Vaccination and Clinical Severity: Is the Effectiveness of Contact Tracing and Case Isolation Hampered by Past Vaccination?
Abstract
:1. Introduction
2. Methods
2.1. Mathematical Model
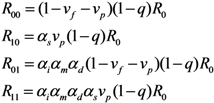
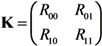
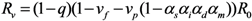
2.2. Epidemic Threshold and Vaccine Effects

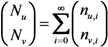
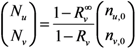
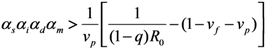
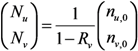
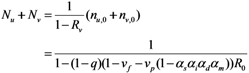
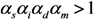
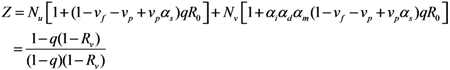
2.3. Probability of Extinction and Vaccine Effects
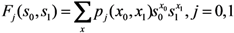
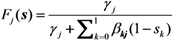
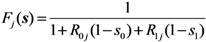
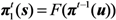
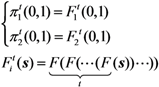
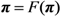
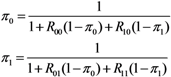
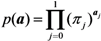
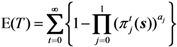
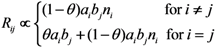
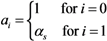
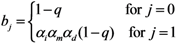
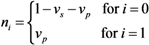
2.4. Numerical Illustration
3. Results
3.1. Epidemic Threshold
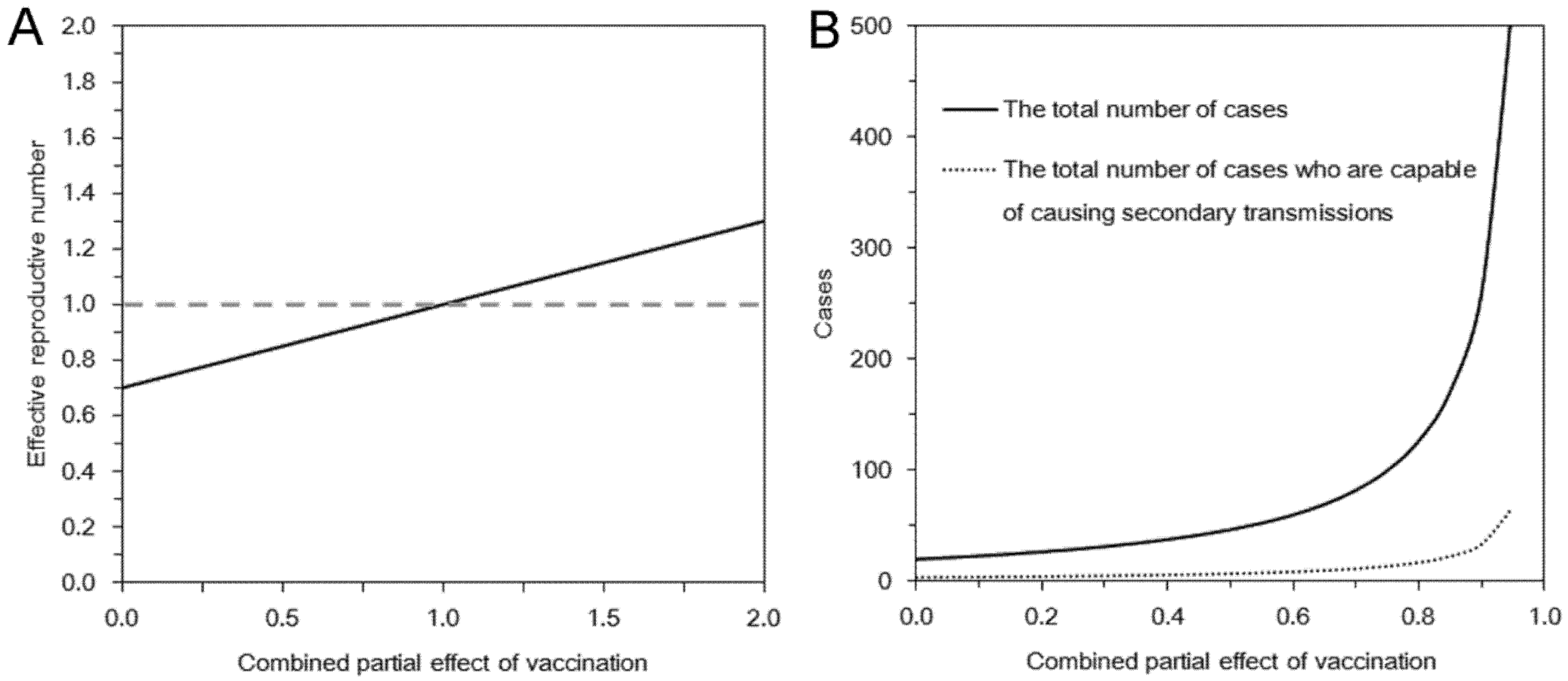
3.2. Multi-Type Branching Process
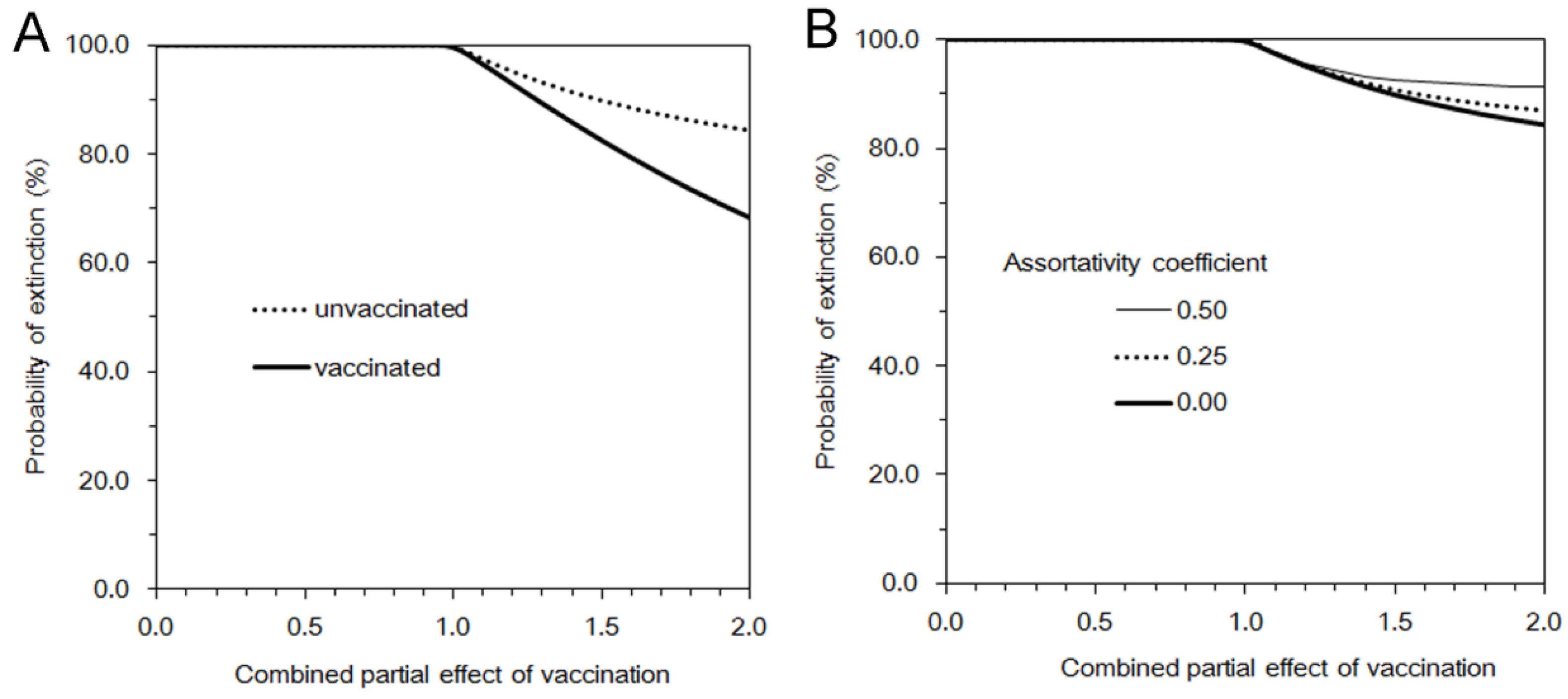
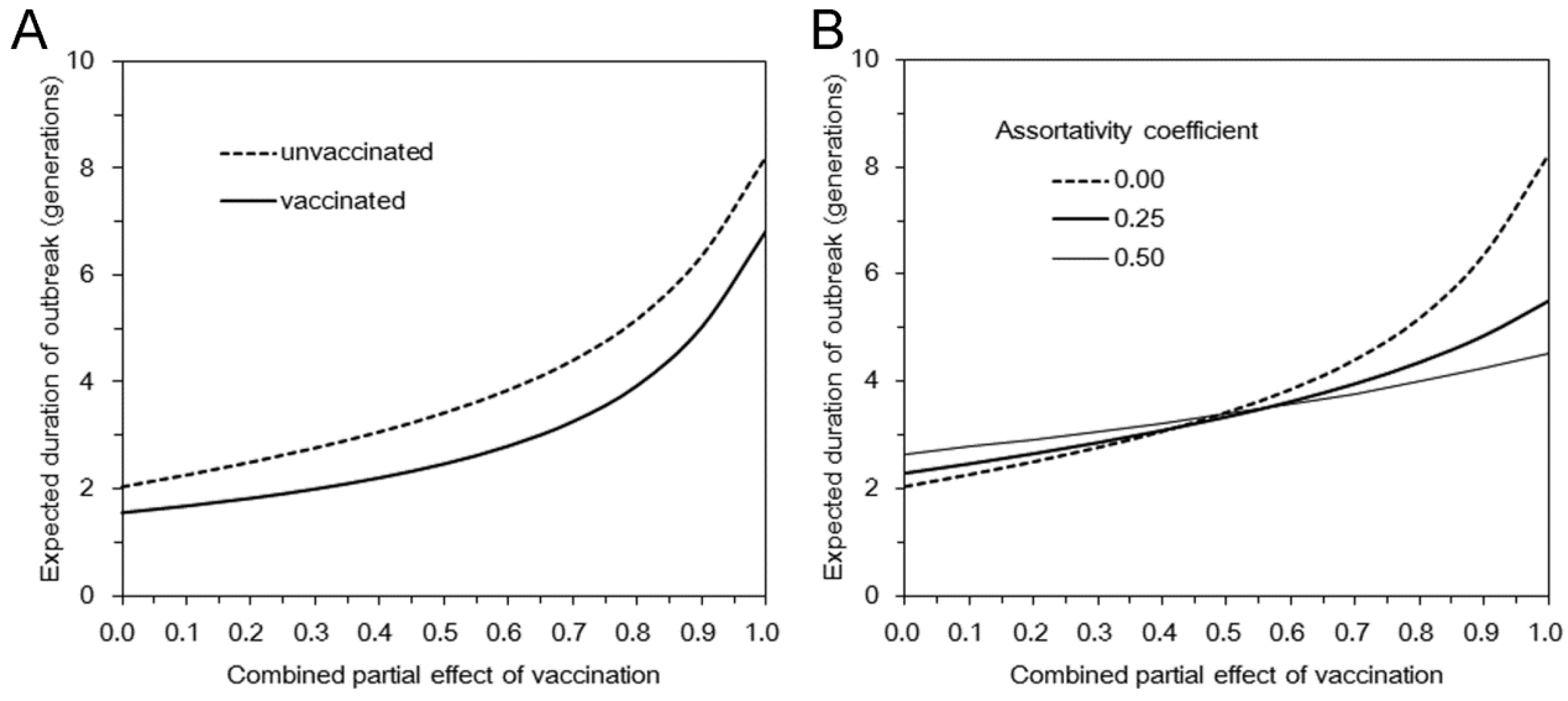
4. Discussion
Acknowledgments
Conflict of Interest
References
- Eichner, M. Case isolation and contact tracing can prevent the spread of smallpox. Am. J. Epidemiol. 2003, 158, 118–128. [Google Scholar] [CrossRef]
- Klinkenberg, D.; Fraser, C.; Heesterbeek, H. The effectiveness of contact tracing in emerging epidemics. PLoS One 2006, 1, e12. [Google Scholar] [CrossRef]
- Riley, S.; Ferguson, N.M. Smallpox transmission and control: Spatial dynamics in Great Britain. Proc. Natl. Acad. Sci. USA 2006, 103, 12637–12642. [Google Scholar] [CrossRef]
- Halloran, M.E.; Longini, I.M.; Struchiner, C.J. Design and Analysis of Vaccine Studies; Springer: Berlin, Germany, 2009. [Google Scholar]
- Basta, N.E.; Halloran, M.E.; Matrajt, L.; Longini, I.M., Jr. Estimating influenza vaccine efficacy from challenge and community-based study data. Am. J. Epidemiol. 2008, 168, 1343–1352. [Google Scholar] [CrossRef]
- Nishiura, H.; Schwehm, M.; Eichner, M. Still protected against smallpox? Estimation of the duration of vaccine-induced immunity against smallpox. Epidemiology 2006, 17, 576–581. [Google Scholar] [CrossRef]
- Nishiura, H.; Eichner, M. Estimation of the duration of vaccine-induced residual protection against severe and fatal smallpox based on secondary vaccination failure. Infection 2006, 34, 241–246. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamic; Princeton University Press: New York, NY, USA, 2012. [Google Scholar]
- Griffiths, D.A. Multivariate birth-and-death processes as approximations to epidemic processes. J. Appl. Prob. 1973, 10, 15–26. [Google Scholar] [CrossRef]
- Ball, F. The threshold behaviour of epidemic models. J. Appl. Prob. 1983, 20, 227–241. [Google Scholar] [CrossRef]
- Nishiura, H.; Cook, A.R.; Cowling, B.J. Assortativity and the probability of epidemic extinction: A case study of pandemic influenza A (H1N1–2009). Interdiscip. Perspect. Infect. Dis. 2011, 2011, 194507. [Google Scholar] [CrossRef]
- Lam, E.H.; Cowling, B.J.; Cook, A.R.; Wong, J.Y.; Lau, M.S.; Nishiura, H. The feasibility of age-specific travel restrictions during influenza pandemics. Theor. Biol. Med. Model. 2011, 8, 44. [Google Scholar] [CrossRef]
- Otter, R. The multiplicative process. Ann. Math. Stat. 1949, 20, 206–224. [Google Scholar] [CrossRef]
- Jacquez, J.A.; Simon, C.P.; Koopman, J.; Sattenspiel, L.; Perry, T. Modeling and analyzing HIV transmission: The effect of contact patterns. Math. Biosci. 1988, 92, 119–199. [Google Scholar] [CrossRef]
- Nishiura, H.; Eichner, M. Predicting residual immunity against smallpox. J. Infect. Dis. 2007, 195, 160–161. [Google Scholar] [CrossRef]
- Nishiura, H.; Brockmann, S.O.; Eichner, M. Extracting key information from historical data to quantify the transmission dynamics of smallpox. Theor. Biol. Med. Model. 2008, 5, 20. [Google Scholar] [CrossRef]
- Eichner, M.; Dietz, K. Transmission potential of smallpox: Estimates based on detailed data from an outbreak. Am. J. Epidemiol. 2003, 158, 110–117. [Google Scholar] [CrossRef]
- Dietz, K.; Heesterbeek, J.A. Daniel Bernoulli’s epidemiological model revisited. Math. Biosci. 2002, 180, 1–21. [Google Scholar] [CrossRef]
- Eames, K.T.; Tilston, N.L.; White, P.J.; Adams, E.; Edmunds, W.J. The impact of illness and the impact of school closure on social contact patterns. Health Technol. Assess. 2010, 14, 267–312. [Google Scholar]
- Halloran, M.E.; Cochi, S.L.; Lieu, T.A.; Wharton, M.; Fehrs, L. Theoretical epidemiologic and morbidity effects of routine varicella immunization of preschool children in the United States. Am. J. Epidemiol. 1994, 140, 81–104. [Google Scholar]
- Massoudi, M.S.; Barker, L.; Schwartz, B. Effectiveness of postexposure vaccination for the prevention of smallpox: Results of a delphi analysis. J. Infect. Dis. 2003, 188, 973–976. [Google Scholar] [CrossRef]
- Eames, K.T. Contact tracing strategies in heterogeneous populations. Epidemiol. Infect. 2007, 135, 443–454. [Google Scholar] [CrossRef]
- Eames, K.T.; Keeling, M.J. Contact tracing and disease control. Proc. R Soc. Lond. Ser. B 2003, 270, 2565–2571. [Google Scholar] [CrossRef]
- House, T.; Keeling, M.J. The impact of contact tracing in clustered populations. PLoS Comput. Biol. 2010, 6, e1000721. [Google Scholar] [CrossRef]
- Mizumoto, K.; Nishiura, H.; Yamamoto, T. Effectiveness of antiviral prophylaxis coupled with contact tracing in reducing the transmission of the influenza A (H1N1–2009): A systematic review. Theor. Biol. Med. Model. 2013, 10, 4. [Google Scholar] [CrossRef]
- Omori, R.; Cowling, B.J.; Nishiura, H. How is vaccine effectiveness scaled by the transmission dynamics of interacting pathogen strains with cross-protective immunity? PLoS One 2012, 7, e50751. [Google Scholar] [CrossRef]
- Nishiura, H.; Yen, H.L.; Cowling, B.J. Sample size considerations for one-to-one animal transmission studies of the influenza a viruses. PLoS One 2013, 8, e55358. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mizumoto, K.; Ejima, K.; Yamamoto, T.; Nishiura, H. Vaccination and Clinical Severity: Is the Effectiveness of Contact Tracing and Case Isolation Hampered by Past Vaccination? Int. J. Environ. Res. Public Health 2013, 10, 816-829. https://doi.org/10.3390/ijerph10030816
Mizumoto K, Ejima K, Yamamoto T, Nishiura H. Vaccination and Clinical Severity: Is the Effectiveness of Contact Tracing and Case Isolation Hampered by Past Vaccination? International Journal of Environmental Research and Public Health. 2013; 10(3):816-829. https://doi.org/10.3390/ijerph10030816
Chicago/Turabian StyleMizumoto, Kenji, Keisuke Ejima, Taro Yamamoto, and Hiroshi Nishiura. 2013. "Vaccination and Clinical Severity: Is the Effectiveness of Contact Tracing and Case Isolation Hampered by Past Vaccination?" International Journal of Environmental Research and Public Health 10, no. 3: 816-829. https://doi.org/10.3390/ijerph10030816
APA StyleMizumoto, K., Ejima, K., Yamamoto, T., & Nishiura, H. (2013). Vaccination and Clinical Severity: Is the Effectiveness of Contact Tracing and Case Isolation Hampered by Past Vaccination? International Journal of Environmental Research and Public Health, 10(3), 816-829. https://doi.org/10.3390/ijerph10030816





