An Insight into Cancer Cells and Disease Progression Through the Lens of Mathematical Modeling
Abstract
1. Introduction
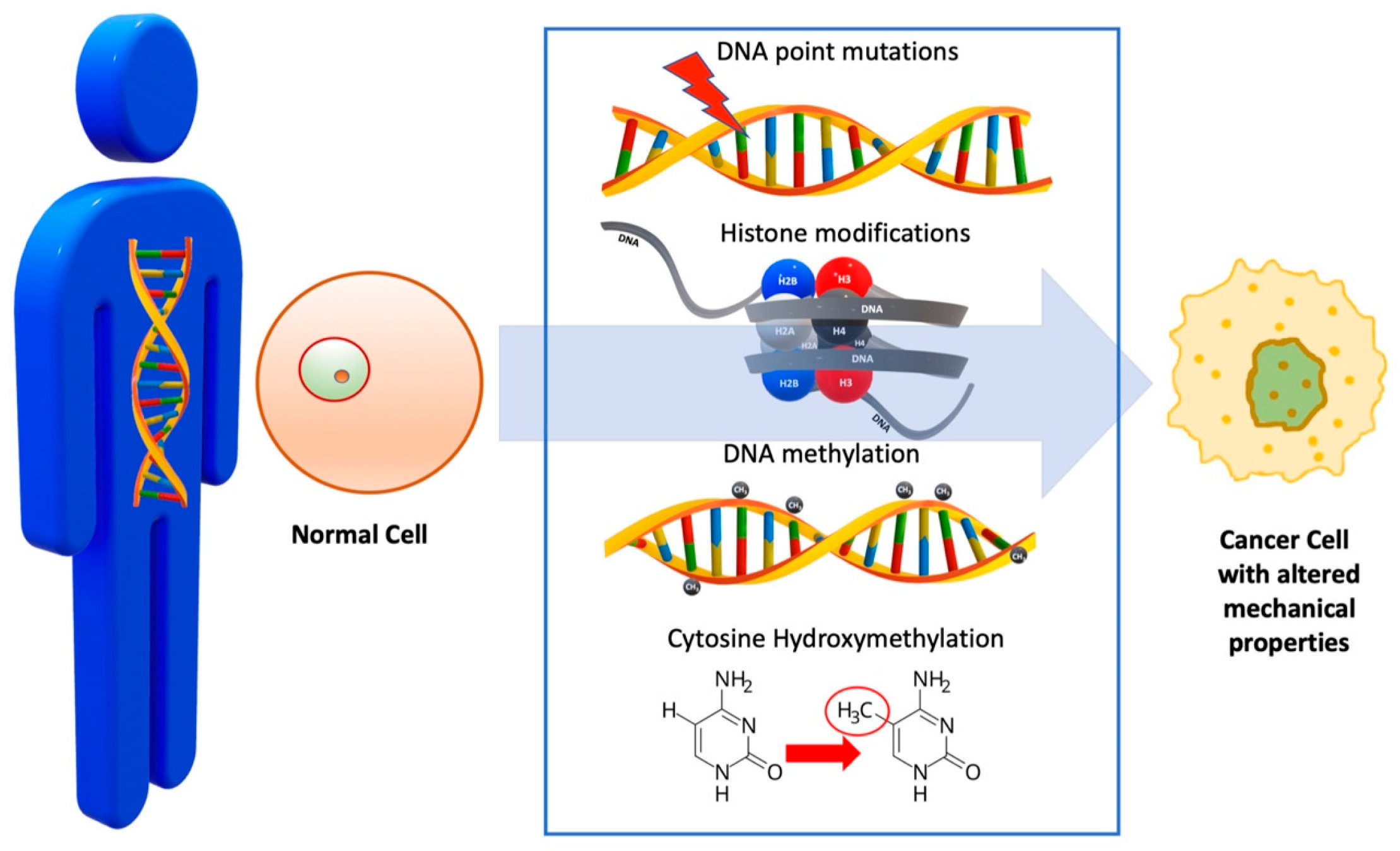
2. Genetic Alteration of Cell
3. DNA
| DNA Change | Mechanism | Effect on Cellular Processes | Impact on Cancer Biology |
|---|---|---|---|
| DNA Point Mutations | Point mutations in driver genes (e.g., BRCA2, TP53, KRAS) [49] | Disruption of crucial processes like DNA repair, apoptosis, and cell division, as well as alterations in cytoskeletal organization, leading to changes in cell stiffness and deformability [50] | Mutations can lead to abnormal cell proliferation, migration, and invasion and impact cancer progression and therapy [50] |
| Histone Modifications | Chemical modifications of histones [35] | Alters chromatin structure, affecting gene expression [35] | Modulates chromatin compaction, influencing oncogene expression, tumor suppressor silencing, and uncontrolled cell growth and proliferation [35] |
| DNA Methylation | Addition of methyl groups to DNA at CpG dinucleotides [36] | Affects DNA accessibility to transcription factors and other regulatory proteins [36] | Modulates gene expression, influencing oncogene activation or tumor suppressor silencing [35,36] |
| Cytosine Hydroxymethylation | Addition of a hydroxymethyl group to cytosine residues [37] | Affects DNA strand separation propensity, thus modulating mechanical stress response [37] | Affects chromatin accessibility, gene expression, and DNA mechanics, influencing cancer cell behavior [37] |
4. Nucleus
5. Mitochondria
6. Cytoskeleton
7. Cytoplasm
8. Plasma Membrane
9. Membrane Receptors—Adherens Junctions
10. Discussion
11. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| COSMIC | Catalog of Somatic Mutations in Cancer |
| ECM | Extracellular Matrix |
| VEGF | Vascular Endothelial Growth Factor |
| DNA | Deoxyribonucleic Acid |
| BRCA2 | Breast Cancer Gene 2 |
| TP53 | Gene Providing Instruction for Tumor Protein p53 |
| KRAS | Gene Providing Instructions for Making a Protein Called K-Ras |
| ATP | Adenosine Triphosphate |
| ROS | Reactive Oxygen Species |
| OXPHOS | Oxidative Phosporylation |
| NAD | Nicotinamide Adenine Dinucleotide |
| FAD | Flavin Adenine Dinucleotide |
| ETC | Electron Transport Chain |
| TCA | Tricarboxylic Acid |
| DPR1 | Dynamin-Related Protein |
| OMM | Outer Mitochondrial Membrane |
| FIS1 | Fission 1 Homolog Protein |
| MID | Mitochondrial Dynamics Proteins |
| MIEF | Mitochondrial Elongation Factor |
| MFF | Mitochondrial Fission Factor |
| ER | Endoplasmic Reticulum |
| MMP | Matrix Metalloproteinase |
| EMT | Epithelial–Mesenchymal Transition |
| GPMV | Giant Plasma Membrane Vesicle |
References
- Kleeff, J.; Korc, M.; Apte, M.; La Vecchia, C.; Johnson, C.D.; Biankin, A.V.; Neale, R.E.; Tempero, M.; Tuveson, D.A.; Hruban, R.H.; et al. Pancreatic cancer. Nat. Rev. Dis. Primers 2016, 2, 16022. [Google Scholar] [CrossRef] [PubMed]
- Richters, A.; Aben, K.K.H.; Kiemeney, L.A.L.M. The global burden of urinary bladder cancer: An update. World J. Urol. 2020, 38, 1895–1904. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Pedraza-Fariña, L.G. Mechanisms of oncogenic cooperation in cancer initiation and metastasis. Yale J. Biol. Med. 2006, 79, 95–103. [Google Scholar] [PubMed] [PubMed Central]
- Forbes, S.A.; Beare, D.; Gunasekaran, P.; Leung, K.; Bindal, N.; Boutselakis, H.; Ding, M.; Bamford, S.; Cole, C.; Ward, S.; et al. COSMIC: Exploring the world’s knowledge of somatic mutations in human cancer. Nucleic Acids Res. 2015, 43, D805–D811. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Futreal, P.A.; Coin, L.; Marshall, M.; Down, T.; Hubbard, T.; Wooster, R.; Rahman, N.; Stratton, M.R. A census of human cancer genes. Nat. Rev. Cancer 2004, 4, 177–183. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Lawrence, M.S.; Stojanov, P.; Mermel, C.H.; Robinson, J.T.; Garraway, L.A.; Golub, T.R.; Meyerson, M.; Gabriel, S.B.; Lander, E.S.; Getz, G. Discovery and saturation analysis of cancer genes across 21 tumour types. Nature 2014, 505, 495–501. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Perou, C.M.; Jeffrey, S.S.; van de Rijn, M.; Rees, C.A.; Eisen, M.B.; Ross, D.T.; Pergamenschikov, A.; Williams, C.F.; Zhu, S.X.; Lee, J.C.; et al. Distinctive gene expression patterns in human mammary epithelial cells and breast cancers. Proc. Natl. Acad. Sci. USA 1999, 96, 9212–9217. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Perou, C.M.; Sørlie, T.; Eisen, M.B.; van de Rijn, M.; Jeffrey, S.S.; Rees, C.A.; Pollack, J.R.; Ross, D.T.; Johnsen, H.; Akslen, L.A.; et al. Molecular portraits of human breast tumours. Nature 2000, 406, 747–752. [Google Scholar] [CrossRef] [PubMed]
- Garber, M.E.; Troyanskaya, O.G.; Schluens, K.; Petersen, S.; Thaesler, Z.; Pacyna-Gengelbach, M.; van de Rijn, M.; Rosen, G.D.; Perou, C.M.; Whyte, R.I.; et al. Diversity of gene expression in adenocarcinoma of the lung. Proc. Natl. Acad. Sci. USA 2001, 98, 13784–13789. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- McBeath, R.; Pirone, D.M.; Nelson, C.M.; Bhadriraju, K.; Chen, C.S. Cell shape, cytoskeletal tension, and RhoA regulate stem cell lineage commitment. Dev. Cell 2004, 6, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Engler, A.J.; Sen, S.; Sweeney, H.L.; Discher, D.E. Matrix elasticity directs stem cell lineage specification. Cell 2006, 126, 677–689. [Google Scholar] [CrossRef] [PubMed]
- Kahn, J.; Shwartz, Y.; Blitz, E.; Krief, S.; Sharir, A.; Breitel, D.A.; Rattenbach, R.; Relaix, F.; Maire, P.; Rountree, R.B.; et al. Muscle contraction is necessary to maintain joint progenitor cell fate. Dev. Cell 2009, 16, 734–743. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Landmann, F.; Zahreddine, H.; Rodriguez, D.; Koch, M.; Labouesse, M. A tension-induced mechanotransduction pathway promotes epithelial morphogenesis. Nature 2011, 471, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Monier, B.; Gettings, M.; Gay, G.; Mangeat, T.; Schott, S.; Guarner, A.; Suzanne, M. Apico-basal forces exerted by apoptotic cells drive epithelium folding. Nature 2015, 518, 245–248. [Google Scholar] [CrossRef] [PubMed]
- Maître, J.L.; Turlier, H.; Illukkumbura, R.; Eismann, B.; Niwayama, R.; Nédélec, F.; Hiiragi, T. Asymmetric division of contractile domains couples cell positioning and fate specification. Nature 2016, 536, 344–348. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Broders-Bondon, F.; Nguyen Ho-Bouldoires, T.H.; Fernandez-Sanchez, M.E.; Farge, E. Mechanotransduction in tumor progression: The dark side of the force. J. Cell Biol. 2018, 217, 1571–1587. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Alberts, B.; Bray, D.; Lewis, J.; Raff, M.; Roberts, K.; Watson, J.D. Molecular Biology of the Cell, 4th ed.; Garland: New York, NY, USA, 2002; pp. 209–235. [Google Scholar]
- Zhang, S.; Xiao, X.; Yi, Y.; Wang, X.; Zhu, L.; Shen, Y.; Lin, D.; Wu, C. Tumor initiation and early tumorigenesis: Molecular mechanisms and interventional targets. Signal Transduct. Target. Ther. 2024, 1, 149. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Rejniak, K.A. A single-cell approach in modeling the dynamics of tumor microregions. Math. Biosci. Eng. 2005, 2, 643–655. [Google Scholar] [CrossRef] [PubMed]
- Liberti, M.V.; Locasale, J.W. The Warburg Effect: How Does it Benefit Cancer Cells? Trends Biochem. Sci. 2016, 41, 211–218, Erratum in Trends Biochem. Sci. 2016, 41, 287. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Qin, X.; Li, T.; Li, S.; Yang, H.; Wu, C.; Zheng, C.; You, F.; Liu, Y. The tumor biochemical and biophysical microenvironments synergistically contribute to cancer cell malignancy. Cell Mol. Immunol. 2020, 17, 1186–1187. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Wicks, E.E.; Semenza, G.L. Hypoxia-inducible factors: Cancer progression and clinical translation. J. Clin. Investig. 2022, 132, e159839. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Xin, Y.; Li, K.; Huang, M.; Liang, C.; Siemann, D.; Wu, L.; Tan, Y.; Tang, X. Biophysics in tumor growth and progression: From single mechano-sensitive molecules to mechanomedicine. Oncogene 2023, 42, 3457–3490. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- De Felice, F.; Malerba, S.; Nardone, V.; Salvestrini, V.; Calomino, N.; Testini, M.; Boccardi, V.; Desideri, I.; Gentili, C.; De Luca, R.; et al. Progress and challenges in integrating nutritional care into oncology practice: Results from a national survey on behalf of the NutriOnc research group. Nutrients 2025, 17, 188. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Jain, R.K. Antiangiogenesis strategies revisited: From starving tumors to alleviating hypoxia. Cancer Cell 2014, 26, 605–622. [Google Scholar] [CrossRef]
- Rejniak, K.A. An immersed boundary framework for modelling the growth of individual cells: An application to the early tumour development. J. Theor. Biol. 2007, 247, 186–204. [Google Scholar] [CrossRef] [PubMed]
- Rejniak, K.A.; Dillon, R.H. A single cell-based model of the ductal tumour microarchitecture. Comput. Math. Methods Med. 2007, 8, 51–69. [Google Scholar] [CrossRef]
- Peskin, C.S. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge Mathematical Library Edition; Cambridge University Press: Cambridge, UK, 2007; pp. 35–44. [Google Scholar]
- Sarkar, S.; Horn, G.; Moulton, K.; Oza, A.; Byler, S.; Kokolus, S.; Longacre, M. Cancer development, progression, and therapy: An epigenetic overview. Int. J. Mol. Sci. 2013, 14, 21087–21113. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Herceg, Z.; Hainaut, P. Genetic and epigenetic alterations as biomarkers for cancer detection, diagnosis and prognosis. Mol. Oncol. 2007, 1, 26–41. [Google Scholar] [CrossRef]
- Bohmann, D.; Bos, T.J.; Admon, A.; Nishimura, T.; Vogt, P.K.; Tjian, R. Human proto-oncogene c-jun encodes a DNA binding protein with structural and functional properties of transcription factor AP-1. Science 1987, 238, 1386–1392. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Qian, X.; Sanchez-Solana, B.; Tripathi, B.K.; Durkin, M.E.; Lowy, D.R. Cancer-associated point mutations in the DLC1 tumor suppressor and other Rho-GAPs occur frequently and are associated with decreased function. Cancer Res. 2020, 80, 3568–3579. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Jurga, S.; Barciszewski, J. The DNA, RNA, and Histone Methylomes; Springer Nature: Cham, Switzerland, 2019; pp. 76–82. [Google Scholar]
- Szyf, M. DNA methylation properties: Consequences for pharmacology. Trends Pharmacol. Sci. 1994, 15, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Severin, P.M.D.; Zou, X.; Schulten, K.; Gaub, H.E. Effects of cytosine hydroxymethylation on DNA strand separation. Biophys. J. 2013, 104, 208–215. [Google Scholar] [CrossRef]
- Marko, J.F.; Siggia, E.D. Fluctuations and supercoiling of DNA. Science 1994, 265, 506–508. [Google Scholar] [CrossRef] [PubMed]
- Odjik, T. Stiff chains and filaments under tension. Macromolecules 1995, 28, 7016–7018. [Google Scholar] [CrossRef]
- Smith, S.B.; Cui, Y.; Bustamante, C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.D.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Stretching DNA with optical tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Gross, P.; Laurens, N.; Oddershede, L.; Bockelmann, U.; Peterman, E.J.G.; Wuite, G.J.L. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011, 7, 731–736. [Google Scholar] [CrossRef]
- Gore, J.; Bryant, Z.; Nöllmann, M.; Le, M.U.; Cozzarelli, N.R.; Bustamante, C. DNA overwinds when stretched. Nature 2006, 442, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Garcia, H.G.; Grayson, P.; Han, L.; Inamdar, M.; Kondev, J.; Nelson, P.C.; Phillips, R.; Widom, J.; Wiggins, P.A. Biological consequences of tightly bent DNA: The other life of a macromolecular celebrity. Biopolymers 2007, 85, 115–130. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Huo, Y.X.; Zhang, Y.T.; Xiao, Y.; Zhang, X.; Buck, M.; Kolb, A.; Wang, Y.P. IHF-binding sites inhibit DNA loop formation and transcription initiation. Nucleic Acids Res. 2009, 37, 3878–3886. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Sharma, M.; Predeus, A.V.; Mukherjee, S.; Feig, M. DNA bending propensity in the presence of base mismatches: Implications for DNA repair. J. Phys. Chem. B 2013, 117, 6194–6205. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Afek, A.; Shi, H.; Rangadurai, A.; Sahay, H.; Senitzki, A.; Xhani, S.; Fang, M.; Salinas, R.; Mielko, Z.; Pufall, M.A.; et al. DNA mismatches reveal conformational penalties in protein-DNA recognition. Nature 2020, 587, 291–296. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Reyes, M.E.; Pulgar, V.; Vivallo, C.; Ili, C.G.; Mora-Lagos, B.; Brebi, P. Epigenetic modulation of cytokine expression in gastric cancer: Influence on angiogenesis, metastasis and chemoresistance. Front. Immunol. 2024, 15, 1347530. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Ondraskova, K.; Sebuyoya, R.; Moranova, L.; Holcakova, J.; Vonka, P.; Hrstka, R.; Bartosik, M. Electrochemical biosensors for analysis of DNA point mutations in cancer research. Anal. Bioanal. Chem. 2023, 415, 1065–1085. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Kim, H.; Verhaak, R.G.W. Silent mutations make some noise. Cell 2014, 156, 1129–1131. [Google Scholar] [CrossRef]
- Tan, K.P.; Kanitkar, T.R.; Kwoh, C.K.; Madhusudhan, M.S. Packpred: Predicting the functional effect of missense mutations. Front. Mol. Biosci. 2021, 8, 646288. [Google Scholar] [CrossRef]
- Wittenstein, A.; Caspi, M.; Rippin, I.; Elroy-Stein, O.; Eldar-Finkelman, H.; Thoms, S.; Rosin-Arbesfeld, R. Nonsense mutation suppression is enhanced by targeting different stages of the protein synthesis process. PLoS Biol. 2024, 22, e3002524, Erratum in PLoS Biol. 2023, 21, e3002355. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Kim, D.H.; Hah, J.; Wirtz, D. Mechanics of the cell nucleus. In Biomechanics in Oncology; Dong, C., Zahir, N., Konstantopoulos, K., Eds.; Springer Nature: Cham, Switzerland, 2018; pp. 41–55. [Google Scholar]
- Zink, D.; Fischer, A.H.; Nickerson, J.A. Nuclear structure in cancer cells. Nat. Rev. Cancer 2004, 4, 677–687. [Google Scholar] [CrossRef]
- Wolf, K.; Te Lindert, M.; Krause, M.; Alexander, S.; Te Riet, J.; Willis, A.L.; Hoffman, R.M.; Figdor, C.G.; Weiss, S.J.; Friedl, P. Physical limits of cell migration: Control by ECM space and nuclear deformation and tuning by proteolysis and traction force. J. Cell Biol. 2013, 201, 1069–1084. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Yamazaki, D.; Kurisu, S.; Takenawa, T. Regulation of cancer cell motility through actin reorganization. Cancer Sci. 2005, 96, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Chaffer, C.L.; Weinberg, R.A. A perspective on cancer cell metastasis. Science 2011, 331, 1559–1564. [Google Scholar] [CrossRef] [PubMed]
- Guilak, F.; Tedrow, J.R.; Burgkart, R. Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Commun. 2000, 269, 781–786. [Google Scholar] [CrossRef] [PubMed]
- Rowat, A.C.; Lammerding, J.; Ipsen, J.H. Mechanical properties of the cell nucleus and the effect of emerin deficiency. Biophys. J. 2006, 91, 4649–4664. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Mathur, A.B.; Truskey, G.A.; Reichert, W.M. Atomic force and total internal reflection fluorescence microscopy for the study of force transmission in endothelial cells. Biophys. J. 2000, 78, 1725–1735. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Lammerding, J.; Fong, L.G.; Ji, J.Y.; Reue, K.; Stewart, C.L.; Young, S.G.; Lee, R.T. Lamins A and C but not lamin B1 regulate nuclear mechanics. J. Biol. Chem. 2006, 281, 25768–25780. [Google Scholar] [CrossRef] [PubMed]
- Harada, T.; Swift, J.; Irianto, J.; Shin, J.W.; Spinler, K.R.; Athirasala, A.; Diegmiller, R.; Dingal, P.C.; Ivanovska, I.L.; Discher, D.E. Nuclear lamin stiffness is a barrier to 3D migration, but softness can limit survival. J. Cell Biol. 2014, 204, 669–682. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Stephens, A.D.; Banigan, E.J.; Adam, S.A.; Goldman, R.D.; Marko, J.F. Chromatin and lamin A determine two different mechanical response regimes of the cell nucleus. Mol. Biol. Cell 2017, 28, 1984–1996. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Stephens, A.D.; Banigan, E.J.; Marko, J.F. Chromatin’s physical properties shape the nucleus and its functions. Curr. Opin. Cell Biol. 2019, 58, 76–84. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Caille, N.; Thoumine, O.; Tardy, Y.; Meister, J.J. Contribution of the nucleus to the mechanical properties of endothelial cells. J. Biomech. 2002, 35, 177–187. [Google Scholar] [CrossRef] [PubMed]
- La Berre, M.; Liu, Y.J.; Hu, J.; Maiuri, P.; Benichou, O.; Voituriez, R.; Chen, Y.; Piel, M. Geometric friction directs cell migration. Phys. Rev. Lett. 2013, 111, 198101. [Google Scholar] [CrossRef] [PubMed]
- Giverso, C.; Grillo, A.; Preziosi, L. Influence of nucleus deformability on cell entry into cylindrical structures. Biomech. Model. Mechanobiol. 2014, 13, 481–502. [Google Scholar] [CrossRef] [PubMed]
- Estabrook, I.D.; Thiam, H.R.; Piel, M.; Hawkins, R.J. Calculation of the force field required for nucleus deformation during cell migration through constrictions. PLoS Comput. Biol. 2021, 17, e1008592. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Sokolnikoff, I.S. Mathematical Theory of Elasticity, 2nd ed.; Krieger Publishing: Malabar, FL, USA, 1983; pp. 98–105. [Google Scholar]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues, 2nd ed.; Springer: New York, NY, USA, 1993; pp. 38–40. [Google Scholar]
- Landau, L.D.; Pitaevskii, L.P.; Lifshitz, E.M.; Kosevich, A.M. Theory of Elasticity, 3rd ed.; Theoretical Physics; Butterworth-Heinemann: Oxford, UK, 1986; Volume 7, pp. 1–26. [Google Scholar]
- Wolf, K.; Müller, R.; Borgmann, S.; Bröcker, E.B.; Friedl, P. Amoeboid shape change and contact guidance: T-lymphocyte crawling through fibrillar collagen is independent of matrix remodeling by MMPs and other proteases. Blood 2003, 102, 3262–3269. [Google Scholar] [CrossRef] [PubMed]
- Davidson, P.M.; Denais, C.; Bakshi, M.C.; Lammerding, J. Nuclear deformability constitutes a rate-limiting step during cell migration in 3-D environments. Cell Mol. Bioeng. 2014, 7, 293–306. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Wu, Y.; Pegoraro, A.F.; Weitz, D.A.; Janmey, P.; Sun, S.X. The correlation between cell and nucleus size is explained by an eukaryotic cell growth model. PLoS Comput. Biol. 2022, 18, e1009400. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Gomes, E.R.; Jani, S.; Gundersen, G.G. Nuclear movement regulated by Cdc42, MRCK, myosin, and actin flow establishes MTOC polarization in migrating cells. Cell 2005, 121, 451–463. [Google Scholar] [CrossRef] [PubMed]
- Tsai, L.H.; Gleeson, J.G. Nucleokinesis in neuronal migration. Neuron 2005, 46, 383–388. [Google Scholar] [CrossRef] [PubMed]
- Calero-Cuenca, F.J.; Janota, C.S.; Gomes, E.R. Dealing with the nucleus during cell migration. Curr. Opin. Cell Biol. 2018, 50, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Skepper, J.N.; Yang, F.; Davies, J.D.; Hegyi, L.; Roberts, R.G.; Weissberg, P.L.; Ellis, J.A.; Shanahan, C.M. Nesprins: A novel family of spectrin-repeat-containing proteins that localize to the nuclear membrane in multiple tissues. J. Cell Sci. 2001, 114, 4485–4498. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, M.L.; Jaalouk, D.E.; Shanahan, C.M.; Burke, B.; Roux, K.J.; Lammerding, J. The interaction between nesprins and sun proteins at the nuclear envelope is critical for force transmission between the nucleus and cytoskeleton. J. Biol. Chem. 2011, 286, 26743–26753. [Google Scholar] [CrossRef] [PubMed]
- Meier, I. LINCing the eukaryotic tree of life—Towards a broad evolutionary comparison of nucleocytoplasmic bridging complexes. J. Cell Sci. 2016, 129, 3523–3531. [Google Scholar] [CrossRef] [PubMed]
- Maniotis, A.J.; Chen, C.S.; Ingber, D.E. Demonstration of mechanical connections between integrins, cytoskeletal filaments and nucleoplasm that stabilize nuclear structure. Proc. Natl. Acad. Sci. USA 1997, 94, 849–854. [Google Scholar] [CrossRef]
- Wang, N.; Tytell, J.D.; Ingber, D.E. Mechanotransduction at a distance: Mechanically coupling the extracellular matrix with the nucleus. Nat. Rev. Mol. Cell Biol. 2009, 10, 75–82. [Google Scholar] [CrossRef]
- Harris, D.A.; Das, A.M. Control of mitochondrial ATP synthesis in the heart. Biochem. J. 1991, 280, 561–573. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Liu, X.; Kim, C.N.; Yang, J.; Jemmerson, R.; Wang, X. Induction of apoptotic program in cell-free extracts: Requirement for dATP and cytochrome c. Cell 1996, 86, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Murphy, M.P. How mitochondria produce reactive oxygen species. Biochem. J. 2009, 417, 1–13. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Warburg, O.; Wind, F.; Negelein, E. The metabolism of tumors in the body. J. Gen. Physiol. 1927, 8, 519–530. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Hitosugi, T.; Kang, S.; Vander Heiden, M.G.; Chung, T.W.; Elf, S.; Lythgoe, K.; Dong, S.; Lonial, S.; Wang, X.; Chen, G.Z.; et al. Tyrosine phosphorylation inhibits PKM2 to promote the Warburg effect and tumor growth. Sci. Signal. 2009, 2, ra73. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Galvan, D.L.; Badal, S.S.; Long, J.; Chang, B.H.; Schumacker, P.T.; Overbeek, P.A.; Danesh, F.R. Real-time in vivo mitochondrial redox assessment confirms enhanced mitochondrial reactive oxygen species in diabetic nephropathy. Kidney Int. 2017, 92, 1282–1287. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Kumari, S.; Badana, A.K.; Murali, M.G.; Shailender, G.; Malla, R. Reactive oxygen species: A key constituent in cancer survival. Biomark. Insights 2018, 13, 1177271918755391. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Scott, I.; Youle, R.J. Mitochondrial fission and fusion. Essays Biochem. 2010, 47, 85–98. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Friedman, J.R.; Lackner, L.L.; West, M.; DiBenedetto, J.R.; Nunnari, J.; Voeltz, G.K. ER tubules mark sites of mitochondrial division. Science 2011, 334, 358–362. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Manor, U.; Bartholomew, S.; Golani, G.; Christenson, E.; Kozlov, M.; Higgs, H.; Spudich, J.; Lippincott-Schwartz, J. A mitochondria-anchored isoform of the actin-nucleating spire protein regulates mitochondrial division. eLife 2015, 4, e08828. [Google Scholar] [CrossRef] [PubMed] [PubMed Central][Green Version]
- Steffen, J.; Koehler, C.M. ER-mitochondria contacts: Actin dynamics at the ER control mitochondrial fission via calcium release. J. Cell Biol. 2018, 217, 15–17. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Sebastián, D.; Palacín, M.; Zorzano, A. Mitochondrial dynamics: Coupling mitochondrial fitness with healthy aging. Trends Mol. Med. 2017, 23, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Mahecic, D.; Carlini, L.; Kleele, T.; Colom, A.; Goujon, A.; Matile, S.; Roux, A.; Manley, S. Mitochondrial membrane tension governs fission. Cell Rep. 2021, 35, 108947. [Google Scholar] [CrossRef] [PubMed]
- Leinheiser, A.K.; Mitchell, C.C.; Rooke, E.; Strack, S.; Grueter, C.E. A dynamical systems model for the total fission rate in Drp1-dependent mitochondrial fission. PLoS Comput. Biol. 2024, 20, e1012596. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Hatch, A.L.; Gurel, P.S.; Higgs, H.N. Novel roles for actin in mitochondrial fission. J. Cell Sci. 2014, 127, 4549–4560. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Mofrad, M.R.K.; Kamm, R.D. Cytoskeletal Mechanics: Models and Measurements; Cambridge University Press: Cambridge, UK, 2010; pp. 50–70. [Google Scholar]
- Gaspar, P.; Holder, M.V.; Aerne, B.L.; Janody, F.; Tapon, N. Zyxin antagonizes the FERM protein expanded to couple F-actin and Yorkie-dependent organ growth. Curr. Biol. 2015, 25, 679–689. [Google Scholar] [CrossRef] [PubMed]
- Kimura, H.; Fumoto, K.; Shojima, K.; Nojima, S.; Osugi, Y.; Tomihara, H.; Eguchi, H.; Shintani, Y.; Endo, H.; Inoue, M.; et al. CKAP4 is a Dickkopf1 receptor and is involved in tumor progression. J. Clin. Investig. 2016, 126, 2689–2705. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Vouyovitch, C.M.; Perry, J.K.; Liu, D.X.; Bezin, L.; Vilain, E.; Diaz, J.J.; Lobie, P.E.; Mertani, H.C. WNT4 mediates the autocrine effects of growth hormone in mammary carcinoma cells. Endocr. Relat. Cancer 2016, 23, 571–585. [Google Scholar] [CrossRef] [PubMed]
- Parshina, E.A.; Eroshkin, F.M.; Orlov, E.E.; Gyoeva, F.K.; Shokhina, A.G.; Staroverov, D.B.; Belousov, V.V.; Zhigalova, N.A.; Prokhortchouk, E.B.; Zaraisky, A.G.; et al. Cytoskeletal Protein Zyxin Inhibits the Activity of Genes Responsible for Embryonic Stem Cell Status. Cell Rep. 2020, 33, 108396. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.K.; Han, S.; Xing, B.; Huang, J.; Liu, B.; Bordeleau, F.; Reinhart-King, C.A.; Zhang, J.J.; Huang, X.Y. Targeted inhibition of fascin function blocks tumour invasion and metastatic colonization. Nat. Commun. 2015, 6, 7465. [Google Scholar] [CrossRef] [PubMed]
- Jiu, Y.; Lehtimäki, J.; Tojkander, S.; Cheng, F.; Jäälinoja, H.; Liu, X.; Varjosalo, M.; Eriksson, J.E.; Lappalainen, P. Bidirectional Interplay between Vimentin Intermediate Filaments and Contractile Actin Stress Fibers. Cell Rep. 2015, 11, 1511–1518. [Google Scholar] [CrossRef] [PubMed]
- Thiery, J.P.; Acloque, H.; Huang, R.Y.; Nieto, M.A. Epithelial-mesenchymal transitions in development and disease. Cell 2009, 139, 871–890. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Pei, Z.; Ji, C.; Zhang, X.; Xu, J.; Wang, J. Novel Insights into the Role of the Cytoskeleton in Cancer. In Cytoskeleton—Structure, Dynamics, Function and Disease; Jimenez-Lopez, J.C., Ed.; InTech: London, UK, 2017. [Google Scholar] [CrossRef]
- Yamasaki, T.; Seki, N.; Yamada, Y.; Yoshino, H.; Hidaka, H.; Chiyomaru, T.; Nohata, N.; Kinoshita, T.; Nakagawa, M.; Enokida, H. Tumor suppressive microRNA-138 contributes to cell migration and invasion through its targeting of vimentin in renal cell carcinoma. Int. J. Oncol. 2012, 41, 805–817. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Kellogg, E.H.; Hejab, N.M.A.; Howes, S.; Northcote, P.; Miller, J.H.; Díaz, J.F.; Downing, K.H.; Nogales, E. Insights into the distinct mechanisms of action of taxane and non-taxane microtubule stabilizers from cryo-EM structures. J. Mol. Biol. 2017, 429, 633–646. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Shoji, K.; Ohashi, K.; Sampei, K.; Oikawa, M.; Mizuno, K. Cytochalasin D acts as an inhibitor of the actin-cofilin interaction. Biochem. Biophys. Res. Commun. 2012, 424, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Ethier, R.C.; Simmons, C.A. Introductory Biomechanics: From Cells to Organisms; Cambridge University Press: Cambridge, UK, 2008; pp. 56–89. [Google Scholar]
- Su, X.; Zhang, L.; Kang, H.; Zhang, B.; Bao, G.; Wang, J. Mechanical, nanomorphological and biological reconstruction of early stage apoptosis in HeLa cells induced by cytochalasin B. Oncol. Rep. 2019, 41, 928–938. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Runel, G.; Lopez-Ramirez, N.; Chlasta, J.; Masse, I. Biomechanical properties of cancer cells. Cells 2021, 10, 887. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Lekka, M.; Laidler, P.; Ignacak, J.; Łabedz, M.; Lekki, J.; Struszczyk, H.; Stachura, Z.; Hrynkiewicz, A.Z. The effect of chitosan on stiffness and glycolytic activity of human bladder cells. Biochim. Biophys. Acta 2001, 1540, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Ramos, J.R.; Pabijan, J.; Garcia, R.; Lekka, M. The softening of human bladder cancer cells happens at an early stage of the malignancy process. Beilstein J. Nanotechnol. 2014, 5, 447–457. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Lodish, H.; Berk, A.; Matsudaira, P.; Kaiser, C.A.; Krieger, M.; Scott, M.P.; Zipursky, L.S.; Darnell, J. Molecular Cell Biology, 5th ed.; Freeman and Co.: New York, NY, USA, 2004; p. 147. [Google Scholar]
- Karp, G. Cell and Molecular Biology: Concepts and Experiments, 6th ed.; Wiley: Hoboken, NJ, USA, 2010; p. 11. [Google Scholar]
- Neurohr, G.E.; Amon, A. Relevance and regulation of cell density. Trends Cell Biol. 2020, 30, 213–225. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Molines, A.T.; Lemière, J.; Gazzola, M.; Steinmark, I.E.; Edrington, C.H.; Hsu, C.T.; Real-Calderon, P.; Suhling, K.; Goshima, G.; Holt, L.J.; et al. Physical properties of the cytoplasm modulate the rates of microtubule polymerization and depolymerization. Dev. Cell 2022, 57, 466–479.e6. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Luby-Phelps, K.; Taylor, D.L.; Lanni, F. Probing the structure of cytoplasm. J. Cell Biol. 1986, 102, 2015–2022. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Moeendarbary, E.; Valon, L.; Fritzsche, M.; Harris, A.R.; Moulding, D.A.; Thrasher, A.J.; Stride, E.; Mahadevan, L.; Charras, G.T. The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 2013, 12, 253–261. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Copos, C.A.; Guy, R.D. A porous viscoelastic model for the cell cytoskeleton. ANZIAM J. 2018, 59, 472–498. [Google Scholar]
- Ong, M.S.; Deng, S.; Halim, C.E.; Cai, W.; Tan, T.Z.; Huang, R.Y.; Sethi, G.; Hooi, S.C.; Kumar, A.P.; Yap, C.T. Cytoskeletal Proteins in Cancer and Intracellular Stress: A Therapeutic Perspective. Cancers 2020, 12, 238. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Holsbeeks, I.; Lagatie, O.; Van Nuland, A.; Van de Velde, S.; Thevelein, J.M. The eukaryotic plasma membrane as a nutrient-sensing device. Trends Biochem. Sci. 2004, 29, 556–564. [Google Scholar] [CrossRef] [PubMed]
- Mow, V.C.; Guilak, F.; Tran-Son-Tay, R.; Hochmuth, R.M. Cell Mechanics and Cellular Engineering; Springer: New York, NY, USA, 1994; pp. 160–181. [Google Scholar]
- Dias, C.; Nylandsted, J. Plasma membrane integrity in health and disease: Significance and therapeutic potential. Cell Discov. 2021, 7, 4. [Google Scholar] [CrossRef] [PubMed]
- Barceló-Coblijn, G.; Martin, M.L.; de Almeida, R.F.; Noguera-Salvà, M.A.; Marcilla-Etxenike, A.; Guardiola-Serrano, F.; Lüth, A.; Kleuser, B.; Halver, J.E.; Escribá, P.V. Sphingomyelin and sphingomyelin synthase (SMS) in the malignant transformation of glioma cells and in 2-hydroxyoleic acid therapy. Proc. Natl. Acad. Sci. USA 2011, 108, 19569–19574. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Brochard, J.; Lennon, F. Frequency spectrum of the flicker phenomenon in erythrocytes. J. Phys. 1975, 36, 1035–1047. [Google Scholar] [CrossRef]
- Sauer, R.A. On the computational modeling of lipid bilayers using thin-shell theory. In The Role of Mechanics in the Study of Lipid Bilayers; CISM International Centre for Mechanical Sciences; Springer International Publishing: Cham, Switzerland, 2017; Volume 577, pp. 221–286. [Google Scholar]
- Rädler, J.O.; Feder, T.J.; Strey, H.H.; Sackmann, E. Fluctuation analysis of tension-controlled undulation forces between giant vesicles and solid substrates. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 1995, 51, 4526–4536. [Google Scholar] [CrossRef] [PubMed]
- Friedl, P.; Wolf, K. Plasticity of cell migration: A multiscale tuning model. J. Cell Biol. 2010, 188, 11–19. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Stillwell, W. An Introduction to Biological Membranes: Composition, Structure and Function, 2nd ed.; Elsevier: New York, NY, USA, 2016; pp. 553–579. [Google Scholar]
- Guck, J.; Schinkinger, S.; Lincoln, B.; Wottawah, F.; Ebert, S.; Romeyke, M.; Lenz, D.; Erickson, H.M.; Ananthakrishnan, R.; Mitchell, D.; et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 2005, 88, 3689–3698. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Händel, C.; Schmidt, S.; Schiller, J.; Dietrich, U.; Möhn, T.; Kießling, T.; Pawlizak, S.; Fritsch, A.; Horn, L.C.; Briest, S.; et al. Cell membrane softening in human breast and cervical cancer cells. New J. Phys. 2015, 17, 083008. [Google Scholar] [CrossRef]
- Gracia, R.; Bezlyepkina, N.; Knorr, R.; Lipowsky, R.; Dimova, R. Effect of cholesterol on the rigidity of saturated and unsaturated membranes: Fluctuation and electrodeformation analysis of giant vesicles. Soft Matter 2010, 6, 1472–1482. [Google Scholar] [CrossRef]
- Goetz, R.J.; Gompper, G.; Lipowsky, R. Mobility and elasticity of self-assembled membranes. Phys. Rev. Lett. 1999, 82, 221–224. [Google Scholar] [CrossRef]
- Jamali, Y.; Azimi, M.; Mofrad, M.R. A sub-cellular viscoelastic model for cell population mechanics. PLoS ONE 2010, 5, e12097. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Sandersius, S.A.; Newman, T.J. Modeling cell rheology with the subcellular element model. Phys. Biol. 2008, 5, 015002. [Google Scholar] [CrossRef] [PubMed]
- Van Liedekerke, P.; Buttenschön, A.; Drasdo, D. Off-Lattice Agent-Based Models for Cell and Tumor Growth: Numerical Methods, Implementation, and Applications. In Numerical Methods and Advanced Simulation in Biomechanics and Biological Processes; Cerrolaza, M., Shefelbine, S.J., Garzon-Alvarado, D., Eds.; Elsevier: St. Louis, MO, USA, 2018; pp. 245–267. [Google Scholar]
- Chiodoni, C.; Di Martino, M.T.; Zazzeroni, F.; Caraglia, M.; Donadelli, M.; Meschini, S.; Leonetti, C.; Scotlandi, K. Cell communication and signaling: How to turn bad language into positive one. J. Exp. Clin. Cancer Res. 2019, 38, 128, Erratum in J. Exp. Clin. Cancer Res. 2019, 38, 425. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Beckmann, A.; Hainz, N.; Tschernig, T.; Meier, C. Facets of Communication: Gap Junction Ultrastructure and Function in Cancer Stem Cells and Tumor Cells. Cancers 2019, 11, 288. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Ramilowski, J.A.; Goldberg, T.; Harshbarger, J.; Kloppmann, E.; Lizio, M.; Satagopam, V.P.; Itoh, M.; Kawaji, H.; Carninci, P.; Rost, B.; et al. A draft network of ligand-receptor-mediated multicellular signaling in human. Nat. Commun. 2015, 6, 7866, Erratum in Nat. Commun. 2016, 7, 10706. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Minc, N.; Burgess, D.; Chang, F. Influence of cell geometry on division-plane positioning. Cell 2009, 144, 414–426. [Google Scholar] [CrossRef]
- Drasdo, D.; Hoehme, S. A cell-based simulation software for multi-cellular systems. Bioinformatics 2012, 26, 2641–2642. [Google Scholar]
- Friedl, P.; Wolf, K.; Lammerding, J. Nuclear mechanics during cell migration. Curr. Opin. Cell Biol. 2011, 23, 55–64, Erratum in Curr. Opin. Cell Biol. 2011, 23, 253. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Dahl, K.N.; Ribeiro, A.J.S.; Lammerding, J. Nuclear shape, mechanics, and mechanotransduction. Circ. Res. 2008, 102, 1307–1318. [Google Scholar] [CrossRef]
- Lammerding, J. Mechanics of the nucleus. Compr. Physiol. 2011, 1, 783–807. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Marko, J.F.; Siggia, E.D.; Smith, S. Entropic elasticity of λ-phage DNA. Science 1994, 265, 1599–1600. [Google Scholar] [CrossRef] [PubMed]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromol. 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Suresh, S. Biomechanics and biophysics of cancer cells. Acta Biomater. 2007, 3, 413–438. [Google Scholar] [CrossRef]
- Cross, S.E.; Jin, Y.S.; Rao, J.; Gimzewski, J.K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2007, 2, 780–783. [Google Scholar] [CrossRef]
- Gardel, M.L.; Shin, J.H.; MacKintosh, F.C.; Mahadevan, L.; Matsudaira, P.; Weitz, D.A. Elastic behavior of cross-linked and bundled actin networks. Science 2004, 304, 1301–1305. [Google Scholar] [CrossRef]
- Storm, C.; Pastore, J.J.; MacKintosh, F.C.; Lubensky, T.C.; Janmey, P.A. Nonlinear elasticity in biological gels. Nature 2005, 435, 191–194. [Google Scholar] [CrossRef]
- Petrie, R.J.; Koo, H.; Yamada, K.M. Generation of compartmentalized pressure by a nuclear piston governs cell motility in a 3D matrix. Science 2014, 345, 1062–1065. [Google Scholar] [CrossRef]
- Charras, G.; Sahai, E. Physical influences of the extracellular environment on cell migration. Nat. Rev. Mol. Cell Biol. 2014, 15, 813–824. [Google Scholar] [CrossRef]
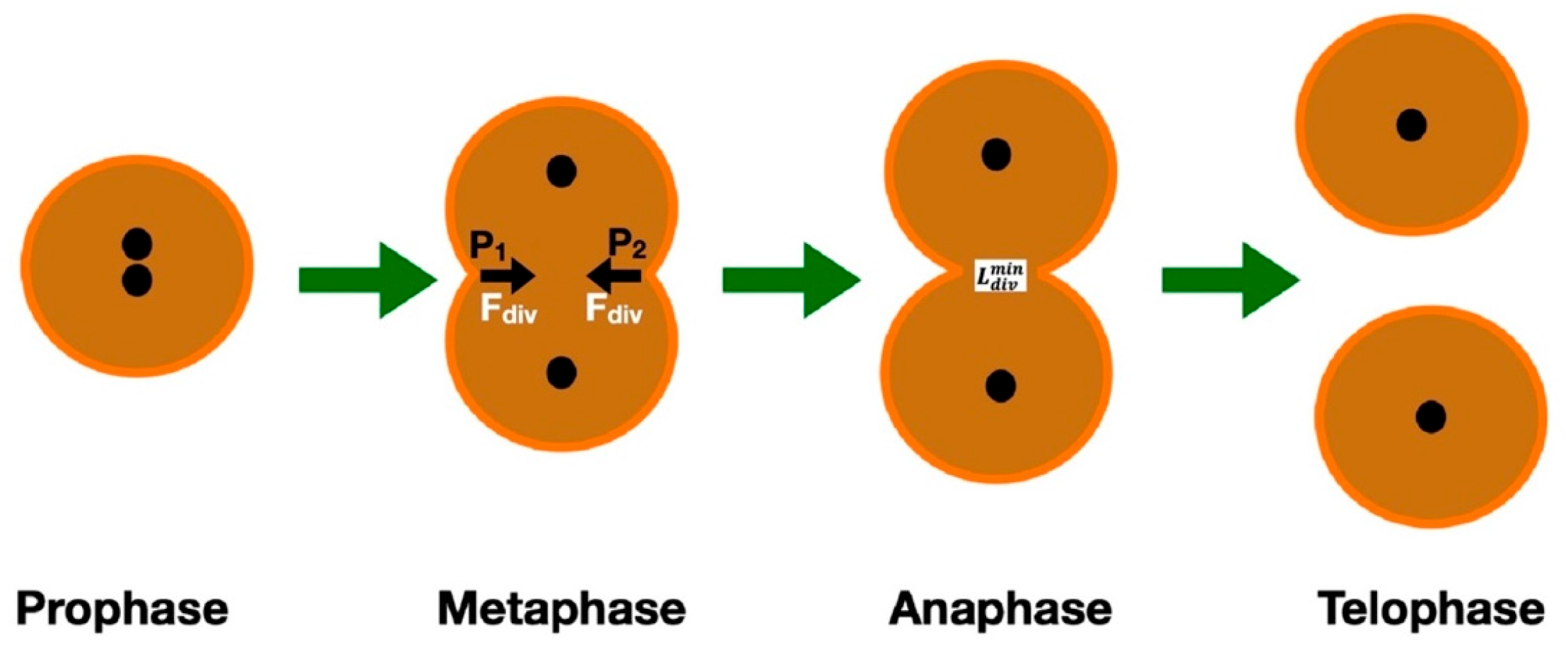
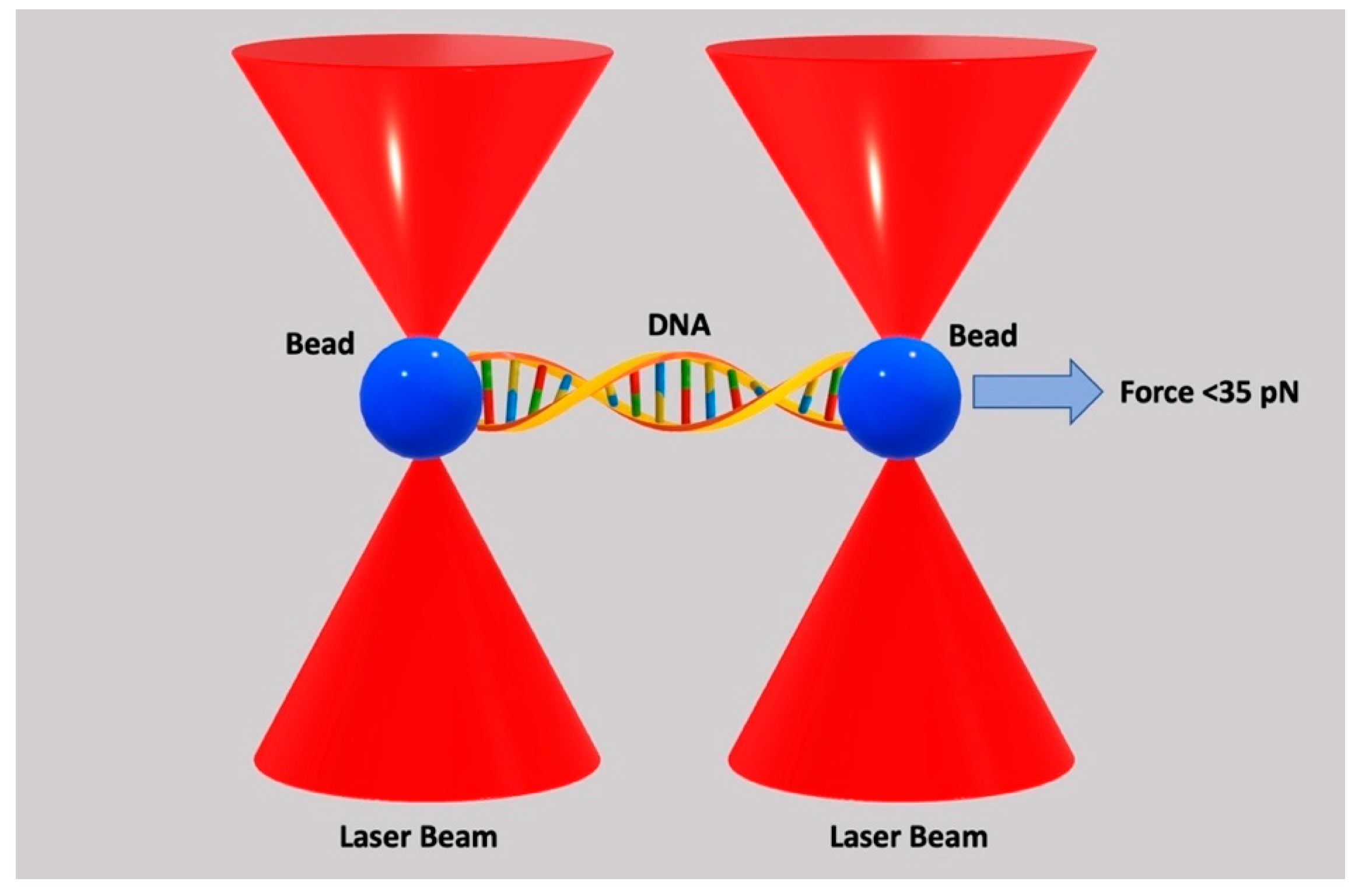
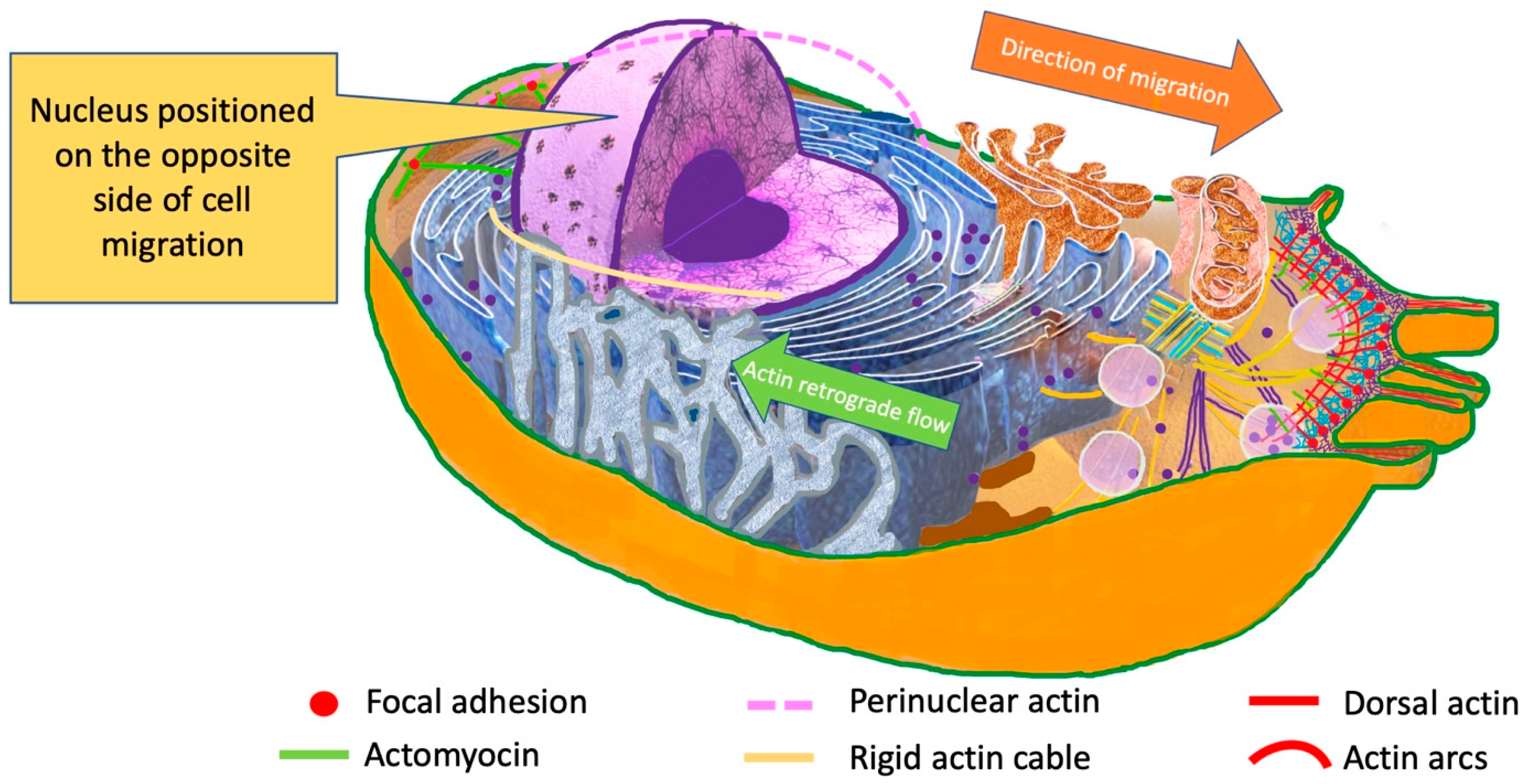
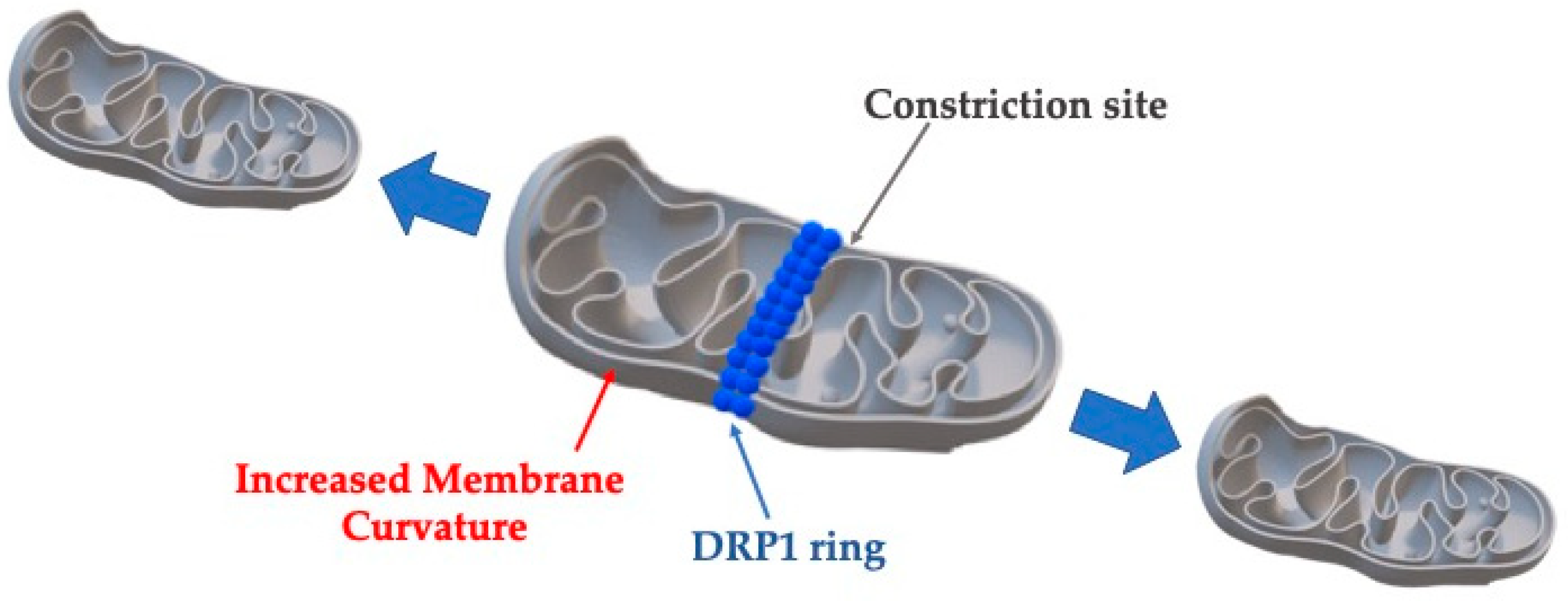

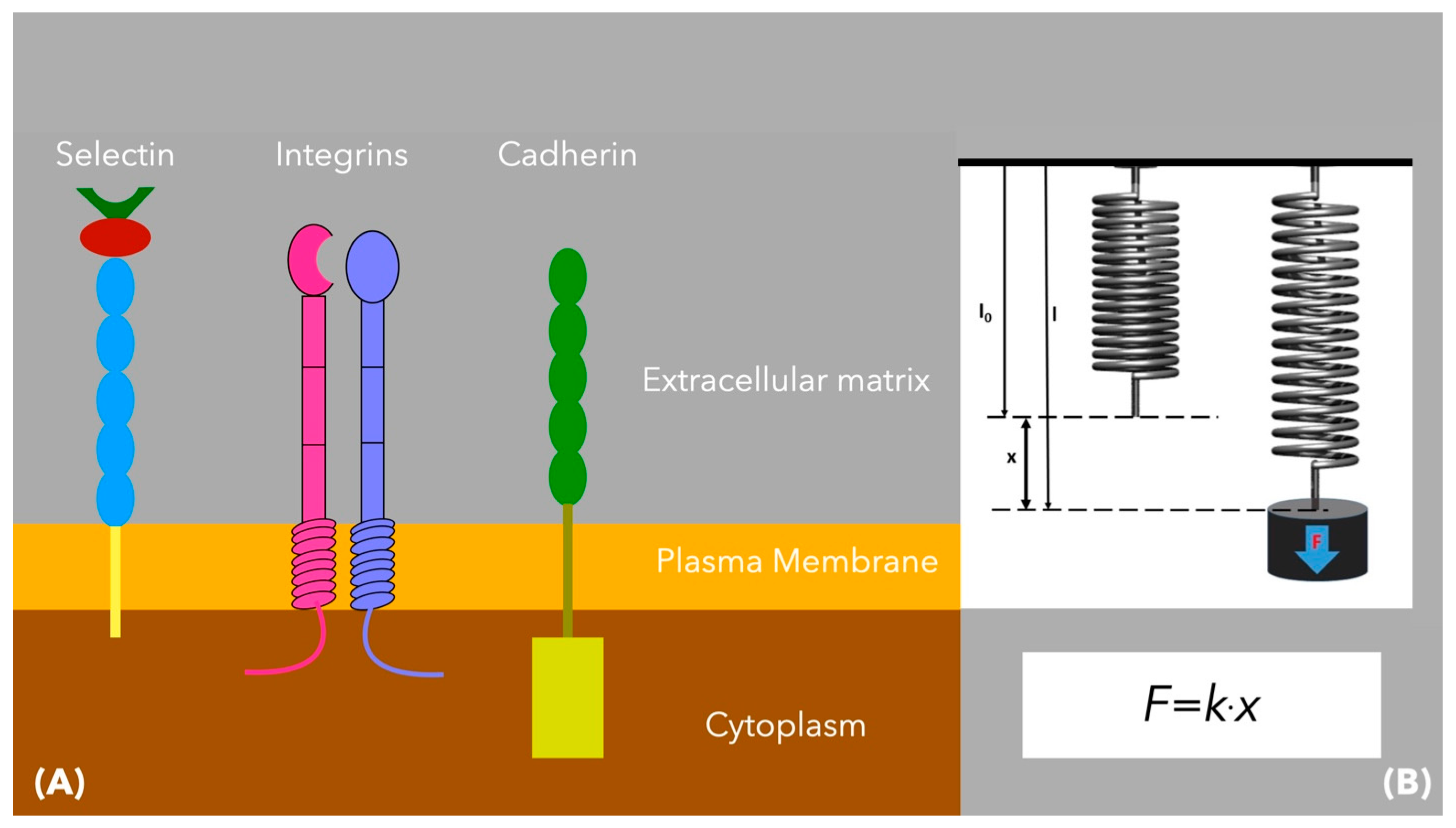
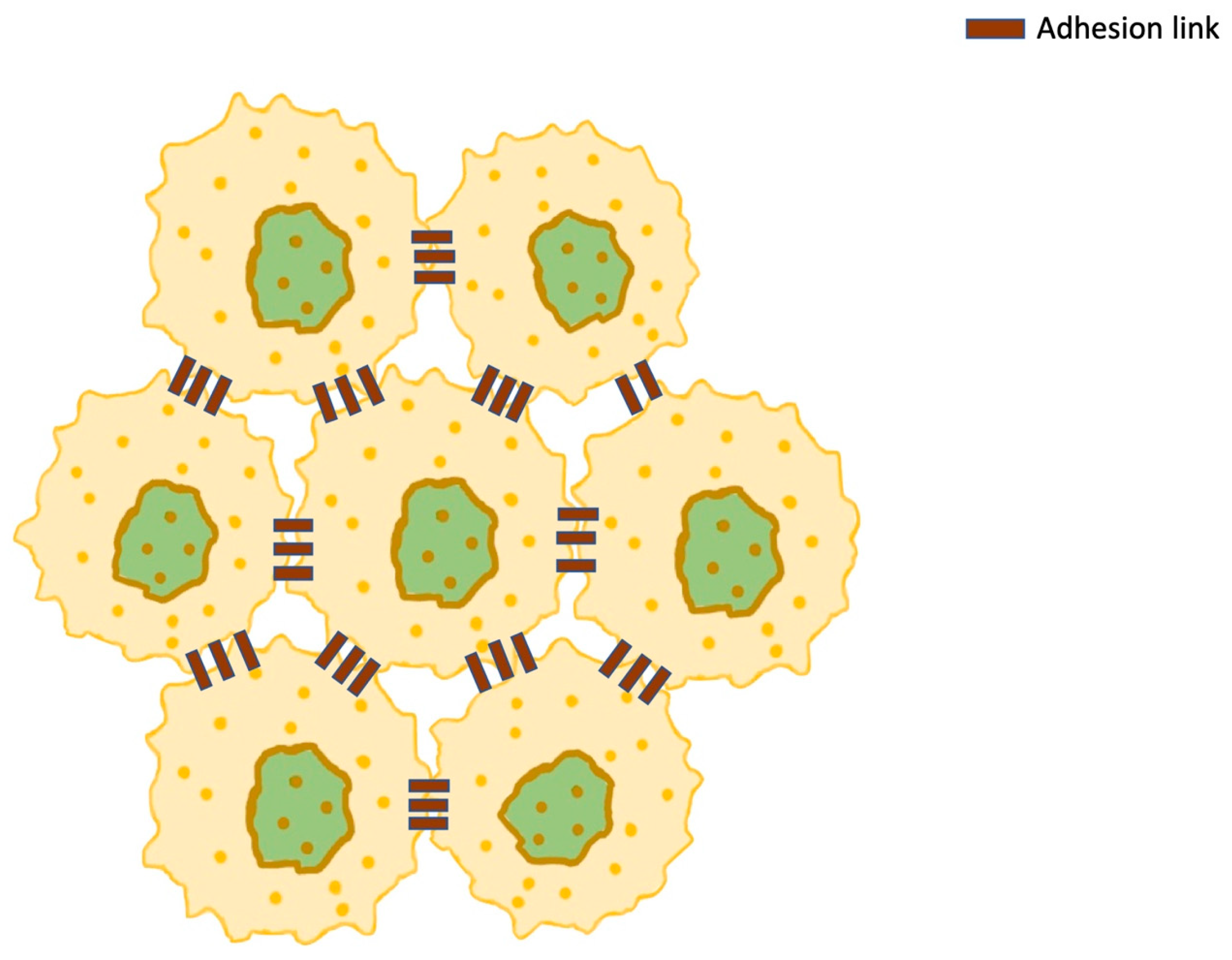
| Organelle | Effect | Mechanism | Molecules Involved |
|---|---|---|---|
| Nucleus | Assists in metastasis and proliferation [55] Guides the cell migration direction [75,76] |
| |
| Cytoskeleton | Adhesion, mechanotransduction, migration and mitosis, probably induces cell proliferation and oncogene activation [84] |
| |
| Cytoplasm | Density variations affect both the physical properties of cytoplasm and the biological processes [103] | Cytoplasm compression and disorganization of the actin cytoskeleton lead to reduction in the elastic/fluid ratio [107] | Protein–protein associations, enzymatic fluxes [103] |
| Plasma membrane | Involved in the cancer process [111] |
| |
| Receptors/adherens | Cancer expansion and disease progress [125] | Malignant cell-to-cell communication and adhesion [125] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michalakis, P.; Vasilaki, D.; Abdallah, A.J.; Asikis, C.; Niakou, A.; Stratos, A.; Tsouknidas, A.; Johnstone, E.; Michalakis, K. An Insight into Cancer Cells and Disease Progression Through the Lens of Mathematical Modeling. Curr. Issues Mol. Biol. 2025, 47, 477. https://doi.org/10.3390/cimb47070477
Michalakis P, Vasilaki D, Abdallah AJ, Asikis C, Niakou A, Stratos A, Tsouknidas A, Johnstone E, Michalakis K. An Insight into Cancer Cells and Disease Progression Through the Lens of Mathematical Modeling. Current Issues in Molecular Biology. 2025; 47(7):477. https://doi.org/10.3390/cimb47070477
Chicago/Turabian StyleMichalakis, Polychronis, Dimitra Vasilaki, Ali Jihad Abdallah, Charilaos Asikis, Athina Niakou, Athanasios Stratos, Alexandros Tsouknidas, Elaine Johnstone, and Konstantinos Michalakis. 2025. "An Insight into Cancer Cells and Disease Progression Through the Lens of Mathematical Modeling" Current Issues in Molecular Biology 47, no. 7: 477. https://doi.org/10.3390/cimb47070477
APA StyleMichalakis, P., Vasilaki, D., Abdallah, A. J., Asikis, C., Niakou, A., Stratos, A., Tsouknidas, A., Johnstone, E., & Michalakis, K. (2025). An Insight into Cancer Cells and Disease Progression Through the Lens of Mathematical Modeling. Current Issues in Molecular Biology, 47(7), 477. https://doi.org/10.3390/cimb47070477









