Abstract
Online retailers offer free shipping services, such as threshold free shipping (TFS) and membership free shipping (MFS), to promote sales and provide a better shopping experience to consumers in online retailing. Although MFS attracts more member-consumers, it encourages consumers to place more small orders than TFS, which significantly increases the operational costs of the online retailer. To address this issue, we propose two price discount policies under the MFS service, namely the limited-time discount and the threshold discount. Then, we build analytical models under these two policies to explore the impacts of offering price discounts on the retailer’s profit and consumers’ welfare. We find that no matter which discount policy is adopted, consumers are more likely to consolidate several small orders from different time periods into a big one to obtain the discount. The economies of scale generated by consumers consolidating their orders under these discount policies can help reduce online retailers’ operational costs. Therefore, regardless of any discount policy offered by the online retailer under the MFS service, consumers will place more big orders and more member-consumers are attracted, i.e., the online retailer can have its cake and eat it too. Our research findings provide decision-making insights for practitioners who offer free shipping services and price discounts to consumers in online retailing.
1. Introduction
1.1. Background and Motivation
Global e-commerce retail sales have grown rapidly in recent years [1,2], increasing from USD 2382 billion in 2017 to USD 5211 billion in 2022 [3]. Given that shipping surcharges play a key role in online consumers’ purchase decisions and satisfaction [4,5], online retailers have incorporated free shipping into their business models. There are two common types of free shipping policies in practice, namely threshold free shipping (TFS) and membership free shipping (MFS). Under TFS, online retailers offer free shipping services for orders with a value above a pre-specified threshold. For example, Macy’s provides a free shipping service for orders above USD 99. Under MFS, online retailers offer free shipping service for their subscribed members. For example, Amazon Prime offers free shipping to its members for an annual fee of USD 119. Unlike TFS, subscribers of MFS have no incentive to place big orders since an order of any amount will include the free shipping service. Instead, they order as needed, resulting in a higher purchasing frequency and a smaller order size. Thus, while MFS may attract more member consumers, online retailers must bear high shipping costs due to the high frequency of small orders. For example, Amazon collected USD 8.9 billion in shipping revenue in 2016 but spent USD 16.2 billion on shipping costs [6].
Motivated by the above challenge, we propose two price discount policies, namely the limited-time discount policy and the threshold discount policy, to encourage consumers to merge orders under MFS. Under the limited-time discount policy, consumers may merge some small orders that may be placed at different times into a big order during a limited time to obtain the discount, whereas under the threshold discount policy, consumers may merge orders to reach the discount threshold.
1.2. Research Questions and Major Findings
In this study, we examine the use of price discounts to address the challenges caused by MFS. The research questions we aim to address in this study are as follows:
RQ1: How do price discount policies affect consumer shopping frequency?
RQ2: What factors influence the decision of an online retailer to offer price discounts?
RQ3: Given the heterogeneity of consumers and the different structures of consumer orders, what is the impact of offering price discounts on online retailers’ profits and consumers’ welfare?
To address the above questions, we develop models of competition between online retailers who offer price discounts and who do not under the MFS service. In addition, we consider two distinct groups of consumers in the market, namely (1) low-sensitivity consumers (LSCs), whose shopping behaviors are not affected by price discounts, and (2) highly sensitive consumers (HSCs), who are more sensitive to price discounts and carefully arrange shopping orders in each shopping period to obtain discounts.
We obtain several intriguing findings. First, we reveal an unexpected result that online retailers can increase profits by offering price discounts even without increasing sales. Second, there exists a Pareto improvement between the buyer and seller, i.e., the seller offers a discount to save more on the delivery cost than its discount concessions, and the buyer places orders that are not urgently needed in order to obtain the discount. Third, the order structure of the consumers is an important factor for the online retailer to offer price discounts.
1.3. Contributions and Paper Arrangement
To the best of our knowledge, this paper is among the first to investigate the impact of offering limited-time discount and threshold discount policies under MFS on online retailers’ profit and consumers’ welfare based on the heterogeneity of consumer shopping behaviors and order structures. The contributions of this study are as follows: (1) We propose limited-time discount and threshold discount policies and derive optimal price discounts for online retailers under the MFS, with the aim of ensuring online retailers are not hindered in profitability because of the high-frequency and small-scale purchase behavior of consumers. Unlike previous studies, we make a theoretical contribution to this field by considering scenarios of consumer order consolidation and additional purchases under different policies. (2) We incorporate consumer shopping behaviors into this study and we develop a competition model under MFS, through which we explore the impacts of discount policies on consumers’ shopping behaviors. Our paper enriches the topic by incorporating the sensitivity of consumers into price discounts and providing analytical models to derive the optimal discount percentage and optimal discount duration. (3) We find a win–win result for both online retailers and consumers where online retailers offering MFS with limited-time or threshold discounts incentivize consumers to place more big orders and e-tailers attract more member-consumers. Our findings not only contribute to the literature but also provide decision-making insights for online retailers that offer free shipping services.
We organize the rest of the paper as follows: In Section 2 we review the literature on membership free shipping and price discount in online retailing. In Section 3 we establish a basic model to capture consumers’ shopping behaviors and the online retailer’s profit. We extend the model to examine the optimal decision under MFS with limited-time discounts in Section 4 and the optimal decision under MFS with threshold discounts in Section 5. We present and discuss the results of numerical studies in Section 6. Finally, we conclude the paper and suggest topics for future research in Section 7. We give the proofs of all the results in the Appendix A.
2. Literature Review
This study is related to three main streams of literature on online retailing operations, namely the membership free shipping policy, threshold free shipping policy, and the price discount strategy.
2.1. Membership Free Shipping in Online Retailing
The paid membership system can improve consumers’ repeated purchases, increase their dependence on shopping routes, and at the same time carry out consumer portraits through member shopping data. Free shipping is a strategy decision for retailers [7]. In e-commerce, MFS is widely used [8,9].
Some of the early literature focuses on analyzing consumers’ shopping behavior using member data [10]. For example, online retailers can analyze the shopping behavior data of members and non-members to determine the difference between them [11,12]. By analyzing the data on members’ shopping behavior, online retailers can further segment market customers [13]. These studies can provide sales decision support for online retailers.
In addition to the impact on consumers’ shopping behavior, MFS also has a greater impact on the online retailer’s cost. Compared with TFS, the revenue that the online retailer receives from the membership fee does not offset the cost incurred from offering member free shipping [8]. Only when the membership fee is lower than a certain value can it be easily accepted by consumers [14]. This is also why online retailers do not easily increase the fees charged to members.
In recent years, many researchers have studied the impact of MFS on business operations development. For example, Wen and Lin examined the impact of MFS in different competitive environments [15]. Sun et al. studied the impact of different sales modes on MFS and showed that it is more profitable to the retailer in the agency mode than in the wholesale mode [16].
Unlike the papers mentioned above, which explore the traditional MFS strategies, our paper focuses on two prevalent price discount policies under MFS and incorporates consumer’s sensitivity into price discounts, as well as their behaviors of order transfer and order consolidation. Specifically, the limited-time discount and threshold discount under MFS are explored and we derive the conditions under which different price discount strategies can be offered.
2.2. Threshold Free Shipping in Online Retailing
Apart from MFS, TFS can also promote consumer purchases and increase the sales of online retailers, so it is widely used in online sales [17,18,19]. The wide range of this marketing policy has attracted much research attention. Past studies have shown that TFS affects consumers’ purchase decisions [20]. When the purchase amount is less than the TFS threshold, consumers have a strong willingness to add purchases to obtain free shipping. The main factor affecting this willingness is the delivery (distribution) cost and threshold. Lewis et al. demonstrated that TFS can increase the purchase amount of customers’ orders. In terms of marketing policy, the threshold can be the number of purchased products [21]. Huang and Cheng showed that piece-based threshold free shipping is more effective than dollar-based shipping [22]. Li et al. found that to make the shopping amount reach the threshold, online retailers can provide additional shopping recommendations to improve consumers’ willingness to buy [23].
In our study, TFS is used directly in reference to the analysis of MFS. We also compare changes in consumers’ shopping behaviors under TFS and MFS policies. Our study is fundamentally different from that of Sun et al., which examines the difference between MFS under the agency mode and the wholesale mode. Our study works on a different way of exploring the impact of combining MFS with other marketing strategies compared to the existing studies [16].
2.3. The Price Discount Strategy in Online Retailing
Offering price discounts is one of the widely used strategies for online retailers to promote sales in practice [23]. Nouri-Harzvili and Hosseini-Motlagh proposed a dynamic model to determine the optimal price discount rate based on inventory and consumers’ reference in online retailing systems [24]. Given that the supplier provides a free shipping service to attract and keep consumers, the supplier’s quantity discount and transport cost are incorporated into the optimal order lot size and retail price decision models [25]. Similarly, the impacts of quantity discount, transport cost, and demand variance on the retailer’s optimal order quantity and pricing decisions for the newsvendor problem with free shipping are determined simultaneously [26]. Zheng et al. considered a fresh produce supply chain with multiple retailers and explored the supplier’s optimal pricing decision and retailers’ optimal procurement decisions under the quantity discount policy [27]. Kwon et al. introduced a quadratic quantity discount contract under price-dependent demand and consumer returns [28]. The time-based temporary discount strategy is also a price discount strategy offered by the supplier to the buyer that places special orders during a sale period [29]. In addition, the joint decisions of the order quantity and selling price are explored when the retailer provides multiple discounts [30]. They found that when the demand distribution information is known, using a small discount in the beginning, and marking down with an accelerating increase rate will benefit the retailer more. Under uncertain demand, the shipping quantity and pricing decisions are investigated when shipping services are provided before order making [31]. The pricing discount strategy is also considered in the context of live-streaming commerce to attract new consumers, and the optimal price discount rate for the selling format is determined to make price discount decisions in supply chains with manufacturers selling online [32].
There are few papers incorporating the consumer’s behavior into the price discount problem. For example, Sheehan et al. examined the impact of price discount on consumers’ purchase intentions in online shopping, and they found that the magnitude of the price discount is more predictive of consumers’ purchase intentions during the online shopping process [33]. Taking consumers’ patience with waiting time into account, Liu et al. incorporated consumers’ patience into the dynamic pricing problem and found that a pricing discount can mitigate revenue loss for homogeneous consumers, and consumers’ patience time results in a high net monetary cost for the time-sensitive consumers [34]. In addition, Li et al. established two-period models to investigate the impacts of the platform’s different discount pricing strategies of online coupons on strategic consumer behavior [35]. Unlike the above-mentioned papers that examine the impact of consumer behaviors on price discount strategies, our paper attempts to incorporate consumer’s behavior of order transfer into the limited-time discount and order consolidation into the threshold discount.
2.4. Research Gaps
Overall, the literature on free shipping and price discounts in online retailing focuses on TFS and MFS itself, but price decision research under MFS is relatively limited. Since price promotion has proven to be an effective marketing strategy, firms’ operational decisions during price promotion have been an important research topic. Hence, it is desirable to explore how price discounts affect consumers’ shopping behavior and the factors that influence online retailers to offer price discounts. In essence, we examine the operations impact of combining price discounts with MFS. Contrary to the existing research on this topic, we mainly study whether online retailers offering MFS can increase revenue by providing limited-time discounts or threshold discounts. Table 1 summarizes the relevant literature and the focus of this paper.

Table 1.
Summary of the relevant literature and the focus of this paper.
3. Model Setup
3.1. Problem Description
MFS has become popular among online retailers in the last decade. MFS is commonly advertised as a premium service included in an online retailer’s loyalty program. Under this policy, consumers pay a membership fee upfront and enjoy free shipping along with other benefits throughout the membership period. Once the membership fee is paid, it becomes a sunk cost for subsequent shopping decisions, so consumers can enjoy membership free shipping on any shopping occasion.
Unlike TFS, subscribers of MFS have no incentive to place big orders. Instead, they order as needed, resulting in a higher purchasing frequency and a smaller order size. With the surging popularity of MFS, high-frequency and small-size ordering may hinder the online retailer’s profitability.
How to reduce the small-size shopping frequency of consumers, while not reducing the total amount of shopping and improving the profit, is a key problem for online retailers. To address this issue, we design discount policies under the MFS service. The discount policies allow consumers to keep the total purchase amount unchanged, or even increase it, but reduce the frequency of shopping. The online retailer can improve its revenue by reducing the frequency of delivery.
For the convenience of reading, we summarize the symbols and descriptions of relevant parameters in Table 2.

Table 2.
Summary of notation and symbols.
3.2. Consumer Shopping Behaviors
In this subsection, we analyze consumers’ shopping behavior under different free shipping policies and make a comparison between them.
3.2.1. Consumer Shopping Behavior under TFS
To increase the number of purchased products per order, a clear understanding of consumers’ shopping behavior is needed. Under TFS, consumers have a plan before shopping, which is called planned shopping. Supposing that the planned purchase amount is , the marginal utility per unit of purchased products is , and the net utility of planned shopping is . When the amount of the consumer’s planned purchase is less than the threshold value under TFS , there are three possibilities for the consumer’s actual purchase amount :
- The consumer buys directly and pays the delivery fee , the marginal negative utility of the delivery fee is , and the actual purchase amount of the consumer is . The consumer utility function is . This linear utility function is widely used in the operations management literature [36,37]. Let , then .
- The additional purchase of items by the consumer brings the purchase amount to the threshold and enables the consumer to receive free shipping. The actual amount of the consumer’s purchase satisfies . The consumer utility function is . Letting , we have . Letting , we have . The purchase amount is the utility undifferentiated plan purchase amount of the first two options.
- The consumer abandons the purchase, i.e., the actual purchase amount is .
Through the above analysis, we can obtain the relationships between the consumer’s shopping utility, the actual purchase amount, and the planned purchase amount, as shown in Figure 1.
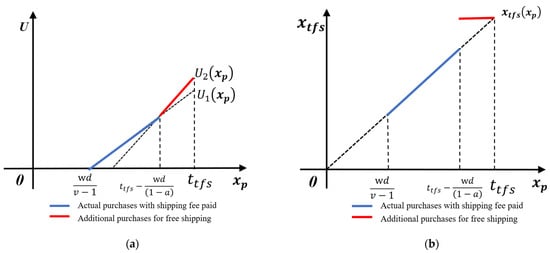
Figure 1.
Consumers’ shopping behavior under TFS. (a) The relationship between the consumer’s utility and the amount of planned purchase; (b) the relationship between the actual purchase amount and the planned purchase amount.
3.2.2. Consumers’ Shopping Behavior under MFS
Under MFS, consumers have a shopping plan before making a purchase and the actual purchase is also based on their plan. The amount purchased by the consumer is . The consumer’s utility function is without considering the payment of the membership fee. We can obtain the consumer’s purchase utility and actual purchase amount, and their relationships with the planned purchase amount, as shown in Figure 2.
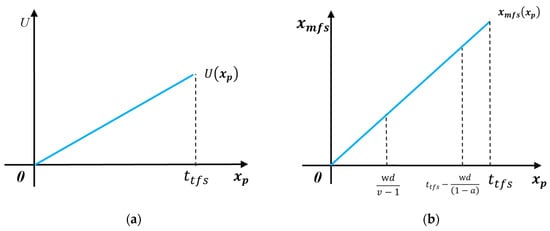
Figure 2.
Consumers’ shopping behavior under MFS. (a) The relationship between the consumer’s utility and the amount of planned purchase; (b) the relationship between the actual purchase amount and the planned purchase amount.
3.2.3. Comparison between Consumers’ Shopping Behaviors under TFS and MFS
Comparing the shopping behaviors of consumers under TFS and MFS, we find that the actual purchase amounts of the two are different. We show the specific differences in Table 3.

Table 3.
Comparison of actual purchase amounts under TFS and MFS.
Without loss of generality, we normalize the planned purchase amount. If the planned purchase amount is uniformly distributed in the [0, 1] interval, i.e., , we have the following result.
Lemma 1.
Compared with TFS, when online retailer adopts MFS, we have the following:
- (1)
- the number of orders will increase by ;
- (2)
- the total amount of purchases will decrease by(or increase by);
- (3)
- the average purchase amount per unit order will decrease by.
All the proofs can be found in the Appendix A.
3.3. Basic Model
We consider competition between two online retailers, one of which does not offer the discount while the other does (see Figure 3). Both online retailers provide MFS. The only difference between the two companies is whether they offer discounts.
Figure 3.
Online retailers that offer and do not offer discounts.
To concentrate our analysis on the impacts of delivery frequency and discount level, we normalize the product cost to zero, which is widely considered in the operations management literature. For the online retailers, the profits with and without price discount are as follows:
The difference in revenue between the two online retailers is
If , the online retailer should provide a discount. In practice, there are such discount policies as limited-time discount or threshold discount offered by online retailers.
4. Limited-Time Discount under MFS
4.1. Problem Description
A limited-time discount refers to a promotional strategy in which an online retailer only offers a discount within a specific time window (e.g., “12% off on Tuesday only”), during which consumers can transfer potential orders to make a concentrated purchase. The obvious motivation for retailers to use time limitation is to engage consumers in purchasing within a specific time window.
We classify a given sales period as a “discount period” and a “non-discount period”. For example, Tuesday is the discount period, and the rest of the week is the non-discount period in a week. Due to consumer heterogeneity, different consumers respond differently to the online retailer’s limited-time discount.
To increase sales and merge some small orders into a big one, online retailers provide a limited-time discount. The sales period is divided into a “discount period” and a “non-discount period”. For example, Freshippo’s members can choose every Tuesday or Wednesday as their membership day and enjoy 12% off on their orders on these days.
In Figure 4, we show the shopping process of MFS participants under the limited-time discount strategy.
Figure 4.
Limited-time discount shopping behaviors.
High-sensitivity consumers are more sensitive to online retailers’ special offers, and they will arrange “transferable orders” during the “non-discount period” to make purchases during the “discount period” to enjoy the benefits of the discount. However, low-sensitivity consumers may not care about these offers and will not make such arrangements. Such a business strategy, without affecting the shopping experience of consumers (which improves their shopping experience, i.e., reduces their consumption), reduces the online retailer’s delivery cost or increases its revenue by consolidating some of the orders. Therefore, this is a win–win business operation.
In China, Freshippo (www.freshippo.com) offers this service to its paid members. Freshippo launched one day a week as a membership day (paid members can choose Tuesday or Wednesday as their membership day) and members enjoy a 12% discount on the membership day, i.e., 12% off on their orders purchased on this day. The membership service, in addition to providing price discounts directly to consumers, allows orders to be shifted and pooled at specific time periods.
For research, we make the following reasonable assumptions.
- Assumption 1: When online retailers do not provide a limited-time discount, consumers’ daily shopping follows the uniform distribution.
- Assumption 2: For orders that are not purchased during a fixed time, consumers will choose to purchase during a specific discounted time to enjoy a price discount.
- Assumption 3: Consumers transferring non-fixed time purchase orders to limited-time discount purchases will not increase the number of orders, i.e., delivery frequency will not increase.
- Assumption 4: The delivery costs are the same for all the orders, regardless of the quantities of the goods ordered.
4.2. The Model with Order Transfer
When an online retailer does not offer limited-time discount, consumers will purchase according to their normal habits. For the convenience of this study, the total number of purchases includes the percentage of purchases during the discount period and the percentage of purchases during the non-discount period . Of course, the total number of purchases can also be divided into two parts according to the type of consumers. Based on Assumption 1, the percentage of purchases made by highly sensitive consumers is , so the percentage of purchases made by low-sensitivity consumers is .
When the online retailer offers a limited-time discount, it changes the highly sensitive consumers’ shopping strategies. They transfer orders from non-discounted periods to discounted periods to enjoy a limited-time discount. The number of transfer orders of the highly sensitive consumers is , where is the transfer ratio, which is proportional to the discount , i.e., = k.
Based on Assumption 3, the transferred order does not increase the number of shopping orders during the discount period but increases the purchase amount. After offering the discount, the online retailer’s delivery will decrease by .
As consumers reduce the number of orders, the online retailer reduces its delivery cost by . At the same time, the online retailer adopts price discount policies, which will reduce profit and revenue by .
If the benchmark revenue of the online retailer is , the revenue including the limited-time discount is
The revenue difference of the online retailer when offering limited-time discount is
From Equations (4) and (5), we have the following Proposition 1.
Proposition 1.
If the online retailer provides limited-time discount under MFS, the optimal discount percentage and discount duration are as follows:
The optimal discount duration is the ratio of the minimum time of the limited-time discount duration , which usually lasts one day, to the total limited-time discount cycle time ; usually, a weekly or monthly discount is offered. Given that consumers are always willing to combine their “high-frequency and small-volume” orders for groceries into a big one in a limited time to obtain a discount, the online retailer usually sets a fixed discount date within a discount cycle. For example, Freshippo offers a limited-time discount for members every Tuesday or Wednesday. Aeon supermarket sets every Wednesday as its regular discount day. Without loss of generality, the minimum limited-time discount duration is normally one day and the total discount cycle time is typically in a short weekly or monthly interval. Therefore, we can conclude that will increase as decreases, which illustrates why the online retailer generally prefers to offer the discount for only one day per week, i.e., .
The following Proposition 2 provides the condition under which the online retailer offers the limited-time discount.
Proposition 2.
The online retailer should offer a limited-time discount, if and only if .
From and , we obtain . We know that is the pre-condition for the online retailer to offer a limited-time discount. When the proportion of highly sensitive consumers in the member group is large enough, and the order transfer caused by discount is large enough, the online retailer can only have economic benefits to offer a limited-time discount. In short, offering a limited-time discount benefits all the stakeholders. The higher the unit delivery cost c is, the smaller is the average unit order amount ; or, the larger the is, the better it is to offer a limited-time discount, and the more favorable it is to the online retailer.
If the online retailer offers a limited-time discount under MFS, the consumer’s revenue is and the online retailer’s revenue is .
4.3. The Model with Order Transfer and Additional Purchases
The online retailer offers a limited-time discount, which allows consumers to transfer orders to qualify for a discount, which increases sales, i.e., additional purchases. That is, the consumer increases the number of purchases during the discount period (excluding the purchase amount transferred during the non-promotional period). Low prices are the easiest and most effective means to entice customers to buy. The increase in shopping is proportional to the discount , i.e., the proportion of shopping growth is and the revenue from this shopping growth is . represents the amount of sales during the sales period before the limited-time discount is offered, the increase rate is , and the profit margin is when the limited-time discount is offered. By analyzing consumers’ shopping behavior, we find the revenue function of the online retailer that offers limited-time discount is
The increased revenue of the online retailer is
From Equations (8) and (9), we have the following Proposition 3.
Proposition 3.
If the retailer offers a limited-time discount under MFS, the optimal discount percentage and discount duration are as follows:
Form Equations (10) and (11), we derive that Only in the case of order transfer, the offering of a limited-time discount does not take into account the profit margin of the sold goods. If the delivery cost saved by the limited-time discount exceeds the discount expenditure, the online retailer benefits from offering a limited-time discount. However, if the sales growth (additional purchases) caused by the discount is considered, when , the more sales growth there is, the greater is the online retailer’s loss.
Comparing with , we have the following results.
Proposition 4.
Considering order transfer and sales growth, we obtain the following:
- (1)
- when , then ;
- (2)
- when , then ;
- (3)
- when , then .
From Proposition 4, we find that when the optimal discount rate is relatively small ), and the discount rate can be increased to promote sales, which is the best decision choice for the online retailer. When the optimal discount rate is , then . When the optimal discount rate is relatively large (), because the increase in discount strength promotes sales growth while also compressing the profit margin, the best decision choice for the online retailer is to reduce the discount.
4.4. Discussion
From Propositions 2 and 3, not all online retailers can adopt this policy under MFS. Whether the adoption of this policy is beneficial to the online retailer depends not only on the delivery cost and sales profit margin of the online retailer, but also on the order structure and shopping behavior of consumers.
When the online retailer provides a limited-time discount under MFS, the optimal discount is and we have . For the online retailer, the higher the delivery cost is, the larger is the potential for promotional activities. From and , we find that when , it is beneficial for the online retailer to offer a limited-time discount.
In real-world online retailing settings, the higher the delivery cost is, the more willing is the online retailer to offer a discount, thereby improving consumers’ shopping behavior. If the delivery cost as a percentage of the purchase value of an order is low, then the impact on the online retailer is also low.
The parameter indicates the proportion of sensitive consumers under the limited-time discount policy, and the parameter represents the elasticity factor for order transfer caused by the discount margin, both of which are exogenous. Their economic implications are how responsive consumers are to the online retailer’s offering of a limited-time discount. The higher and are, the larger the impact of the limited-time discount is, and the better it is to adopt this discount policy.
From and , we find that when , it is beneficial for the online retailer to offer a limited-time discount. This result shows that the smaller the average purchase amount is, the more conducive it is to adopt this policy. Without taking sales growth into account, the sales margin has no impact on the decision to offer a limited-time discount.
Offering a limited-time discount under MFS will bring benefits to the online retailer. However, there exist some obvious problems in adopting this policy: (1) insufficient service capacity of the online retailer during the discount periods and (2) excess service capacity during the non-discount periods. Therefore, we examine the order consolidation that does not occur during a specific time in the extended model.
From Equation (5), we find that the shorter the discount period is, the larger is the profit of the online retailer. It is noted that if a discount period lasts too long, consumers are not able to transfer many orders due to the uncertainty in their shopping plans. In addition, if the duration of the discount is too short, it is not convenient for consumers to make a shopping plan. Therefore, the online retailer generally offers the discount for a period of no less than one day in practice. To provide the discount policy continuously, it is necessary to consider the interval period in addition to the duration. In addition, if the interval between two discounts becomes longer, the consumer’s expectation of the discount becomes lower, resulting in a lower probability of order transfer. Therefore, the online retailer usually offers a discount in regular periods, while the most important discount usually lasts for only one day. The model of the fresh produce online retailer Freshippo (www.freshippo.com) is a good example; Freshippo offers a discount of 88% in a weekly discount period, i.e., one day per week is defined as a member’s day.
5. Threshold Discount under MFS
In Section 4, the online retailer provides a limited-time discount under MFS to encourage consumers to make bigger orders within a specific limited-time period. This section examines the case where the online retailer offers a threshold discount to encourage consumers to merge orders of different purchase amounts into bigger orders.
5.1. Problem Description
A threshold discount refers to a promotional strategy in which a consumer will enjoy a price discount when their order amount reaches a threshold. In this section, we examine the possibility of using a threshold discount to encourage consumers to merge small orders into a big one under MFS. During the sales period of products, the online retailer sets a shopping threshold and discount ratio . Then, the saving on costs for a consumer is if they purchase . Obviously, when the discount ratio is higher, the consumer is more likely to participate in the policy, and vice versa.
When the planned purchase amount is less than , the consumer has the following three choices: (1) purchase as planned and pay the purchase amount; (2) merge different planned purchase orders into one to reach , and pay ; (3) merge different planned purchase orders and add unscheduled shopping to reach , and pay .
We consider two scenarios based on consumers’ decision-making processes: (1) no unplanned purchases, i.e., case 1 and case 2, and (2) unplanned purchases, i.e., all the cases.
The order of the consumer’s planned shopping is divided into two categories: (1) orders with an amount less than , the order quantity is , and the average purchase amount per order is ; (2) orders with an amount greater than or equal to and the order quantity is 1 − γ.
5.2. The Model with Order Consolidation
Consumers combine small orders to a big order to reach the threshold . The proportion of consolidated small orders is and the quantity of consolidated orders is . Then, the total payment of the consolidated orders is . After consolidation, the total order quantity is reduced by and the online retailer reduces the delivery cost by .
The consumer’s benefits have two parts: (1) cashback from purchasing more than and (2) cashback through the consolidation of small orders.
The online retailer reduces the delivery cost by , and pays more cashback . The benefit of adopting this policy to the online retailer is
The incremental benefit under this policy is
From Equations (12) and (13), we derive the following result.
Proposition 5.
If the online retailer offers a threshold discount under MFS, the equilibrium discount ratio and the threshold for the discount are as follows:
Based on Proposition 5, from Equation (14) and , we have the following result.
Proposition 6.
Under MFS, the online retailer should offer a threshold discount only if the shipping fee satisfies , the number of small orders satisfies , and the average purchase amount of their orders satisfies .
In practice, regardless of whether the online retailer’s delivery system is self-operated or provided by a third party, the delivery cost is almost fixed. The online retailer can use members’ historical transactions data to decide whether to provide a threshold discount.
5.3. The Model with Order Consolidation and Additional Purchases
When online retailers provide a threshold discount, consumers’ purchases reach a threshold through consolidating small orders and additional purchases. Suppose that the consolidated order ratio is proportional to the discount ratio , i.e., . The quantity of the consolidated order is equal to and the purchase amount of the consolidated order is equal to .
Assuming that additional shopping is proportional to the consolidated orders, then the additional shopping ratio is proportional to the discount ratio , with , and the additional purchase amount is equal to .
For the online retailer, the benefits are twofold: (1) added revenue due to a decrease in consumers’ shopping frequency (reduction in the delivery cost), and (2) added revenue due to increased purchases by consumers.
For the consumer, there are also multiple benefits: (1) discount income for planned orders more than , (2) cashback through the consolidation of small orders, and (3) discount income through the consolidation of small orders and additional purchases.
After adopting the threshold discount policy, the revenue of the online retailer is
The added revenue of the online retailer is
Substituting and into Equation (17), we find the added revenue of the online retailer is
In the real-world online retailing market, the larger the , the higher the proportion of small-order mergers. Hence, there will be more savings in delivery costs, but a greater loss of profit for the online retailers. Therefore, is the optimal discount ratio for online retailers.
From Equations (16) and (18), we have Proposition 7.
Proposition 7.
If the online retailer provides a threshold discount under MFS, the optimal discount ratio and the threshold for the discount are as follows:
where , , and .
For the threshold values, if is too large, consumers need to merge more small orders in order to enjoy discounts, thereby reducing their willingness to merge small orders. If is too small, consumers can obtain discounts by merging a small number of small orders, while increasing the discount for some orders that do not need to be merged.
5.4. Discussion
Whether the threshold discount policy is worth adopting is related to the order structure and shopping behavior of consumers. The order structure includes the quantity and the average purchase amount per order less than the threshold . The smaller is, the larger is . At this time, the profit erosion of the online retailer is larger. It can be obtained from Proposition 5 that only when should the online retailer adopt this policy. At the same time, we find that only when will the online retailer benefit from adopting this policy.
Under the limited-time discount policy, the discount activities are not limited by the number of purchases, but by the time. However, the threshold discount policy is the opposite and is limited only by the number of purchases and not by time. If the consumer enjoys MFS for small orders, they cannot enjoy the threshold discount. Consumers cannot enjoy both discount policies at the same time, which provides an opportunity for online retailers to make profits. For example, JD Group provides free shipping coupons and threshold discount coupons to plus members, i.e., consumers can choose either one to use. Using the free shipping coupon can only save on the delivery cost, while the threshold discount coupon can reduce the payment. Some sensitive consumers are willing to combine orders (make additional purchases) in order to enjoy the threshold discount. Therefore, this policy is applicable to comprehensive online retailers, such as JD Group.
6. Numerical Studies
In this section we conduct numerical studies to illustrate the results and generate managerial insights from the analytical findings by using data from some leading online retailing platforms such as JD Group, Taobao, and Tmall.
6.1. Parameter Settings
The numerical parameters are set with respect to real-world practices, which are important to reflect the real free shipping delivery services and discount policies offered by online retailers. Following the setting of parameters in this section, the results obtained can be extended to other similar scenarios and provide practical guidance for online retailers. The parameters are set according to the following principles:
- (1)
- Data from mainstream e-commerce platforms. With reference to the shipping charges and free shipping thresholds of several important online retailers in mainland China (e.g., JD Group, Tmall, Dangdang.com, and Suning.com), we set the parameters of the order delivery cost and the average purchase amount for small orders. To be reasonable, the purchase amount parameter for small orders is taken as half of the free shipping threshold. The limited-time discount offer period parameter is taken from Freshippo and the threshold discount threshold parameter is taken from JD Group’s plus members. The delivery cost is taken as or . The average purchase amount for small orders is or . The discount threshold is 105.
- (2)
- Data are based on reasonable assumptions. In order to facilitate the numerical analysis, reasonable assumptions are made for the annual number of orders, percentage of small orders, order transfer coefficient, sales growth coefficient, and margin of gross profit on sales.
6.2. Numerical Analysis
To investigate the impacts of the average purchase amount of small orders and the delivery cost per order of buyers on profitability under limited-time and threshold discounts, the numerical results are displayed based on the above parameters, as shown in Figure 5 and Figure 6.
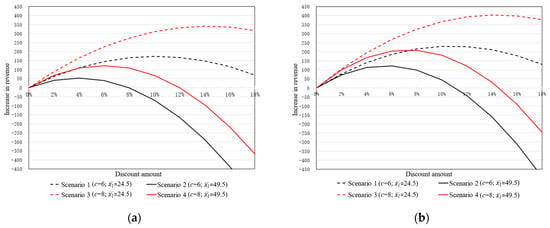
Figure 5.
The online retailer’s profit changes under the limited-time discount policy. Note: (a) shows the online retailer’s profit changes when only considering the impact of order transfer. (b) shows the online retailer’s profit changes when considering the impacts of both order transfer and additional purchases.
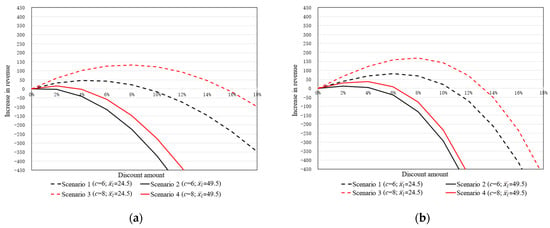
Figure 6.
The online retailer’s profit changes under the threshold discount policy. Note: (a) shows the online retailer’s profit changes when only considering the impact of order transfer. (b) shows the online retailer’s profit changes when considering the impacts of both order transfer and additional purchases.
Observations 1. A limited-time discount under the free shipping policy for members allows for increased profits even without increasing sales. Observation 1 is against the real-life intuition that a discount hurts profits without increasing sales.
Observations 2. A limited-time discount is more effective only if the delivery cost is relatively high or if the average purchase amount is low for small orders. This phenomenon is more intuitive because when more orders are consolidated, more delivery costs are saved, and more profit is generated.
Comparing the results shown in Figure 5a,b we have the following observation.
Observations 3. The discount that can be offered by the online retailer is more significant in terms of increasing sales.
7. Conclusions
In the past decade, online retailers have widely used TFS and MFS policies to promote online retailing. TFS is extensively used as a promotion strategy to induce bigger orders. However, there is a lack of customer loyalty. MFS is a common service included in an online retailer’s loyalty program. However, it generates many small orders. This paper built analytical models to examine how price discount policies affect consumer shopping frequency and the impact of offering limited-time discount and threshold discount policies on online retailers’ profits and consumers’ welfare in online retailing.
From the consumer’s perspective, we find that whether the adoption of these strategies is profitable is related to the order structure (order proportion and average purchase amount) and the consumer’s reactions. From the online retailer’s perspective, we find that whether the online retailer has the motivation to adopt these strategies is related to the delivery cost. We suggest that the online retailer examines members’ order structure and changes in consumers’ purchasing behavior when offering price discount policies.
This paper has both theoretical and managerial implications for managerial practices. First, we propose a limited-time discount or threshold discount under MFS to address the disadvantages of the above two conventional price discount policies. The proposed price discount managerial strategies are efficient in reducing the order frequency of consumers and saving the delivery cost of online retailers. Second, under the limited-time discount policy with order transfers and the threshold discount with order consolidation, the resulting revenue is distributed between the online retailer and consumers to achieve a win–win outcome. Third, this paper can shed light on how to make decisions on offering optimal price discount policies based on consumer shopping behaviors in online retailing.
There are some limitations in this study, which provide opportunities for future research. First, it should be noted that we only examined orders transferred or combined as a whole. In real-world practice, consumers may transfer or combine products they want to purchase in different orders. Although it does not affect the overall policy adoption, it affects the optimal solution. Second, this paper focused on the impact of order structure including the order quantity and the average purchase amount of small orders. The impact of the uncertainty of changes in the prices of consumables on discounting prices and the risk of uncertainties can also be explored in the future. Third, we can also treat the discount threshold as a decision variable and examine the impact of other consumer shopping behaviors in future research.
Author Contributions
Conceptualization, Z.T. and G.H.; methodology, Z.T. and G.H.; software, Z.T.; validation, G.H., T.C.E.C., X.L. and J.D.; formal analysis, Z.T. and X.L.; investigation, Z.T. and G.H.; writing—original draft preparation, Z.T.; writing—review and editing, T.C.E.C., X.L. and J.D.; supervision, G.H.; funding acquisition, G.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 71831001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this paper.
Acknowledgments
We would like to express our gratitude to the anonymous reviewers and editors for their insightful comments on this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Proof of Lemma 1.
Under TFS, the total number of orders is = , the total payment of the order is , and the average payment per order is .
Under MFS, the total number of orders is , the total payment of orders is , and the average payment per unit order is .
From the above, the number of orders will increase by , the total payment will decrease by (or increase by ), and the average payment per unit order will decrease by . □
Proof of Proposition 1.
From Equation (5), we know that is a first-order function of , and the first-order derivative is less than zero. From and , we obtain the optimal discount duration as follows:
The optimal discount duration is the ratio of the minimum time of the limited-time discount duration , i.e., usually one day, to the total limited-time discount cycle time , i.e., usually weekly or monthly.
The first-order condition for the online retailer’s revenue change is
Solving the above equation, we obtain the optimal discount percentage in terms of the wholesale discount as follows:
We further verify that the second-order condition fulfils the following condition
From , we obtain the discount range , which is the maximum value of the online retailer. Plugging and into Equation (5), we obtain:
□
Proof of Proposition 2.
From and , we obtain .
Solving the above equation, we obtain . □
Proof of Proposition 3.
From Equation (9), we know that is a first-order function of , and the first-order derivative is less than zero. From and , we obtain the optimal discount duration as follows:
The optimal discount duration is the ratio of the minimum time of the limited-time discount duration , i.e., usually one day, to the total limited-time discount cycle time , i.e., usually weekly or monthly.
The first-order condition for the retail optimization problem under MFS with limited-time discount is
Solving the above equation, we obtain the optimal limited-time discount .
We further verify that the second-order condition fulfils the following condition
From , we obtain the discount range , which is the maximum value of the online retailer. Plugging and into Equation (5), we obtain:
□
Proof of Proposition 4.
From and , when , then .
Substituting into , we derive .
Similarly, when , then ; when , then and when , then . □
Proof of Proposition 5.
Finding the first and second derivatives of Equation (13), we have
From the Hessian matrix, if , a maximum exists, so it is necessary that . Given
we have and .
Letting , we have .
From and and .
Substituting and into Equation (13), we have
□
Proof of Proposition 6.
From Equation (14) and , we obtain .
Solving the above equation, we obtain , and . □
Proof of Proposition 7.
Finding the first and the second derivatives of Equation (18), we have
Let , , and .
From the Hessian matrix, if , a maximum exists, so it is necessary that . Given
we have and .
Letting , we have .
From and , letting ,, and , we have , and .
Substituting and into Equation (18), we find the online retailer’s optimal added revenue as . □
References
- Zhang, X.; Li, Y.; Zhu, J.; Zhou, X. Pricing game models of hybrid channel supply chain: A strategic consumer behavior perspective. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1177–1195. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, W.; Jiang, M. Human services or non-human services? How online retailers make service decisions. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 1791–1811. [Google Scholar] [CrossRef]
- Retail E-Commerce Sales Worldwide from 2014 to 2026. Available online: https://www.statista.com/statistics/379046/worldwide-retail-e-commerce-sales/ (accessed on 18 March 2023).
- Janda, S.; Trocchia, P.J.; Gwinner, K.P. Consumer perceptions of internet retail service quality. Int. J. Serv. Ind. Manag. 2022, 13, 412–431. [Google Scholar] [CrossRef]
- Trocchia, P.J.; Janda, S. How do consumers evaluate internet retail service quality? J. Serv. Mark. 2003, 17, 243–253. [Google Scholar] [CrossRef]
- Amazon Lost over $7 Billion Last Year by Providing Free Shipping. Available online: https://www.marketplacepulse.com/articles/amazon-lost-over-7-billion-by-providing-free-shipping (accessed on 18 March 2023).
- Niu, B.; Xu, H.; Xie, F. Free shipping in cross-border supply chains considering tax disparity and carrier’s pricing decisions. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102369. [Google Scholar] [CrossRef]
- Fang, Z.; Ho, Y.C.; Tan, X.; Tan, Y. Show me the money: The economic impact of membership-based free shipping programs on e-tailers. Inf. Syst. Res. 2021, 32, 1115–1127. [Google Scholar] [CrossRef]
- Sun, G.; Cavusoglu, H.; Raghunathan, S. Strategic implications of online retail platforms’ membership-based free shipping programs. Inf. Syst. Res. 2023. [Google Scholar] [CrossRef]
- Guo, F.; Liu, Y. The effectiveness of membership-based free shipping: An empirical investigation of consumers’ purchase behaviors and revenue contribution. J. Mark. 2023, 87, 869–888. [Google Scholar] [CrossRef]
- Leenheer, J.; Van Heerde, H.J.; Bijmolt, T.H.; Smidts, A. Do loyalty programs really enhance behavioral loyalty? An empirical analysis accounting for self-selecting members. Int. J. Res. Mark. 2007, 24, 31–47. [Google Scholar] [CrossRef]
- Meyer-Waarden, L. The influence of loyalty programme membership on customer purchase behaviour. Eur. J. Mark. 2008, 42, 87–114. [Google Scholar] [CrossRef]
- Allaway, A.W.; Gooner, R.M.; Berkowitz, D.; Davis, L. Deriving and exploring behavior segments within a retail loyalty card program. Eur. J. Mark. 2006, 40, 1317–1339. [Google Scholar] [CrossRef]
- Xu, L.; Meng, Z. Dynamic analysis of retailers’ paid membership strategy. Discret. Dyn. Nat. Soc. 2021, 2021, 6412614. [Google Scholar] [CrossRef]
- Wen, Z.; Lin, L. Membership free shipping programs: Effect on competition and optimality of member fees. In Proceedings of the 50th Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 4–7 January 2017; pp. 3935–3939. [Google Scholar]
- Sun, G.; Cavusoglu, H.; Raghunathan, S. Value of membership-based free shipping in online retailing: Impact of upstream pricing model. Prod. Oper. Manag. 2022, 31, 4131–4153. [Google Scholar] [CrossRef]
- Shao, X.-F. Free or calculated shipping: Impact of delivery cost on supply chains moving to online retailing. Int. J. Prod. Econ. 2017, 191, 267–277. [Google Scholar] [CrossRef]
- Hua, Z.; Hou, H.; Bian, Y. Optimal shipping strategy and return service charge under no-reason return policy in online retailing. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 3189–3206. [Google Scholar] [CrossRef]
- Sainathan, A. Customer differentiation with shipping as an ancillary service? Free service, prioritization, and strategic delay. Decis. Sci. 2018, 49, 690–727. [Google Scholar] [CrossRef]
- Li, G.; Sheng, L.; Zhan, D. Designing shipping policies with top-up options to qualify for free delivery. Prod. Oper. Manag. 2023, 32, 2704–2722. [Google Scholar] [CrossRef]
- Lewis, M. The effect of shipping fees on customer acquisition, customer retention, and purchase quantities. J. Retail. 2006, 82, 13–23. [Google Scholar] [CrossRef]
- Huang, W.-H.; Cheng, Y.-C. Threshold free shipping policies for internet shoppers. Transp. Res. Part A Policy Pract. 2015, 82A, 193–203. [Google Scholar] [CrossRef]
- Li, C.; Chu, M.; Zhou, C.; Xie, W. Is it always advantageous to add-on item recommendation service with a contingent free shipping policy in platform retailing? Electron. Commer. Res. Appl. 2019, 37, 100883. [Google Scholar] [CrossRef]
- Nouri-Harzvili, M.; Hosseini-Motlagh, S.M. Dynamic discount pricing in online retail systems: Effects of post-discount dynamic forces. Expert Syst. Appl. 2023, 232, 120864. [Google Scholar] [CrossRef]
- Hua, G.; Wang, S.; Cheng, T.C.E. Optimal order lot sizing and pricing with free shipping. Eur. J. Oper. Res. 2012, 218, 435–441. [Google Scholar] [CrossRef]
- Hua, G.; Wang, S.; Cheng, T.C.E. Optimal pricing and order quantity for the newsvendor problem with free shipping. Int. J. Prod. Econ. 2012, 135, 162–169. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhou, L.; Fan, T.; Ieromonachou, P. Joint procurement and pricing of fresh produce for multiple retailers with a quantity discount contract. Transp. Res. Part E Logist. Transp. Rev. 2019, 130, 16–36. [Google Scholar] [CrossRef]
- Kwon, Y.W.; Sheu, J.B.; Yoo, S.H. Quadratic quantity discount contract under price-dependent demand and consumer returns. Transp. Res. Part E Logist. Transp. Rev. 2022, 164, 102756. [Google Scholar] [CrossRef]
- Sari, D.P.; Rusdiansyah, A.; Huang, L. Models of joint economic lot-sizing problem with time-based temporary price discounts. Int. J. Prod. Econ. 2012, 139, 145–154. [Google Scholar] [CrossRef]
- Ma, S.; Jemai, Z.; Bai, Q. Optimal pricing and ordering decisions for a retailer using multiple discounts. Eur. J. Oper. Res. 2022, 299, 1177–1192. [Google Scholar] [CrossRef]
- Xu, X.; Chen, C.; Zou, B.; Wang, H.; Li, Z. Shipping before order making: Optimal shipping quantity and pricing decisions under uncertain demand. Transp. Res. Part E Logist. Transp. Rev. 2023, 169, 102986. [Google Scholar] [CrossRef]
- Ji, G.; Fu, T.; Li, S. Optimal selling format considering price discount strategy in live-streaming commerce. Eur. J. Oper. Res. 2023, 309, 529–544. [Google Scholar] [CrossRef]
- Sheehan, D.; Hardesty, D.M.; Ziegler, A.H.; Chen, H.A. Consumer reactions to price discounts across online shopping experiences. J. Retail. Consum. Serv. 2019, 51, 129–138. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.; Bo, R.; Meng, F.; Xu, Y.; Li, P. Increases or discounts: Price strategies based on customers’ patience times. Eur. J. Oper. Res. 2023, 305, 722–737. [Google Scholar] [CrossRef]
- Li, C.; Chu, M.; Zhou, C.; Zhao, L. Two-period discount pricing strategies for an e-commerce platform with strategic consumers. Comput. Ind. Eng. 2020, 147, 106640. [Google Scholar] [CrossRef]
- Radhi, M. Service decisions in a two-echelon retailing system with customer returns. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 1219–1242. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, J.; Zhou, C.; Ren, Y. Strategic business mode choices for e-commerce platforms under brand competition. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 1769–1790. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).