Integrating Non-Positional Numbering Systems into E-Commerce Platforms: A Novel Approach to Enhance System Fault Tolerance

Abstract

In the dynamic landscape of electronic commerce, the robustness of platforms is a critical determinant of operational continuity and trustworthiness, necessitating innovative approaches to fault tolerance. This study pioneers an advanced strategy for enhancing fault tolerance in e-commerce systems, utilizing non-positional numbering systems (NPNS) inspired by the mathematical robustness of the Chinese Remainder Theorem (CRT). Traditional systems rely heavily on positional numbering, which, despite its ubiquity, harbors limitations in flexibility and resilience against computational errors and system faults. In contrast, NPNS, characterized by their independence, equitability, and residue independence, introduce a transformative potential for system architecture, significantly increasing resistance to disruptions and computational inaccuracies. Our discourse extends beyond theoretical implications, delving into practical applications within contemporary e-commerce platforms. We introduce and elaborate on new terminologies, concepts, and a sophisticated classification system for fault-tolerance mechanisms within the framework of NPNS. This nuanced approach not only consolidates understanding but also identifies underexplored pathways for resilience in digital commerce infrastructure. Furthermore, this research highlights the empirical significance of adopting NPNS, offering a methodologically sound and innovative avenue to safeguard against system vulnerabilities. By integrating NPNS, platforms can achieve enhanced levels of redundancy and fault tolerance, essential for maintaining operational integrity in the face of unforeseen system failures. This integration signals a paradigm shift, emphasizing proactive fault mitigation strategies over reactive measures. Conclusively, this study serves as a seminal reference point for subsequent scholarly endeavors, advocating for a shift towards NPNS in e-commerce platforms. The practical adaptations suggested herein are poised to redefine stakeholders’ approach to system reliability, instigating a new era of confidence in e-commerce engagements.

1. Introduction

In the rapidly advancing landscape of electronic commerce (e-commerce), system reliability and fault tolerance are becoming paramount for delivering seamless user experiences and maintaining trust [1,2,3]. As digital transactions and interactions via e-commerce platforms proliferate, ensuring the fault tolerance of underlying computing systems becomes indispensable, especially given their ubiquity in sectors like finance, retail, and services, where system hitches could translate to substantial financial or reputational losses [4,5,6].

Notwithstanding the current strides in system reliability, there exists an identifiable research gap [2,7]: the need for systems that can sustain increasingly complex e-commerce transactions with more considerable fault tolerance than that provided by conventional positional systems. Hence, this paper introduces a novel, potentially transformative approach to addressing this lacuna by integrating non-positional numbering systems (NPNS) based on the Chinese Remainder Theorem (CRT) into the fabric of e-commerce computing systems [8].

Current e-commerce systems predominantly rely on traditional positional numbering, including binary and decimal forms, which have shaped digital commerce’s foundational architecture [9,10]. However, as platforms face burgeoning transactional demands and heightened expectations for zero-error operations, these systems reveal limitations in their ability to adapt and maintain fault tolerance [11,12]. NPNS emerge as a promising alternative, touting attributes such as independence, equality, and residue independence [13,14]. These features not only differentiate them from their positional counterparts but also poise NPNS as pivotal in the re-engineering of e-commerce platforms, potentially enhancing their resilience and reducing vulnerability to disruptions.

1.1. Specificity of E-Commerce Platforms

E-commerce platforms represent a unique ecosystem within the digital landscape, characterized by their high transactional volumes, the necessity for real-time user interaction, and the multifaceted nature of these transactions [15,16]. Unlike other digital systems, e-commerce operations are not only about processing large quantities of data but also about maintaining seamless, uninterrupted user engagement. Any disruption, even transient, can fracture consumer trust and translate into significant competitive disadvantages and revenue losses [17].

The singular nature of e-commerce comes into sharper focus considering the diversity of transactions, encompassing B2B, B2C, C2C, and more recently, D2C models [18]. Each transaction type poses distinct challenges in data processing, security, and fault tolerance [19,20]. Additionally, e-commerce platforms interface with numerous third-party services, such as payment gateways, digital wallets, and courier services [21,22]. This interdependence amplifies the complexity of maintaining high reliability and fault tolerance due to the increased risk of cascading failures [23].

Moreover, the competitive nature of the e-commerce industry has led to an unprecedented focus on customer experience, necessitating platforms to ensure zero-error operations and 24/7 availability. The intolerance for downtime and the expectation for instantaneous processing and grievance redressal are far more pronounced than in many other sectors [24].

This environment, where high stakes, an immense scale, and an extraordinary rate of interactions converge, justifies the concentrated examination of e-commerce platforms within the fault-tolerance discourse. Traditional fault-tolerance mechanisms, while somewhat effective, do not fully meet these platforms’ unique demands, necessitating novel approaches attuned to their specific operational dynamics [20,25]. It is within this context that our study proposes the integration of NPNS to enhance the resilience and reliability of e-commerce platforms.

1.2. Fault Tolerance in E-Commerce: Defining the Need and Scope

Following the uniqueness established in e-commerce systems, a critical aspect that comes to the forefront is fault tolerance [14,23]. Fault tolerance in the context of e-commerce is the built-in ability of a system to robustly handle both the internal inconsistencies, like software bugs or hardware failures, and external pressures, such as surges in user traffic or targeted cyber-attacks, thereby ensuring uninterrupted and secure service [23]. For instance, during high-volume events like Black Friday sales, systems must handle enormous, erratic transaction loads without faltering, maintaining data integrity and user trust [26,27].

Existing systems have ingrained limitations impacting their fault tolerance. Traditional architectures, reliant on positional numbering and binary logic, are ill-equipped for the dynamism and scale of modern high-reliability computing [28,29,30]. They struggle with issues like “single points of failure”, where one component’s malfunction can halt entire operations, leading to cascading consequences for interconnected services [29,30]. Furthermore, they often fail in situations requiring real-time error correction and recovery, crucial for continuous transactional activities, customer satisfaction, and retention [31].

Addressing these limitations necessitates a reimagining of system design, moving beyond incremental adjustments to existing models. The incorporation of NPNS based on the CRT offers a paradigm shift [32,33]. By leveraging the CRT’s mathematical robustness, e-commerce platforms can achieve enhanced fault tolerance through distributed processing capabilities, reducing the systemic reliance on any single component and enabling real-time error mitigation [28,29,30].

Moreover, fault tolerance, particularly in e-commerce, is not just about preventing service disruptions but also about safeguarding data integrity, user privacy, and overall system security [29,34]. Cybersecurity breaches, a notorious issue, can compromise user data, eroding the trust that takes years to build. Here, the proposed CRT-based NPNS demonstrate superiority by providing a framework that inherently disperses information, making it less susceptible to traditional hacking methods [34,35].

The imperative for such advanced fault-tolerance strategies in e-commerce is unequivocal. It is not merely about sustaining operations; it is about preserving an ecosystem’s economic viability, consumer trust, and market competitiveness. The proposed integration of NPNS represents a frontier in this regard, promising a transformative approach to systemic resilience in the digital commerce arena. Thus, this research does not just contribute a novel solution—it advocates for a fundamental shift in how we conceptualize and ensure reliability within the pulsating realm of e-commerce.

1.3. Article Structure

This manuscript is organized into distinct sections, each adding a unique layer to the overarching narrative. Post this introduction, the subsequent section elucidates the theoretical underpinnings of NPNS in the context of e-commerce platforms. Following that, new concepts and definitions of fault tolerance are unveiled, setting the stage for the in-depth exploration of the topic. An innovative classification to achieve fault tolerance in NPNS-based e-commerce platforms is then presented, offering clarity and direction for subsequent research endeavors. A case study highlighting the superiority of CRT-based platforms over traditional architectures is detailed subsequently. The penultimate segment forecasts potential research trajectories, and the concluding section encapsulates the core revelations and their broader implications.

2. State of the Art

The domain of electronic commerce (e-commerce) has been subject to significant advancements over the past decades, given its pivotal role in the global economy and its constant interplay with evolving digital technologies. One of the primary areas of concern in the domain, particularly given the surging online transactions, is ensuring seamless system reliability and fault tolerance.

The foundational structure of e-commerce dates back to the late 20th century, with the evolution of electronic data interchange replacing traditional mail and fax [36]. Over the years, the e-commerce landscape has morphed, with the integration of multimedia content, personalized user experiences, and most notably, mobile commerce [37]. The core principles, although refined, have maintained their integrity throughout this evolution, ensuring a sustainable and user-centric digital trading environment.

The need for reliable and fault-tolerant systems in e-commerce is not a new concept. In fact, the principles of fault tolerance have been applied in various computing systems, from mission-critical aerospace systems to online banking and e-commerce systems [38]. Recent advancements have seen the incorporation of cloud-based solutions, decentralized platforms, and artificial intelligence for the prediction and mitigation of potential system faults, ensuring uninterrupted service delivery [39].

While NPNS present a relatively fresh perspective in the context of e-commerce platforms, their mathematical foundations have been explored extensively. The CRT, which serves as the cornerstone of NPNS, has historical significance in number theory and has seen applications in coding theory and cryptography [40]. The integration of NPNS into e-commerce platforms to enhance fault tolerance is a promising yet nascent area of exploration, bringing together mathematical rigor and practical computing applications.

Redundancy mechanisms, whether structural, informational, or functional, have been leveraged to ensure system reliability. Especially in e-commerce, where a single system glitch can cost millions in revenue, redundancy mechanisms serve as a critical backbone. Techniques like data mirroring, load balancing, and distributed databases have been vital in ensuring that e-commerce platforms remain functional even in the face of hardware failures or data corruption [41].

2.1. Literature Review in the Field of Reliability and Fault Tolerance

The research literature provides considerable insights into various aspects of fault tolerance in computing systems. However, the application of NPNS, especially based on the CRT, as a mechanism for enhancing fault tolerance is a relatively unexplored area.

• Pradhan, in his book, provides an exhaustive discussion on designing computer systems that are resistant to different types of faults, emphasizing hardware and software redundancy mechanisms [42]. Despite providing comprehensive coverage, the book does not consider alternative numbering systems such as NPNS.
• In the book Fault-Tolerant Systems, Koren and Krishna discuss the fundamentals of fault tolerance, including definitions, fault types, and fault-tolerance measures, from a systems perspective [23]. Despite providing an excellent foundation, the authors do not explore the use of NPNS.
• Shooman explores various strategies for achieving reliability in computer systems and networks, with a focus on modeling techniques [43]. However, the work does not cover the use of NPNS as a strategy for achieving fault tolerance.
• Avizienis et al. provide a thorough overview of basic concepts and terminologies of fault tolerance in their landmark paper [44]. However, they do not delve into the advantages of NPNS in enhancing fault tolerance.
• Siewiorek and Swarz, in their book Reliable Computer Systems, provide a comprehensive examination of fault tolerance and system reliability, with detailed discussions on redundancy and error-correction methods [45]. However, they do not consider NPNS in their discussions.
• Trivedi provides a detailed explanation of various quantitative reliability and performance models for computer systems [46]. Although valuable, this work does not explore the impact of different numbering systems on fault tolerance.
• In Introduction to Reliable and Secure Distributed Programming, Cachin, Guerraoui, and Rodrigues address reliable distributed programming, including the incorporation of fault tolerance [47]. However, they do not consider NPNS as a potential approach for enhancing fault tolerance.

The literature review reveals a gap in the existing body of knowledge concerning the application of NPNS as a strategy for enhancing fault tolerance in computing systems. While significant work has been conducted in the broader field of fault tolerance, the specific potential of NPNS remains underexplored. This paper aims to fill this gap, presenting novel concepts, classifications, and a case study that demonstrate the potential of NPNS for enhancing fault tolerance in computing systems.

2.2. Literature Review in Applying Residue Number Systems for Reliability and Fault Tolerance

These recent publications present further evidence of the emerging research interest in applying residue number systems (RNS) for fault tolerance:

• Phalakarn, K.; Surarerks, A. [48] propose a novel approach to constructing a redundant RNS (RRNS) using redundant residue representations. This RRNS construction is designed to enhance error detection and correction, improving fault tolerance. However, this approach results in higher costs for performing addition and multiplication operations. While the authors acknowledge the need for further investigation to improve the efficiency of their proposed RRNS, the study does not explore the inherent properties of NPNS such as RNS for enhancing fault tolerance in a broader context.
• Res. [49] offer an innovative approach by incorporating AN codes into RRNS to improve reliability in neural networks. Despite its significant contribution to improving the redundancy and reliability of neural networks, the focus of this study is highly application-specific. The broader utilization of RNS for enhancing fault tolerance in various computing systems is not explored.
• Huang, T.-C. [50] propose a systematic approach to design a low-power, compact, reliable neural network based on RRNS. This research contributes significantly to self-checking in neural networks, reducing power, time, and area costs. However, it does not comprehensively address how the general properties of NPNS can be used to enhance fault tolerance in computing systems.

The commonality in these works is the focus on specific applications, without broader consideration of the principles of NPNS for enhancing fault tolerance. Our study bridges this gap by comprehensively examining the inherent properties of NPNS and illustrating how they can be applied to enhance fault tolerance in a case study.

Continuing with the analysis of the recent literature, the following works have further contributed to the understanding and application of RNS:

• Mohan’s monograph Residue Number Systems provides a comprehensive overview of RNS, including a detailed explanation of core and quotient functions, CRT, and large integer operations [30]. It also outlines applications to practical communication systems and cryptography, such as FIR filters and elliptic curve cryptography. However, the text mainly serves as a foundation and does not delve into the specific use of RNS for enhancing fault tolerance.
• The paper [51] offers a theoretical foundation for the cryptographic protection of color image pixels using RNS, highlighting the speed increase of algorithm operations. While the paper presents valuable insights on using RNS for cryptographic protection, the application of RNS for fault tolerance is not explored.
• Hiasat, A. [52] broaden the classical moduli sets for designing residue-based arithmetic components, presenting multiplicative inverses and introducing general frameworks for component design. This work expands the available options for designing an RNS processor, contributing significantly to the versatility of RNS. However, the paper does not explicitly address the use of these frameworks in enhancing system fault tolerance.

In our prior work, we have delved deeper into the utilization of RNS for fault tolerance:

• Krasnobayev, V.A.; Koshman, S.A. [53] proposed a time-efficient method for diagnosing data errors in RNS-based data, thereby increasing the efficiency of diagnosis. This method, thereby, contributed to enhancing the overall efficiency of computing systems with non-positional code structures in RNS.
• Krasnobayev, V.A. et al. [54] presented detailed a method for executing the arithmetic operation of the modulo addition of two numbers in RNS, thereby improving the efficiency of RNS operations.

Our current work further builds on these foundations, focusing on the inherent properties of NPNS and their applicability in enhancing fault tolerance in computing systems.

In conclusion, the e-commerce domain, while mature in many aspects, still offers fertile ground for research, especially in the realm of fault tolerance and system reliability. With the continued integration of advanced mathematical models like NPNS and the incessant demand for 24/7 platform availability, the interplay between theory and practice in this domain will likely remain an exciting area of exploration for years to come.

3. Research Design

This research project is firmly situated within the methodological framework of applied computational mathematics and systems engineering, specifically tailored for the complex and dynamic field of electronic commerce (e-commerce). The selection of e-commerce platforms, as the central focus for applying the proposed advanced fault-tolerance strategy, is anchored in several critical considerations, reflecting both the sector’s unique challenges and its transformative role in global economics and consumer behavior.

3.1. Rationale for E-Commerce Focus

E-commerce platforms represent a nexus of multifaceted computational processes, high-volume transactional activities, and stringent requirements for reliability and user trust [55]. These systems are characterized by their need to support a vast array of online transactions, manage colossal databases, ensure user data security, and accommodate surges in user demand, particularly during peak shopping periods [21].

The realm of e-commerce has been undergoing rapid evolution, necessitating platforms that are not only robust under normal operational parameters but also resilient in the face of unexpected disruptions or malicious cyber-threats. The recent surge in online retail, accelerated by global shifts in shopping behaviors, further underscores the urgency of fortifying the e-commerce infrastructure [21,55]. In light of these factors, e-commerce platforms present an ideal case study for exploring the efficacy of innovative fault-tolerance strategies, offering a context in which computational theory and market realities intersect.

3.2. Adaptation of Methodology to E-Commerce Specifics

The unique challenges and operational dynamics of e-commerce necessitate a tailored approach to developing fault-tolerant systems. Within this context, our research introduces structural schemes of a Fault-Tolerant Computing System in Residue Classes (FTCSRC) [8,13], exploring its operation in various modes to ensure resilience and continuity in e-commerce applications. This exploration becomes indispensable when acknowledging the e-commerce sector’s idiosyncrasies, such as its non-negotiable demand for uptime, the necessity to handle vast transactional volumes, and the imperativeness of data integrity and security [9,26].

Our methodology is particularly attentive to the operational pressures exerted on e-commerce platforms. We delve into two specific modes of system functioning: the first mode without degradation (pristine operational state) and the second with degradation (following a failure incident). These modes are reflective of real-world e-commerce operational scenarios, where systems must maintain service continuity in both optimal conditions and periods of strain or partial failure.

Within each mode, we scrutinize multiple failure possibilities of one or more computational modules—a critical aspect considering the diversity of interactions and the plethora of backend processes inherent in e-commerce transactions. Each failure scenario corresponds to realistic challenges e-commerce platforms face, such as surges during high-traffic periods, security threats, or hardware malfunctions, emphasizing the relevance and applicability of our research to actual industry circumstances.

For each operational mode and system degradation level, we propose specific parameters of the FTCSRC, grounded in the RNS, that uphold the integrity and reliability of the computational environment. This nuanced approach recognizes that e-commerce systems require graduated responses to issues, balancing resource allocation, system stability, and performance maintenance, particularly in degraded states.

The proposed parameters and subsequent reliability strategies are derived from a detailed examination of e-commerce platform requirements. These include real-time transaction processing, data encryption for security, inventory management interfacing, and user experience considerations, each placing distinct demands on the system.

3.3. Basic Properties of the RNS

In the RNS, each number is represented as several low-order positional numbers, which are the remainders from dividing the original number by mutually primed bases [56]. Unlike the conventional binary positional system, where operations such as the addition of two numbers are carried out sequentially by digits, starting from the least significant, the RNS allows for the parallelization of this process [57]. All operations over the remainders for each base are conducted separately and independently, making them easy and fast due to their low bit-depth [13].

The low bit-depth of the remainders facilitates the implementation of table-based arithmetic, where the operation’s result is not computed every time. Instead, it is calculated once, stored in a memory device, and then retrieved as needed [58]. Therefore, an operation in RNS with table-based arithmetic is performed within a single period of the synchronizing frequency (machine cycle). However, issues may arise with number representation range overflow and rounding results, which have demanded substantial mathematical effort and intellect to address.

The table method in RNS enables not only the execution of basic operations but also complex functions, all within a single machine cycle [58]. This leads to one of the paradoxical properties of RNS: the effective performance of a modular computer system can be significantly, even exponentially, higher than a positional system with the same clock frequency [56]. Indeed, an operation that a typical system performs in 100 cycles, an RNS system executes in a single cycle, naturally resulting in a 100-fold increase in effective performance under otherwise equal conditions.

Another remarkable property of RNS is the introduction of additional redundancy [30,59]. By adding supplementary bases to the main RNS information bases, we introduce additional informational redundancy into the system. This redundancy enables error detection and correction during operation execution, which is one of the most significant advantages of RNS codes (arithmetical code property) over all systems in the positional number system [29,30]. No existing system in the positional number system allows for error detection, let alone correction, during arithmetic operation execution [28,30,32]. On the contrary, in an arithmetic device of a system in the positional number system, once an error occurs, it propagates uncontrollably. As a result, error control and correction in systems operating in traditional positional number systems (parity check, redundant coding, majority voting, etc.) are ensured only in data storage and transmission systems. Arithmetic-logic devices—a major source of system failures and errors—remain uncontrolled [29].

In this article, research methods related to number theory (comparison theory section) and the results of the “Chinese Remainder Theorem” were used.

3.4. CRT Explanation: Theoretical Insights into the Chinese Remainder Theorem

The CRT is a pivotal mathematical construct with profound implications in various computational realms [40], particularly in constructing fault-tolerant systems within electronic commerce infrastructures. To comprehend the versatility and applicability of CRT in enhancing system robustness, it is imperative to first unravel its fundamental principles and operational logic.

At its core, the CRT deals with solving systems of simultaneous congruences by exploiting the unique properties of modular arithmetic. The theorem posits that for any system of congruences, where the moduli are pairwise coprime (i.e., the greatest common divisor of each pair is one), there exists a unique solution modulo the product of these moduli. This foundational aspect of CRT allows for the reconstruction of a unique composite number from its residues modulo several other numbers.

Expressed more formally, suppose we have $n$ linear congruences as follows [40]:

$$\begin{array}{l}\begin{array}{l}x\equiv a_1\left(\mathrm{mod}{m}_1\right),\hfill \\ x\equiv a_2\left(\mathrm{mod}{m}_2\right),\hfill \\ \dots \hfill \end{array}\\ x\equiv a_n\left(\mathrm{mod}{m}_n\right),\end{array}$$

where $m_1,m_2,\dots ,m_n$ are pairwise coprime. CRT guarantees that there is a unique solution $x$ modulo $M$ (where $M=m_1\cdot m_2\cdot \dots \cdot m_n$) that satisfies all these congruences concurrently.

In the context of electronic commerce systems, the CRT’s capability to piece together information from different modular domains facilitates a high level of fault tolerance. Specifically, the theorem supports the establishment of systems where operations continue unimpeded, even with partial data, since original data can be reconstructed using the residues [13,14]. This inherent redundancy is a bulwark against data loss, a critical attribute for e-commerce platforms where transactional integrity and continuity are paramount.

Furthermore, the CRT finds profound utility in cryptographic communications, an integral element of secure digital transactions [34,60]. It undergirds several cryptographic protocols by enabling secure information transmission over public channels and plays a significant role in algorithms for public key cryptography, such as RSA [35,60].

By leveraging the mathematical robustness and reconstructive capability of the CRT, e-commerce platforms can significantly enhance their computational efficiency, fault tolerance, and data security. This resilience, especially in high-transaction environments, underscores CRT’s importance and growing relevance in advanced e-commerce system architectures [61,62,63].

4. Experimental Section

As an experiment, this study comprehensively investigates the fault-tolerant operation of a CS in the RNS, defined by the information bases $m_1=3$, $m_2=4$, $m_3=5$, and $m_4=7$ and a single control base $m_k=m_5=23$. The fault tolerance of the CS is achieved using the primary properties of RNS, an active fault-tolerance method, and a procedure of progressive degradation. The CS’s fault-tolerance level in RNS is enhanced by reducing the calculation accuracy. The CS allows for the execution of specified computational functions after failures, either without degrading performance metrics or by reducing the calculation accuracy.

Analysis of a fault-tolerant CS functioning in RNS, defined by the information bases $m_1=3$, $m_2=4$, $m_3=5$, and $m_4=7$ and a single control base $m_k=m_5=23$, revealed that the use of RNS ensures more operable CS states with diminished quality (a higher number of degradation levels) than the number of operable CS states in the positional number system. In this example, a specific metric serves to quantify and compare the fault tolerance of the CS.

In general, a CS in RNS with $n$ informational and one control base includes the following elements (Figure 1):

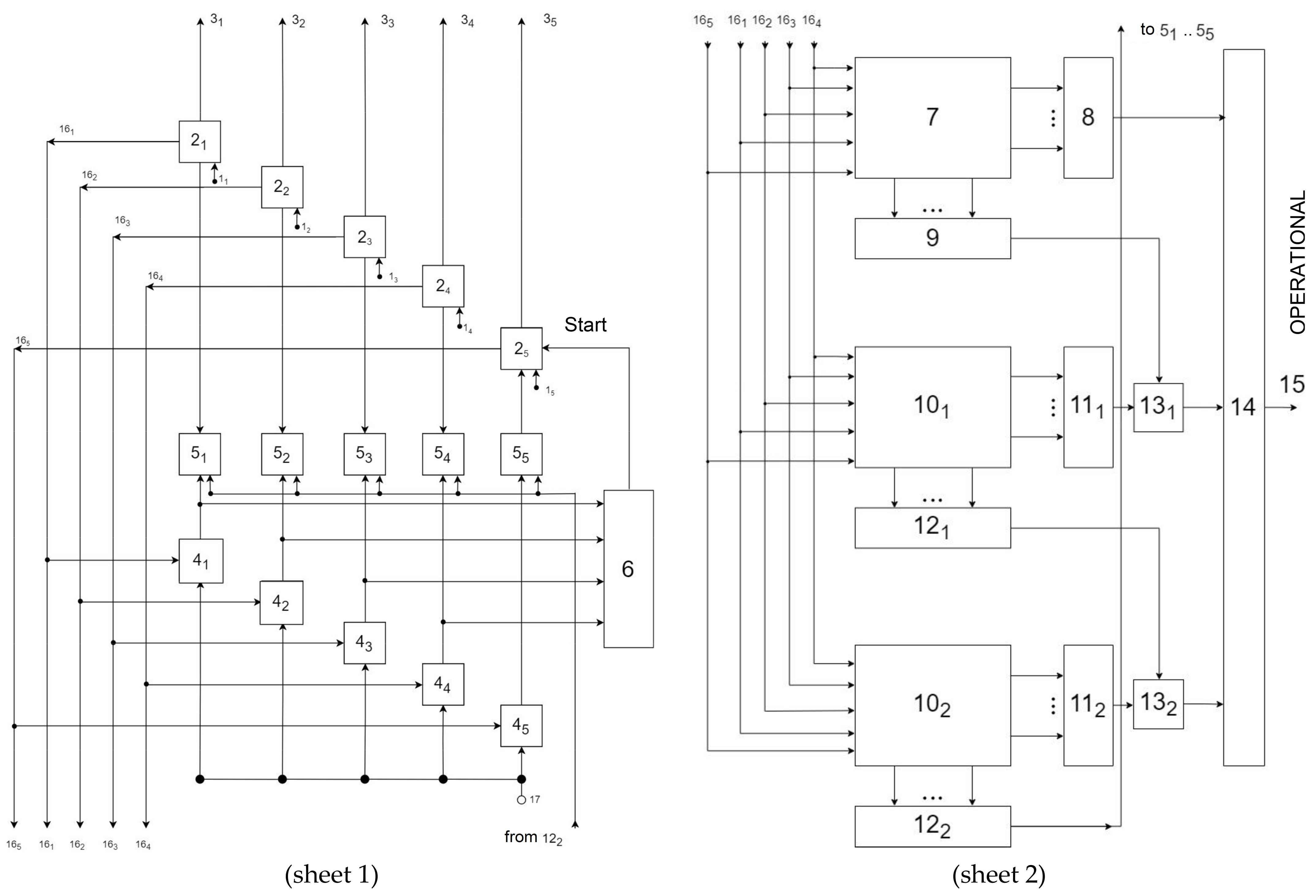
• $1_1,\dots ,1_{n+1}$: the first (informational) CS inputs;
• $2_1,\dots ,2_n$: informational bases;
• $2_{n+1}$: control base;
• $3_1,\dots ,3_{n+1}$: informational CS outputs;
• $4_1,\dots ,4_{n+1}$: the first group of elements AND;
• $5_1,\dots ,5_{n+1}$: the first group of OR elements;
• $6$: the first OR element;
• $7$: decoder (device for binary to unary code conversion);
• $8$: the second OR element;
• $9$: the third OR element;
• ${10}_1,\dots ,{10}_k$: group of decoders;
• ${11}_1,\dots ,{11}_k$: second group of OR elements;
• ${12}_1,\dots ,{12}_k$: third group of OR elements;
• ${13}_1,\dots ,{13}_k$: second group of elements AND;
• $14$: the fourth OR element;
• $15$: CS operational output in RNS;
• ${16}_1,\dots ,{16}_{n+1}$: CS control block outputs in RNS;
• $17$: device’s clock input.

The Figure 1 presents a block diagram of the fault-tolerant CS in the RNS, characterized by given informational bases and a single control basis. This CS operates with two levels of degradation, each defined by a specific range. The conditions for degradation are determined by the number of operational computing elements for each degradation level. The need for two sheets is to comprehensively represent the intricate scheme with a multitude of computational elements, ensuring clarity and precision in presentation.

A CS in RNS can operate in two modes. We will explore each mode for an arbitrary RNS with $n$ informational and one ($k=1$) control base.

The first mode

The first mode is a non-degradation mode of fault-tolerant CS operation, i.e., without a decrease in calculation accuracy (data processing is carried out in the information range $[0,D_0)$). This mode is achieved under the following conditions:

• All informational $2_1{..2}_n$ and control $2_{n+1}$ computational tracks (CTs) are operational;
• All informational $2_1{..2}_n$ CTs are operational, and the control $2_{n+1}$ CT has failed;
• The control $2_{n+1}$ CT is operational, and a part $r$ of informational CTs out of a total $n$ $2_1{..2}_n$ CTs have failed, where condition (1) is met:

$$m_{n+1}\ge {\displaystyle \prod _{i=1}^r{m}_l{}_{{}_i}},$$

(1)

where $r$ is the number of RNS bases.

Calculations will be carried out in the operational information range $D_0$, where $D_0={\displaystyle \prod _{i=1}^n{m}_i}$. The number of output buses ${16}_1{\dots 16}_{n+1}$ of the CT control blocks $2_1{\dots 2}_{n+1}$ of the fault-tolerant CS equals the value of $D_0$.

The presence of a signal on the $i$-th originating bus (a unit in the binary code of the CT control block states $2_1{\dots 2}_{n+1}$) conditions the failure of the $i$-th CT.

The decoder $7$ converts the original binary code of CT control block states into a unary code. The first group of decoder outputs ${10}_1,\dots ,{10}_k$, which combine buses for which the original binary code of CT states defines the operational state of the fault-tolerant CS, are connected through OR elements $8$ and $14$ to the “OPERATIONAL” output $15$ of the CS in RNS.

The control signal for the non-degradation operation mode is generated at the output of the OR element $8$. The signal or signals of the failure of the $i$-th CT (or a set of computational tracks $2_1{\dots 2}_{n+1}$) also arrive at the first inputs of the AND elements $4_1{\dots 4}_{n+1}$, to the second inputs of which the clock bus signal $17$ arrives. Through the open AND element (or AND elements $4_1{..4}_n$), the signal (or signals) through the OR element $6$ activates (“Start”) the control CT $2_{n+1}$ on the base $m_k$, and simultaneously, the original signal (or signals) of the AND element (AND elements $4_1{\dots 4}_{n+1}$) through the corresponding OR element (or elements) $5_1{\dots 5}_{n+1}$ disables the corresponding CT (or CTs) $2_1{\dots 2}_{n+1}$. If there is a set of inoperative informational computational tracks $2_1{\dots 2}_{n+1}$ and condition (2) is not met, then the fault-tolerant CS is considered to have failed.

The second mode

The second mode of the fault-tolerant CS operation is the mode with a degradation of the system’s quality, i.e., a decrease in calculation accuracy.

The control signal for the first ($k=1$) level of degradation is formed at the output of the OR element $9$. The control signal for the ($i+1$)-th level of degradation is formed at the output of the OR element ${12}_k$.

Let us assume the $j$-th level of degradation is implemented. In this case, the original signal from the ($j-1$)-th OR element ${12}_{j-1}$ serves as a control signal for the CS in the degradation mode.

Under these conditions, and assuming that condition (2) is met:

$${\displaystyle \prod _{z=1}^{Q_j}{m}_{i_z}}\ge D_j,$$

(2)

where $Q$ is the number of RNS bases, calculations will be performed in the numerical range (0, $D_j$].

If condition (2) is met, then the signal from the decoder output ${10}_j$ through the OR element ${11}_j$, the open AND element ${13}_j$, and the OR element $14$ is sent to the “OPERATIONAL” output $15$ of the CS. Simultaneously, the signal (or signals) from the output buses ${16}_1{..16}_{n+1}$ of the control blocks, corresponding to the CTs $2_1{\dots 2}_{n+1}$ of the CS, through the corresponding open AND elements $4$ and the corresponding OR elements $5$, disable the corresponding CTs among the possible CTs $2_1{\dots 2}_{n+1}$.

If condition (2) is not met, then the signal from the second group of decoder outputs ${10}_j$ through the OR element ${12}_j$ opens the ($i+1$)-th AND element ${11}_{k+1}$. In other words, this signal serves as a control signal for the ($i+1$)-th level of degradation.

The block diagram of the fault-tolerant CS in the RNS is represented in the Figure 1 (sheets 1, 2), which is defined by the information bases $m_1=3$, $m_2=4$, $m_3=5$, and $m_4=7$ and one control base $m_k=m_5=23$ of the RNS. Let us consider an example of a specific implementation of the CS operation process in the RNS (refer to the figure).

Suppose we consider that the CS has two ($k=2$) levels of degradation ($j=1,2$) with the corresponding adopted values $D_1=139$ and $D_2=61$.

For this RNS, we have $D_0={\displaystyle \prod _{i=1}^4{m}_i}=420$, i.e., the information range in which calculations are performed is [0, $D_0$). For the first level of degradation ($j=1$), this range is [0, 139), and for the second level of degradation ($j=2$), this range is [0, 61).

The degradation conditions for each level (see condition (2)) are defined as follows: for the first level of degradation, ${\displaystyle \prod _{z=1}^{Q_1}{m}_{i_z}}\ge D_1$, and for the second level of degradation, ${\displaystyle \prod _{z=1}^{Q_2}{m}_{i_z}}\ge D_2$. In general, the value of $Q$ is the number of operational CTs of the CS.

For the information computation range (zero level of degradation), the condition for normal operation of the CS is determined (see condition (1)) by the relationship $m_{n+1}=23\ge {\displaystyle \prod _{i=1}^r{m}_l{}_{{}_i}}$, where $r$ is the number of operational information CTs.

The operational conditions of the Fault-Tolerant System (FTS) in the RNS are tabulated below. Herein, the variable $\mathsf{\Omega }$ represents the quantity of functional states of the computational modules (CMs), indicated by the “+” symbol in columns 4, 6, and 8, respectively, corresponding to the FTS operation modes.

In the first mode ($j=0$), the non-degraded operational mode of the FTS, the number of functional states ${\mathsf{\Omega }}_0=10$ is equivalent to the quantity of initial buses from the first group of outputs from the decoder 7 (i.e., the number of “+” symbols in column 4).

In the second mode of operation, the first degradation level ($j=1$), the number of functional states ${\mathsf{\Omega }}_1=14$ is equivalent to the quantity of initial buses from the first group of outputs of the decoder group ${10}_1$ (i.e., the number of “+” symbols in column 6).

For the third mode of operation, the second degradation level ($j=2$), the quantity of functional states ${\mathsf{\Omega }}_2=19$ is equivalent to the quantity of initial buses from the first group of outputs of the decoder group 10${}_2$ (i.e., the number of “+” symbols in column 8).

The second group of outputs from decoders 7, 10${}_1$, and 10${}_2$, which unify buses with numbers corresponding to non-functional states of the FTS CMs (indicated by the “-” symbol in columns 4, 6, and 8), are connected to the inputs of the OR elements 9, 12${}_1$, and 12${}_2$, respectively.

4.1. The First Mode: “Non-Degraded Mode of Operation”

Let us examine the first mode of operation for the Fault-Tolerant System (FTS)—the non-degraded operational mode.

Variant 1.1 All computational modules (CMs) 2${}_1$ to 2${}_5$ are operational. The binary code representing the states of the CMs, 00000, is sent from the outputs of CMs 2${}_1$ to 2${}_5$, via buses 16${}_1$ to 16${}_5$, to the input of the decoder 7. The signal from the zeroth output is then passed through the OR element 8 and OR element 14 to the “OPERATIONAL” output 15 (see

Table 1. Operating Conditions of the FTS in the RNS.

Control Block Output Buses 161 to 165 Indicators					Failed FTS CM Numbers	First Mode		Second Mode
m5	m1	m2	m3	m4		RNS Base Relationship for Information m1 + m4 and Control m5	Set Ω0 of Operational FTS States (D0 = 420)	First Level of Degradation (D1 = 139)		Second Level of Degradation (D2 = 61)
23	3	4	5	7				RNS Base Relationship	Set Ω1 of Operational FTS States	RNS Base Relationship	Set Ω2 of Operational FTS States
1					2	3	4	5	6	7	8
0	0	0	0	0	-	-	+	-	+	-	+
0	0	0	0	1	4	7 < 23	+	23·3·4·5 > 139	+	23·3·4·5 > 61	+
0	0	0	1	0	3	5 < 23	+	23·3·4·7 > 139	+	23·3·4·7 > 61	+
0	0	0	1	1	3, 4	5·7 > 23	-	23·3·4·> 139	+	23·3·4 > 61	+
0	0	1	0	0	2	4 < 23	+	23·3·5·7 > 139	+	23·3·5·7 > 61	+
0	0	1	0	1	2, 4	4·7 > 23	-	23·3·5 > 139	+	23·3·5 > 61	+
0	0	1	1	0	2, 3	4·5 < 23	+	23·3·7 > 139	+	23·3·7 > 61	+
0	0	1	1	1	2, 3, 4	4·5·7 > 23	-	23·3 < 139	-	23·3 > 61	+
0	1	0	0	0	1	3 < 23	+	23·4·5·7 > 139	+	23·4·5·7 > 61	+
0	1	0	0	1	1, 4	3·7 < 23	+	23·4·5 > 139	+	23·4·5 > 61	+
0	1	0	1	0	1, 3	3·5 < 23	+	23·4·7 > 139	+	23·4·7 > 61	+
0	1	0	1	1	1, 3, 4	3·5·7 > 23	-	23·4 < 139	-	23·4 > 61	+
0	1	1	0	0	1, 2	3·4 < 23	+	23·5·7 > 139	+	23·5·7 > 61	+
0	1	1	0	1	1, 2, 4	3·4·7 > 23	-	23·5 < 139	-	23·5 > 61	+
0	1	1	1	0	1, 2, 3	3·4·5 > 23	-	23·7 > 139	+	23·7 > 61	+
0	1	1	1	1	1, 2, 3, 4	3·4·5·7 > 23	-	23 < 139	-	23 < 61	-
1	0	0	0	0	5	3·4·5·7 = 420	+	3·4·5·7 > 139	+	3·4·5·7 > 61	+
1	0	0	0	1	5, 4	-	-	3·4·5 < 139	-	3·4·5 < 61	-
1	0	0	1	0	5, 3	-	-	3·4·7 < 139	-	3·4·7 > 61	+
1	0	0	1	1	5, 3, 4	-	-	3·4 < 139	-	3·4 < 61	-
1	0	1	0	0	5, 1	-	-	3·5·7 < 139	-	3·5·7 > 61	+
1	0	1	0	1	5, 1, 4	-	-	3·5 < 139	-	4·5·7 > 61	-
1	0	1	1	0	5, 1, 3	-	-	3·7 < 139	-	3·7 < 61	-
1	0	1	1	1	5, 1, 3, 4	-	-	3 < 139	-	3 < 61	-
1	1	0	0	0	5, 1	-	-	4·5·7 > 139	+	4·5·7 > 61	+
1	1	0	0	1	5, 1, 4	-	-	4·5 < 139	-	4·5 < 61	-
1	1	0	1	0	5, 1, 3	-	-	4·7 < 139	-	4·7 < 61	-
1	1	0	1	1	5, 1, 3, 4	-	-	4 < 139	-	4 < 61	-
1	1	1	0	0	5, 1, 2	-	-	5·7 < 139	-	5·7 < 61	-
1	1	1	0	1	5, 1, 2, 4	-	-	5 < 139	-	5 < 61	-
1	1	1	1	0	5, 1, 2, 3	-	-	7 < 139	-	7 < 61	-
1	1	1	1	1	1, 2, 3, 4, 5	-	-	-	-	-	-
							Ω = 10		Ω = 14		Ω = 19

, columns 1–4).

Variant 1.2 All information CMs 2${}_1$ to 2${}_4$ are operational, while the control CM 2${}_5$ is not. The binary code representing the states of CMs, 10000, is transmitted via buses 16${}_1$ to 16${}_5$ to the input of the decoder 7. The signal from its output goes through the sixteenth original bus, then via OR elements 8 and 14 to the “OPERATIONAL” output 15 (see Table 1, columns 1–4).

Variant 1.3 The control CM 2${}_5$ is operational, but some of the information CMs have failed.

Variant 1.3.1 Suppose CMs for bases m${}_1$ and m${}_2$, i.e., tracks 2${}_1$ and 2${}_2$, have failed. The binary code, 01100, representing the states of CMs 2${}_1$ to 2${}_5$, is transmitted via buses 16${}_1$ to 16${}_5$ to the input of the decoder 7. The signal from its output passes through the twelfth original bus via OR elements 8 and 14 to the “OPERATIONAL” output 15 (see Table 1, columns 1–4). Concurrently, the signals from the code 01100 activate AND elements 4${}_1$ and 4${}_2$. The signal from bus 17, firstly, passes through OR elements 5${}_1$ and 5${}_2$ to the “STOP” inputs, disabling CMs 2${}_1$ and 2${}_2$. Secondly, it passes through OR element 6 to the “START” input of the control CM 2${}_5$. Consequently, the FTS remains operational, with information processing undertaken by CMs 2${}_3$ to 2${}_5$.

Variant 1.3.2 Suppose CMs 2${}_3$ and 2${}_4$ have failed. The binary code, 00011, representing the states of CMs 2${}_1$ to 2${}_4$, is sent via buses 16${}_1$ to 16${}_5$ to the input of the decoder 7. The signal from its output (second group of outputs from decoder 7) passes through the third bus via OR element 9 (second group of outputs, see column 4, “-” symbol), activating the first AND element 13${}_1$ of the group (control signal of the first level of degradation). In this case, the FTS operates at the first level of degradation mode.

Variant 1.4 One or several information CMs, 2${}_1$ to 2${}_4$, and the control CM 2${}_5$ have simultaneously failed. In this case, with the existence of a signal on the first (left) position (control CM 2${}_5$ failure) and a signal in any other arbitrary position of the original binary code of buses 16${}_1$ to 16${}_5$, all CMs 2${}_1$ to 2${}_5$ stop, rendering the FTS inoperable in the RNS. In this scenario, the FTS will operate in the second mode—the degradation mode.

4.2. The Second Mode: “Mode with Degradation of Work”

Consider the second operational mode of the Fault-Tolerant System (FTS), i.e., the degraded mode. Assume the device operates at the second level ($D_2=61$) of degradation. As per the reference table (columns 1, 7, and 8), the first group of outputs from decoder 10${}_2$ combines the set of buses corresponding to the operational states ${\mathsf{\Omega }}_2=19$ of the second level of degradation (denoted by the “+” symbol in column 8 of the table), while the second group of outputs amalgamates the set of buses corresponding to the non-operational states (denoted by the “-” symbol in column 8 of the table).

Variant 2.1 Let us assume computational tracks 2${}_1$, 2${}_2$, and 2${}_3$ have failed. In this case, the state code of CMs 2${}_1$ to 2${}_5$, 01110, is sent via buses 16${}_1$ to 16${}_5$ to the input of the decoder 10${}_2$ (see table columns 1, 7, and 8). From the output of the decoder, the signal proceeds through the fourteenth bus (first group of outputs), then through AND elements 11${}_2$, 13${}_2$, and 14, reaching the “OPERATIONAL” output 15 of the FTS.

Variant 2.2 Assume computational tracks 2${}_1$, 2${}_2$, 2${}_3$, and 2${}_4$ have failed. In this scenario, the state code of CMs 2${}_1$ to 2${}_5$, 01111, is sent via buses 16${}_1$ to 16${}_5$ to the input of the decoder 10${}_2$ (see table columns 1, 7, and 8). From its output, the signal travels through the fifteenth bus (second group of outputs of decoder 10${}_2$) and then via AND element ${12}_2$ and AND elements 5${}_1$ to 5${}_5$ to the second inputs of all computational tracks 2${}_1$ to $2_5$ of the FTS. In this case, the “OPERATIONAL” signal from bus 15 is absent, meaning that the FTS in the RNS is non-operational.

5. Results

In computational technology, non-positional number systems in RNS have long been recognized and employed in practice to enhance the execution speed of integer arithmetic operations such as addition, subtraction, and multiplication [53,54]. This renewed interest is driven mainly by the following circumstances:

• There has been an influx of scientific-theoretical publications both domestically and internationally, dedicated to the theory and practice of creating high-performance, reliable, resilient, and fault-tolerant computer systems and components operating in RNS. In particular, elements of the theory for ensuring fault tolerance and the classification of CS based on the use of RNS are being developed.
• There is a widespread distribution of mobile device processors that demand high data processing performance coupled with minimal energy consumption. The use of RNS for arithmetic operations of addition and multiplication ensures high speed due to the absence of inter-bit transfers during arithmetic operations. During the operation of mobile devices, the use of RNS can significantly reduce energy consumption.
• There is considerable interest from banking structures that require the reliable and accurate real-time processing of large data sets. They necessitate high-performance computational tools for highly reliable computations with potential self-error correction—a feature inherent to correction codes in RNS.
• The increasing density of component placement on a single chip does not always allow for the thorough and comprehensive testing of computer components. In such scenarios, ensuring the fault-tolerant operation of the CS becomes crucial. Preliminary research results have shown that fault-tolerant CS operations can be organized using RNS.
• The need for specialized CS to perform a vast number of operations on multidimensional numerical structures in real time necessitates the high-speed execution of integer operations of addition and multiplication. This is applicable to tasks such as matrix multiplication, vector dot product computation, Fourier transformations, etc.
• The widespread implementation of microelectronics in all areas of human life has significantly increased the relevance and importance of previously infrequent, but now ubiquitous, scientific-practical tasks such as digital signal and image processing, pattern recognition, cryptographic transformations, the processing and storage of multi-digit information, etc. This situation requires massive computational resources, exceeding the capabilities of CS operating in binary positional numeral systems (PNS).
• The literature suggests that, from the perspective of ensuring necessary performance, reliability, and fault tolerance in the real-time processing of large data sets, existing and prospective CS and components operating in PNS cannot provide this.
• Specialists in computational technology acknowledge that the current level of microelectronics development is approaching its limits. The prospective avenues for further development in microelectronics, succeeding nanoelectronics—such as molecular and biological electronics, micromechanics, optical, optoelectronic, and photonic CS, and other exotic directions for improving existing CS—are still far from widespread industrial production and practical use.

Suppose it is necessary to ensure the necessary (specified) level of reliability of the CS during the design phase. Enhancing (ensuring) reliability is possible if the CS possesses a particular property that allows this. Such a property is defined and termed fault tolerance [43]. Regarding CS, the concept of fault tolerance can be understood as the ability of the CS to maintain its operational state despite the failure of its constituent elements.

In defining the term fault tolerance, three main aspects of its use are highlighted:

• Fault tolerance is incorporated by developers in the design of the CS to increase its reliability; the necessary level of fault tolerance is mainly achieved through the use of redundant (additional) technical means (introduction of artificial structural and/or other redundancy) compared to the minimum necessary to fully perform all required CS functions.
• The use of the property of fault tolerance allows for maintaining the full or partial operationality of the CS.
• It is assumed that the failure of CS elements is not associated with effects not provided for in the operating conditions.

In most cases, developers are interested in ensuring fault tolerance only while maintaining full operationality, i.e., without reducing the quality of CS operation. In the future, when considering the concept of fault tolerance, we will be interested only in such a variant of CS operation.

To provide the CS with the property of fault tolerance at the design stage, it is necessary to not only provide for the introduction and use of artificial redundancy (AR), i.e., the use of various types of backups: structural, informational, functional, temporal, and load, but also to identify and use the possible natural (“inherent”) redundancy (NR) of the system. In this regard, the main task of designers in ensuring the necessary level of reliability is to identify (determine) and use the internal reserves (NR) of the CS for fault tolerance at the pre-design stages of design, due to the used numbering system (NS), and, taking this into account, to subsequently select and apply the necessary methods of redundancy (introduction of AR). Taking into account and using NR will increase the reliability of the CS.

In [53,54], partial definitions of primary redundancy (PR) and secondary redundancy (SR) are introduced in relation to computational technology. In this aspect, it is considered that PR is conditioned by the NS used in the CS. Obviously, SR is redundancy caused by the application of traditional redundancy methods, widely used in information systems of various purposes to improve their individual characteristics. Primary redundancy for CS coincides with the concept of the NR of information processing systems, and SR coincides with the concept of AR. The need to introduce and use SR is determined by the requirements for characteristics at the design stage of the CS. Note that the selected and used NS significantly influences the following characteristics of the CS: structure (architecture); principles of information processing (to a greater extent, the methods and algorithms for performing arithmetic operations); requirements for the use of a new element base; system and user performance; reliability; survivability; accuracy and fault tolerance; operational characteristics and indicators of the CS, etc.

When researching and developing methods to increase the reliability of CS, it is advisable and convenient to divide the concept of fault tolerance into two components, i.e., use two separate concepts: natural fault tolerance and artificial fault tolerance. The introduced terms, NFT and AFT, are convenient to use when analyzing and synthesizing the reliability structures of CS. These concepts adequately reflect the essence of methods for calculating and improving reliability. Let us give definitions to these terms.

Definition 1.

The natural fault tolerance of CS is the ability of CS to maintain a functional state due to the use of NR only.

Definition 2.

The artificial fault tolerance of CS is a property laid down in the design of CS, the use of which allows for maintaining a functional state in case of element failures due to the simultaneous use of NR and AR.

Unquestionably, natural fault tolerance determines the inherent (existing) level of system reliability, while artificial fault tolerance determines the aggregate (required, set) level of reliability. The overarching goal of reliability enhancement can be formulated as ensuring system resilience through the simultaneous use of natural and artificial redundancies. The enhancement of reliability, as a feature of system dependability, can be achieved through either passive or active fault-tolerance methodologies.

Definition 3.

PFT is a method of improving fault tolerance through the concurrent utilization of natural and artificial redundancies without reconfiguring (i.e., constant reservation) the system structure. This method is used during the design phase to elevate the system reliability to a pre-specified (required) level of fault tolerance.

Definition 4.

AFT is a method of improving fault tolerance through the concurrent utilization of natural and artificial redundancies by reconfiguring (i.e., dynamic reservation) the system structure. This method is also employed during the design phase to augment the system reliability to a pre-specified (required) level of fault tolerance.

Let us examine the influence of the primary properties of the CRT on system resilience (i.e., the structure and principles of system functioning).

5.1. Independence of Residues

This property enables the formation of the system as a collection of independent, temporally parallel computational data processing paths, functioning independently and concurrently, each according to its specific module $m_i$ of RNS. Therefore, a system operating within RNS possesses resilience, owing to the capability of detecting and rectifying computational path failures and errors by substituting a malfunctioning path with a functional one without interrupting task resolution. Additionally, errors arising due to circuit failures (malfunctions) in any computational path do not “multiply” into adjacent computational paths (i.e., errors remain within one residue modulo $m_i$), thereby enhancing the computational accuracy within RNS. An error occurring in a computational path of the base $m_i$ either persists in this path until computations conclude or self-eliminate during subsequent computations (for example, by multiplying the number residue by zero). This unique RNS property allowed for the creation of a unique error monitoring and correction system within the dynamic computational process, without interrupting the computational process, and introducing minimal informational code redundancy, which is vital for real-time data processing systems.

5.2. Equality of Residues

Based on the principle of number formation in RNS, it is apparent that any residue $a_i$ of a number $A=(a_1,a_2,\dots ,a_p)$ carries information about the entire original number $A$. This provides an opportunity to replace a malfunctioning computational path with module $m_i$ with a functional path with module $m_j$ (assuming that $m_i<m_j$), without interrupting task resolution. A system operating within RNS, which, for instance, has two control bases (ensuring a minimum code distance of three), maintains its operability upon the failure of any two computational paths. If failures occur in the third or fourth computational path, the system remains operational, albeit with some degradation of characteristics (e.g., reduced computational precision). Thus, a system within RNS possesses the property of resilience, which is implemented through a method of gradual degradation. This property determines a distinctive feature of system operation within RNS: the computer system can exhibit varied levels of fault tolerance, computational precision, and arithmetic operation speed, depending on the requirements imposed on it. If needed, during the task resolution process, the system’s fault tolerance, computational precision, and operational speed can be varied without interrupting the system’s computations.

Indeed, suppose data in RNS are defined by a non-positional code structure of the form $A_{RNS}=(a_1|\left|a_2\right||\dots |\left|a_{i-1}\right|\left|a_i\right|\left|a_{i+1}\right||\dots |\left|a_n\right||\dots ||a_{n+k})$, represented by the set of bases {$m_i$}, where $i=\overline{1,n+k}$. It is known that the execution time of arithmetic operations and the solution’s precision depend on the number $n$ of informational bases, while the reliability and the accuracy of computations depend on the number $k$ of control bases of the RNS. Let us say there is a need to increase the system’s reliability and/or the computations’ accuracy during the computations. In this case, without interrupting the computations, the RNS bases {$m_i$} are redistributed in real time as follows: $i=\overline{1,n^{\prime }+k^{\prime }}$ where $n^{\prime }<n$ and $k^{\prime }>k$, and $n+k=n^{\prime }+k^{\prime }=const$. This results in decreased computation precision and increased arithmetic operation speed, defined by the number of informational bases $n’$. If a need arises to increase the solution’s precision for a specific part of the computed program, the program is redistributed as follows: $i=\overline{1,n^{″}+k^{″}}$, with $n+k=n^{″}+k^{″}=const$. In this case, with the increase in computation precision ($n^{″}>n$), the reliability (computation accuracy) decreases and the task solution time increases. A similar redistribution of informational $n$ and control $k$ bases also occurs with non-modular operation (control operation, correction, comparison, etc.) execution within RNS. The time needed to execute non-modular operations in RNS is proportional to the number $n$ of informational bases, i.e., to the number of bases defining the computation precision. Transitioning to computations with lower precision allows for increased operation speed. If an ordered ($m_i<m_{i+1}$) RNS is extended by adding $l$ bases, each larger than the previous base of the original RNS, the minimum code distance $d_{min}$ automatically increases by the amount $l$. The same can be achieved by decreasing the number $n$ of informational bases, i.e., transitioning to computations with lower precision. Consequently, an inversely proportional relationship exists between the correcting capabilities of codes in RNS and the computation precision.

Indeed, the joint use of the first and second properties of RNS entails the simultaneous presence of three types of redundancy: structural, informational, and functional.

Based on the idea of structural redundancy, the combined use of the first and second properties allows for synthesizing reliability mathematical models in RNS, corresponding to the models of constant and dynamic redundancy in the positional numbering system. In this case, the information paths $m_1..m_n$ serve as operating elements, and the $m_{n+1}..m_{n+k}$ computing tracks serve as reserve elements, where $k$ is the number of control (reserve) bases of RNS.

In structural redundancy, there are spare components within the system to replace failing components. Informational redundancy uses additional bits to ensure the accuracy of the data. Functional redundancy provides redundant or duplicate systems in case one fails.

This approach helps maintain system functionality even in the event of partial failures, improving overall system reliability and robustness. This is a critical feature in various fields where high reliability and continuous operation are necessary, such as in space exploration or critical infrastructure.

5.3. Low Bit-Length Residue

This property significantly enhances both the reliability and speed of the RNS-based CS. This is achieved through the low bit-length construction of RNS-based CS tracks, and the ability to employ (unlike the positional numbering system, PNS) table arithmetic, where arithmetic operations such as addition, subtraction, and multiplication are executed in almost a single machine cycle. In particular, the low bit-length residue representation in RNS allows for a wide array of system technical solutions in implementing modular arithmetic operations, based on the following principles:

• Accumulative principle (based on the usage of low bit-length binary adders module-wise).
• Table principle (based on the utilization of small-sized Read-Only Memory (ROM) units).
• Ring shift principle, based on the usage of ring shift registers.

By analyzing the potential application of the three main properties listed above (independence, equality, and low bit length of residues that define non-positional code structure), non-positional arithmetic in RNS, compared to PNS, has several substantial advantages:

• The ability to parallelize calculations at the operand decomposition level significantly increases speed.
• The potential for the spatial separation of data elements with the capacity for subsequent asynchronous independent processing.
• The possibility of the table (matrix) execution of arithmetic operations from the basic set and polynomial functions with the single-cycle ROM-result extraction of modular operations.
• The capability to implement a control and correction system with the effective detection and rectification of failures and faults.
• The opportunity to monitor and correct errors dynamically during the computation process.
• The ability to efficiently use passive and active fault tolerance based on prompt structural reconfiguration.
• Reduced computational and temporal complexity for certain classes (types) of integer tasks.
• The manifestation of a unique property of the structure in RNS that prevents the error propagation effect when implementing arithmetic integer operations like addition, subtraction, and multiplication.
• The structure’s suitability in RNS for conducting the prompt diagnoses of computation blocks and nodes.
• The possibility to increase reliability in RNS through the efficient simultaneous utilization of passive and active fault tolerance.

The unique features of the fault-tolerant functioning of a CS in RNS are conditioned by the influence of the primary properties of the non-positional numbering system, which are as follows.

• The principles of constructing non-positional code structures have inherently predisposed the CS structure in RNS to ensure fault-tolerant operation.
• In RNS, the application of one type of redundancy implies the simultaneous presence of other types of redundancies, i.e., it stipulates other forms of redundancy. For instance, the application of information redundancy (the introduction of redundant information by incorporating check bases) for increasing computational accuracy implies the presence of structural redundancy, which can be further exploited to enhance the CS’s fault tolerance.
• There exists a direct analogy between the CS structure in RNS and the redundancy structure in PNS. This aspect, using known approaches and mathematical relationships in reliability theory for corresponding methods and ways of redundancy in PNS, enables the synthesis of mathematical models for conducting computations, evaluations, and comparative analyses of fault tolerance and reliability of the CS in RNS.

6. Discussion

In the rapidly evolving domain of e-commerce, where system reliability can make or break businesses, enhancing fault tolerance becomes not just a technical endeavor but a strategic imperative. The exploration of NPNS based on the CRT illuminates a path toward a robust computational architecture, specifically designed to mitigate risks inherent in online commercial environments.

6.1. Advantages of NPNS in E-Commerce Resilience

NPNS represents more than a shift in computational paradigms; it is an innovative response to the exigencies faced by e-commerce platforms. Traditional binary systems, with their susceptibility to compounded errors and downtime, contrast sharply with the multi-faceted redundancy that NPNS introduces. This redundancy is not linear but dimensional, offering multiple independent pathways for information processing, thereby reducing the risk of systemic failures.

In practical e-commerce scenarios, this means that a platform could withstand multiple simultaneous discrepancies—from traffic surges to hardware failures—without a breakdown in transactional integrity. For instance, during high-volume events like Black Friday sales, when the strain on resources is immense, the NPNS’s ability to continue operations unhindered by failures in individual computational elements ensures consistent user experience and sales completion rates. This resilience extends to both hardware robustness and software error minimization—a crucial dual advantage in an ecosystem increasingly underpinned by complex software interactions.

6.2. Overcoming Inertia in Established Systems

Transitioning to a new operational logic, especially in systems deeply entrenched in conventional binary frameworks, is an undertaking fraught with technological and organizational inertia. The challenges stem from the need to overhaul not just hardware and software but also to retrain personnel, adapt operational procedures, and realign customer expectations. This inertia is characterized by more than resistance to change; it encompasses several dimensions of operational disruption and investment. However, the proposed NPNS structure offers a counterbalance by promising significantly higher system reliability and, consequently, customer trust and satisfaction—essential currencies in e-commerce competitiveness.

6.3. Practical and Theoretical Implications for E-Commerce

Implementing NPNS within e-commerce platforms entails confronting a learning curve and the intricacies of novel system behaviors. However, these are surmountable, given the profound implications for operational reliability. On a practical level, for example, the avoidance of transactional downtimes or data inconsistencies—common issues under binary systems during failures—directly translates to customer retention and revenue preservation.

Theoretically, this study pioneers an approach that could redefine fault tolerance standards within digital commerce. It challenges current norms, pushing for a shift from recovery-focused strategies to an emphasis on failure prevention and consistent operation. Such a shift could set new industry benchmarks, prompting a wide-ranging reassessment of what merchants and customers can expect from online commercial experiences.

6.4. Operational Trade-Offs and System Optimization

Enhancing computational systems’ (CS) fault tolerance via CRT exploitation incurs specific trade-offs, critical to understanding and leveraging the unique attributes of RNS within the e-commerce landscape:

• The efficacy of RNS in computational systems materializes predominantly in integer processing, aligning with the transactional nature of e-commerce.
• Positional operations within RNS introduce an additional layer of temporal and technical intricacy, given their necessity in functions pivotal to e-commerce such as data control and transactional integrity.
• While RNS adoption in non-redundant computational systems necessitates augmented hardware investments compared to positional number systems (PNS), this is mitigated by the imperative for enhanced fault tolerance in the high-stakes e-commerce environment.
• The performance surplus intrinsic to computational systems within RNS provides a strategic avenue for bolstering fault tolerance, albeit with potential impacts on operational velocity, necessitating a balanced approach especially critical in the time-sensitive e-commerce sector.

For instance, it can be shown that the non-positional code structure (NPCS) in RNS is an advanced development of multi-residue arithmetic codes in PNS. It is known that a multi-residue code can be represented as

$$A_k^{\prime }=[A_k,A_k(\mathrm{mod}{m}_1),\hspace{0.33em}{A}_k(\mathrm{mod}{m}_2),\hspace{0.33em}\dots ,\hspace{0.33em}{A}_k(\mathrm{mod}{m}_i),\hspace{0.33em}\dots ,A_k(\mathrm{mod}{m}_{n-1}),A_k(\mathrm{mod}{m}_n)]$$

i.e.,

$$A_k^{\prime }=(A_k,a_1,a_2,\dots ,a_n)$$

where

$$a_i=A_k-[A_k/m_i]m_i.$$

When the inequality ${\displaystyle \prod _{i=1}^n{m}_i\ge A_k}$ holds, the set of remainders $\left\{a_i\right\}$ (NPCS) uniquely identifies the number $A_k$ and the numerical value $A_k$ becomes unnecessary. The multi-residue code then takes the form of the RNS code $A_k^{\prime }=(a_1,a_2,\dots ,a_n)$, which facilitates the implementation of modular operations via separate independent tracts, operating solely with remainders $\left\{a_i\right\}$. This encoding of numbers allows for the construction of a CS, where the processing of all number digits (remainders $a_i$) occurs in parallel over time. In this case, the generalized structural diagram of CS in RNS represents a set of separate calculators, functioning independently and in parallel over time, each according to its specific modulus $m_i$.

Thus, the “trade-offs” of utilizing the RNS within the NPNS framework involve several considerations, including its optimal function with integer processing and the complexities of positional operations. However, these are mitigated by the system’s heightened fault-tolerance level, even though it necessitates additional hardware resources and could marginally impact the speed of arithmetic operations. In the context of e-commerce, these trade-offs are justified by enhanced system stability, particularly during critical high-stake scenarios, thereby solidifying the business’s market position and customer trust.

In conclusion, while NPNS presents certain operational and transitional challenges, its integration represents a forward-thinking solution to the perennial issues of system reliability in e-commerce. By reinforcing the technical infrastructure that underpins these platforms, NPNS offers a practical route to enhanced operational resilience, customer confidence, and overall business continuity in the ever-expanding digital commerce sphere.

7. Conclusions

Electronic commerce, with its vast expanse and intricate web of transactions, stands at the forefront of digital transformation, commanding both technological innovation and methodical precision. Our exploration into enhancing fault tolerance within this domain, specifically through the incorporation of NPNS based on the CRT, has unveiled both potential avenues for advancement and critical considerations for effective deployment.

NPNS, by virtue of its unique mathematical properties, offers an exciting alternative to traditional computing paradigms. Its promise of heightened resilience against system faults is particularly relevant in today’s e-commerce landscape, where even transient glitches can lead to significant economic losses and eroded consumer trust. The central premise of NPNS—providing multiple layers of redundancy and system independence—resonates with the foundational needs of a robust e-commerce platform, namely reliability, security, and efficiency.

However, as underscored in our discussions, the transition to such an innovative system demands a holistic approach. Beyond the immediate technological challenges lie broader implications, encompassing workforce training, organizational change management, and evolving customer expectations. As with any transformative innovation, the promise of potential benefits is invariably accompanied by a suite of challenges, each requiring strategic foresight and agile response mechanisms.

As the world of e-commerce continues its relentless pace of evolution, staying abreast of technological advancements becomes paramount. NPNS, while nascent in its application, holds the promise of charting a new trajectory in fault tolerance, potentially redefining the benchmarks of system reliability.

This paper has explored the unique characteristics of CS operation based on the CRT. The peculiarities of computer data processing are conditioned by the influence of the key properties of CRT on the operating principles and structure of CS. This feature allows for the organization of the fault-tolerant functioning of the original CS in RNS, in contrast to the PNS, even without the implementation of additional means of ensuring fault tolerance (introducing additional types of redundancy).

In this study, some concepts, terms, and definitions of fault tolerance were introduced. A classification of various methods of ensuring CS fault tolerance in RNS was conducted for the first time. The results of this classification directly or indirectly facilitate the selection, justification, and implementation of the necessary methods to enhance CS fault tolerance, depending on the field of CS application. Moreover, the terms “elementary operation” and “independent operation” were introduced, which are convenient for analyzing and synthesizing reliable CS structures. These concepts adequately reflect the essence of the methods for calculating and enhancing reliability.

The practical importance and usefulness of the research conducted in this paper are as follows:

• A pathway for effectively increasing the fault tolerance of CS; specifically, the use of RNS as the number system in CS was demonstrated.
• The presented classification of various fault-tolerance methods provides an opportunity for the synthesis and quantitative assessment of CS fault tolerance in RNS.

Based on the results of the research conducted in this paper, the following main conclusions can be drawn:

The non-positional number system in residue classes presents an effective means for enhancing the fault tolerance of CS. This is underpinned by the following circumstances:

• The initial structure of CS in the CRT, without the introduction of additional redundancy, exhibits an inherent predisposition for the possibility of fault-tolerant CS operation. This is due to the influence of the primary properties of RNS on the CS structure. The CS structure in RNS is similar to the structure of multiprocessor CS in the PNS.
• There is a direct analogy between the structure of CS in RNS and the structure of a redundant system in PNS. This parallelism allows us, using established approaches and mathematical relationships from reliability theory for corresponding methods and means of redundancy in PNS, to synthesize mathematical models for performing calculations, evaluation, and comparative analysis of the fault tolerance and reliability of CS in RNS.
• In RNS, the application of one type of redundancy implicitly introduces other types of redundancy. For instance, the use of information redundancy (introducing information excess through control bases) to enhance computation reliability introduces structural redundancy, which can be further used to enhance CS fault tolerance.
• The results of the analysis of an example one-byte CS in RNS functioning with given information bases ($m_1=3$, $m_2=4$, $m_3=5$, and $m_4=7$) and only one control base ($m_k=m_5=23$) (detailed in Section 4) demonstrate the following. The use of RNS ensures a higher level of CS fault tolerance due to the consideration of additional operational states of CS with a reduced quality of operation. The level of fault tolerance increases by reducing computation accuracy by taking into account an additional number of operational CS states.

Possible future research prospects, in our view, lie in a more detailed analysis of the influence of the properties of the CRT on the reliability (fault tolerance) of real-time functioning CS. This would involve the following steps:

• Based on the methods of passive (Definition 3) and active (Definition 4) fault tolerance, synthesize mathematical models of reliability for different modes of CS operation in RNS.
• Calculate the reliability of CS in RNS using a selected metric.
• Conduct a comparative analysis of the reliability of the synthesized CS in RNS with the existing CS.
• Develop technical recommendations for choosing the location for the effective application of CS in RNS.

This paper demonstrates that the effect of ensuring a given level of reliability of CS functioning in RNS is achieved with fewer hardware expenses (with less additional equipment introduced), i.e., at a lower cost, compared to the widely used method in high-reliability computing system creation practice, which involves tripling identical CS. This is due to the fact that, firstly, the proposed mathematical model most fully accounts for the primary properties of RNS: independence, equality, and independence of residues defining the non-positional code structure. The analysis and consideration of the basic properties of RNS ensure the presence and use in CS of various types of redundancy simultaneously: structural, informational, and functional.

In closing, our exploration into NPNS is not an endpoint but rather a starting juncture—an invitation for researchers, technologists, and industry practitioners to delve deeper, test rigorously, and innovate continually. The confluence of mathematical rigor and practical application, as epitomized by NPNS, offers a beacon of potential in the ever-evolving journey of e-commerce, marking a significant stride toward building a more resilient, secure, and efficient digital commerce ecosystem.

In acknowledging the constraints of this study, it is pertinent to note that while the proposed CRT-based approach significantly enhances fault tolerance in e-commerce systems, there are inherent limitations. The complexity of real-world e-commerce environments may present unpredictable challenges that are not fully encapsulated within the scope of this research. Additionally, the applicability of our method requires extensive stakeholder buy-in and rigorous compliance with security protocols, which may not always be feasible across diverse operational contexts. Future studies might seek to address these factors by exploring adaptive fault-tolerance models and conducting comprehensive field tests in varied e-commerce settings.