Unveiling the Power of ARIMA, Support Vector and Random Forest Regressors for the Future of the Dutch Employment Market
Abstract
1. Introduction
- To what extent do the selected models demonstrate efficacy in predicting job vacancies categorized as “innovative” and “non-innovative” when confronted with an imbalanced dataset?
- To what extent do the models perform in predicting a reduced number of online job vacancies, taking into consideration the required education degree?
- To what extent does the performance of the selected models differ when the granularity of the data transitions from the national level to the provincial level?
2. Related Work
2.1. Demand Forecasting
2.2. Comparative Models Studies in the Time Series Domain
3. Methodology
3.1. Data Description, Pre-Processing and Exploratory Data Analysis
3.1.1. Datasets Description
3.1.2. Data Pre-Processing
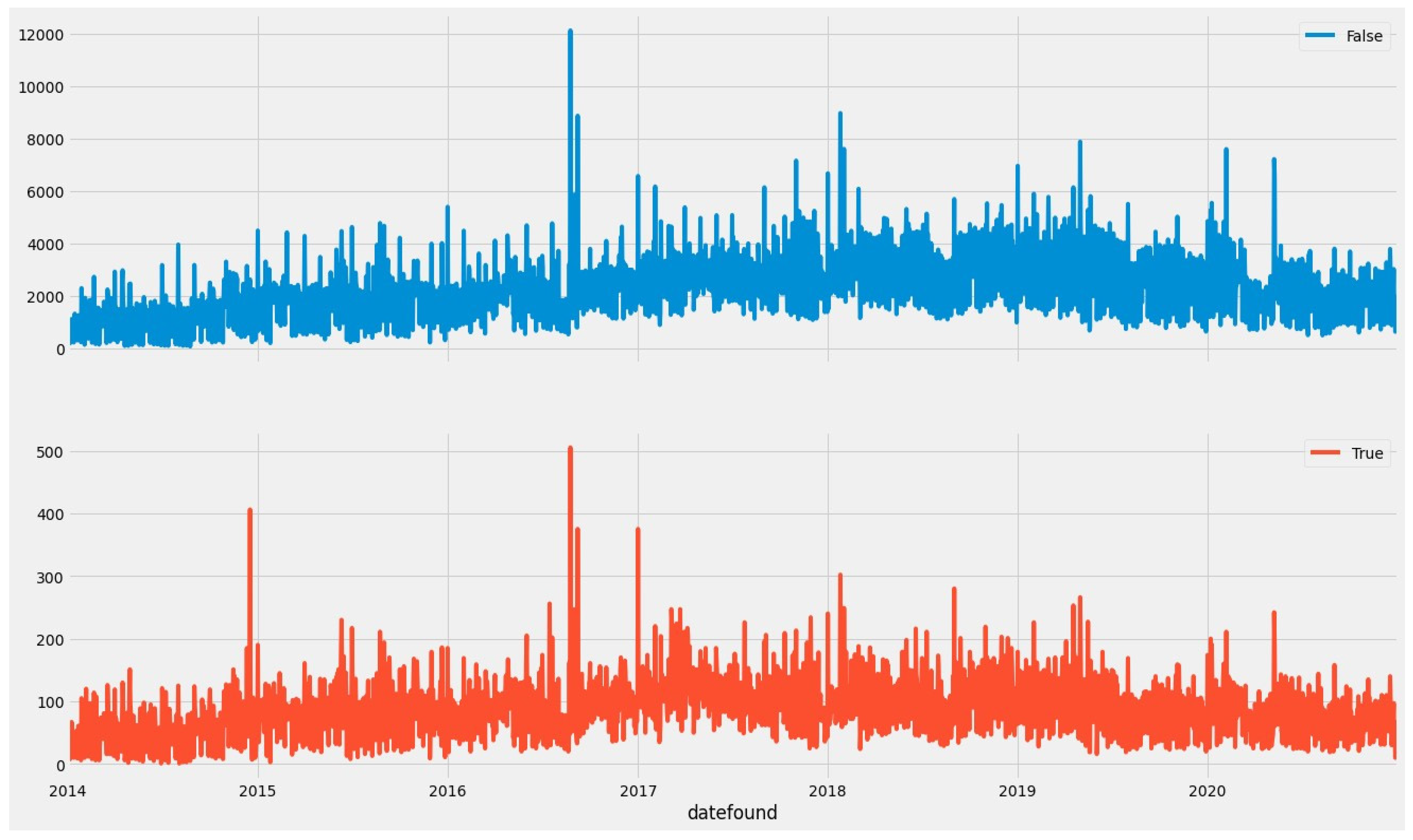
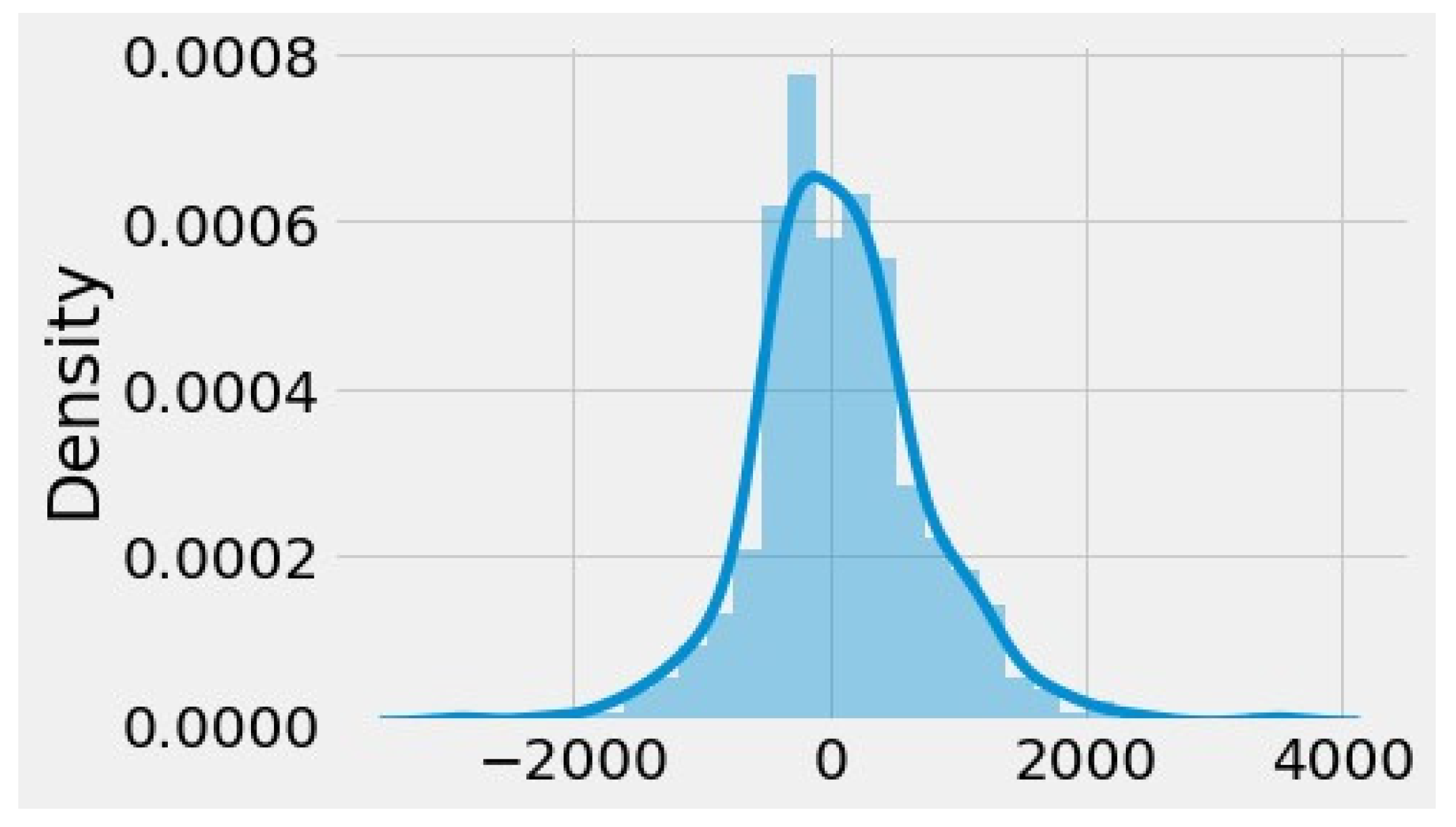
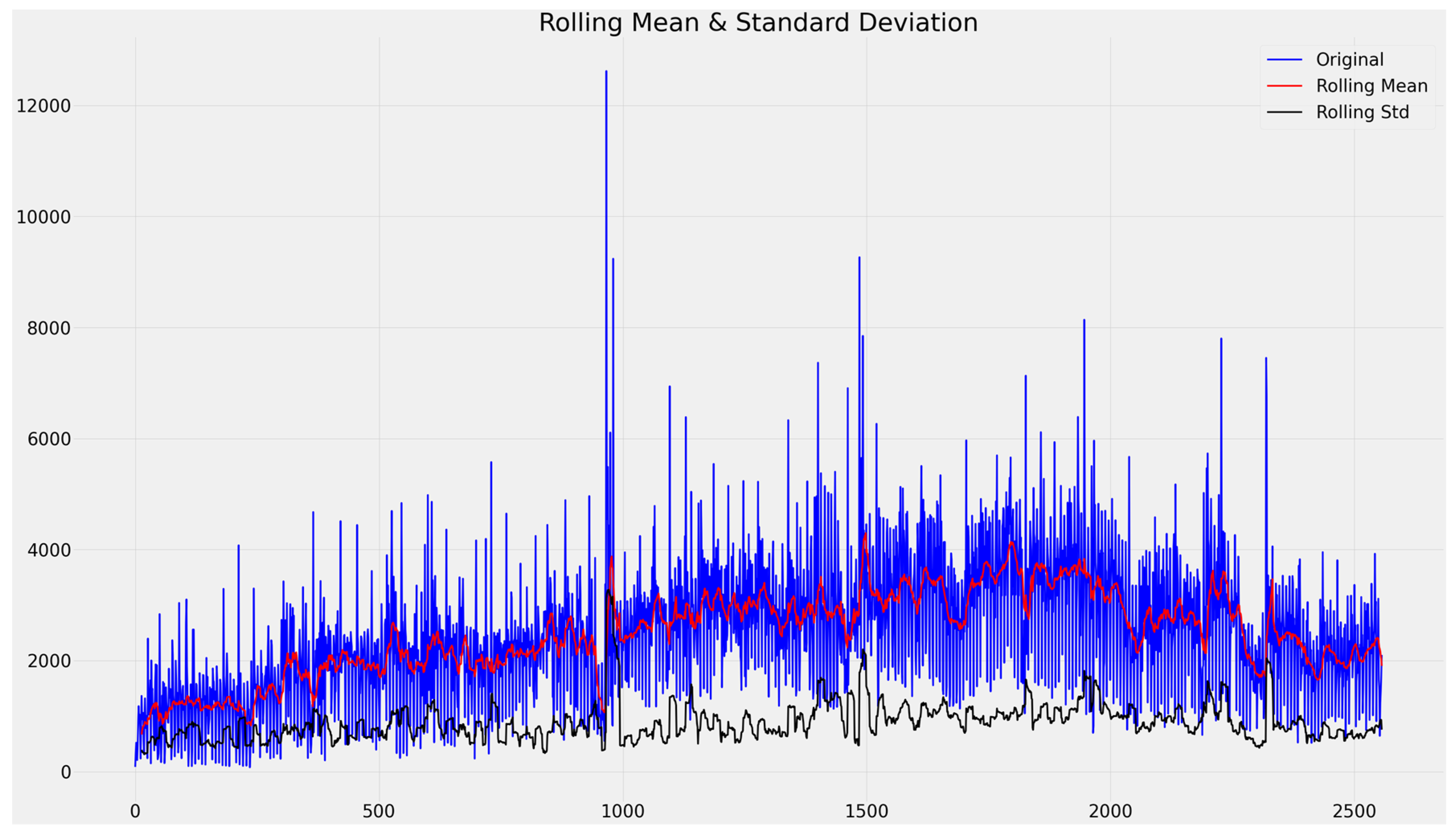
3.1.3. Exploratory Data Analysis (EDA)
3.2. Algorithms
3.2.1. ARIMA
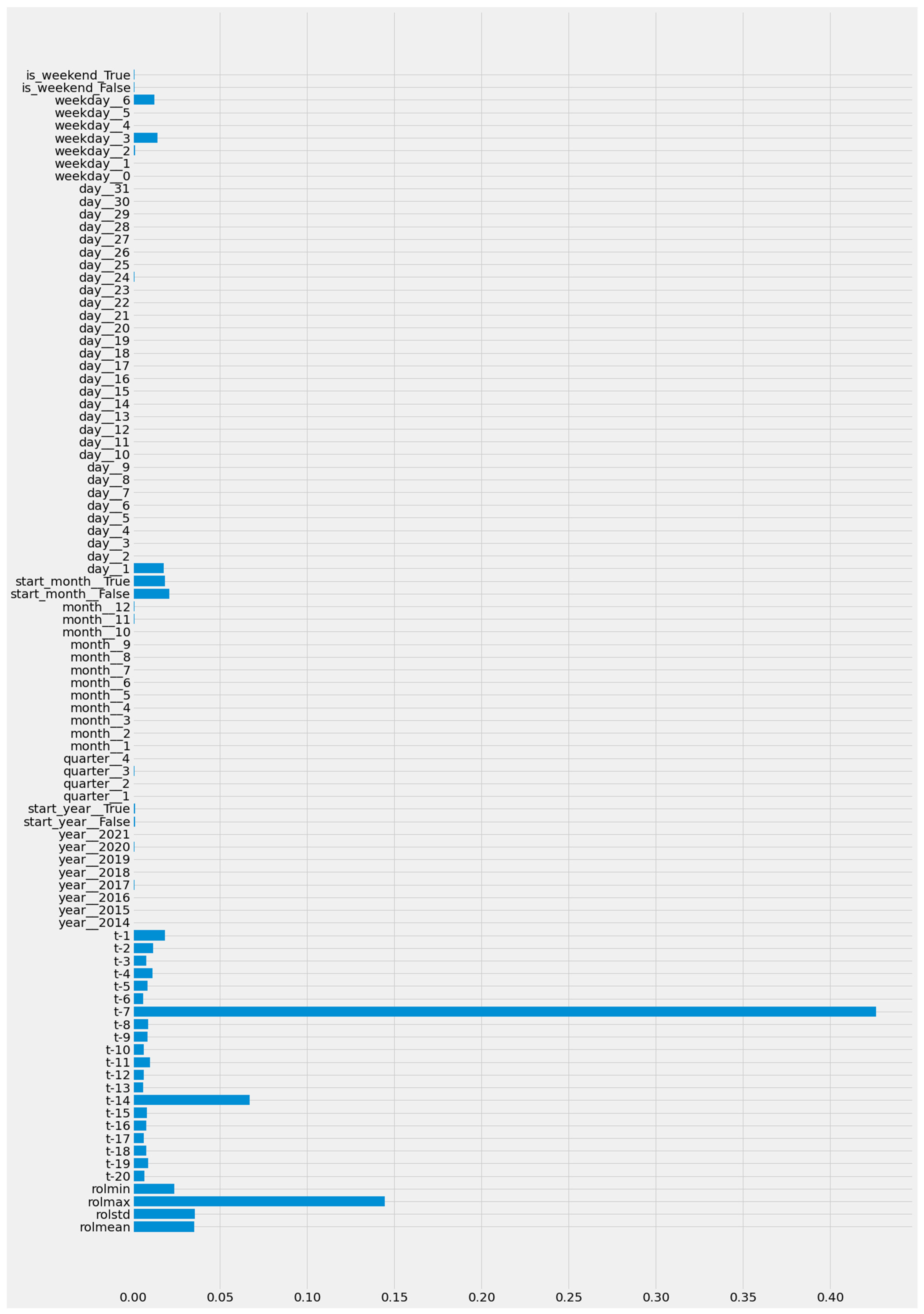
3.2.2. Random Forest Regressor
3.2.3. Support Vector Regressor
3.3. Experimental Set-Up
3.3.1. Training and Hyper-Parameter Tuning
3.3.2. Model Evaluation
3.3.3. Model Performance Metrics
4. Results
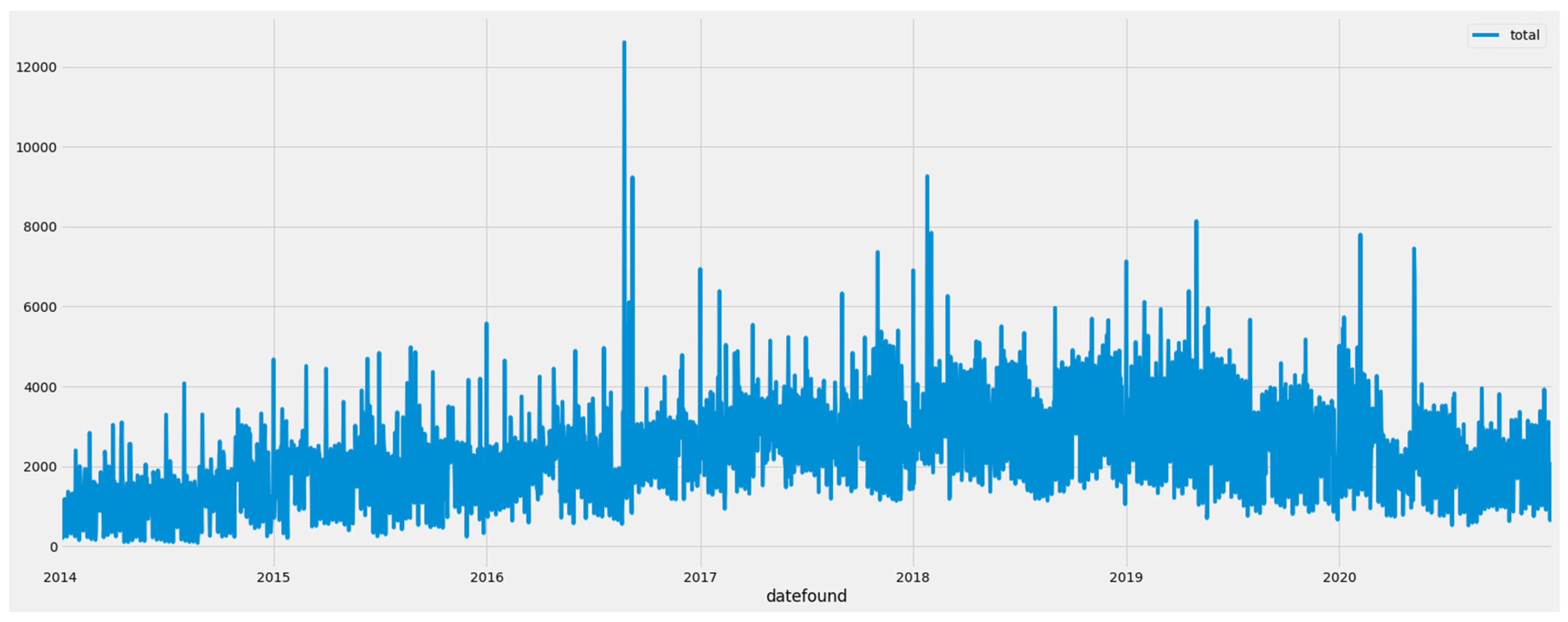
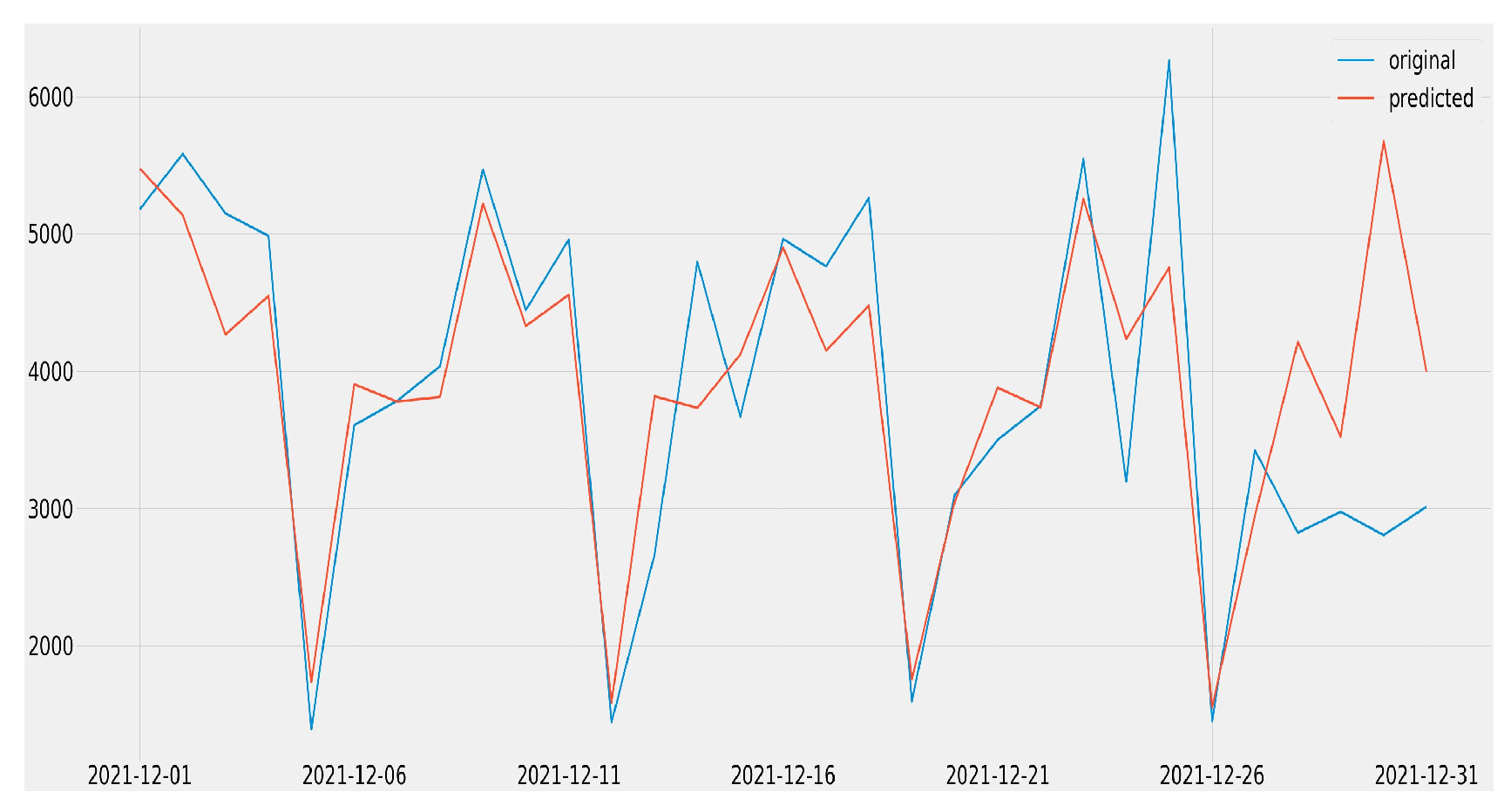
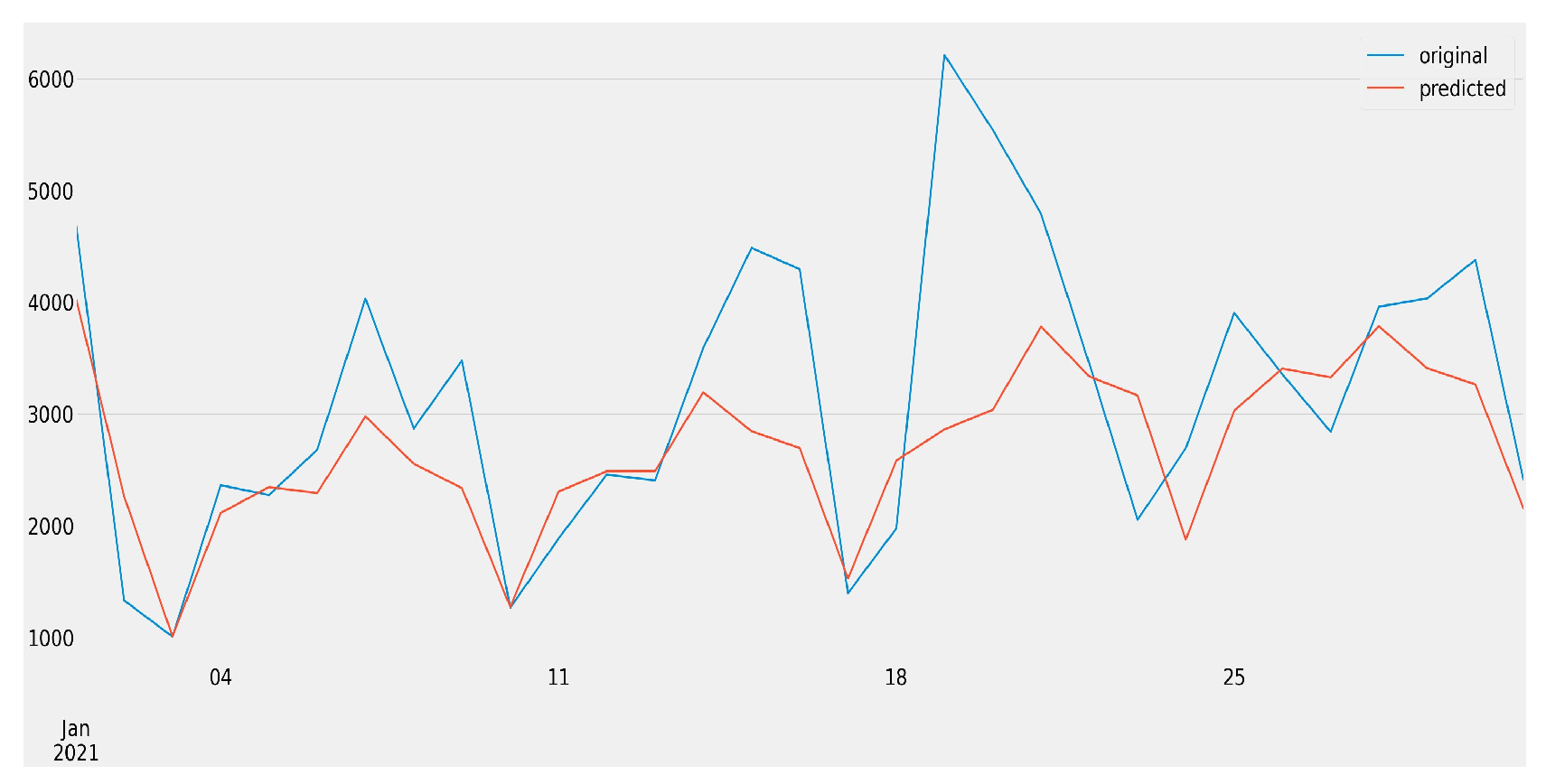
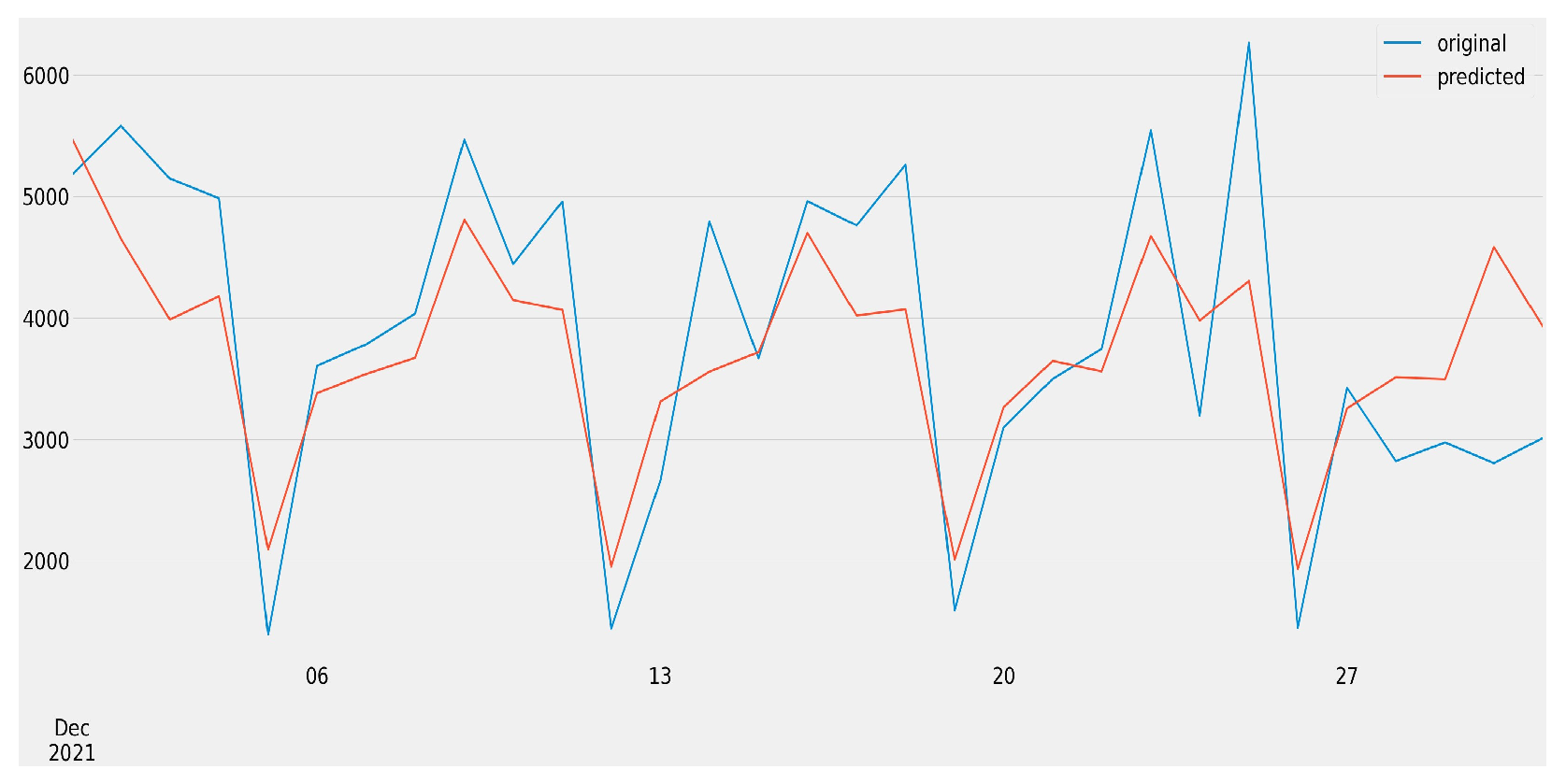
4.1. Forecasting All Job Openings
4.2. Forecasting Vacancies Split by the Innovative Feature
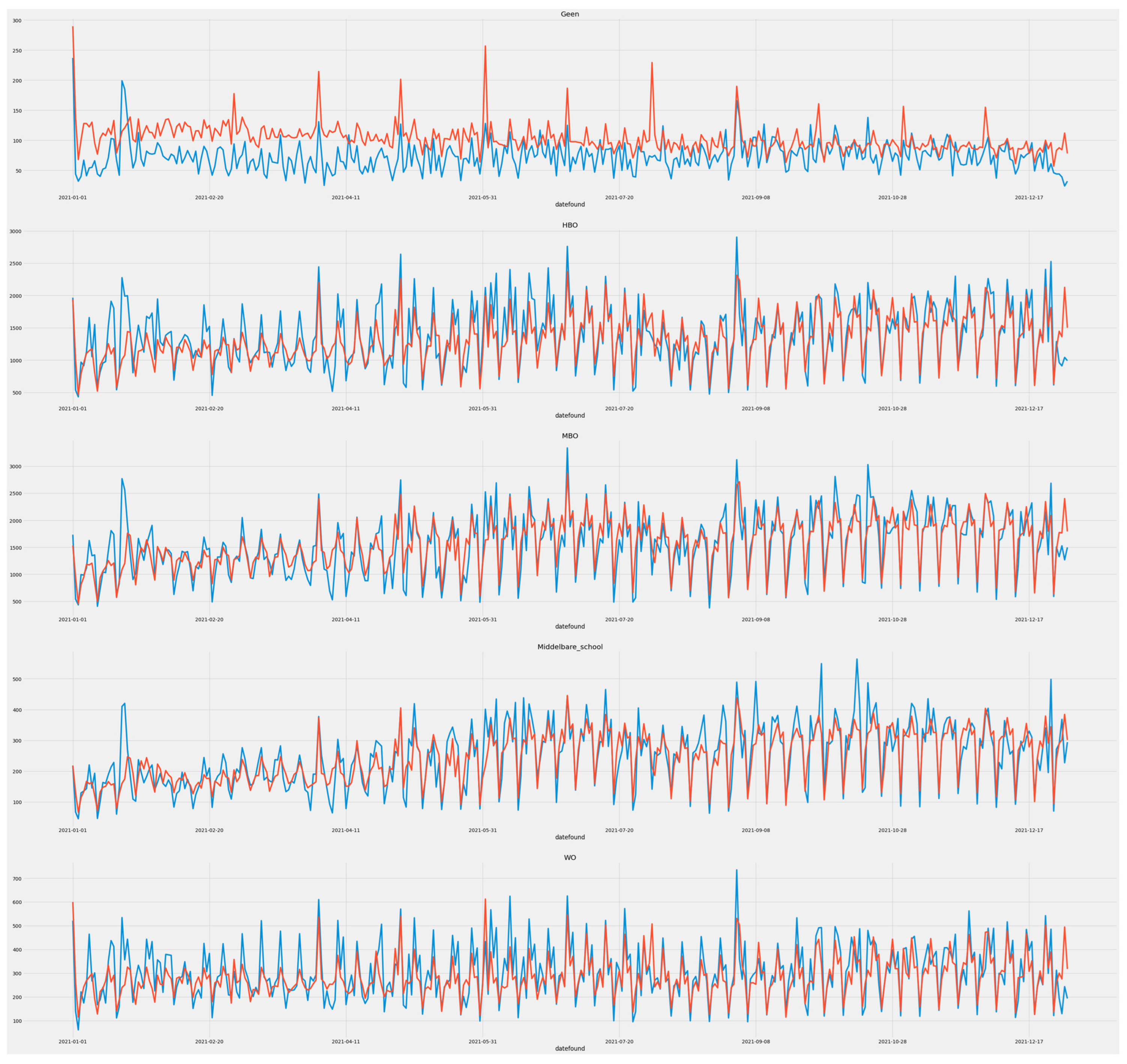
4.3. Forecasting Vacancies by Educational Requirements
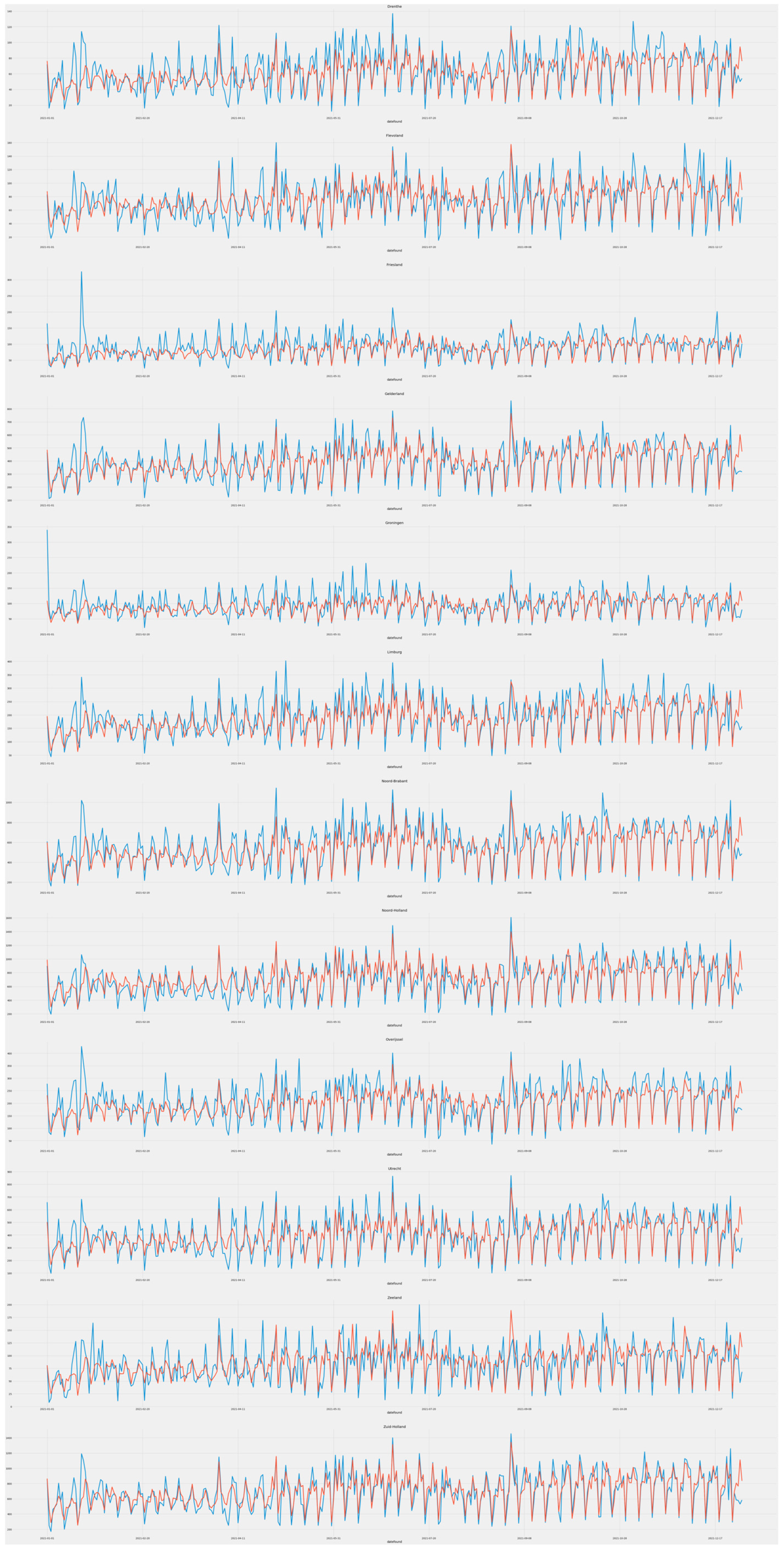
4.4. Forecasting Job Openings by Provinces
5. Discussion
5.1. Limitations
5.2. Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| All available features in the main database |
| organization name, organization name generalized, education degree minimum required detailed, education degree minimum required, education degree generalized, education degree, Industry code, industry description, date found, date deactivated, closing date, starting date, active weeks, organization place, organization_id, nr of employees physical location municipality, physical location place, physical location province, jdcocode, jdcodescription, jdcoisco, position title, position title cleaned, selected text |
| All available features in the EU Industrial R&D Investment Scoreboard for the Worldwide companies for 2021 database |
| World rank, Company, Country, Region, Industry-ICB3 sector name, R&D 2020 (EUR million), R&D one-year growth (%), Net sales (EUR million), Net sales one-year growth (%), R&D intensity (%), Capex (EUR million), Capex one-year growth (%), Capex intensity (%), Op.profits (EUR million), Op.profits one-year growth (%), Profitability (%), Employees, Employees one-year growth (%), Market cap (EUR million), Market cap one-year growth (%) |
| All available features in the EU Industrial R&D Investment Scoreboard for the European companies for 2021 database |
| EU rank, Company, Country, Region, Industry-ICB3 sector name, R&D 2020 (EUR million), R&D one-year growth (%), Net sales (EUR million), Net sales one-year growth (%), R&D intensity (%), Capex (EUR million), Capex one-year growth (%), Capex intensity (%), Op.profits (EUR million), Op.profits one-year growth (%), Profitability (%), Employees, Employees one-year growth (%), Market cap (EUR million), Market cap one-year growth (%) |
| Original Feature | Final Feature after Transformation |
|---|---|
| VWO HAVO VMBO LBO | MIDDELBARE_SCHOOL |
| Nan ONBEKEND | np.NaN |
| Series | Test Result | p-Value | Decision |
|---|---|---|---|
| Total | −3.173956 | 0.021543 | Stationary |
| Non-innovative | −4.105082 | 0.000950 | Stationary |
| Innovative | −3.138486 | 0.023833 | Stationary |
| Geen | −3.169272 | 0.021834 | Stationary |
| HBO | −3.821251 | 0.002697 | Stationary |
| MBO | −2.307436 | 0.169581 | Non-Stationary |
| MIDDELBARE | −2.144197 | 0.227118 | Non-Stationary |
| WO | −4.841603 | 0.000045 | Stationary |
| Drenthe | −3.717743 | 0.003870 | Stationary |
| Flevoland | −3.366402 | 0.012159 | Stationary |
| Friesland | −3.628962 | 0.005231 | Stationary |
| Gelderland | −3.477303 | 0.008590 | Stationary |
| Groningen | −4.211969 | 0.000629 | Stationary |
| Limburg | −3.003770 | 0.034544 | Stationary |
| Noord-Brabant | −3.189875 | 0.020578 | Stationary |
| Noord-Holland | −3.420469 | 0.010281 | Stationary |
| Overijssel | −3.702140 | 0.004083 | Stationary |
| Utrecht | −3.362788 | 0.012295 | Stationary |
| Zeeland | −2.945658 | 0.040290 | Stationary |
| Zuid-Holland | −3.346154 | 0.012937 | Stationary |
| Test Result | p-Value | Decision |
|---|---|---|
| 0.96517 | 2.75 × 10−24 | Data non-normally distributed |
| p | d | q |
|---|---|---|
| 9 | 1 | 5 |
| Forecasting | Min_Samples_Split | Min_Samples_Leaf | Max_Depth |
|---|---|---|---|
| 1st | 4 | 2 | 80 |
| 2nd | 6 | 2 | 30 |
| 3rd | 6 | 2 | None |
| 4th | 2 | 4 | 30 |
| 5th | 2 | 2 | 80 |
| Forecasting | Kernel | Gamma | Epsilon | C |
|---|---|---|---|---|
| 1st | rbf | 0.001 | 0.1 | 10,000 |
| 2nd | sigmoid | 0.01 | 0.001 | 1000 |
| 3rd | sigmoid | 0.001 | 0.1 | 10,000 |
| 4th | sigmoid | 0.01 | 0.001 | 1000 |
| 5th | rbf | 0.1 | 0.001 | 100 |
| Model | Non-Innovative | Innovative |
|---|---|---|
| ARIMA | [998.47, 33.45%, 1262.46] | [49.72, 42.43%, 62.79] |
| RFR | [488.52, 16.1%, 684.03] | [30.43, 23.51%, 40.73] |
| SVR | [490.81, 15%, 648.61] | [29.21, 21.96%, 39.58] |
| ARIMA | |||
|---|---|---|---|
| Series | MAE | MAPE | RMSE |
| Geen | 21.34 | 30.23% | 30.04 |
| HBO | 346.04 | 26.25% | 442.75 |
| MBO | 452.17 | 35.32% | 570.41 |
| MIDDELBARE | 80.87 | 40.69% | 102.46 |
| WO | 93.97 | 36.54% | 120.67 |
| Random Forest Regressor | |||
|---|---|---|---|
| Series | MAE | MAPE | RMSE |
| Geen | 32.67 | 55% | 39.47 |
| HBO | 212 | 16.19% | 290.56 |
| MBO | 234.85 | 18% | 323.71 |
| MIDDELBARE | 41.91 | 20.2% | 57.9 |
| WO | 58.16 | 20.1% | 77.57 |
| Support Vector Regressor | |||
|---|---|---|---|
| Series | MAE | MAPE | RMSE |
| Geen | 18.58 | 27.9% | 24.48 |
| HBO | 213.65 | 15.9% | 290.47 |
| MBO | 237.54 | 18% | 308.47 |
| MIDDELBARE | 43.77 | 20.4% | 59.38 |
| WO | 40.28 | 14.15% | 54.28 |
| ARIMA | |||
|---|---|---|---|
| Series | MAE | MAPE | RMSE |
| Drenthe | 20.08 | 38.36% | 24.76 |
| Flevoland | 24.02 | 38.91% | 30.9 |
| Friesland | 29.09 | 37.71% | 38.82 |
| Gelderland | 109.3 | 32.63% | 135.59 |
| Groningen | 31.37 | 36.97% | 42.8 |
| Limburg | 49.24 | 28.15% | 63.78 |
| Noord-Brabant | 137.40 | 26% | 176.9 |
| Noord-Holland | 201.08 | 34% | 251.19 |
| Overijssel | 64.11 | 37.28% | 79.82 |
| Utrecht | 101.37 | 28.72% | 128.88 |
| Zeeland | 32.38 | 51.92% | 40.71 |
| Zuid-Holland | 200.28 | 33.5% | 254.01 |
| Random Forest Regressor | |||
|---|---|---|---|
| Series | MAE | MAPE | RMSE |
| Drenthe | 13.14 | 24.81% | 17.04 |
| Flevoland | 14.91 | 26.36% | 19.37 |
| Friesland | 19.67 | 22.48% | 28.52 |
| Gelderland | 61.64 | 18.4% | 83.26 |
| Groningen | 20.67 | 22.9% | 29.62 |
| Limburg | 34.61 | 20.16% | 46.04 |
| Noord-Brabant | 88.75 | 16.51% | 120.55 |
| Noord-Holland | 108.89 | 19.29% | 139.40 |
| Overijssel | 37.06 | 19.98% | 49.3 |
| Utrecht | 65.15 | 19.31% | 86.61 |
| Zeeland | 20.29 | 32.87% | 26.99 |
| Zuid-Holland | 101.19 | 17.16% | 135.32 |
| Support Vector Regressor | |||
|---|---|---|---|
| Series | MAE | MAPE | RMSE |
| Drenthe | 8.29 | 15.2% | 10.05 |
| Flevoland | 10.27 | 16.36% | 13.45 |
| Friesland | 16.05 | 18.74% | 23.58 |
| Gelderland | 49.89 | 14.18% | 69.69 |
| Groningen | 16.02 | 17.49% | 23 |
| Limburg | 23.49 | 13.82% | 31.95 |
| Noord-Brabant | 55.16 | 10.25% | 72.36 |
| Noord-Holland | 86.65 | 14.44% | 114.63 |
| Overijssel | 20.2 | 10.56% | 26.73 |
| Utrecht | 50.18 | 14.45% | 65.97 |
| Zeeland | 16.81 | 24.1% | 21.96 |
| Zuid-Holland | 93.4 | 14.6% | 125.99 |




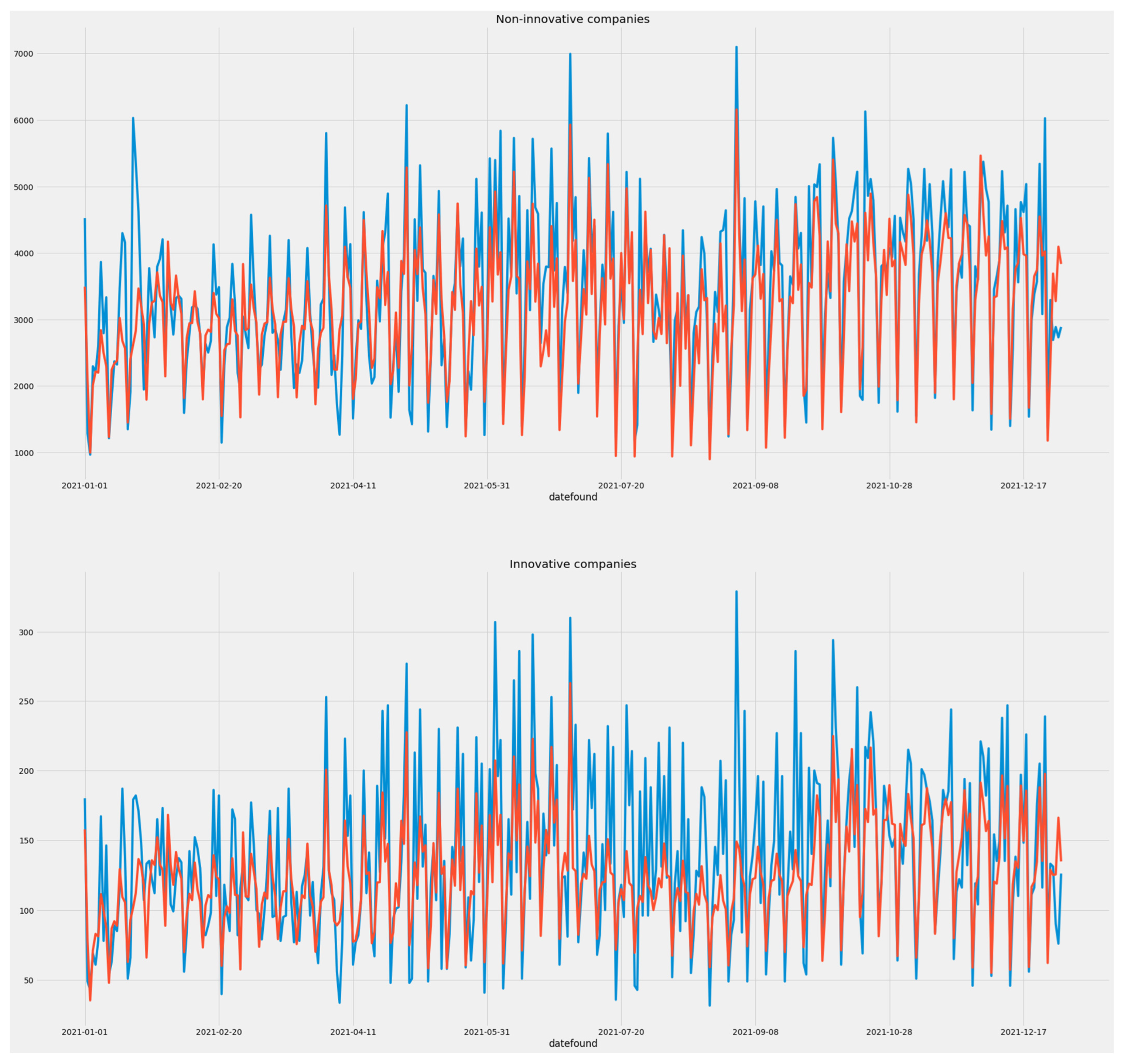




References
- Colombo, E.; Mercorio, F.; Mezzanzanica, M. Applying Machine Learning Tools on Web Vacancies for Labour Market and Skill Analysis, Terminator or the Jetsons? The Economics and Policy Implications of Artificial Intelligence. 2018. Available online: https://www.agraria.unirc.it/documentazione/materiale_didattico/1465_2017_437_29328.pdf (accessed on 10 December 2022).
- Cedefop. The Online Job Vacancy Market in the EU; Publications Office: Luxembourg, 2019. [Google Scholar] [CrossRef]
- Kureková, L.M.; Beblavý, M.; Thum-Thysen, A. Using online vacancies and web surveys to analyse the labour market: A methodological inquiry. IZA J. Labor Econ. 2015, 4, 18. [Google Scholar] [CrossRef]
- Wiggers, K. AI Weekly: Can AI Predict Labor Market Trends? Available online: https://venturebeat.com/ai/ai-weekly-can-ai-predict-labormarket-trends/ (accessed on 25 December 2022).
- Green, F.; Henseke, G. Europe’s evolving graduate labour markets: Supply, demand, underemployment and pay. J. Labour Mark. Res. 2021, 55, 2. [Google Scholar] [CrossRef]
- Juricic, B.B.; Galic, M.; Marenjak, S. Review of the construction labour demand and shortages in the EU. Buildings 2021, 11, 17. [Google Scholar] [CrossRef]
- Bakens, J.; Fouarge, D.; Peeters, T. Labour Market Forecasts by Education and Occupation up to 2022; Technical Reports; Maastricht University, Research Centre for Education and the Labour Market (ROA): Maastricht, The Netherlands, 2018. [Google Scholar]
- Meagher, G.; Pang, F. Labour Market Forecasting, Reliability and Workforce Development; Centre of Policy Studies (CoPS): Melbourne, Australia, 2011. [Google Scholar]
- Skobleva, A.; Eremina, I. Lysanov, Labour Market Forecasting of the Russian Federation. In Second Conference on Sustainable Development: Industrial Future of Territories (IFT 2021); Atlantis Press: Amsterdam, The Netherlands, 2021; pp. 219–223. [Google Scholar]
- Sarycheva, T.V.; Shvetsov, M.N. Statistical approaches to the evaluation of the demand and supply at the labour market based on panel data. Rev. Eur. Stud. 2015, 7, 356. [Google Scholar] [CrossRef]
- Rublikova, E.; Lubyova, M. Estimating arima-arch model rate of unemployment in Slovakia. Forecast. Pap. Progn. Práce 2013, 5, 275–289. [Google Scholar]
- Weber, E.; Zika, G. Labour market forecasting in germany: Is disaggregation useful? Appl. Econ. 2016, 48, 2183–2198. [Google Scholar] [CrossRef]
- Adenomon, M. Modelling and forecasting unemployment rates in nigeria using arima model. FUW Trends Sci. Technol. J. 2017, 2, 525–531. [Google Scholar]
- Jelena, M.; Ivana, I.; Zorana, K. Modeling the Unemployment Rate at the Eu Level by Using Box-Jenkins Methodology. KnE Soc. Sci. 2017, 1, 1–13. [Google Scholar] [CrossRef]
- Petrusevich, D. Time series forecasting using high order arima functions. Int. Multidiscip. Sci. GeoConf. SGEM 2019, 19, 673–679. [Google Scholar]
- Shobana, G.; Umamaheswari, K. Forecasting by machine learning techniques and econometrics: A review. In Proceedings of the 2021 6th International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 20–22 January 2021; pp. 1010–1016. [Google Scholar] [CrossRef]
- Gogas, P.; Papadimitriou, T.; Sofianos, E. Forecasting Unemployment in the Euro Area with Machine Learning. J. Forecast. 2022, 41, 551–566. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/for.2824 (accessed on 20 December 2022). [CrossRef]
- Fabo, B.; Kureková, L.M. Methodological Issues Related to the Use of Online Labour Market Data; Technical Reports, ILO Working Paper; International Labour Organization (ILO): Geneva, Switzerland, 2022. [Google Scholar]
- Turulja, L.; Vugec, D.S.; Bach, M.P. Big Data and Labour Markets: A Review of Research Topics. Procedia Comput. Sci. 2023, 217, 526–535. [Google Scholar] [CrossRef]
- Jošić, H.; Žmuk, B. A Machine Learning Approach to Forecast International Trade: The Case of Croatia. Bus. Syst. Res. Int. J. Soc. Adv. Innov. Res. Econ. 2022, 13, 144–160. [Google Scholar] [CrossRef]
- Elkamel, M.; Schleider, L.; Pasiliao, E.L.; Diabat, A.; Zheng, Q.P. Longterm electricity demand prediction via socioeconomic factors—A machine learning approach with florida as a case study. Energies 2020, 13, 3996. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using cnn-lstm neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Muralitharan, K.; Sakthivel, R.; Vishnuvarthan, R. Neural network based optimization approach for energy demand prediction in smart grid. Neurocomputing 2018, 273, 199–208. [Google Scholar] [CrossRef]
- Amini, M.; Karabasoglu, O.; Ili, M.D.; Boroojeni, K.G.; Iyengar, S.S. Arima-based demand forecasting method considering probabilistic model of electric vehicles’ parking lots. In Proceedings of the 2015 IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Noureen, S.; Atique, S.; Roy, V.; Bayne, S. Analysis and application of seasonal arima model in energy demand forecasting: A case study of small scale agricultural load. In Proceedings of the 2019 IEEE 62nd International Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, TX, USA, 4–7 August 2019; pp. 521–524. [Google Scholar] [CrossRef]
- Ediger, V.; Akar, S. Arima forecasting of primary energy demand by fuel in turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Dacrema, M.F.; Cremonesi, P.; Jannach, D. Are we really making much progress? A worrying analysis of recent neural recommendation approaches. In Proceedings of the 13th ACM Conference on Recommender Systems, Copenhagen, Denmark, 16–20 September 2019; pp. 101–109. [Google Scholar]
- Bi, J.-W.; Han, T.-Y.; Li, H. International tourism demand forecasting with machine learning models: The power of the number of lagged inputs. Tour. Econ. 2022, 28, 621–645. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Al-Bugharbee, H.; Muhsen, Y.R.; Hashim, K.; Alkhaddar, R.M.; Hmeesh, W.H. The prediction of municipal water demand in iraq: A case study of baghdad governorate. In Proceedings of the 2019 12th International Conference on Developments in eSystems Engineering (DeSE), Kazan, Russia, 7–10 October 2019; pp. 274–277. [Google Scholar] [CrossRef]
- Nwokike, C.C.; Okereke, E.W. Comparison of the performance of the sann, sarima and arima models for forecasting quarterly gdp of Nigeria. Asian Res. J. Math. 2021, 17, 1–20. [Google Scholar] [CrossRef]
- Sehrawat, P.K.; Vishwakarma, D.K. Comparative analysis of time series models on covid-19 predictions. In Proceedings of the 2022 International Conference on Sustainable Computing and Data Communication Systems (ICSCDS), Erode, India, 20–22 March 2022; pp. 710–715. [Google Scholar] [CrossRef]
- Noureen, S.; Atique, S.; Roy, V.; Bayne, S. A comparative forecasting analysis of arima model vs. random forest algorithm for a case study of small-scale industrial load. Int. Res. J. Eng. Technol. 2019, 6, 1812–1821. [Google Scholar]
- Rady, E.; Fawzy, H.; Fattah, A.M.A. Time series forecasting using tree based methods. J. Stat. Appl. Probab. 2021, 10, 229–244. [Google Scholar]
- Milunovich, G. Forecasting australia’s real house price index: A comparison of time series and machine learning methods. J. Forecast. 2020, 39, 1098–1118. [Google Scholar] [CrossRef]
- Jain, M.; AlSkaif, T.; Dev, S. Are deep learning models more effective against traditional models for load demand forecasting? In Proceedings of the 2022 International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, The Netherlands, 5–7 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Cerqueira, V.; Torgo, L.; Mozetič, I. Evaluating time series forecasting models: An empirical study on performance estimation methods. Mach. Learn. 2020, 109, 1997–2028. [Google Scholar] [CrossRef]
- Cerqueira, V.; Torgo, L.; Smailović, J.; Mozetič, I. A comparative study of performance estimation methods for time series forecasting. In Proceedings of the 2017 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Tokyo, Japan, 19–21 October 2017; pp. 529–538. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, S.; Liwen, L.; Xia, Q. Forecasting agricultural commodity prices using model selection framework with time series features and forecast horizons. IEEE Access 2020, 8, 28197–28209. [Google Scholar] [CrossRef]
- Savrul, M.; Incekara, A. The effect of R&D intensity on innovation performance: A country level evaluation. Procedia-Soc. Behav. Sci. 2015, 210, 388–396. [Google Scholar] [CrossRef]
- Deschryvere, M.; Husso, K.; Suominen, A. Targeting & Intensity in Finnish Innovation Policy. 2021. Available online: https://www.oecd-ilibrary.org/content/paper/51c767c9-en (accessed on 20 December 2022).
- Trovero, M.A.; Leonard, M.J. Time Series Feature Extraction. Paper SAS2020 (2018). 2018, pp. 1–18. Available online: https://www.sas.com/content/dam/SAS/support/en/sas-global-forum-proceedings/2018/2020-2018.pdf (accessed on 5 December 2022).
- Scikit-Learn, Compare the Effect of Different Scalers on Data with Outliers. Available online: https://scikitlearn.org/stable/autoexamples/preprocessing/plotallscaling.html (accessed on 28 December 2022).
- Brockwell, P.J.; Davis, R.A. Time Series: Theory and Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Mehtab, S.; Sen, J.; Dutta, A. Stock Price Prediction Using Machine Learning and Lstm-Based Deep Learning Models. In Proceedings of the Symposium on Machine Learning and Metaheuristics Algorithms, and Applications, Chennai, India, 14–17 October 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 88–106. [Google Scholar]
- Amin, M.A.A.; Hoque, M.A. Comparison of arima and svm for shortterm load forecasting. In Proceedings of the 2019 9th Annual Information Technology, Electromechanical Engineering and Microelectronics Conference (IEMECON), Jaipur, India, 13–15 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Lei, C.; Deng, J.; Cao, K.; Xiao, Y.; Ma, L.; Wang, W.; Ma, T.; Shu, C. A comparison of random forest and support vector machine approaches to predict coal spontaneous combustion in gob. Fuel 2019, 239, 297–311. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, W.; Gutierrez, M. Effectiveness of predicting tunneling-induced ground settlements using machine learning methods with small datasets. J. Rock Mech. Geotech. Eng. 2022, 14, 1028–1041. [Google Scholar] [CrossRef]
- Candelieri, A.; Giordani, I.; Archetti, F.; Barkalov, K.; Meyerov, I.; Polovinkin, A.; Sysoyev, A.; Zolotykh, N. Tuning hyperparameters of a svm-based water demand forecasting system through parallel global optimization. Comput. Oper. Res. 2019, 106, 202–209. [Google Scholar] [CrossRef]
- Bhoj, N.; Bhadoria, R.S. Time-series based prediction for energy consumption of smart home data using hybrid convolution-recurrent neural network. Telemat. Inform. 2022, 75, 101907. [Google Scholar] [CrossRef]
- Claveria, O.; Monte, E.; Torra, S. Modelling tourism demand to spain with machine learning techniques. the impact of forecast horizon on model selection. arXiv 2018, arXiv:1805.00878. [Google Scholar]
- Sun, Y.; Ding, S.; Zhang, Z.; Jia, W. An improved grid search algorithm to optimize svr for prediction. Soft Comput. 2021, 25, 5633–5644. [Google Scholar] [CrossRef]





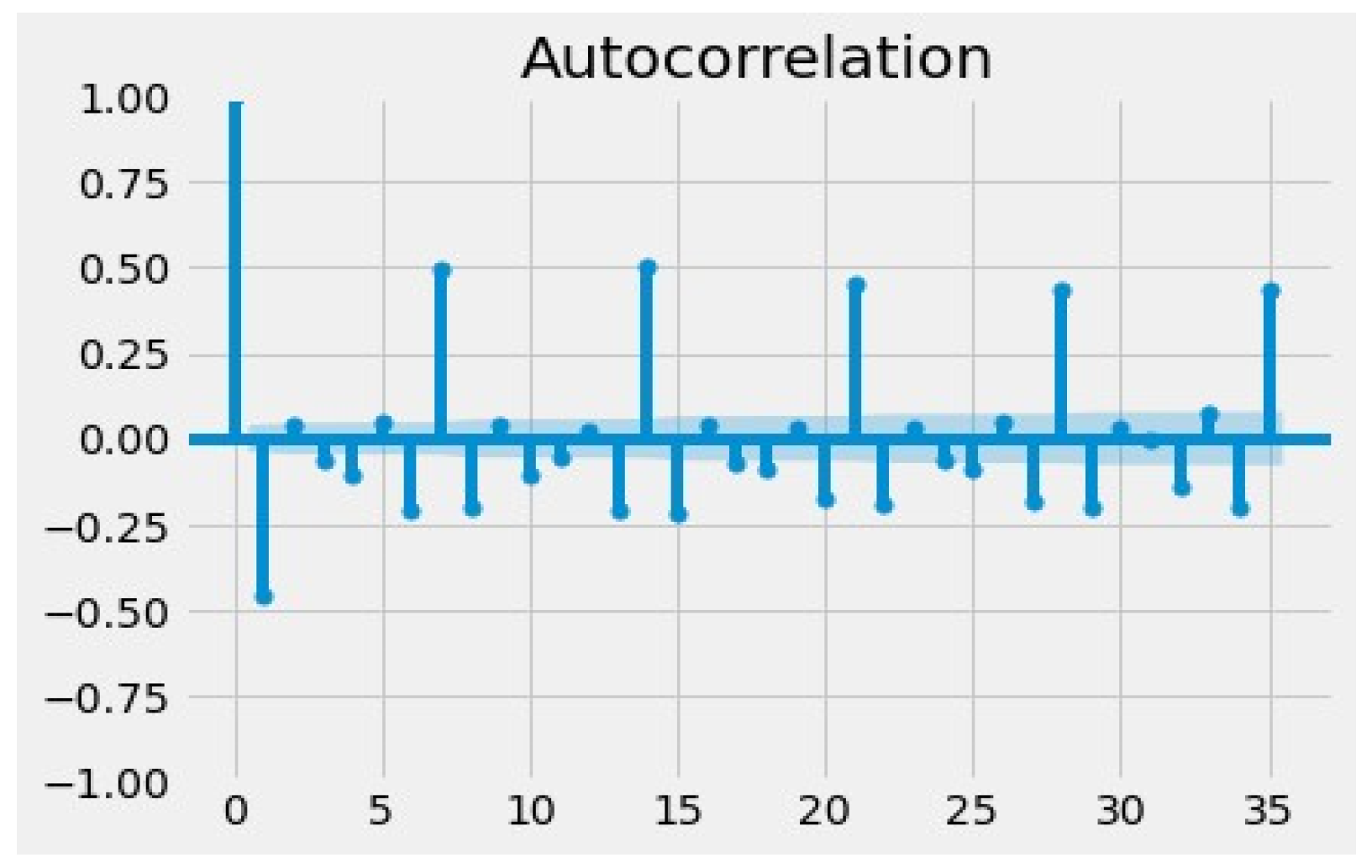
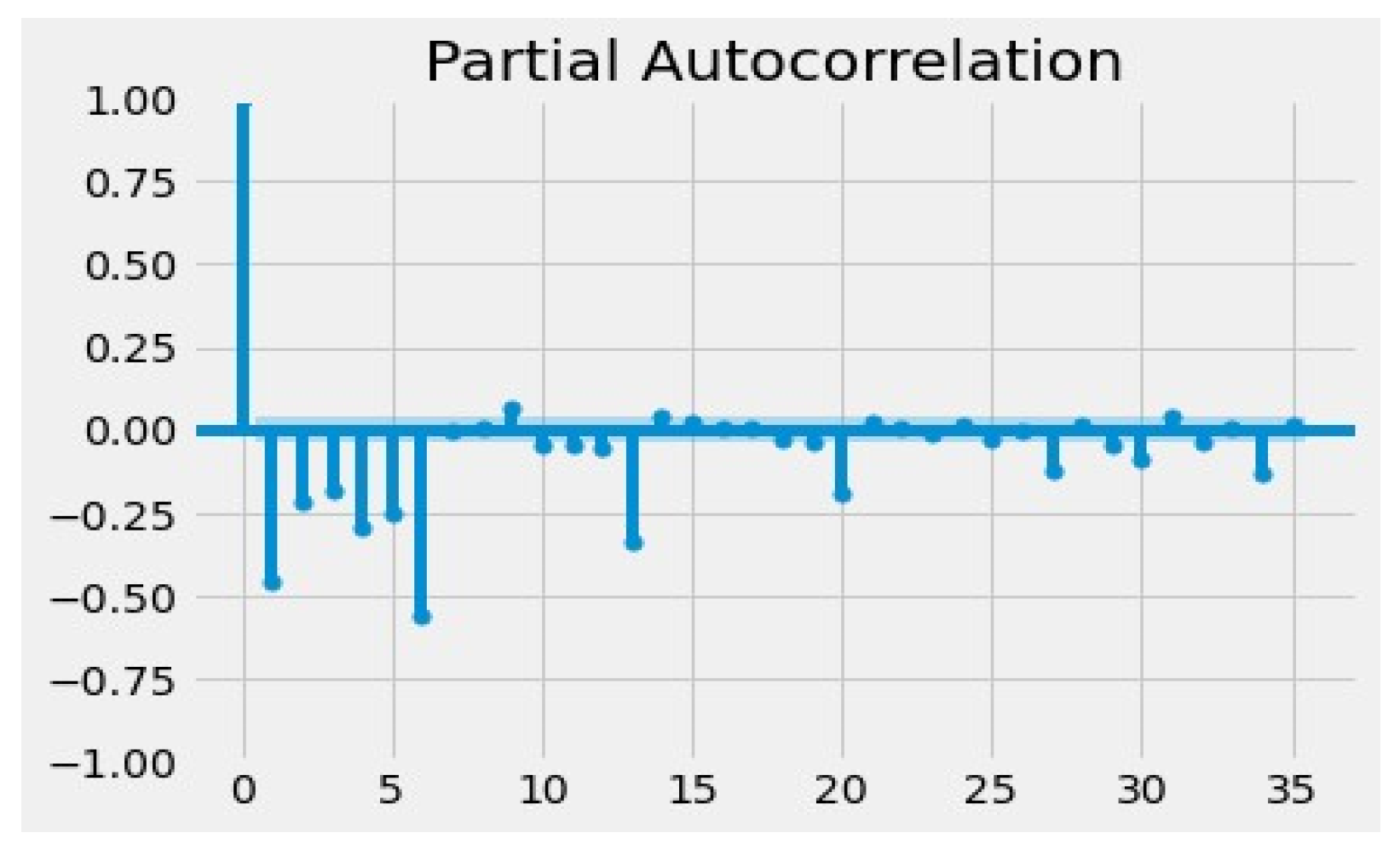
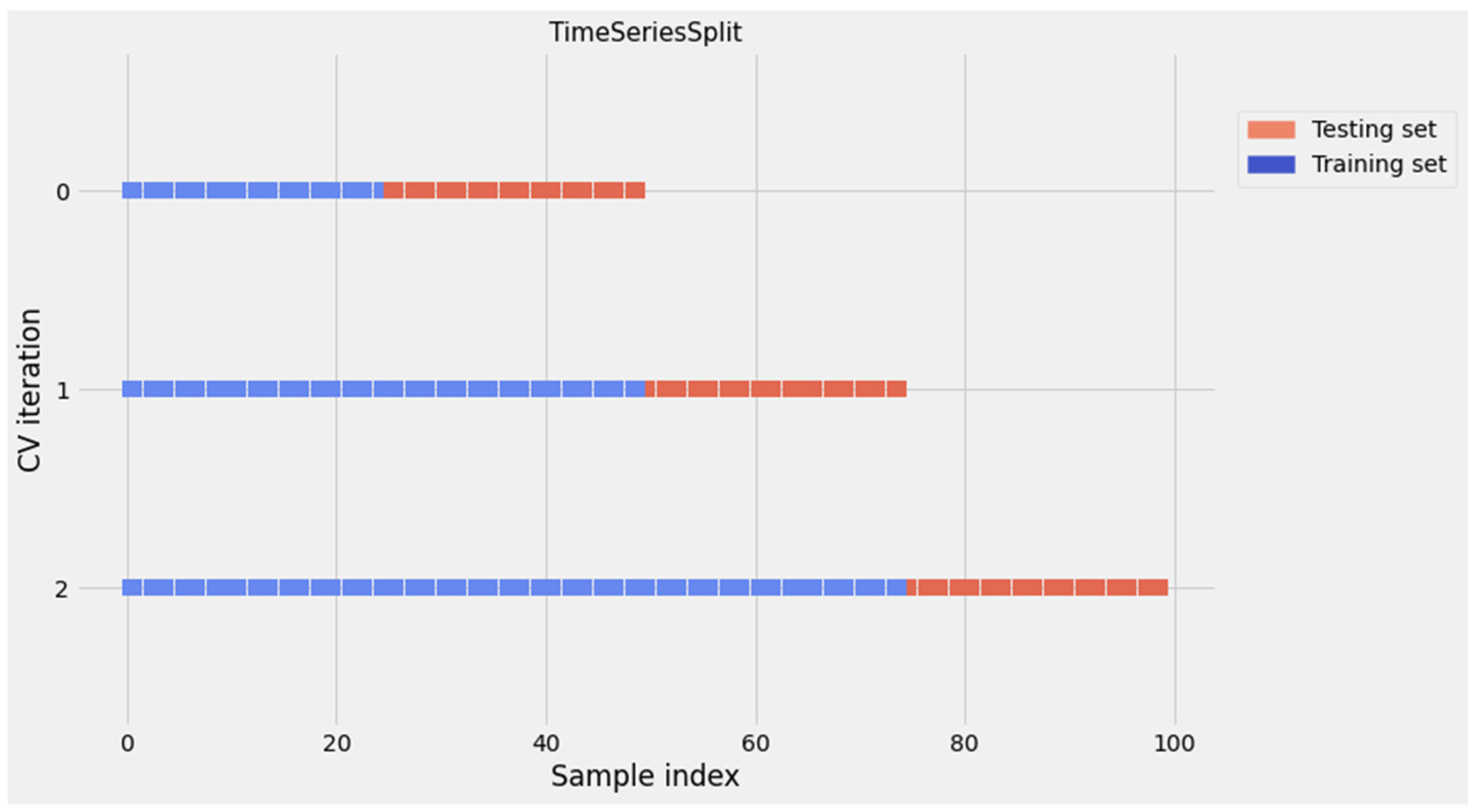


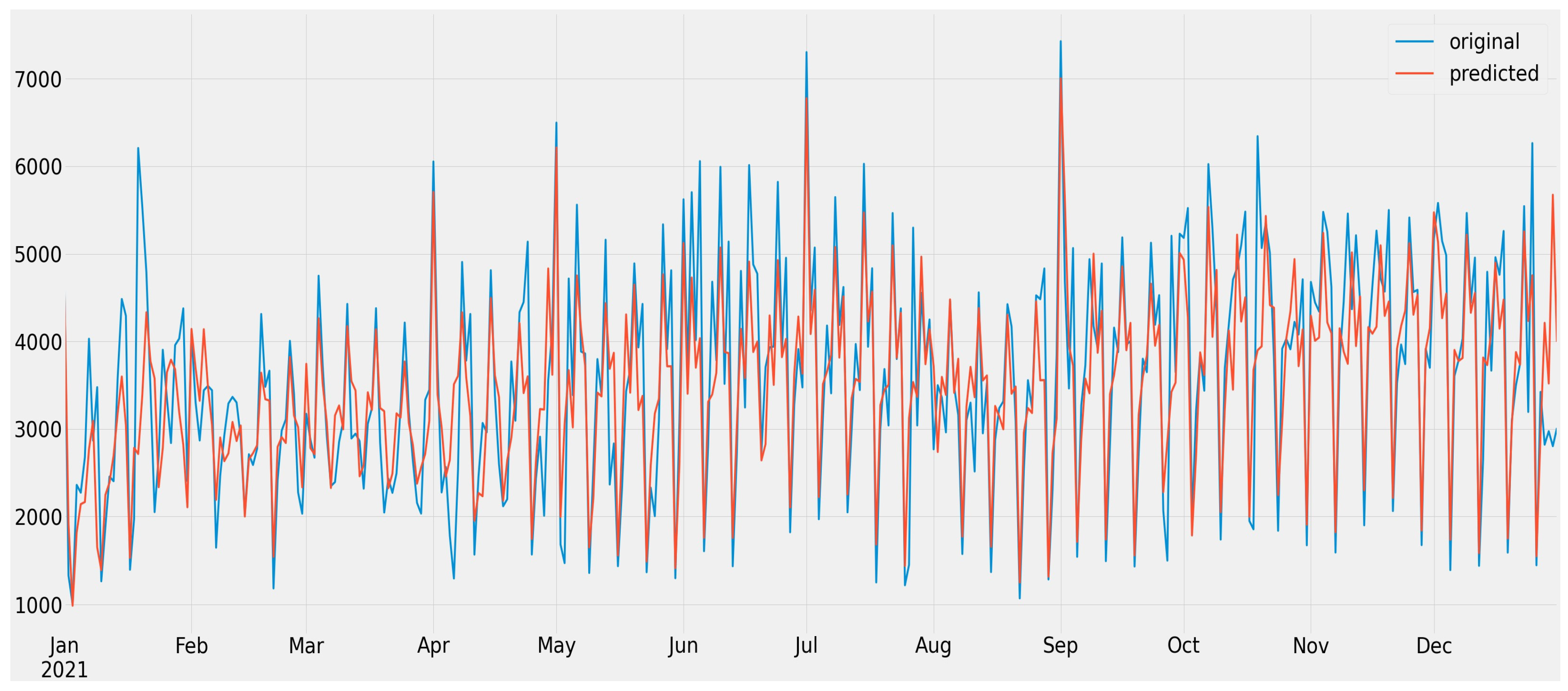
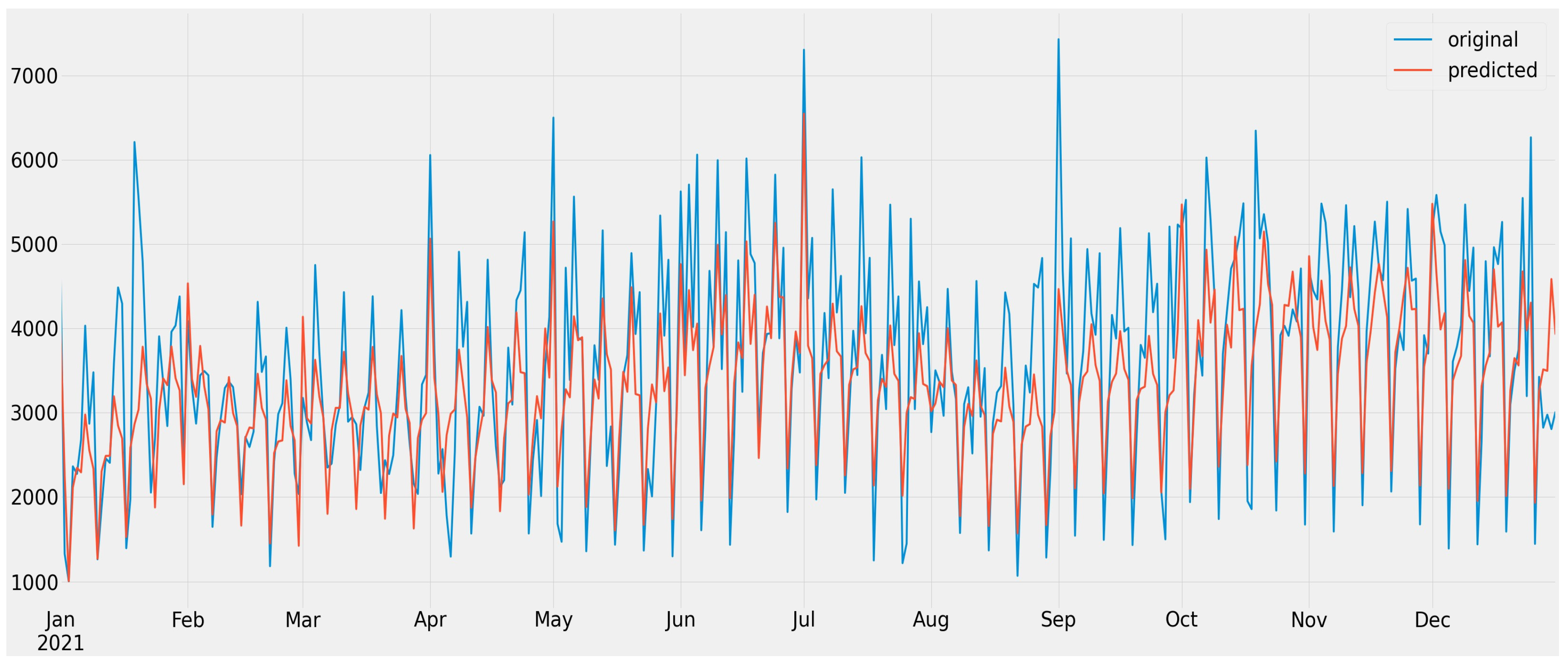
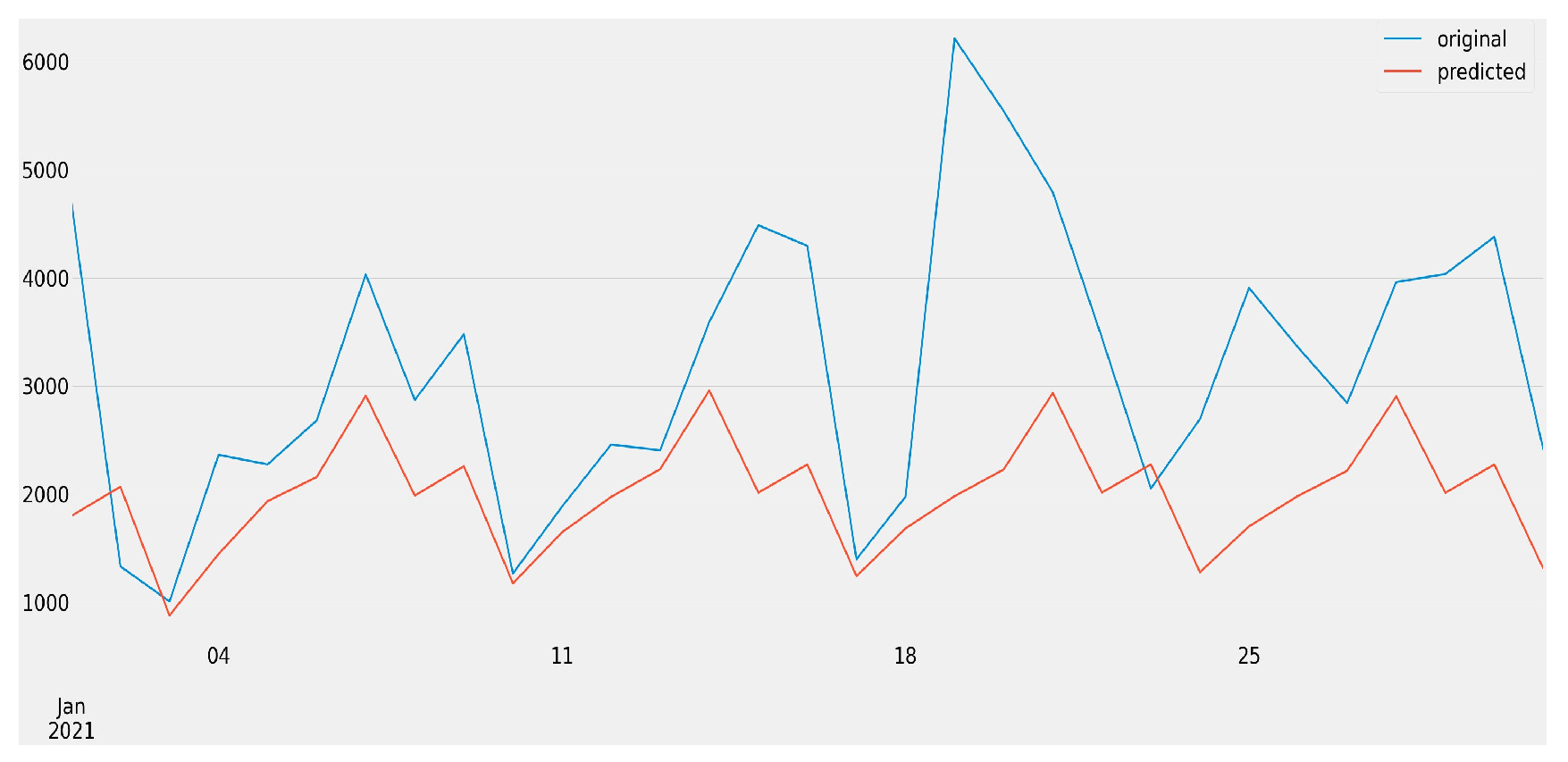
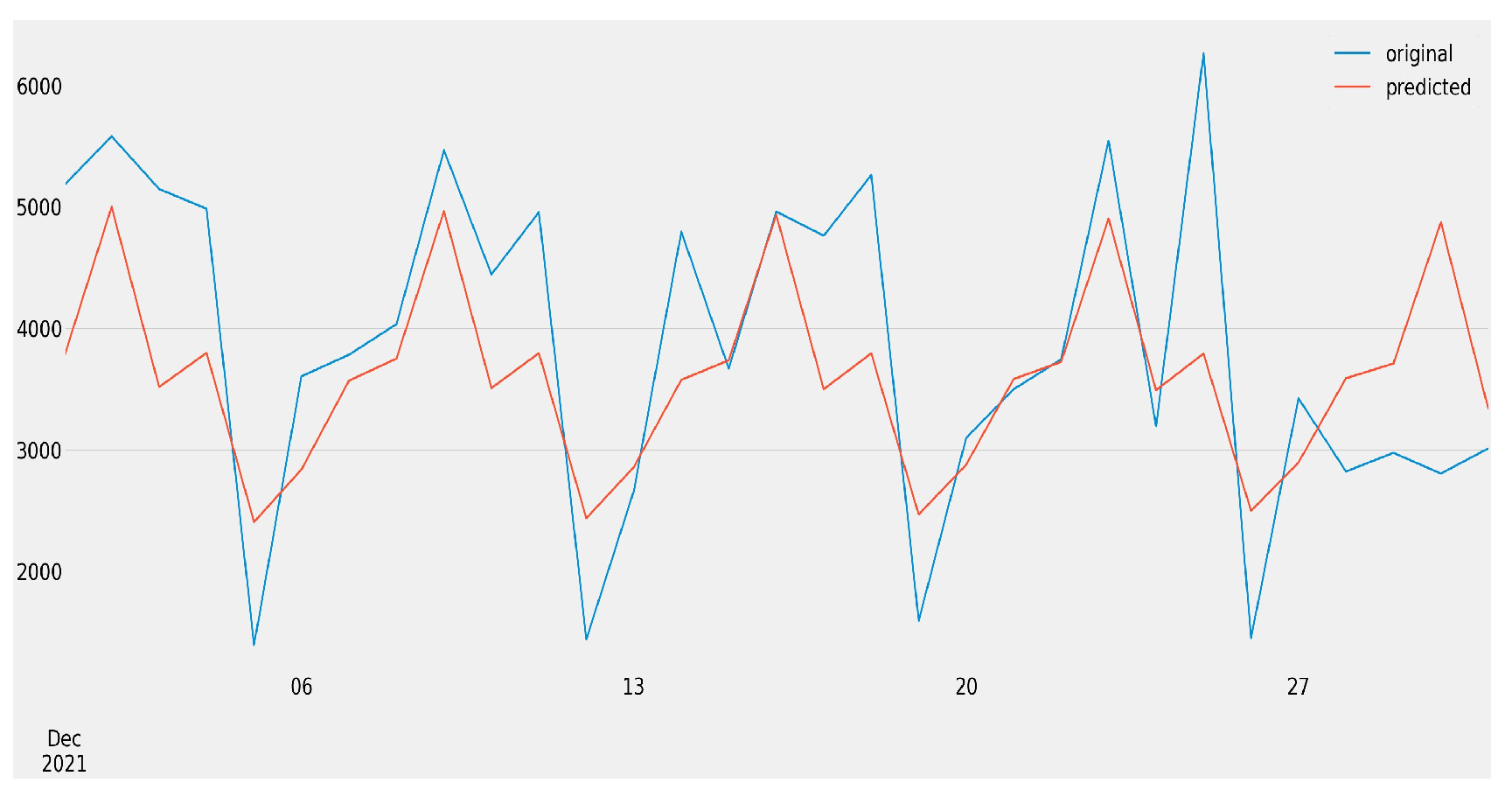
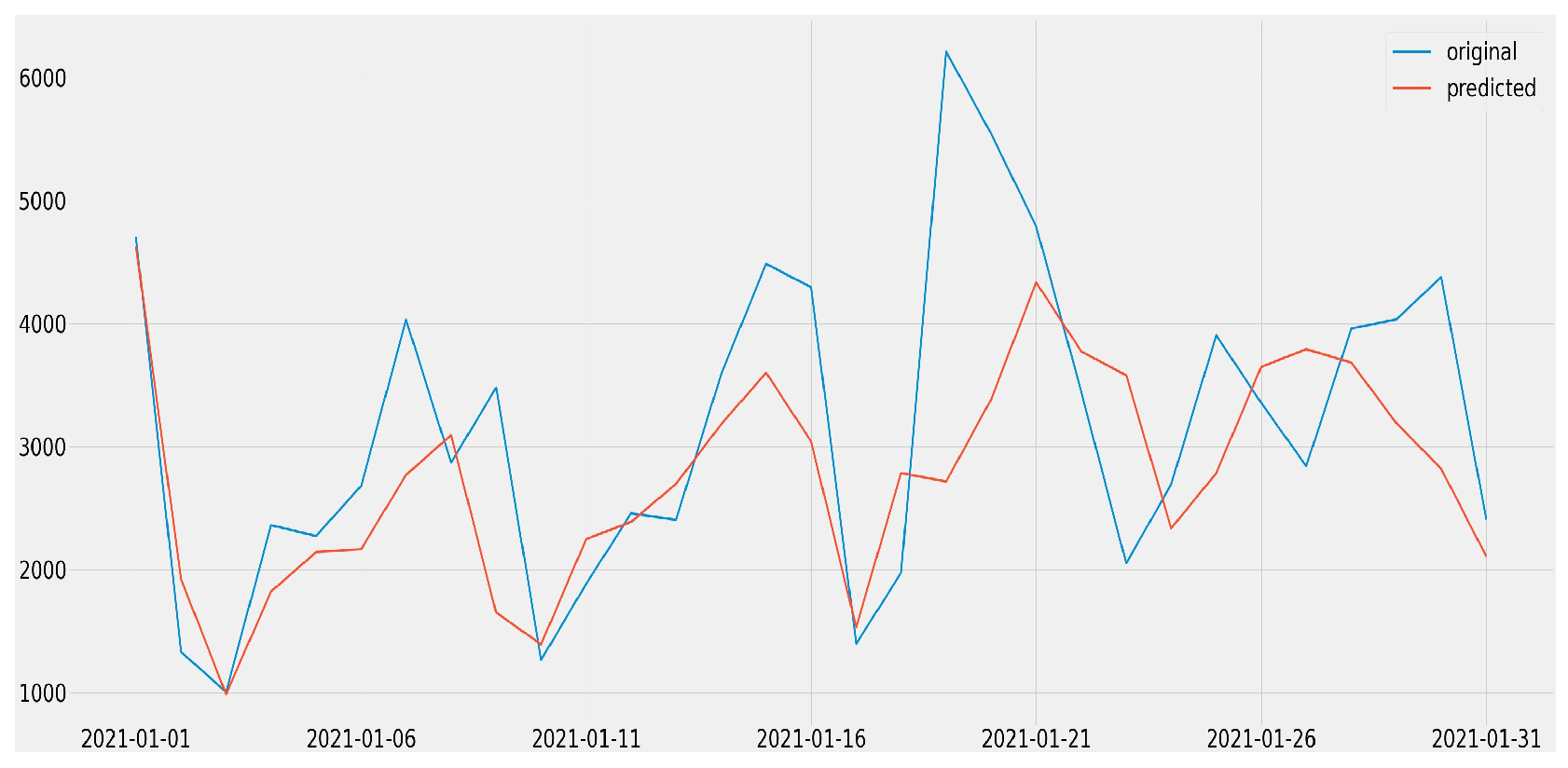
| Name of the Dataset | A Feature Used to Aggregate | Levels of the Feature |
|---|---|---|
| All vacancies | - | 1 |
| Innovativness | innovative | 2 |
| Educational | educationdegreeminimumrequired | 4 |
| Province | physicallocationprovince | 12 |
| Name of the Feature | Original Type |
|---|---|
| year | categorical |
| is year start | binary |
| quarter | categorical |
| month | categorical |
| is month start | binary |
| day | categorical |
| day of week | categorical |
| weekend | binary |
| Name of the Feature | Size of Window Function |
|---|---|
| Rolling mean | 14 |
| Rolling standard deviation | 14 |
| Rolling minimum | 7 |
| Rolling maximum | 7 |
| Forecasting Dataset | Number of Lags |
|---|---|
| All vacancies | 20 |
| Innovative | 27 |
| Educational | 28 |
| Province | 28 |
| Property | Minimal Value | Maximal Value | Value |
|---|---|---|---|
| p | 1 | 10 | - |
| q | 1 | 10 | - |
| d | - | - | 1 |
| stepwise | - | - | True |
| maxiter | - | - | 50 |
| Hyper-Parameter | Selected Values |
|---|---|
| max depth | [None, 30, 50, 80] |
| min samples leaf | [1, 2, 4, 6] |
| min samples split | [2, 4, 6, 8] |
| n estimators | [100, 200] |
| Hyper-Parameter | Selected Values |
|---|---|
| kernel | [’rbf’, ’sigmoid’] |
| gamma | [1 × 10−4, 1 × 10−3, 0.01, 0.1] |
| C | [1, 10, 100, 1000, 10,000] |
| epsilon | [0.001, 0.01, 0.1] |
| Model | MAE | MAPE | RMSE | Execution Time in Minutes [0.5 ex] |
|---|---|---|---|---|
| ARIMA | 869.79 | 26.1% | 1119.64 | <1 |
| RFR | 512.09 | 15.69% | 698.85 | ~6 |
| SVR | 597.90 | 17.85% | 781.32 | <1 |
| Model | MAE | MAPE | RMSE [0.5 ex] |
|---|---|---|---|
| RFR without tuning | 516.19 | 15.81% | 707.64 |
| RFR with tuning | 512.09 | 15.69% | 698.85 |
| RFR with extra predictors and tuning | 506.70 | 15.54% | 695.71 |
| SVR without tuning | 1349.28 | 36.18% | 1647.86 |
| SVR with tuning | 597.90 | 17.85% | 781.32 |
| Model | MAE | MAPE | RMSE | Execution Time in Minutes [0.5 ex] |
|---|---|---|---|---|
| ARIMA | 524.09 | 37.9% | 893.79 | 8 |
| RFR | 259.47 | 19.8% | 484.53 | 14 |
| SVR | 260 | 18.48% | 459.49 | <1 |
| Model | MAE | MAPE | RMSE | Execution Time in Minutes [0.5 ex] |
|---|---|---|---|---|
| ARIMA | 198.87 | 33.81% | 330.87 | ~12 |
| RFR | 115.91 | 25.9% | 200.07 | ~47 |
| SVR | 110.76 | 19.27% | 193.18 | ~3 |
| Model | MAE | MAPE | RMSE | Execution Time in Minutes [0.5 ex] |
|---|---|---|---|---|
| ARIMA | 83.31 | 35.35% | 132.57 | ~30 |
| RFR | 48.86 | 21.68% | 78.71 | 82 |
| SVR | 37.2 | 15.35% | 62.63 | ~14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajewski, P.; Čule, B.; Rankovic, N. Unveiling the Power of ARIMA, Support Vector and Random Forest Regressors for the Future of the Dutch Employment Market. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1365-1403. https://doi.org/10.3390/jtaer18030069
Gajewski P, Čule B, Rankovic N. Unveiling the Power of ARIMA, Support Vector and Random Forest Regressors for the Future of the Dutch Employment Market. Journal of Theoretical and Applied Electronic Commerce Research. 2023; 18(3):1365-1403. https://doi.org/10.3390/jtaer18030069
Chicago/Turabian StyleGajewski, Piotr, Boris Čule, and Nevena Rankovic. 2023. "Unveiling the Power of ARIMA, Support Vector and Random Forest Regressors for the Future of the Dutch Employment Market" Journal of Theoretical and Applied Electronic Commerce Research 18, no. 3: 1365-1403. https://doi.org/10.3390/jtaer18030069
APA StyleGajewski, P., Čule, B., & Rankovic, N. (2023). Unveiling the Power of ARIMA, Support Vector and Random Forest Regressors for the Future of the Dutch Employment Market. Journal of Theoretical and Applied Electronic Commerce Research, 18(3), 1365-1403. https://doi.org/10.3390/jtaer18030069







