Return Policy Selection Analysis for Brands Considering MCN Click Farming and Customer Disappointment Aversion
Abstract
1. Introduction
2. Literature Review
2.1. Live Streaming E-Commerce and Click Farming
2.2. Return Policy Selection
2.3. Disappointment Aversion
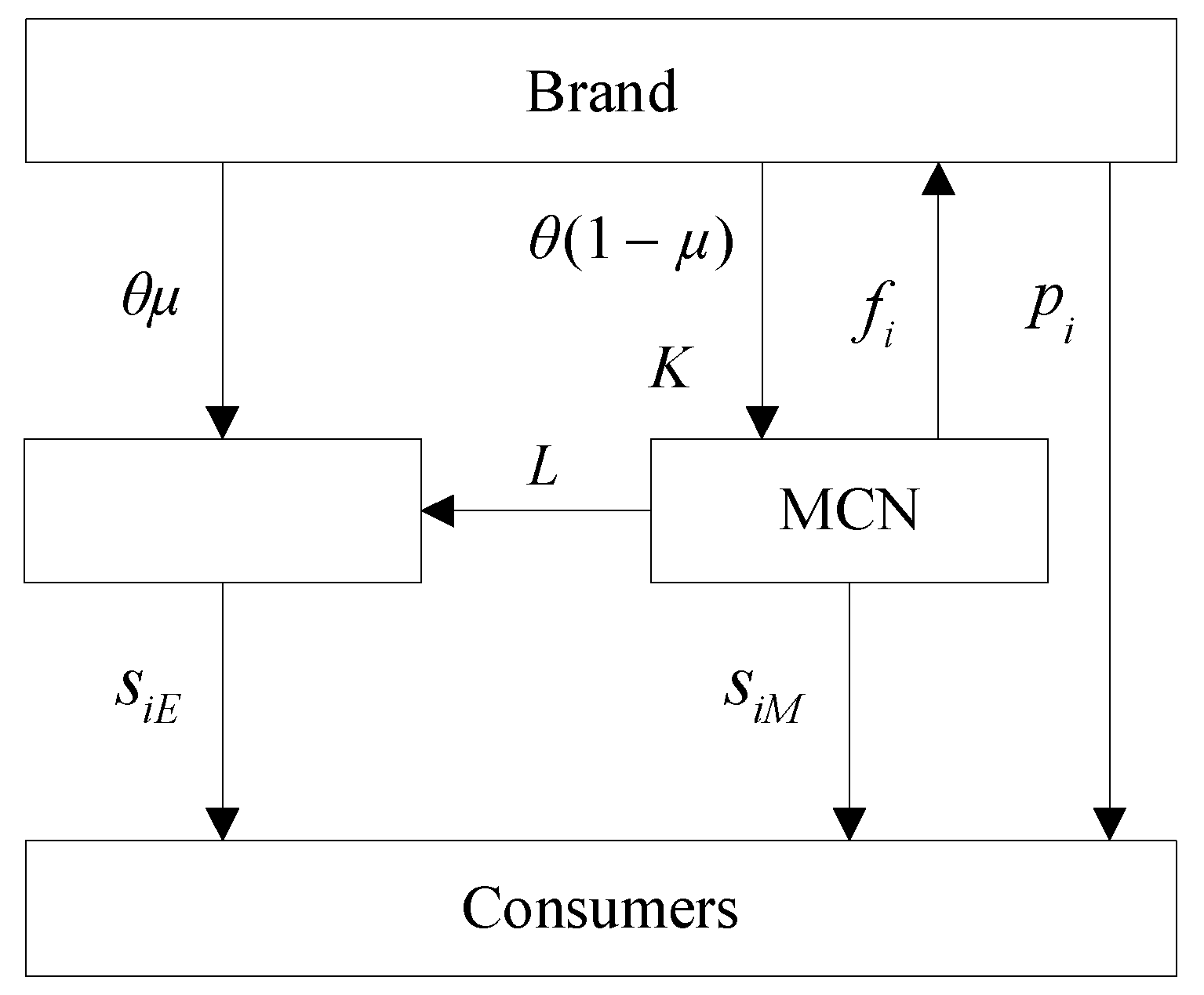
3. Problem Formulation
3.1. Subsection
3.2. Assumptions
4. The Models
4.1. Model H for Return-Freight Insurance by Brand
4.2. Model C for Return-Freight Insurance by Consumers
4.3. Model T for Return-Freight Insurance Jointly by Brand and MCN
5. Numerical Experiments
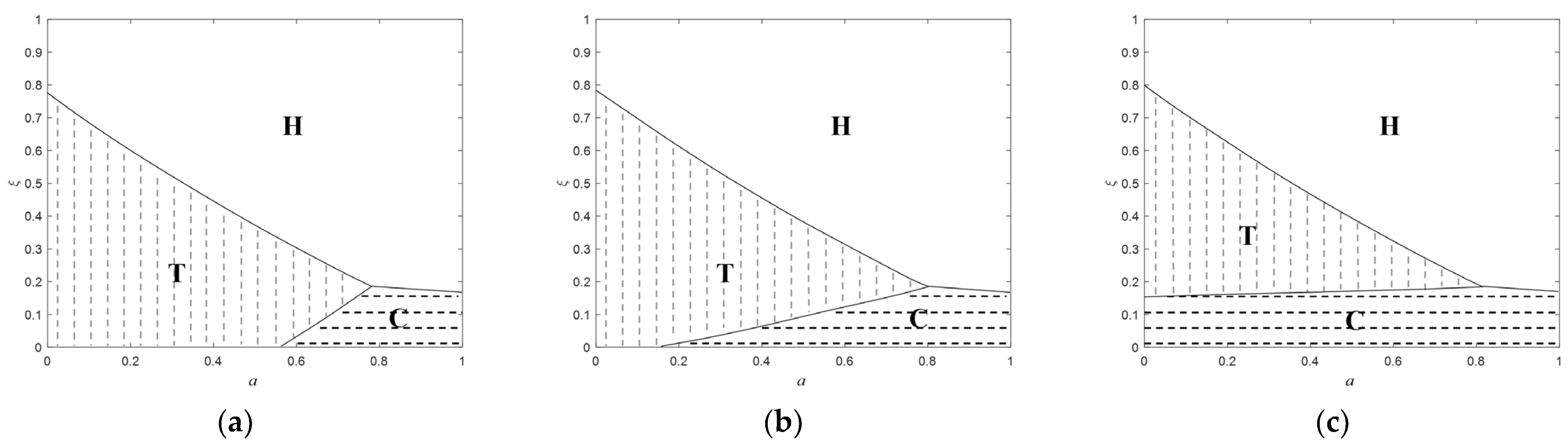
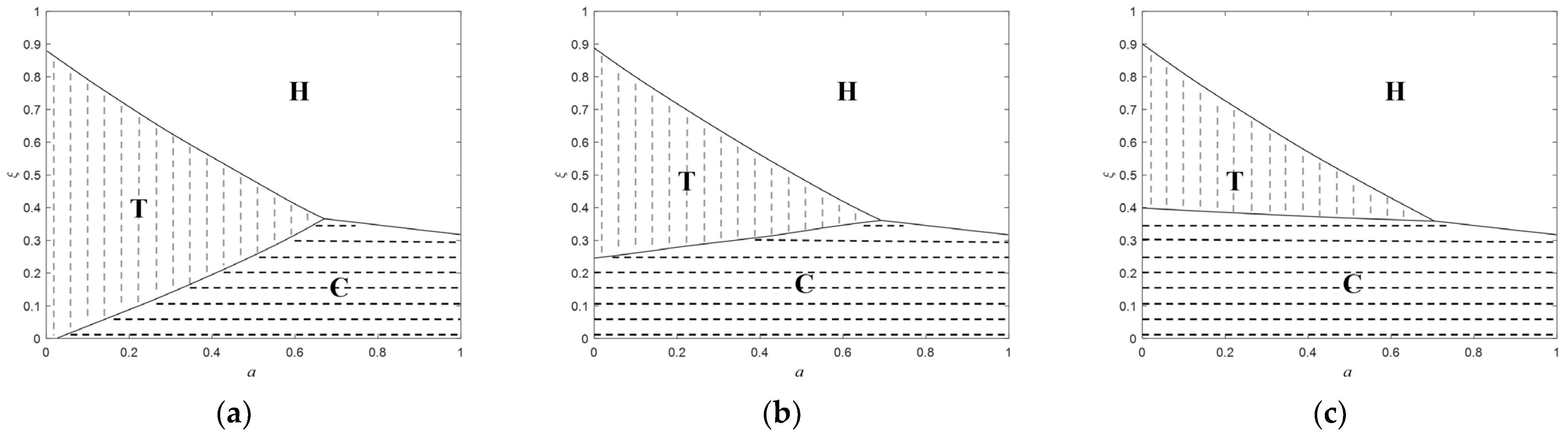
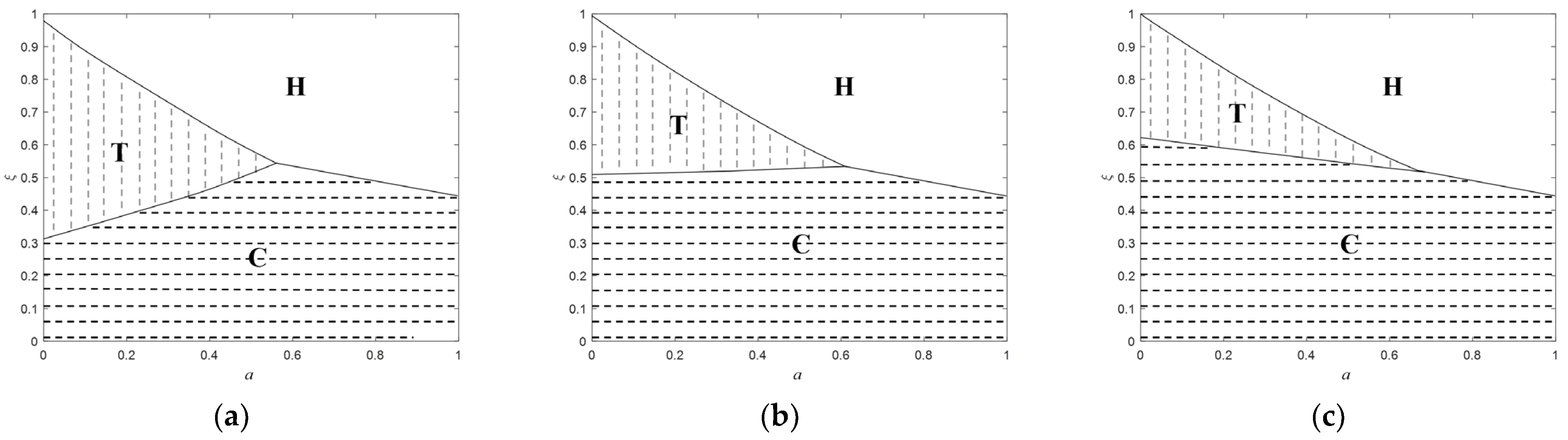
5.1. Return Policy Selection
5.1.1. Low Commission Rate Scenario ()
5.1.2. Medium Commission Rate Scenario ()
5.1.3. High Commission Rate Scenario ()
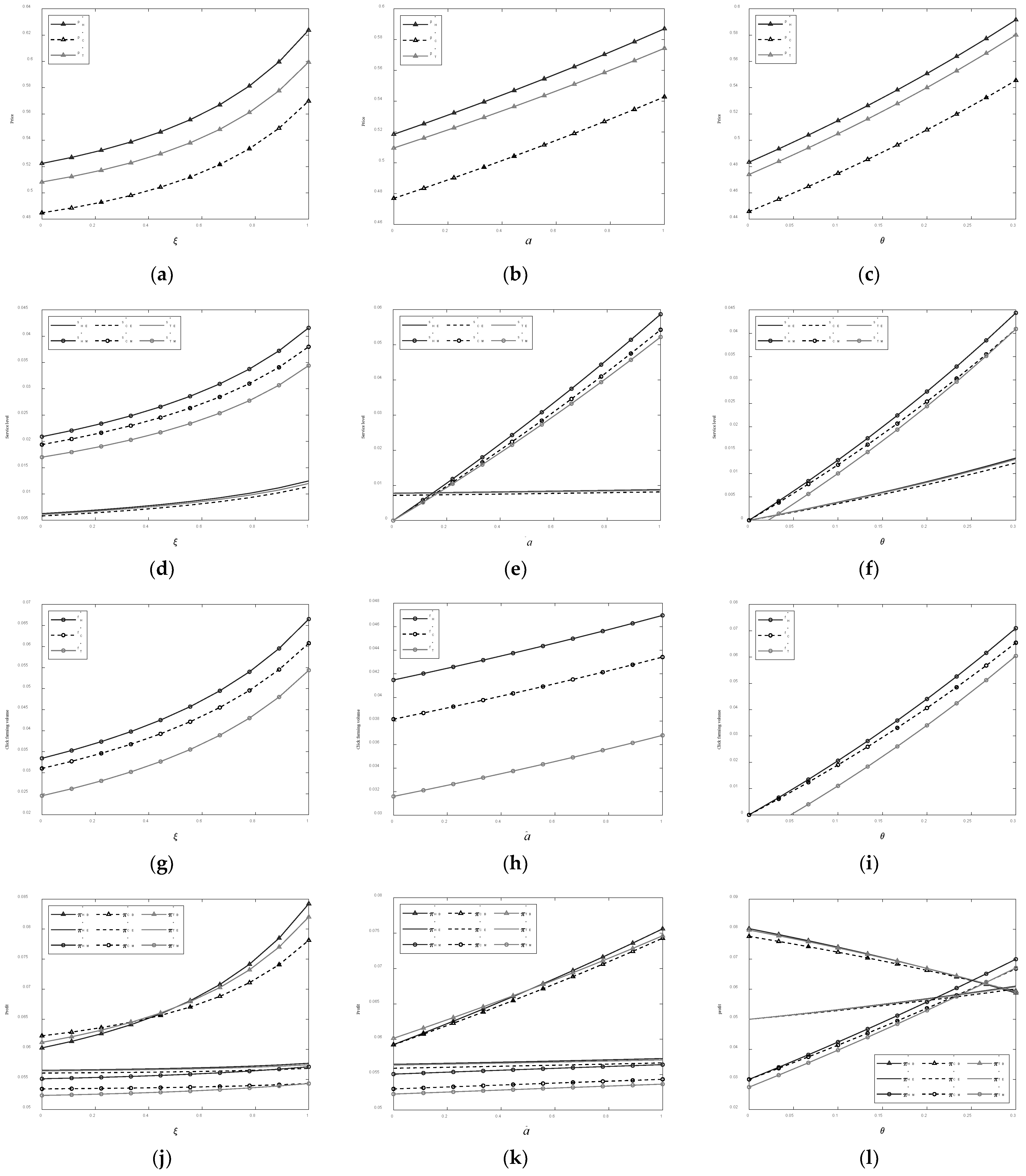
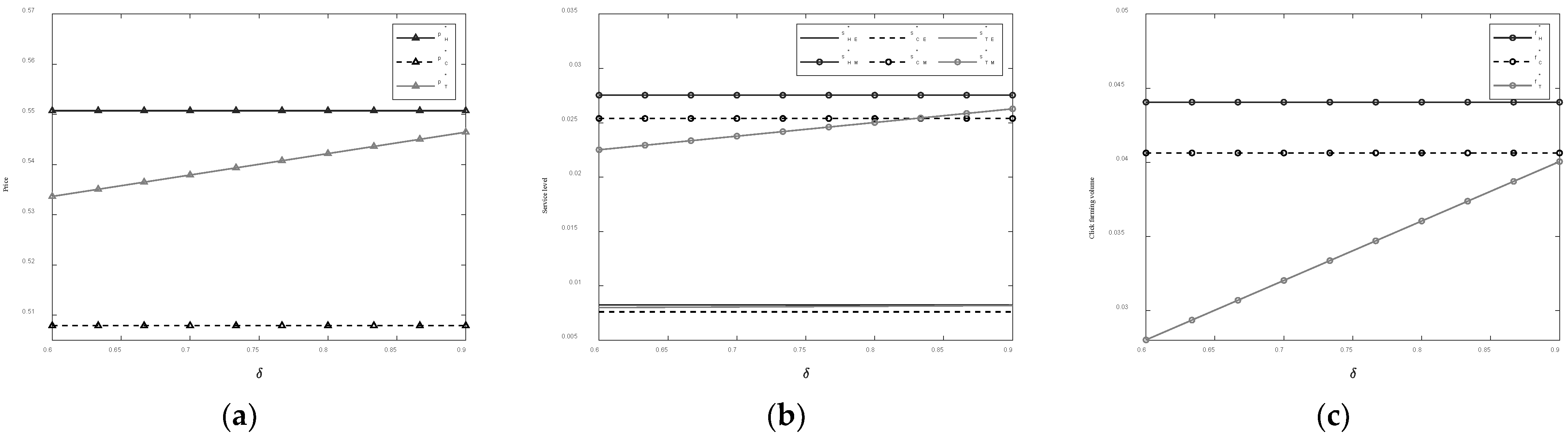
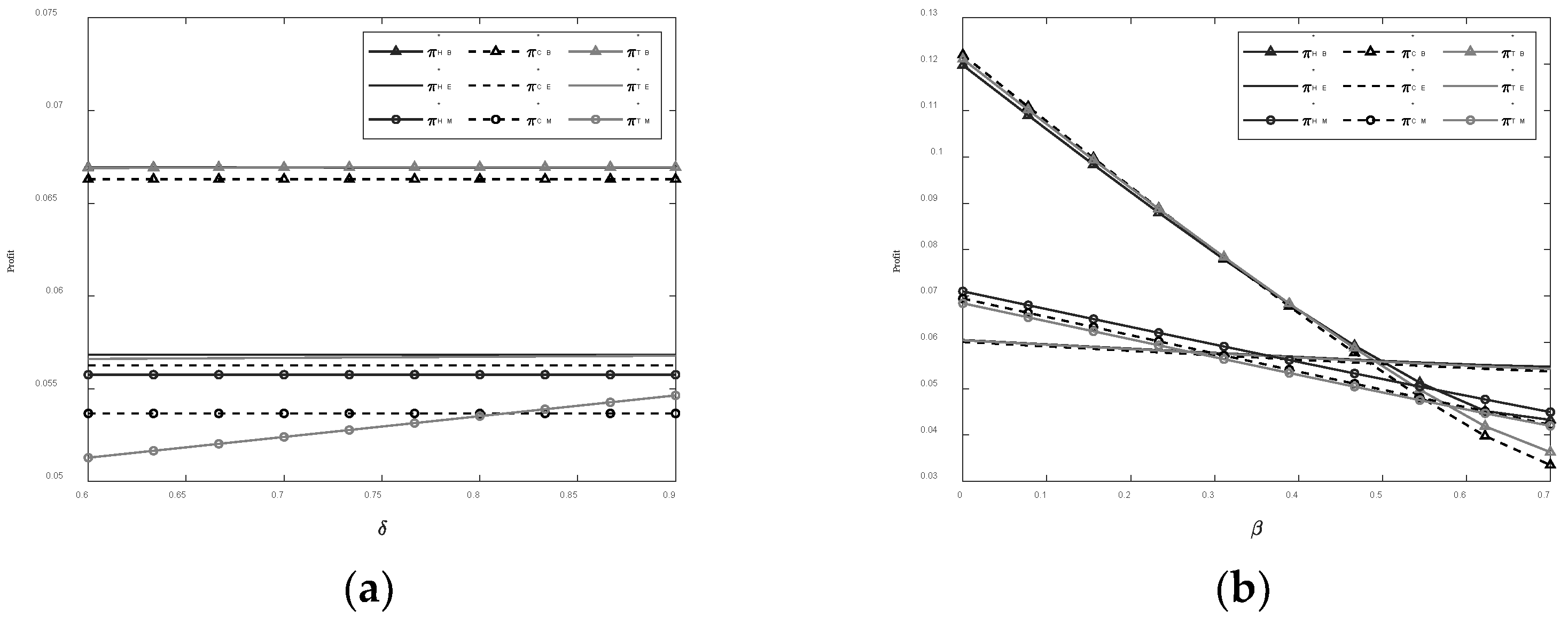
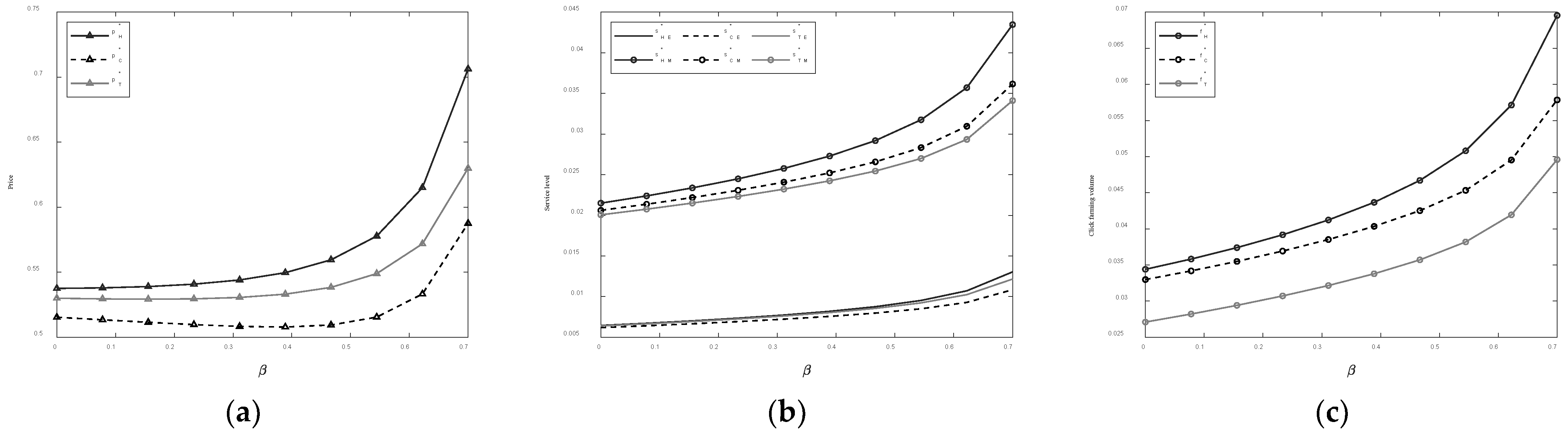
5.2. Sensitivity Analysis of Optimal Decisions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Bell, D.E. Disappointment in decision making under uncertainty. Oper. Res. 1985, 33, 1–27. [Google Scholar] [CrossRef]
- Chen, S.J.; Guan, Z.Z. Research on return policies of omni-channel retailer considering consumers disappointment aversion. China J. Manag. Sci. 2021. [Google Scholar] [CrossRef]
- Du, S.F.; Li, W.; Li, H. Omnichannel management with consumer disappointment aversion. Int. J. Prod. Econ. 2019, 215, 84–101. [Google Scholar] [CrossRef]
- Wongkitrungrueng, A.; Dehouche, N.; Assarut, A. Live streaming commerce from the sellers’ perspective: Implications for online relationship marketing. J. Market. Manag. 2020, 36, 488–518. [Google Scholar] [CrossRef]
- Lu, B.J.; Chen, Z.J. Live streaming commerce and consumers’ purchase intention: An uncertainty reduction perspective. Inf. Manag. 2021, 58, 103509. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.L.; Cai, J.L. How attachment affects user stickiness on live streaming platforms: A socio-technical approach perspective. J. Retail. Consum. Serv. 2021, 60, 102478. [Google Scholar] [CrossRef]
- Iimedia Research. China’s Live Streaming E-Commerce Industry: The Total Scale is Expected to Reach 2137.3 Billion Yuan by 2025. 2022. Available online: https://mp.weixin.qq.com/s/kauGkdsQ8qDq4r_MA4GJZA (accessed on 3 July 2022).
- Zhang, P.P. Internet celebrity “Factory”: The development history, rise logic and future trend of MCN. Future Commun. 2021, 28, 48–54. [Google Scholar] [CrossRef]
- Huang, M.; Chu, X.P. The Problem and Governance of Internet Traffic in Live Streaming E-Commerce. 2021. Available online: https://d.wanfangdata.com.cn/periodical/ChlQZXJpb2RpY2FsQ0hJTmV3UzIwMjIwOTAxEgx4d2MyMDIxMDEwMDQaCGR5d2ZhN21t (accessed on 25 February 2021).
- Jiang, C.X.; Zhu, J.; Xu, Q.F. Dissecting click farming on the Taobao platform in China via PU learning and weighted logistic regression. Electron. Commer. Res. 2020, 22, 157–176. [Google Scholar] [CrossRef]
- Bao, L.J.; Zhong, W.J.; Mei, Z.E. The influence of “Click farming” on the sellers’ competition in e-commerce platform. Syst. Eng. Theory Pract. 2021, 41, 2876–2886. [Google Scholar]
- 36 Kr Research Institute. 2020 China Live Streaming E-Commerce Industry Research Report. 2020. Available online: https://36kr.com/p/986332005917833 (accessed on 2 December 2020).
- Fan, Z.P.; Chen, Z.W. When should the e-tailer offer complimentary return-freight insurance? Int. J. Prod. Econ. 2020, 230, 107890. [Google Scholar] [CrossRef]
- Ang, T.; Wei, S.; Anaza, N.A. Livestreaming vs. pre-recorded: How social viewing strategies impact consumers’ viewing experiences and behavioral intentions. Eur. J. Market. 2018, 52, 2075–2104. [Google Scholar] [CrossRef]
- Hou, F.F.; Guan, Z.Z.; Li, B.Y.; Chong, A.Y.L. Factors influencing people’s continuous watching intention and consumption intention in live streaming: Evidence from China. Internet Res. 2020, 1, 141–163. [Google Scholar] [CrossRef]
- Ma, Y.Y. To shop or not: Understanding Chinese consumers’ live-stream shopping intentions from the perspectives of uses and gratifications, perceived network size, perceptions of digital celebrities, and shopping orientations. Telemat. Inform. 2021, 59, 101562. [Google Scholar] [CrossRef]
- Sun, Y.; Shao, X.; Li, X.T.; Guo, Y.; Nie, K. How live streaming influences purchase intentions in social commerce: An IT affordance perspective. Electron. Commer. Res. Appl. 2019, 37, 100886. [Google Scholar] [CrossRef]
- Xu, X.Y.; Wu, J.H.; Li, Q. What drives consumer shopping behavior in live streaming commerce? J. Electron. Commer. Res. 2020, 21, 144–167. Available online: http://www.jecr.org/node/609 (accessed on 1 August 2020).
- Zhang, M.; Sun, L.; Qin, F.; Wang, G.A. E-service quality on live streaming platforms: Swift guanxi perspective. J. Serv. Mark. 2021, 35, 312–324. [Google Scholar] [CrossRef]
- Wang, X.; Tao, Z.Y.; Liang, L.; Gou, Q.L. An analysis of salary mechanisms in the sharing economy: The interaction between streamers and unions. Int. J. Prod. Econ. 2019, 214, 106–124. [Google Scholar] [CrossRef]
- Xing, P.; You, H.Y.; Fan, Y.C. Optimal quality effort strategy in service supply chain of live streaming e-commerce based on platform marketing effort. Control Decis. 2022, 37, 205–212. [Google Scholar]
- Hu, J.; Li, L.; Zhang, H.; Zhu, X.Z.; Yang, W.S. Dynamic pricing strategies for live broadcast platform considering reference effect and anchor influence. Syst. Eng. Theory Pract. 2022, 42, 756–766. [Google Scholar]
- Liu, H.Y.; Liu, S.L. Optimal decisions and coordination of live streaming selling under revenue-sharing contracts. Manag. Decis. Econ. 2021, 42, 1022–1036. [Google Scholar] [CrossRef]
- Zhao, J.; Lau, R.Y.K.; Zhang, W.P.; Zhang, K.H.; Chen, X.; Tang, D. Extracting and reasoning about implicit behavioral evidences for detecting fraudulent online transactions in e-commerce. Decis. Support Syst. 2016, 86, 109–121. [Google Scholar] [CrossRef]
- Li, N.; Du, S.G.; Zheng, H.Z.; Xue, M.H.; Zhu, H.J. Fake reviews tell no tales? Dissecting click farming in content-generated social networks. China Commun. 2018, 15, 98–109. [Google Scholar] [CrossRef]
- Jiang, C.X.; Zhu, J.; Xu, Q.F. Which goods are most likely to be subject to click farming? An evidence from the Taobao platform. Electron. Commer. Res. Appl. 2021, 50, 101107. [Google Scholar] [CrossRef]
- Fang, X.L. The control of “False transaction and credit standing” behavior in the network trading platform from the perspective of evolutionary game. Inf. Sci. 2018, 36, 89–92. [Google Scholar] [CrossRef]
- McWilliams, B. Money-back guarantees: Helping the low-quality retailer. Manag. Sci. 2012, 58, 1521–1524. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.J.; Govindan, K.; Xu, X.L. Consumer returns policies with endogenous deadline and supply chain coordination. Eur. J. Oper. Res. 2015, 242, 88–99. [Google Scholar] [CrossRef]
- Ren, M.; Liu, J.Q.; Feng, S.; Yang, A.F. Pricing and return strategy of online retailers based on return insurance. J. Retail. Consum. Serv. 2021, 59, 102350. [Google Scholar] [CrossRef]
- Chen, Z.W.; Fan, Z.P.; Zhao, X. Offering return-freight insurance or not: Strategic analysis of an e-seller’s decisions. Omega-Int. J. Manag. Sci. 2021, 103, 102447. [Google Scholar] [CrossRef]
- Chen, B.T.; Chen, J. When to introduce an online channel, and offer money back guarantees and personalized pricing? Eur. J. Oper. Res. 2017, 257, 614–624. [Google Scholar] [CrossRef]
- Radhi, M.; Zhang, G.Q. Optimal cross-channel return policy in dual-channel retailing systems. Int. J. Prod. Econ. 2019, 210, 184–198. [Google Scholar] [CrossRef]
- Jin, D.; Caliskan-Demirag, O.; Chen, F.; Huang, M. Omnichannel retailers’ return policy strategies in the presence of competition. Int. J. Prod. Econ. 2020, 225, 107595. [Google Scholar] [CrossRef]
- Loomes, G.; Sugden, R. Disappointment and dynamic consistency in choice under uncertainty. Rev. Econ. Stud. 1986, 53, 271–282. [Google Scholar] [CrossRef]
- Delquie, P.; Cillo, A. Expectations, disappointment, and rank-dependent probability weighting. Theory Decis. 2006, 60, 193–206. [Google Scholar] [CrossRef]
- Koszegi, B.; Rabin, M. Reference dependent risk attitudes. Am. Econ. Rev. 2007, 97, 1047–1073. [Google Scholar] [CrossRef]
- Liu, Q.; Shum, S. Pricing and capacity rationing with customer disappointment aversion. Prod. Oper. Manag. 2013, 22, 1269–1286. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.L. Strategic customer behavior with disappointment aversion customers and two alleviation policies. Int. J. Prod. Econ. 2017, 191, 170–177. [Google Scholar] [CrossRef]
- Wang, H.; Guan, Z.Z.; Dong, D.Y.; Zhao, N. Optimal pricing strategy with disappointment-aversion and elation-seeking consumers: Compared to price commitment. Int. Trans. Oper. Res. 2021, 28, 2810–2840. [Google Scholar] [CrossRef]
- Simon, A.H. Models of Bounded Rationality; The MIT Press: Cambridge, MA, USA, 1982; Volume 2. [Google Scholar]
- Cao, B.B.; Fan, Z.P.; You, T.H. The newsvendor problem with reference dependence, disappointment aversion and elation seeking. Chaos Solitons Fractals 2017, 104, 568–574. [Google Scholar] [CrossRef]
- Cao, B.B.; Fan, Z.P. Ordering and sales effort investment for temperature-sensitive products considering retailer’s disappointment aversion and elation seeking. Int. J. Prod. Res. 2018, 56, 2411–2436. [Google Scholar] [CrossRef]
- Rintamäki, T.; Kanto, A.; Kuusela, H.; Spence, M.T. Decomposing the value of department store shopping into utilitarian, hedonic and social dimensions: Evidence from Finland. Int. J. Retail Distrib. Manag. 2006, 34, 6–24. [Google Scholar] [CrossRef]
- Chen, J.; Bell, P. The impact of customer returns on decisions in a newsvendor problem with and without buyback policies. Int. Trans. Oper. Res. 2011, 18, 473–491. [Google Scholar] [CrossRef]
- Letizia, P.; Pourakbar, M.; Harrison, T. The impact of consumer returns on the multichannel sales strategies of manufacturers. Prod. Oper. Manag. 2017, 27, 323–349. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Yu, Z.Q. Research on the dominant models and commission coordination mechanism of e-supply chain based on e-commerce sales platform. China J. Manag. Sci. 2019, 27, 109–118. [Google Scholar]
| Set | Definition |
|---|---|
| , indicate the return policy of return-freight insurance by brand, return-freight insurance by consumers, and return-freight insurance jointly by brand and MCN respectively | |
| Parameter | Definition |
| Disappointment-aversion level, | |
| Brand’s return-freight insurance purchasing ratio under the return policy T, | |
| Unit return-freight insurance price, | |
| Under the return policy i, consumer’s valuation of product when the expected utility is 0 | |
| Pit fee | |
| Entry fee | |
| Function | Definition |
| Demand function under the return policy i | |
| Profit function of brand under the return policy i | |
| Profit function of platform under the return policy i | |
| Profit function of MCN under the return policy i | |
| Variable | Definition |
| Price of per unit product under the return policy i | |
| Service level of platform under the return policy i | |
| Service level of MCN under the return policy i | |
| Click farming volume of MCN under the return policy i |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, G.; Xu, W.; Li, Y.; Zhu, X. Return Policy Selection Analysis for Brands Considering MCN Click Farming and Customer Disappointment Aversion. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 1543-1563. https://doi.org/10.3390/jtaer17040078
Lin G, Xu W, Li Y, Zhu X. Return Policy Selection Analysis for Brands Considering MCN Click Farming and Customer Disappointment Aversion. Journal of Theoretical and Applied Electronic Commerce Research. 2022; 17(4):1543-1563. https://doi.org/10.3390/jtaer17040078
Chicago/Turabian StyleLin, Guihua, Wenxuan Xu, Yuwei Li, and Xide Zhu. 2022. "Return Policy Selection Analysis for Brands Considering MCN Click Farming and Customer Disappointment Aversion" Journal of Theoretical and Applied Electronic Commerce Research 17, no. 4: 1543-1563. https://doi.org/10.3390/jtaer17040078
APA StyleLin, G., Xu, W., Li, Y., & Zhu, X. (2022). Return Policy Selection Analysis for Brands Considering MCN Click Farming and Customer Disappointment Aversion. Journal of Theoretical and Applied Electronic Commerce Research, 17(4), 1543-1563. https://doi.org/10.3390/jtaer17040078






