1. Introduction
The last 20 years have seen worldwide outbreaks of various epidemics such as severe acute respiratory syndrome (SARS) in 2002 and the 2014–2016 Ebolan epidemic in West Africa. The recent eruption of the COVID-19, in particular, was upgraded from an epidemic to a pandemic by the World Health Organization (WHO) in March 2020, because of its wide and severe impacts on various aspects of social development (e.g., health, economy, politics, and culture) all over the world. According to Worldometers, a well-known website updating real time world statistics, up to the 7th of April 133,015,276 people in the world caught COVID-19 and 2,885,894 of them have sadly died. The United States alone has recorded a COVID-19 related death toll which even exceeds that of the US Army in World War II.
Governments in various countries have responded to large epidemics such as COVID-19 and the 2014–2016 Ebola epidemic in West African by restricting movement of people and trade [
1,
2]. As a result, E-commerce is deeply suffering from logistics constraints as well. This is because fulfilling e-commerce orders depends on fast logistics, safe transportation (e.g., avoiding the spoilage of goods), and low transport costs [
3]. Poor logistics, having an adverse effect on the reputation of e-commerce retailers [
4], result in low sales and profits [
5]. Through the rapid development of the past two decades, e-commerce has become the most commonly used way of purchasing. With numerous physical stores closed, COVID-19 even impels more consumers to turn to online purchasing for daily life necessities [
3,
6]. However, a large number of e-commerce retailers selling products on platforms (i.e.,
platform–retailer systems) cannot get rid of the transport predicament during an epidemic scenario. A research reported by Paidai.com, a famous community for e-commerce industry in China, shows that during early COVID-19, more than 80% of e-commerce retailers’ revenue fall and 53.93% of retailers claim that the main difficulties are logistics constraints [
7].
Logistics constraints as well as other negative factors due to epidemics result in lower earnings and high risk of e-commerce retailers, which draws the e-commerce platforms’ attention. The platforms act as trade bridges linking retailers and consumers in the two-side e-commerce markets. The role of trade bridges and network effects in platform economy mean that the platforms and the retailers are symbiotic relationships, as their profits are interdependent on each other [
8,
9,
10,
11]. To cushion the blows of epidemics to the retailers and maintain sustainable development of platform economy, various subsidies to the retailers are implemented by the platforms during an epidemic scenario like COVID-19. In fact, subsidies just like paid product reviews [
12], can boost the platforms’ reputation in e-commerce. For instance, Buy Together, a well-known e-commerce platform for group purchasing in China, provided sales subsidies, that is, 3 yuan per order to its retailers from January to February of 2020. What is more, AliExpress, the third largest cross-border e-commerce platform in the world, claims that as to overseas warehouse orders, its retailers can be subsidized 3 dollars per order from 15 March 2020.
Many studies have examined the operational decisions of the platform-retailer systems [
8,
9,
13,
14,
15]. However, few previous scholarly efforts consider logistics constraints and subsidy programs (some concern about government subsidies, other than platforms subsidies, in e-commerce environment, like [
16]) simultaneously. This presents a gap in our understanding of the subsidy decisions of the platform-retailer systems. This lack of understanding motivates us to focus on the subsidy programs and investigate how the platforms make optimal decisions on subsidizing the retailers with logistics constraints during an epidemic scenario. By filling the gap, our research enhances understanding of the platform-retailer systems’ optimal decisions on subsidies, pricing and logistics services in situations of an epidemic, and thus helps promote the sustainability and symbiotic relationship of the systems.
In this study we consider two factors to further research on the subsidy programs. The first is altruistic preference. The decision-makers with altruistic preference have intrinsic concerns for other parties’ interests, in addition to their own payoffs. Symbiotic relationships can easily arouse altruistic preference and change the objectives of business transactions from narrow economic optimization to the goal of maintaining relationships [
17]. Thus, it is quite natural that the platforms exhibit altruistic preference. Altruistic preference has been investigated in a large amount of literature on operational decisions [
17,
18,
19,
20], but relatively little work has been done to examine the platform-retailer systems with logistics constraints during an epidemic. Our study fills this gap by explaining the role of logistic constraints in the platforms’ behavior of subsidizing the retailers.
Power structure is another key factor to be considered, as the subsidies provided by the platforms are usually proportionate to their bargaining power during COVID-19. The literature on supply chains is concerned with this concept and conceptualizes difference in bargaining power among manufacturers and retailers as different power structures [
21,
22,
23]. Power structure is also existed in the systems consisting of platforms and retailers. For instance, many live platforms in China give their popular anchors (e.g., Viya who guided gross merchandise volume (GMV) over 310 billion RMB on 2020, nearly 10% of GMV in Taobao live platform) more bargaining power when they sell products. Moreover, large manufactures (e.g., HUAWEI and Haier) have more bargaining power with the platforms (e.g., Buy Together and Suning) during COVID-19. According to the literature review in
Section 2, few studies about the power structure in e-commerce supply chains as well as logistics constraints are simultaneously explored. This paper theorizes and models the effects of power structure on the platforms’ decision on subsidies during an epidemic scenario.
New business practices in the time of COVID-19 should be paid more attention to [
24]. To sum up, this paper aims to answer the flowing questions by examining a system consisting of a platform and a retailer during an epidemic scenario:
- (1)
How should e-commerce platforms subsidize retailers with logistics constraints during an epidemic scenario?
- (2)
How power structure and altruistic preference jointly affect the platform’s decision on subsidies?
- (3)
How the retailers’ profits and the platforms’ utility are affected by power structure, altruistic preference and other market parameters?
The study contributes to the literature in three ways. First, previous research on marketplace platforms assumes that the platforms engage in service decisions or pricing decisions but ignores that they also need to make decisions on subsidies in situations of an epidemic (e.g., COVID-19 and Ebola epidemic). Our study examines the optimal sales subsidy provided by a platform and investigates the effect of various environmental parameters on it under different power structures. Second, prior research does not consider altruistic preference and logistics constraints simultaneously in the platform decision-making models under different power structures. Our study fills this gap and extends this literature stream (e.g., [
23,
25,
26,
27]) by adding both factors into a new subsidy decision model of a platform and quantifying the impact of power structure on the decision-making of platforms. Finally, the research on game models between platforms and retailers focuses on logistics services but rarely considers logistics constraints. To account for the reality of COVID-19, logistics constraints are introduced into our game model which helps enrich the understanding of what shapes the operational decisions of marketplace platforms.
The rest of this paper is organized as follows.
Section 2 reviews the related literature.
Section 3 shows the methodology and constructs the basic model to analyze the system consisting of a platform and a retailer with logistics constraints during an epidemic scenario.
Section 4 calculates the optimal subsidy with different power structures.
Section 5 further explores the joint effects of power structure, altruistic preference, and logistics constraints on the optimal subsidy and other results. Numerical experimentation is carried out to simulate the impacts of environmental parameters and verify the reliability of the propositions in
Section 6. All proofs are available in the
Appendix A.
2. Literature Review
This paper is related to four streams of the literature: the operational decisions of marketplace platforms, power structure in e-commerce supply chains, the operational decisions with altruistic preference, and the effects of logistics service on the operational decisions of e-commerce platforms. The differences between these studies and our study are summarized in
Table 1.
2.1. The Operational Decisions of Marketplace Platforms
Marketplace platforms refer to the platforms who provide online sales platform for retailers and they share revenue with each other, contrary to the reseller platforms buying products from retailers and reselling them to consumers [
13,
28,
51]. A key distinction between marketplace platforms and reseller platforms is whether the platforms can set the retail price—reseller platforms can decide the retail price, whereas marketplace platforms cannot because it should be decided by the retailers. The marketplace platforms run operational decisions (e.g., subsidy programs, revenue sharing fee, delivery services, and sales services) to maximize their utility. However, subsidy programs (e.g., sales subsidy and delivery subsidy) are ignored in the research on marketplace platforms. The research can be divided into two streams based on the number of distribution channels.
One considers only one distribution channel in which the providers sell their services/products to the consumers through the marketplace platforms. A few scholars in this stream pay attention to the price and revenue sharing fee decided by the marketplace platforms. Rochet and Tirole [
29] build a model of pricing competition with two-sided platforms. Economides and Katsamakas [
8] describe the optimal pricing decisions on the users of a platform as well as firms offering applications in the platform. Recently, more factors are considered in the pricing model of marketplace platforms. As to bundling price, Chao and Derdenger [
30] construct a game model to analyze the optimal two-side price as well as the bundling price charged by the platform in the presence of installed base effects. Geng et al. [
15] further examine the retailing format and pricing decision of a platform while the manufacturer determines to adopt add-on strategy or bundling strategy. In view of surge pricing, Cachon et al. [
31] discover that surge pricing strategy increases the platform’s profit relative to fixed pricing as well as the welfare of providers and consumers. For risk attitudes, Choi et al. [
14] analyze the optimal service pricing decision of the on-demand platform based on three different risk attitudes of customers. Wen and Siqin [
32] identify the optimal average quality levels and prices made by sharing economy platforms when the risk-averse attitudes of decision makers prevail. Considering platform delivery service, Kung and Zhong [
33] explore the pricing strategies for platform delivery where online platforms provide delivery services by making independent shoppers deliver goods from retailers to consumers. Wei et al. [
34] study how two suppliers that produce complementary goods, considering the combined impacts of e-retailer’s referral fees, goods’ differences in the level of complementarity and goods’ differences in potential demand.
However, the other stream considers the competition between different distribution channels (e.g., online channels and offline channels). In this stream, platforms operate with a marketplace mode and providers can also sell their products through their brick-and-mortar stores or own website except for on the platforms [
9,
10,
11,
13,
29,
35,
36,
37]. Our paper considers one distribution channel but differs from the first stream in two key aspects. First, the power structure is introduced into the sales subsidy model and compares the operational decisions of the platform in the case of the platform-dominant with retailer-dominant. Second, this paper considers the impact of altruistic preference and logistics constraints on the operational decisions of marketplace platforms.
2.2. Power Structure in E-Commerce Supply Chains
The literature on supply chains has first concerns for the power structure and argues that different bargaining power among manufacturers and retailers refers to different power structures [
38,
39]. The members who own huge brand and user resources (e.g., major traditional retailers like Wal-Mart) usually have dominant bargaining power. As a result, the members with weaker bargaining power must accept the decisions made by the dominant members and follow them to make decisions. Power structure is widely considered an important factor influencing the behavior of supply chain members. As to the e-commerce supply chains, power structure has been studied in two different streams. The first stream focuses on the scenario in which the manufacturers control online direct channels and sell wholesale to offline retailers who resell it to customers [
21,
22,
39,
40,
41]. The e-commerce platforms as decision-makers are ignored in this scenario.
In contrast to the first stream, the other stream turns its attention to the scenario in which the e-commerce platforms act as an important role in the decision making. On the one hand, the scenarios where platforms act as resellers by reselling the products which they purchase from upriver manufacturers are studied. Jia [
42] discusses the decisions of the supply chain consisting of one manufacturer and one online platform which act as a reseller with three power structures. Given the risk attitude, Chen et al. [
43] study whether the e-commerce platforms can introduce the online channel under different power structures. On the other hand, the scenario where platforms act as marketplaces by allowing upriver manufacturers to run their own online stores on platforms and sell products directly to consumers are investigated. Considering the service decision of e-commerce platform, Wang et al. [
25] investigate the pricing and service behavior of e-commerce supply chain participants under different power structures with fairness concern. In the case of introducing two manufacturers who sell substitutable products, Wei et al. [
23] depict the principle to choose the best sales formats, that is, resellers or marketplaces model for online platforms with different power structures. Liu and Ke [
26] investigate the impacts of power structure on pricing policies under dual-format retailing mode adopted by an online platform. Qin et al. [
27] develop an analytical model to examine how the online platform’s selling mode choice interacts with the logistics service strategy under different power structures. Our study is closely related to the second stream where the platforms act as marketplaces. Nonetheless, the study differs previous studies in that it considers the subsidy programs implemented by the platforms and logistics constraints as well as altruistic preference.
2.3. The Operational Decisions with Altruistic Preference
Previous studies suggest that decision-makers are influenced by social preferences and they are usually not fully rational economic men. An important kind of social preferences is altruistic preference. The decision-makers with altruistic preference have intrinsic concerns for other parties’ interests, in addition to their own payoffs [
17]. Altruistic preference has a significant impact on the operational decisions. Loch and Wu [
17] first introduce altruistic preference into operational decisions and reveal that it systematically influences the behavior in the supply chain with two members depending on game models and experimental studies. Based on a supply chain with one manufacturer and two altruistic retailers, Lin [
44] further illustrates that altruistic preference can improve the profits of the supply chain under certain conditions. Assuming both the logistics service integrator and functional logistics service provider have altruistic preferences, Liu et al. [
18] identify the optimal investment decisions in the logistics service supply chain. Hua et al. [
19] extend their work by taking uncertain demand and capital-constrained retailers into consideration and identify when the supplier’s relationship concern can improve the supply chain’s efficiency. As to altruistic consumers, Zhou et al. [
20] investigate how poor farmers choose the traditional mode or the crowd-funding mode for poverty alleviation. They discover that the optimal mode is determined by the scale of altruistic consumers. Beyond that, other research issues about altruistic preference in low-carbon supply chains have also received attention, such as low-carbon tourism supply chain [
45], low-carbon e-commerce closed-loop supply chain [
46], and low-carbon supply chain in cap-and-trade system [
47]. However, power structure and logistics constraints are not considered in their models.
2.4. The Effects of Logistics Service on the Operational Decisions of E-Commerce Platforms
It is widely accepted that “demand-enhancing services” play an important role in the operational decisions of e-commerce platforms. Obviously, logistics service is one of demand-enhancing services because consumers prefer to products with lower delivery time and commodity wastage [
48,
49,
50,
51,
52,
53,
54,
55,
56]. A massive amount of literature examine how logistics services can affect the operational decisions of e-commerce platforms. One stream of literature refers to the optimal logistics systems including routing problems and dispatching operations designed by e-commerce platforms based on programming models [
48,
49,
50].
In contrast to the first stream, some scholars explore the influence of logistics services on the interaction between the decision of e-commerce platforms and other parties (e.g., upstream suppliers), relying on game models. Considering two competing suppliers selling two substitutable products through an e-commerce platform, Tian et al. [
51] assume that they all provide logistics service, and discover how the platform chooses the optimal model among marketplace, reseller, or hybrid. Subsequently, more studies examine whether the platform should provide logistics services. Wang et al. [
52] introduce two supplier’s entry modes which are FBP and SOP, respectively. As a marketplace, the e-commerce platform provides logistics service in FBP case, while does not in SOP case. By establishing a differential game model, they identify how the supplier’s entry mode affects the operational decisions of the e-commerce platform. Zhong et al. [
53] introduce terminal distributors to his model and illustrate the complexity of logistics service strategies provided by a platform. Based on multi-oligopolies Cournot competition model, Ma et al. [
54] analyze when the platform should self-operate logistics or utilize the third-party logistics in the scenario that
n online stores sell homogeneous products on the platform. Qin et al. [
27] further discuss how the online platform’s selling mode choice (i.e., marketplace or reseller) interacts with his logistics service strategy.
In addition, more platforms build self-supporting logistics service systems and share it with the sellers, which is examined by [
55,
56,
57] in depth. However, this stream has been little argument on logistics constraints, and they also ignore the platforms with altruistic preference subsidizing the retailer during an epidemic scenario. This paper further studies the effects of logistics service on the operational decisions of e-commerce platforms by introducing logistics constraints and altruistic preference to the subsidy decision of an e-commerce platform.
3. Methodology and Basic Model Setup
3.1. Methodology
This study applies the method of game theory to investigate an e-commerce platform’s decision on subsidizing a retailer selling on it with logistics constraints during an epidemic scenario, with a focus on the role of power structure and altruistic preference. Game theory is used by a large amount of research (e.g., [
14,
29,
30,
31,
32,
58]) to analyze the coopetition between the platforms and the retailers in the field of operations management in e-commerce. In particular, the Stackelberg game models, which reflect the competitive equilibria between two sides with different market powers, are appropriate for studying the effects of power structure on the players’ decision in the game [
23,
28,
39].
The steps of our research are detailed as follows.
First, we setup the environment of a basic model. In the basic model, this paper defines the competition between the platform and the retailer by introducing logistics constraints, altruistic preference, and other basic parameters (
Section 3).
Second, this paper constructs a Stackelberg game model to analyze the system consisting of a dominant platform and a weaker retailer. In this model, the platform has higher market power and the retailer has lower market power. Logistics constraints and altruistic preference are considered in the model. The optimal sales subsidy, optimal price, and optimal logistics service level are studied (
Section 4.1).
Third, in contrast, the other system consisting of a weaker platform and a dominant retailer is explored in the second Stackelberg game model. In this model, the retailer has higher market power and the platform has lower market power. Additionally, logistics constraints and altruistic preference are considered in the model. The optimal sales subsidy, optimal price, and optimal logistics service level in this model are calculated (
Section 4.2).
Fourth, this paper compares the optimal sales subsidy in the two models to discover the joint effects of power structure and altruistic preference on the platforms’ decision on subsidies with logistics constraints (
Section 5).
Finally, numerical experimentation is finally carried out to simulate the impacts of environmental parameters and verify the reliability of the propositions. We run the program of numerical experimentation in MATLAB 2016 more than 10 times. In addition to the authors, three experts were invited to run the program again. The outcome is consistent and thus our conclusions have a good scientific robustness (
Section 6).
3.2. Basic Model Setup
Consider a system that consists of one e-commerce platform
E (She) and one retailer
R (He) selling only one kind of product on the platform at retail price
p during an epidemic scenario like COVID-19. The platform acts as a marketplace for the retailer and charges him (1 −
φ)
p per order as commission, which is common in real world like Amazon.com and Taobao.com. This marketplace-mode system has been widely studied in some literature [
27,
59,
60]. The demand function can be assumed as follows:
In Equation (1),
d denotes the consumers’ demand, and
v indicates the primary demand potential.
β represents the price elasticity of demand.
t refers to the effort level of logistics service determined by the retailer since most platforms have no self-run logistics systems and retailers realize delivery with the help of third-party logistics providers. The higher the service level, the higher the cost. It is assumed that the service cost function of the retailer is
kt2/2. Following some literature [
61,
62,
63], without loss of generality, the study assumes
β = 1 and
k = 1 to simplify expressions. The parameter
n, called logistics service coefficient, shows the linear influence degree of logistics service level on demand [
64,
65]. The consumers’ degree of sensitivity to price is greater than to logistics services [
61,
62], that is,
n ≤ 1. Many enterprises have disruptions in their logistic hubs and delivery routes due to restricted locations and closures during COVID-19 [
66], so that they cannot provide sufficient logistics service. It can be assumed
t ≤
T to show this special phenomenon.
T is exogenous and denotes the upper limit of logistics service level. It decreases monotonously with the intensity of the epidemic.
During COVID-19, as mentioned in the introduction, many e-commerce platforms, for instance, Buy Together and AliExpress set up the sales subsidy programs that the retailers receive unit subsidies when they sell a product to consumers. In according with [
67,
68] and without loss of generality, the research focuses on the sales subsidy program (a typical subsidy program) in our model, although other subsidy programs are also implemented. It is assumed that the platform subsidizes the retailer
m per his order. To summarize, we determine the profit function of the platform and retailer as follows:
In Equations (2) and (3),
denotes the profit of the e-commerce platform and retailer, respectively. Based on altruistic preference, the platform’s utility function can be expressed as follows:
In Equation (4),
b (0 ≤
b ≤ 1) represents the altruistic preference coefficient of the platform [
17,
46].
b ≤ 1 indicates that even if the platform is altruistic, she cares more about her own profits than the retailer’s profits. The higher
b indicates that the platform is concerned more with the retailer’s profits. When
b = 0, the platform is completely self-interest and cares only about maximizing her own profits. In contrast,
b = 1 indicates the platform is fully altruistic. In order to ensure the decision variables
p,
m, and
t are positive, the relationship between variables is satisfied that 4 − 4
b −
n2 > 0.
Table 2 shows the notations of the model.
4. Analysis of Subsidy Models with Different Power Structures
4.1. Model 1: Optimal Subsidy with a Dominant Platform
Based on the above section, the platform determines her subsidies to the retailer, while the retailer decides the sales price and logistics service level. In the process of decision-making, the platform and the retailer play games with each other. The sequence and outcome of the game depends on the power structure between them. The dominant platform means she obtains strong bargaining power with huge user resources, while the weaker retailer can only accept the decision made by the platform. For instance, Tmall and JD.com, the famous e-commerce platforms in China, can easily dominate numerous small sellers on it.
To summarize, the timing of the Stackelberg game with a dominant platform is as follows. In the first stage, the platform determines her sales subsidy
m. In the second stage, the retailer determines his price
p and logistics service level
t simultaneously after observing the sales subsidy decision by the platform. This paper uses the superscript
ed to denote this mode and its decision problem can be determined by the following:
We solve the game backward and obtain its subgame-perfect Nash equilibrium as follows:
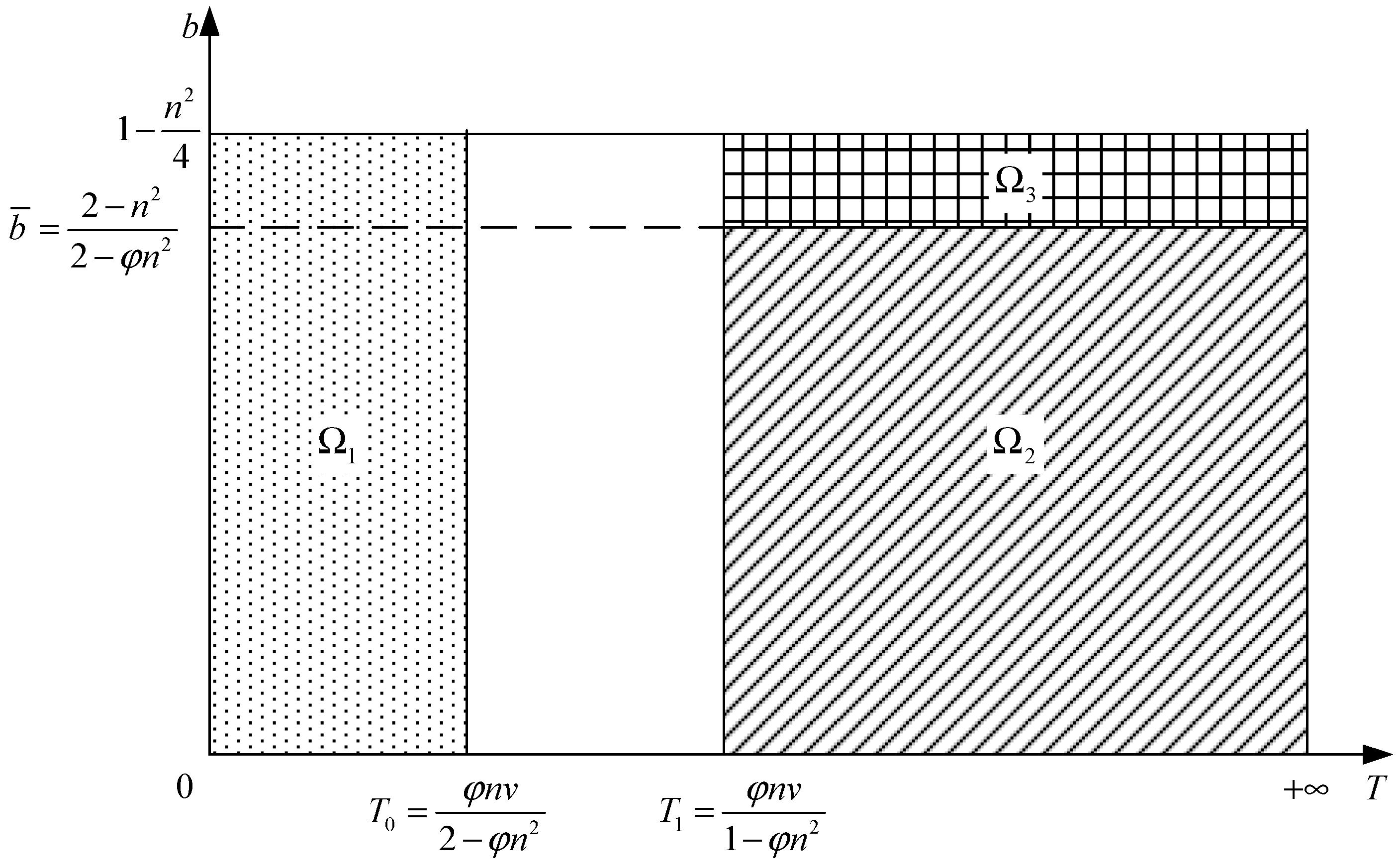
Lemma 1. With the platform dominating the retailer, the optimal sales subsidy med*, the optimal price ped*, and the optimal logistics service level ted* are as follows:where
,,,,,. This decision spaces with dominant platform can be clearly understood in Figure 1. Substituting (6)–(8) into Equation (4), it can be obtained that:
Proposition 1. When and only when logistics constraints T and the altruistic preference coefficient b are both higher than a certain value, respectively, the platform will give the retailer a certain subsidy med. At this time, .
Proposition 1 indicates the conditions of giving sales subsidy. It can be understood the platform with higher altruistic preference is more likely to give the retailer sales subsidies, because it can lower the price and attract more buyers to improve the retailer’s profit and clove to her altruistic ideal. However, when the logistics service level is limited to a low value, the market demand is limited as well. At this time, the sales subsidies can only help the retailer increase few profits which cannot make up for the decrease of platform utility caused by subsidizing the retailer. That is the reason why the conditions of giving sales subsidy hold. When the platform has no altruistic preference (b = 0), she will not subsidize the retailer even there is no limitation on the logistics service level (i.e., T = +∞).
When the platform implements the sales subsidy program, med is increasing in b and n. The higher n indicates the higher value of logistics service, and the platform is also willing to give more subsidies to the retailer to encourage him to improve his logistics service level and attract more customers. In reality, the platforms highly subsidize the retailers who sell badly needed products (higher n) like mask during COVID-19. For instance, JD.com gives 50% sales subsidies to the retailers who sell badly needed products, while 30% sales subsidies to the retailers who sell general products from 11 February 2020 to 31 March 2020.
Proposition 2. (i) ped is increasing in n and φ, decreasing in b. (ii) ted is increasing in n, φ and b.
Proposition 2 can be proved by and .
The platform with higher altruistic preference should improve the subsidies to the retailer, which stimulates him to increase market demand by charging lower price and providing higher logistics service level. From Equation (1), the higher n allows the retailer to charge higher price to keep the demand unchanged and obtain more profits. Furthermore, it also indicates that higher logistics service level can attract more consumers and obtain more profits. The higher φ means boosting the market demand can obtain more profits, so the retailer will provide higher logistics service level. However, he will not lower price for that, because it cannot compensate the profits obtained by charging a higher price when the higher φ holds. In China, some platforms lower the commission and advance altruistic preference to stabilize the price of badly needed product which is called by the government during early COVID-19.
Proposition 3. (i) When , is increasing in n, decreasing in φ. (ii) When , is increasing in n and φ.
Proposition 3 depicts the impacts of n and φ on the platform’s utility. Obviously, the market demand is increasing in n, and the platform and the retailer can both benefit from higher n. φ involves profit sharing between the platform and the retailer, and its impact on the platform’s utility is more complex. When T or b is low, the platform will not implement sales subsidy, and they show a competitive relationship. In such conditions is decreasing in φ.
On the contrary, when T and b are all high enough, the platform should implement a sales subsidy, and they show a cooperative relationship. The higher the profit that the platform transfers to the retailer, the greater the utility it gets. It can be observed that many platforms lower their commission during COVID-19 to clove to their altruistic ideal. For instance, Tophatter, a cross border e-commerce platform in North America, claims that it remains a commission at 9% which should have risen after the Spring Festival on 20 February 2020 because of COVID-19. In China, MOGU, the most famous platform focusing on fashionable female consumers, announces that the cooperative brands will not need to pay the platform commission before the end of March 2020 within 10 million RMB on 4 February.
4.2. Model 2: Optimal Subsidy with a Dominant Retailer
The preceding
Section 4.1 studies the optimal sales subsidy with a dominant platform who fully control the bargaining power. However, some dominant retailers and weaker platforms in reality. Dominant retailer means he can move first to decide his retail margin and the weaker platform has to accept the decision made by him. Some large brand retailers always take the role of dominant retailers because they have won massive loyal customers and can impact on the reputation of weaker platforms.
To summarize, the timing of the Stackelberg game with a dominant retailer is as follows. In the first stage, the retailer determines his retail margin
h = φ p + m and logistics service level
t simultaneously. In the second stage, the platform determines her sales subsidy
m after observing the decision by the retailer. This paper uses the superscript
rd to denote this mode and its decision problem can be determined by the following:
Solving the game backward and obtain its subgame-perfect Nash equilibrium as follows:
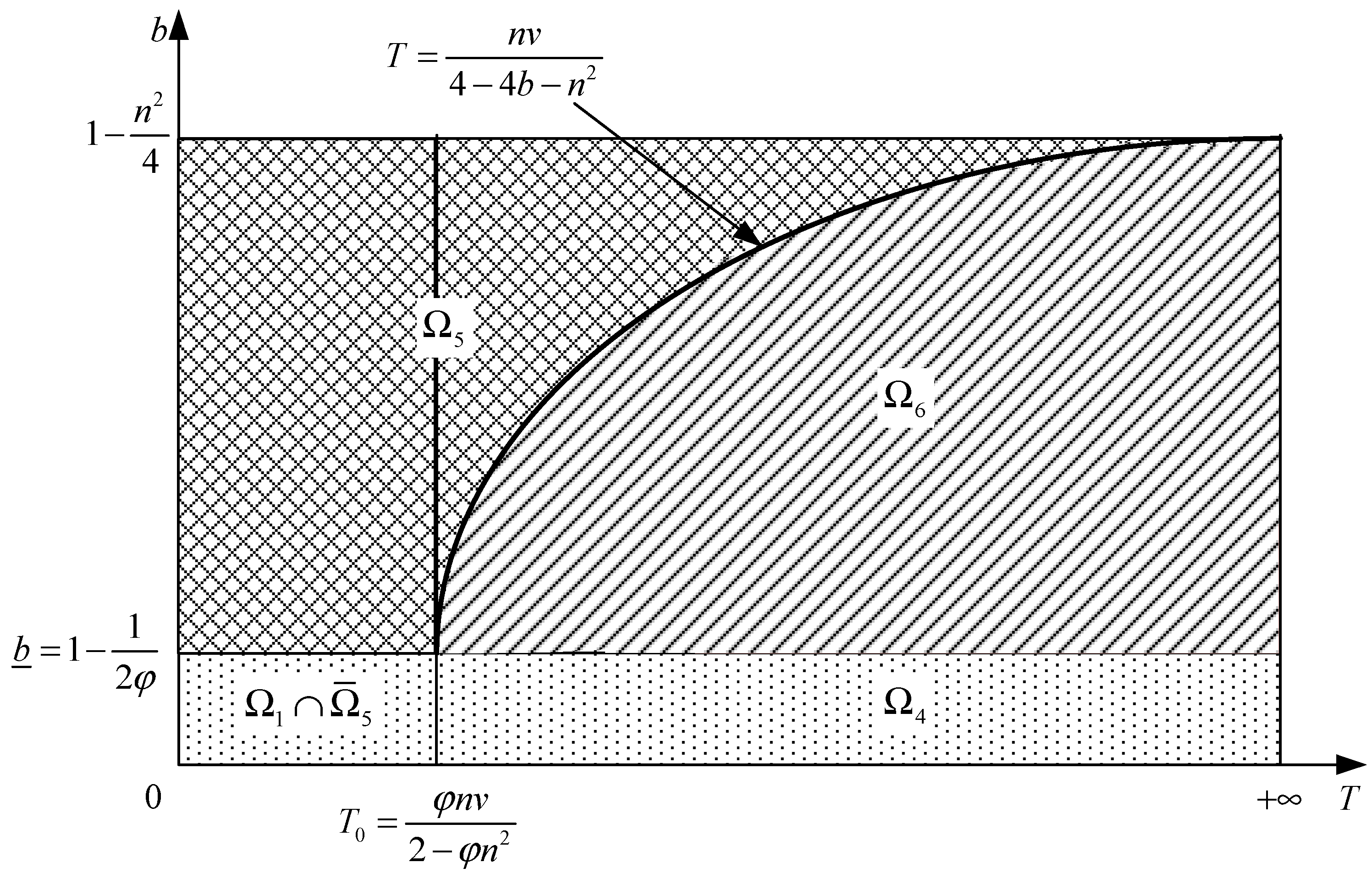
Lemma 2. With the retailer dominating the platform, the optimal sales subsidy mrd*, the optimal price prd*, and the optimal logistics service level trd* are as follows: where,,,,. This decision spaces with dominant retailer can be clearly understood in Figure 2. Substituting (11)–(13) into Equation (4), it can be obtained that
Proposition 4. When and only when the altruistic preference coefficient b is higher enough to meet , the weaker platform will give the retailer a certain subsidy mrd*. At this time, (i) mrd* is increasing in n and b, but decreasing in φ; (ii) prd* is increasing in n and b.
Propositions 1 and 4 indicate the higher b can ensure the implementation of sales subsidy no matter what the power structure is. It is decreasing in φ because higher φ means the retailer can obtain more profits and the platform can give few subsidies to achieve the same incentives. Furthermore, an interesting conclusion is that the price is increasing in b, while decreasing in b with a dominant platform. The reason is the dominant retailer should charge a higher retail margin because he sees that the weaker platform can only accept it. The more altruistic preference, the higher retail margin she can accept, and the price goes up. That first move advantage can be described as “all lay loads on a willing house”.
Proposition 5. If the weaker platform can select his altruistic preference b, he will find the best choice is mrd* = 0 when .
We define this selection as a weaker platform which will lower her altruistic preference b if it can improve his utility. The definition is based on the cost-benefit analysis that lowering her altruistic preference does not cost anything but can obtain more utility.
Proposition 5 is interesting that the weaker platform can get more utility by lowering her altruistic preference. It is contrary to our common sense that the platform’s utility is increasing in her altruistic preference from Equation (4). The reason is the dominant retailer should charge a higher h considering the weaker platform with higher b. The higher h would seriously damage her profits and utility, and the weaker platform would rather have a lower b. This proposition can explain the reality that most weaker platforms have low altruistic preference and give the dominant retailers few sales subsidies during an epidemic scenario considering most platforms’ commission is below 1/2.
5. Comparison of Results in Two Models: Joint Effects of Power Structure and Altruistic Preference
This section compares the optimal sales subsidy, the retailer’s profits, and the platform’s utility under different power structures to analyze the joint effects of power structure and altruistic preference on them. To simplify analysis and without loss of generality, considering two scenarios in which T is larger or smaller, that is, or . Through comparison and analysis, Lemma 3 has been illustrated.
Lemma 3. (i) When , . (ii) When and , . (iii) When and , . (iv) When and , .
Lemma 3 can be clearly understood in
Figure 3 which shows the optimal sales subsidy under different power structures. Although
and
is assumed in this figure, we can move the lines
b = 0 and
b = 1 −
n2/4 up and down to analyze other scenarios as well.
Proposition 6. When and only when,. Otherwise,.
Proposition 6 represents the joint effects of power structure and altruistic preference on sales subsidies. When b is lower, the platform will give no subsidy to the retailer no matter what power she has. However, the influence mechanisms of b on sales subsidy are different under different power structures. The dominant platform does not care about the retailer’s profits and is not willing to give the retailer more subsidies to boost his profits. As to the weaker platform, she passively accepts the decision of the dominant retailer. From Equation (A10), the dominant retailer should increase his retail margin to decrease market demand and let the weaker platform give sales subsidies. When b is lower, he realizes the few sales subsidies given by the weaker platform cannot compensate for the loss of his profits caused by increasing his retail margin. Thus, he would rather she give no subsidy.
When b is higher, the weaker platform can give the retailer more sales subsidies than the dominant platform. The reason is the dominant retailer can decide his retail margin h first and then partly decide the sales subsidy because of h = φ p + m, while the dominant platform can move first and decide the sales subsidy independently. The dominant retailer should boost h considering the weaker platform must accept it. To ensure p > 0, the weaker platform has to improve her sales subsidies to a higher value.
In reality, many dominant platforms (e.g., Buy Together and JD.com) give the retailers more sales subsidies than weaker platforms during COVID-19. According to Propositions 5 and 6, two reasons should be taken into account. The first is dominant platforms usually have higher altruistic preference than weaker platforms because of their far-sighted and high-altruistic character that makes the former dominant power. The second is the phenomenon that weaker platforms even with high altruistic preference would rather choose
from Proposition 5, which can be deducted that they have lower altruistic preference and corporate social responsibility. Although this phenomenon has been proved by empirical research in some literature [
69,
70], our conclusions provide a reasonable theoretical explanation for it.
Based on the above analysis, it can be inferred that platforms give the weaker retailers (e.g., small and medium enterprises) more sales subsidies than dominant retailers (e.g., large brand retailers). For example, Taobao exclusively allocates 1 billion yuan to subsidize small and medium enterprises selling agricultural products on 13 February 2020. 1688.com, a global leading B2B e-platform for purchasing and wholesale, launches escort activities for small and medium enterprises to subsidize them on 8 February 2020.
Proposition 7. When and only when , , . Otherwise, , .
Proposition 7 indicates power structure is the main influencing factor affecting the platform’s utility and the retailer’s profits in our model. Its impact is more than any other factors (e.g., logistics constraints, commission, and logistics cost). Dominant platforms’ utility is higher than weaker platforms’ utility because the former can decide the sales subsidy independently and obtain the first mover advantage. This proposition indicates even the platforms with higher altruistic preference should give the retailer more sales subsidies or charge lower commission, but should not lower her bargain power during an epidemic scenario.
6. Numerical Experimentation
In order to verify the reliability of the above propositions, and compare the impacts of various important parameters (e.g., b, T, n, and φ) on the optimal sales subsidy, the platform’s utility and the retailer’s profit, the paper conducts the analysis of numerical experimentation. It can be assumed that the potential demand (parameter v) is 1. Our paper only considers T > T1 for better comparison.
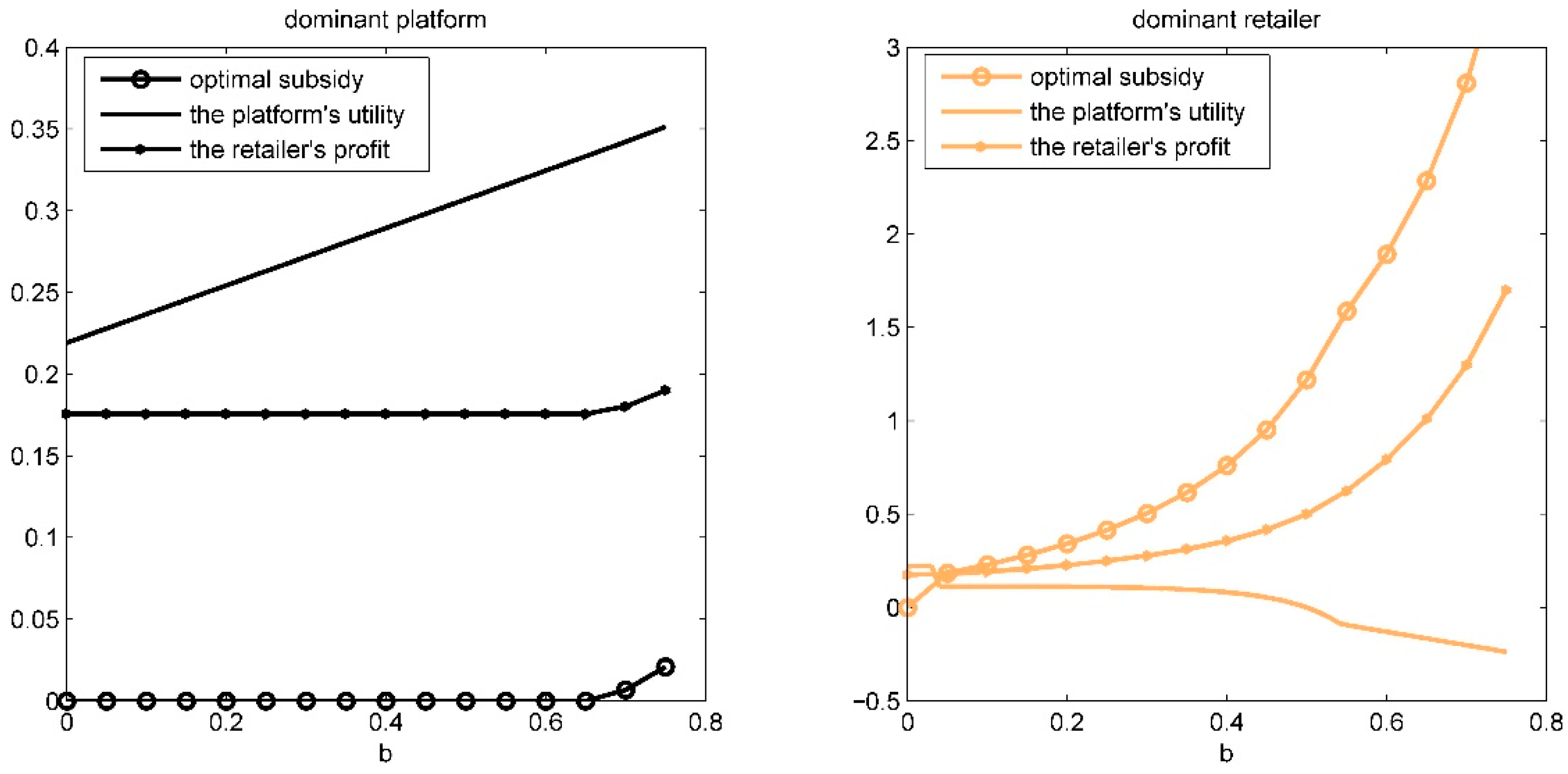
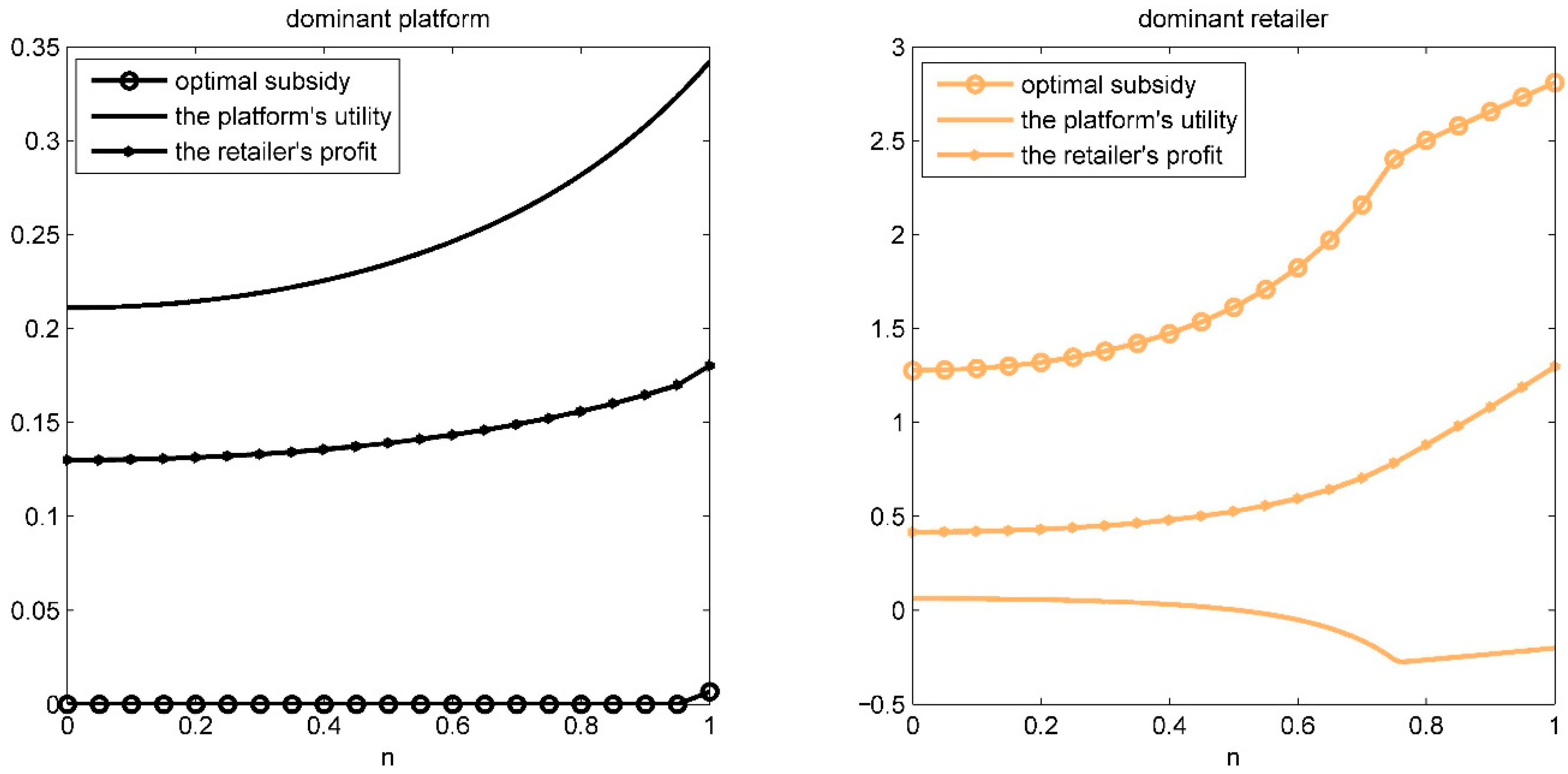
6.1. Impacts of Altruistic Preference b
Case 1: Fixed
T = 1.2,
n = 1 and
φ = 0.52. MATLAB 2016 is used to carry out simulation calculations to obtain the optimal sales subsidy, the platform’s utility, and the retailer’s profit under different power structures with the change of altruistic preference
b (
Figure 4). Change
b from 0 to 0.75 (1 −
n2/4).
Figure 4 shows that it is only when
b is higher that the platform gives subsidies no matter what the power structure is. The threshold of
b for the dominant platform (about 0.65) to give subsidies is higher than the weaker platform (about 0.03). The sales subsidy is increasing in
b. These results validate Propositions 1 and 4. Furthermore, the sales subsidy with a dominant platform is not less than a weaker platform no matter what
b is, which is consistent with Proposition 6.
Figure 4 also shows the impacts of
b on the platform’s utility and the retailer’s profit. It can be observed that
,
, which is consistent with Proposition 7. The weaker platform’s utility is decreasing in b even to a negative value, which correlates with a lower altruistic preference. Proposition 5 depicts and analyzes this result.
6.2. Impacts of Logistics Constraints T
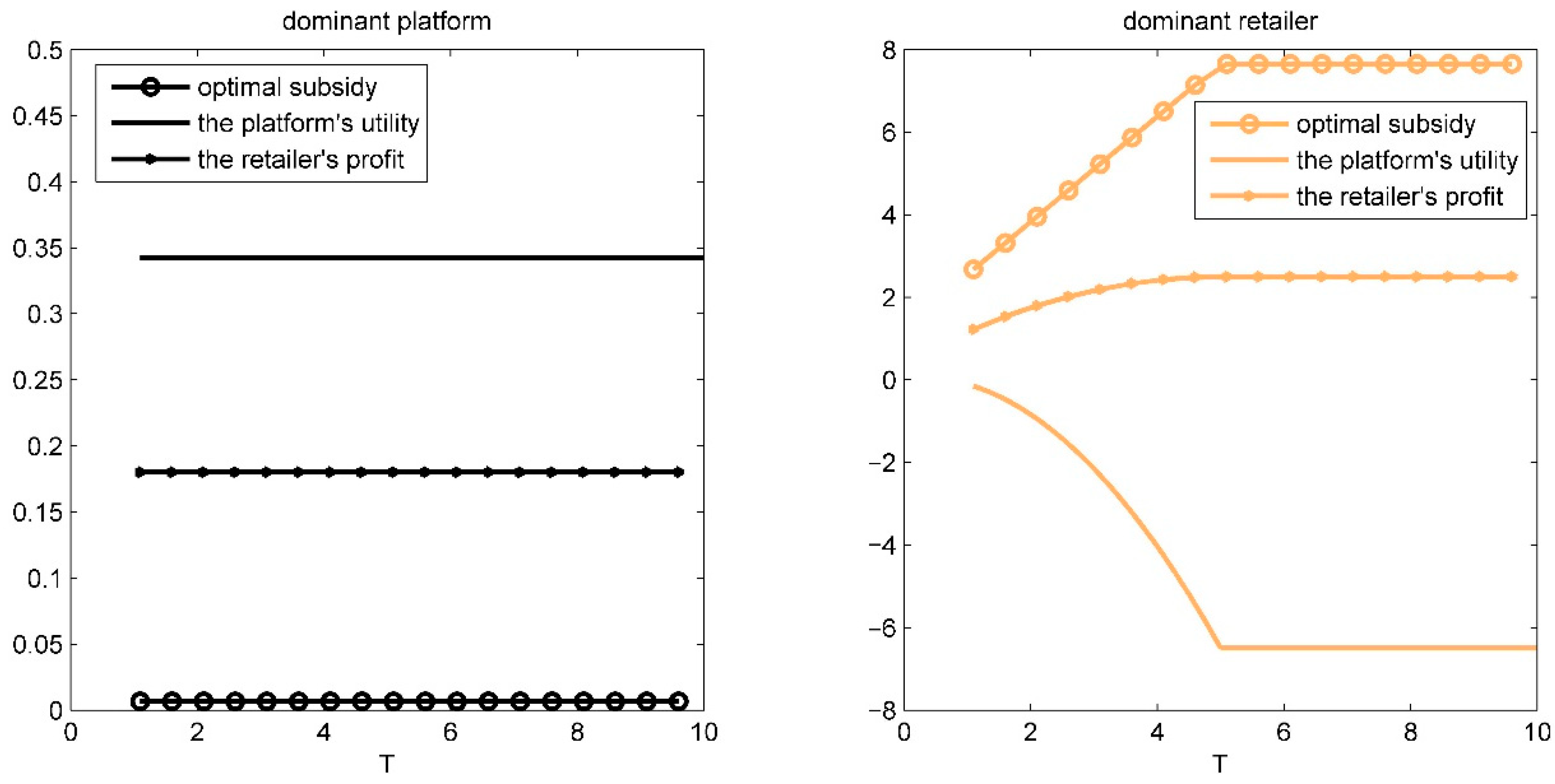
Case 2: Fixed
b = 0.7,
n = 1 and
φ = 0.52. MATLAB 2016 is used to carry out simulation calculations to obtain the optimal sales subsidy, the platform’s utility, and the retailer’s profit under different power structures with the change of logistics constraints
T (
Figure 5). Change
T from 1.1 to 10 because of
T >
T1.
Figure 5 shows in the scenario of the dominant platform, the optimal sales subsidy, the platform’s utility, and the retailer’s profit are all independent of
T when logistics constraints are not strictly limited to
T1. However, in the scenario of the dominant retailer, they vary with
T unless
T is high enough. As logistics constraints have been lifted, the optimal sales subsidy increases, the platform’s utility decreases, and the retailer’s profit increases. These results are inconsistent with
Figure 1 and
Figure 2.
Figure 5 also shows
,
,
, which are consistent with Propositions 6 and 7.
6.3. Impacts of Logistics Service Coefficient n
Case 3: Fixed
b = 0.7,
T = 1.2 and
φ = 0.52. MATLAB 2016 is used to carry out simulation calculations to obtain the optimal sales subsidy, the platform’s utility, and the retailer’s profit under different power structures with the change of logistics service coefficient
n (
Figure 6). Change
n from 0 to 1.
It can be observed that only when
n is high enough, the dominant platform gives subsidies from
Figure 6. It depicts that the optimal subsidy is increasing in
n when the platform gives subsidies, which validates Propositions 1 and 4. Dominant platform’s utility is increasing in
n, which is consistent with Proposition 3.
Figure 6 also shows
,
,
. That are consistent with Propositions 6 and 7.
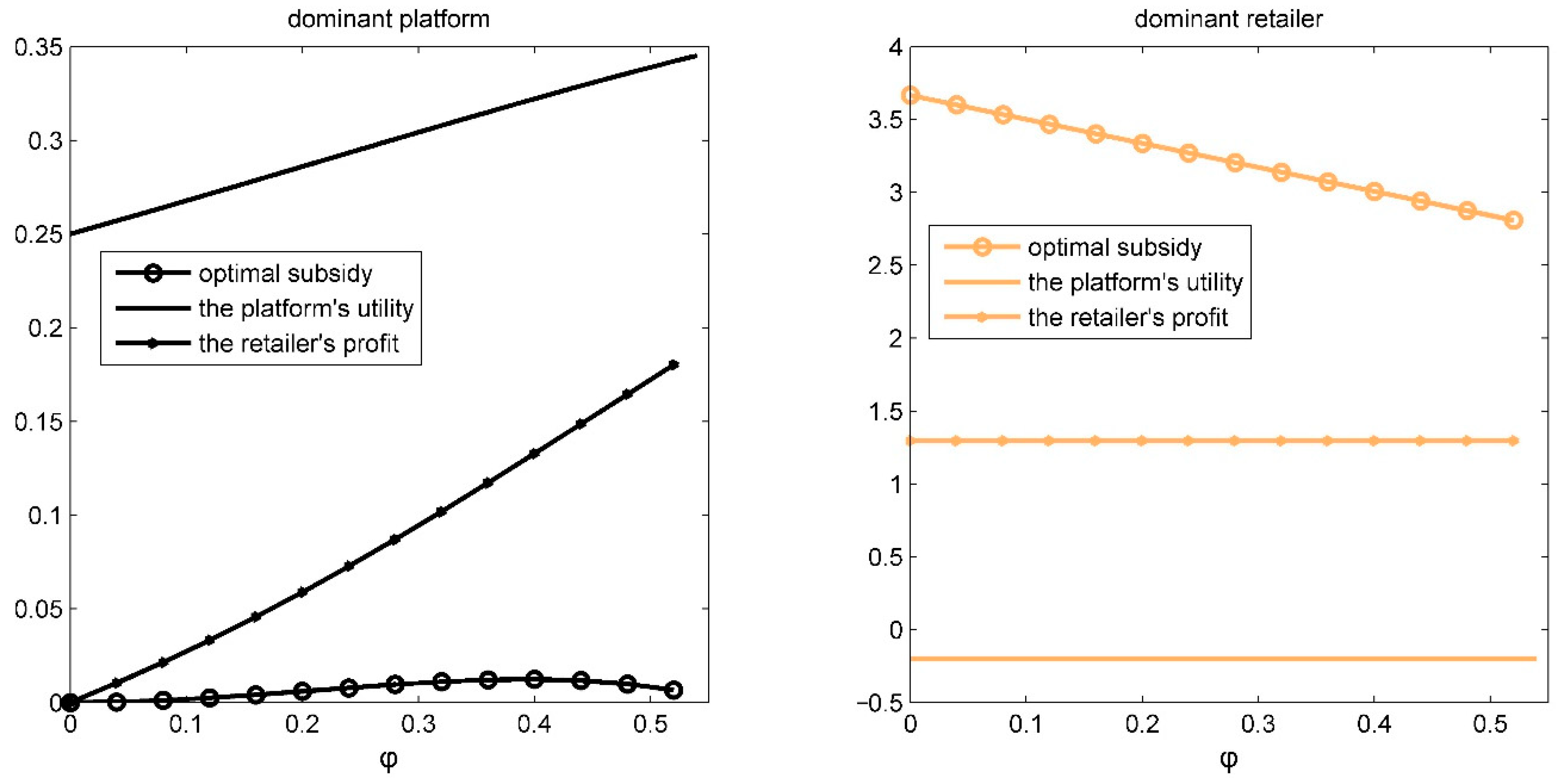
6.4. Impacts of Commission φ
Case 4: Fixed
b = 0.7,
T = 1.2 and
n = 1. MATLAB 2016 is used to carry out simulation calculations to obtain the optimal sales subsidy, the platform’s utility, and the retailer’s profit under different power structures with the change of commission
φ (
Figure 7). Change
φ from 0 to 0.54 because of
T >
T1.
Figure 7 illustrates that both the platform’s utility and the retailer’s profit are increasing in
φ when the dominant platform gives subsidies, which is consistent with Proposition 3. The impacts of
φ on the optimal sales subsidy of the dominant platform increases firstly and then decrease as
φ increases, which indicates the dominant platform should not give too many subsidies to the weaker retailer when the commission is higher or lower enough.
Figure 7 depicts the monotonically decreasing impacts of
φ on the optimal sales subsidies given by the weaker platform, which is shown in Proposition 4. The weaker platform’s utility and the dominant retailer’s profit are irrelevant to
φ.
Figure 7 also shows
,
,
. That are consistent with Propositions 6 and 7.
7. Conclusions and Managerial Implications
This paper considers an epidemic scenario in which logistics services are constrained due to restricted locations and closures. The power structure and altruistic preference are introduced to explore how should e-commerce platforms subsidize retailers with logistics constraints during the scenario. Applying a game-theoretic modeling framework, this study construct two Stackelberg game models to investigate this theme. The first model analyzes the system consisting of a dominant platform and a weaker retailer. In contrast, the other system consisting of a weaker platform and a dominant retailer is explored in the second model. The optimal sales subsidy, optimal price, and optimal logistics service level are studied in the two models, respectively. Furthermore, this paper compares them to discover the joint effects of power structure and altruistic preference on the platforms’ decision on subsidies, the platforms’ utility, and the retailers’ profits with logistics constraints. Numerical experimentation is finally carried out to simulate the impacts of environmental parameters and verify the reliability of the propositions.
Analytical and numerical results demonstrate that the weaker platform will give the dominant retailer a certain subsidy just when altruistic preference is higher enough. However, to make the dominant platform give the weaker retailer subsidies, both altruistic preference and logistics constraints should be higher enough. Considering the same setting (i.e., the same parameters such as altruistic preference and commission fee), the optimal subsidy provided by the weaker platform is always not less than the dominant platform. It is increasing in logistics service coefficient and altruistic preference no matter what the power structure is. Both the retailer’s profits and the platform’s utility are the same under different power structures when and only when altruistic preference is lower enough. Otherwise, the dominant retailer’s profits are higher than the weaker retailer, and the dominant platform’s utility is higher than the weaker platform, which is caused by “the first mover advantage”. There is a thought-provoking conclusion that the weaker platform can get more utility by lowering her altruistic preference voluntarily when the commission fee is low.
From our conclusions, various managerial implications can be identified during an epidemic scenario as follows. First, the sales subsidy provided by e-commerce platforms and the pricing and logistics service strategy of retailers should be adjusted under different conditions. The sufficiently high logistics constraints are necessary conditions for the dominant platforms subsidizing weaker retailers. It implies that excessively strict logistics constraints can result in the platforms standing by and make the retailers more difficult. No matter what the power structure is, the sales subsidy should be increasing in logistics service coefficient, which indicates that the platforms should give more sales subsidies to the retailers who sell badly needed products like masks and fresh agricultural products. The prices of badly needed products are high. To stabilize it, which is called by the government, the platforms can lower their commission and advance altruistic preference. In addition, the managerial implications about logistics service strategy can be obtained by the analysis of the impacts of various parameters on it.
Second, our findings illustrate that the weaker platform can get more utility by lowering her altruistic preference voluntarily when the commission fee is low. This conclusion provides a reasonable theoretical explanation for why weaker platforms often show lower altruistic preference. This paper further finds that the optimal sales subsidy provided by the weaker platform is always not less than the dominant platform with the same altruistic preference. It implies that their sales subsidies are lower than dominant platforms in reality. In other words, platforms should give the weaker retailers (e.g., small and medium enterprises) more sales subsidies than dominant retailers. Finally, power structure is the main influencing factor affecting the platform’s utility and the retailer’s profits. Its impact is more than any other factors (e.g., logistics constraints, commission, and logistics cost).
This paper has several limitations. The first is that the platform can provide logistics services and other service such as matching service. However, this study only considers the platform charging commission fee and subsidizing retailers. Second, the platform-retailer systems are more complicated than the system that consists of one platform and one retailer in real world. For instance, two or more competitive retailers selling their substitute or complementary products on a platform are easily seen at Buy Together. These complex systems should be paid more attention. There are some further constraints upon the sustaining of a Stackelberg equilibrium. The leader must know that the follower observes its action. The follower must have no means of committing to a future non-Stackelberg leader’s action and the leader must know this. Indeed, if the “follower” could commit to a Stackelberg leader action and the “leader” knew this, the leader’s best response would be to play a Stackelberg follower action. These constraints should be considered to fully understand the conditions of our model.
Follow-up studies could further investigate the optimal subsidy considering the platforms providing logistics services. At this time, the subsidies may vary with the delivery capacity of the platforms. In addition, further research could focus on more complicated platform-retailer systems consisting of two competitive platforms and two competitive retailers selling substitute or complementary goods during an epidemic. It can be inferred that the competitive environment compels the platforms to increase their subsidies. Above extensive studies will get more interesting conclusions and provide reference for the e-commerce platforms subsidizing retailers.