1. Introduction
Global e-commerce has developed rapidly in recent years. As the largest two markets for global e-commerce, online retail sales of China reached 1815.76 billion dollars in 2020, and eMarketer forecasts that US retail ecommerce sales will reach 908.73 billion dollars in 2021. Despite its rapid growth, online retail faces a challenge, i.e., e-tailers deliver product information only through word and picture and lack physical experience. Namely, consumers cannot make sure whether the product fits their needs before receiving the product. This results in the fact that some product categories, which need to be touched and felt, such as household products, apparel and accessories, are confronted with large amounts of returns [
1,
2].
Under this background, the offline showroom model (showroom for short) emerges to solve the high return rate issue of the online channel. In the showroom model, showrooms provide a physical experience for products sold by e-tailers instead of selling competing products directly. Then, consumers can touch and feel these products in showrooms before buying them from e-tailers directly. In practice, many e-tailers have adopted this channel cooperation model. For example, Warby Parker, a fashion eyewear brand in America, cooperates with local retailers to showcase all glasses sold online [
3]. Further, some showrooms serve more than one e-tailer to satisfy consumers’ heterogeneous demand. For example, Home Times, a showroom of household products opened by Yintai Retails (a leading traditional retailer in China) provides experience service for many brands.
Besides, as the market environment becomes more uncertain, showrooms face huge challenges on operational decisions. For example, if showrooms are too optimistic about the market condition, it may result in overinvestment. In a word, acquiring demand information is crucial to showrooms. In practice, Home Times invests in big data to analyze consumers’ purchasing behaviors. However, showrooms must invest large sums of money in the information gathering system, demand forecast system and so on, leading to higher operational costs. Thus, showrooms need to make the trade-off between cost and revenue of information acquisition. For competing e-tailers, information can also guide their operational decisions. Thus, they have the incentive to encourage showrooms to acquire and share the information. However, it may intensify competition between e-tailers, which may lead to new interest conflict. Therefore, it has practical and theoretical values for channel cooperation to study information acquisition strategy and its incentives.
Based on this background, this paper aims at solving the following questions.
- (1)
What is the impact of information acquisition on the e-commerce supply chain members?
- (2)
What is the optimal information acquisition strategy of the showroom?
- (3)
How do the competing e-tailers design the optimal information acquisition incentive contract to obtain Pareto improvement?
The contribution of this paper is twofold. First, this paper studies operational decisions under the competition scenario where the showroom exerts experience service for two competing e-tailers, while the existing research studies mostly focuses on the scenario without competition. Second, the existing research on information acquisition and its incentives mainly focuses on the traditional supply chain in which manufacturers cooperate with retailers through a wholesale model. Differently, this paper explores information acquisition and its incentives in an e-commerce supply chain, where a showroom cooperates with two competing retailers through an agent model.
The rest of this paper is organized as follows.
Section 2 reviews the related literature.
Section 3 describes how to build the mathematical model, and
Section 4 gives the methodology on how to solve the mathematical model.
Section 5 and
Section 6 study the optimal information acquisition strategy of the showroom and the optimal information acquisition incentive contract of competing e-tailers, respectively.
Section 7 provides the discussion and conclusion of this paper.
2. Literature Review
2.1. Literature on Showroom Model
Literature on the showroom model can be divided into two streams. In the first stream of literature, some retailers are forced to be showrooms due to showrooming (the behavior that consumers examine products offline and then buy them from e-tailers at lower prices). Therefore, scholars mainly focused on the impact of showrooming [
4,
5,
6,
7] and how to cope with showrooming [
8,
9,
10,
11,
12]. Later, some scholars considered the vital role of manufacturers in the distribution channel and introduced them to this research stream [
13,
14,
15].
As more and more consumers use both online and offline channels to purchase, some scholars put forward a showroom mechanism from the aspect of channel cooperation [
16]. This stream of literature on showroom mainly includes two aspects: the aspect of a single firm and the aspect of a supply chain. From the aspect of a single firm, some scholars investigated the impact of a showroom on the e-tailer [
3]; some scholars studied operational decisions of the retailer operating both an online channel and a showroom, such as inventory decision [
17], product placement strategy [
18,
19,
20,
21], pricing decision [
22,
23]. From the aspect of a supply chain, some scholars examined the cooperation strategy of supply chain members without competition, such as Liu et al., who explored how to open the online and showroom channel in a supply chain with a manufacturer and a retailer [
24]; Li et al. studied the cooperative advertising contract design of the e-tailer to the showroom [
25]. Some scholars considered the scenario with competition. For instance, Zhang et al. investigated a retailer’s information service decision and two competing manufacturers’ pricing decisions when the retailer operates both the online channel and showroom [
26]; Li et al. studied whether a showroom cooperating with an existing e-tailer introduces a competing e-tailer under information asymmetry [
27]; Zhang et al. studied an online manufacturer’s response strategy to a retailer when it introduces a competing product in its showroom [
28].
The second stream of literature under competition is more related, but Zhang et al. [
26] mainly focused on the competition between manufacturers, and the online channel and showroom belong to one retailer; Li et al. [
27] mainly studied whether a showroom introduces a competitor; Zhang et al. [
28] focused on product competition in a one-to-one supply chain. Differently, we consider a supply chain with a showroom and two competing e-tailers, and explore information acquisition and its incentives of supply chain members.
2.2. Literature on Information Acquisition and Its Incentives
This paper also relates literature on information acquisition and its incentives, which can be divided into scenarios without competition and with competition. In the first stream of literature, some scholars mainly focused on information acquisition decisions [
29]; some scholars investigated the impact of information acquisition at different timing [
30,
31]; some scholars designed different contracts to encourage the retailer to acquire information [
32,
33].
In the second stream of literature, some scholars studied information acquisition and its incentives with downstream competition. For instance, in a supply chain with a supplier and two or more competing retailers, Shin and Tunca examined the reason for the retailers’ overinvestment in information acquisition, and designed a contract based on market behavior [
34]; Li et al. considered that the supplier can obtain information by itself and the retailers, and explored the optimal information acquisition decision and side payment contract of the supplier [
35]. Besides, some scholars considered a supply chain with channel competition. For instance, Huang et al. studied the optimal information acquisition incentive contract of the manufacturer and information acquisition decision of the retailer in a dual-channel supply chain [
36].
This paper relates more on information acquisition and its incentives under competition. However, these research studies mainly focused on the traditional supply chain where suppliers cooperate with retailers through a wholesale model. Differently, we focus on the supply chain where e-tailers cooperate with the showroom through an agent model.
Table 1 summarizes the difference between this paper and the most relevant research studies.
3. Mathematical Model Building
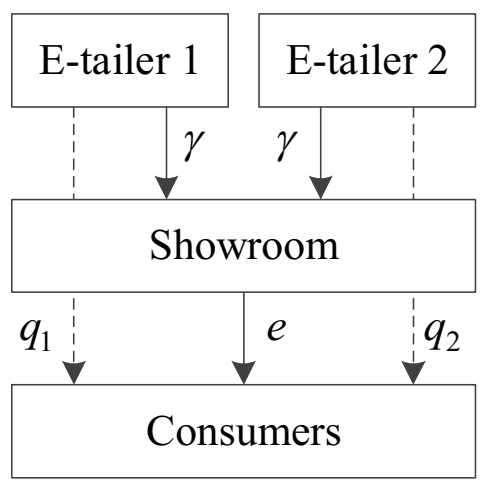
Consider a supply chain with a showroom (
) and two competing e-tailers (
). E-tailer
sells product
to consumers at selling quantity
. The showroom exerts experience service to attract consumers to experience products offline and then buy them online, and charges a certain proportion of revenue for each transaction as commission. Let
and
denote experience service level and commission rate. We draw
Figure 1 to illustrate the supply chain structure intuitively.
Experience service does not deliver product information, rather, it brings a unique experience to consumers; therefore,
can increase market demand. Besides, consumers always prefer different channels to purchase [
19]. Thus, we assume that there exist consumers preferring online channel and consumers preferring offline channel. Meanwhile, this paper mainly focuses on the cooperation problem where the showroom exerts experience service to attract consumers preferring offline channel to touch and feel products. Therefore, similar to [
37], we assume that the demand of consumers preferring online channel is exogenous, which is normalized to 0. Then, we have inverse demand function of e-tailer
:
where
denotes market-clearing price of product
,
denotes base market demand of consumers preferring offline channel (base market demand for short),
denotes competition intensity between the e-tailers. Considering the impact of market uncertainty, we assume base market demand
is random, which can be either high (H type) or low (L type) with equal probability, i.e.,
. Further, we assume
and
, where
denotes the mean of base market demand,
denotes demand uncertainty and satisfies
. The showroom and e-tailers only know the prior distribution type of
.
Due to serving consumers directly, the showroom always possesses extensive data. Then, before the selling season, the showroom can obtain demand forecast information
at a fixed cost
. Information
has two states:
and
, which correspond to the two demand states
and
, respectively. Besides, it is an unbiased estimator of the real demand state, i.e.,
,
; and also satisfies regularity conditions, i.e.,
and
. In real life, the showroom can only forecast limited information, and we define forecast accuracy as
, and
. Then, we have:
From Equation (3), is the combination of forecast accuracy and demand uncertainty, which measures how much the expected demand varies from the showroom’s forecast. Thus, we refer to as forecast variability for convenience.
Let
denote side payment offered by e-tailer
to incent the showroom to acquire and share the information. Besides, considering the increasing marginal cost of experience service, we assume that the cost function of experience service is
. Then, we have profit functions of supply chain members:
Before the selling season, the e-tailers decide whether to provide information acquisition incentives, if provided, then decide side payment . Then the showroom makes the information acquisition decision. At the beginning of the selling season, the showroom decides the experience service level ; then e-tailer decides product quantity . At the end of the selling season, demand is achieved and supply chain members obtain their profit.
Besides, we acknowledge some constraints of our model. First, this paper mainly studies information acquisition decision of the showroom and information acquisition incentive contract design of the e-tailers. As a result, the mathematical model is only applied to the product categories which require touch and feel, such as household products, apparel and accessories. Second, in this model, the showroom does not sell competing products directly; therefore, this model may not fit for the scenario where offline stores sell competing products and consumers exhibit price comparison behavior. Third, this paper mainly focuses on cooperation instead of competition between showroom and e-tailers. Thus, this model cannot apply to the scenario where offline and online channels are significantly different, i.e., the different return date and return methods between online and offline channels.
4. Methodology
For convenience, let F and N strategies represent the showroom acquire information and does not acquire information, respectively.
4.1. Methodology under F Strategy
Under F strategy, we use backward induction to solve our mathematical model based on signaling game theory. The reason is as follows. Under F strategy, the showroom does not share information
to e-tailer
, i.e., e-tailer
does not know
. However, e-tailer
can make a rational inference through experience service. Anticipating this reaction, the showroom may distort information to maximize profit. Signaling game between the showroom and e-tailer
happens. There always exist separating equilibrium and pooling equilibrium in a signaling game. When more than one equilibrium result exists, it is necessary to refine the equilibrium results. Due to intuitive criterion, a classical equilibrium refinement tool proposed by Cho and Kreps [
38], it is easy to verify that the pooling equilibrium cannot survive the intuitive criterion [
27,
39,
40]. Thus, the rest of this paper mainly focuses on the separating equilibrium.
In the separating equilibrium, the showroom exerts different levels of experience service
due to information
. E-tailer
upgrades its belief on the type of
after observing
. Intuitively, with higher base market demand, the showroom tends to exert a higher
. Therefore, belief structure of e-tailer
satisfies the rules: if
, e-tailer
regards information as
; otherwise, e-tailer
regards information as
, where
denotes threshold of experience service level. Based on this belief structure, e-tailer
can infer the true type of
. Then, the expected profits of supply chain members are:
Solving the above optimization problems, we have Theorem 1.
Theorem 1. ,,,, where,,,; and when,.
Proof of Theorem 1. Due to backward induction, we first derive the optimal selling quantity decisions. It is easy to verify that
is concave in
. Let
, we have
. Next, we derive the optimal experience service level. Due to the belief structure of e-tailer
, there exists a unique perfect Bayesian equilibrium of the signaling game if and only if the following constraints are satisfied:
where
denotes expected profit of H type showroom which mimics as L type;
denotes expected profit of H type showroom which delivers its true information;
denotes expected profit of L type showroom which delivers its true information;
denotes expected profit of L type showroom which mimics as H type. The above two constraints ensure that the showroom cannot obtain higher profit by mimicking as the other type.
From , we can easily obtain that the optimal experience service level is . Then, the optimal expected profit of H type showroom is . It is also easy to obtain that . Then, Constraint 1 equals to . To guarantee this inequality, experience service level of L type should satisfy ; otherwise H type showroom can always obtain higher profit by mimicking as L type. Thus, under the perfect Bayesian equilibrium, e-tailer has the unique belief structure, i.e., . Besides, it is easy to verify that Constraint 2 is always satisfied. Therefore, we have the optimal experience service level of L type showroom as without constraint. Combined with the belief structure of e-tailer , if , L type showroom will choose the optimal experience service level as ; otherwise, L type showroom will choose the optimal experience service level as . □
Theorem 1 shows that L type showroom has to lower when forecast variability is relatively small. The reason for this downward distortion is as follows. When is relatively small, H type showroom has the incentive to mimic L type. Anticipating this incentive, e-tailer will infer showroom when its experience service level is higher than , as H type further increases product selling quantity. This will intensify competition between e-tailers under L type demand and result in a profit loss of L type showroom. Then, to avoid being misunderstood, L type showroom has to lower . This reveals that under information asymmetry, the showroom has to pay a certain signal cost to deliver its true information.
4.2. Methodology under N Strategy
Under N strategy, all supply chain members are not aware of the actual demand state. Thus, we use backward induction to solve the mathematical model based on the expected profit maximization. Then, the expected profits of supply chain members are:
Solving the above optimization problems, we have the equilibrium decisions in Theorem 2.
Theorem 2. ;.
Proof of Theorem 2. Due to backward induction, we first solve the optimal selling quantity decisions. It is easy to verify that is concave in . Let , we have . Then we can verify that is concave in . Let , we have . □
5. Results
5.1. The Optimal Information Acquisition Strategy
Let
and
, where
and
denote value brought by information acquisition to the showroom and e-tailer
. Substituting equilibrium results in Theorems 1 and 2, we have:
where
and
denote forecast revenue brought by information acquisition to the showroom and e-tailer
,
and
denote signal cost brought by information asymmetry to the showroom and e-tailer
, and
,
;
,
.
Analyzing the impact of information acquisition on supply chain members, we have Proposition 1.
Proposition 1. (1) Forecast revenue: if, then,; if, then,; (2) Signal cost: if, then; if,and, then .
Where , is the solution of , ; , , , .
Proof of Proposition 1. From Equations (10) and (11), we have:
From the above equation, we have . Due to the nature of the quadratic function, we have when ; when . The proof of , as well as the proof of Proposition 1(2) is similar to that mentioned before. □
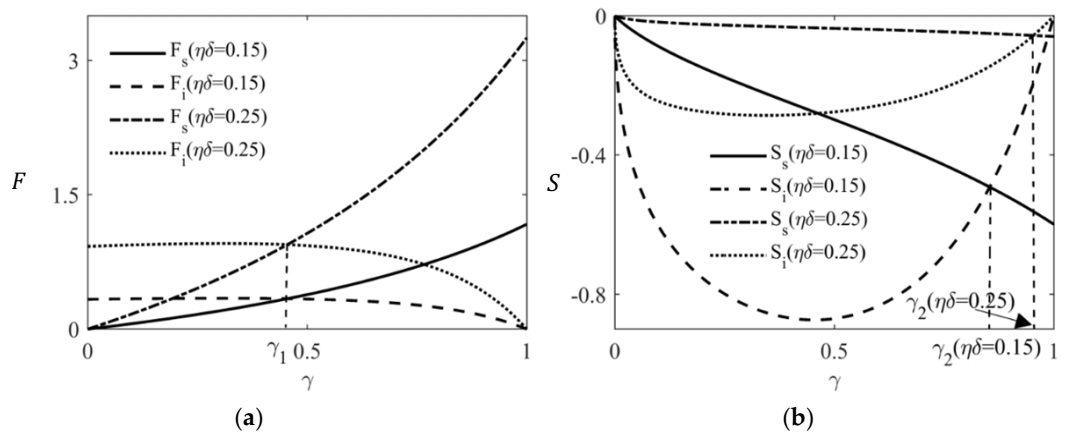
To illustrate Proposition 1 intuitively, we used Matlab-R2017a to draw
Figure 2 based on
and
. Proposition 1(1) shows that information acquisition always brings positive forecast revenue to supply chain members, which is also illustrated in
Figure 2a. It is noteworthy that when commission rate is low, forecast revenue of the e-tailers is higher than that of the showroom. Proposition 1(1) also shows that forecast variability
has a positive effect on forecast revenue. Proposition 1(2) indicates that when
is small, information asymmetry generates signal cost to supply chain members, which is also illustrated in
Figure 2b, and when
is high and
is medium, signal cost of the showroom is higher than that of the e-tailers.
Analyzing , we have the optimal information acquisition decision of the showroom in Proposition 2.
Proposition 2. (1) When, for any, N strategy is optimal to the showroom; (2) When, if then F strategy is optimal to the showroom; otherwise, N strategy is the optimal strategy; where .
Proof of Proposition 2. The proof of Proposition 2 is similar to that of Proposition 1. □
Proposition 2 shows that the optimal information acquisition strategy depends on the joint impact of forecast revenue, signal cost and information acquisition cost. To be more specific, when forecast variability is small, signal cost dominates forecast revenue. Thus, even when information acquisition cost approaches 0, the showroom will not acquire information. As becomes bigger, forecast revenue dominates, then the showroom will acquire information if the information acquisition cost is no larger than its total value. This suggests whether the showroom should acquire information needs to consider information asymmetry besides information acquisition cost.
5.2. The Optimal Information Acquisition Incentive Contract
Analyzing the impact of the optimal information acquisition strategy on the e-tailers, we have Proposition 3.
Proposition 3. The impact of the optimal strategy on the e-tailers is given in Table 2.
Proof of Proposition 3. The proof of Proposition 3 is similar to that of Proposition 1. □
Proposition 3 indicates that the optimal information acquisition strategy benefits the e-tailers in some conditions but hurts them in others, and there exist three different reasons for profit loss. In region R2, low commission rate makes that revenue forecast of the e-tailers dominates their signal cost. Thus, information acquisition brings higher profits to them. In region R4 and region R9, information acquisition always generates higher profits for the e-tailers. In region R6, high commission rate makes forecast revenue of the e-tailers lower than signal cost. Thus, information acquisition hurts the e-tailers.
When the optimal strategy hurts the e-tailers, they have incentives to encourage the showroom to change its strategy. However, only when the increased profit of e-tailers can offset profit loss of the showroom caused by changing the optimal strategy is information acquisition incentive contract feasible. Thus, it is necessary to analyze the impact of the optimal strategy on the whole supply chain. Let , where denotes value brought by information acquisition to the whole supply chain. From Equations (10) and (11), we have , where and denote forecast revenue and signal cost of the whole supply chain, and , . Analyzing the impact of the optimal strategy on the whole supply chain, we have Proposition 4.
Proposition 4. The impact of the optimal strategy on the whole supply chain is given in Table 3.
Proof of Proposition 4. The proof of Proposition 4 is similar to that of Proposition 1. □
Proposition 4 indicates that only in regions R2b, R4a, R6a and R9a, the e-tailers can design contract to encourage the showroom to change its strategy.
In region R6a, the e-tailers encourage the showroom not to acquire information; in regions R2b, R4a and R9a, the e-tailers encourage the showroom to acquire information. For convenience, we refer to SN contract and SF contract as the two contracts.
5.2.1. SN Contract
In practice, firms always determine side payment by negotiation. Thus, we assume that side payment
is determined by one-to-one negotiation. Let
denote bargaining power of e-tailer
to the showroom. Under SN contract, the Nash bargaining problem is:
where
,
,
.
Due to backward induction, we obtain the equilibrium SN contract in Proposition 5.
Proposition 5. (1);;; (2) When,; otherwise,.
Proof of Proposition 5. Due to backward induction, we first solve the optimal sell quantity decisions and the optimal experience service level decision during the selling season, which is similar to the proof of Theorem 2. Then, we solve the optimal side payment in Equation (12) without constraint, and we have . It is easy to verify that can satisfy the constraint in Equation (12), i.e., is the optimal Nash negotiation solution. It is easy to prove the solution in Proposition 5(2). □
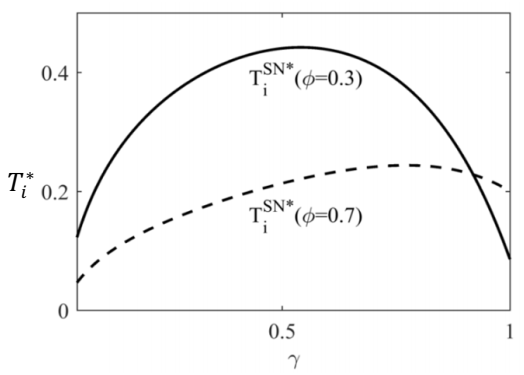
To illustrate Proposition 5 intuitively, we use Matlab-R2017a to draw
Figure 3 based on
,
and
. Comparing Theorem 2 and Proposition 5(1), SN contract only changes the optimal information acquisition strategy. Proposition 5(2) indicates that when information acquisition value of the showroom is relatively high (
), side payment increases as bargaining power of the e-tailers increases, which is also illustrated in
Figure 3.
5.2.2. SF Contract
Under SF contract, if the showroom accepts side payment, it will acquire and share the information to the e-tailers. Then, the Nash bargaining problem is:
where
,
,
.
Due to backward induction, we obtain the equilibrium SF contract as shown in Proposition 6.
Proposition 6. (1);;;;; (2) When,; otherwise,.
Proof of Proposition 6. The proof of Proposition 6 is similar to that of Proposition 5. □
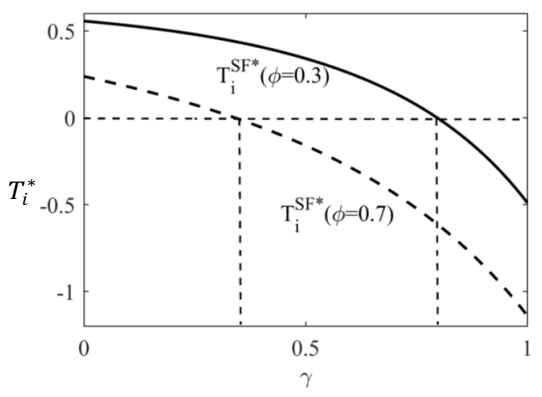
To illustrate Proposition 6 intuitively, we use Matlab-R2017a to draw
Figure 4 based on
,
and
. Comparing Theorem 1 and Proposition 6(1), SF contract does not encourage the showroom to change the optimal strategy, but also changes the optimal decisions. Proposition 6(2) shows that when the bargaining power of the e-tailers is strong, the showroom can get higher side payment with higher competition intensity. On the one hand, it is easy to verify that
and
, which indicates that the increase of competition intensity has a negative impact on forecast revenues. On the other hand, when the bargaining power of the e-tailers is strong, the negative impact of competition on forecast revenue of the showroom dominates that of the e-tailers. As a result, the showroom can get higher side payment with higher competition intensity.
6. Discussion
This paper studies the impact of information acquisition on the optimal decisions of supply chain members, and finds that information acquisition generates both positive forecast revenue and negative signal cost. These results are in line with literature [
29] and [
36], i.e., information acquisition may distort the optimal decisions of supply chain members and lead to negative signal cost. However, comparing with the literature considering the traditional supply chain with supplier(s) and retailer(s), our study points out that the negative signal cost may hurt the showroom more severely than the e-tailers in the e-commerce supply chain. To be more specific, the reason for the generation of signal cost is that the showroom lowers the optimal experience service level to deliver true forecast information under information asymmetry, leading to lower demand and lower profit of supply chain members. Notably, high commission rate means high signal cost shared by the showroom. Meanwhile, the decrease of experience service level can lower the operational cost of the showroom to a certain extent. Thus, when forecast variability is medium, the showroom suffers higher signal cost than the e-tailers.
This paper also studies the optimal information acquisition incentive contract for e-tailers to achieve Perato improvement. The existing literature mainly explores how suppliers design different contracts to encourage retailers to forecast demand information [
32,
33,
34,
35]. Differently, in SN contract, the e-tailers offer contracts to encourage the showroom not to acquire demand information. This is because in the SN contract region, forecast revenue of the showroom dominates its signal cost, but the profit the showroom obtained by acquiring information cannot offset the negative effect on the e-tailers. Besides, we also find that SF contract can eliminate the ill effect of signal cost; as a result, side payment is negative when commission rate is high.
7. Conclusions
In recent years, showrooms have developed fast to provide experience service for e-tailers, which can solve consumers’ fit uncertainty when purchasing online. However, with the increasing uncertainty of the market, the mismatch between demand and supply brings a considerable challenge to supply chain members. How to acquire information is crucial for channel cooperation. Under this background, this paper considered a supply chain consisting of a showroom and two competing e-tailers, and examined the optimal information acquisition and its incentives.
The main results are summarized as follows. On the one hand, information acquisition prompts the showroom to adjust experience service level, which further delivers information to the e-tailers indirectly and then prompts them to adjust their optimal decisions. As a result, all supply chain members obtain positive forecast revenue. On the other hand, when forecast variability is relatively small, the showroom needs to lower the optimal experience service level to deliver true information. This leads to lower consumers’ demand and then generates negative signal cost to supply chain members. The optimal information acquisition strategy of the showroom depends on the joint impact of forecast revenue, signal cost and information acquisition cost. Specifically, in some conditions, even information acquisition cost approaches 0, and the showroom will not acquire information. In some conditions, the optimal strategy harms profits of the e-tailers and the whole supply chain. Then, we design SN and SF contracts to encourage the showroom to change its optimal strategy.
The above conclusions have important implications. From the perspective of the enterprise itself, the more demand information it has the better. However, from the perspective of the whole supply chain, information asymmetry among supply chain members may hurt the one possessing more demand information. Therefore, when making demand acquisition decisions, showrooms should consider their relationship with other supply chain members, especially the information asymmetry and the cooperation model among them.
It is notable that in some conditions information acquisition hurts the whole supply chain due to negative signal cost caused by information asymmetry. Under this condition, the e-tailers should offer side payment to encourage showrooms not to acquire demand information. The existing literature mainly explores how to design contracts to encourage information acquisition behavior. Therefore, this finding is also the contribution of our paper to the theory.
We acknowledge some limitations in this paper. First, e-tailers may cooperate with more than one showroom in practice, but we only consider the competition issue between e-tailers in this paper, which is one of the limitations of this paper. As a result, studying how e-tailers cooperate with more than one showroom will be an interesting direction. Second, in this paper we find that the showroom possessing more demand information may obtain lower profits, which indicates that the showroom can strategically share its information to obtain more profits. However, limited by the length of the article, this paper fails to explore forecast information sharing in the e-commerce supply chain, which is another limitation of this paper. Thus, future research can explore how showrooms strategically share information with e-tailers in an e-commerce supply chain.