Measuring Customer Equity in Noncontractual Settings Using a Diffusion Model: An Empirical Study of Mobile Payments Aggregator
Abstract
1. Introduction
2. Literature Review
2.1. Brief Introduction of CE
2.2. CE Measurement Model
- In terms of the relationship between a firm and its customers, the approaches of customer equity measurement can be divided into contractual models and noncontractual models [21,22]. In contractual settings, such as insurance, telecommunications, and magazine subscriptions, firms can accurately understand the cash flow generated by their customers as customers usually sign long-term contracts with the firms. In such cases, the measurement of customer equity should focus on the prediction of whether customers in the following period will continue to subscribe for products or services of the firm (i.e., investigation of the retention rate) [7]. Noncontractual models are used, for example, in the retail industry, where customers and firms are not bound by contracts and customers may shift among different products or service providers. In such cases, the measurement of customer equity involves not only the prediction of the frequency of customers’ future purchases but also the prediction of customers’ future purchase amount [23]. The measurement of customer equity under a noncontractual relationship thus appears to be more complicated.
- In terms of the data source, the measurement of customer equity can be based on firm-level data (such as financial data from annual reports) or individual-level data (such as individual transaction data) [24]. For the former, the average customer lifetime value is calculated through financial data and is multiplied by the number of customers to obtain customer equity. As no individual customer lifetime value is involved in this top-down approach, it is also called an aggregate-level approach [3,9,25,26]. For the latter, the lifetime value of each customer is calculated based on individual transaction data. Customer equity is then calculated by summing up the lifetime value of all customers. This bottom-up approach is also referred to as a disaggregate-level approach [23].
- In terms of the model type, customer equity can be calculated by taking deterministic and stochastic approaches [2,27]. For the former, there are no random components involved in the model. The heterogeneity among individual customers is usually not considered. Customer equity can thus be directly calculated based on a simple formula [7,25]. For the latter, the stochastic factors and the heterogeneity among customers are fully considered. Although the stochastic approach is more complicated, it can make the calculation of customer equity more accurate [11].
- In terms of the specific modeling approach, customer equity can be calculated using probability models, econometric models, persistence models, computer science models, and diffusion/growth models. Probability models are built under certain probability distribution assumptions of customers’ purchasing behaviors. For example, the customers’ future purchasing frequency can be predicted using a Pareto/NBD model [16] and a BG/NBD model [28], the amount of customers’ future purchase can be predicted using the normal distribution [29] or log-gamma distribution [30], and the Conway–Maxwell–Poisson distribution is used to jointly model the purchase frequency and purchase quantity [31]. The central concept of econometric models is to explain different purchasing behaviors of customers through a series of covariates. This approach emphasizes factors that affect customer equity and its components. Commonly used econometric models include the simple regression model, the logit/probit model [32,33] and the survival analysis model [34]. When the time series data is long enough, persistence models, including the unit root test, cointegration model, and VAR model, can be established to predict customer equity, quantifying the long-term dynamic effects of different covariates in customer equity modeling [35,36]. Computer science models introduce machine learning and modern nonparametric statistics to the measurement of customer equity. These models need no theoretical assumptions and generally have stronger predictive ability than parametric models. The main models used are the support vector machine (SVM) [37], random forest [38], Lasso regression, and generalized additive model (GAM) [39]. Diffusion/growth models emphasize the prediction of the number of future customers and thus lay a foundation for customer equity measurement. The diffusion models are discussed in detail below.
2.3. CE Measurement Using a Diffusion Model
3. Theoretical Model
3.1. Customer Segmentation Based on a Diffusion Model
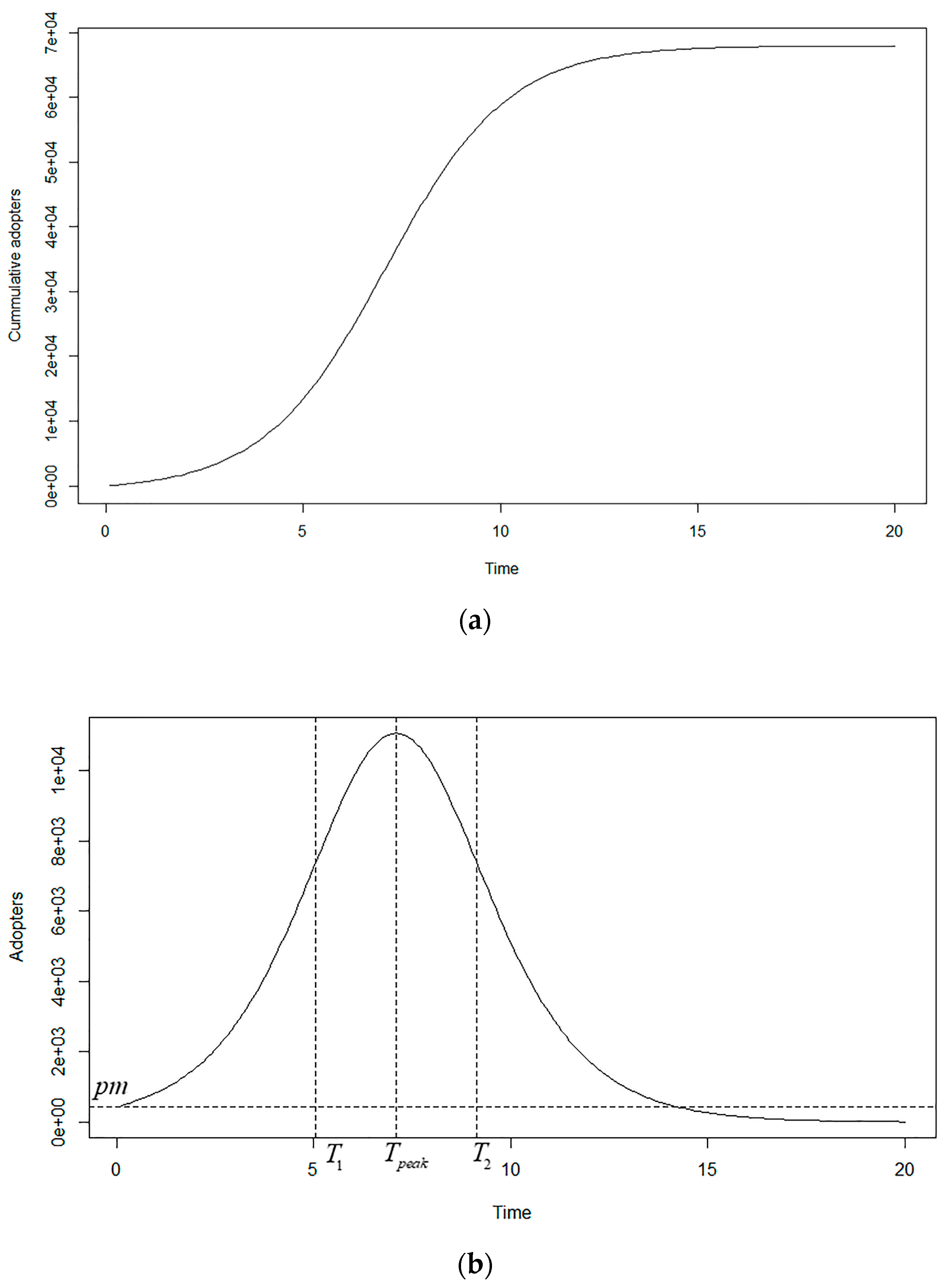
3.1.1. Bass Model
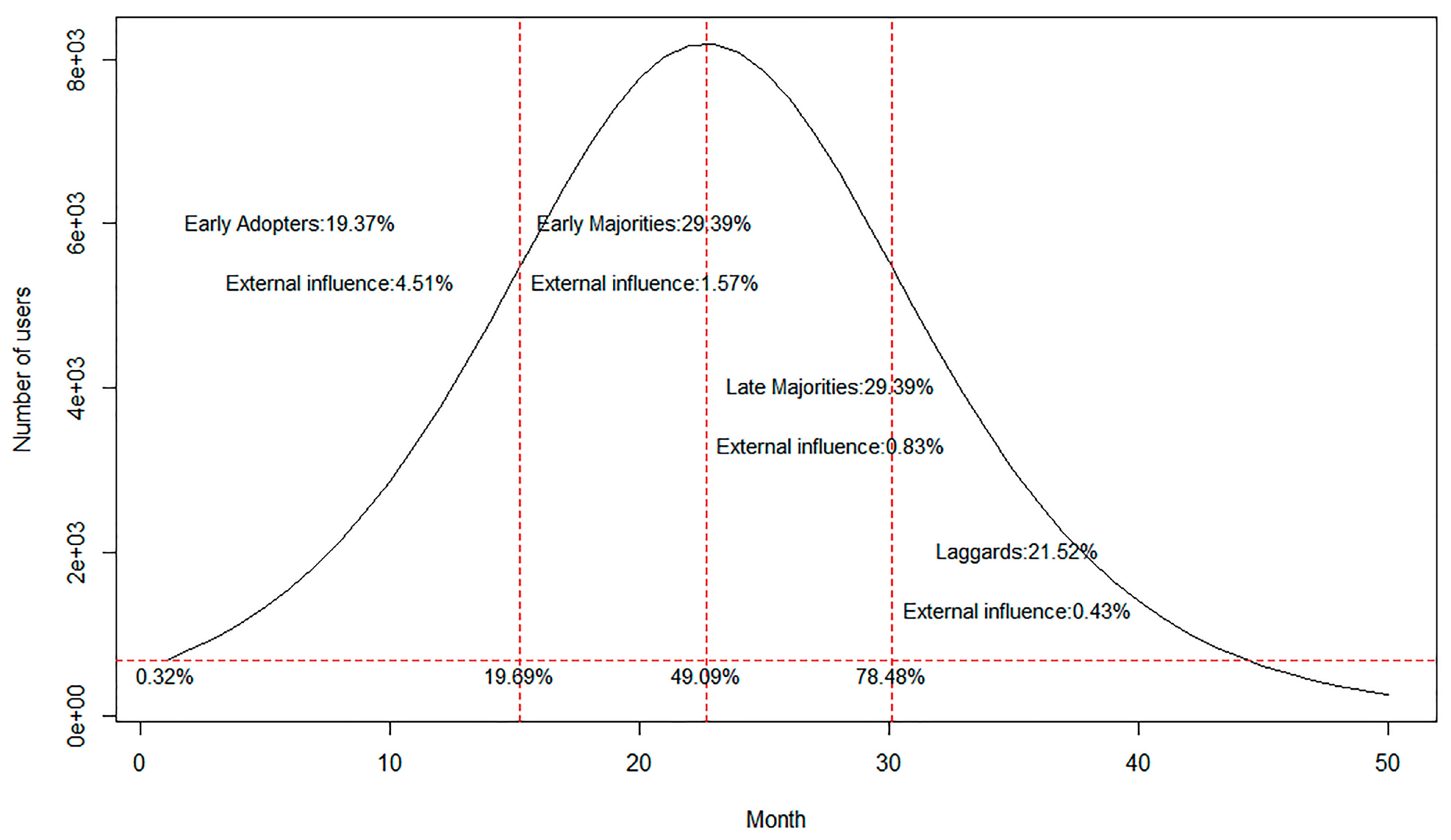
3.1.2. Bass Model and Adopter Categories Proposed by Rogers
3.2. Estimation of CE and CESR
3.2.1. Estimation of CE
3.2.2. Estimation of CESR
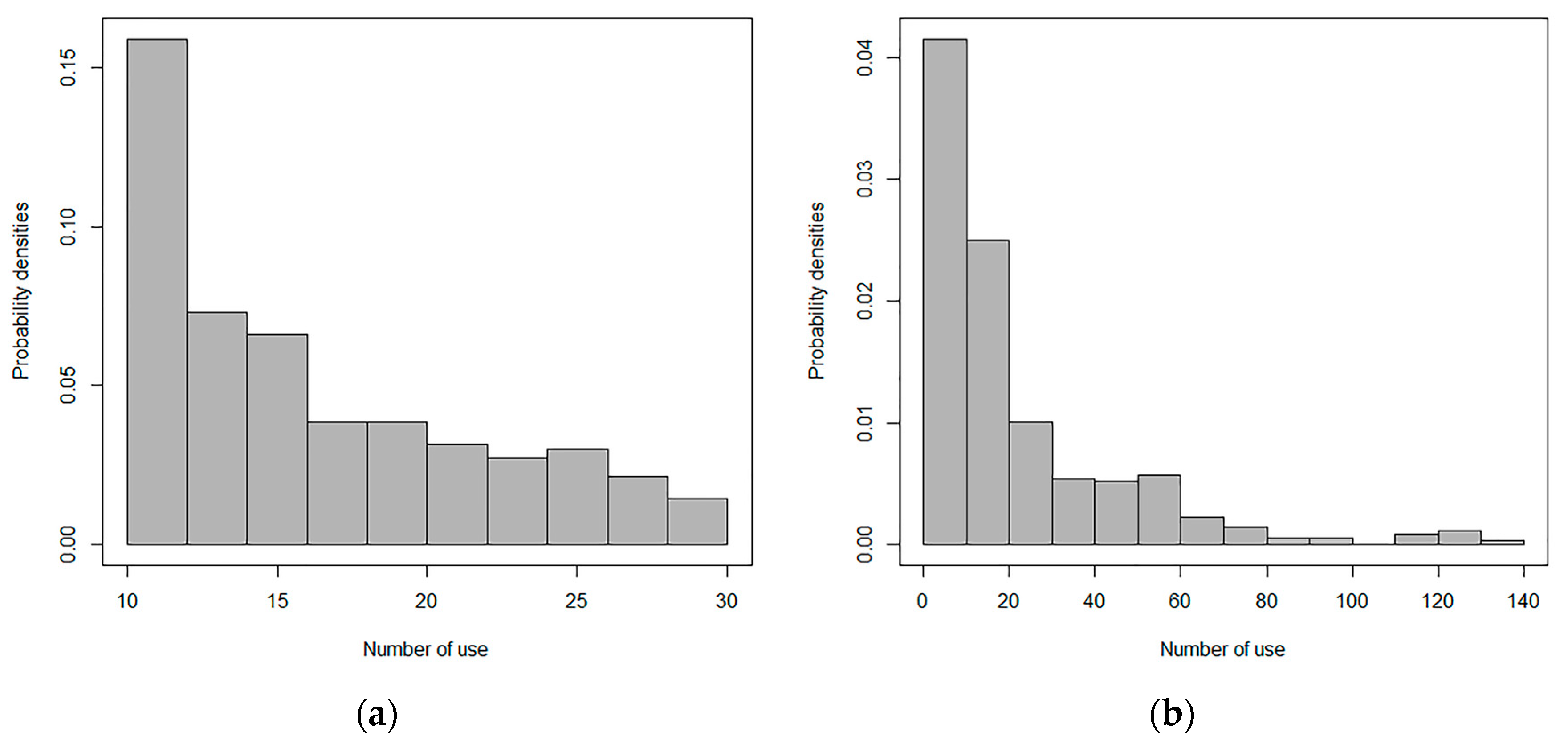
3.3. Estimation of Customer Purchase and Retention Rates Using a Pareto/NBD Model
- 1.
- The time when a customer becomes “inactive” is exponentially distributed with churn rate μ. The probability density function is:
- 2.
- There is a difference in the transaction rate of individual customers. The transaction rate λ across customers follows a gamma distribution. The probability density function is:
- 3.
- There is a difference in the churn rates of individual customers. The churn rate μ across customers follows a gamma distribution. The probability density function is:
- 4.
- Transaction rate λ is independent of the death rate μ. The expected number of transactions from the initial transaction period T0 to the observation period T is therefore
4. Methodology
4.1. Research Framework
4.2. Data
5. Empirical Results and Analysis
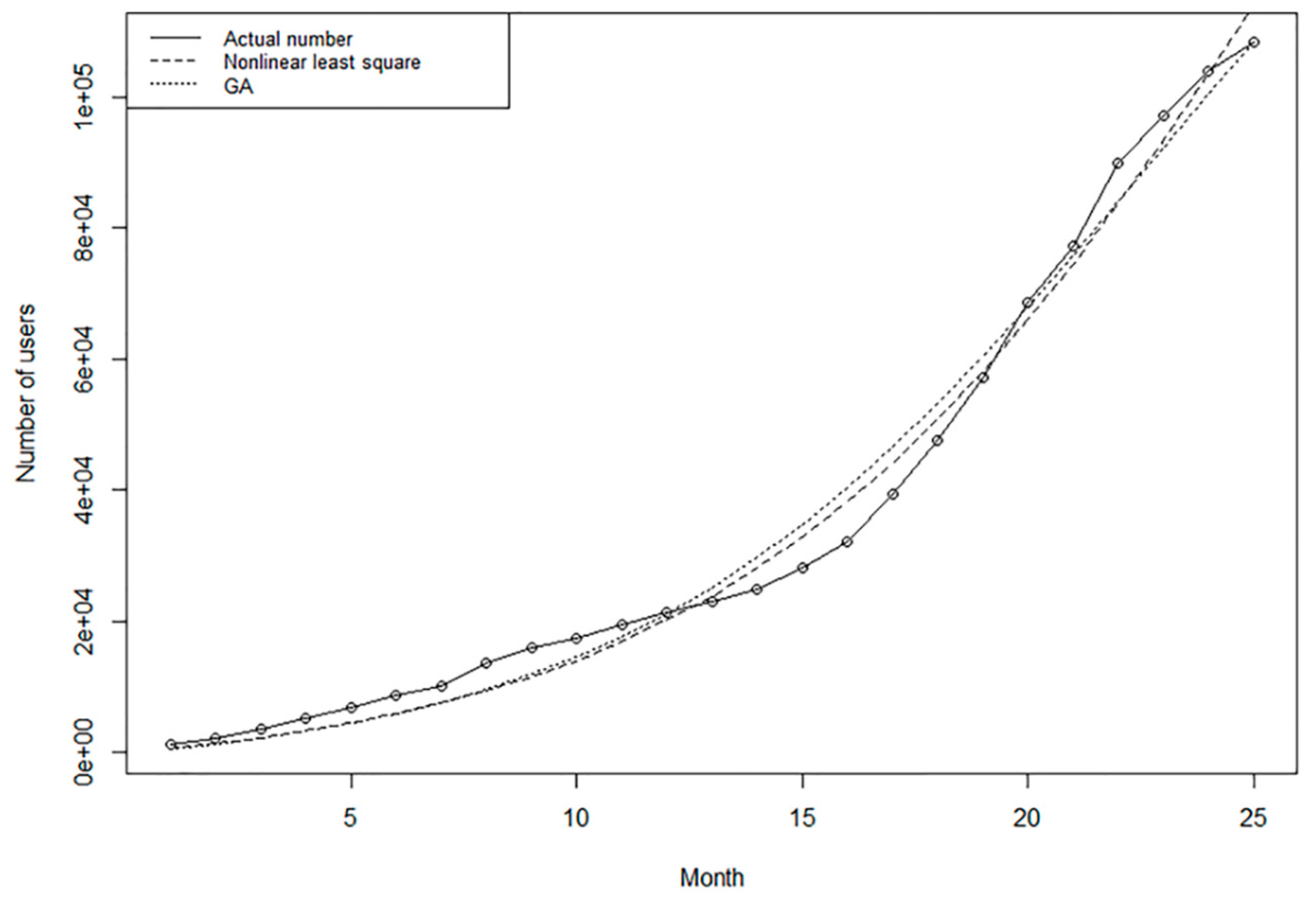
5.1. Parameter Estimation for the Bass Diffusion Model
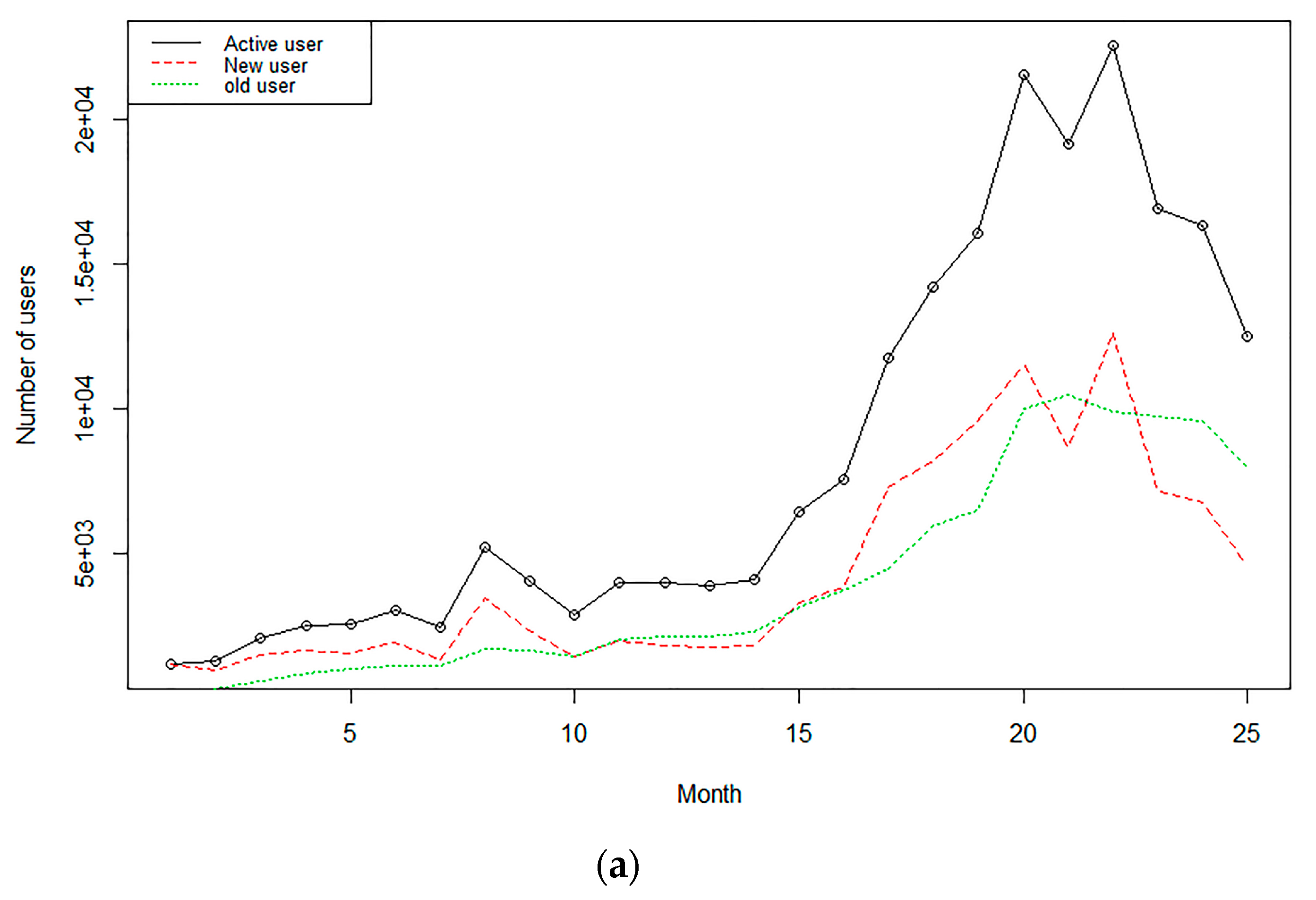
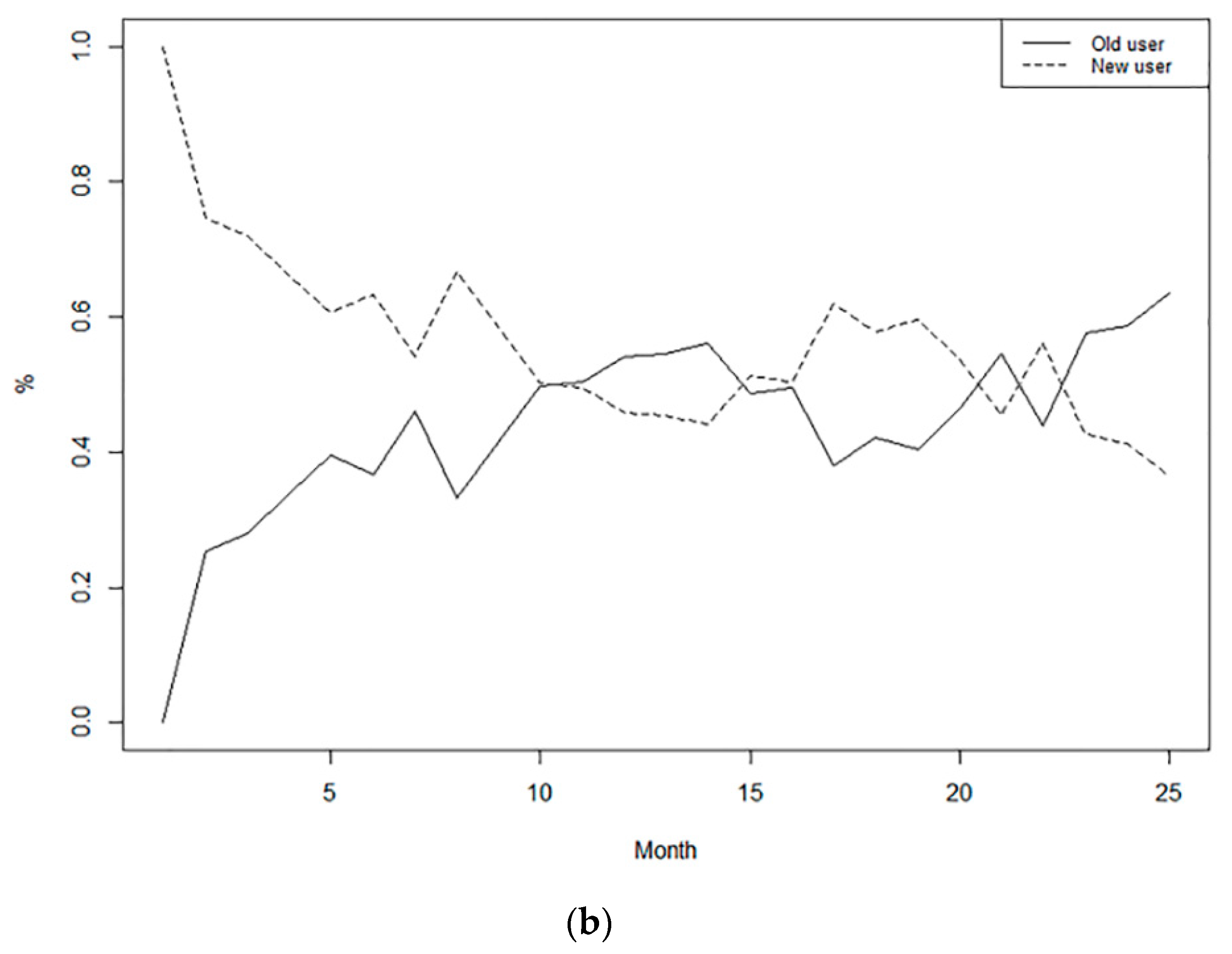
5.2. User Segmentation Based on the Diffusion Model
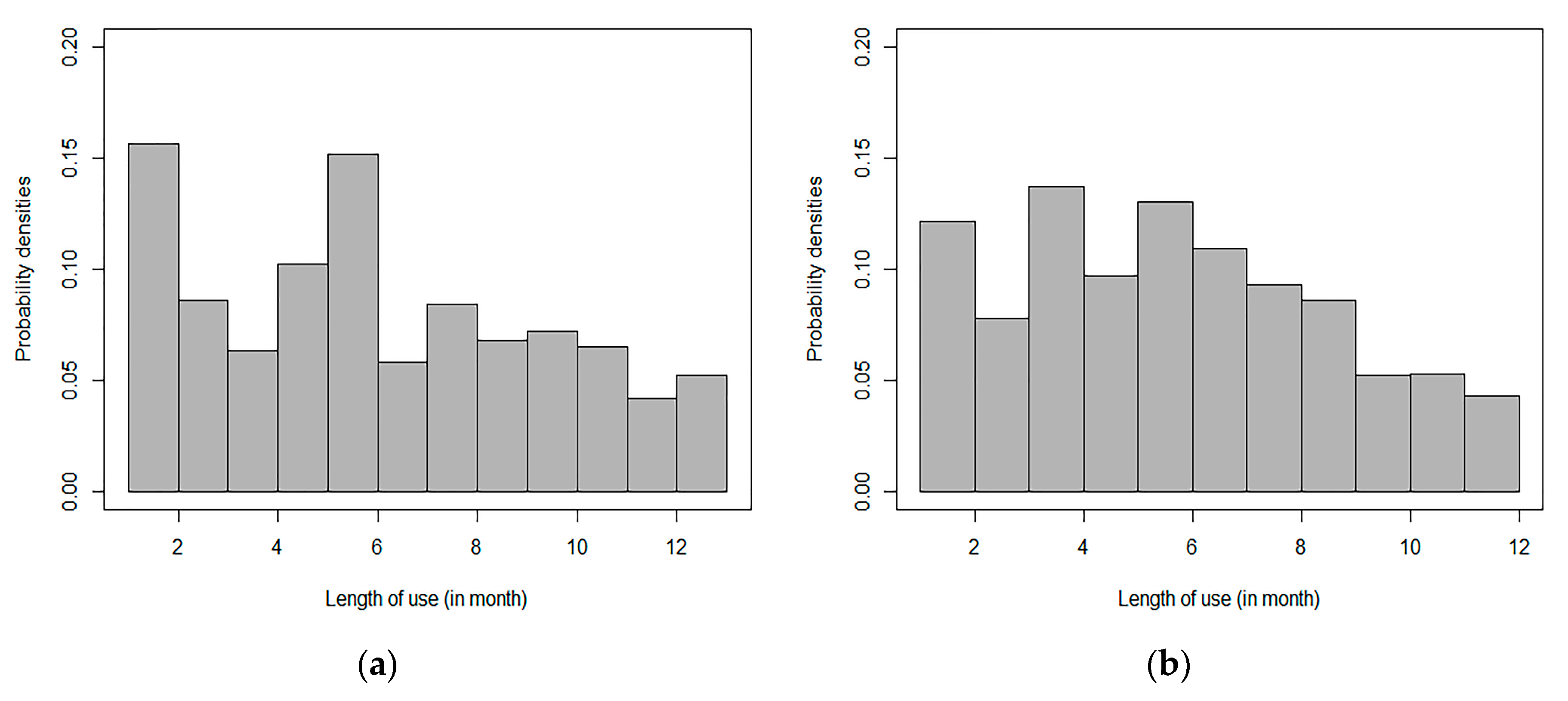
5.3. Modeling Customer Behavior Using a Pareto/NBD Model
5.4. CE and CESR Calculation
5.4.1. Calculating Customer Equity of Current Users
5.4.2. Calculating Customer Equity of Potential Users
6. Managerial Relevance and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Concept | Definition | Abbreviation |
|---|---|---|
| Customer lifetime value | The net present value of profits that a customer can bring to a firm during his or her entire life of transactions with the firm | CLV |
| Customer equity | The sum of the lifetime value for all customers of the firm | CE |
| Customer equity sustainability ratio | The ratio of a customer’s (or all customers’) future CLV (or CE) to the customer’s (or their) total CLV (or CE) | CESR |
References
- Blattberg, R.; Getz, G.; Thomas, J.S. Customer Equity: Building and Managing Relationships as Valuable Assets; Harvard Business School Press: Boston, MA, USA, 2001. [Google Scholar]
- Estrella-Ramón, A.M.; Sánchez-Pérez, M.; Swinnen, G.; Vanhoof, K. A Marketing View of the Customer Value: Customer Lifetime Value and Customer Equity. South Afr. J. Bus. Manag. 2013, 44, 47–64. [Google Scholar] [CrossRef]
- Gupta, S.; Lehmann, D.R. Customers as Assets. J. Interact. Mark. 2003, 17, 9–24. [Google Scholar] [CrossRef]
- Kumar, V. A Theory of Customer Valuation: Concepts, Metrics, Strategy, and Implementation. J. Mark. 2018, 82, 1–19. [Google Scholar] [CrossRef]
- Gupta, S.; Zeithaml, V. Customer Metrics and Their Impact on Financial Performance. Mark. Sci. 2006, 25, 718–739. [Google Scholar] [CrossRef]
- Wiesel, T.; Skiera, B.; Villanueva, J. Customer Equity: An Integral Part of Financial Reporting. J. Mark. 2008, 72, 1–14. [Google Scholar] [CrossRef]
- Blattberg, R.C.; Deighton, J. Manage Marketing by the Customer Equity Test. Harv. Bus. Rev. 1996, 74, 136–144. [Google Scholar]
- Gupta, S.; Lehmann, D.R.; Stuart, J.A. Valuing Customers. J. Mark. Res. 2004, 41, 7–18. [Google Scholar] [CrossRef]
- Rust, R.T.; Lemon, K.N.; Zeithaml, V.A. Return on Marketing: Using Customer Equity to Focus Marketing Strategy. J. Mark. 2004, 68, 109–127. [Google Scholar] [CrossRef]
- Gupta, S.; Hanssens, D.; Hardie, B.; Kahn, W.; Kumar, V.; Lin, N.; Ravishanker, N.; Sriram, S. Modeling Customer Lifetime Value. J. Serv. Res. 2006, 9, 139–155. [Google Scholar] [CrossRef]
- Reinartz, W.J.; Kumar, V. The Impact of Customer Relationship Characteristics on Profitable Lifetime Duration. J. Mark. 2003, 67, 77–99. [Google Scholar] [CrossRef]
- Kumar, V.; Shah, D. Building and Sustaining Profitable Customer Loyalty for the 21st Century. J. Retail. 2004, 80, 317–329. [Google Scholar] [CrossRef]
- Skiera, B.; Bermes, M.; Horn, L. Customer Equity Sustainability Ratio: A New Metric for Assessing a Firm’s Future Orientation. J. Mark. 2011, 75, 118–131. [Google Scholar] [CrossRef]
- Tuli, K.R.; Bharadwaj, S.G.; Kohli, A.K. Ties that Bind: The Impact of Multiple Types of Ties with a Customeron Sales Growth and Sales Volatility. J. Mark. Res. 2010, 47, 36–50. [Google Scholar] [CrossRef]
- Bass, F.M. A New Product Growth for Model Consumer Durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Schmittlein, D.C.; Morrison, D.G.; Colombo, R. Counting Your Customers: Who-Are They and What Will They Do Next? Manag. Sci. 1987, 33, 1–24. [Google Scholar] [CrossRef]
- McCarthy, D.M.; Fader, P.S. How to Value a Company by Analyzing Its Customers. Harv. Bus. Rev. 2020, 91, 51–55. [Google Scholar]
- McCarthy, D.M.; Fader, P.S. Customer-Based Corporate Valuation for Publicly Traded Non-Contractual Firms. J. Mark. Res. 2018, 55, 617–635. [Google Scholar] [CrossRef]
- Kumar, V.; Shah, D. Introduction: The Evolution of Customer Equity. In Handbook of Research on Customer Equity in Marketing; Edward Elgar Publishing: Cheltenham, UK, 2015; pp. 1–14. [Google Scholar]
- Kumar, V.; Shah, D. Handbook of Research on Customer Equity in Marketing; Edward Elgar Publishing: Cheltenham, UK, 2015; pp. 283–305. [Google Scholar]
- Dwye, F.R. Customer Lifetime Valuation to Support Marketing Decision Making. J. Direct Mark. 1997, 11, 7–13. [Google Scholar]
- Reinartz, W.J.; Kumar, V. On the Profitability of Long-Life Customers in a Non-Contractual Setting: An Empirical Investigation and Implications for Marketing. J. Mark. 2000, 64, 17–35. [Google Scholar] [CrossRef]
- Venkatesan, R.; Kumar, V. A Customer Lifetime Value Framework for Customer Selection and Resource Allocation Strategy. J. Mark. 2004, 68, 106–125. [Google Scholar] [CrossRef]
- Kumar, V.; George, M. Measuring and Maximizing Customer Equity: A Critical Analysis. J. Acad. Mark. Sci. 2007, 35, 157–171. [Google Scholar] [CrossRef]
- Calciu, M. Deterministic and Stochastic Customer Lifetime Value Models. Evaluating the Impact of Ignored Heterogeneity in Non-Contractual Contexts. J. Target. Meas. Anal. Mark. 2009, 17, 257–271. [Google Scholar] [CrossRef]
- Berger, P.D.; Nasr, N.I. Customer Lifetime Value: Marketing Models and Applications. J. Interact. Mark. 1998, 12, 17–30. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Martell, M. Does Attitudinal Loyalty Influence behavioral Loyalty: A Theoretical and Empirical Study. J. Retail. Consum. Serv. 2007, 14, 35–44. [Google Scholar] [CrossRef]
- Fader, P.S.; Hardie, B.G.S.; Lee, K.L. Counting Your Customers the Easy Way: An Alternative to the Pareto/NBD Model. Mark. Sci. 2005, 24, 275–284. [Google Scholar] [CrossRef]
- Schmittlein, D.C.; Peterson, R.A. Customer Base Analysis: An Industrial Purchase Process Application. Mark. Sci. 1994, 13, 41–67. [Google Scholar] [CrossRef]
- Colombo, R.; Jiang, W. A Stochastic RFM Model. J. Interact. Mark. 1999, 13, 2–12. [Google Scholar] [CrossRef]
- Boatwright, P.; Borle, S.; Kadane, J.B. A Model of the Joint Distribution of Purchase Quantity and Timing. J. Am. Stat. Assoc. 2003, 98, 564–572. [Google Scholar] [CrossRef]
- Thomas, J.S. A Methodology for Linking Customer Acquisition to Customer Retention. J. Mark. Res. 2001, 38, 262–268. [Google Scholar] [CrossRef]
- Thomas, J.S.; Blattberg, R.C.; Fox, E.J. Recapturing Lost Customers. J. Mark. Res. 2004, 41, 31–45. [Google Scholar] [CrossRef]
- Meyer-Waarden, L. The Effects of Loyalty Programs on Customer Lifetime Duration and Share of Wallet. J. Retail. 2007, 83, 223–236. [Google Scholar] [CrossRef]
- Yoo, S.; Hanssens, D.M. Modeling the Sales and Customer Equity Effects of the Marketing MIX. UCLA Anderson Sch. Manag. 2005, 2, 1–42. [Google Scholar]
- Bandyopadhyay, S. A Dynamic Model of Cross-Category Competition: Theory, Tests, and Application. J. Retail. 2009, 85, 468–479. [Google Scholar] [CrossRef]
- Chen, Z.-Y.; Fan, Z.-P. Dynamic Customer Lifetime Value Prediction Using Longitudinal Data: An Improved Multiple Kernel SVR Approach. Knowl. Based Syst. 2013, 43, 123–134. [Google Scholar] [CrossRef]
- Ying, W. The Research on Random Forests and the Application in Customer Churn Prediction. Manag. Rev. 2012, 24, 140–145. [Google Scholar]
- Coussement, K.; Benoit, D.F.; Poel, D.V.D. Improved Marketing Decision Making in a Customer Churn Prediction Context Using Generalized Additive Models. Expert Syst. Appl. 2010, 37, 2132–2143. [Google Scholar] [CrossRef]
- Schumpeter, J. The Instability of Capitalism. Econ. J. 1928, 38, 361. [Google Scholar] [CrossRef]
- Mansfield, E. Technical Change and the Rate of Innovation. Econometrica 1961, 29, 741–766. [Google Scholar] [CrossRef]
- Libai, B.; Muller, E.; Peres, R. The Diffusion of Services. J. Mark. Res. 2009, 46, 163–175. [Google Scholar] [CrossRef]
- Hogan, J.E.; Lemon, K.N.; Libai, B. What Is the True Value of a Lost Customer? J. Serv. Res. 2003, 5, 196–208. [Google Scholar] [CrossRef]
- Silveira, C.S.; De Oliveira, M.O.R.; Luce, F.B.; Alejandro, T.B. Comparing Alternative Approaches to Estimate Customer Equity. Mark. Intell. Plan. 2017, 35, 611–625. [Google Scholar] [CrossRef]
- Rogers, E.M. Diffusion of Innovations; The Free Press: New York, NY, USA, 1983. [Google Scholar]
- Mahajan, V.; Muller, E.; Srivastava, R.K. Determination of Adopter Categories by Using Innovation Diffusion Models. J. Mark. Res. 1990, 27, 37–50. [Google Scholar] [CrossRef]
- Pfeifer, P.E. On Estimating Current-Customer Equity Using Company Summary Data. J. Interact. Mark. 2011, 25, 1–14. [Google Scholar] [CrossRef]
- Venkatesan, R.; Kumar, V. A Genetic Algorithms Approach to Growth Phase Forecasting of Wireless Subscribers. Int. J. Forecast. 2002, 18, 625–646. [Google Scholar] [CrossRef]

| Reference | Customer-Firm Relationship | Data Source | Model Type | Modeling Approach |
|---|---|---|---|---|
| [7] | contractual | firm-level | deterministic | econometric |
| [25] | contractual/noncontractual | firm-level | deterministic | econometric |
| [22] | noncontractual | individual-level | stochastic | probability |
| [3] | contractual | firm-level | deterministic | econometric |
| [11] | noncontractual | individual-level | stochastic | probability |
| [8] | contractual | firm-level | deterministic | diffusion/growth |
| [23] | noncontractual | individual-level | stochastic | probability/econometric |
| [9] | noncontractual | firm-level | stochastic | econometric |
| [42] | contractual | firm-level | deterministic | diffusion/growth |
| [35] | contractual | individual-level | stochastic | persistence |
| [38] | contractual | individual-level | stochastic | computer science |
| [37] | noncontractual | individual-level | stochastic | computer science |
| User Categories | Number of Uses per Month | Churn Rate |
|---|---|---|
| Innovators | 1.28 | 0.011 |
| Early adopters | 0.41 | 0.0003 |
| Early majorities | 0.52 | 0.00012 |
| Late majorities and laggards | 0.56 | 0.028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, W.; Sun, Y.; Bandyopadhyay, S.; Cheng, D. Measuring Customer Equity in Noncontractual Settings Using a Diffusion Model: An Empirical Study of Mobile Payments Aggregator. J. Theor. Appl. Electron. Commer. Res. 2021, 16, 409-431. https://doi.org/10.3390/jtaer16030026
Xue W, Sun Y, Bandyopadhyay S, Cheng D. Measuring Customer Equity in Noncontractual Settings Using a Diffusion Model: An Empirical Study of Mobile Payments Aggregator. Journal of Theoretical and Applied Electronic Commerce Research. 2021; 16(3):409-431. https://doi.org/10.3390/jtaer16030026
Chicago/Turabian StyleXue, Wei, Yinglu Sun, Subir Bandyopadhyay, and Dong Cheng. 2021. "Measuring Customer Equity in Noncontractual Settings Using a Diffusion Model: An Empirical Study of Mobile Payments Aggregator" Journal of Theoretical and Applied Electronic Commerce Research 16, no. 3: 409-431. https://doi.org/10.3390/jtaer16030026
APA StyleXue, W., Sun, Y., Bandyopadhyay, S., & Cheng, D. (2021). Measuring Customer Equity in Noncontractual Settings Using a Diffusion Model: An Empirical Study of Mobile Payments Aggregator. Journal of Theoretical and Applied Electronic Commerce Research, 16(3), 409-431. https://doi.org/10.3390/jtaer16030026








