Head Orientation Estimation Based on Multiple Frequency Bands Using Sparsely Aligned Microphones

Abstract

We describe the problem of estimating the speaker’s head orientation from the asynchronous multi-channel waveforms observed by microphones distributed in a room. In particular, we address a novel problem of estimating head orientation from sound captured by fewer microphones than the number of distinct head orientations to be distinguished. This is because the head orientation is an important clue indicating the speaker’s intended conversational partners. Head orientation estimation technology is an essential technology within environmental intelligence technology, which uses sensors embedded in rooms to monitor and support people’s activities. We propose a head orientation estimation method that aims to achieve high angular resolution using a small number of microphones. The proposed method achieves high estimation accuracy by using the spatial radiation pattern of the sound source as clues and by integrating information from multiple frequency bands. We conducted an experiment to estimate head orientation with an angular resolution of $15\mathrm{degrees}$ under observation conditions using six microphones. Experimental results showed that higher estimation accuracy was obtained than the conventional method using distributed microphone arrays (Oriented Global Coherence Field method) and the conventional method using distributed microphones (Radiation Pattern Matching method). The proposed method utilizing multiple frequency bands achieved the best performance with a mean absolute error of $10.58\mathrm{degrees}$ in the task of classifying 24 distinct head orientations.

1. Introduction

Many people participate in large-scale events, such as international conferences and exhibitions. They interact with various people at the event venue. If we can analyze their interactive activities, various applications are realized based on these analysis results. For example, it is possible to identify booths and times when dialogue activities are most likely to occur. It is also possible to identify a key person who generates dialogue groups and facilitates them. Based on the number of people who participated in each dialogue, it is possible to estimate which dialogues covered topics that are of interest to many people.

The analysis of people’s dialogic activities requires the ability to monitor them. Research of monitoring dialogue activities is progressing due to research on the position of each speaker (sound source localization [1]), the orientation of each speaker’s head (head orientation estimation [2,3,4]), the utterance period (Voice Activity Detection [5]), the content of the utterance (Automatic Speech Recognition [6]), the identification of the speaker (Speaker Identification [7]), sound source separation [8], etc. With the development of these elemental technologies for acoustic signal processing and speech signal processing, it is becoming possible to analyze actual dialog activities in the real world. The elemental technologies are related to each other, so if the speaker’s position and head direction are known, it becomes easier to separate the spoken sounds. If specific utterances can be separated from other utterances, background noise and environmental sounds, utterance intervals can be easily detected. Furthermore, by linking with downstream applications such as automatic speech recognition and speaker identification, it is possible to recognize the utterances of separated speech and identify the speaker. The high-level analysis function of a dialogue activity monitoring system is realized by the function of clarifying the relationships between speakers, that is, who is speaking with whom and, therefore, requires the cooperation of many elemental technologies. Analysis from a higher-order meta-perspective, such as analyzing multiple conversations simultaneously, requires the collaboration of even more elemental technologies.

Although many of the functions [1,9] expected of dialogue activity monitoring systems are attractive, these functions have not been sufficiently developed. Although we have so far been able to estimate the speaker’s position [1], we have not been able to integrate other elemental technologies such as estimating the speaker’s head direction. This is because we are proceeding with development while satisfying the requirement of being able to cover a wide observation range that conventional methods have not considered. In the analysis of real dialogue, the positions of the speakers are not determined in advance, so it is necessary to cover a wide observation range in order to deal with the problem of not knowing when and where the dialogue will begin. In the case of a simulated dialogue, it is possible to teach the speakers to start a dialogue within the observation range, but the speakers will be analyzing their speech activities according to a script, which poses different problems than analyzing actual dialogue activities.

We believe that it is necessary to develop a real-time system that assumes that microphones are distributed over a wide area and that they collect sound all the time. Based on this belief, we proposed a dialogue monitoring method [1] in which microphone arrays are distributed at each vertex of a repeating regular hexagon with sides of $1.5\text{m}$. The system has a distributed arrangement of 4-channel microphone arrays and has a structure that does not require time synchronization between the microphone arrays. This system has a structure that allows the addition of an unlimited number of microphone arrays, so the observation range can be expanded by the number of microphone arrays added. This system makes it possible to simultaneously monitor the positions of multiple sound sources. In other words, it is now possible to capture the actual dialogue of the speakers whose sound will be captured without the need to alert them to the existence of the sound collection system.

In this work, we expand the speaker position estimation system developed by the authors that can observe a wide range of areas and describe the results of our study to add a function for estimating the speaker’s head direction. Specifically, we focus on head orientation estimation based on a hexagonal distributed arrangement of microphones. We propose a head orientation estimation method that can be integrated into our sound source localization system [1]. We also propose a method that handles multiple frequency bands for head orientation estimation and experimentally demonstrate effective band combinations for estimation.

The following sections are organized as follows. Section 2 provides a head orientation estimation and conventional methods for estimating head orientation. Section 3 details the proposed methodology, including theoretical framework. Section 4 details experimental design, and implementation specifics. Section 5 represents the experimental results, with a focus on performance metrics and comparative analysis against conventional approaches. Finally, Section 6 concludes the paper with a summary of contributions and future works.

2. Method of Estimating Head Orientation

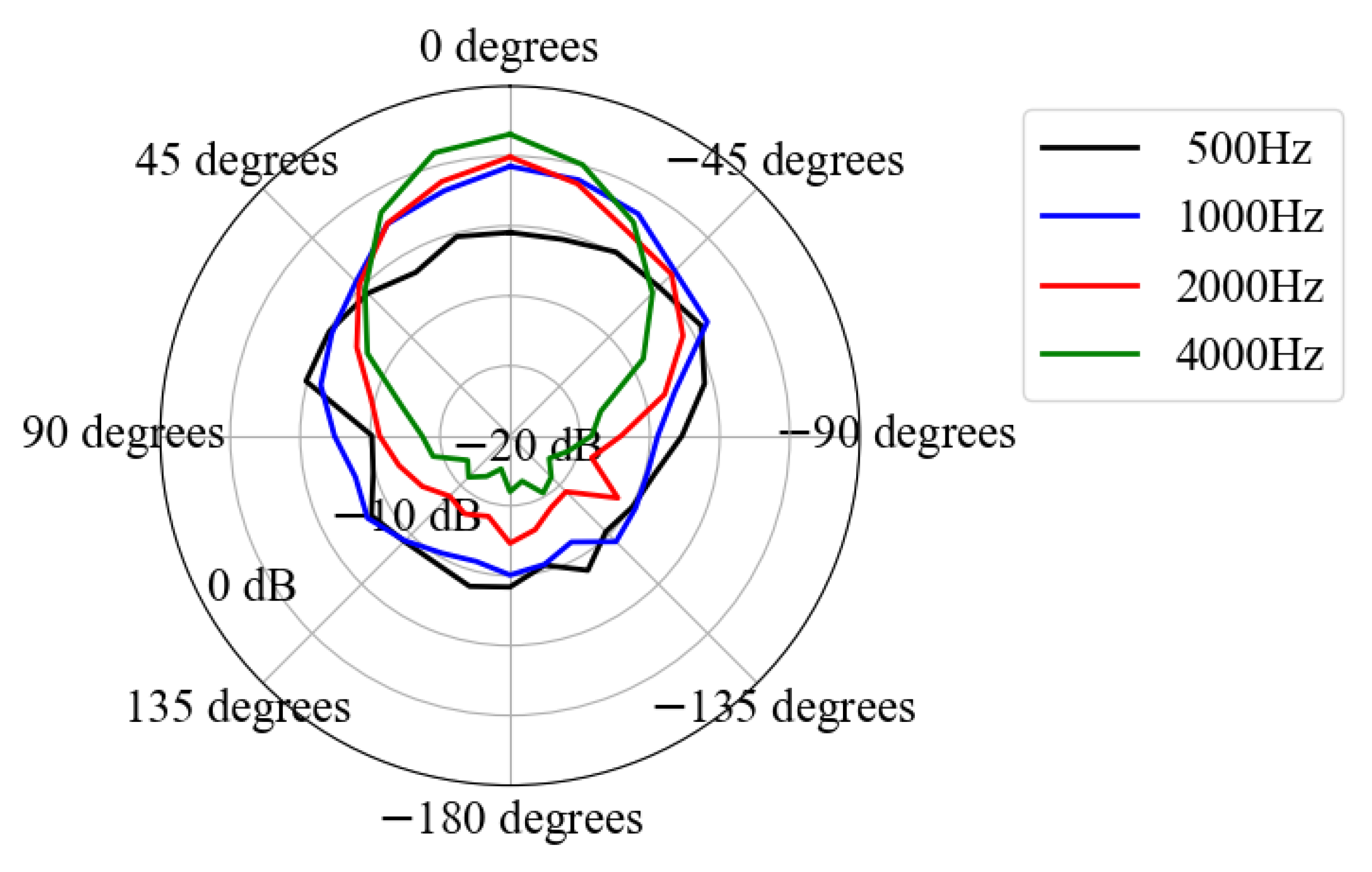
An objective of head orientation estimation is to find a direction where energy radiated from a sound source is maximum. When microphones are placed in all directions, we can find head orientation by selecting a microphone with maximum energy observed among all microphones. However, a required angular resolution is limited and the number of microphones M is also limited. When the angular resolution is $R\mathrm{degrees}$, we have to discriminate $J=360/R$ kinds of directions. When $M>J$, it is easy to estimate accurately. In this paper, we describe head orientation estimation under the condition of $M<J$ (i.e., $M=6$ and $J=24$). Figure 1 shows alignment of directional sound source and six microphone arrays. The black solid lines formed a hexagon show the alignment of microphones. The gray dashed lines are shown to represent that the directional sound source is located at the coordinate origin for convenience. Like this figure, microphone arrays, instead of microphones, are often used for head orientation estimation. Although the proposed method is based on six microphones, we compare our method with both microphone-based and microphone-array-based methods.

Conventional head orientation estimation methods include the Oriented Global Coherence Field (OGCF) [10] method and the RAdiation Pattern Matching (RAPM) [11] method. OGCF is a head orientation estimation method that uses distributed microphone arrays without prior knowledge. OGCF is known to perform with high accuracy among estimation methods using microphone arrays. On the other hand, RAPM is a head orientation estimation method that uses distributed microphones like the proposed method. RAPM is a method that uses the radiation pattern of sound source as prior knowledge and is, therefore, performed with high estimation performance without using microphone arrays. We compare the estimation performance of these two methods and the proposed method and demonstrate the effectiveness of the proposed method. In the following sections, we explain the conventional methods OGCF and RAPM.

2.1. Oriented Global Coherence Field (OGCF) Method

Oriented Global Coherence Field (OGCF) [10] is one of the acoustic processing based on the use of a coherence measure derived from the cross-power spectrum phase analysis. Although the cross-power spectrum is typically used for speaker localization, the coherence measure is used for head orientation estimation with microphone arrays.

We describe classifying J kinds of orientations by using M microphone arrays. OGCF method estimates head orientation by maximizing OGCF value ($OGC{F}_j\left(S\right)$) with respect to index j of hypothesis orientation ${\theta }_j=-\pi +{\displaystyle \frac{2\pi (j-1)}{J}}$.

$$\widehat{j}=arg\underset{j}{max}OGC{F}_j\left(S\right)$$

(1)

Once $\widehat{j}$ is calculated, head orientation is estimated as ${\theta }_{\widehat{J}}$. Let J be equispaced points $P_j,j=1,2,\dots ,J$ on a circle C, centered at a sound source location S and radius r, and M equispaced points $Q_m,m=1,2,\dots ,M$ on the circle C. $Q_m$ is the location of m-th microphone array. ${\theta }_j$ is orientation to the $P_j$ at a point of the sound source S.

OGCF of orientation to the $P_j$ is defined at a point of the sound source S as

$$OGC{F}_j\left(S\right)=\sum _{m=1}^{M}GCF\left(Q_m\right)\omega \left({\theta }_{mj}\right),$$

(2)

$$GCF\left(Q_m\right)=\sum _{(i,k)\in G}CS{P}_{i,k}(t,\tau (i,k,Q_m)),$$

(3)

where G is a set which contains all possible microphone element pairs on a microphone array, and $CS{P}_{ik}(t,\tau (i,k,Q_m))$ is Crosspower Spectrum Phase (CSP [12]) coefficient at time t and lag $\tau (i,k,Q_m)$. $\tau (i,k,Q_m)$ is theoretically derived from a distance between S and $Q_m$. ${\theta }_{mj}\in [-\pi ,\pi ]$ is the angle between $P_j$ and $Q_m$. $\omega \left({\theta }_{mj}\right)$ is a weight computed from Gaussian function:

$$\omega \left(\theta \right)={\displaystyle \frac{1}{\sqrt{2\pi }}}exp\left(-{\displaystyle \frac{{\theta }^2}{2}}\right).$$

(4)

As a result, the weights $\omega \left({\theta }_{mj}\right)$ related to the j-the orientation emphasize the contributions of GCFs in points $Q_m$ closer to $P_j$ and suppress the contributions corresponding to points in the opposite direction. A estimation performance of the OGCF method basically depends on Equation (4). When we use Equation (4), we implicitly assume there are more M than J. This is because, unless it is assumed that at least one microphone array is located near the extension line in the head orientation, there will be no GCF contributing to the OGCF.

2.2. Radiation Pattern Matching (RAPM) Method

Radiation Pattern Matching (RAPM) [11] is one of the acoustic processing based on the similarity between predefined radiation pattern of sound source and observed pattern captured by distributed M microphones. These patterns are M dimensional vector and consist of short-time-frame energy $ϵ\left(n_t\right)$ at time index $n_t$ with frame length N defined as

$$ϵ\left(n_t\right)=\sum _{n=0}^{N-1}{x}^2(n_t-N/2+n),$$

(5)

where $x\left(n\right)$ is time series observed by one microphone element.

We describe classifying J orientations by using M microphones. RAPM estimates head orientation by maximizing similarity function $J\left(\theta \right)$ with respect to index j of hypothesis orientation ${\theta }_j=-\pi +{\displaystyle \frac{2\pi (j-1)}{J}}$.

$$\widehat{j}=arg\underset{j}{max}J\left({\theta }_j\right)$$

(6)

Once $\widehat{j}$ is calculated, head orientation is estimated as ${\theta }_{\widehat{J}}$. The similarity function is based cosine similarity. It is defined as

$$J\left(\theta \right)={\displaystyle \frac{1}{\left|B\right|}}\sum _{b\in B}{\displaystyle \frac{{\varphi }_b^T{P}_b\left(\theta \right)}{\left|\right|{\varphi }_b\left|\right|·\left|\right|P_b\left(\theta \right)\left|\right|}}$$

(7)

where B is a set of 1/3-octave band b, $\left|\right|\left|\right|$ represents L2 norm, and superscript T represents vector transpose. And a frequency predefined radiation pattern and an observed pattern are

$${\varphi }_b={[{\varphi }_{1,b},\dots ,{\varphi }_{M,b}]}^T,$$

(8)

$$P_b={[P_{1,b}\left(\theta \right),\dots ,P_{M,b}\left(\theta \right)]}^T.$$

(9)

${\varphi }_{m,b}$ is the short-time power spectral density of each microphone m in 1/3-octave bands, defined as

$${\varphi }_{m,b}={\displaystyle \frac{1}{|K_b|}}\sum _{k\in K_b}{\varphi }_m\left(k\right),$$

(10)

${\varphi }_m\left(k\right)$ is power spectrum density calculated from observed signal captured from m-th microphone. $K_b$ is a set containing all frequency bins of 1/3-octave band b.

$P_{m,b}\left(\theta \right)={\left|D_b({\theta }_m-\theta )\right|}^2$, and $D_b({\theta }_m-\theta )$ is the speech directivity towards microphone m with azimuth ${\theta }_m$.

3. Head Orientation Estimation Method Using Multi-Frequency Bands (Proposed Method)

The information that the proposed method uses to estimate head orientation is information about how energy is diffused in space after sound is radiated. With directional sound sources, the amount of energy diffused is biased toward the front, so if you know the orientation in which the strongest energy is radiated, you can determine the orientation of the sound source. Therefore, by distributing microphones around the sound source and observing the energy, the orientation of the sound source can be estimated from the position of the microphone where the maximum energy is observed. For example, if you want to distinguish between 72 different audio directions, you can easily estimate the orientation by using 72 microphones. However, it is not realistic to arrange a large number of microphones such as 72 in the first place. Therefore, the number of microphones must be reduced. If you reduce the number of microphones placed, a situation will arise in which the observation microphone is not necessarily placed exactly in front of the sound source. If no microphone is placed in front of the sound source, the orientation will be estimated from nearby microphones. Previous research has been evaluated as a problem in which the orientation of the sound source is distinguished between at most four to eight orientations. The history of research on estimating the orientation of a sound source has generally focused on simple tasks, where the number of orientations that can be distinguished is limited and it is possible to use a relatively large number of microphones compared to the orientations to be distinguished. We aim to achieve high angular resolution under the conditions that the number of orientations to be distinguished is 24 and the number of microphones used is 6 and to consider sound source orientation estimation when the number of microphones distributed around the sound source is clearly smaller than the number of orientations of the sound source to be discriminated. To cope with the relative deterioration of the information obtained from the microphone, we take measures to utilize the radiation characteristics of the sound source.

The reason RAPM and other methods were unable to achieve high angular resolution is because they did not use band-splitting processing. Normally, the radiation characteristics of a sound source tend to be sharper as the frequency increases, emitting strong energy toward the front, and becoming duller as the frequency decreases, emitting energy uniformly in all directions. Since a powerful clue for orientation estimation is the bias in the spread of energy, it is expected that the estimation accuracy will be higher as a higher frequency band is used. On the other hand, to estimate the strongest radiation direction of a signal whose energy varies depending on the frequency band, such as voice, the signal-to-noise ratio will differ depending on the frequency band due to noise and reverberation. Therefore, we thought it would be possible to improve estimation accuracy by estimating orientation by combining a band with the high energy of the sound source signal, a band with little fluctuation, and a band with less influence on noise and reverberation. We believe that the problem with conventional methods processed in ranges from one frequency to another is that it is difficult to select only the frequency bands that are effective for estimation. Therefore, we thought that if we proposed a method that uses multiple bands and integrates the similarity of each band after the fact, it would be possible to achieve higher estimation accuracy with higher resolution than before.

Our method is similar to RAPM [11]. We also use a radiation pattern. One difference between these methods is cost function. Our cost function is the Euclidean distance based on the power spectrum. Therefore, the proposed method estimates head orientation by minimizing the Euclidean distance with respect to hypothesis orientation $\theta$. The cost function of proposed method is defined as

$$J\left(\theta \right)=\sum _{b\in B}Dist({\varphi }_b,P_b\left(\theta \right)),$$

(11)

$$Dist({\varphi }_b,P_b\left(\theta \right))={\left(\sum _{m=1}^M{((10{log}_{10}{\varphi }_{m,b}-\alpha )-(10{log}_{10}{P}_b\left(\theta \right)-\beta ))}^2\right)}^{{\displaystyle \frac{1}{2}}},$$

(12)

where

$$\alpha ={\displaystyle \frac{1}{M}}\sum _{m=1}^{M}10{log}_{10}{\varphi }_{m,b},$$

(13)

$$\beta ={\displaystyle \frac{1}{M}}\sum _{m=1}^{M}10{log}_{10}{P}_b\left(\theta \right).$$

(14)

The cost function of RAPM is designed to measure a similarity between radiation pattern and observed pattern. As RAPM focuses on shape of energy patterns, the cost function is based on cosine similarity. One of the advantages is that the cost is independent of observed energy. However, this is one of the disadvantages since RAPM completely ignores amount of energy.

The cost function of proposed method is designed to measure a similarity between radiation pattern and observed pattern based on shape of energy patterns and amount of energy. First of all, we use power as feature vector instead of energy. Then we use the Euclidean distance to account for the amount of power. When we simply use the Euclidean distance, a range mismatch between radiation vector and observed vector deteriorates the cost even if shape of these vectors is similar. To avoid this problem, we apply mean subtraction to the vectors before measuring the Euclidean distance.

3.1. Technique of Integrating Multiple Frequency Band

In the proposed and RAPM methods, a set of the 1/3-octave band is used. In a set B, continuous bands from the lowest band to the highest are usually included. However contribution of head orientation estimation is different from frequency bands. The bands including a set B do not need continuous 1/3-octave bands.

Radiation pattern depends on the frequency band. In some bands the radiation pattern is sharp; in other bands, it is dull. We use both continuous and non-continuous bands for a set B. To find the best estimation performance, we try all possible combinations of the bands.

3.2. Contribution of the Proposed Method

Our method is positioned as a solution that is similar in approach to RAPM in that it uses the radiation characteristics of the sound source as a template in advance. There are two main differences. Although they are similar in how they estimate head orientation based on the match between observed and template patterns, they differ in the criterion used. The proposed method measures the similarity after normalizing the difference in gain between the template and observation. On the other hand, RAPM does not have a gain normalization mechanism. In other words, the difference is whether the similarity evaluation criterion has a gain normalization mechanism or not.

Next, the proposed method uses a multi-band matching procedure, whereas RAPM is a single-band matching procedure. Although it is not impossible to interpret the original RAPM’s band as a multi-band connection of several bands, it is assumed that the series of bands is a continuous region.

On the other hand, the proposed method divides the band into multiple bands, calculates the similarity in each band with a gain normalization mechanism, and then performs fusion to obtain the final similarity. This method makes it possible to fuse multiple discontinuous bands. In other words, the proposed method is clearly different from RAPM in that it has a mechanism for pattern matching templates in multiple bands and post-fusion of similarities in multiple bands, and it aims to improve estimation accuracy.

In the following experimental section, we will verify the effects of gain normalization for each band, template matching for each band, and fusion of the similarity of multiple bands.

4. Experiments

4.1. Radiation Pattern

The radiation pattern from a directional sound source was created by measuring the impulse responses of points on a circle centered on the source point. A loudspeaker (GENELEC 8020DPM) was used as a directional sound source. The impulse response was measured on the azimuth plane at a height of 1 m above the floor. We placed the low-frequency speaker cone so that its center was $1\text{m}$ away, and we measured the angle from $0\mathrm{degrees}$ to $360\mathrm{degrees}$ at 15-degree intervals around a circle with a radius of $1.5\text{m}$. The microphone used was an 8-channel circular microphone array called Kurage, manufactured by System In Frontier Inc., Tokyo, Japan [13]. Kurage means jellyfish in Japanese, and the microphone was named after it because of its jellyfish-like appearance when attached to the tripod. Kurage is equipped with a MEMS microphone element, and only channel 1 was used for measuring the impulse response. Channel 1 was positioned $1\text{m}$ above the floor. The measurement signal used was a time-stretched pulse with a signal length of 32,768 samples. We applied 16 synchronous addition processes to the measurements and synchronized the playback of the measurement signals and recording them. A System In Frontier RASP-24 AD/DA converter was used for playback and recording, with a sampling rate of 48,000 Hz and a quantization bit depth of 24 bits. The measurement location was Osaka Sangyo University, Building 15, Laboratory 15806. The volume of the room is approximately $\text{H}2.5\text{m}\times \text{W}13.4\text{m}\times \text{D}8.2\text{m}$, the background noise level is ${\mathrm{LA}}_{\mathrm{eq}}=44.6\mathrm{dB}$, and the reverberation time is about $T_{60}=0.4\text{s}$. The 1/3 octave band energy with center frequencies of $500\mathrm{Hz}$, $1000\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$ was calculated from the impulse responses obtained at 15-degree intervals, and the radiation characteristics were calculated for each frequency band.

Figure 2 shows the radiation patterns from the loudspeaker in a polar coordinates with $0\mathrm{degrees}$ at the top and positive angles counterclockwise. The radiation level at the center of the circle corresponds to −25 dB, and the radiation level at the outer circle corresponds to $0\mathrm{dB}$. The four lines (green, red, blue, and black) represent the radiation pattern when the speaker is pointed at $0\mathrm{degrees}$. The green line represents the energy radiation pattern of a 1/3 octave band with a center frequency of $4000\mathrm{Hz}$. Similarly, the red, blue, and black lines represent the energy radiation patterns of the 1/3 octave bands with center frequencies of $2000\mathrm{Hz}$, $1000\mathrm{Hz}$, and $500\mathrm{Hz}$, respectively. Figure 2 shows that the higher the frequency band, the more radiated energy tends to be biased toward the front of the sound source. The proposed method aims to improve the accuracy of head orientation estimation by using these four radiation patterns as prior knowledge. It can be confirmed that the actually measured radiation pattern differs from the true radiation pattern in that it has an uneven shape that includes measurement errors, and that it is a rough measurement result. By improving the measurement environment, it is possible to obtain a highly accurate loudspeaker radiation pattern. Additionally, a theoretical radiation pattern can be created based on the speaker’s shape and size. The reason for evaluating the estimation method using roughly measured patterns, as shown in Figure 2, is that we aim to estimate the head orientation using a person as a sound source. A human’s radiation pattern must be determined by measurement, and measurement distortion is inevitable. There are also individual differences in humans’ radiation patterns. The radiation pattern of the average human is usually different from that of a subject for head direction estimation. Based on these assumptions, we will evaluate estimation methods under the mismatch condition using a roughly measured radiation pattern.

4.2. Evaluation Dataset for Comparing Head Orientation Estimation Method

In this subsection, we describe about the evaluation database. The evaluation database must be composed of audio files under a variety of conditions in order to enable stable performance comparisons that are not affected by a variety of conditions. The essential variation for evaluating head orientation estimation is the variation in the speaker’s head orientation. There are other variations that need to be considered, such as variations in the speaker and the content of the utterance. We constructed an evaluation database taking these three variations into consideration.

The evaluation database contains 24 head orientation variations, divided into 15-degree increments from $0\mathrm{degrees}$ to $360\mathrm{degrees}$. There are 10 speaker variations (5 male speakers and 5 female speakers) and 10 variations of the utterance. All utterances are in Japanese, and their audio files are from the Japanese Newspaper Article Speech Database (JNAS) [14]. As described above, there are 100 ($(5+5)\mathrm{speaker}\times 10\mathrm{sentence}$) types of evaluation audio files per orientation.

The generation of 24 types of audios file for evaluation with different head orientations is achieved by convolving the actually measured impulse response using a loudspeaker as a substitute for the human head into the audio waveform. The evaluation database contains 2400 types of audio files ($24\mathrm{orientation}\times (5+5)\mathrm{speaker}\times 10\mathrm{sentence}$). The sampling rate is 16,000 Hz, and the quantization bit rate is $16\mathrm{bit}$.

We measured the impulse response with time-stretched pulse (TSP) method [15], which applied sixteen-times synchronous additions in the laboratory room 15806, Building 15, Osaka Sangyo University. A period of the TSP signal was 16,384 samples. A GENELEC 8020DMP was used to reproduce the measurement signal. For recording, we used a Seeed Studio ReSpeaker USB Mic Array [16]. The laboratory room was covered with standard office floor carpet, the background noise level was ${\mathrm{LA}}_{\mathrm{eq}}=44.6\mathrm{dB}$, and the reverberation time was approximately $T_{60}=0.4\text{s}$.

The evaluation results described in the following section correspond to the estimation results when calibrated to the same sensitivity for all microphones. In the experiment, we created an evaluation database by actually measuring the impulse response and convolving it with the audio signal. Impulse responses were measured in sequence, using the same MEMS microphone under all combinations of sound source position, sound source orientation, and microphone position. Using the procedure, we constructed an experiment in which all microphones were calibrated to the same sensitivity.

5. Results and Discussion

We performed head orientation estimation from the audio file in the evaluation database using three methods, namely OGCF, RAPM, and the proposed method, where the proposed method is a single-band frequency band using four 1/3 octave bands with central frequencies, $500\mathrm{Hz}$, $1000\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$. All methods use frame length $N=8192$, and 512 sample points frame shift. 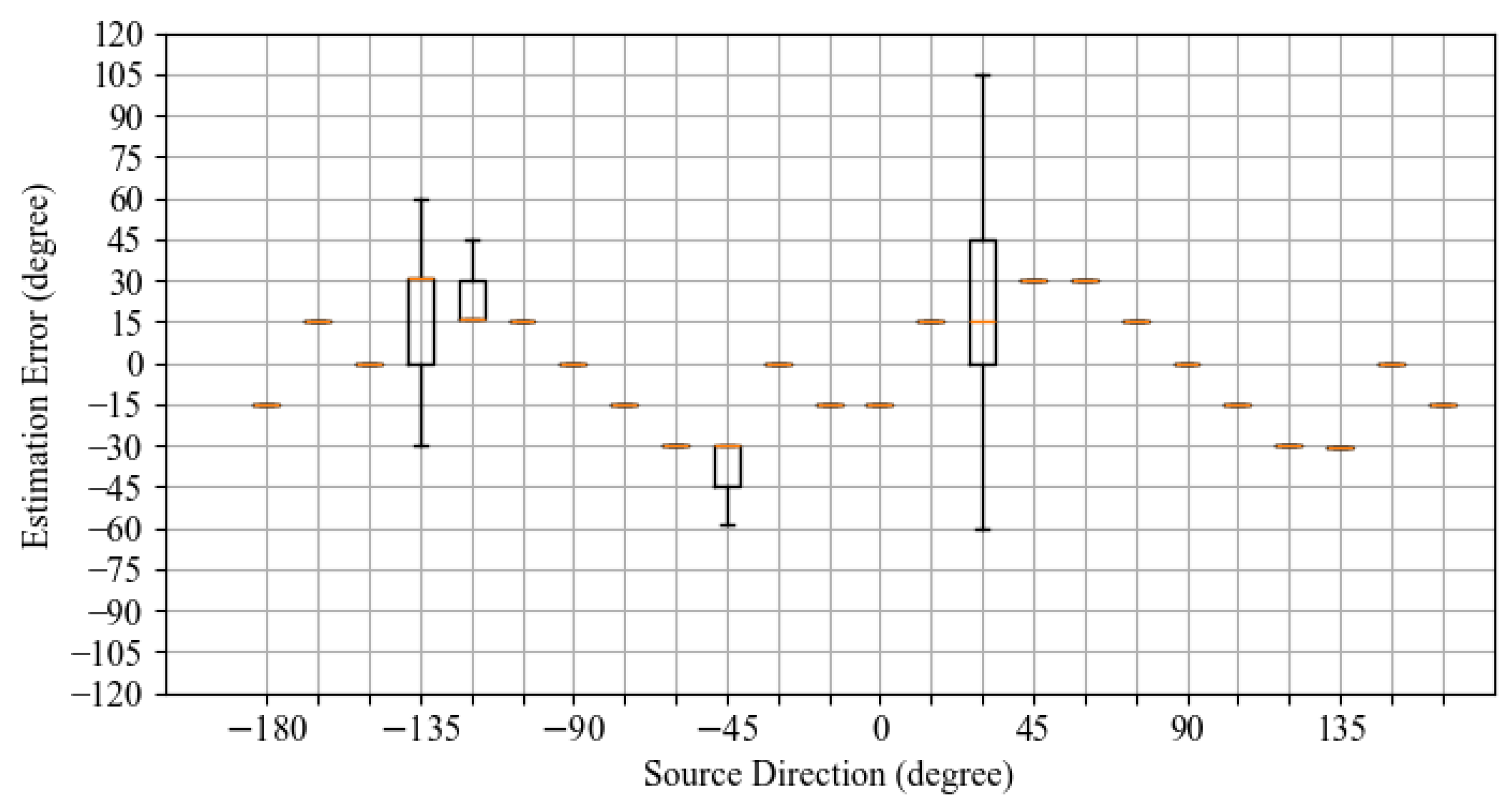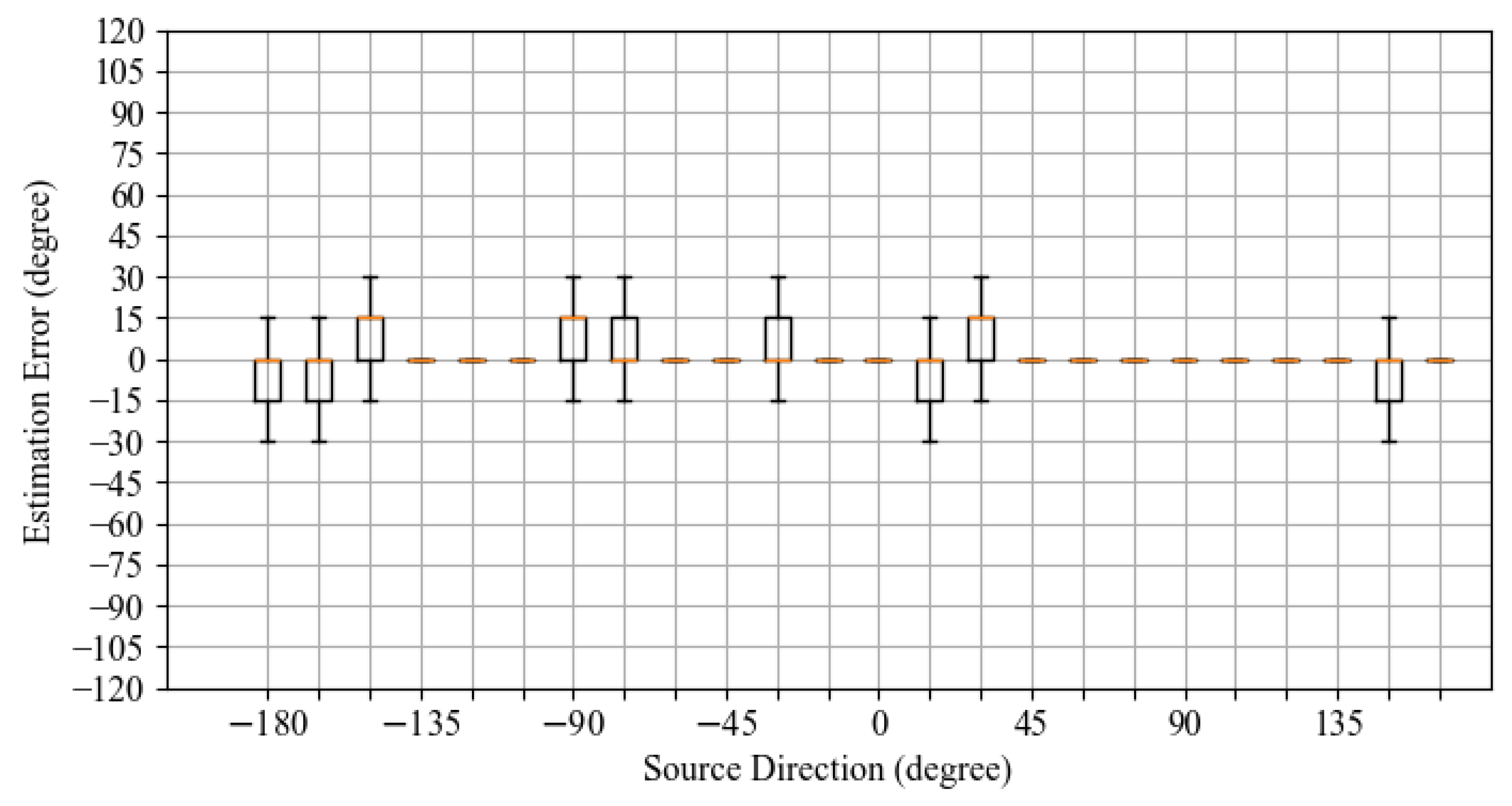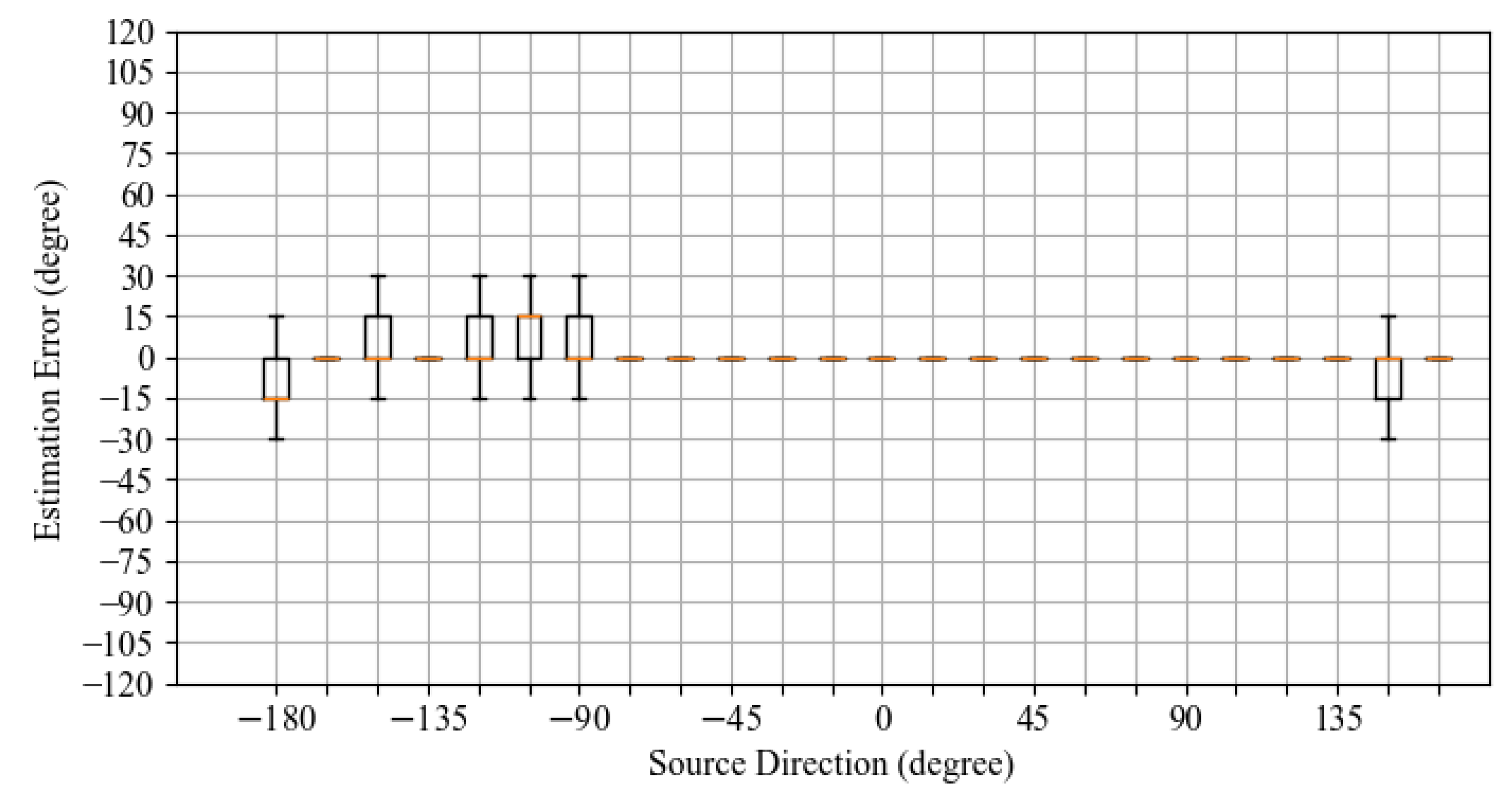Figure 3, Figure 4 and Figure 5 show boxplots of the distribution of estimation errors. The horizontal axis represents the speaker’s orientation, i.e., the correct direction. The vertical axis represents the estimation error. The orange bar represents the second quartile (median), and the top and bottom of the black box represent the third and first quartiles. Please note that in some boxplots, all the estimation results were the same value, so the boxes do not spread, and the boxes are collapsed and appear as a single orange line.

Figure 3 shows that the distribution of estimation errors tends to differ depending on the sound source direction. The second quartile ranges from $-30$ to $+30$, depending on the direction of the sound source. There is more variability than in RAPM (Figure 4) and the proposed method (Figure 5). This is thought to be due to the effect of Equation (4). In this experiment, there were $J=24$ variations in the sound source direction, but the number of microphones was only six; $M=6$.

The distribution of the estimation errors for the RAPM method (Figure 4) and the proposed method (Figure 5) is narrower than that for the OGCF method. The second quartile appears near $0\mathrm{degrees}$ and $\pm 15\mathrm{degrees}$, and stable results independent of direction are obtained. RAPM and the proposed method are superior to OGCF, but no significant differences are observed between RAPM and the proposed method.

Next, the error distributions of the OGCF, RAPM, and the proposed method are compared from another viewpoint. The differences among these methods are shown in

Table 1. Characteristics of methods.

Methods	Device	Prior Knowledge	Frequency Band
OGCF	Microphone Arrays	No	Single Band
RAPM	Distributed Microphones	Radiation Pattern	Single Band/Multiple Bands
PROP	Distributed Microphones	Radiation Pattern	Single Band/Multiple Bands

. We show the error distributions as histograms in Figure 6. The horizontal axis represents the estimation error, and the vertical axis represents the frequency. Since the 2400 audio files are composed of 427,104 frames, the total number of estimations is 427,104. We also compared derivative methods that applied multiple frequency bands to the proposed method. PROP $+500\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ is a proposed method that uses three bands with center frequencies: $500\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$. This method is the best according to the mean errors and mean absolute errors for all possible combinations in

Table 2. Effectiveness of using multi-frequency bands.

Methods	Mean Error	Mean Absolute Error
OGCF	$-2.07\mathrm{degrees}$	$24.21\mathrm{degrees}$
RAPM $+500\mathrm{Hz}$	$4.34\mathrm{degrees}$	$28.74\mathrm{degrees}$
RAPM $+1000\mathrm{Hz}$	$3.36\mathrm{degrees}$	$24.15\mathrm{degrees}$
RAPM $+2000\mathrm{Hz}$	$0.21\mathrm{degrees}$	$14.41\mathrm{degrees}$
RAPM $+4000\mathrm{Hz}$	$-1.82\mathrm{degrees}$	$15.08\mathrm{degrees}$
PRAM $+500\mathrm{Hz}+1000\mathrm{Hz}$	$4.33\mathrm{degrees}$	$22.22\mathrm{degrees}$
PRAM $+500\mathrm{Hz}+2000\mathrm{Hz}$	$1.25\mathrm{degrees}$	$14.55\mathrm{degrees}$
PRAM $+500\mathrm{Hz}+4000\mathrm{Hz}$	$-1.45\mathrm{degrees}$	$14.46\mathrm{degrees}$
PRAM $+1000\mathrm{Hz}+2000\mathrm{Hz}$	$1.76\mathrm{degrees}$	$14.20\mathrm{degrees}$
PRAM $+1000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.49\mathrm{degrees}$	$14.32\mathrm{degrees}$
PRAM $+2000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.99\mathrm{degrees}$	$11.81\mathrm{degrees}$
PRAM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}$	$2.58\mathrm{degrees}$	$14.30\mathrm{degrees}$
PRAM $+500\mathrm{Hz}+1000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.03\mathrm{degrees}$	$14.07\mathrm{degrees}$
PRAM $+500\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.61\mathrm{degrees}$	$11.70\mathrm{degrees}$
PRAM $+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.20\mathrm{degrees}$	$11.69\mathrm{degrees}$
RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$	$0.21\mathrm{degrees}$	$11.60\mathrm{degrees}$
PROP $+500\mathrm{Hz}$	$4.52\mathrm{degrees}$	$29.61\mathrm{degrees}$
PROP $+1000\mathrm{Hz}$	$0.83\mathrm{degrees}$	$24.72\mathrm{degrees}$
PROP $+2000\mathrm{Hz}$	$0.40\mathrm{degrees}$	$14.93\mathrm{degrees}$
PROP $+4000\mathrm{Hz}$	$-1.46\mathrm{degrees}$	$14.13\mathrm{degrees}$
PROP $+500\mathrm{Hz}+1000\mathrm{Hz}$	$2.49\mathrm{degrees}$	$22.58\mathrm{degrees}$
PROP $+500\mathrm{Hz}+2000\mathrm{Hz}$	$2.10\mathrm{degrees}$	$15.35\mathrm{degrees}$
PROP $+500\mathrm{Hz}+4000\mathrm{Hz}$	$-0.45\mathrm{degrees}$	$13.41\mathrm{degrees}$
PROP $+1000\mathrm{Hz}+2000\mathrm{Hz}$	$1.29\mathrm{degrees}$	$14.72\mathrm{degrees}$
PROP $+1000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.95\mathrm{degrees}$	$13.91\mathrm{degrees}$
PROP $+2000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.77\mathrm{degrees}$	$11.03\mathrm{degrees}$
PROP $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}$	$2.36\mathrm{degrees}$	$14.87\mathrm{degrees}$
PROP $+500\mathrm{Hz}+1000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.13\mathrm{degrees}$	$13.39\mathrm{degrees}$
PROP $+500\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.27\mathrm{degrees}$	$10.58\mathrm{degrees}$
PROP $+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.51\mathrm{degrees}$	$11.37\mathrm{degrees}$
PROP $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$	$-0.09\mathrm{degrees}$	$11.07\mathrm{degrees}$

.

RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ is original version of RAPM. Although we applied multiple frequency bands to the RAPM, a positive effect was not obtained for RAPM (See Table 2). Therefore, we show RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ in Figure 6. PROP $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ is a proposed method that uses four 1/3 octave bands with center frequencies: $500\mathrm{Hz}$, $1000\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$. This version of proposed method is not applied to multiple frequency band technique. This version is for comparison with the original RAPM.

Blue, orange, green, and red bars represent OGCF, RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$, PROP $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$, and PROP $+500\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ results, respectively.

It can be confirmed that the mode (that is, the most frequent bin) of the estimation error of OGCF is $-15\mathrm{degrees}$, and the errors are mainly distributed around $-30\mathrm{degrees}$, $-15\mathrm{degrees}$, $0\mathrm{degrees}$, $15\mathrm{degrees}$, and $30\mathrm{degrees}$. The mode of estimation error for RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ is $0\mathrm{degrees}$, and it can be confirmed that the errors are mainly districuted around $-15\mathrm{degrees}$, $0\mathrm{degrees}$, and $15\mathrm{degrees}$. The frequency is concentrated in $0\mathrm{degrees}$, which is a narrower range than OGCF, indicating that RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ is $0\mathrm{degrees}$ is superior to OGCF in estimating head orientation. PROP $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ is mainly distributed around $-15\mathrm{degrees}$, $0\mathrm{degrees}$, and $15\mathrm{degrees}$. It shows similar trend as RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$. This result suggests that the estimation accuracy of PROP $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ and that of RAPM $+500\mathrm{Hz}+1000\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ are almost equivalent.

The error distribution of PROP $+500\mathrm{Hz}+2000\mathrm{Hz}+4000\mathrm{Hz}$ shows the best because shape of the error distribution is most concentrated at $0\mathrm{degrees}$. By applying multiple frequency band technique, estimation becomes more accurate.

Evaluation for Processing Based on Multi-Frequency Bands

The frequency bands used for this evaluation are four 1/3 octave bands with center frequencies of $500\mathrm{Hz}$, $1000\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$. There are a total of 15 combinations of multi-frequency band processing, and we compared them. These 15 types include 4 types of single band processing, 6 types of two band processing, 4 types of three band processing, and 1 type of four band processing. The mean absolute error is used for the evaluation. This is because comparisons using the mean error are inappropriate, as the positive and negative estimation errors cancel each other out, and the mean error becomes a small value. Table 2 shows the comparison results. For reference, the average error is also listed in Table 2.

It was shown that RAPM had no effect on multiple frequency band technique. On the other hand, by applying techniques to the proposed method, it is experimentally shown that the most accurate combination of frequency bands is $500\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$.

The proposed method and RAPM can be said to be methods based on pattern matching between radiation characteristic templates and observed patterns. The accuracy of orientation estimation is determined by how precisely the similarity of patterns can be evaluated. The essential difference between the proposed method and PAPM is the criteria used during matching. The proposed method applies mean subtraction to the template and the observed patterns, so it realizes pattern matching with the radiation characteristics that is not affected by the gain of the observed pattern. Since mean subtraction is applied to each band, precise matching is possible for each band.

Next, further improvement in estimation accuracy can be expected by solving the problem of selecting a combination of bands that are effective for orientation estimation. As this paper did not propose a method to find the optimal combination, we tried all combinations to find an optimal one. Through this experiment, we were able to show that dividing the band into several bands and selecting an appropriate band from among them contributes to improving head direction estimation, although the optimal frequency band division and the band to be selected may vary depending on the sound source. In this paper, four 1/3-octave bands (i.e., $500\mathrm{Hz}$, $1000\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$) are selected as the multiple frequency bands because energy of human speech signal is distributed to these frequencies. We believe that there will be a need in the future to develop methods for automatically dividing bands and adjusting multiple optimal bands according to the characteristics of the sound source.

On the other hand, RAPM does not have a mechanism to normalize the difference in gain between the radiation characteristic template and the observed sound. Therefore, even if the band is divided, it does not necessarily result in more precise matching than before division, and we believe that the band division process was not sufficiently effective and the estimation accuracy was inferior to the proposed method.

6. Conclusions

We propose a head orientation estimation method. It is based on minimizing the Euclidean distance between mean-subtracted power spectra. We also propose a multiple frequency band technique. Our method with a multiple frequency band technique achieve mean absolute error of $10.58\mathrm{degrees}$. This accuracy is sufficient for the dialogue activity monitoring system that we aim to realize. The mean absolute error of the proposed method without multiple frequency band technique is reduced by $0.53\mathrm{degrees}$ compared to that of the original RAPM method. By applying multiple frequency band technique, the mean absolute error of the proposed method using $500\mathrm{Hz}$, $2000\mathrm{Hz}$, and $4000\mathrm{Hz}$ is reduced by $1.11\mathrm{degrees}$ compared to that of the original RAPM method. We experimentally demonstrated that multiple frequency band technique is effective for the proposed method and not effective for RAPAM.

Future works are an evaluation of head orientation estimation when the sound source is not at the center of six microphones and the integration of sound source localization and head orientation estimation. There is an urgent need to support multi-tracking of each speaker as a dialogue activity monitoring system. Improvements in elemental technology are also necessary, and measures against noise and reverberation are particularly important.

The proposed method directly evaluates the energy pattern of the multi-channel acoustic signal observed by six microphones, and is likely to be easily affected by noise and reverberation. Although it is important to evaluate robustness against noise and reverberation, this time we evaluated head orientation estimation in a specific environment assumed by the application. However, under conditions where Gaussian noise is constantly observed in all microphones, it has been confirmed in experiments using four or eight distributed microphones that there is no significant effect on estimation accuracy even if the SNR changes to $0\mathrm{dB}$, $10\mathrm{dB}$, or $20\mathrm{dB}$, as described in [17]. In other words, the proposed method is robust to stationary noise. As it will be necessary to extend our method when the directional sound sources interfere, this is a topic for future research.

By fusing other sensor data, such as visual data, to estimate head orientation, we can expect further improvement in the accuracy of head orientation estimation. On the other hand, audio signals have the advantage of not being affected by occlusion, and camera images have the advantage of not being affected by noise. Estimation using audio signals and estimation using camera images have a complementary relationship, and we believe that improving estimation accuracy using audio signals is still essential.