Comparison of Alternative Port-Hamiltonian Dynamics Extensions to the Thermodynamic Domain Toward IDA-PBC-Like Control: Application to a Heat Transfer Model
Abstract
1. Introduction
2. Object of the Study
2.1. Mathematical Model
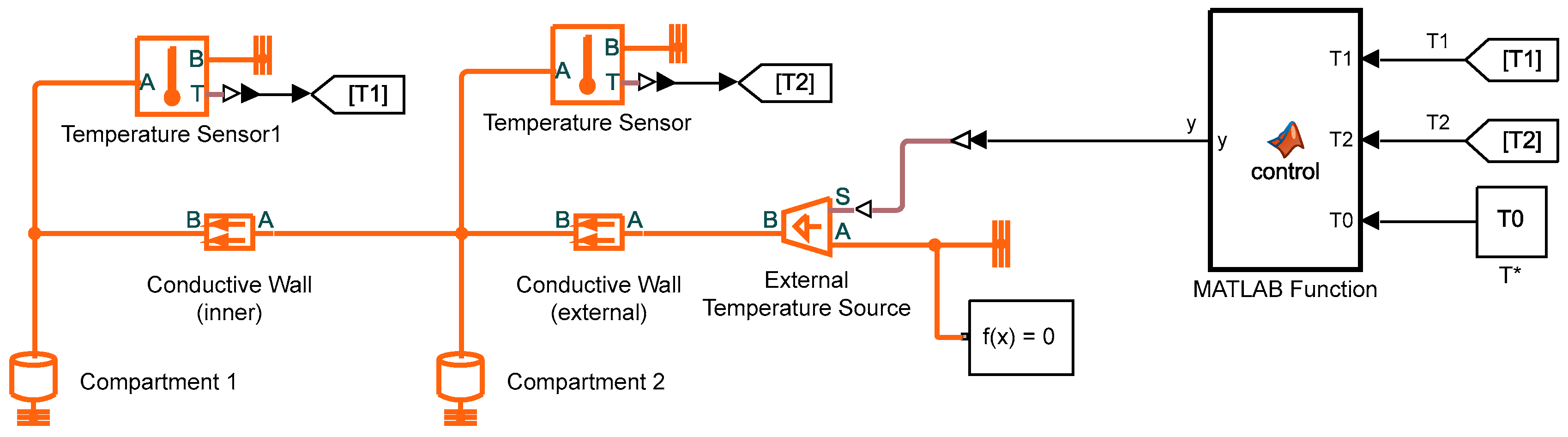
2.2. Computer Model for Simulation Studies
3. Port-Hamiltonian Systems and IDA-PBC
4. Irreversible Port-Hamiltonian Systems Framework
4.1. Theory
4.2. Application to HEX
4.3. Control Law Derivation
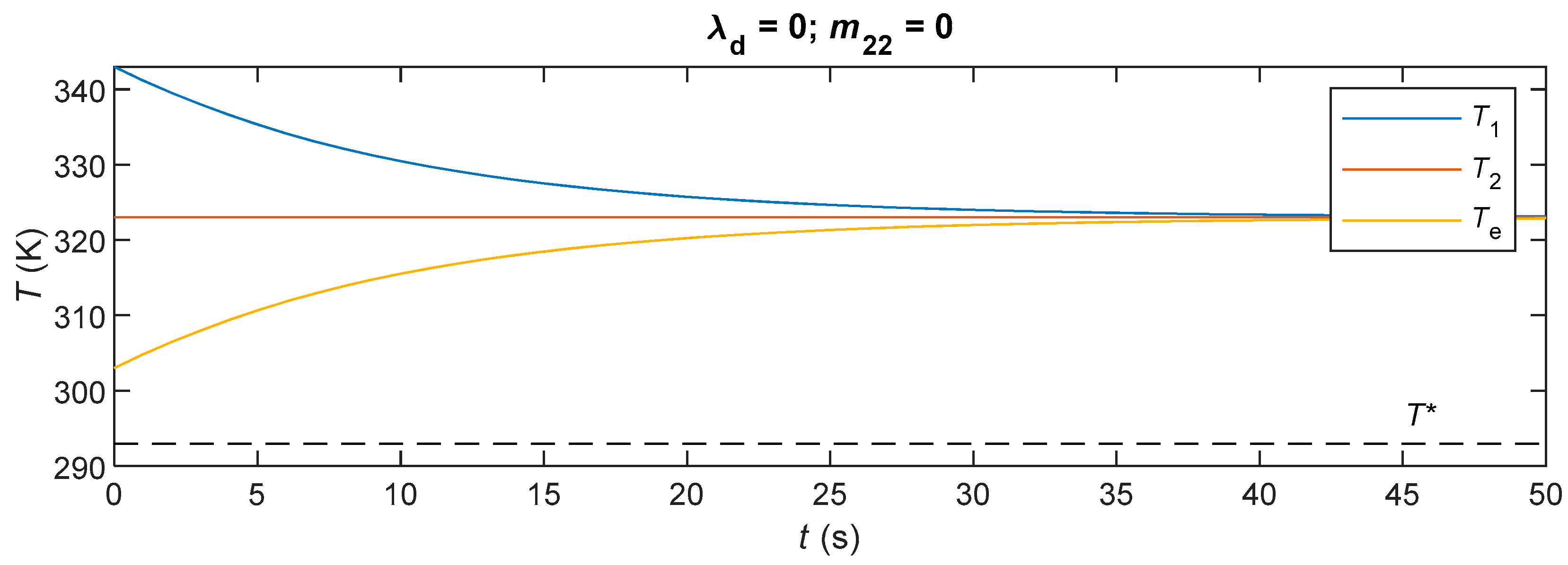
4.4. Simulations and Discussions
5. Entropy-Based Generalized Hamiltonian Framework
5.1. Theory
5.2. Application to HEX
5.3. Control Law Based on a Thermodynamic Availability Function
5.4. Modified Control Law
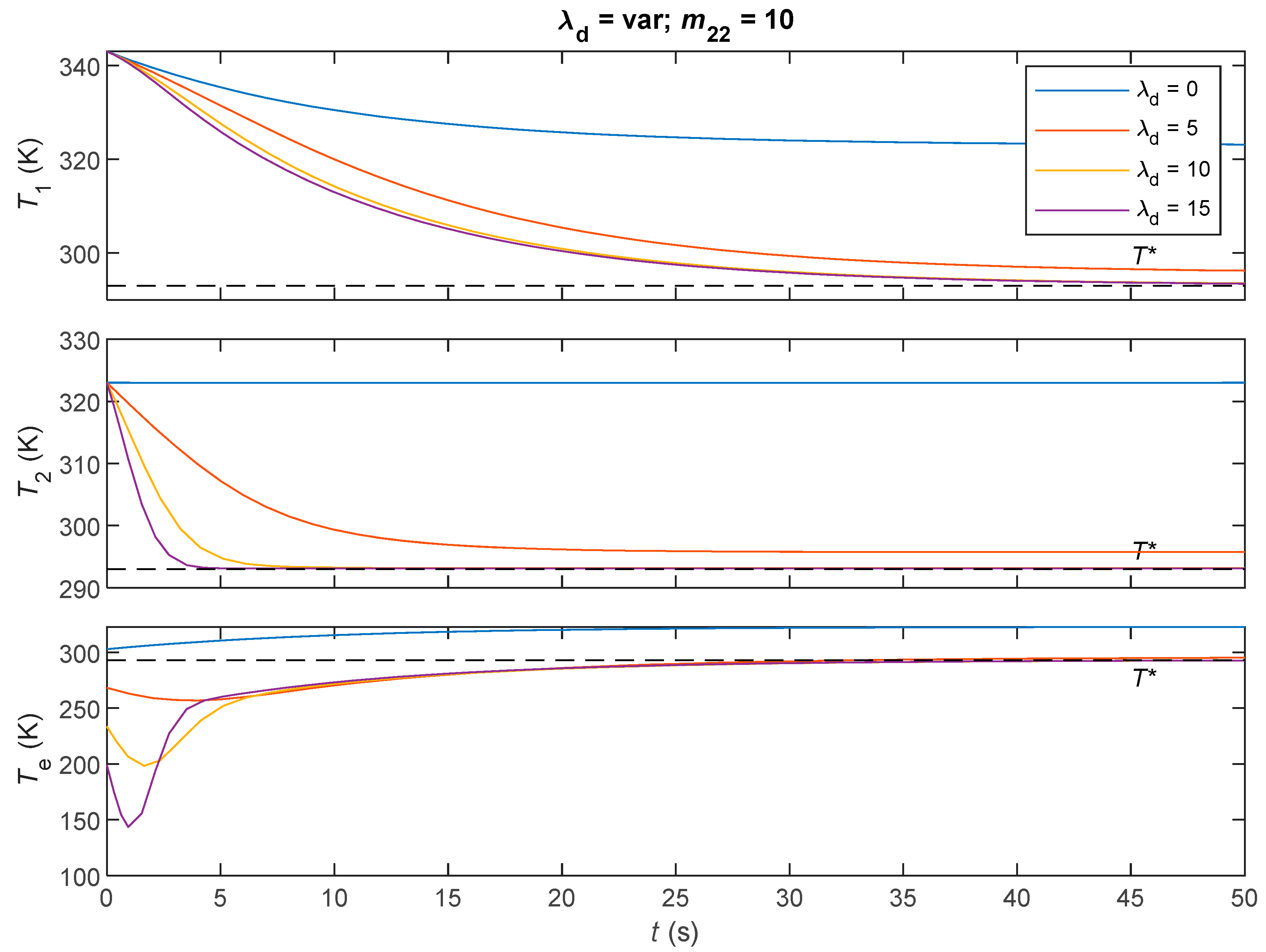
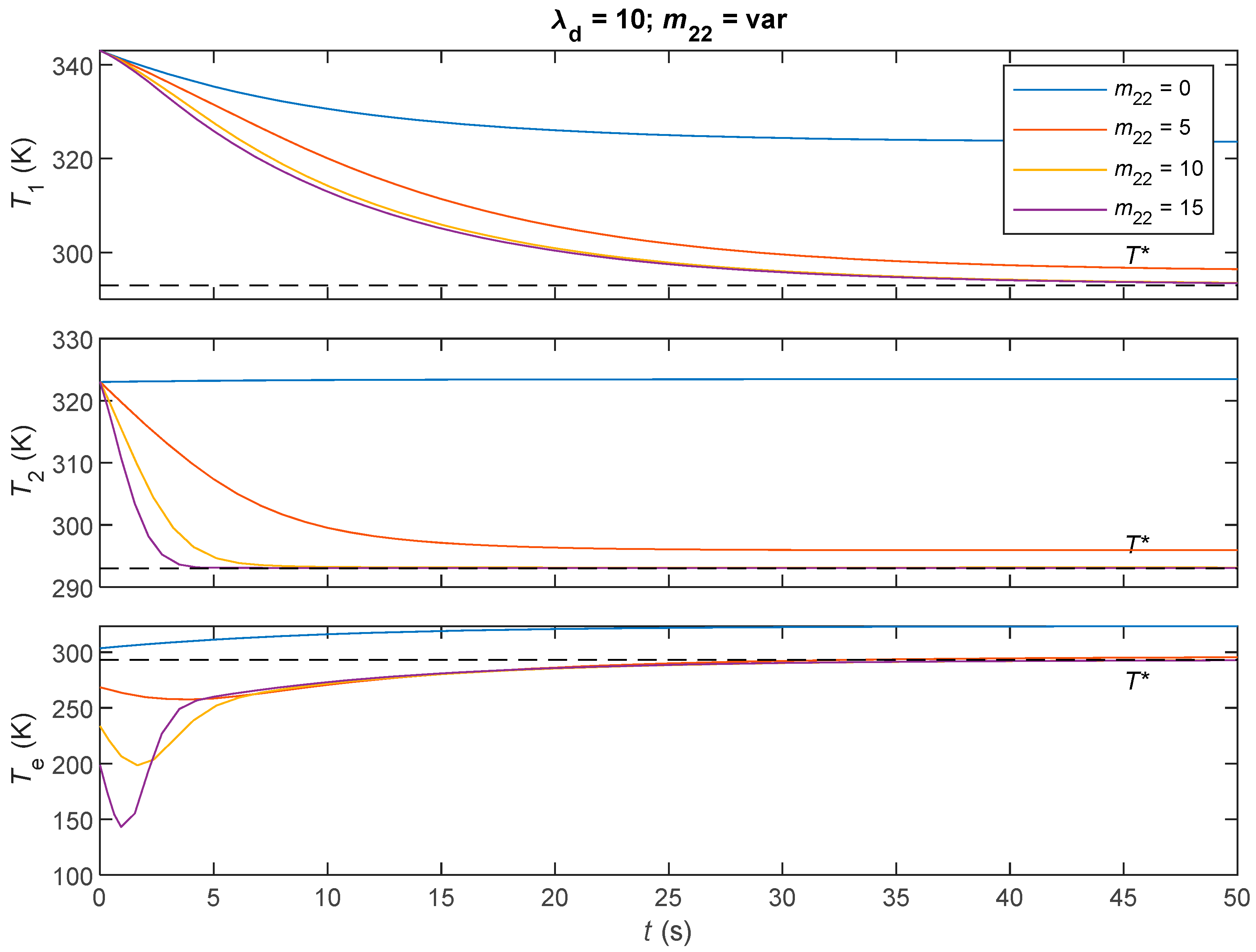
5.5. Simulations and Discussions
6. Entropy-Production-Metric-Based PHS
6.1. Theory
6.2. Application to HEX and Control Law Derivation
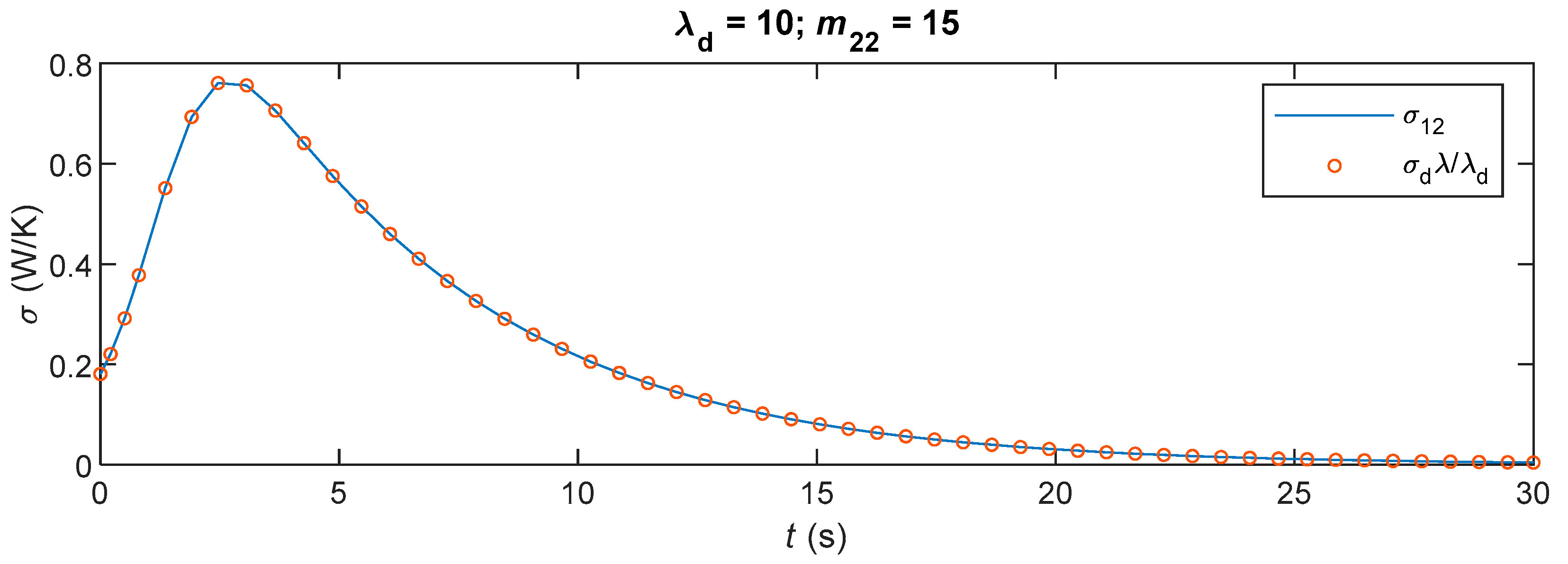
6.3. Simulations and Discussions
7. Comparative Analysis of the Three Frameworks
7.1. General Discussion on the Three Frameworks
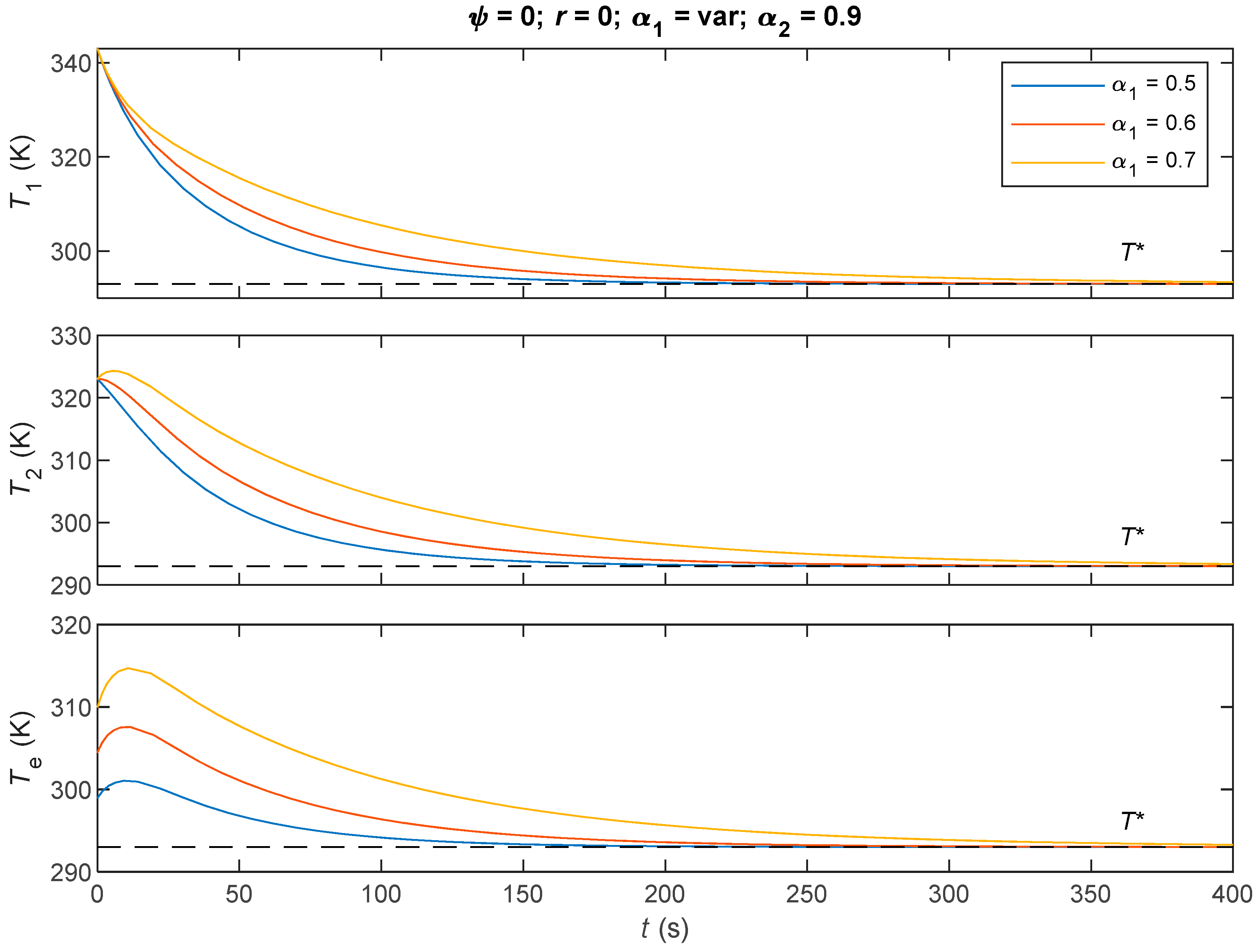
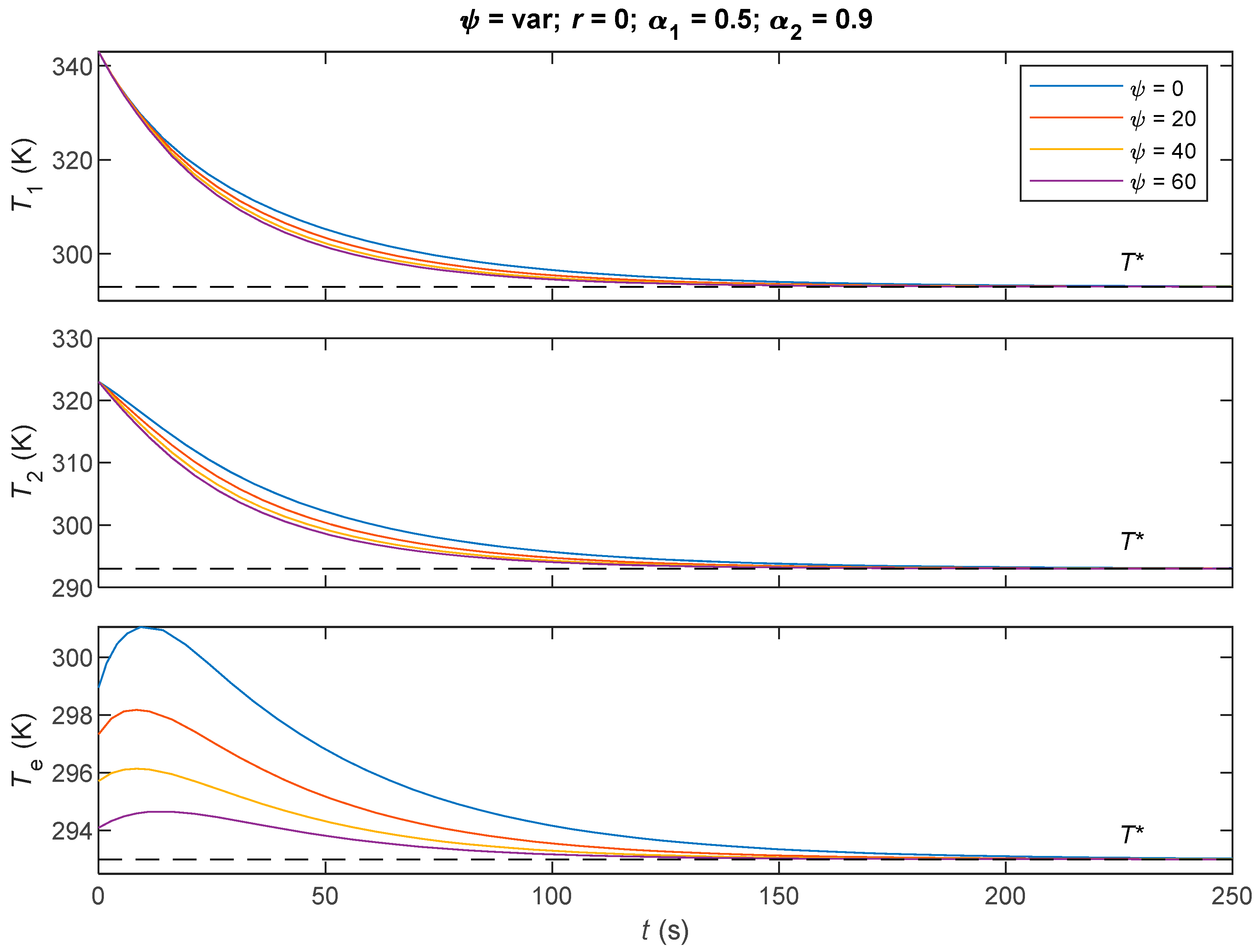
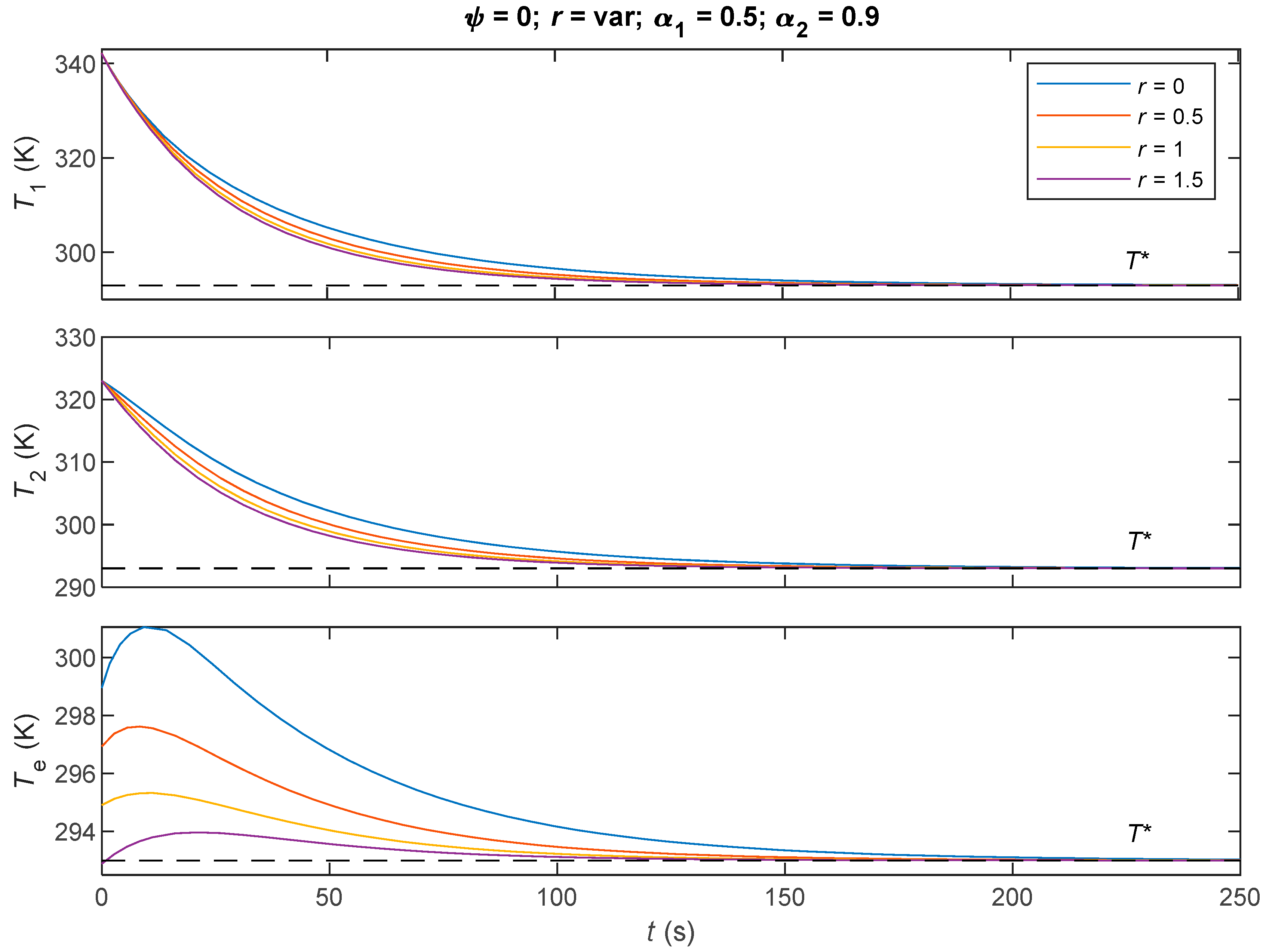
7.2. Comparative Analysis of the Three Derived Control Laws
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Notation | |
| Symbols | |
| availability function | |
| constant volume heat capacity | |
| the vector field characterizing the system dynamics | |
| vector of external flows | |
| input matrix | |
| Hamiltonian function | |
| elements of matrix | |
| interconnection matrix | |
| driving force matrix | |
| elements of matrix | |
| dissipation shaping matrix (IPHS approach) | |
| matrix of stoichiometric coefficients (EBGH approach) | |
| heat | |
| elements of matrix | |
| nonlinear modulating function | |
| damping matrix | |
| -th compartment | |
| entropy function | |
| weighted entropy function | |
| temperature of external source | |
| -th compartment | |
| temperature at the equilibrium state | |
| input vector | |
| internal energy function | |
| state vector | |
| equilibrium state | |
| output vector | |
| th weight coefficient | |
| control law expression | |
| nonlinear dissipative gain | |
| deviation of variable from its equilibrium value | |
| vector of intensive variables | |
| vector of extensive variables | |
| vector of extensive variables of the environment/surrounding | |
| thermal conductance between compartments | |
| thermal conductance to the external source | |
| chemical potential Hessian | |
| entropy flow | |
| isothermal compressibility | |
| element of matrix | |
| generalized conductivity matrix | |
| zero matrix | |
| added function or matrix (for a target system) | |
| desired function or matrix (for a target system) | |
| vector differential operator | |
| Poisson bracket operator | |
| Ginzburg-Landau bracket operator | |
| Abbreviations | |
| HEX | heat exchanger |
| IDA-PBC | interconnection and damping assignment passivity-based control |
| IPHS | irreversible port-Hamiltonian systems |
| PH | port-Hamiltonian |
| PHS | port-Hamiltonian system |
| EBGH | entropy-based generalized Hamiltonian |
| -PHS | entropy-production-metric-based port-Hamiltonian systems |
References
- Duindam, V.; Macchelli, A.; Stramigioli, S.; Bruyninckx, H. (Eds.) Modeling and Control of Complex Physical Systems: The Port-Hamiltonian Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- van der Schaft, A.; Jeltsema, D. Port-Hamiltonian systems theory: An introductory overview. Found. Trends® Syst. Control 2014, 1, 173–378. [Google Scholar] [CrossRef]
- Feng, W.; Deng, Y.; Li, H.; Chen, D.; Li, F. Design of a novel hybrid control for permanent magnet synchronous generator–based wind energy conversion system. J. Vib. Control 2021, 28, 2357–2372. [Google Scholar] [CrossRef]
- Vu, N.M.T.; Lefèvre, L. A connection between optimal control and IDA-PBC design. IFAC-PapersOnLine 2018, 51, 205–210. [Google Scholar] [CrossRef]
- Alkrunz, M.; Yalçın, Y. Adaptive interconnection and damping assignment passivity-based control for linearly parameterized discrete-time port controlled Hamiltonian systems via I&I approach. Int. J. Adapt. Control Signal Process. 2021, 35, 69–88. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, Z.; Wu, B.; Song, M.; Wu, X. An air-cooled system with a control strategy for efficient battery thermal management. Appl. Therm. Eng. 2024, 236 Pt B, 121578. [Google Scholar] [CrossRef]
- Liu, K.; Gao, Y.; Zhu, C.; Li, K.; Fei, M.; Peng, C.; Zhang, X.; Han, Q.-L. Electrochemical modeling and parameterization towards control-oriented management of lithium-ion batteries. Control Eng. Pract. 2022, 124, 105176. [Google Scholar] [CrossRef]
- Sanz i López, V.; Costa-Castelló, R.; Batlle, C. Literature review of energy management in combined heat and power systems based on high-temperature proton exchange membrane fuel cells for residential comfort applications. Energies 2022, 15, 6423. [Google Scholar] [CrossRef]
- Miao, S.; Ezawa, T.; Honda, K.; Harano, K.; Sumita, M.; Katayama, N.; Dowaki, K. Enhancing energy efficiency through combined PEMFC and MH systems and advanced exhaust management strategies. Int. J. Hydrogen Energy 2025, 144, 992–1000. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Ahmad, A.D.; Abubaker, A.M.; Mohamed, M.A. An integrated photovoltaic/wind/biomass and hybrid energy storage systems towards 100% renewable energy microgrids in university campuses. Sustain. Energy Technol. Assess. 2021, 46, 101273. [Google Scholar] [CrossRef]
- Wrobel, R. A technology overview of thermal management of integrated motor drives—Electrical machines. Therm. Sci. Eng. Prog. 2022, 29, 101222. [Google Scholar] [CrossRef]
- Bai, S.; Liu, C. Overview of energy harvesting and emission reduction technologies in hybrid electric vehicles. Renew. Sustain. Energy Rev. 2021, 147, 111188. [Google Scholar] [CrossRef]
- Farhat, O.; Faraj, J.; Hachem, F.; Castelain, C.; Khaled, M. A recent review on waste heat recovery methodologies and applications: Comprehensive review, critical analysis and potential recommendations. Clean. Eng. Technol. 2022, 6, 100387. [Google Scholar] [CrossRef]
- Akbar, A.; Najafi, G.; Gorjian, S.; Kasaeian, A.; Mazlan, M. Performance enhancement of a hybrid photovoltaic-thermal-thermoelectric (PVT-TE) module using nanofluid-based cooling: Indoor experimental tests and multi-objective optimization. Sustain. Energy Technol. Assess. 2021, 46, 101276. [Google Scholar] [CrossRef]
- Shakouri, A.; Gorjian, S.; Ghobadian, B. Energy, exergy, and exergoeconomic (3E) evaluation of a hybrid multigeneration system based on a solar tower. Appl. Therm. Eng. 2024, 252, 123660. [Google Scholar] [CrossRef]
- Pathak, S.K.; Sharma, P.O.; Goel, V.; Bhattacharyya, S.; Aybar, H.Ş.; Meyer, J.P. A detailed review on the performance of photovoltaic/thermal system using various cooling methods. Sustain. Energy Technol. Assess. 2022, 51, 101844. [Google Scholar] [CrossRef]
- Dongellini, M.; Naldi, C.; Morini, G.L. Influence of sizing strategy and control rules on the energy saving potential of heat pump hybrid systems in a residential building. Energy Convers. Manag. 2021, 235, 114022. [Google Scholar] [CrossRef]
- van der Schaft, A.; Rao, S.; Jayawardhana, B. On the mathematical structure of balanced chemical reaction networks governed by mass action kinetics. SIAM J. Appl. Math. 2013, 73, 953–973. [Google Scholar] [CrossRef]
- Makkar, M.; Dieulot, J.-Y. Energy-based modeling and control of continuous chemical reactors under isothermal conditions. Control Eng. Appl. Inf. 2016, 18, 30–40. [Google Scholar]
- Ydstie, B.E.; Alonso, A.A. Process systems and passivity via the Clausius-Planck inequality. Syst. Control Lett. 1997, 30, 253–264. [Google Scholar] [CrossRef]
- Hoang, H.; Couenne, F.; Jallut, C.; Le Gorrec, Y. Hamiltonian formulation and IDA-PBC control of non-isothermal continuous stirred tank reactors. IFAC Proc. Vol. 2010, 43, 715–720. [Google Scholar] [CrossRef]
- Hangos, K.M. Engineering model reduction and entropy-based Lyapunov functions in chemical reaction kinetics. Entropy 2010, 12, 772–797. [Google Scholar] [CrossRef]
- Krishna, A.; Schiffer, J. A port-Hamiltonian approach to modeling and control of an electro-thermal microgrid. IFAC-PapersOnLine 2021, 54, 287–293. [Google Scholar] [CrossRef]
- Hoang, H.; Couenne, F.; Jallut, C.; Le Gorrec, Y. The port Hamiltonian approach to modeling and control of continuous stirred tank reactors. J. Process Control 2011, 21, 1449–1458. [Google Scholar] [CrossRef]
- García-Sandoval, J.P.; Hudon, N.; Dochain, D.; González-Álvarez, V. Stability analysis and passivity properties of a class of thermodynamic processes: An internal entropy production approach. Chem. Eng. Sci. 2016, 139, 261–272. [Google Scholar] [CrossRef]
- García-Sandoval, J.P.; Hudon, N.; Dochain, D. Generalized Hamiltonian representation of thermo-mechanical systems based on an entropic formulation. J. Process Control 2017, 51, 18–26. [Google Scholar] [CrossRef]
- Romo-Hernandez, A.; Hudon, N.; Ydstie, B.E.; Dochain, D. Internal entropy production as a Lyapunov function for thermal equilibrium in irreversible multiphase systems. IFAC-PapersOnLine 2022, 55, 27–32. [Google Scholar] [CrossRef]
- Ramirez, H.; Le Gorrec, Y.; Maschke, B.; Couenne, F. Passivity Based Control of Irreversible Port Hamiltonian Systems. IFAC Proc. Vol. 2013, 46, 84–89. [Google Scholar] [CrossRef]
- Ramírez, H.; Le Gorrec, Y.; Maschke, B.; Couenne, F. On the passivity based control of irreversible processes: A port-Hamiltonian approach. Automatica 2016, 64, 105–111. [Google Scholar] [CrossRef]
- Tefera, D.T.; Dubljevic, S.; Prasad, V. A port Hamiltonian approach to dynamical chemical process systems network modeling and analysis. Chem. Eng. Sci. 2022, 261, 117907. [Google Scholar] [CrossRef]
- Márquez, F.M.; Zufiria, P.J.; Yebra, L.J. Port-Hamiltonian modeling of thermofluid systems and object-oriented implementation with Modelica I: Thermodynamic part. IEEE Access 2021, 9, 131496–131519. [Google Scholar] [CrossRef]
- Dong, Z.; Li, J.; Zhang, Z.; Dong, Y.; Huang, X. The definition of entropy production metric with application in passivity-based control of thermodynamic systems. Renew. Sustain. Energy Rev. 2025, 209, 115065. [Google Scholar] [CrossRef]
- Li, J.; Dong, Z. Passivity-based control for methane steam reforming in nuclear cogeneration systems. Int. J. Hydrogen Energy 2025, 140, 473–482. [Google Scholar] [CrossRef]
- Tangde, V.M.; Bhalekar, A.A.; Andresen, B. Thermodynamic stability theories of irreversible processes and the Fourth Law of Thermodynamics. Entropy 2024, 26, 442. [Google Scholar] [CrossRef]
- Ramirez, H.; Le Gorrec, Y.; Maschke, B. Interconnection and Damping Assignment—Passivity Based Control of Irreversible Port Hamiltonian Systems. IFAC Proc. Vol. 2014, 47, 9111–9116. [Google Scholar] [CrossRef]
- Gay-Balmaz, F.; Yoshimura, H. From Lagrangian Mechanics to Nonequilibrium Thermodynamics: A Variational Perspective. Entropy 2019, 21, 8. [Google Scholar] [CrossRef] [PubMed]
- Yoshimura, H.; Gay-Balmaz, F. Hamiltonian variational formulation for non-simple thermodynamic systems. In Geometric Science of Information. GSI 2023. Lecture Notes in Computer Science; Nielsen, F., Barbaresco, F., Eds.; Springer: Cham, Switzerland, 2023; Volume 14072. [Google Scholar] [CrossRef]
- de León, M.; Bajo, J. A geometric description of some thermodynamical systems. J. Phys. A Math. Theor. 2025, 58, 175203. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Grmela, M. GENERIC guide to the multiscale dynamics and thermodynamics. J. Phys. Commun. 2018, 2, 032001. [Google Scholar] [CrossRef]
- Morrison, P.J. Bracket formulation for irreversible classical fields. Phys. Lett. A 1984, 100, 423–428. [Google Scholar] [CrossRef]
- Zaidni, A.; Morrison, P.J.; Benjelloun, S. Thermodynamically consistent Cahn–Hilliard–Navier–Stokes equations using the metriplectic dynamics formalism. Physica D 2024, 468, 134303. [Google Scholar] [CrossRef]
- Ramirez, H.; Maschke, B.; Sbarbaro, D. Modelling and control of multi-energy systems: An irreversible port-Hamiltonian approach. Eur. J. Control 2013, 19, 513–520. [Google Scholar] [CrossRef]
- Ortega, R.; Garcia-Canseco, E. Interconnection and damping assignment passivity-based control: A survey. Eur. J. Control 2004, 10, 432–450. [Google Scholar] [CrossRef]
- van der Schaft, A. Classical thermodynamics revisited: A systems and control perspective. IEEE Control Syst. 2021, 41, 32–60. [Google Scholar] [CrossRef]
- van der Schaft, A. Geometric modeling for control of thermodynamic systems. Entropy 2023, 25, 577. [Google Scholar] [CrossRef] [PubMed]
- Philipp, F.M.; Schaller, M.; Worthmann, K.; Faulwasser, T.; Maschke, B. Optimal control of port-Hamiltonian systems: Energy, entropy, and exergy. Syst. Control Lett. 2024, 194, 105942. [Google Scholar] [CrossRef]





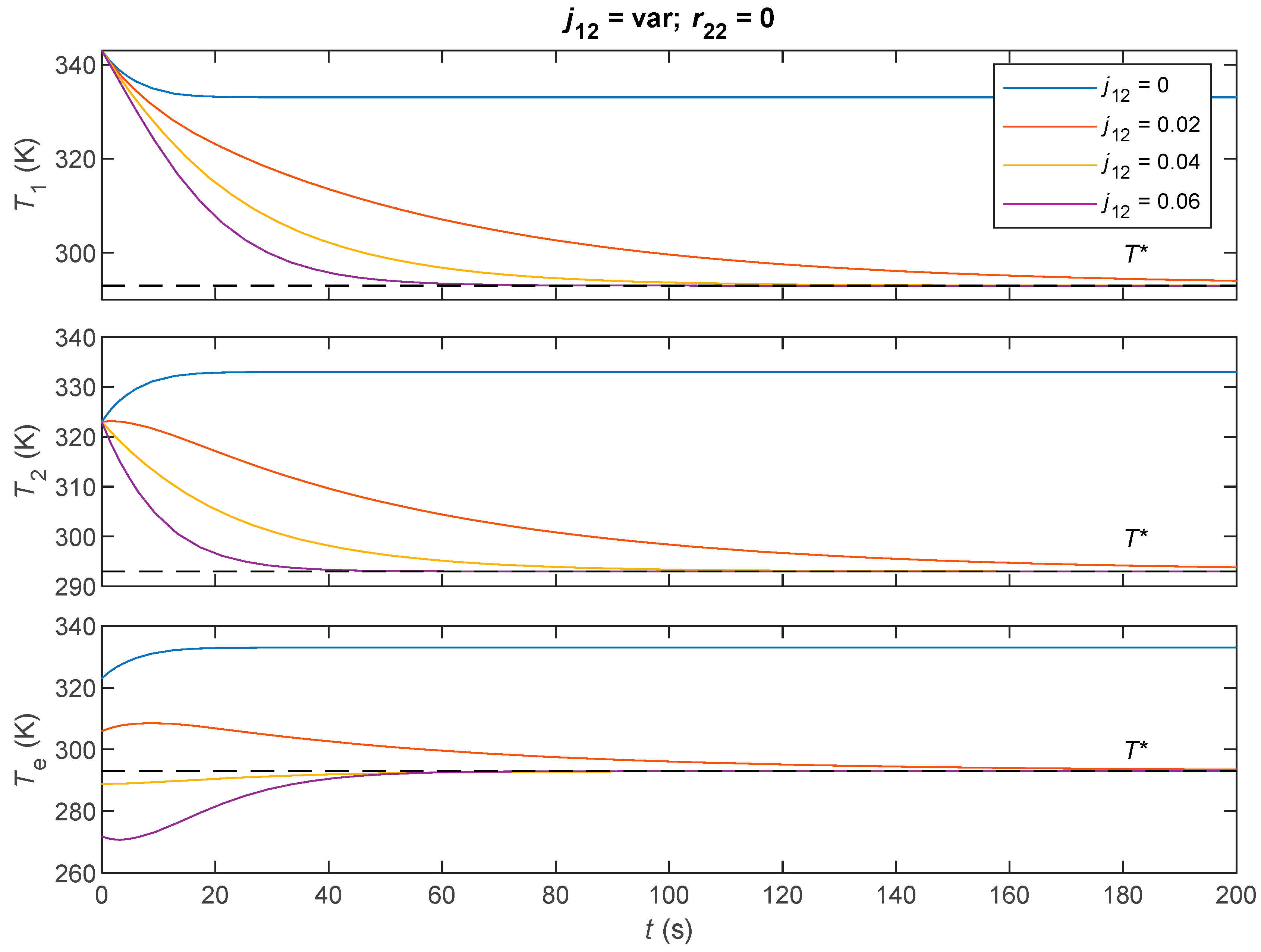
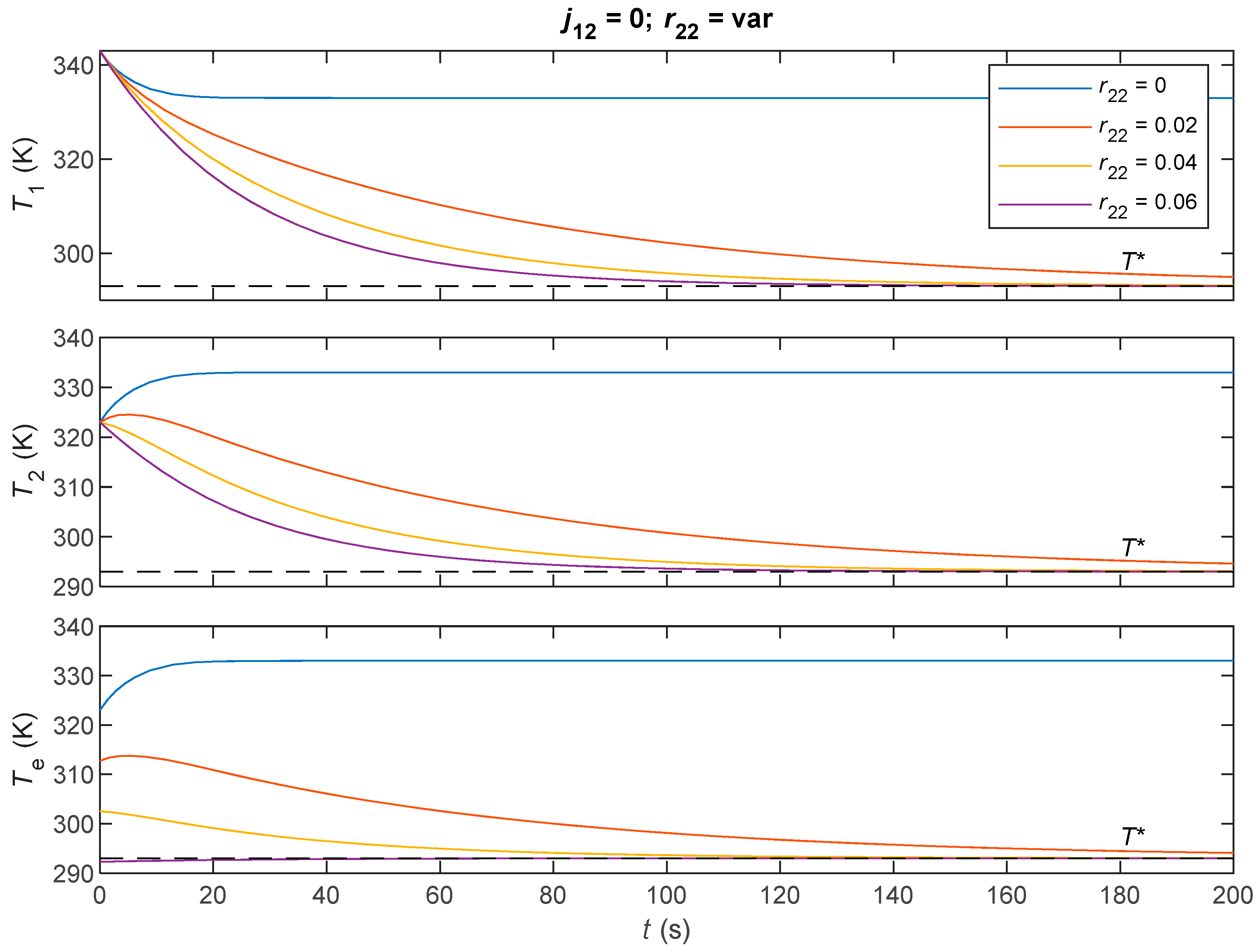
| Parameter | Value |
|---|---|
| Compartments | |
| 1 kg | |
| 500 J/(K·kg) | |
| Conductive walls | |
| 10 cm2 | |
| 1 cm | |
| 50 W/(m·K) | |
| 50 W/K | |
| 50 W/K | |
| Initial temperature | |
| 343 K | |
| 323 K | |
| 293 K | |
| Criterion | IPHS | EBGH | -PHS |
|---|---|---|---|
| Selection of state variables, in particular, for thermodynamic domain | aligned with the PH approach; entropy for thermodynamic domain | extensive quantities; internal energies for thermal domain | for the thermodynamic domain |
| Storage function (Hamiltonian-like) of an open-loop system | internal energy function | entropy function | second-order deviation of the entropy production metric function |
| Co-variables definition | gradient of internal energy; temperature for thermodynamic domain | gradient of the entropy function; reverse temperature for thermal domain | gradient of the entropy-production-metric-based storage function, dependent on the model structure |
| Thermodynamic compliance via the first law (energy conservation) | explicit by design, using the storage function time derivative | enforced by deriving thermodynamic relations based on the Gibbs equation | enforced by deriving the storage function based on the Gibbs equation |
| Thermodynamic compliance via the second law (entropy production conservation) | intrinsic, using the entropy production | explicit by design, using entropy as a storage function | explicit by design, using the entropy production metric |
| Development of passivity-based control in general | thoroughly developed theory | undeveloped in literature | extended-state passivity-based control |
| Development of IDA-PBC-like control in literature | yes | no | no |
| Possibility of developing the IDA-PBC-like control | yes | yes | yes |
| Storage function for the target system | energy-based availability function | thermodynamic availability function | second-order deviation of the entropy production metric function |
| Stability analysis tools | convexity of the availability function with a strict minimum at the equilibrium | concavity of the availability function with the maximum at the equilibrium | convexity of the storage function with a strict minimum at the origin |
| Possibility of using free parameters of the control to adjust the transient behavior | yes | yes | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznyetsov, O. Comparison of Alternative Port-Hamiltonian Dynamics Extensions to the Thermodynamic Domain Toward IDA-PBC-Like Control: Application to a Heat Transfer Model. Dynamics 2025, 5, 42. https://doi.org/10.3390/dynamics5040042
Kuznyetsov O. Comparison of Alternative Port-Hamiltonian Dynamics Extensions to the Thermodynamic Domain Toward IDA-PBC-Like Control: Application to a Heat Transfer Model. Dynamics. 2025; 5(4):42. https://doi.org/10.3390/dynamics5040042
Chicago/Turabian StyleKuznyetsov, Oleksiy. 2025. "Comparison of Alternative Port-Hamiltonian Dynamics Extensions to the Thermodynamic Domain Toward IDA-PBC-Like Control: Application to a Heat Transfer Model" Dynamics 5, no. 4: 42. https://doi.org/10.3390/dynamics5040042
APA StyleKuznyetsov, O. (2025). Comparison of Alternative Port-Hamiltonian Dynamics Extensions to the Thermodynamic Domain Toward IDA-PBC-Like Control: Application to a Heat Transfer Model. Dynamics, 5(4), 42. https://doi.org/10.3390/dynamics5040042







