Modeling, Validation, and Controllability Degradation Analysis of a 2(P-(2PRU–PRPR)-2R) Hybrid Parallel Mechanism Using Co-Simulation
Abstract
1. Introduction
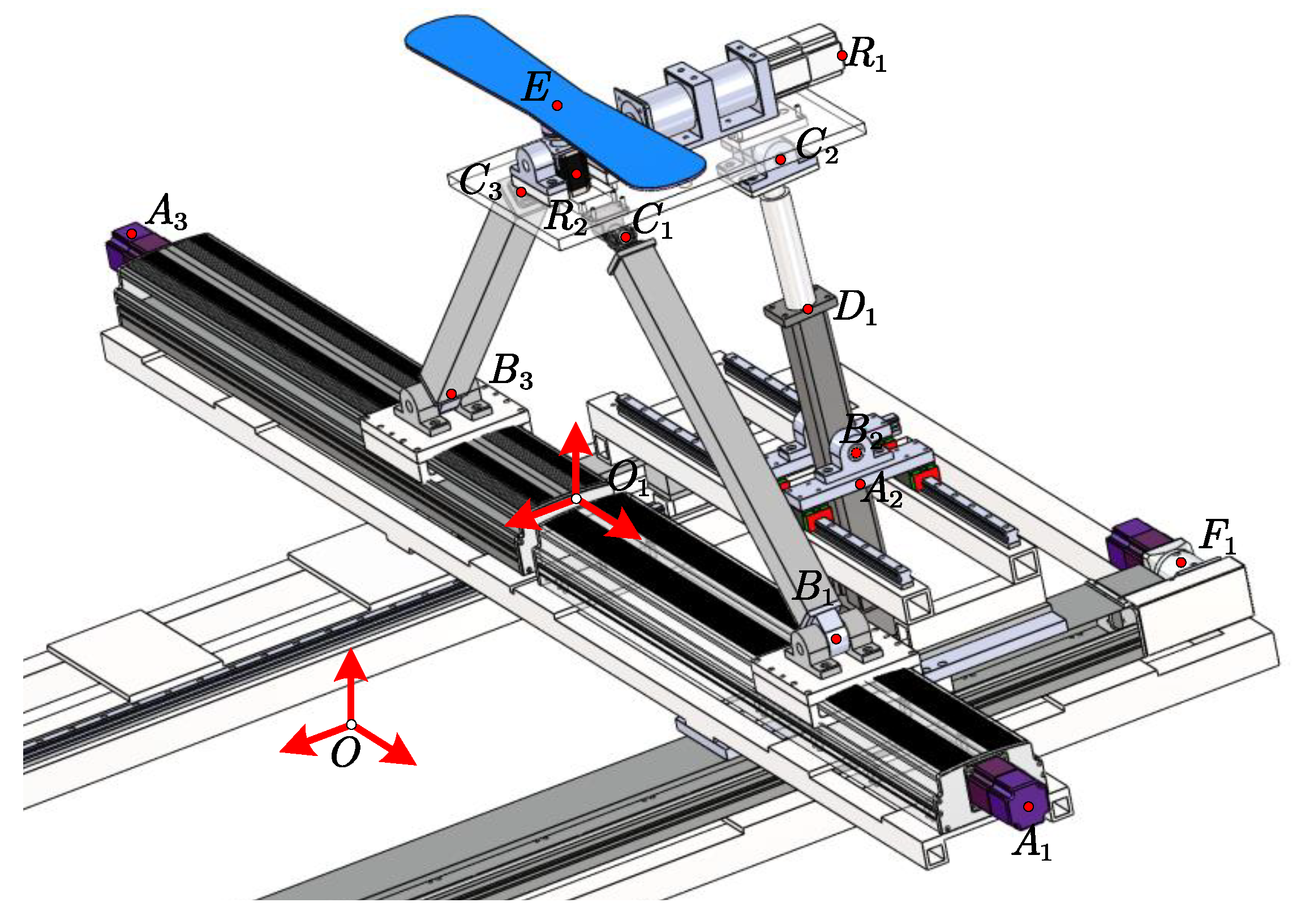
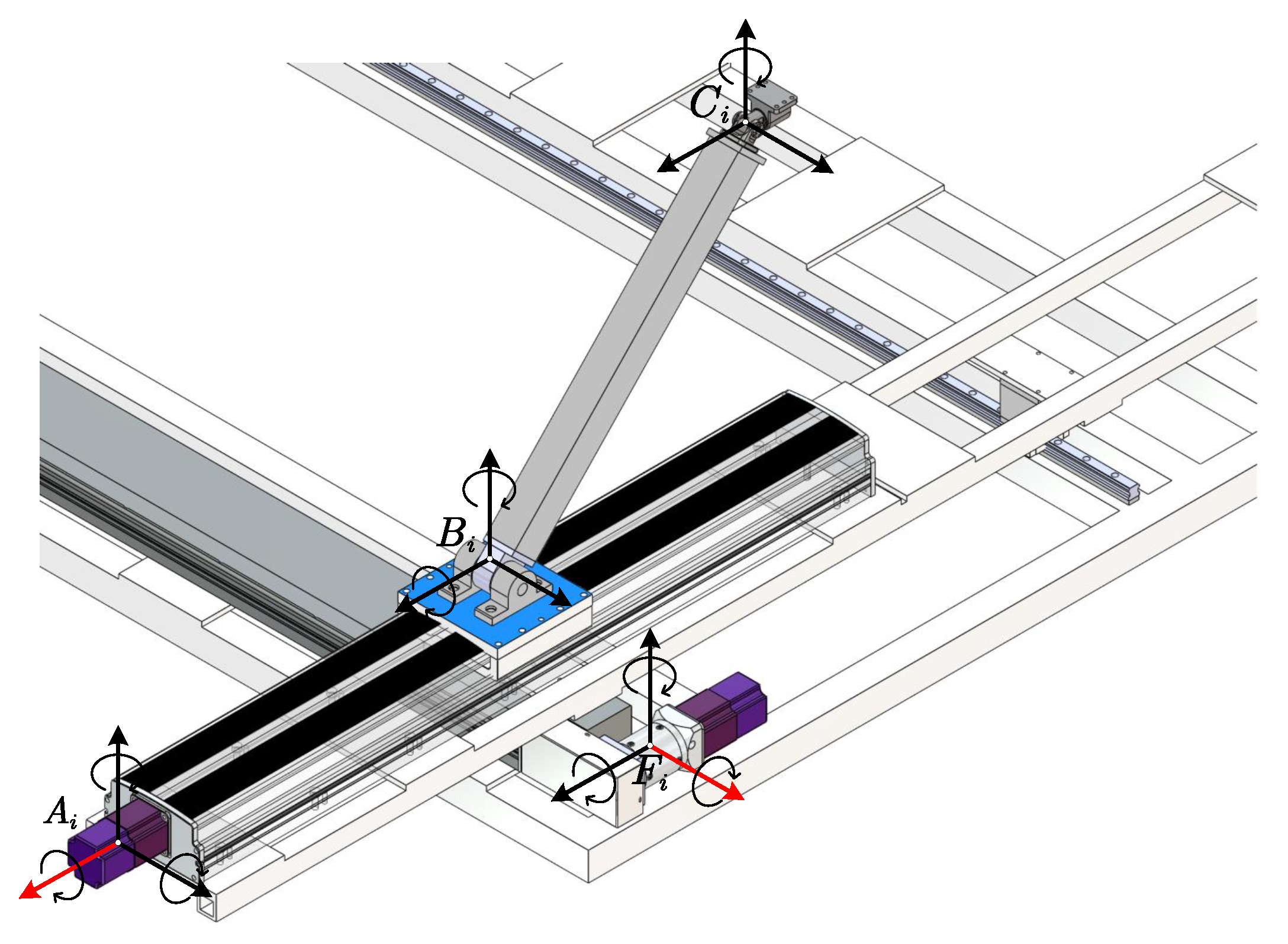
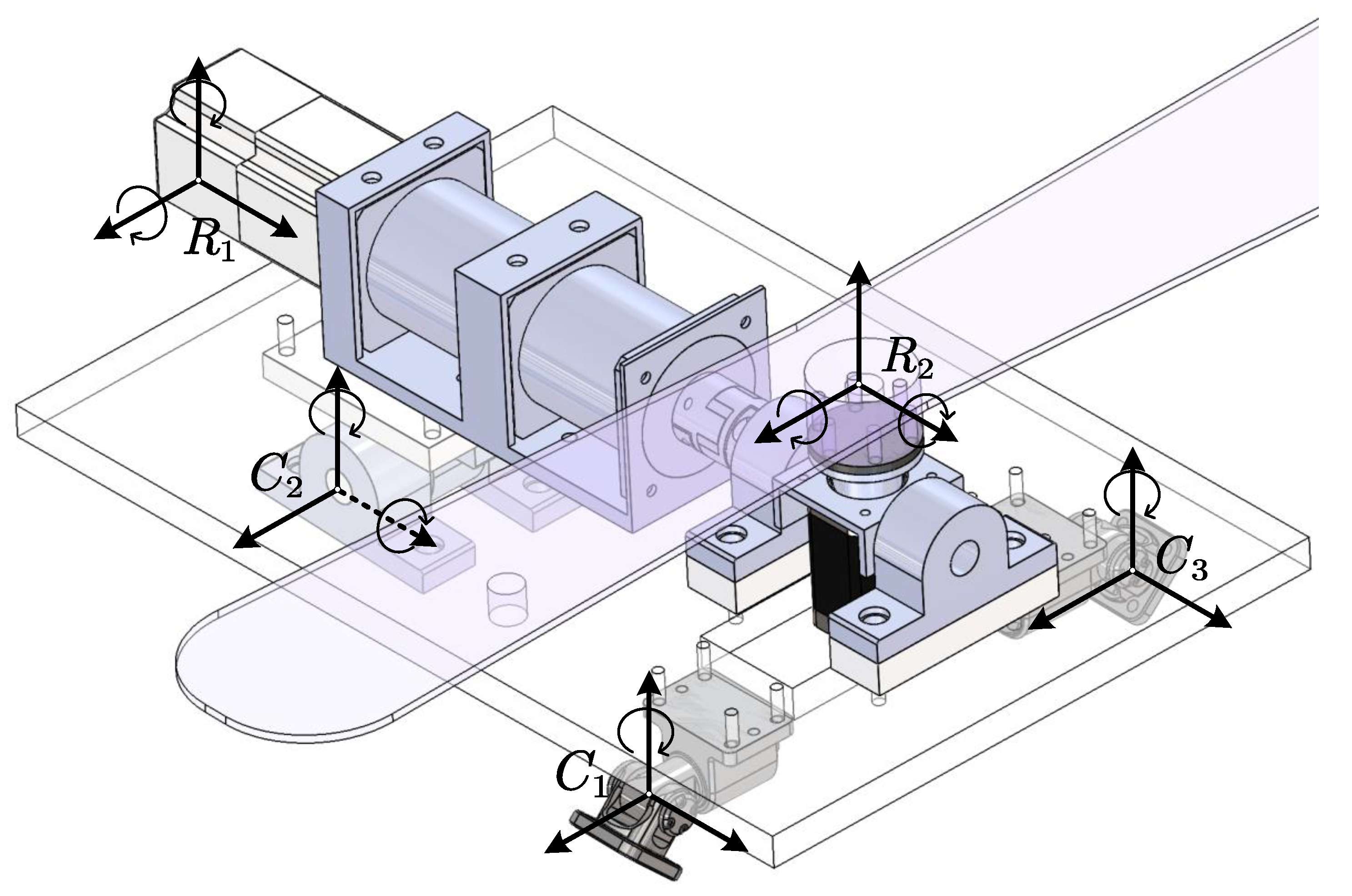
2. Mechanism Description and Kinematic Analysis
2.1. Mechanism Description
2.2. Inverse Kinematics for Hybrid Mechanisms
2.3. Kinematic Analysis of Ski Simulation Platform
2.3.1. Kinematic Analysis of PRU Chains
2.3.2. Kinematic Analysis of PRPR Subchains
2.3.3. Kinematic Analysis of Serial Subchains
3. Dynamic Modeling and Analysis of Hybrid Mechanisms
3.1. Dynamic Force/Torque Analysis of Kinematic Components
3.1.1. Force/Torque Analysis of PRU-Pulley Subsystem
3.1.2. Force/Torque Analysis of PRPR Hybrid Subsystem
3.1.3. Force/Torque Analysis of End-Effector Subsystem
3.2. Dynamic Model Validation Through Numerical Simulation
4. Mechanism Deformation Compatibility Analysis
Deformation Compatibility Formulation for Kinematic Chain
5. Conclusions
- •
- 82.3% moment accuracy improvement (final deviation ≤ 0.98%)
- •
- Force precision enhancement to 0.12% relative error Cross-platform consistency (MATLAB/Adams RMS error < 0.15%)
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Guo, F.; Lu, W.; Li, Y.; Zhang, L. Non-inertial System Dynamic Modeling of 3UPS/S Ship Stability Platform. J. Mech. Eng. 2020, 56, 20–29. [Google Scholar]
- Cai, A.-Y.; Yao, X.-L. Trajectory optimization with constraints for alpine skiers based on multi-phase nonlinear optimal control. Front. Inf. Technol. Electron. Eng. 2020, 21, 1521–1535. [Google Scholar] [CrossRef]
- SONG, C.j.; Xiao-dan, C.; Si-wen, S. Design and Implementation of Visual System of Simulated Ski Machine Based on Unity3D. Ind. Appl. Commun. 2021, 40, 158–161. [Google Scholar]
- Yu, Z.; Liu, Y.; Liu, Y.; Wan, Y.; Yang, W.; Daoai, W.; Feng, Z. Wearable Snow Friction Harvester Based on Traditional Skis. Tribology 2024, 44, 97–106. [Google Scholar] [CrossRef]
- Guan, L.; Cong, X.; Zhang, Q.; Zhou, X. Design of visualization system for indoor skiing teaching and training based on micro-inertia and Unity3D. Exp. Technol. Manag. 2021, 38, 152–156. [Google Scholar] [CrossRef]
- Gao, H.; Qiao, R.; Liu, J. Design of Ski Training Equipment Based on Industrial Robot Technology. Mech. Eng. 2024, 135–140. [Google Scholar]
- Cheng, Y.; Ren, G.; Dai, S. The multi-body system modelling of the Gough-Stewart platform for vibration control. J. Sound Vib. 2004, 271, 599–614. [Google Scholar] [CrossRef]
- Engin, M. Controller Design for Parallel Mechanism Solar Tracker. Machines 2023, 11, 372. [Google Scholar] [CrossRef]
- Olar, M.L.; Panaite, A.F.; Leba, M.; Sibisanu, R. Stewart Platform Modified into a Bio-inspirational Device of the Human Shoulder. In Trends and Applications in Information Systems and Technologies, VOL 4, Proceedings of the 9th World Conference on Information Systems and Technologies (WorldCIST), Electr Network, 30 March–2 April 2021; Advances in Intelligent Systems and Computing; Rocha, A., Adeli, H., Dzemyda, G., Moreira, F., Correia, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 1368, pp. 151–160. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, J. Design of virtual interactive educational games based on human perception. Entertain. Comput. 2025, 52, 100891. [Google Scholar] [CrossRef]
- Liu, C.; He, Q.; Tang, Q.; Ren, K.; Gong, J.; Zhang, D. Novel control strategy for the energy recovery system of a hydraulic excavator. Int. J. Agric. Biol. Eng. 2024, 17, 94–101. [Google Scholar] [CrossRef]
- Liu, B.; Gan, J.; Xu, J.; Ellis, D.; Zou, R.; Yu, A.; Zhou, Z. Numerical simulation of operations of hydraulic excavators for polydisperse bulk materials and different configurated buckets. Autom. Constr. 2024, 157, 105154. [Google Scholar] [CrossRef]
- Jaiswal, S.; Jiang, D.; Xiang, S.; Nikitina, A.; Khadim, Q.; Mikkola, A. Gamification of control valves in real-time multibody simulation of an excavator. Multibody Syst. Dyn. 2024. [Google Scholar] [CrossRef]
- Song, H.; Li, G.; Li, Z.; Xiong, X. Trajectory Control Strategy and System Modeling of Load-Sensitive Hydraulic Excavator. Machines 2023, 11, 10. [Google Scholar] [CrossRef]
- Ding, J.; Ding, H.; Yang, W. Dynamic Modeling of a Novel Multi-Loop Multi-Body Mechanism of Face-Shovel Excavator. Chin. J. Mech. Eng. 2025, 38, 38. [Google Scholar] [CrossRef]
- Hu, B.; Zhang, L.; Yu, J. Kinematics and dynamics analysis of a novel serial-parallel dynamic simulator. J. Mech. Sci. Technol. 2016, 30, 5183–5195. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Y.; Zhang, Y.; Zhang, L. Dynamic Modeling Method of Spatial Passive Over-constrained Parallel Mechanism Based on Newton Euler Method. J. Mech. Eng. 2020, 56, 48–57. [Google Scholar]
- Huang, H.; Han, H.; Li, D.; Xu, Z.; Wu, Q. Inverse dynamics analysis of a 6-RR-RP-RR parallel manipulator with offset universal joints. Robotica 2024, 42, 1549–1567. [Google Scholar] [CrossRef]
- Zhao, J.S.; Wei, S.T.; Sun, X.C. Dynamics of a 3-UPS-UPU-S Parallel Mechanism. Appl. Sci. 2023, 13, 3912. [Google Scholar] [CrossRef]
- Boyer, F.; Gotelli, A.; Tempel, P.; Lebastard, V.; Renda, F.; Briot, S. Implicit Time-Integration Simulation of Robots With Rigid Bodies and Cosserat Rods Based on a Newton-Euler Recursive Algorithm. IEEE Trans. Robot. 2024, 40, 677–696. [Google Scholar] [CrossRef]
- Chen, Z.; Song, J.; Li, N.; Yan, W.; Zhao, C. Design and dynamics modeling of a novel 2R1T 3-DOF parallel motion simulator. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 234. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, G.; Rui, X.; Wu, G.; Tang, J.; Gu, L. Modeling and simulation framework for missile launch dynamics in a rigid-flexible multibody system with slider-guide clearance. Nonlinear Dyn. 2024, 112, 21701–21728. [Google Scholar] [CrossRef]
- Liu, K.; Song, T.; Xu, X.; Wang, H.; Meng, Q. Dynamics modeling and typical motion performance analysis for a multi-joint autonomous underwater vehicle. Ocean. Eng. 2023, 281, 114999. [Google Scholar] [CrossRef]
- Liu, T. Analysis of human lower limb dynamics and gait reconstruction. J. Mech. Med. Biol. 2024, 24, 2440027. [Google Scholar] [CrossRef]
- Urbas, A.; Augustynek, K.; Martsenyuk, V. The Influence of the Load Modelling Methods on Dynamics of a Mobile Crane. In Perspectives in Dynamical Systems I-Applications, DSTA 2021, Proceedings of the 16th International Conference on Dynamical Systems—Theory and Applications (DSTA), Electr Network, 6–9 December 2021; Springer Proceedings in Mathematics and Statistics; Awrejcewicz, J., Ed.; Lodz Univ Technol, Dept Automat, Biomechan & Mechatron: Łódź, Poland; Polish Minister Educ & Sci: Warsaw, Poland, 2024; Volume 453, pp. 559–569. [Google Scholar] [CrossRef]
- Chen, R.; Gu, Y.; Qiu, G.; Huang, P. Dynamic analysis of planetary gear transmission based on Lagrange interpolation polynomials. Meas. Sci. Technol. 2024, 35, 11. [Google Scholar] [CrossRef]
- Yang, H.; Ni, T.; Wang, Z.; Wang, Z.; Zhao, D. Dynamic modeling and analysis of traction operation process for the shipboard helicopter. Aerosp. Sci. Technol. 2023, 142, 108661. [Google Scholar] [CrossRef]
- Qiu, J.; Qiu, W.; Niu, A.; Han, G.; Wang, S.; Sun, Y. Modeling and Analysis of Offshore Gangway under Dynamic Load. J. Mar. Sci. Eng. 2023, 11, 77. [Google Scholar] [CrossRef]
- Luo, Z.; Xiao, J.; Liu, S.; Wang, M.; Zhao, W.; Liu, H. A dynamic parameter identification method for the 5-DOF hybrid robot based on sensitivity analysis. Ind. Robot.- Int. J. Robot. Res. Appl. 2024, 51, 340–357. [Google Scholar] [CrossRef]
- Zhu, R.; Yang, G.; Fang, Z.; Chen, C.Y.; Li, H.; Zhang, C. Quasi-Coordinates-Based Closed-Form Dynamic Modeling and Analysis for a 2R1T PKM with a Rigid-Flexible Structure. Machines 2023, 11, 260. [Google Scholar] [CrossRef]
- Wu, N.; Yang, H.; Afsar, H.; Wang, B.; Fan, J. Analysis of Train-Track-Bridge Coupling Vibration Characteristics for Heavy-Haul Railway Based on Virtual Work Principle. Sensors 2023, 23, 8550. [Google Scholar] [CrossRef]
- Di Gregorio, R. Dynamic model of single-DOF spherical mechanisms based on instantaneous pole axes and Eksergian’s equation. Mech. Mach. Theory 2024, 200, 105720. [Google Scholar] [CrossRef]
- ISO 14839-1:2018; Mechanical Vibration—Vibration of Rotating Machinery Equipped with Active Magnetic Bearings—Part 3: Evaluation of Stability Margin. ISO: Geneva, Switzerland, 2006.
- Gupta, A.; Lee, C. Real-time control benchmarks for multi-axis motion platforms. Mechatronics 2020, 65, 102301. [Google Scholar]
- Feng, G.; Jia, S.; Chen, J.; Zhou, X. Newton-Eulerian Dynamics of a Walkable Lander. Spacecr. Recovery Remote Sens. 2024, 45, 53–64. [Google Scholar]
- Liu, Y.; Cao, X.; Wang, X.; Wang, F.; Xu, Z.; Lu, H. Forward kinematics of the 6-DOF parallel mechanism based on homogeneous transformation matrix numerical solution. J. Harbin Eng. Univ. 2013, 34, 894–898. [Google Scholar]
- Zhang, J.; Xie, F.; Liu, X.J. Dynamic modeling of hybrid robots through stiffness directionally releasing and multiple-node dynamics assembling. Mech. Mach. Theory 2025, 209, 106002. [Google Scholar] [CrossRef]
- Yang, J.; Harsono, E.; Yu, H. Dynamic modeling and validation of a hybrid-driven continuum robot with antagonistic mechanisms. Mech. Mach. Theory 2024, 197, 105635. [Google Scholar] [CrossRef]
- Shen, N.; Yuan, H.; Li, J.; Wang, Z.; Lu, N.; Lu, Y. Dynamic Modeling and Simulation of a Hybrid Robot. J. Mech. Robot.-Trans. Asme 2023, 15, 011012. [Google Scholar] [CrossRef]
- Gao, F.; Yang, J.; Ge, Q. GF Set Theory for Type Synthesis of Parallel Mechanisms; China Machine Press: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Cammarata, A.; Maddio, P.D.; Sinatra, R.; Tian, Y.; Zhao, Y.; Xi, F. Elastostatic analysis of a module-based shape morphing snake-like robot. Mech. Mach. Theory 2024, 194, 105580. [Google Scholar] [CrossRef]








| i | ||||
|---|---|---|---|---|
| 1 | 0 | 0 | ||
| 2 | 0 |
| Parameters | Values |
|---|---|
| Stroke of Pulley/m | 5 |
| Stroke of Servo motor 1/rad | |
| Stroke of Servo motor 2/rad | |
| Length of fixing rod/m | 0.8 |
| Stroke of electric cylinder/m | |
| Length of servo motor/m | 0.12 |
| Size of intermediate platform/m | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Q.; Wu, Z.; Li, Y.; Tao, H.; Li, B.; Li, W. Modeling, Validation, and Controllability Degradation Analysis of a 2(P-(2PRU–PRPR)-2R) Hybrid Parallel Mechanism Using Co-Simulation. Dynamics 2025, 5, 30. https://doi.org/10.3390/dynamics5030030
Gu Q, Wu Z, Li Y, Tao H, Li B, Li W. Modeling, Validation, and Controllability Degradation Analysis of a 2(P-(2PRU–PRPR)-2R) Hybrid Parallel Mechanism Using Co-Simulation. Dynamics. 2025; 5(3):30. https://doi.org/10.3390/dynamics5030030
Chicago/Turabian StyleGu, Qing, Zeqi Wu, Yongquan Li, Huo Tao, Boyu Li, and Wen Li. 2025. "Modeling, Validation, and Controllability Degradation Analysis of a 2(P-(2PRU–PRPR)-2R) Hybrid Parallel Mechanism Using Co-Simulation" Dynamics 5, no. 3: 30. https://doi.org/10.3390/dynamics5030030
APA StyleGu, Q., Wu, Z., Li, Y., Tao, H., Li, B., & Li, W. (2025). Modeling, Validation, and Controllability Degradation Analysis of a 2(P-(2PRU–PRPR)-2R) Hybrid Parallel Mechanism Using Co-Simulation. Dynamics, 5(3), 30. https://doi.org/10.3390/dynamics5030030





