Aerodynamic Optimization and Thermal Deformation Effects on Mid-Altitude Sounding Rockets: A Computational and Structural Analysis

Abstract

Mid-altitude sounding rockets are essential for atmospheric research and suborbital experimentation, where aerodynamic optimization and structural integrity are crucial for achieving targeted apogees. This study uses OpenRocket v23.09 for preliminary flight performance prediction and SolidWorks 2024 to integrate aerodynamic and structural analyses through Computational Fluid Dynamics (CFD) and Finite Element Analysis (FEA). SolidWorks Flow Simulation and SolidWorks Simulation are used to assess how nose cone and fin geometries, as well as thermal deformation, influence flight performance. Among nine tested configurations, the ogive nose cone with trapezoidal fins achieved the highest simulated apogee of 2639 m, with drag coefficients of 0.480 (OpenRocket) and 0.401 (SolidWorks Flow Simulation). Thermal–structural analysis revealed a maximum nose tip displacement of 0.7249 mm for the rocket with the ogive nose cone, leading to an increasing drag coefficient of 0.404. However, thermal deformation of the ellipsoid nose cone led to a reduction in the drag coefficient from 0.419 to 0.399, even though it exhibited a slightly higher maximum displacement of 0.7443 mm. Mesh independence was confirmed with outlet velocity deviations below 1% across refinements. These results highlight the importance of integrated CFD–FEA approaches, geometric optimization, and material resilience for enhancing the aerodynamic performance of subsonic sounding rockets.

1. Introduction

Sounding rockets, serving as pivotal tools for scientific exploration, have a rich history of contributions to atmospheric and aerospace research. These suborbital rockets are designed to carry payloads to altitudes ranging from tens to hundreds of kilometres, providing a platform for experiments in microgravity, atmospheric sampling, and space environment studies [1,2,3]. Unlike orbital rockets, sounding rockets follow a parabolic trajectory, making them ideal for short-duration missions that demand quick turnaround and cost-effectiveness. Over the years, advancements in material science, aerodynamic modeling, and computational simulations have driven significant innovations in their design and performance [4,5].

The aerodynamic performance of a sounding rocket is heavily influenced by its geometry, structural integrity, and material properties. Key aerodynamic principles such as drag, lift, and stability coefficients are critical in determining the rocket’s trajectory and overall efficiency. Drag, which opposes the rocket’s motion, is minimized through streamlined designs, while lift coefficients are optimised to enhance stability during ascent [6,7]. Computational tools, such as Computational Fluid Dynamics (CFD), play a central role in analyzing and optimizing these aerodynamic parameters. By simulating various flight conditions, CFD enables engineers to predict performance metrics and identify potential areas for improvement, reducing reliance on costly prototypes or wind tunnel testing [8].

One of the significant challenges in sounding rocket design is addressing the pressure effects on components, particularly the nose cone, which experiences extreme temperatures during flight. The use of 3D-printed materials such as Polylactic Acid (PLA) introduces unique thermal and mechanical challenges. PLA, while lightweight and cost-effective, is prone to deformation under high thermal loads, potentially compromising aerodynamic efficiency and structural integrity. This research focuses on investigating these thermal effects and their implications for the aerodynamic performance of mid-altitude sounding rockets.

The integration of advanced software tools such as SolidWorks for geometric modeling and OpenRocket for flight simulations further enhances the design process [9]. These tools enable the precise modeling of rocket components and provide insights into the interplay between design variables and performance outcomes [10]. Additionally, thermal analysis using finite element methods offers a deeper understanding of how temperature variations impact structural behaviour, informing iterative design modifications to mitigate thermal deformation [11].

The existing literature lacks comprehensive studies that combine structural mechanics, aerodynamics, and thermal deformation analysis, particularly for mid-altitude rockets. This study is novel in its coupling of Finite Element Analysis (FEA) and Computational Fluid Dynamics (CFD) to quantify how thermal stress-induced deformation affects the aerodynamics and flight performance of the mid-altitude sounding rocket. It also provides comparative assessments of different fin and nose cone geometries under both ideal and deformed states. By bridging this methodological gap, the research contributes to the design of high-performing and thermally resilient sounding rockets capable of achieving consistent apogees between 2.3 km and 3 km. The findings not only advance the field of aerospace engineering but also provide a foundation for future innovations in suborbital rocket technology, with potential applications in scientific research, atmospheric studies, and competitive events such as TEKNOFEST [12] or European Rocketry Challenge (EuRoC).

The remainder of this paper is organized as follows. Section 2 describes the research methodology, including rocket component design, material selection, and simulation setup. Section 3 presents and discusses the results from aerodynamic, structural, and thermal analyses, including performance comparisons and flow behaviour. Section 4 provides the main conclusions drawn from this study, along with recommendations for future research in the field of mid-altitude sounding rocket development.

2. Methodology

In this study, the Finite Element Analysis (FEA) was conducted using SolidWorks 2024 to simulate the thermal behaviour of the PLA nose cone under high-temperature conditions experienced during mid-altitude rocket launches. SolidWorks Flow Simulation was employed for Computational Fluid Dynamics (CFD) analysis to evaluate the aerodynamic performance of the rocket. Simulations were conducted for both undeformed and thermally deformed nose cone geometries to assess parameters, such as the drag coefficient, lift-to-drag ratio, and flow separation points. Finally, the aerodynamic and structural performance metrics of the original and deformed nose cone designs were compared. Metrics, such as apogee height, drag force, and stress deformation thresholds, were analyzed to assess the overall impact of thermal effects on rocket performance.

2.1. Component of Mid-Altitude Sounding Rocket

The mid-altitude sounding rocket analyzed in this study has been specifically designed for participation in the TEKNOFEST competition [12]. The general design and layout were developed using OpenRocket v23.09 software, which provided simulation-based insights into the rocket’s aerodynamic behaviour. Emphasis was placed on achieving an aerodynamic shape to minimize drag while considering the effects of structural stress.

The rocket features a fiberglass airframe with a body diameter of 137 mm and is powered by the Aerotech M1850W solid rocket motor, capable of delivering 250 N of thrust over a 3-s burn time. It is equipped with dual recovery hardware to enable two-stage parachute deployment and includes a duty payload subsystem designed to measure G-forces experienced during descent. The finalised design specifies a total length of 2530 mm, a dry weight of 20,874 g, and a lift-off weight of 27,567 g. The rocket is engineered to carry its payload to a target altitude of 8400 feet (2560 m) above ground level.

Table 1. General information regarding the mid-altitude sounding rocket.

Criterion	Measurement
Length, L (mm)	2530
Diameter, D (mm)	137
Dry Weight of Rocket (grams)	20,874
Fuel Mass (grams)	3951
Engine Dry Weight (grams)	2472
Duty Payload Weight (grams)	4500
Total Take-off Weight (grams)	27,567
Take-off Thrust/Weight Ratio (T/W)	8.92
Ramp Ascent Speed (m/s)	28.3
Stability (for 0.3 Mach)	2.18
Peak Acceleration (g)	77.4
Top Speed (m/s)	219
Top Speed, M (Mach)	0.648
Apogee Altitude (m)	2561

summarizes the rocket’s physical specifications and predicted performance parameters.

Parameters such as the T/W at lift-off, ramp ascent speed, aerodynamic stability margin, peak acceleration, top speed, and apogee were obtained from OpenRocket simulations, based on the rocket’s actual geometry and propulsion data for the selected Aerotech M1850W motor. This motor configuration results in a top speed of 219 m/s, which corresponds to approximately Mach 0.648 under standard atmospheric conditions. These values served as key inputs for both the aerodynamic (CFD) and structural (FEA) analyses conducted in this study.

Figure 1 shows the design and configuration of the rocket as generated in OpenRocket software. It illustrates the main components of the mid-altitude sounding rocket, with key elements labeled, including the nose cone, drogue parachute, payload and payload parachute, recovery system, avionics compartment, center of gravity (CG), center of pressure (CP), engine compartment, fin root chord, fin height, and rocket diameter. Based on this initial configuration, SolidWorks was used to create a 3D model of the rocket’s structure.

The nose cone is a critical component of the rocket because its design significantly influences aerodynamic performance by minimizing drag and improving stability. In this study, three distinct nose cone designs were selected for analysis: conical, ogive, and ellipsoid [13,14,15]. All three nose cone designs were constructed with the same base diameter (137 mm) and axial length (300 mm) to ensure consistent slenderness ratios and fair aerodynamic comparison. The conical nose cone was defined by a straight-line profile forming a sharp vertex at the tip. The ogive shape was modeled using a tangent ogive curve, which blends smoothly into the body tube to reduce pressure drag. The elliptical nose cone was designed as a prolate ellipsoid generated by revolving a half-ellipse around the rocket’s longitudinal axis. These geometries were selected based on standard rocket design practices [14,15], providing a representative range of sharp to blunt profiles suitable for subsonic flight. In OpenRocket, the nose cone designs were assessed for basic aerodynamic parameters, such as drag coefficient and overall stability.

The fins also play a crucial role in stabilizing the rocket during flight. Three distinct fin shapes, including elliptical, trapezoidal, and tube form, were tested using OpenRocket software for initial results [16]. Following that, two of the best fin designs were modeled and analyzed using SolidWorks. These designs were chosen based on their contrasting characteristics in terms of aerodynamic performance and ease of integration into the rocket’s structure [17]. The fin configurations were evaluated for their ability to ensure stability, minimize drag, and control the center of pressure relative to the center of gravity. For the nose cone, fin, and body tube, lightweight composite materials were prioritized due to their superior strength-to-weight ratio and durability.

2.2. Materials and Geometric Modeling

The structural and aerodynamic assessment of a rocket nose cone intended for mid-altitude sounding rockets is the primary focus of the materials and geometric modeling used in this study. The selected material is Polylactic Acid (PLA), a thermoplastic polymer commonly used in 3D printing because of its mechanical properties, ease of fabrication. PLA, availability, low cost, and ease of processing, which make it highly suitable for rapid prototyping and student-led aerospace development projects, such as those carried out for TEKNOFEST competitions. It also offers acceptable mechanical strength for subsonic rocket structures under moderate loading conditions. Furthermore, Slavković et al. [18] demonstrated that PLA exhibits temperature-dependent mechanical degradation below its glass transition temperature, making it an ideal candidate for simulating and analyzing thermal deformation in subsonic flight conditions.

PLA is modeled as an isotropic material with key thermal properties, as summarized in

Table 2. Key thermal and mechanical properties of Polylactic Acid (PLA) [10,18].

Property	Value
Density, ρ (kg/m3)	900
Specific heat capacity, cp (J/kgK)	1200
Thermal conductivity, k (W/mK)	0.15
Young’s Modulus, E (MPa)	3000
Poisson’s Ratio, ν	0.45

[10,18]. These key material properties are essential to simulate the thermal and structural behaviour of the nose cone under the high-temperature conditions encountered during ascent. The simulations evaluated von Mises stress, strain, and displacement to assess the impact of stress deformation on structural performance, ensuring a comprehensive analysis.

2.3. Structural Deformation Analysis

Structural deformation analysis evaluated the rocket nose cone’s performance under thermomechanical loading conditions, with a focus on structural integrity and its implications for aerodynamic performance. SolidWorks Simulation was utilized for Finite Element Analysis (FEA), in which temperature and pressure distributions obtained from SolidWorks Flow Simulation were applied as spatially varying external loads. This constitutes a one-way fluid–structure interaction (FSI) approach, where aerodynamic and thermal loads from CFD are mapped onto the structural model to capture deformation effects without iterative coupling [19]. By adopting this sequential method, this study accounts for the influence of realistic in-flight conditions on the structural behaviour of the 3D-printed PLA nose cone.

Figure 2 illustrates the computational setup and boundary conditions used in the structural deformation analysis. External thermal and pressure loads were applied to the nose cone, rocket body, and fins, while the aft end of the rocket body was fixed in all degrees of freedom. These loads were mapped directly from the SolidWorks Flow Simulation results to more accurately represent conditions during high-speed ascent, capturing the non-uniform distribution of temperature and aerodynamic pressure across the rocket surface. The inner surface of the nose cone was assumed to be insulated, simulating thermal isolation from internal payload compartments. In the SolidWorks Simulation setup, the nose cone material was defined as PLA, while the rocket body and fins were modeled using fiberglass. PLA’s isotropic thermal and mechanical properties, as listed in Table 2, were incorporated in the FEA setup to ensure accurate thermomechanical response modeling.

In structural deformation analysis, von Mises stress, strain, and displacement were the primary evaluation metrics. A displacement exceeding the 0.15 mm threshold was deemed a failure criterion because it indicates potential aerodynamic and structural compromises.

2.4. CFD Simulation

Computational Fluid Dynamics (CFD) simulations using SolidWorks Flow Simulation were performed to evaluate the aerodynamic performance of the rocket under thermally induced deformation. A simplified one-way fluid–structure interaction (FSI) strategy was adopted, consisting of three main stages:

(i)

Stage 1: Initial flow simulation on the undeformed rocket to obtain external pressure and thermal loads;

(ii)

Stage 2: Structural deformation analysis using the CFD-derived pressure and temperature fields;

(iii)

Stage 3: Follow-up flow simulations on the thermally deformed geometries to assess the impact of the deformation on aerodynamics performance.

This integrated CFD–FEA setup established the basis for evaluating the aerodynamic effects of thermal deformation.

To accurately replicate in-flight conditions, a rectangular computational domain was constructed around the rocket geometry with dimensions scaled to the rocket length (L). The upstream boundary was placed 1L ahead of the nose cone tip, while the downstream boundary extended 4L behind the rocket. The vertical and lateral boundaries were each set at a distance of L from the rocket’s central axis to ensure sufficient clearance for capturing wake and boundary layer effects. The applied boundary conditions included a velocity inlet (219 m/s) at the front face, a pressure outlet (101,325 Pa) at the rear face, symmetry conditions at the top and bottom surfaces, and no-slip adiabatic walls on the rocket body. The full boundary condition and simulation settings are summarized in

Table 3. Boundary conditions and simulation settings for the CFD simulation.

Boundary Type/ Settings	Specification
Inlet Velocity	Uniform velocity, 219 m/s (based on max flight speed)
Far-field	Ambient pressure (101,325 Pa)
Pressure Outlet	101,325 Pa (atmospheric)
Wall	No-slip, adiabatic (at nose cone, rocket body, and fins)
Turbulence Model	k–ε (default in SolidWorks Flow Simulation)
Flow Type	External, steady-state
Fluid	Ideal gas
Initial conditions	Atmospheric pressure (101,325 Pa), ambient temperature (293.2 K)

, and the computational domain configuration is illustrated in Figure 3.

As shown in Figure 4, the computational domain was discretized using a structured Cartesian mesh in SolidWorks Flow Simulation. The mesh is created based on the setting listed in

Table 4. Mesh configuration parameters.

Parameter	Value/Setting
Mesh type	Cartesian (hexahedral structured grid)
Refinement method	Manual local refinement
Global mesh	Automatic mesh setting (initial mesh level = 3) with contracting ratio factor of 3
Local refinement level	Four times finer than global mesh
Refined zones	Nose cone tip, fin edges, rocket base
Near-wall treatment	Wall function approach (k–ε model)

. The global mesh level was initially set to 3 and later varied to generate coarse, medium, and fine meshes for mesh independence analysis. The global mesh contracting factor was fixed at 3, and a local refinement level of 4 was applied to critical regions, including the nose cone tip, fin edges, and rocket base. These settings ensured sufficient resolution in areas with steep pressure and velocity gradients. The zoomed insets in Figure 4 highlight the mesh density in refined zones. Although SolidWorks Flow Simulation does not support structured boundary layer meshes, it applies a wall function approach under the k–ε turbulence model to estimate near-wall flow behaviour [20]. Mesh independence was verified by varying the global mesh level while maintaining the contracting factor and local refinement constant, ensuring that the numerical results were not affected by discretization errors.

2.5. Mesh Independence Study

A mesh independence study was conducted to ensure the reliability and numerical stability of the CFD simulations. Three levels of global mesh resolution were evaluated: coarse, medium, and fine, corresponding to the total cell counts of 236,433, 684,232, and 1,329,124, respectively. These cell counts were obtained by varying the global mesh level from 3 to 5, while keeping the global mesh contraction factor and local refinement level fixed at 3 and 4, respectively. Local refinement was applied in critical regions, including the nose cone tip, fin edges, and rocket base, to ensure accurate resolution of boundary layer behaviour and wake structures.

The percentage difference in average outlet velocity was used as the primary metric to assess mesh sensitivity. A change of less than 5% between successive mesh levels is generally considered acceptable for mesh convergence [21]. In this study, the difference between the medium and fine mesh results was less than 1%, confirming mesh independence. As shown in

Table 5. Mesh independence study results.

Mesh Level	Cell Count	Global Mesh Level	Outlet Velocity
			Min	% Diff.	Max	% Diff.
Coarse	236,433	3	196.807	-	219.027	-
Medium	684,232	4	197.568	0.39	219.024	0.001
Fine	1,329,124	5	198.387	0.41	219.018	0.003

, the results stabilized as the mesh was refined, indicating that further mesh densification would not significantly impact accuracy. Given its balance between computational efficiency and accuracy, the medium mesh was selected for subsequent simulations.

Since SolidWorks Flow Simulation employs a Cartesian mesh and wall function-based near-wall treatment, traditional mesh quality metrics, such as skewness and orthogonality, are not computed. However, the suitability of the mesh for resolving boundary layer effects was evaluated using y⁺ values, as shown in the contour plot in Figure 5. The y⁺ distribution over the rocket surface ranges from approximately 30 to over 300, with the majority of the surface falling between 50 and 200. These values fall within the acceptable range for wall function applicability (typically y⁺ ≈ 30–300) [22,23], ensuring that the turbulent boundary layer is reasonably well captured. Local peaks near the nose cone and fin tips indicate areas of higher shear and steep velocity gradients, which are appropriately refined through manual local mesh control. This supports the validity of the selected mesh configuration for accurate aerodynamic predictions.

2.6. Assumptions and Limitations

The CFD analysis conducted in this study was subjected to several limitations and assumptions, which are outlined below to provide a clearer understanding of the research scope and constraints.

• Steady-State Thermal Conditions: The analysis assumed steady-state heat transfer across the nose cone surface, which did not fully capture transient thermal variations during ascent.
• Material Homogeneity: PLA material properties were assumed isotropic and homogeneous, excluding variations from 3D printing inconsistencies or defects. All simulations use standardized 3D printing parameters to ensure consistency.
• Boundary Condition Simplifications: External environmental factors, such as crosswinds or atmospheric turbulence, were excluded to focus solely on idealized conditions.
• Surface Smoothness: The nose cone surface was assumed to be perfectly smooth, neglecting surface roughness effects that could influence flow dynamics.
• Flight Envelope: This study presumed that the rocket operated within its designed flight parameters without unexpected deviations or catastrophic failures.
• Flow Simulation Limitations: SolidWorks Flow Simulation did not model highly complex chemical reactions or real gas effects, which might have occurred under extreme conditions. The air was considered an ideal gas.
• Validation Scope: Validation was based on grid independence tests but did not include real-world flight testing.

3. Results and Discussions

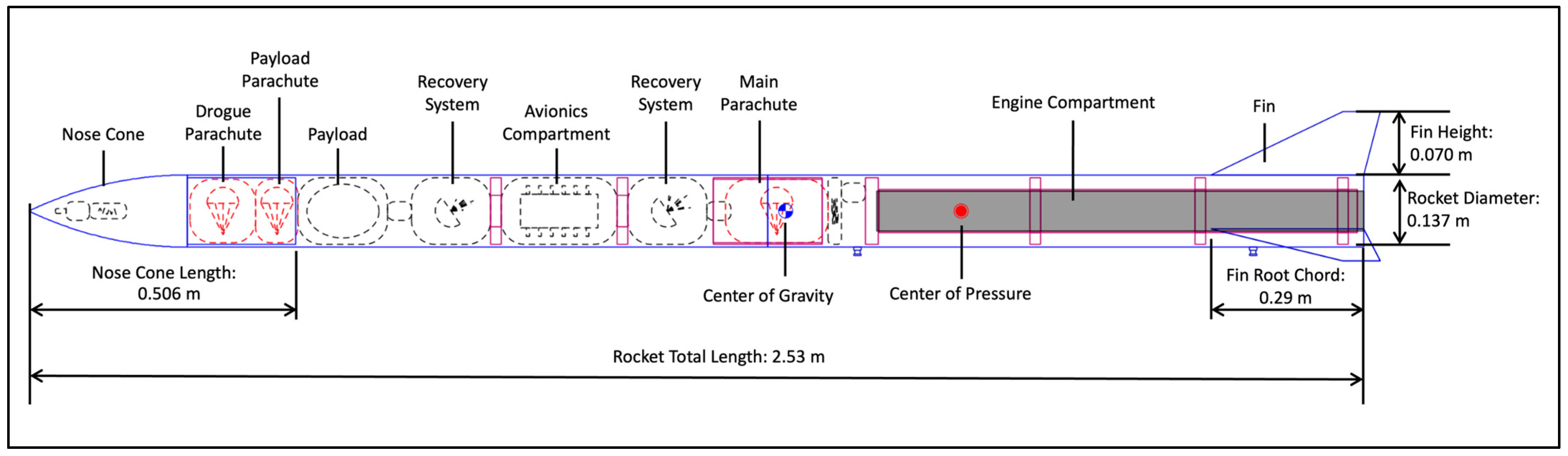
3.1. Aerodynamics Performance and Stability Analysis

As mentioned in the previous section, each fin configuration was paired with three different nose cones, and their aerodynamic performance was evaluated using OpenRocket. The simulation results, listed in

Table 6. Aerodynamics characteristics comparison.

Fin Type	Nose Cone Type	Apogee (m)	Drag Coefficient		Stability (CP and CG LOCATION)
					At Engine Burnout		At Apogee
			At Max Velocity	At Apogee	CP	CG	CP	CG
Trapezoidal	Conical	2496	0.523	0.465	179.516	133.130	176.062	133.130
	Ogive	2639	0.480	0.435	178.000	132.500	202.000	132.500
	Ellipsoid	2508	0.504	0.435	176.472	132.057	173.151	132.057
Elliptical	Conical	2433	0.580	0.519	178.357	132.463	176.877	132.463
	Ogive	2470	0.539	0.488	176.550	131.824	172.848	131.824
	Ellipsoid	2444	0.562	0.490	175.374	131.390	174.600	131.390
Tube form	Conical	1928	1.002	0.926	200.885	135.231	206.835	135.231
	Ogive	1946	0.964	0.895	200.260	134.594	205.981	134.594
	Ellipsoid	1930	0.982	0.896	199.950	134.162	205.535	134.162

, were analyzed based on key aerodynamic characteristics, including apogee, drag coefficient, and stability margin. Among the tested configurations, the trapezoidal fin design paired with the ogive nose cone exhibited the most favourable aerodynamic performance in terms of drag reduction. This allowed the rocket to achieve the highest apogee (2639 m) among the tested configurations.

In rocketry, stability is typically ensured when the center of pressure (CP) is behind the center of gravity (CG) by a sufficient margin (larger separation, often measured in calibers). A larger stability margin, defined as the distance between the CG and CP, usually means the rocket will naturally self-correct more strongly (more stable), whereas a very small separation approaches neutral stability. In this study, the apex of the nose is defined as the origin, with positive distance extending toward the tail. Based on this definition, Table 6 shows that the CP values are larger than the CG values; hence, CP is behind the CG for all configurations, indicating that all designs are statically stable.

Moreover, the stability margin was relatively large for the trapezoidal fin design paired with the ogive nose cone (CP = 202.000 cm, CG = 132.500 cm at apogee). While this larger CP–CG distance suggests a strong restoring moment and greater static stability, it may also lead to over-stability, which can cause the rocket to resist necessary course corrections.

In contrast, the conical and ellipsoid nose cone configurations exhibited higher drag coefficients at apogee, resulting in greater aerodynamic resistance. Both nose cone designs experienced higher pressure drag because of their blunt shape, which limited their maximum altitude compared with the ogive nose cone. However, the ellipsoid nose cone, when analyzed for stability margin, had the smallest CP–CG distance during engine burnout and at apogee, indicating a lower static stability margin. This could make the rocket more responsive to minor disturbances but also more susceptible to instability if not properly controlled.

The elliptical fin configuration exhibited lower aerodynamic efficiency than the trapezoidal fin design for all nose cone configurations, resulting in a lower apogee because of higher drag at maximum velocity and apogee. However, the ogive nose cone with elliptical fins showed a moderate stability margin, achieving a CP of 172.84 cm and a CG of 131.824 cm at apogee. This smaller CP–CG separation resulted in a lower static stability margin, making the configuration more manoeuvrable but potentially more prone to instability under external disturbances.

On the other hand, the tube form fin design consistently underperformed compared with the trapezoidal and elliptical fin designs, regardless of the nose cone used in the simulations. Even though the ogive nose cone resulted in the highest apogee and the lowest drag, the CP–CG distance or static margin for all nose cone designs in the tube–fin configuration was larger, leading to higher static stability but reduced manoeuvrability.

3.2. Structural Behaviour of Nose Cone Under Thermal Stress Load

The structural response of the ogive and ellipsoid nose cones under applied thermal stress loads was evaluated using three crucial parameters: resultant or total displacement (URES), equivalent strain (ESTRN), and von Mises stress.

Table 7. Structural response parameters.

Parameter	Ogive		Ellipsoid
	Min	Max	Min	Max
URES (mm)	0	7.25 × 10−1	0	7.44 × 10−1
Equivalent Strain	0	2.46 × 10−3	0	2.81 × 10−3
von Mises stress	5.76 × 101	7.54 × 107	3.45 × 102	7.45 × 107

summarizes the key crucial parameters arising from the structural deformation simulations, including maximum displacement, equivalent strain, and von Mises stress.

Both the ogive and ellipsoid nose cone geometries exhibit comparable levels of maximum displacement—0.7249 mm and 0.7443 mm, respectively—suggesting that both are susceptible to deformation at the nose tip under thermal loads. However, the ellipsoid nose cone shows a slightly higher peak strain and a wider region of displacement, indicating a more distributed deformation pattern. The ogive, in contrast, exhibits more concentrated strain regions, which may result in higher local stresses but potentially less impact on overall shape retention.

Meanwhile, Figure 6, Figure 7, and Figure 8 show the total displacement, equivalent strain, and von Mises stress distributions, respectively, for both nose cone configurations. As the deformation values are small relative to the overall rocket size, a deformation scale factor of 100 was applied in the visualizations to emphasize the effects of thermal stress and displacement. In Figure 6, the red regions denote maximum displacement, concentrated near the nose cone apex, while the blue regions indicate minimal displacement, primarily at the rocket body because of its fibreglass material. The apex deformation is a result of thermal expansion and stress concentration in this slender region. Quantitatively, both nose cones exhibit similar maximum total displacement values. However, the ellipsoid shows a wider region of high maximum displacement compared with the ogive, suggesting comparable deformation levels, but with marginally higher susceptibility to the ellipsoid design because of its broader surface curvature.

Figure 7 shows the distribution of equivalent strain (ESTRN). For both geometries, strain is predominantly concentrated at the junction between the nose cone and cylindrical body, with values gradually tapering off toward the aft section. The ogive exhibits a more localized and slightly sharper strain concentration, whereas the ellipsoid displays a broader strain distribution along the same region. This indicates that the ogive nose cone is more prone to localized deformation, while the ellipsoid shape allows a more even dissipation of strain energy.

Figure 7 illustrates the von Mises stress distribution, highlighting critical areas where yielding may occur. Both nose cones experience maximum von Mises stress at the nose–body interface, reaching up to 7.54 × 10⁷ N/m². The ogive exhibits a more sharply defined stress zone, whereas the ellipsoid presents a smoother gradient. This suggests that, although both geometries reach similar peak stress levels, the ellipsoid shape better distributes the stress, potentially offering enhanced resistance to localized failure.

Table 8. Structural analysis trade-off table.

Parameter	Ogive Nose	Ellipsoid Nose	Trade-Off Analysis
Maximum URES (mm)	0.7249	0.7443	Displacement concentrated at the nose tip in both cases
Maximum ESTRN (×10−3)	1.0746	1.1123	Slightly higher strain in ellipsoid indicates more distributed deformation
Maximum von Mises Stress (×107 N/m2)	7.5383	7.5379	Similar stress magnitudes; ogive stress more localized
Displacement Concentration Region	Nose tip	Nose tip	Same deformation location
Stress Distribution Pattern	Localized	Broader	Ellipsoid geometry distributes stress more evenly

provides a comparative assessment of structural behaviour between the ogive and ellipsoid nose cones under identical thermal loading conditions. The maximum displacement for both is similar and exceeds 0.7 mm, indicating that thermal expansion significantly affects the nose tip region regardless of geometry. However, the ellipsoid nose cone shows more evenly distributed strain and stress contours, reducing the likelihood of localized failure and improving fatigue resistance. The von Mises stress values for both profiles reach up to 7.54 × 10⁷ N/m², but in the ogive case, this stress is more localized around the nose–body junction. The ellipsoid profile, with its smoother curvature, better distributes stress, which could be advantageous in repetitive thermal cycling. On the other hand, the sharper ogive geometry exhibits slightly better shape retention, contributing to higher aerodynamic stability in precision flight applications.

3.3. Impact of Nose Cone Deformation on Aerodynamics Performance

For the undeformed (ideal) rocket configurations, the highest surface pressure was recorded at the stagnation point located at the tip of the nose cone. As shown in Figure 9, this region experienced direct impingement of airflow, leading to maximum pressure accumulation. The ogive nose cone recorded a peak pressure of approximately 119,375.95 Pa, whereas the ellipsoid nose cone exhibited a higher stagnation pressure of 134,190.13 Pa (

Table 9. Drag and maximum surface pressure.

Parameter	Ogive N.C.		Ellipsoid N.C.
	Ideal	Deformed	Ideal	Deformed
Drag (Average) [N]	173.532	174.951	181.352	172.933
Drag Coefficient, Cd	0.401	0.404	0.419	0.399
Maximum Surface Pressure [Pa]	119,375.95	115,876.43	134,190.13	111,999.50

). This difference reflects the blunter geometry of the ellipsoid profile, which results in a broader stagnation zone and consequently greater form drag.

Correspondingly, the undeformed ellipsoid nose cone generated the highest drag force of 181.352 N, compared with 173.532 N for the undeformed ogive configuration. This difference is also evident in the calculated drag coefficients, with values of 0.419 for the ellipsoid and 0.401 for the ogive, consistent in magnitude and trend with the estimates obtained using OpenRocket (see Table 6).

Figure 9 illustrates the pressure distribution around the ideal (undeformed) rocket configurations with ogive and ellipsoid nose cones. For the ogive profile (see Figure 9a), the pressure peaks at the stagnation point with a value of approximately 111,000 Pa, then decreases smoothly along the nose to the teal zone near the nose–body intersection (98,000 Pa). A slight pressure recovery occurs along the midsection (100,000 Pa), before the pressure drops again to about 95,000 Pa near the trailing edges of the fins, marking the onset of the wake. This smooth gradient, with only minor localized increases at the fin leading edges, indicates minimal flow separation and a well-controlled boundary layer. The confined wake and gradual pressure transitions contribute to the aerodynamic efficiency of the ogive configuration, with relatively low drag and stable flow.

In contrast, the ellipsoid nose cone (see Figure 9b) exhibits a broader high-pressure region at the nose tip, reaching up to 134,190 Pa because of its blunt geometry. Similar to the ogive profile, the pressure then decreases downstream to around 98,000 Pa near the nose–body intersection, followed by a slight pressure recovery along the midsection to approximately 100,000 Pa. The wake region, identified by pressure values of about 95,000 Pa near the fin trailing edges, also resembles that of the ogive configuration in shape and extent. However, despite these similarities in flow behaviour, the ellipsoid nose cone generates higher form drag and exhibits less favourable pressure gradients overall, primarily because of its significantly higher stagnation pressure and larger frontal area. These characteristics confirm that the ellipsoid profile is aerodynamically less efficient than the ogive configuration under subsonic flight conditions.

Figure 10a shows the pressure distribution for the deformed ogive nose cone. The stagnation point remains clearly defined at the tip, with a peak pressure of approximately 111,000 Pa, slightly reduced from the undeformed case (119,375.95 Pa, Table 9) because of minor surface distortions. The deformation introduces geometric asymmetry, causing the high-pressure region to shift slightly off-axis. This results in an uneven pressure field that may induce lateral aerodynamic forces, potentially affecting flight stability. Pressure then decreases steadily along the body, reaching about 98,000 Pa near the nose–body intersection, followed by a modest recovery along the midsection. Near the rocket base, pressure drops again to approximately 95,000 Pa at the trailing edges of the fins, indicating the onset of a confined wake. Compared with the undeformed case, the deformed ogive shows a minimal degradation in aerodynamic performance. The drag force increases slightly from 173.532 N to 174.951 N, and the drag coefficient rises marginally from 0.401 to 0.404 in Table 9, suggesting the overall aerodynamic efficiency is largely preserved.

In contrast, the deformed ellipsoid nose cone, shown in Figure 10b, exhibits more substantial aerodynamic penalties. Although the stagnation pressure drops from 134,190.13 Pa (undeformed) to about 111,000 Pa, the broader and blunter shape causes the high-pressure region to remain more expansive. Pressure decreases sharply to around 98,000 Pa near the shoulder, followed by a modest recovery, and ultimately falls to about 95,000 Pa at the fin trailing edges. While the drag force decreases from 181.352 N to 172.933 N, the drag coefficient also drops from 0.419 to 0.399 (Table 9). However, this reduction does not indicate improved aerodynamic efficiency. Rather, it reflects the redistribution of flow energy into turbulent motion and enlarged wake structures. These outcomes are consistent with blunt-body aerodynamic theory, where flow separation occurs earlier and more severely, forming larger turbulent wakes and increasing pressure drag [24,25]. Deformation worsens these effects by introducing asymmetry and disturbing streamline attachment, leading to greater instability and energy loss. Similar conclusions have been drawn in studies of nose bluntness in hypersonic and re-entry configurations, which consistently show reduced aerodynamic performance for blunter shapes under compressible and viscous flow conditions [24].

Additionally, a line graph was generated to compare the surface pressure distribution along the rocket body for different nose cone configurations. Figure 11 presents the pressure coefficient (Cp) distributions along the surface of the rocket from aft to nose for both ideal and deformed configurations, comparing the ogive (Figure 11a) and ellipsoid (Figure 11b) nose cones. The Cp profiles reveal the effects of thermally induced geometric deformation on aerodynamic pressure behaviour.

In the ogive configuration, both the ideal and deformed cases follow a similar trend. Cp values are nearly constant (~0) along the cylindrical body, followed by a sharp increase approaching the nose. At the nose tip, the ideal ogive exhibits a maximum Cp close to 0.6, characteristic of a mild stagnation point pressure. The deformed case, while closely matching this profile, shows a slight reduction in peak Cp, indicating the redistribution of surface pressure due to geometric asymmetry. This aligns with the pressure field visualization shown in Figure 10a and the numerical results reported in Table 9, where drag and maximum pressure increase only marginally for the deformed ogive.

The ellipsoid configuration (Figure 11b) shows more pronounced effects of deformation. The ideal ellipsoid has a higher peak Cp, reaching values above 1.1, reflecting a broader and more intense stagnation zone. In the deformed case, the Cp distribution is visibly dampened, causing the peak Cp to drop, and the curve becomes smoother and flatter around the nose. This softening indicates a wider pressure plateau, consistent with the larger stagnation area and pressure drag observed in Figure 9b and Figure 10b. While the average drag decreases, as shown in Table 9, the pressure coefficient data reinforce that this is due to redistributed and dissipated aerodynamic forces, not improved aerodynamic efficiency. The broader wake and earlier separation associated with this flatter Cp profile confirm increased turbulence and energy loss, in line with blunt-body flow behaviour [25,26].

Overall, the Cp plots in Figure 11 quantitatively validate the flow behaviour discussed earlier: the ogive nose cone maintains its aerodynamic sharpness under deformation, while the ellipsoid nose cone exhibits stronger performance degradation because of its inherently blunt and deformation-sensitive profile.

Figure 12 presents the velocity magnitude contours and streamlines around the deformed ogive and ellipsoid nose cone rockets. Both configurations show a comparable freestream velocity field around the rocket body and a visible stagnation zone at the nose tip. The velocity drops sharply in the wake region behind the rocket base, with the lowest velocity values (~13 m/s) concentrated in the base and fin areas for both geometries. The streamlines remain aligned with the flow direction and do not exhibit significant divergence or recirculation zones.

The similarity in streamline behaviour and wake structure suggests that, under the simulated subsonic conditions, nose cone deformation alone does not drastically alter the external velocity field in a way that is easily distinguishable in streamline visualizations. However, when considered alongside pressure distribution (Figure 9 and Figure 10) and pressure coefficient trends (Figure 11), subtle differences in surface pressure behaviour and stagnation region intensity still support the conclusion that the ogive nose cone maintains better aerodynamic performance.

3.4. Fin Analysis

In this analysis, only two fins were focused on, trapezoidal and elliptical, because only these fins gave the best performance aerodynamically when studied using OpenRocket software, as mentioned in Section 3.1. The analysis focuses on pressure distribution around each fin, obtained via CFD simulations, as illustrated in Figure 13 and Figure 14.

Figure 13 illustrates the pressure distribution around the trapezoidal fin from three different perspectives: rear (a), side (b), and surface (c). In the rear view, distinct high-pressure zones are visible near the fin tips, indicating the presence of localized aerodynamic loading and tip vortex formation. The side view highlights a concentrated stagnation region at the leading edge, where the oncoming flow decelerates sharply. This is followed by a steep pressure gradient along the fin surface, suggesting early flow separation. On the fin surface, pressure is highest at the leading edge and decreases toward the trailing edge, resulting in asymmetrical loading that may contribute to side forces and rolling moments. Despite this, the trapezoidal fin maintains good pressure anchoring and flow stability, as seen from the contour transitions.

In comparison, Figure 14 shows the pressure distribution for the elliptical fin. Compared with the trapezoidal fin, the rear view reveals a more symmetrical and smoother pressure field with less tip-induced pressure distortion. The side view depicts a broader, more evenly distributed stagnation region at the leading edge, reflecting improved flow attachment. Surface contours show a gradual and continuous pressure gradient along the chord, with minimal abrupt changes. This behaviour is consistent with the aerodynamic characteristics of elliptical fins, which typically promote smoother boundary layer development and reduced flow separation across the surface.

However, when comparing the aerodynamic performance quantitatively, the trapezoidal fin demonstrates a lower drag. CFD results in

Table 10. Comparison of drag forces and surface pressure for trapezoidal and elliptical fins.

Fin Type	Drag [N]	Max. Pressure [Pa]	Min. Pressure [Pa]
Trapezoidal	33.120	106,588.66	85,093.86
Elliptical	41.412	137,408.89	87,389.15

show that the trapezoidal fin generates an average drag force of 33.120 N, while the elliptical fin produces a higher drag force of 41.412 N, a difference of over 25%. This is supported by OpenRocket simulation results (see Table 6), where the trapezoidal configuration also recorded lower drag coefficients, 0.480 versus 0.539 for the elliptical fin when paired with an ogive nose cone. The higher drag observed in the elliptical fin is likely due to its larger wetted surface area and increased frontal curvature, which contribute to greater form drag despite its favorable surface pressure characteristics.

In summary, although CFD visualization indicates that the elliptical fin provides a smoother pressure distribution and potentially better directional stability, the trapezoidal fin offers superior aerodynamic efficiency by generating lower drag forces and drag coefficients. This reinforces the importance of integrating both visual flow diagnostics and quantitative simulation data when evaluating fin designs for sounding rocket applications.

4. Conclusions

This study presents an integrated aerodynamic and structural analysis of mid-altitude sounding rockets, focusing on the effects of nose cone and fin geometry, as well as thermally induced deformation. Using a one-way fluid–structure interaction (FSI) approach, the work combines CFD and FEA simulations to evaluate aerodynamic efficiency and structural resilience under high-speed flight conditions.

Among the nine tested configurations, the ogive nose cone with trapezoidal fins demonstrated the best aerodynamic performance, achieving the highest simulated apogee of 2639 m and the lowest drag coefficient (0.401) in the ideal, undeformed geometry. In contrast, blunter geometries, such as the ellipsoid and conical nose cones, produced higher pressure drag and broader stagnation zones, leading to reduced aerodynamic efficiency. Structural deformation analyses under spatially varying thermal and pressure loads revealed that PLA-based nose cones experienced tip displacements exceeding 0.7 mm, with the ellipsoid shape exhibiting wider stress and strain distributions. While this suggests improved load dispersion, it also resulted in greater shape distortion, particularly in the ellipsoid design.

The pressure coefficient distributions and the drag comparisons in Table 8 confirm that thermal deformation leads to asymmetric pressure fields, expanded wake regions, and minor increases in drag. Despite similar maximum displacements, the ogive nose cone retained more favourable pressure gradients and lower flow separation, highlighting its robustness under thermal–mechanical loading. The ellipsoid nose cone, on the other hand, behaved more similarly to a bluff body post-deformation, consistent with reduced aerodynamic sharpness and increased energy losses. Regarding fin configurations, the elliptical fin produced smoother pressure contours and better flow attachment along its surface, which may reduce rolling moments. However, the trapezoidal fin consistently resulted in higher apogees, likely because of its smaller projected area and improved aerodynamic alignment with the nose cone.

This study highlights the importance of geometry selection and material performance in mid-altitude rocket design. The combined CFD–FEA simulation framework effectively captures the thermal–structural–aerodynamic interplay, offering critical insight for the design of thermally resilient, aerodynamically stable rocket structures. For future work, a study should explore the use of alternative heat-resistant and thermally stable materials, such as carbon fiber-reinforced PLA or polycarbonate, to minimize deformation under thermal loads. Real-world validation of simulation results through subscale or full-scale experimental launches is also crucial to confirm the computational findings. In addition, extending the study to supersonic flow regimes and incorporating transient thermal–structural coupling effects would provide a more comprehensive understanding of rocket performance.