A New Approach for Solving Nonlinear Oscillations with an m-Degree Odd-Power Polynomial Restoring Force
Abstract
1. Introduction
2. Deriving a New Equation
3. Comparison with Numerical Results for
4. Physical Systems That Demonstrate the Applicability of the Proposed Method
4.1. The Rotating Pendulum
4.2. Electrical Oscillations
5. The 9th Degree Polynomial Case
6. Discussion and Further Considerations
- A simple equation (Equation (11)) was derived that can be used to approximate the angular frequency of any undamped nonlinear oscillation with an m-degree odd-power polynomial restoring force.
- The proposed equation can be applied regardless of the oscillation’s amplitude, as demonstrated in Section 3.
- It is valid for both ’hardening’ and ’softening’ systems, as shown in the example of the rotating pendulum (Section 4.1).
- It can be used for real industrial applications (e.g., electrical oscillations in Section 4.2).
- It provides significantly more accurate results for large amplitudes compared to classic equations in the literature (e.g., Equation (44)).
- It is a valuable method for solving many classic systems, such as the simple pendulum, the capillary oscillator, and the oscillator with cubic and harmonic restoring forces, among others, since in the aforementioned cases, the restoring force can be written in the form of an m-degree odd-power polynomial using a Maclaurin series expansion.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Abouelregal, A.E.; Mohammad-Sedighi, H.; Faghidian, S.A.; Shirazi, A.H. Temperature-dependent physical characteristics of the rotating nonlocal nanobeams subject to a varying heat source and a dynamic load. Facta Univ. Ser. Mech. 2021, 19, 633–656. [Google Scholar] [CrossRef]
- Sedighi, H.M.; Shirazi, K.H. Dynamic pull-in instability of double-sided actuated nano-torsional switches. Acta Mech. Solida Sin. 2015, 28, 91–101. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Two modifications of the homotopy perturbation method for nonlinear oscillators. J. Appl. Comput. Mech. 2020, 6, 1420–1425. [Google Scholar]
- Anjum, N.; He, J.H. Homotopy perturbation method for N/MEMS oscillators. Math. Meth. Appl. Sci. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Higher-order homotopy perturbation method for conservative nonlinear oscillators generally and microelectromechanical systems’ oscillators particularly. Int. J. Mod. Phys. 2020, 34, 2050313. [Google Scholar] [CrossRef]
- Qie, N.; Houa, W.F.; He, J.H. The fastest insight into the large amplitude vibration of a string. Rep. Mech. Eng. 2021, 2, 1–5. [Google Scholar] [CrossRef]
- Hosen, M.A.; Chowdhury, M.S.H. A new reliable analytical solution for strongly nonlinear oscillator with cubic and harmonic restoring force. Results Phys. 2015, 5, 111–114. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Malamou, A. Exploring oscillations with a nonlinear restoring force. Eur. J. Phys. 2022, 43, 015006. [Google Scholar] [CrossRef]
- Xu, L. Application of He’s parameter-expansion method to an oscillation of a mass attached to a stretched elastic wire. Phys. Lett. A 2007, 368, 259–262. [Google Scholar] [CrossRef]
- Li, S.; Niu, J.; Li, X. Primary resonance of fractional-order Duffing–van der Pol oscillator by harmonic balance method. Chin. Phys. B 2018, 27, 120502. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Mazi, I.; Malamou, A. A Note on a Simple Equation for Solving Nonlinear Undamped Oscillations. J. Vib. Eng. Technol. 2024, 12, 8235–8248. [Google Scholar]
- Ju, P.; Xue, X. Global residue harmonic balance method to periodic solutions of a class of strongly nonlinear oscillators. Appl. Math. Model. 2014, 38, 6144–6152. [Google Scholar]
- Wu, B.; Liu, W.; Chen, X.; Lim, C.W. Asymptotic analysis and accurate approximate solutions for strongly nonlinear conservative symmetric oscillators. Appl. Math. Model. 2017, 49, 243–254. [Google Scholar]
- He, J.H.; Yang, Q.; He, C.H.; Khan, Y. A simple frequency formulation for the tangent oscillator. Axioms 2021, 10, 320. [Google Scholar] [CrossRef]
- Tian, Y. Frequency formula for a class of fractal vibration system. Rep. Mech. Eng. 2022, 3, 55–61. [Google Scholar]
- Mickens, R.E. A generalization of the method of harmonic balance. J. Sound Vib. 1986, 111, 515–518. [Google Scholar]
- Mickens, R.E. Truly Nonlinear Oscillations; World Scientific Publishing: Singapore, 2010. [Google Scholar]
- He, J.H.; Wu, X.H. Variational iteration method: New development and applications. Comput. Math. Appl. 2007, 54, 881–894. [Google Scholar]
- Wu, H.G.; Hu, Y. On variational iteration method for fractional calculus. Therm. Sci. 2017, 21, 1707–1712. [Google Scholar]
- Liao, S.J.; Cheung, A.T. Application of homotopy analysis method in nonlinear oscillations. ASME J. Appl. Mech. 1998, 65, 914–922. [Google Scholar]
- Zhang, G.Q.; Wu, Z.Q. Homotopy analysis method for approximations of Duffing oscillator with dual frequency excitations. Chaos Soliton Fract. 2019, 127, 342–353. [Google Scholar]
- Wu, Y.; He, J.H. Homotopy perturbation method for nonlinear oscillators with coordinate-dependent mass. Results Phys. 2018, 10, 270–271. [Google Scholar]
- He, J.H.; El-Dib, Y.O.; Mady, A.A. Homotopy perturbation method for the fractal Toda oscillator. Fractal Fract. 2021, 5, 93. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H.; Ain, Q.T.; Tian, D. Li–He’s modified homotopy perturbation method for doubly-clamped electrically actuated microbeams-based microelectromechanical system. Facta Univ. Ser. Mech. 2021, 19, 601–612. [Google Scholar]
- He, J.H.; El-Dib, Y.O. The enhanced homotopy perturbation method for axial vibration of strings. Facta Univ. Ser. Mech. 2021, 19, 735–750. [Google Scholar]
- Belendez, A.; Hernandez, A.; Belendez, T. Asymptotic representation of the period for the nonlinear oscillator. J. Sound Vib. 2007, 299, 403–408. [Google Scholar]
- Cveticanin, L.; Kovacic, I.; Rakaric, Z. Asymptotic methods for vibrations of the pure non-integer order oscillator. Comput. Math. Appl. 2010, 60, 2616–2628. [Google Scholar]
- Molla, M.H.U.; Alam, M.S. Higher accuracy analytical approximations to nonlinear oscillators with discontinuity by energy balance method. Results Phys. 2017, 7, 2104–2110. [Google Scholar]
- Ebaid, A.E. Approximate periodic solutions for the non-linear relativistic harmonic oscillator via differential transformation method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1921–1927. [Google Scholar]
- Wang, S.Q.; He, J.H. Nonlinear oscillator with discontinuity by parameter expansion method. Chaos Soliton Fract. 2008, 35, 688–691. [Google Scholar]
- Sedighi, H.M.; Shirazi, K.H.; Noghrehabadi, A.R.; Yildirim, A.H.M.E.T. Asymptotic investigation of buckled beam nonlinear vibration. Iran. J. Sci. Technol. Trans. Mech. Eng. 2012, 36, 107–116. [Google Scholar]
- He, J.H.; Anjum, N.; Skrzypacz, P. A variational principle for a nonlinear oscillator arising in the microelectromechanical system. J. Appl. Comput. Mech. 2021, 7, 78–83. [Google Scholar]
- He, J.H.; Houa, W.F.; Qie, N.; Gepreel, K.A.; Shirazi, A.H.; Mohammad-Sedighi, H. Hamiltonian-based frequency-amplitude formulation for nonlinear oscillators. Facta Univ. Ser. Mech. 2021, 19, 199–208. [Google Scholar] [CrossRef]
- Hosen, M.A.; Ismail, G.M.; Yildirim, A.; Kamal, M.A.S. A modified energy balance method to obtain higher-order approximations to the oscillators with cubic and harmonic restoring force. J. Appl. Comput. Mech. 2020, 6, 320–331. [Google Scholar]
- El-Dib, Y.O.; Matoog, R.T. The rank upgrading technique for a harmonic restoring force of nonlinear oscillators. J. Appl. Comput. Mech. 2021, 7, 782–789. [Google Scholar]
- Kontomaris, S.V.; Mazi, I.; Chliveros, G.; Malamou, A. Generic numerical and analytical methods for solving nonlinear oscillators. Phys. Scr. 2024, 99, 025231. [Google Scholar] [CrossRef]
- Lu, J. Global residue harmonic balance method for strongly nonlinear oscillator with cubic and harmonic restoring force. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1402–1410. [Google Scholar] [CrossRef]
- Big-Alabo, A. Approximate periodic solution for the large-amplitude oscillations of a simple pendulum. Int. J. Mech. Eng. Educ. 2020, 48, 335–350. [Google Scholar] [CrossRef]
- He, J.H. The simplest approach to nonlinear oscillators. Results Phys. 2019, 15, 102546. [Google Scholar] [CrossRef]
- Chen, B.; Lu, J.; Xia, Z. Numerical investigation of the fractal capillary oscillator. J. Low Freq. Noise Vib. Act. Control 2023, 42, 579–588. [Google Scholar] [CrossRef]
- Jin, X.; Liu, M.; Pan, F.; Li, Y.; Fan, J. Low frequency of a deforming capillary vibration, part 1: Mathematical model. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1676–1680. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Chliveros, G.; Malamou, A. Approximate Solutions for Undamped Nonlinear Oscillations Using He’s Formulation. J 2023, 6, 140–151. [Google Scholar] [CrossRef]
- Kauderer, H. Nichtlineare Mechanik; Springer: Berlin/Göttingen/Heidelberg, Germany, 1958. [Google Scholar]
- Cveticanin, L. Oscillator with Fractional Order Restoring Force. J. Sound Vib. 2009, 320, 1064–1077. [Google Scholar] [CrossRef]
- He, J.-H.; Amer, T.S.; Elnaggar, S.; Galal, A.A. Periodic property and instability of a rotating pendulum system. Axioms 2021, 10, 191. [Google Scholar] [CrossRef]
- Ismail, G.M.; El-Moshneb, M.M.; Zayed, M. Analytical technique for solving strongly nonlinear oscillator differential equations. Alex. Eng. J. 2023, 74, 547–557. [Google Scholar] [CrossRef]
- Srisoontorn, S.; Charoenmee, A.; Panikhom, S.; Janda, T.; Fungdetch, S.; Patimaprakorn, K.; Jantakun, A. Reconfigurable current-mode differentiator and integrator based on current conveyor transconductance amplifiers. Int. J. Electr. Comput. Eng. 2022, 12, 208–218. [Google Scholar] [CrossRef]
- Alimisis, V.; Gennis, G.; Gourdouparis, M.; Dimas, C.; Sotiriadis, P.P. A low-power analog integrated implementation of the support vector machine algorithm with on-chip learning tested on a bearing fault application. Sensors 2023, 23, 3978. [Google Scholar] [CrossRef]
- Gilbert, B. Translinear circuits: An historical overview. Analog Integr. Circuits Signal Process. 1996, 9, 95–118. [Google Scholar] [CrossRef]
- Al-Tamimi, K.M.; Al-Absi, M.A. An ultra low power high accuracy current-mode CMOS squaring circuit. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 24–26 October 2012; Volume 2. [Google Scholar]
- Alimisis, V.; Eleftheriou, N.P.; Kamperi, A.; Gennis, G.; Dimas, C.; Sotiriadis, P.P. A radar-based system for detection of human fall utilizing analog hardware architectures of decision tree model. IEEE Open J. Circuits Syst. 2024, 5, 224–242. [Google Scholar] [CrossRef]
- Cveticanin, L.; Ismail, G.M. Higher-order approximate periodic solution for the oscillator with strong nonlinearity of polynomial type. Eur. Phys. J. Plus 2019, 134, 266. [Google Scholar] [CrossRef]
- Liu, J.F. He’s variational approach for nonlinear oscillators with high nonlinearity. Comput. Math. Appl. 2009, 58, 2423–2426. [Google Scholar] [CrossRef][Green Version]
- Yazdi, M.K.; Ahmadian, H.; Mirzabeigy, A.; Yildirim, A. Dynamic analysis of vibrating systems with nonlinearities. Commun. Theor. Phys. 2012, 57, 183–187. [Google Scholar]
- Younesian, D.; Askari, H.; Saadatnia, Z.; Kalami Yazdi, M. Frequency analysis of strongly nonlinear generalized Duffing oscillators using He’s frequency-amplitude formulation and He’s energy balance method. Comput. Math. Appl. 2010, 59, 3222–3228. [Google Scholar]
- Ren, Z.F.; Hu, G.F. He’s frequency-amplitude formulation with average residuals for nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1050–1059. [Google Scholar]
- Qian, Y.; Ren, D.; Chen, S.; Ping, L. Homotopy analysis method for large-amplitude free vibrations of strongly nonlinear generalized Duffing oscillators. Mod. Mech. Eng. 2012, 2, 167–175. [Google Scholar] [CrossRef]
- Big-Alabo, A.; Ezekwem, C. Periodic solution of capillary vibration in lotus-rhizome-node-like deforming structure using quasistatic quintication method. UJESR 2021, 5, 131–139. [Google Scholar]
- White, D.J.; William, P.E.; Hoffman, M.W.; Balkir, S. Low-power analog processing for sensing applications: Low-frequency harmonic signal classification. Sensors 2013, 13, 9604–9623. [Google Scholar] [CrossRef]
- Dobkin, B.; Williams, J. (Eds.) Analog Circuit Design: A Tutorial Guide to Applications and Solutions; Newnes: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Min, R.; Bhardwaj, M.; Cho, S.H.; Shih, E.; Sinha, A.; Wang, A.; Chandrakasan, A. Low-power wireless sensor networks. In VLSI Design 2001. Fourteenth International Conference on VLSI Design; IEEE: Piscataway, NJ, USA, 2001; pp. 205–210. [Google Scholar]
- Jingtao, H. Motor energy management based on non-intrusive monitoring technology and wireless sensor networks. Energy Manag. 2008, 29, 57–76. [Google Scholar]
- Hoque, M.R. Analog Circuit Blocks for Power Management; University of Arkansas: Fayetteville, AR, USA, 2008. [Google Scholar]
- MacLennan, B.J. A Review of Analog Computing; Technical Report UT-CS-07-601; Department of Electrical Engineering & Computer Science, University of Tennessee: Knoxville, TN, USA, 2007; pp. 19798–19807. [Google Scholar]
- Garg, S.; Lou, J.; Jain, A.; Guo, Z.; Shastri, B.J.; Nahmias, M. Dynamic precision analog computing for neural networks. IEEE J. Sel. Top. Quantum Electron. 2022, 29, 1–12. [Google Scholar] [CrossRef]
- Ulmann, B. Analog Computing; Oldenbourg Wissenschaftsverlag: Berlin, Germany, 2013. [Google Scholar]
- Alimisis, V.; Eleftheriou, N.P.; Kamperi, A.; Gennis, G.; Dimas, C.; Sotiriadis, P.P. General methodology for the design of bell-shaped analog-hardware classifiers. Electronics 2023, 12, 4211. [Google Scholar] [CrossRef]
- Haensch, W.; Gokmen, T.; Puri, R. The next generation of deep learning hardware: Analog computing. Proc. IEEE 2018, 107, 108–122. [Google Scholar]
- Alimisis, V.; Gennis, G.; Dimas, C.; Gourdouparis, M.; Sotiriadis, P.P. An ultra-low power analog integrated radial basis function classifier for smart IoT systems. Analog Integr. Circuits Signal Process. 2022, 112, 225–236. [Google Scholar] [CrossRef]
- Kumar, P.; Nandi, A.; Chakrabartty, S.; Thakur, C.S. Process, bias, and temperature scalable CMOS analog computing circuits for machine learning. IEEE Trans. Circuits Syst. I Regul. Papers 2022, 70, 128–141. [Google Scholar] [CrossRef]
- Franco, S. Design with Operational Amplifiers and Analog Integrated Circuits; McGraw-Hill: New York, NY, USA, 2002; Volume 1988. [Google Scholar]
- Tietze, U.; Schenk, C. Advanced Electronic Circuits; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- MacLennan, B.J. The promise of analog computation. Int. J. Gen. Syst. 2014, 43, 682–696. [Google Scholar] [CrossRef]
- Johns, D.A.; Martin, K. Analog Integrated Circuit Design; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Tapashetti, P.; Gupta, A.; Mithlesh, C.; Umesh, A.S. Design and simulation of op-amp integrator and its applications. Int. J. Eng. Adv. Technol. (IJEAT) 2012, 1, 12–19. [Google Scholar]
- Clayton, G.B.; Winder, S. Operational Amplifiers; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Elías-Zúñiga, A. Analytical solution of the damped Helmholtz–Duffing equation. Appl. Math. Lett. 2012, 25, 2349–2353. [Google Scholar] [CrossRef]
- Kontomaris, S.V.; Alimisis, V.; Malamou, A.; Chliveros, G.; Dimas, C. A simple method for solving damped Duffing oscillators. Meccanica 2025, 60, 95–118. [Google Scholar] [CrossRef]
- Yao, S.W. Variational principle for nonlinear fractional wave equation in a fractal space. Therm. Sci. 2021, 25, 1243–1247. [Google Scholar] [CrossRef]
- Liu, H.Y.; Li, Z.M.; Yao, S.W.; Yao, Y.J.; Liu, J. A variational principle for the photocatalytic NOx abatement. Therm. Sci. 2020, 24, 2515–2518. [Google Scholar] [CrossRef]
- He, J.-H. The simpler, the better: Analytical methods for nonlinear oscillators and fractional oscillators. J. Low Freq. Noise Vib. Act Control 2019, 38, 1252–1260. [Google Scholar] [CrossRef]


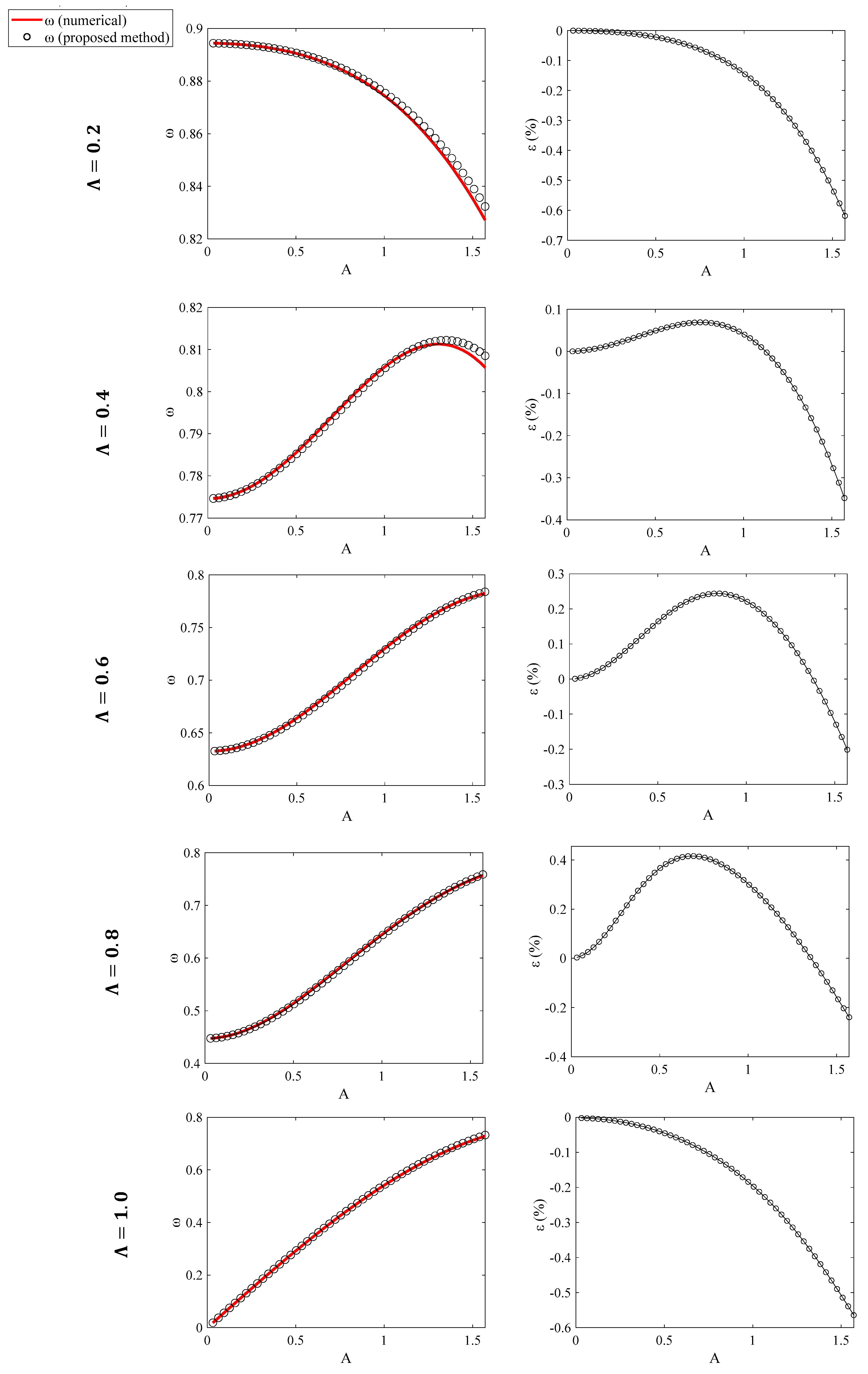



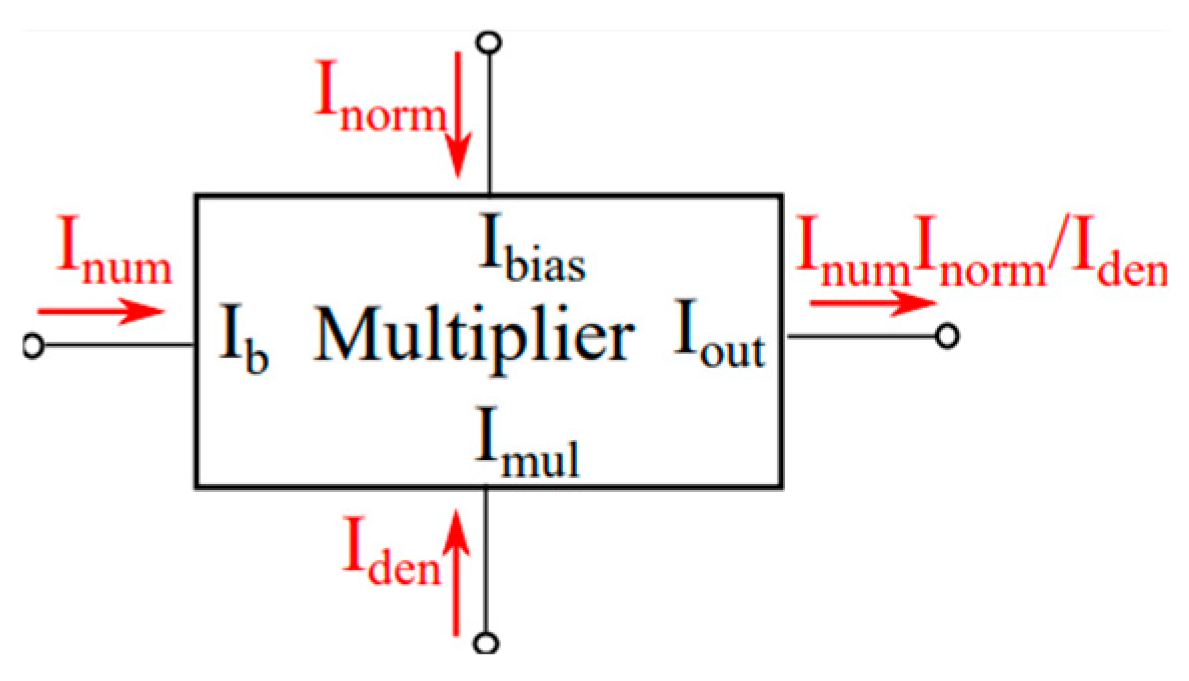


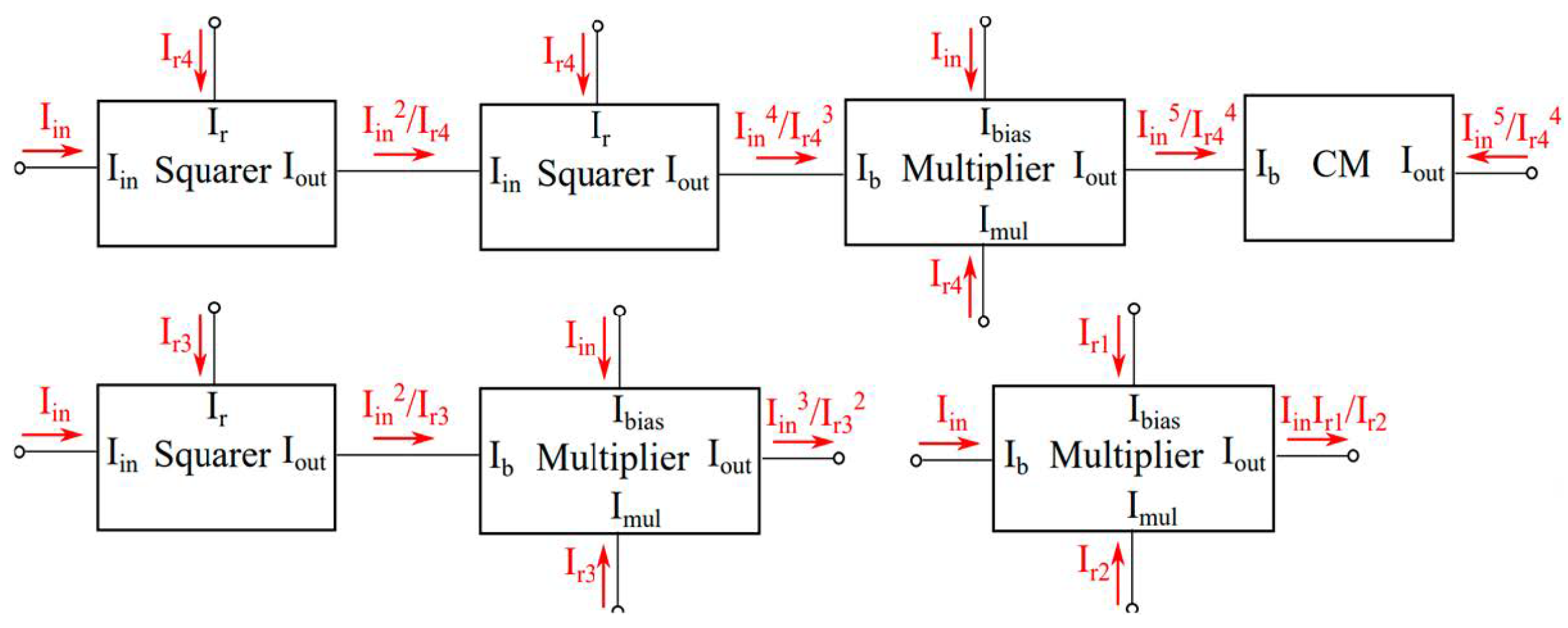

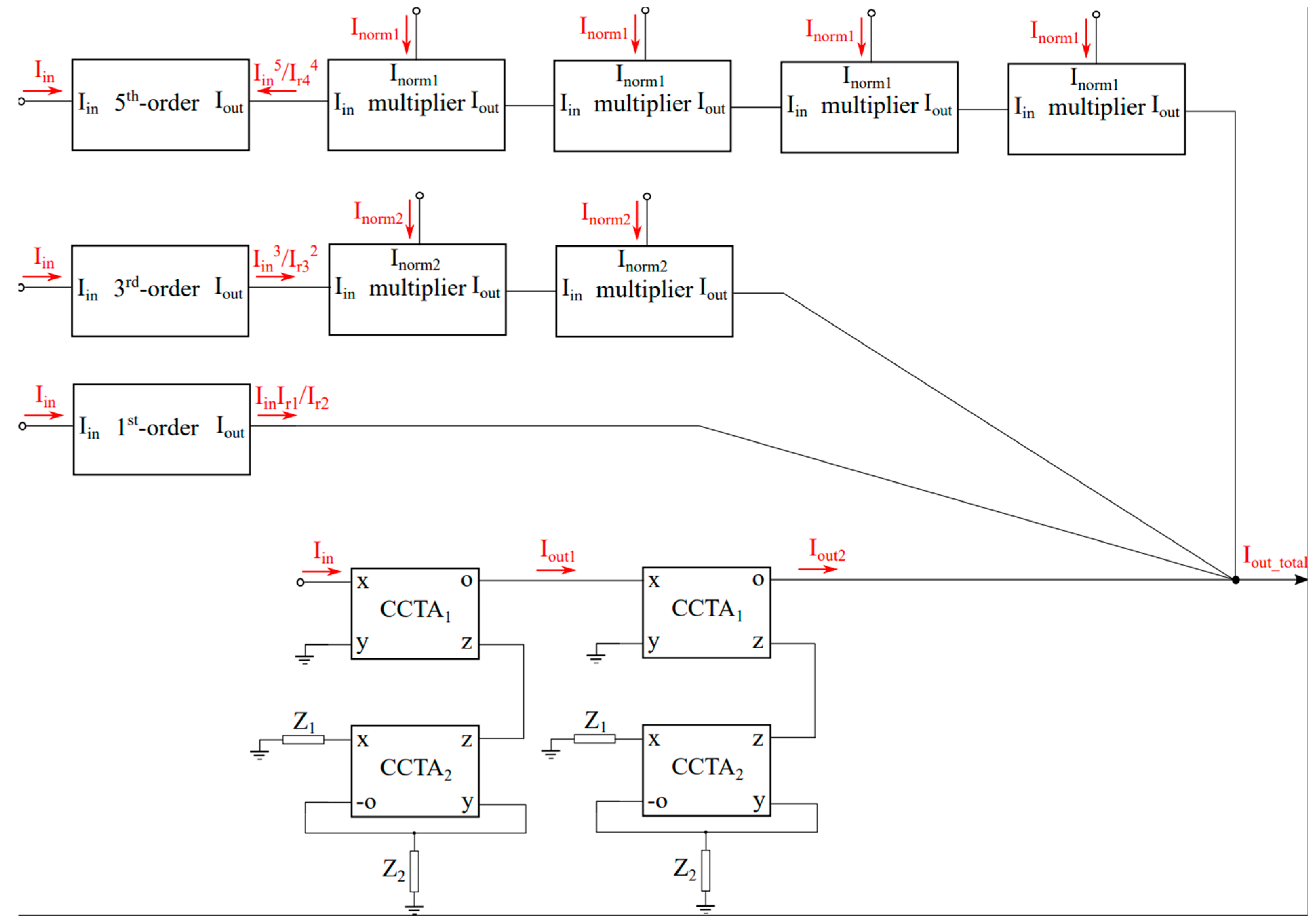


| Λ = 0.2 | |||||||
| A | |||||||
| π/10 | 0.8930 | 0.8931 | 0.8884 | 0.8928 | −0.0112 | 0.0035 | 0.0224 |
| π/5 | 0.8879 | 0.8883 | 0.8795 | 0.8875 | −0.0450 | 0.0532 | 0.0451 |
| 3π/10 | 0.8772 | 0.8783 | 0.8644 | 0.8766 | −0.1252 | 0.2535 | 0.0684 |
| 4π/10 | 0.8581 | 0.8606 | 0.8409 | 0.8575 | −0.2905 | 0.7411 | 0.0700 |
| π/2 | 0.8272 | 0.8323 | 0.8930 | 0.8271 | −0.6128 | 1.6554 | 0.0121 |
| Λ = 0.4 | |||||||
| A | |||||||
| π/10 | 0.7792 | 0.7790 | 0.7793 | 0.7797 | 0.0257 | −0.0114 | −0.0641 |
| π/5 | 0.7908 | 0.7903 | 0.7921 | 0.7932 | 0.0632 | −0.1676 | −0.3026 |
| 3π/10 | 0.8038 | 0.8034 | 0.8099 | 0.8102 | 0.0498 | −0.7520 | −0.7899 |
| 4π/10 | 0.8111 | 0.8117 | 0.8279 | 0.8238 | −0.0739 | −2.0653 | −1.5416 |
| π/2 | 0.8057 | 0.8085 | 0.8409 | 0.8271 | −0.3463 | −4.3665 | −2.5873 |
| Λ = 0.6 | |||||||
| A | |||||||
| π/10 | 0.6456 | 0.6451 | 0.6458 | 0.6471 | 0.0775 | −0.0291 | −0.2318 |
| π/5 | 0.6797 | 0.6783 | 0.6824 | 0.6862 | 0.2064 | −0.3892 | −0.9472 |
| 3π/10 | 0.7225 | 0.7208 | 0.7337 | 0.7378 | 0.2358 | −1.5576 | −2.0737 |
| 4π/10 | 0.7604 | 0.7597 | 0.7897 | 0.7886 | 0.0921 | −3.8508 | −3.5760 |
| π/2 | 0.7824 | 0.7840 | 0.8409 | 0.8271 | −0.2041 | −7.4730 | −5.4044 |
| Λ = 0.8 | |||||||
| A | |||||||
| π/10 | 0.4758 | 0.4748 | 0.4763 | 0.4791 | 0.2106 | −0.0930 | −0.6888 |
| π/5 | 0.5460 | 0.5437 | 0.5512 | 0.5589 | 0.4230 | −0.9619 | −2.3081 |
| 3π/10 | 0.6295 | 0.6273 | 0.6487 | 0.6575 | 0.3507 | −3.0523 | −4.2586 |
| 4π/10 | 0.7045 | 0.7038 | 0.7495 | 0.7518 | 0.0995 | −6.3919 | −6.2916 |
| π/2 | 0.7569 | 0.7587 | 0.8409 | 0.8271 | −0.2372 | −11.1007 | −8.4875 |
| Λ = 1.0 | |||||||
| A | |||||||
| π/10 | 0.1864 | 0.1864 | 0.1914 | 0.2008 | 0.0000 | −2.6936 | −7.1713 |
| π/5 | 0.3619 | 0.3622 | 0.3769 | 0.3924 | −0.0828 | −4.1373 | −7.7727 |
| 3π/10 | 0.5164 | 0.5173 | 0.5507 | 0.5659 | −0.1740 | −6.6287 | −8.7471 |
| 4π/10 | 0.6410 | 0.6431 | 0.7071 | 0.7131 | −0.3265 | −10.3140 | −10.1108 |
| π/2 | 0.7284 | 0.7325 | 0.8409 | 0.8271 | −0.5597 | −15.4450 | −11.9333 |
| t (s) | Num. Results (θ) | HPM (θ) | Proposed App. (θ) | ||
|---|---|---|---|---|---|
| 0 | 1.0000 | 1.0000 | 0 | 1.0000 | 0 |
| 1 | 0.6309 | 0.6278 | 0.490 | 0.6244 | 1.0303 |
| 2 | −0.2196 | −0.2254 | 2.653 | −0.2202 | −0.2732 |
| 3 | −0.8995 | −0.9032 | 0.410 | −0.8994 | 0.0111 |
| 4 | −0.9082 | −0.9031 | 0.559 | −0.9030 | 0.5726 |
| 5 | −0.2397 | −0.2247 | 6.275 | −0.2284 | 4.7142 |
| 6 | 0.6148 | 0.6287 | 2.268 | 0.6179 | −0.5042 |
| 7 | 0.9998 | 1.0007 | 0.091 | 1.0000 | −0.0200 |
| 8 | 0.6467 | 0.6302 | 2.555 | 0.6310 | 2.4277 |
| 9 | −0.1993 | −0.2251 | 12.935 | −0.2120 | −6.3723 |
| 10 | −0.8904 | −0.9035 | 1.474 | −0.8957 | −0.5952 |
| t (s) | Num. Results (θ) | HPM (θ) | Proposed App. (θ) | ||
|---|---|---|---|---|---|
| 0 | 1.0000 | 1.0000 | 0.000 | 1.0000 | 0 |
| 1 | 0.7001 | 0.6831 | 2.432 | 0.7058 | −0.8142 |
| 2 | −0.0052 | −0.0394 | 664.055 | −0.0038 | 26.9231 |
| 3 | −0.7076 | −0.7397 | 4.543 | −0.7111 | −0.4946 |
| 4 | −0.9999 | −0.9953 | 0.469 | −1.0000 | −0.0100 |
| 5 | −0.6926 | −0.6111 | 11.764 | −0.7004 | −1.1262 |
| 6 | 0.0155 | 0.1297 | 739.304 | 0.0114 | 26.4516 |
| 7 | 0.7149 | 0.7940 | 11.056 | 0.7165 | −0.2238 |
| 8 | 0.9998 | 0.9839 | 1.591 | 0.9999 | −0.0100 |
| 9 | 0.6850 | 0.5187 | 24.277 | 0.6949 | −1.4453 |
| 10 | −0.0258 | −0.2527 | 881.111 | −0.0190 | 26.3566 |
| 0.1 | 0.7097 | 0.7080 | 0.7079 |
| 0.2 | 0.7168 | 0.7106 | 0.7104 |
| 0.3 | 0.7283 | 0.7148 | 0.7145 |
| 0.4 | 0.7402 | 0.7205 | 0.7199 |
| 0.5 | 0.7543 | 0.7273 | 0.7266 |
| 0.6 | 0.7688 | 0.7351 | 0.7342 |
| 0.7 | 0.7845 | 0.7434 | 0.7424 |
| 0.8 | 0.7907 | 0.7521 | 0.7510 |
| 0.9 | 0.7992 | 0.7607 | 0.7596 |
| 1.0 | 0.8003 | 0.7690 | 0.7680 |
| A | Exact Numerical Solution (ω) | (Equation (44)) | (Equation (18)) | ||
|---|---|---|---|---|---|
| 0.5 | 1.1111 | 1.1122 | 0.0990 | 1.1059 | 0.4680 |
| 1 | 1.7950 | 1.8477 | 2.9359 | 1.7652 | 1.6602 |
| 2 | 11.879 | 13.229 | 11.3646 | 11.853 | 0.2189 |
| 5 | 397.331 | 448.57 | 12.8958 | 397.286 | 0.0113 |
| 10 | 6241.195 | 7054.9 | 13.0376 | 6241.085 | 0.0018 |
| 20 | 13.0755 | 99,411.667 | 0.0002 | ||
| 100 | 13.0829 | 0.0016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontomaris, S.V.; Ismail, G.M.; Alimisis, V.; Dimas, C.; Malamou, A. A New Approach for Solving Nonlinear Oscillations with an m-Degree Odd-Power Polynomial Restoring Force. Dynamics 2025, 5, 9. https://doi.org/10.3390/dynamics5010009
Kontomaris SV, Ismail GM, Alimisis V, Dimas C, Malamou A. A New Approach for Solving Nonlinear Oscillations with an m-Degree Odd-Power Polynomial Restoring Force. Dynamics. 2025; 5(1):9. https://doi.org/10.3390/dynamics5010009
Chicago/Turabian StyleKontomaris, Stylianos Vasileios, Gamal M. Ismail, Vassilis Alimisis, Christos Dimas, and Anna Malamou. 2025. "A New Approach for Solving Nonlinear Oscillations with an m-Degree Odd-Power Polynomial Restoring Force" Dynamics 5, no. 1: 9. https://doi.org/10.3390/dynamics5010009
APA StyleKontomaris, S. V., Ismail, G. M., Alimisis, V., Dimas, C., & Malamou, A. (2025). A New Approach for Solving Nonlinear Oscillations with an m-Degree Odd-Power Polynomial Restoring Force. Dynamics, 5(1), 9. https://doi.org/10.3390/dynamics5010009








