Derivation of an Analytical Solution of a Forced Cantilevered Tube Conveying Fluid
Abstract
1. Introduction
2. Tube Conveying Fluid General Equation of Motion
3. Exact Analytical Solution
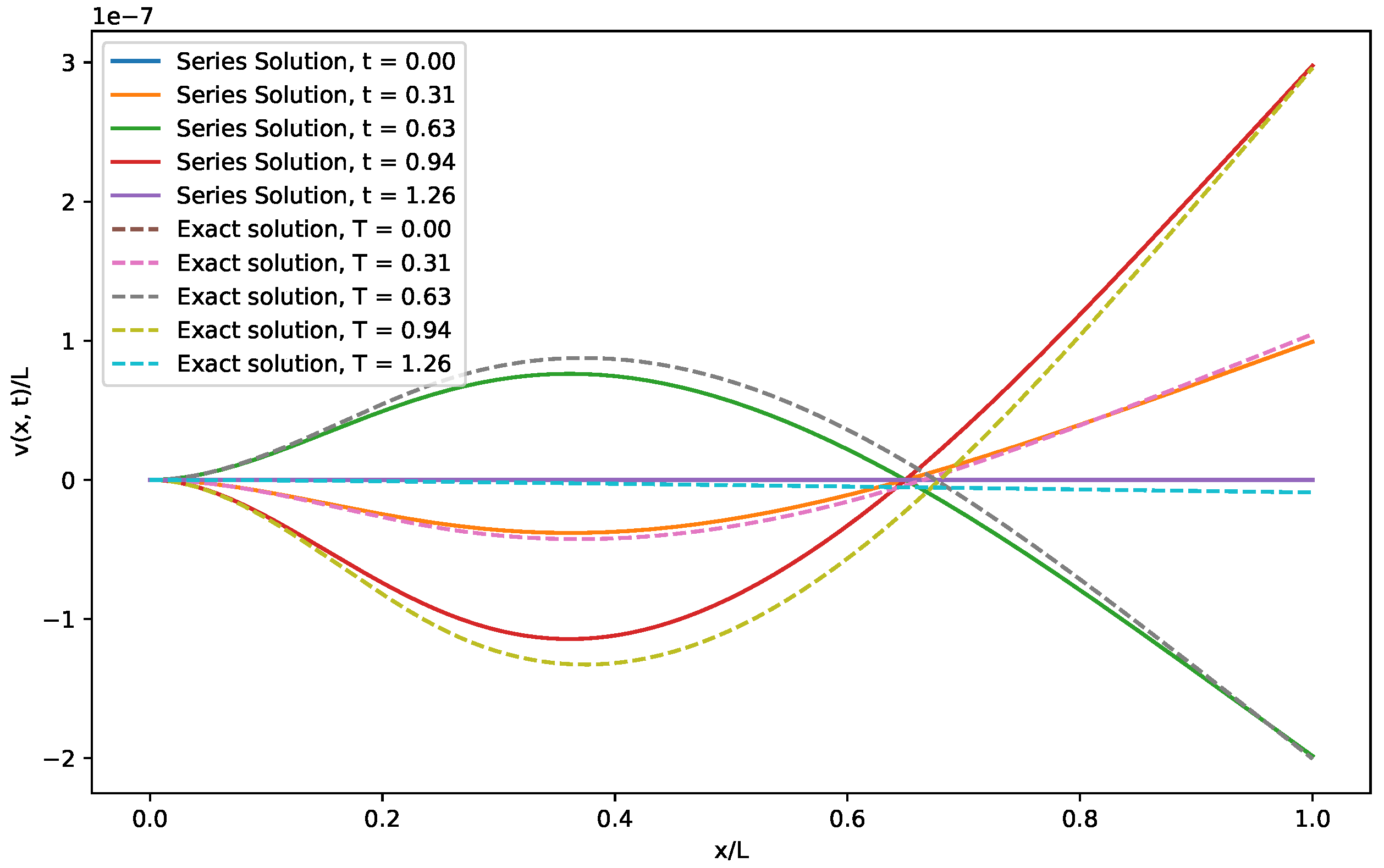
4. Model Validation
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Cantilevered Tube Series Solutions for Pointwise Harmonic Forcing
References
- Paidoussis, M.P. Fluid-Structure Interactions: Slender Structures and Axial Flow, 2nd ed.; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2014. [Google Scholar]
- Tembely, M.; Lecot, C.; Soucemarianadin, A. Prediction and evolution of drop-size distribution for a new ultrasonic atomizer. Appl. Therm. Eng. 2011, 31, 656–667. [Google Scholar] [CrossRef]
- Lin, Y.H.; Chu, C.L. Active Flutter Control Of A Cantilever Tube Conveying Fluid Using Piezoelectric Actuators. J. Sound Vib. 1996, 196, 97–105. [Google Scholar] [CrossRef]
- Housner, G.W. Bending Vibrations of a Pipe Line Containing Flowing Fluid. J. Appl. Mech. 2021, 19, 205–208. [Google Scholar] [CrossRef]
- Weaver, D.S.; Unny, T.E. On the Dynamic Stability of Fluid-Conveying Pipes. J. Appl. Mech. 1973, 40, 48–52. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P. Dynamical stability of pipe conveying fluid with various lateral distributed loads. Arch. Appl. Mech. 2023, 93, 4093–4106. [Google Scholar] [CrossRef]
- Sepehri-Amin, S.; Faal, R.; Das, R. Analytical and numerical solutions for vibration of a functionally graded beam with multiple fractionally damped absorbers. Thin-Walled Struct. 2020, 157, 106711. [Google Scholar] [CrossRef]
- Yang, Z.; Naumenko, K.; Altenbach, H.; Ma, C.C.; Oterkus, E.; Oterkus, S. Some analytical solutions to peridynamic beam equations. ZAMM—J. Appl. Math. Mech. Z. FüR Angew. Math. Und Mech. 2022, 102, e202200132. [Google Scholar] [CrossRef]
- Hozhabrossadati, S.M.; Aftabi Sani, A.; Mehri, B.; Mofid, M. Green’s function for uniform Euler–Bernoulli beams at resonant condition: Introduction of Fredholm Alternative Theorem. Appl. Math. Model. 2015, 39, 3366–3379. [Google Scholar] [CrossRef]
- García García, F.J.; Fariñas Alvariño, P. On an analytic solution for general unsteady/transient turbulent pipe flow and starting turbulent flow. Eur. J. Mech.—B/Fluids 2019, 74, 200–210. [Google Scholar] [CrossRef]
- García García, F.J.; Fariñas Alvariño, P. On the influence of Reynolds shear stress upon the velocity patterns generated in turbulent starting pipe flow. Phys. Fluids 2020, 32, 105119. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Stosiak, M.; Deptuła, A.; Karpenko, M. Navier-Stokes solutions for accelerating pipe flow—A review of analytical models. Energies 2023, 16, 1407. [Google Scholar] [CrossRef]
- Urbanowicz, K.; Bergant, A.; Stosiak, M.; Karpenko, M.; Bogdevičius, M. Developments in analytical wall shear stress modelling for water hammer phenomena. J. Sound Vib. 2023, 562, 117848. [Google Scholar] [CrossRef]
- Henclik, S. Analytical solution and numerical study on water hammer in a pipeline closed with an elastically attached valve. J. Sound Vib. 2018, 417, 245–259. [Google Scholar] [CrossRef]
- Bayle, A.; Plouraboué, F. Laplace-domain fluid–structure interaction solutions for water hammer waves in a pipe. J. Hydraul. Eng. 2023, 150, 04023062-1–12. [Google Scholar] [CrossRef]
- Païdoussis, M.P.; Semler, C.; Wadham-Gagnon, M.; Saaid, S. Dynamics of cantilevered pipes conveying fluid. Part 2: Dynamics of the system with intermediate spring support. J. Fluids Struct. 2007, 23, 569–587. [Google Scholar] [CrossRef]
- Ammari, K.; Tucsnak, M. Stabilization of Bernoulli–Euler Beams by Means of a Pointwise Feedback Force. SIAM J. Control Optim. 2000, 39, 1160–1181. [Google Scholar] [CrossRef]
- Spiegel, M.R. Mathematical Handbook of Formulas and Tables, 1st ed.; Schaum, McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]




| Parameters | Value | Description | Unit |
|---|---|---|---|
| L | [1, 10, 15] | Length | m |
| 7800 | Density of the material | kg/m3 | |
| [0, 1000] | Fluid density | kg/m3 | |
| 0.05 | Tube inner radius | m | |
| 0.06 | Tube outer radius | m | |
| E | Young’s modulus | Pa | |
| U | [0, 0.1, 1] | Velocity | m/s |
| 10.0 | Excitation frequency | rad/s | |
| 10.0 | Amplitude of the forcing function | N | |
| L/4 | Position where the force is applied | m | |
| I | Area moment of inertia | - | |
| Mass per unit length of the tube | - | ||
| Added mass per unit length due to fluid | - | ||
| a | - | ||
| b | - | - | |
| c | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tembely, M. Derivation of an Analytical Solution of a Forced Cantilevered Tube Conveying Fluid. Dynamics 2024, 4, 889-899. https://doi.org/10.3390/dynamics4040046
Tembely M. Derivation of an Analytical Solution of a Forced Cantilevered Tube Conveying Fluid. Dynamics. 2024; 4(4):889-899. https://doi.org/10.3390/dynamics4040046
Chicago/Turabian StyleTembely, Moussa. 2024. "Derivation of an Analytical Solution of a Forced Cantilevered Tube Conveying Fluid" Dynamics 4, no. 4: 889-899. https://doi.org/10.3390/dynamics4040046
APA StyleTembely, M. (2024). Derivation of an Analytical Solution of a Forced Cantilevered Tube Conveying Fluid. Dynamics, 4(4), 889-899. https://doi.org/10.3390/dynamics4040046






