Classical and Quantum Physical Reservoir Computing for Onboard Artificial Intelligence Systems: A Perspective
Abstract
1. Introduction
2. What Is This Review Article About?
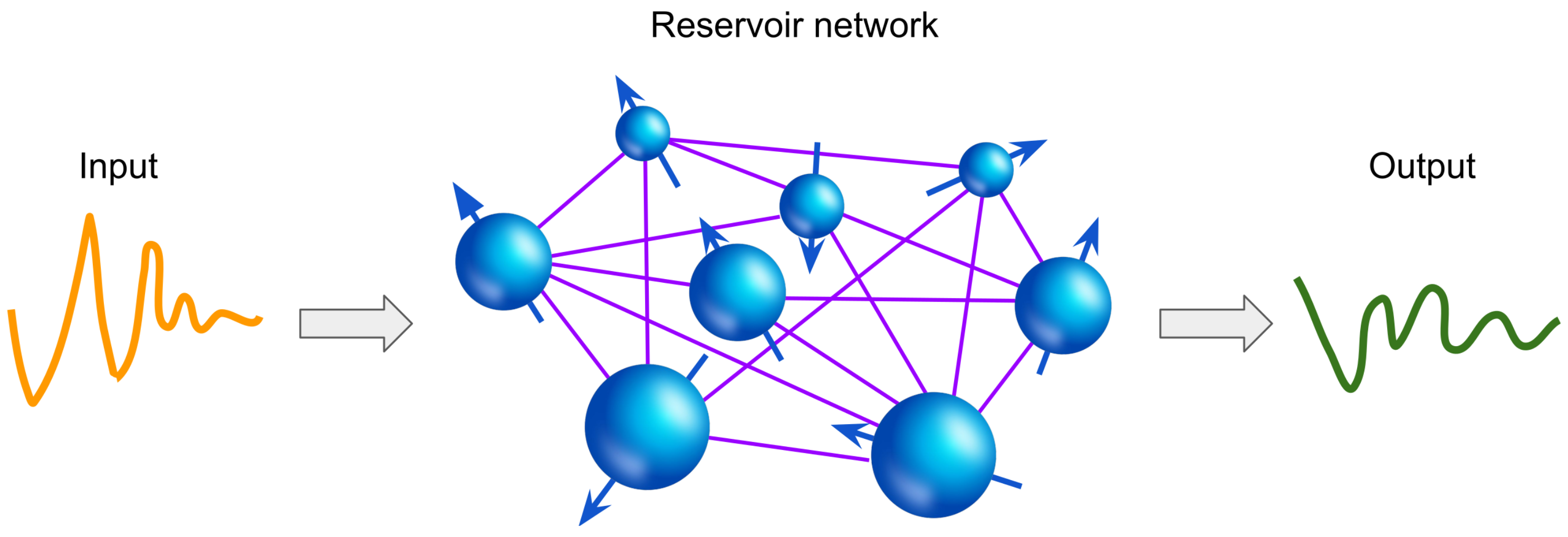
3. Reservoir Computing
3.1. Traditional Reservoir Computing Approach
3.2. Physical Reservoir Computing
4. Reservoir Computing Using the Physical Properties of Fluids
4.1. State-of-the-Art
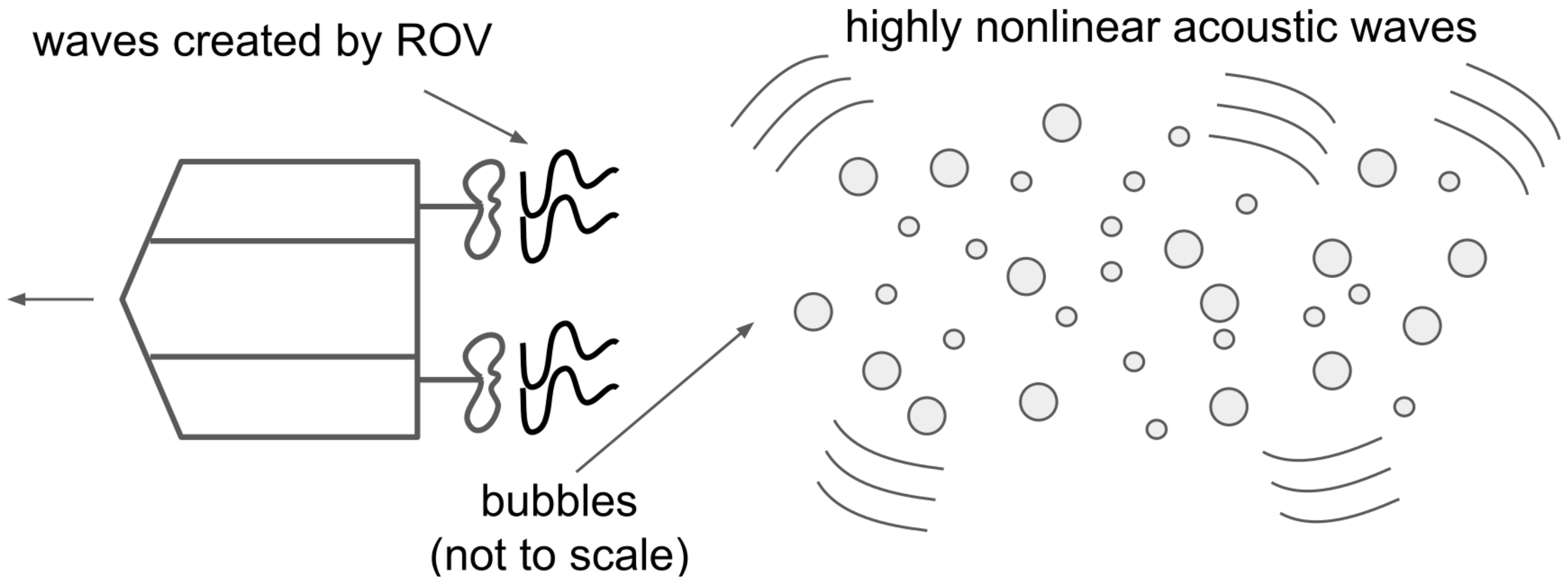
4.2. Towards Reservoir Computing with Water Waves Created by an ROV
4.3. Physical Reservoir Computing Using Fluid-Flow Disturbances
4.4. Acoustic-Based Reservoir Computing
5. Physical Reservoir Computing for UGVs
6. Adjacent Technologies for Onboard Reservoir Computations
7. Quantum Reservoir Computing
7.1. Spin Network-Based Reservoir
7.2. Quantum Oscillator for Reservoir Computing
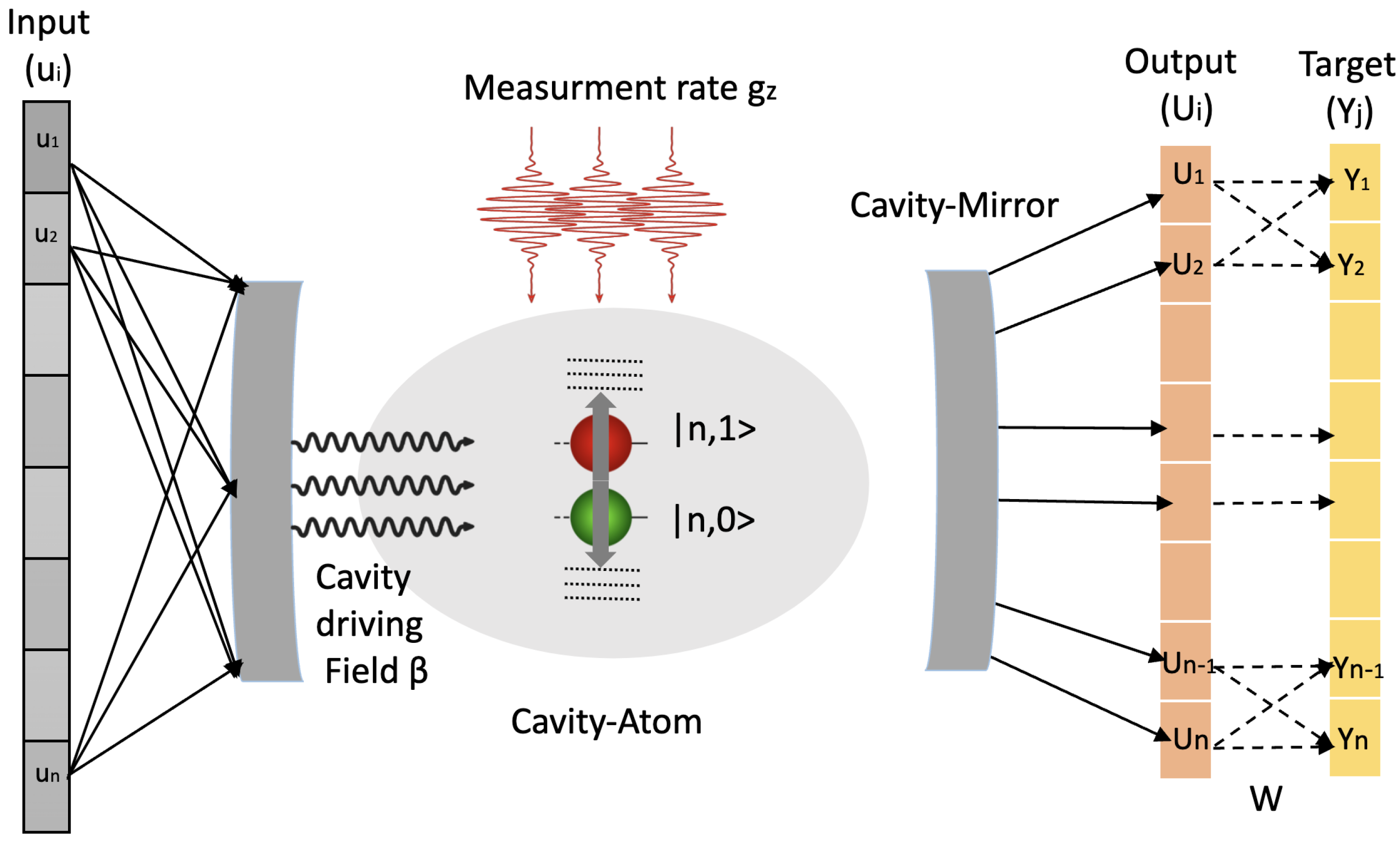
7.3. Quantum Reservoir with Controlled-Measurement Dynamics
- Restarting protocol (RSP): Repeats the entire experiment for each measurement, maintaining unperturbed dynamics but requiring significant resources.
- Rewinding protocol (RWP): Restarts dynamics from a recent past state (washout time ), optimising resources compared to RSP.
- Online protocol (OLP): Uses weak measurements to continuously monitor the system, preserving memory with less back-action but introducing more noise.
- The efficiency of these measurement protocols was evaluated by tasking a QRC system to solve a number of standard benchmarking problems. It was established that RSP and RWP require strong measurements to minimise statistical errors, whereas OLP with weak measurements effectively preserves the state of the reservoir while providing sufficient information for time-series processing [207].
8. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| LIDAR | light detection and ranging |
| NMR | nuclear magnetic resonance |
| OLP | online protocol |
| QNP | quantum neuromorphic processor |
| QRC | quantum reservoir computing |
| RC | reservoir computing |
| ROV | remotely operated vehicle |
| RSP | restarting protocol |
| RWP | rewinding protocol |
| SNAILs | superconducting nonlinear asymmetric inductive elements |
| UAV | unmanned aerial vehicle |
| UGV | unmanned ground vehicle |
References
- Boylen, M.J. The Drone Age: How Drone Technology Will Change War and Peace; Oxford University Press: New York, NY, USA, 2020. [Google Scholar]
- Davies, S.; Pettersson, T.; Öberg, M. Organized violence 1989–2021 and drone warfare. J. Peace Res. 2022, 59, 593–610. [Google Scholar] [CrossRef]
- Kunertova, D. The war in Ukraine shows the game-changing effect of drones depends on the game. Bull. At. Sci. 2023, 79, 95–102. [Google Scholar] [CrossRef]
- Giannaros, A.; Karras, A.; Theodorakopoulos, L.; Karras, C.; Kranias, P.; Schizas, N.; Kalogeratos, G.; Tsolis, D. Autonomous vehicles: Sophisticated attacks, safety issues, challenges, open topics, blockchain, and future directions. J. Cybersecur. Priv. 2023, 3, 493–543. [Google Scholar] [CrossRef]
- Zhang, Q.; Wallbridge, C.D.; Jones, D.M.; Morgan, P.L. Public perception of autonomous vehicle capability determines judgment of blame and trust in road traffic accidents. Transp. Res. A Policy Pract. 2024, 179, 103887. [Google Scholar] [CrossRef]
- de Vries, A. The growing energy footprint of artificial intelligence. Joule 2023, 7, 2191–2194. [Google Scholar] [CrossRef]
- Verdecchia, R.; Sallou, J.; Cruz, L. A systematic review of Green AI. WIREs Data Min. Knowl. 2023, 13, e1507. [Google Scholar] [CrossRef]
- Takeno, J. Creation of a Conscious Robot: Mirror Image Cognition and Self-Awareness; CRS Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Ghimire, S.; Nguyen-Huy, T.; AL-Musaylh, M.S.; Deo, R.C.; Casillas-Pérez, D.; Salcedo-Sanz, S. A novel approach based on integration of convolutional neural networks and echo state network for daily electricity demand prediction. Energy 2023, 275, 127430. [Google Scholar] [CrossRef]
- Rozite, V.; Miller, J.; Oh, S. Why AI and Energy Are the New Power Couple; IEA: Paris, France, 2023. [Google Scholar]
- Faghihian, H.; Sargolzaei, A. Energy Efficiency of Connected Autonomous Vehicles: A Review. Electronics 2023, 12, 4086. [Google Scholar] [CrossRef]
- Grant, A. Autonomous Electric Vehicles Will Guzzle Power Instead of Gas. Hyperdrive, Bloomberg, 27 February 2024. [Google Scholar]
- Zewe, A. Computers That Power Self-Driving Cars Could Be a Huge Driver of Global Carbon Emissions. MIT News, 13 January 2023. [Google Scholar]
- Othman, K. Exploring the implications of autonomous vehicles: A comprehensive review. Innov. Infrastruct. Solut. 2022, 7, 165. [Google Scholar] [CrossRef]
- Rauf, M.; Kumar, L.; Zulkifli, S.A.; Jamil, A. Aspects of artificial intelligence in future electric vehicle technology for sustainable environmental impact. Environ. Chall. 2024, 14, 100854. [Google Scholar] [CrossRef]
- Yang, Y.; Sciacchitano, A.; Veldhuis, L.L.M.; Eitelberg, G. Analysis of propeller-induced ground vortices by particle image velocimetry. J. Vis. 2018, 21, 39–55. [Google Scholar] [CrossRef]
- Sun, Q.; Shi, Z.; Sun, Z.; Chen, S.; Chen, Y. Characteristics of the shedding vortex around the Coanda surface and its impact on circulation control airfoil performance. Phys. Fluids 2023, 35, 027103. [Google Scholar] [CrossRef]
- Yusvika, M.; Prabowo, A.R.; Tjahjana, D.D.D.P.; Sohn, J.M. Cavitation prediction of ship propeller based on temperature and fluid properties of water. J. Mar. Sci. Eng. 2020, 8, 465. [Google Scholar] [CrossRef]
- Ju, H.J.; Choi, J.S. Experimental study of cavitation damage to marine propellers based on the rotational speed in the coastal Waters. Machines 2022, 10, 793. [Google Scholar] [CrossRef]
- Arndt, R.; Pennings, P.; Bosschers, J.; van Terwisga, T. The singing vortex. Interface Focus 2015, 5, 20150025. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Zhou, B.; Liu, H.; Han, X.; Hu, G.; Zhang, T. Study of propeller vortex characteristics under loading conditions. Symmetry 2023, 15, 445. [Google Scholar] [CrossRef]
- Adamatzky, A. Advances in Unconventional Computing. Volume 2: Prototypes, Models and Algorithms; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Adamatzky, A. A brief history of liquid computers. Philos. Trans. R. Soc. B 2019, 374, 20180372. [Google Scholar] [CrossRef]
- Shastri, B.J.; Tait, A.N.; de Lima, T.F.; Pernice, W.H.P.; Bhaskaran, H.; Wright, C.D.; Prucnal, P.R. Photonics for artificial intelligence and neuromorphic computing. Nat. Photon. 2020, 15, 102–114. [Google Scholar] [CrossRef]
- Marcucci, G.; Pierangeli, D.; Conti, C. Theory of neuromorphic computing by waves: Machine learning by rogue waves, dispersive shocks, and solitons. Phys. Rev. Lett. 2020, 125, 093901. [Google Scholar] [CrossRef]
- Marković, D.; Mizrahi, A.; Querlioz, D.; Grollier, J. Physics for neuromorphic computing. Nat. Rev. Phys. 2020, 2, 499–510. [Google Scholar] [CrossRef]
- Suárez, L.E.; Richards, B.A.; Lajoie, G.; Misic, B. Learning function from structure in neuromorphic networks. Nat. Mach. Intell. 2021, 3, 771–786. [Google Scholar] [CrossRef]
- Rao, A.; Plank, P.; Wild, A.; Maass, W. A long short-term memory for AI applications in spike-based neuromorphic hardware. Nat. Mach. Intell. 2022, 4, 467–479. [Google Scholar] [CrossRef]
- Sarkar, T.; Lieberth, K.; Pavlou, A.; Frank, T.; Mailaender, V.; McCulloch, I.; Blom, P.W.M.; Torricelli, F.; Gkoupidenis, P. An organic artificial spiking neuron for in situ neuromorphic sensing and biointerfacing. Nat. Electron. 2022, 5, 774–783. [Google Scholar] [CrossRef]
- Schuman, C.D.; Kulkarni, S.R.; Parsa, M.; Mitchell, J.P.; Date, P.; Kay, B. Opportunities for neuromorphic computing algorithms and applications. Nat. Comput. Sci. 2022, 2, 10–19. [Google Scholar] [PubMed]
- Krauhausen, I.; Coen, C.T.; Spolaor, S.; Gkoupidenis, P.; van de Burgt, Y. Brain-inspired organic electronics: Merging neuromorphic computing and bioelectronics using conductive polymers. Adv. Funct. Mater. 2024, 34, 2307729. [Google Scholar] [CrossRef]
- Mittal, S. A survey of techniques for approximate computing. ACM Comput. Surv. 2016, 48, 62. [Google Scholar] [CrossRef]
- Liu, W.; Lombardi, F.; Schulte, M. Approximate Computing: From Circuits to Applications. Proc. IEEE 2020, 108, 2103–2107. [Google Scholar] [CrossRef]
- Henderson, A.; Yakopcic, C.; Harbour, S.; Taha, T.M. Detection and Classification of Drones Through Acoustic Features Using a Spike-Based Reservoir Computer for Low Power Applications. In Proceedings of the 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Ullah, S.; Kumar, A. Introduction. In Approximate Arithmetic Circuit Architectures for FPGA-Based Systems; Springer International Publishing: Cham, Switzerland, 2023; pp. 1–26. [Google Scholar]
- Maksymov, I.S.; Pototsky, A.; Suslov, S.A. Neural echo state network using oscillations of gas bubbles in water. Phys. Rev. E 2021, 105, 044206. [Google Scholar] [CrossRef]
- Nomani, T.; Mohsin, M.; Pervaiz, Z.; Shafique, M. xUAVs: Towards efficient approximate computing for UAVs-low power approximate adders with single LUT delay for FPGA-based aerial imaging optimization. IEEE Access 2020, 8, 102982–102996. [Google Scholar] [CrossRef]
- Maksymov, I.S. Analogue and physical reservoir computing using water waves: Applications in power engineering and beyond. Energies 2023, 16, 5366. [Google Scholar] [CrossRef]
- Adamatzky, A.; Tarabella, G.; Phillips, N.; Chiolerio, A.; D’Angelo, P.; Nicolaidou, A.; Sirakoulis, G.C. Kombucha electronics. arXiv 2023, arXiv:2302.03984. [Google Scholar]
- Sharma, S.; Mahmud, A.; Tarabella, G.; Mougoyannis, P.; Adamatzky, A. Information-theoretic language of proteinoid gels: Boolean gates and QR codes. arXiv 2024, arXiv:2405.19337. [Google Scholar]
- Maass, W.; Natschläger, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Nakajima, K.; Fisher, I. Reservoir Computing; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Miller, K.; Lohn, A. Onboard AI: Constraints and Limitations; Center for Security and Emerging Technology: Washington, DC, USA, 2023. [Google Scholar] [CrossRef]
- Okulski, M.; Ławryńczuk, M. A small UAV optimized for efficient long-range and VTOL missions: An experimental tandem-wing quadplane drone. Appl. Sci. 2022, 12, 7059. [Google Scholar] [CrossRef]
- Tanaka, G.; Yamane, T.; Héroux, J.B.; Nakane, R.; Kanazawa, N.; Takeda, S.; Numata, H.; Nakano, D.; Hirose, A. Recent advances in physical reservoir computing: A review. Neural Netw. 2019, 115, 100–123. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, K. Physical reservoir computing–an introductory perspective. Jpn. J. Appl. Phys. 2020, 59, 060501. [Google Scholar] [CrossRef]
- Cucchi, M.; Abreu, S.; Ciccone, G.; Brunner, D.; Kleemann, H. Hands-on reservoir computing: A tutorial for practical implementation. Neuromorph. Comput. Eng. 2022, 2, 032002. [Google Scholar] [CrossRef]
- Maksymov, I.S. Quantum-inspired neural network model of optical illusions. Algorithms 2024, 17, 30. [Google Scholar] [CrossRef]
- Mujal, P.; Martínez-Peña, R.; Nokkala, J.; García-Beni, J.; Giorgi, G.L.; Soriano, M.C.; Zambrini, R. Opportunities in quantum reservoir computing and extreme learning machines. Adv. Quantum Technol. 2021, 4, 2100027. [Google Scholar] [CrossRef]
- Govia, L.C.G.; Ribeill, G.J.; Rowlands, G.E.; Krovi, H.K.; Ohki, T.A. Quantum reservoir computing with a single nonlinear oscillator. Phys. Rev. Res. 2021, 3, 013077. [Google Scholar] [CrossRef]
- Suzuki, Y.; Gao, Q.; Pradel, K.C.; Yasuoka, K.; Yamamoto, N. Natural quantum reservoir computing for temporal information processing. Sci. Rep. 2022, 12, 1353. [Google Scholar] [CrossRef] [PubMed]
- Govia, L.C.G.; Ribeill, G.J.; Rowlands, G.E.; Ohki, T.A. Nonlinear input transformations are ubiquitous in quantum reservoir computing. Neuromorph. Comput. Eng. 2022, 2, 014008. [Google Scholar] [CrossRef]
- Dudas, J.; Carles, B.; Plouet, E.; Mizrahi, F.A.; Grollier, J.; Marković, D. Quantum reservoir computing implementation on coherently coupled quantum oscillators. NPJ Quantum Inf. 2023, 9, 64. [Google Scholar] [CrossRef]
- Götting, N.; Lohof, F.; Gies, C. Exploring quantumness in quantum reservoir computing. Phys. Rev. A 2023, 108, 052427. [Google Scholar] [CrossRef]
- Llodrà, G.; Charalambous, C.; Giorgi, G.L.; Zambrini, R. Benchmarking the role of particle statistics in quantum reservoir computing. Adv. Quantum Technol. 2023, 6, 2200100. [Google Scholar] [CrossRef]
- Čindrak, S.; Donvil, B.; Lüdge, K.; Jaurigue, L. Enhancing the performance of quantum reservoir computing and solving the time-complexity problem by artificial memory restriction. Phys. Rev. Res. 2024, 6, 013051. [Google Scholar] [CrossRef]
- Veelenturf, L.P.J. Analysis and Applications of Artificial Neural Networks; Prentice Hall: London, UK, 1995. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Pearson-Prentice Hall: Singapore, 1998. [Google Scholar]
- Galushkin, A.I. Neural Networks Theory; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- McKenna, T.M.; McMullen, T.A.; Shlesinger, M.F. The brain as a dynamic physical system. Neuroscience 1994, 60, 587–605. [Google Scholar] [CrossRef]
- Korn, H.; Faure, P. Is there chaos in the brain? II. Experimental evidence and related models. C. R. Biol. 2003, 326, 787–840. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Nonlinear Dynamical Systems in Engineering; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yan, M.; Huang, C.; Bienstman, P.; Tino, P.; Lin, W.; Sun, J. Emerging opportunities and challenges for the future of reservoir computing. Nat. Commun. 2024, 15, 2056. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H. A Tutorial on Training Recurrent Neural Networks, Covering BPPT, RTRL, EKF and the “Echo State Network” Approach; GMD Report 159; German National Research Center for Information Technology: Karlsruhe, Germany, 2005. [Google Scholar]
- Lukoševičius, M. A Practical Guide to Applying Echo State Networks. In Neural Networks: Tricks of the Trade, Reloaded; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 659–686. [Google Scholar]
- Bala, A.; Ismail, I.; Ibrahim, R.; Sait, S.M. Applications of metaheuristics in reservoir computing techniques: A Review. IEEE Access 2018, 6, 58012–58029. [Google Scholar] [CrossRef]
- Damicelli, F.; Hilgetag, C.C.; Goulas, A. Brain connectivity meets reservoir computing. PLoS Comput. Biol. 2022, 18, e1010639. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Vargas, D.V. A survey on reservoir computing and its interdisciplinary applications beyond traditional machine learning. IEEE Access 2023, 11, 81033–81070. [Google Scholar] [CrossRef]
- Lee, O.; Wei, T.; Stenning, K.D.; Gartside, J.C.; Prestwood, D.; Seki, S.; Aqeel, A.; Karube, K.; Kanazawa, N.; Taguchi, Y.; et al. Task-adaptive physical reservoir computing. Nat. Mater. 2023, 23, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Riou, M.; Torrejon, J.; Garitaine, B.; Araujo, F.A.; Bortolotti, P.; Cros, V.; Tsunegi, S.; Yakushiji, K.; Fukushima, A.; Kubota, H.; et al. Temporal pattern recognition with delayed-feedback spin-torque nano-oscillators. Phys. Rep. Appl. 2019, 12, 024049. [Google Scholar] [CrossRef] [PubMed]
- Watt, S.; Kostylev, M. Reservoir computing using a spin-wave delay-line active-ring resonator based on yttrium-iron-garnet film. Phys. Rev. Appl. 2020, 13, 034057. [Google Scholar] [CrossRef]
- Allwood, D.A.; Ellis, M.O.A.; Griffin, D.; Hayward, T.J.; Manneschi, L.; Musameh, M.F.K.; O’Keefe, S.; Stepney, S.; Swindells, C.; Trefzer, M.A.; et al. A perspective on physical reservoir computing with nanomagnetic devices. Appl. Phys. Lett. 2023, 122, 040501. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, X.; Cheng, H.; Qiu, J.; Liu, X.; Wang, M.; Liu, Q. Emerging dynamic memristors for neuromorphic reservoir computing. Nanoscale 2022, 14, 289–298. [Google Scholar] [CrossRef]
- Liang, X.; Tang, J.; Zhong, Y.; Gao, B.; Qian, H.; Wu, H. Physical reservoir computing with emerging electronics. Nat. Electron. 2024, 7, 193–206. [Google Scholar] [CrossRef]
- Sorokina, M. Multidimensional fiber echo state network analogue. J. Phys. Photonics 2020, 2, 044006. [Google Scholar] [CrossRef]
- Rafayelyan, M.; Dong, J.; Tan, Y.; Krzakala, F.; Gigan, S. Large-scale optical reservoir computing for spatiotemporal chaotic systems prediction. Phys. Rev. X 2020, 10, 041037. [Google Scholar] [CrossRef]
- Coulombe, J.C.; York, M.C.A.; Sylvestre, J. Computing with networks of nonlinear mechanical oscillators. PLoS ONE 2017, 12, e0178663. [Google Scholar] [CrossRef] [PubMed]
- Kheirabadi, N.R.; Chiolerio, A.; Szaciłowski, K.; Adamatzky, A. Neuromorphic liquids, colloids, and gels: A review. ChemPhysChem 2023, 24, e202200390. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.; Gaur, P.; Rubin, S.; Fainman, Y. Thin liquid film as an optical nonlinear-nonlocal medium and memory element in integrated optofluidic reservoir computer. Adv. Photon. 2022, 4, 046005. [Google Scholar] [CrossRef]
- Marcucci, G.; Caramazza, P.; Shrivastava, S. A new paradigm of reservoir computing exploiting hydrodynamics. Phys. Fluids 2023, 35, 071703. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Pototsky, A. Reservoir computing based on solitary-like waves dynamics of liquid film flows: A proof of concept. Europhys. Lett. 2023, 142, 43001. [Google Scholar] [CrossRef]
- Fernando, C.; Sojakka, S. Pattern Recognition in a Bucket. In Advances in Artificial Life; Banzhaf, W., Ziegler, J., Christaller, T., Dittrich, P., Kim, J.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 588–597. [Google Scholar]
- Nakajima, K.; Aoyagi, T. The memory capacity of a physical liquid state machine. IEICE Tech. Rep. 2015, 115, 109–113. [Google Scholar]
- Remoissenet, M. Waves Called Solitons: Concepts and Experiments; Springer: Cham, Switzerland, 1994. [Google Scholar]
- Maksymov, I.S. Physical reservoir computing enabled by solitary waves and biologically inspired nonlinear transformation of input data. Dynamics 2024, 4, 119–134. [Google Scholar] [CrossRef]
- Aguirre-Castro, O.A.; Inzunza-González, E.; García-Guerrero, E.E.; Tlelo-Cuautle, E.; López-Bonilla, O.R.; Olguín-Tiznado, J.E.; Cárdenas-Valdez, J.R. Design and construction of an ROV for underwater exploration. Sensors 2019, 19, 5387. [Google Scholar] [CrossRef]
- Bohm, H. Build Your Own Underwater Robot; Westcoast Words: Vancouver, BC, Canada, 1997. [Google Scholar]
- Perrusquía, A.; Guo, W. Reservoir computing for drone trajectory intent prediction: A physics informed approach. IEEE Trans. Cybern. 2024. early access. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.; Yan, Y. UAV formation trajectory planning algorithms: A review. Drones 2023, 7, 62. [Google Scholar] [CrossRef]
- Goto, K.; Nakajima, K.; Notsu, H. Twin vortex computer in fluid flow. New J. Phys. 2021, 23, 063051. [Google Scholar] [CrossRef]
- Vincent, T.; Gunasekaran, S.; Mongin, M.; Medina, A.; Pankonien, A.M.; Buskohl, P. Development of an Experimental Testbed to Study Cavity Flow as a Processing Element for Flow Disturbances. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Vincent, T.; Nelson, D.; Grossmann, B.; Gillman, A.; Pankonien, A.; Buskohl, P. Open-Cavity Fluid Flow as an Information Processing Medium. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023. [Google Scholar] [CrossRef]
- Vargas, A.; Ireland, M.; Anderson, D. System identification of multirotor UAV’s using echo state networks. In Proceedings of the AUVSI’s Unmanned Systems 2015, Atlanta, GA, USA, 4–7 May 2015. [Google Scholar]
- Sears, W.R. Introduction to Theoretical Aerodynamics and Hydrodynamics; Americal Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011. [Google Scholar]
- Saban, D.; Whidborne, J.F.; Cooke, A.K. Simulation of wake vortex effects for UAVs in close formation flight. Aeronaut. J. 2009, 113, 727–738. [Google Scholar] [CrossRef]
- Hrúz, M.; Pecho, P.; Bugaj, M.; Rostáš, J. Investigation of vortex structure behavior induced by different drag reduction devices in the near field. Transp. Res. Proc. 2022, 65, 318–328. [Google Scholar] [CrossRef]
- Nathanael, J.C.; Wang, C.H.J.; Low, K.H. Numerical studies on modeling the near- and far-field wake vortex of a quadrotor in forward flight. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2022, 236, 1166–1183. [Google Scholar] [CrossRef]
- Wu, J.Z.; Ma, H.Y.; Zhou, M.D. Vorticity and Vortex Dynamics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Billah, K.Y.; Scanlan, R.H. Resonance, Tacoma Narrows bridge failure, and undergraduate physics textbooks. Am. J. Phys. 1991, 59, 118–124. [Google Scholar] [CrossRef]
- Williamson, C.H.K. Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 1996, 28, 477–539. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–445. [Google Scholar] [CrossRef]
- Asnaghi, A.; Svennberg, U.; Gustafsson, R.; Bensow, R.E. Propeller tip vortex mitigation by roughness application. Appl. Ocean Res. 2021, 106, 102449. [Google Scholar] [CrossRef]
- Meffan, C.; Ijima, T.; Banerjee, A.; Hirotani, J.; Tsuchiya, T. Non-linear processing with a surface acoustic wave reservoir computer. Microsyst. Technol. 2023, 29, 1197–1206. [Google Scholar] [CrossRef]
- Yaremkevich, D.D.; Scherbakov, A.V.; Clerk, L.D.; Kukhtaruk, S.M.; Nadzeyka, A.; Campion, R.; Rushforth, A.W.; Savel’ev, S.; Balanov, A.G.; Bayer, M. On-chip phonon-magnon reservoir for neuromorphic computing. Nat. Commun. 2023, 14, 8296. [Google Scholar] [CrossRef]
- Phang, S. Photonic reservoir computing enabled by stimulated Brillouin scattering. Opt. Express 2023, 31, 22061–22074. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.K.; Liu, L. Finite-Difference, Time-Domain Simulation of Sound Propagation in a Dynamic Atmosphere; US Army Corps of Engineers, Engineer Research and Development Center: Washington, DC, USA, 2004. [Google Scholar]
- Rubin, W.L. Radar-acoustic detection of aircraft wake vortices. J. Atmos. Ocean. Technol. 1999, 17, 1058–1065. [Google Scholar] [CrossRef]
- Manneville, S.; Robres, J.H.; Maurel, A.; Petitjeans, P.; Fink, M. Vortex dynamics investigation using an acoustic technique. Phys. Fluids 1999, 11, 3380–3389. [Google Scholar] [CrossRef]
- Digulescu, A.; Murgan, I.; Candel, I.; Bunea, F.; Ciocan, G.; Bucur, D.M.; Dunca, G.; Ioana, C.; Vasile, G.; Serbanescu, A. Cavitating vortex characterization based on acoustic signal detection. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 082009. [Google Scholar] [CrossRef]
- Onasami, O.; Feng, M.; Xu, H.; Haile, M.; Qian, L. Underwater acoustic communication channel modeling using reservoir computing. IEEE Access 2022, 10, 56550–56563. [Google Scholar] [CrossRef]
- Lidtke, A.K.; Turnock, S.R.; Humphrey, V.F. Use of acoustic analogy for marine propeller noise characterisation. In Proceedings of the Fourth International Symposium on Marine Propulsors, Austin, TX, USA, 31 May–4 June 2015. [Google Scholar]
- Made, J.E.; Kurtz, D.W. A Review of Aerodynamic Noise From Propellers, Rofors, and Liff Fans; Technical Report 32-7462; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1970. [Google Scholar]
- Plesset, M.S. The dynamics of cavitation bubbles. J. Appl. Mech. 1949, 16, 228–231. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Lauterborn, W.; Kurz, T. Physics of bubble oscillations. Rep. Prog. Phys. 2010, 73, 106501. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Nguyen, B.Q.H.; Suslov, S.A. Biomechanical sensing using gas bubbles oscillations in liquids and adjacent technologies: Theory and practical applications. Biosensors 2022, 12, 624. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Nguyen, B.Q.H.; Pototsky, A.; Suslov, S.A. Acoustic, phononic, Brillouin light scattering and Faraday wave-based frequency combs: Physical foundations and applications. Sensors 2022, 22, 3921. [Google Scholar] [CrossRef] [PubMed]
- Lauterborn, W.; Mettin, R. Nonlinear Bubble Dynamics. In Sonochemistry and Sonoluminescence; Crum, L.A., Mason, T.J., Reisse, J.L., Suslick, K.S., Eds.; Springer: Dordrecht, The Netherlands, 1999; pp. 63–72. [Google Scholar]
- Maksymov, I.S.; Greentree, A.D. Coupling light and sound: Giant nonlinearities from oscillating bubbles and droplets. Nanophotonics 2019, 8, 367–390. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, Y.; Leech, P.W.; Manasseh, R. Production of monodispersed micron-sized bubbles at high rates in a microfluidic device. Appl. Phys. Lett. 2009, 95, 144101. [Google Scholar] [CrossRef]
- Suslov, S.A.; Ooi, A.; Manasseh, R. Nonlinear dynamic behavior of microscopic bubbles near a rigid wall. Phys. Rev. E 2012, 85, 066309. [Google Scholar] [CrossRef]
- Dzaharudin, F.; Suslov, S.A.; Manasseh, R.; Ooi, A. Effects of coupling, bubble size, and spatial arrangement on chaotic dynamics of microbubble cluster in ultrasonic fields. J. Acoust. Soc. Am. 2013, 134, 3425–3434. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, B.Q.H.; Maksymov, I.S.; Suslov, S.A. Spectrally wide acoustic frequency combs generated using oscillations of polydisperse gas bubble clusters in liquids. Phys. Rev. E 2021, 104, 035104. [Google Scholar] [CrossRef] [PubMed]
- Patterson, A.; Schiller, N.H.; Ackerman, K.A.; Gahlawat, A.; Gregory, I.M.; Hovakimyan, N. Controller Design for Propeller Phase Synchronization with Aeroacoustic Performance Metrics. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Su, P.; Chang, G.; Wu, J.; Wang, Y.; Feng, X. Design and experimental study of an embedded controller for a model-based controllable pitch propeller. Appl. Sci. 2024, 14, 3993. [Google Scholar] [CrossRef]
- Prosperetti, A. Nonlinear oscillations of gas bubbles in liquids: Steady-state solutions. J. Acoust. Soc. Am. 1974, 56, 878–885. [Google Scholar] [CrossRef]
- Keller, J.B.; Miksis, M. Bubble oscillations of large amplitude. J. Acoust. Soc. Am. 1980, 68, 628–633. [Google Scholar] [CrossRef]
- Paul, A.R.; Jain, A.; Alam, F. Drag reduction of a passenger car using flow control techniques. Int. J. Automot. Technol. 2019, 20, 397–410. [Google Scholar] [CrossRef]
- Nakamura, Y.; Nakashima, T.; Yan, C.; Shimizu, K.; Hiraoka, T.; Mutsuda, H.; Kanehira, T.; Nouzawa, T. Identification of wake vortices in a simplified car model during significant aerodynamic drag increase under crosswind conditions. J. Vis. 2022, 25, 983–997. [Google Scholar] [CrossRef]
- Miau, J.J.; Li, S.R.; Tsai, Z.X.; Phung, M.V.; Lin, S.Y. On the aerodynamic flow around a cyclist model at the hoods position. J. Vis. 2020, 23, 35–47. [Google Scholar] [CrossRef]
- Garcia-Ribeiro, D.; Bravo-Mosquera, P.D.; Ayala-Zuluaga, J.A.; Martinez-Castañeda, D.F.; Valbuena-Aguilera, J.S.; Cerón-Muñoz, H.D.; Vaca-Rios, J.J. Drag reduction of a commercial bus with add-on aerodynamic devices. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 1623–1636. [Google Scholar] [CrossRef]
- Trautmann, E.; Ray, L. Mobility characterization for autonomous mobile robots using machine learning. Auton. Robot. 2011, 30, 369–383. [Google Scholar] [CrossRef]
- Otsu, K.; Ono, M.; Fuchs, T.J.; Baldwin, I.; Kubota, T. Autonomous terrain classification with co- and self-training approach. IEEE Robot. Autom. Lett. 2016, 1, 814–819. [Google Scholar] [CrossRef]
- Christie, J.; Kottege, N. Acoustics based terrain classification for legged robots. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3596–3603. [Google Scholar] [CrossRef]
- Valada, A.; Burgard, W. Deep spatiotemporal models for robust proprioceptive terrain classification. Int. J. Robot. Res. 2017, 36, 1521–1539. [Google Scholar] [CrossRef]
- Santana, P.; Guedes, M.; Correia, L.; Barata, J. Stereo-based all-terrain obstacle detection using visual saliency. J. Field Robot. 2011, 28, 241–263. [Google Scholar] [CrossRef]
- Nava, M.; Guzzi, J.; Chavez-Garcia, R.O.; Gambardella, L.M.; Giusti, A. Learning long-range perception using self-supervision from short-range sensors and odometry. IEEE Robot. Autom. Lett. 2019, 4, 1279–1286. [Google Scholar]
- Konolige, K.; Agrawal, M.; Blas, M.R.; Bolles, R.C.; Gerkey, B.; Solà, J.; Sundaresan, A. Mapping, navigation, and learning for off-road traversal. J. Field Robot. 2009, 26, 88–113. [Google Scholar] [CrossRef]
- Zhou, S.; Xi, J.; McDaniel, M.W.; Nishihata, T.; Salesses, P.; Iagnemma, K. Self-supervised learning to visually detect terrain surfaces for autonomous robots operating in forested terrain. J. Field Robot. 2012, 29, 277–297. [Google Scholar] [CrossRef]
- Engelsman, D.; Klein, I. Data-driven denoising of stationary accelerometer signals. Measurement 2023, 218, 113218. [Google Scholar] [CrossRef]
- Brooks, C.; Iagnemma, K. Vibration-based terrain classification for planetary exploration rovers. IEEE Trans. Robot. 2005, 21, 1185–1191. [Google Scholar] [CrossRef]
- Giguere, P.; Dudek, G. A simple tactile probe for surface identification by mobile robots. IEEE Trans. Robot. 2011, 27, 534–544. [Google Scholar] [CrossRef]
- Yu, Z.; Sadati, S.M.H.; Perera, S.; Hauser, H.; Childs, P.R.N.; Nanayakkara, T. Tapered whisker reservoir computing for real-time terrain identification-based navigation. Sci. Rep. 2023, 13, 5213. [Google Scholar] [CrossRef]
- Nakajima, K.; Hauser, H.; Kang, R.; Guglielmino, E.; Caldwell, D.; Pfeifer, R. A soft body as a reservoir: Case studies in a dynamic model of octopus-inspired soft robotic arm. Front. Comput. Neurosci. 2013, 7, 91. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Liu, J.; Liu, B.; Wang, H.; Si, J.; Xu, P.; Xu, M. Potential applications of whisker sensors in marine science and engineering: A review. J. Mar. Sci. Eng. 2023, 11, 2108. [Google Scholar] [CrossRef]
- Trigona, C.; Sinatra, V.; Fallico, A.R.; Puglisi, S.; Andò, B.; Baglio, S. Dynamic Spatial Measurements based on a Bimorph Artificial Whisker and RTD-Fluxgate Magnetometer. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Furuta, T.; Fujii, K.; Nakajima, K.; Tsunegi, S.; Kubota, H.; Suzuki, Y.; Miwa, S. Macromagnetic simulation for reservoir computing utilizing spin dynamics in magnetic tunnel junctions. Phys. Rev. Appl. 2018, 10, 034063. [Google Scholar] [CrossRef]
- Taniguchi, T.; Ogihara, A.; Utsumi, Y.; Tsunegi, S. Spintronic reservoir computing without driving current or magnetic field. Sci. Rep. 2022, 12, 10627. [Google Scholar] [CrossRef]
- Vidamour, I.T.; Swindells, C.; Venkat, G.; Manneschi, L.; Fry, P.W.; Welbourne, A.; Rowan-Robinson, R.M.; Backes, D.; Maccherozzi, F.; Dhesi, S.S.; et al. Reconfigurable reservoir computing in a magnetic metamaterial. Commun. Phys. 2023, 6, 230. [Google Scholar] [CrossRef]
- Edwards, A.J.; Bhattacharya, D.; Zhou, P.; McDonald, N.R.; Misba, W.A.; Loomis, L.; García-Sánchez, F.; Hassan, N.; Hu, X.; Chowdhury, M.F.; et al. Data-driven denoising of stationary accelerometer signals. Commun. Phys. 2023, 6, 215. [Google Scholar] [CrossRef]
- Ivanov, E.N.; Tobar, M.E.; Woode, R.A. Microwave interferometry: Application to precision measurements and noise reduction techniques. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 1526–1536. [Google Scholar] [CrossRef]
- Maksymov, I.S.; Kostylev, M. Broadband stripline ferromagnetic resonance spectroscopy of ferromagnetic films, multilayers and nanostructures. Phys. E 2015, 69, 253–293. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Jeske, J.; Cole, J.H.; Greentree, A.D. Laser threshold magnetometry. New J. Phys. 2016, 18, 013015. [Google Scholar] [CrossRef]
- Templier, S.; Cheiney, P.; d’Armagnac de Castanet, Q.; Gouraud, B.; Porte, H.; Napolitano, F.; Bouyer, P.; Battelier, B.; Barrett, B. Tracking the vector acceleration with a hybrid quantum accelerometer triad. Sci. Adv. 2022, 8, eadd3854. [Google Scholar] [CrossRef]
- Tasker, J.F.; Frazer, J.; Ferranti, G.; Matthews, J.C.F. A Bi-CMOS electronic photonic integrated circuit quantum light detector. Sci. Adv. 2024, 10, eadk6890. [Google Scholar] [CrossRef] [PubMed]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Martinis, M. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Fujii, K.; Nakajima, K. Harnessing disordered-ensemble quantum dynamics for machine learning. Phys. Rev. Appl. 2017, 8, 024030. [Google Scholar] [CrossRef]
- Abbas, A.H.; Maksymov, I.S. Reservoir Computing Using Measurement-Controlled Quantum Dynamics. Electronics 2024, 13, 1164. [Google Scholar] [CrossRef]
- Barreiro, J.; Müller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.; Zoller, P.; Blatt, R. An open-system quantum simulator with trapped ions. Nature 2011, 470, 486–491. [Google Scholar] [CrossRef]
- Hu, Z.; Xia, R.; Kais, S. A quantum algorithm for evolving open quantum dynamics on quantum computing devices. Sci. Rep. 2020, 10, 3301. [Google Scholar] [CrossRef] [PubMed]
- Del Re, L.; Rost, B.; Kemper, A.F.; Freericks, J.K. Driven-dissipative quantum mechanics on a lattice: Simulating a fermionic reservoir on a quantum computer. Phys. Rev. B 2020, 102, 125112. [Google Scholar] [CrossRef]
- Zheng, C. Universal quantum simulation of single-qubit nonunitary operators using duality quantum algorithm. Sci. Rep. 2021, 11, 3960. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Baek, H.; Yoon, J.W.; Lee, Y.K.; Kim, J. AQUA: Analytics-driven quantum neural network (QNN) user assistance for software validation. Future Gener. Comput. Syst. 2024, 159, 545–556. [Google Scholar] [CrossRef]
- Sannia, A.; Martínez-Peña, R.; Soriano, M.C.; Giorgi, G.L.; Zambrini, R. Dissipation as a resource for Quantum Reservoir Computing. Quantum 2024, 8, 1291. [Google Scholar] [CrossRef]
- Marković, D.; Grollier, J. Quantum neuromorphic computing. Appl. Phys. Lett. 2020, 117, 150501. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Quantum Mechanics; Prentice Hall: Hoboken, NJ, USA, 2004. [Google Scholar]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Zhang, J.; Pagano, G.; Hess, P.W.; Kyprianidis, A.; Becker, P.; Kaplan, H.; Gorshkov, A.V.; Gong, Z.X.; Monroe, C. Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator. Nature 2017, 551, 601–604. [Google Scholar] [CrossRef] [PubMed]
- Pino, J.M.; Dreiling, J.M.; Figgatt, C.; Gaebler, J.P.; Moses, S.A.; Allman, M.S.; Baldwin, C.H.; Foss-Feig, M.; Hayes, D.; Mayer, K.; et al. Demonstration of the trapped-ion quantum CCD computer architecture. Nature 2021, 592, 209–213. [Google Scholar] [CrossRef] [PubMed]
- Negoro, M.; Mitarai, K.; Fujii, K.; Nakajima, K.; Kitagawa, M. Machine learning with controllable quantum dynamics of a nuclear spin ensemble in a solid. arXiv 2018, arXiv:1806.10910. [Google Scholar]
- Chen, J.; Nurdin, H.I.; Yamamoto, N. Temporal information processing on noisy quantum computers. Phys. Rev. Appl. 2020, 14, 024065. [Google Scholar] [CrossRef]
- Dasgupta, S.; Hamilton, K.E.; Banerjee, A. Characterizing the memory capacity of transmon qubit reservoirs. In Proceedings of the 2022 IEEE International Conference on Quantum Computing and Engineering (QCE), Broomfield, CO, USA, 18–23 September 2022; pp. 162–166. [Google Scholar]
- Cai, Y.; Roslund, J.; Ferrini, G.; Arzani, F.; Xu, X.; Fabre, C.; Treps, N. Multimode entanglement in reconfigurable graph states using optical frequency combs. Nat. Commun. 2017, 8, 15645. [Google Scholar] [CrossRef]
- Nokkala, J.; Arzani, F.; Galve, F.; Zambrini, R.; Maniscalco, S.; Piilo, J.; Treps, N.; Parigi, V. Reconfigurable optical implementation of quantum complex networks. New J. Phys. 2018, 20, 053024. [Google Scholar] [CrossRef]
- Bravo, R.A.; Najafi, K.; Gao, X.; Yelin, S.F. Quantum Reservoir Computing Using Arrays of Rydberg Atoms. PRX Quantum 2022, 3, 030325. [Google Scholar] [CrossRef]
- Nakajima, K.; Fujii, K.; Negoro, M.; Mitarai, K.; Kitagawa, M. Boosting Computational Power through Spatial Multiplexing in Quantum Reservoir Computing. Phys. Rev. Appl. 2019, 11, 034021. [Google Scholar] [CrossRef]
- Marzuoli, A.; Rasetti, M. Computing spin networks. Ann. Phys. 2005, 318, 345–407. [Google Scholar] [CrossRef]
- Tserkovnyak, Y.; Loss, D. Universal quantum computation with ordered spin-chain networks. Phys. Rev. A 2011, 84, 032333. [Google Scholar] [CrossRef]
- Chen, J.M.; Nurdin, H.I. Learning nonlinear input–output maps with dissipative quantum systems. Quantum Inf. Process 2019, 18, 1440–1451. [Google Scholar]
- Mujal, P.; Nokkala, J.; Martínez-Peña, R.; Giorgi, G.L.; Soriano, M.C.; Zambrini, R. Analytical evidence of nonlinearity in qubits and continuous-variable quantum reservoir computing. J. Phys. Complex. 2021, 2, 045008. [Google Scholar] [CrossRef]
- Martínez-Peña, R.; Nokkala, J.; Giorgi, G.L. Information processing capacity of spin-based quantum reservoir computing systems. Cogn. Comput. 2023, 15, 1440–1451. [Google Scholar] [CrossRef]
- Hanson, R.; Awschalom, D.D. Coherent manipulation of single spins in semiconductors. Nature 2008, 453, 1043–1049. [Google Scholar] [CrossRef]
- Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120. [Google Scholar] [CrossRef]
- Wendin, G. Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef]
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031–1042. [Google Scholar] [CrossRef] [PubMed]
- Blatt, R.; Wineland, D. Entangled states of trapped atomic ions. Nature 2008, 453, 1008–1015. [Google Scholar] [CrossRef]
- Monroe, C.; Kim, J. Scaling the ion trap quantum processor. Science 2013, 339, 1164–1169. [Google Scholar] [CrossRef]
- Singh, S.P. The Ising Model: Brief Introduction and Its Application. In Metastable, Spintronics Materials and Mechanics of Deformable Bodies; Sivasankaran, S., Nayak, P.K., Günay, E., Eds.; IntechOpen: Rijeka, Croatia, 2020; Chapter 8. [Google Scholar] [CrossRef]
- Lüders, G. Über die Zustandsänderung durch den Meßprozeß. Ann. Phys. 1950, 443, 322–328. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Xia, W.; Zou, J.; Qiu, X. The reservoir learning power across quantum many-body localization transition. Front. Phys. 2022, 17, 33506. [Google Scholar] [CrossRef]
- Ponte, P.; Chandran, A.; Papić, Z.; Abanin, D.A. Periodically driven ergodic and many-body localized quantum systems. Ann. Phys. 2015, 353, 196–204. [Google Scholar] [CrossRef]
- Altshuler, B.; Krovi, H.; Roland, J. Anderson localization makes adiabatic quantum optimization fail. Proc. Natl. Acad. Sci. USA 2010, 28, 12446–12450. [Google Scholar] [CrossRef]
- Horodecki, P.; Rudnicki, L.; Życzkowski, K. Five open problems in quantum information theory. PRX Quantum 2022, 3, 010101. [Google Scholar] [CrossRef]
- Qiu, P.H.; Chen, X.G.; Shi, Y.W. Detecting entanglement with deep quantum neural networks. IEEE Access 2019, 7, 94310–94320. [Google Scholar] [CrossRef]
- Peral-García, D.; Cruz-Benito, J.; García-Peñalvo, F.J. Systematic literature review: Quantum machine learning and its applications. Comput. Sci. Rev. 2024, 51, 100619. [Google Scholar] [CrossRef]
- Campaioli, F.; Cole, J.H.; Hapuarachchi, H. A Tutorial on Quantum Master Equations: Tips and tricks for quantum optics, quantum computing and beyond. arXiv 2023, arXiv:2303.16449. [Google Scholar]
- Bollt, E. On explaining the surprising success of reservoir computing forecaster of chaos? The universal machine learning dynamical system with contrast to VAR and DMD. Chaos 2021, 31, 013108. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, D.J.; Bollt, E.; Griffith, A.; Barbosa, W.A.S. Next generation reservoir computing. Nat. Commun. 2021, 12, 5564. [Google Scholar] [CrossRef]
- Kalfus, W.D.; Ribeill, G.J.; Rowlands, G.E.; Krovi, H.K.; Ohki, T.A.; Govia, L.C.G. Hilbert space as a computational resource in reservoir computing. Phys. Rev. Res. 2022, 4, 033007. [Google Scholar] [CrossRef]
- Frattini, N.E.; Sivak, V.V.; Lingenfelter, A.; Shankar, S.; Devoret, M.H. Optimizing the nonlinearity and dissipation of a SNAIL parametric amplifier for dynamic range. Phys. Rev. Appl. 2018, 10, 054020. [Google Scholar] [CrossRef]
- Yasuda, T.; Suzuki, Y.; Kubota, T.; Nakajima, K.; Gao, Q.; Zhang, W.; Shimono, S.; Nurdin, H.I.; Yamamoto, N. Quantum reservoir computing with repeated measurements on superconducting devices. arXiv 2023, arXiv:2310.06706. [Google Scholar]
- Mujal, P.; Martínez-Peña, R.; Giorgi, G.L.; Soriano, M.C.; Zambrini, R. Time-series quantum reservoir computing with weak and projective measurements. NPJ Quantum. Inf. 2023, 9, 021008. [Google Scholar] [CrossRef]
- Harrington, P.M.; Monroe, J.T.; Murch, K.W. Quantum Zeno Effects from Measurement Controlled Qubit-Bath Interactions. Phys. Rev. Lett. 2017, 118, 240401. [Google Scholar] [CrossRef]
- Raimond, J.M.; Facchi, P.; Peaudecerf, B.; Pascazio, S.; Sayrin, C.; Dotsenko, I.; Gleyzes, S.; Brune, M.; Haroche, S. Quantum Zeno dynamics of a field in a cavity. Phys. Rev. A 2012, 86, 032120. [Google Scholar] [CrossRef]
- Lewalle, P.; Martin, L.S.; Flurin, E.; Zhang, S.; Blumenthal, E.; Hacohen-Gourgy, S.; Burgarth, D.; Whaley, K.B. A Multi-Qubit Quantum Gate Using the Zeno Effect. Quantum 2023, 7, 1100. [Google Scholar] [CrossRef]
- Kondo, Y.; Matsuzaki, Y.; Matsushima, K.; Filgueiras, J.G. Using the quantum Zeno effect for suppression of decoherence. New J. Phys. 2016, 18, 013033. [Google Scholar] [CrossRef]
- Monras, A.; Romero-Isart, O. Quantum Information Processing with Quantum Zeno Many-Body Dynamics. arXiv 2009, arXiv:0801.1959. [Google Scholar] [CrossRef]
- Paz-Silva, G.A.; Rezakhani, A.T.; Dominy, J.M.; Lidar, D.A. Zeno effect for quantum computation and control. Phys. Rev. Lett. 2012, 108, 080501. [Google Scholar] [CrossRef]
- Burgarth, D.K.; Facchi, P.; Giovannetti, V.; Nakazato, H.; Yuasa, S.P.K. Exponential rise of dynamical complexity in quantum computing through projections. Nat. Commun. 2014, 5, 5173. [Google Scholar] [CrossRef]
- Feynman, R.P. There’s Plenty of Room at the Bottom. In Proceedings of the Annual Meeting of the American Physical Society at the California Institute of Technology, Pasadena, CA, USA, 29 December 1959. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.H.; Abdel-Ghani, H.; Maksymov, I.S. Classical and Quantum Physical Reservoir Computing for Onboard Artificial Intelligence Systems: A Perspective. Dynamics 2024, 4, 643-670. https://doi.org/10.3390/dynamics4030033
Abbas AH, Abdel-Ghani H, Maksymov IS. Classical and Quantum Physical Reservoir Computing for Onboard Artificial Intelligence Systems: A Perspective. Dynamics. 2024; 4(3):643-670. https://doi.org/10.3390/dynamics4030033
Chicago/Turabian StyleAbbas, A. H., Hend Abdel-Ghani, and Ivan S. Maksymov. 2024. "Classical and Quantum Physical Reservoir Computing for Onboard Artificial Intelligence Systems: A Perspective" Dynamics 4, no. 3: 643-670. https://doi.org/10.3390/dynamics4030033
APA StyleAbbas, A. H., Abdel-Ghani, H., & Maksymov, I. S. (2024). Classical and Quantum Physical Reservoir Computing for Onboard Artificial Intelligence Systems: A Perspective. Dynamics, 4(3), 643-670. https://doi.org/10.3390/dynamics4030033






