Preliminary Numerical Modelling of a Dynamic Spring-Mounted Wing System to Reduce the Drag of Vehicles at Higher Speeds
Abstract
1. Introduction
2. Methodology
2.1. Geometry
2.2. Numerical Modelling
2.3. Modelling Assumptions
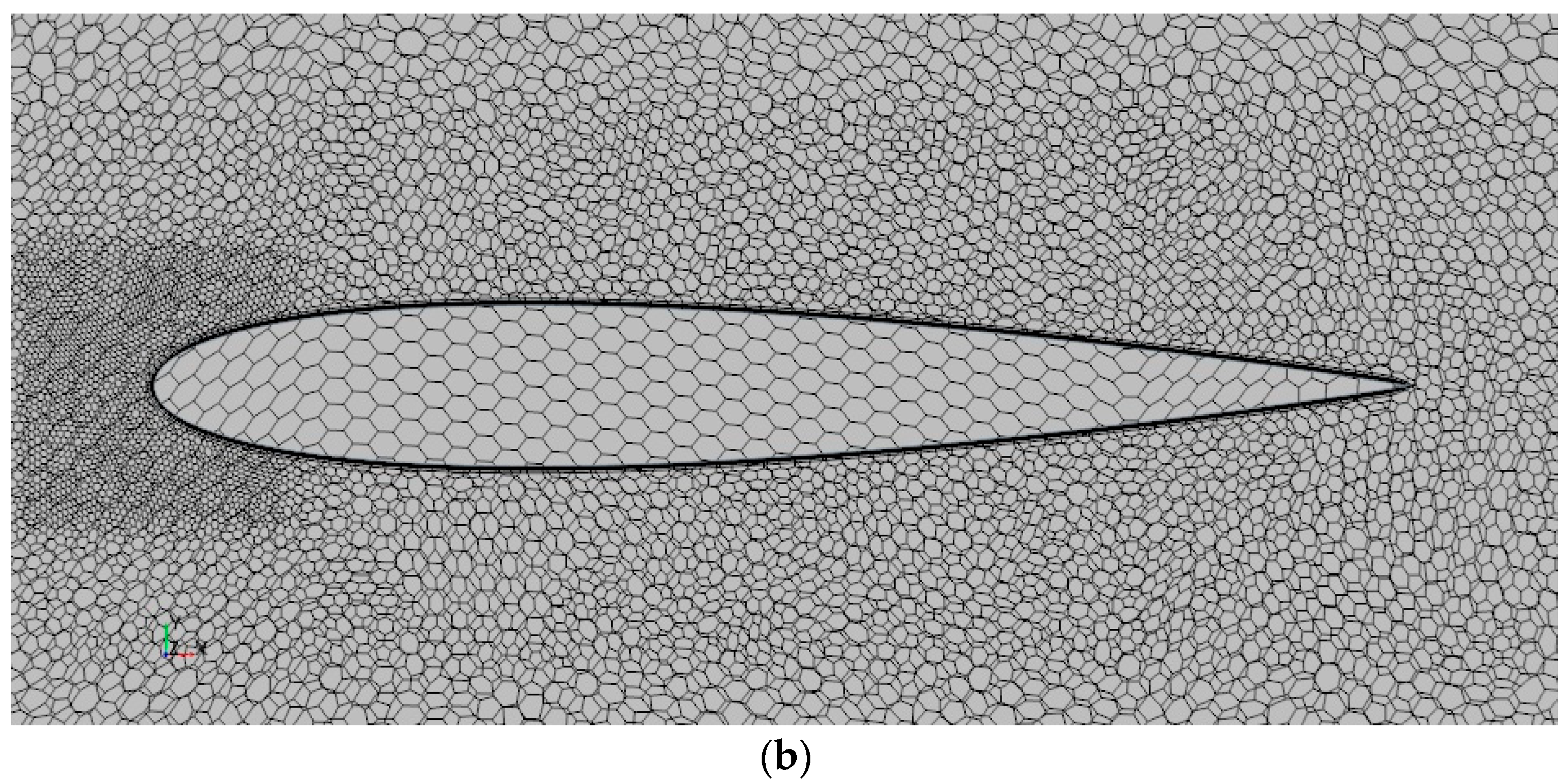
2.4. Mesh
2.5. Fluid–Structure Interaction Modelling
3. Results
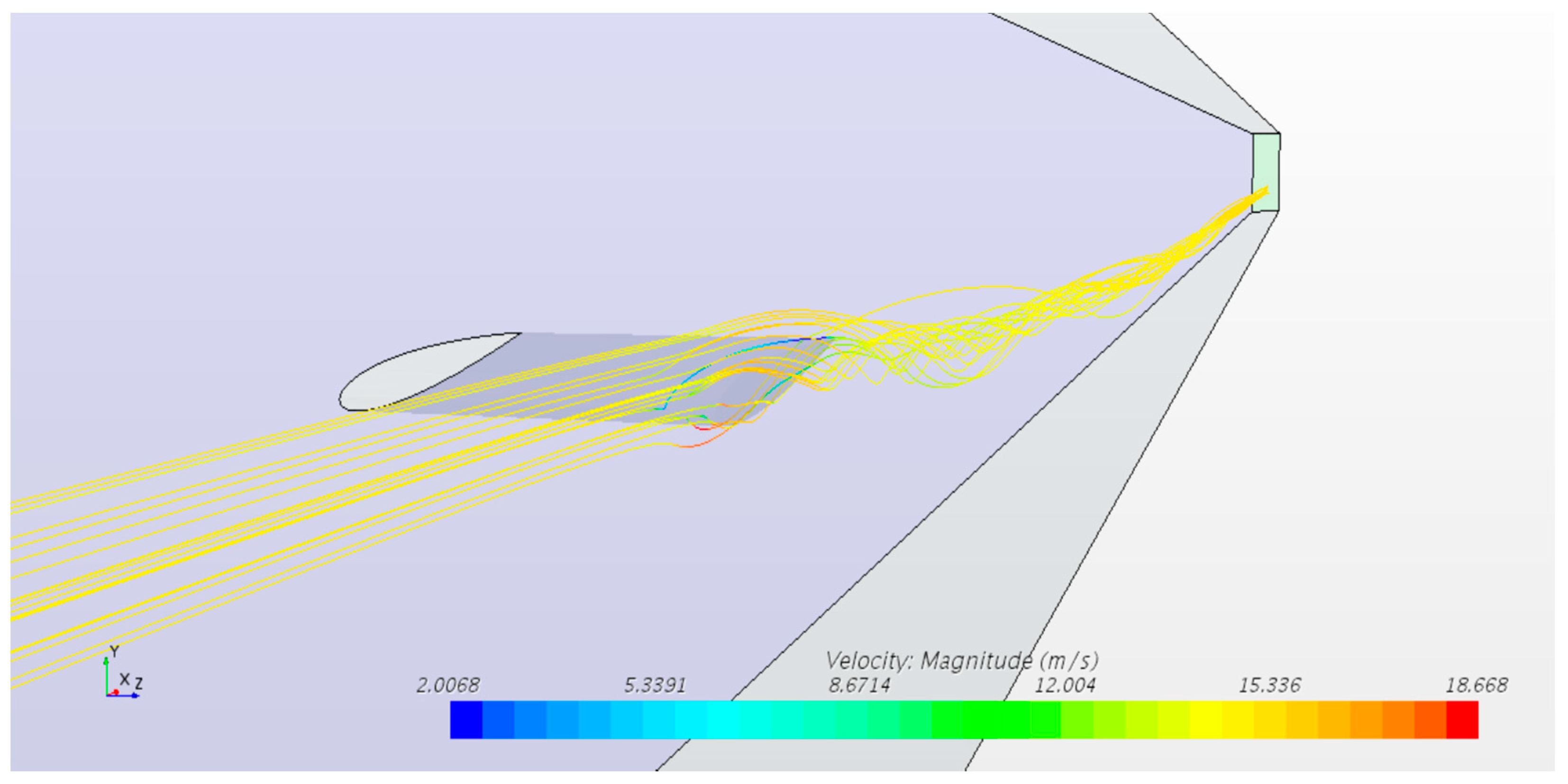
3.1. Initial Findings
3.2. Variation of Preload
3.3. Validation with Experiment
3.4. Variation of Downforce
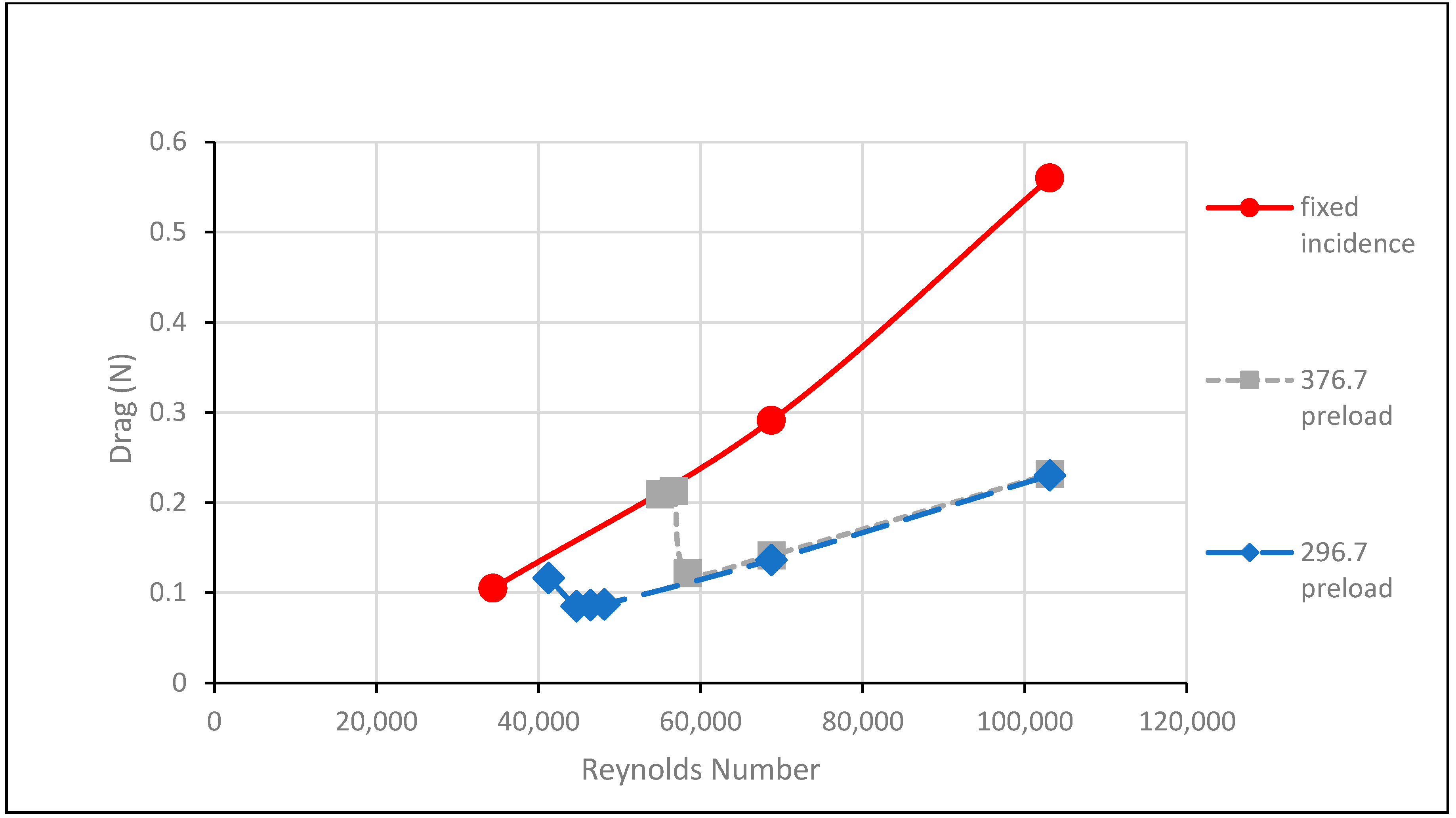
3.5. Variation in Drag
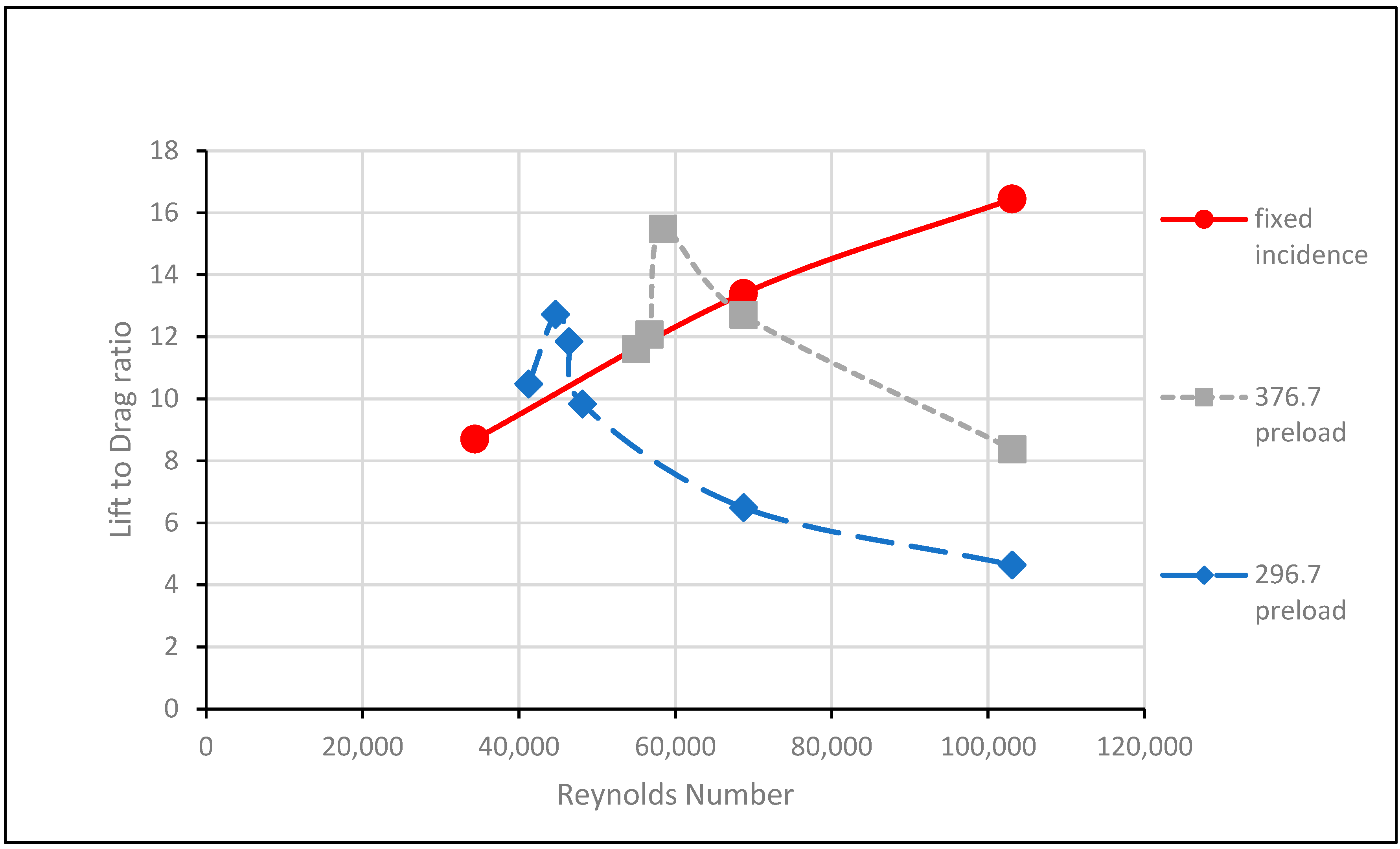
3.6. Efficiency
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buresti, G. Vortex Shedding from Bluff Bodies. In Wind Effects on Buildings and Structures; Reira, J.D., Davenport, A.G., Eds.; Balkema: Rotterdam, The Netherlands, 1998; pp. 61–95. [Google Scholar]
- Morgenthal, G. Fluid-Structure Interaction in Bluff-Body Aerodynamics and Long-Span Bridge Design_Phenomena and Methods; University of Cambridge: Cambridge, UK, 2000. [Google Scholar]
- Szabó, G.; Györgyi, J. Three-dimensional Fluid-Structure Interaction Analysis for Bridge Aeroelasticity. In Lecture Notes in Engineering and Computer Science; Springer: Berlin, Germany, 2009; Volume 2179, pp. 1–81. [Google Scholar]
- Zhang, H.; Liu, L.; Dong, M.; Sun, H. Analysis of wind-induced vibration of fluid-structure interaction system for isolated aqueduct bridge. Eng. Struct. 2013, 46, 28–37. [Google Scholar] [CrossRef]
- Lee, Y.J.; Jhan, Y.T.; Chung, C.H. Fluid–structure interaction of FRP wind turbine blades under aerodynamic effect. Compos. Part B Eng. 2012, 43, 2180–2191. [Google Scholar] [CrossRef]
- Knight, J.; McConnell, M.R.; Ledger, A.; Azcueta, R. Fluid structure interaction of hydrofoils. In Proceedings of the ICMET Oman 2019—International Conference on Marine Engineering and Technology, Muscat, Oman, 5–7 November 2019. [Google Scholar]
- Garelli, L.; Paz, R.; Storti, M. Fluid-structure interaction study of the start-up of a rocket engine nozzle. Comput. Fluids 2010, 39, 1208–1218. [Google Scholar] [CrossRef]
- Pelosi, M. An Investigation of the Fluid-Structure Interaction of Piston/Cylinder Interface; Purdue University: West Lafayette, IN, USA, 2012. [Google Scholar]
- Rehnberg, S.; Börjesson, L.; Svensson, R.; Rice, J. Race Car Aerodynamics—The Design Process of an Aerodynamic Package for the 2012 Chalmers Formula SAE Car. 2013. Available online: https://www.sae.org/publications/technical-papers/content/2013-01-0797/ (accessed on 4 July 2024).
- Barnard, R.H. Road Vehicle Aerodynamics, 3rd ed.; Mechaero Publishing: St Albans, UK, 2010. [Google Scholar]
- Katz, J. New Directions in Race Car Aerodynamics: Designing for Speed, 2nd ed.; Bentley Publishers: Cambridge, MA, USA, 2008. [Google Scholar]
- Jung, F. All vehicles can benefit from active aerodynamics. ATZ Worldw. 2021, 123, 22–25. [Google Scholar] [CrossRef]
- Maughmer, S.S.; Lesieutre, G.A. Formula 1 Race Car Performance Improvement by Optimization of the Aerodynamic Relationship between the Front and Rear Wings. Master’s Thesis, Penn State University Libraries, State College, PA, USA, 2 December 2014. [Google Scholar]
- Cakir, M. Scholar Commons CFD Study on Aerodynamic Effects of a Rear Wing/Spoiler on a Passenger Vehicle. 2012. Available online: http://scholarcommons.scu.edu/mech_mstr/1 (accessed on 4 July 2024).
- Koike, M.; Nagayoshi, T.; Hamamoto, N. Research on Aerodynamic Drag Reduction. Mitsubishi Mot. Tech. Rev. 2004, 11, 49. [Google Scholar]
- Buljac, A.; Džijan, I.; Korade, I.; Krizmanić, S.; Kozmar, H. Automobile aerodynamics influenced by airfoil-shaped rear wing. Int. J. Automot. Technol. 2016, 17, 377–385. [Google Scholar] [CrossRef][Green Version]
- Knight, J.; Spicak, M.; Kuzenko, A.; Haritos, G.; Ren, G. Investigation of Vehicle Ride Height and Diffuser Ramp Angle on Downforce and Efficiency. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 233, 2139–2145. [Google Scholar] [CrossRef]
- GPfans.com. F1 DRS Explained: What Is Drag Reduction System and How Does It Work? 2024. Available online: https://www.gpfans.com/en/f1-news/102569/drs-f1/ (accessed on 9 May 2024).
- Knight, J.; Fels, S.; Haritos, G.; Carolus, T. Fluid-Structure Interaction of a Spring-Mounted Symmetrical Rigid Wing for Drag Reduction of Cars at Higher Wind Velocities. SAE Technical Papers. 2020, pp. 1–13. Available online: https://www.sae.org/publications/technical-papers/content/2020-01-5037/ (accessed on 4 July 2024).
- Siemens Digital Industries Software. Simcenter STAR-CCM+, version 2023.1; Siemens: Munich, Germany, 2023. [Google Scholar]
- Airfoil Tools. NACA 0012 AIRFOILS (n0012-il). Airfoiltools.com. 2019. Available online: http://airfoiltools.com/airfoil/details?airfoil=n0012-il (accessed on 4 July 2024).
- Narayan, G.; John, B. Effect of winglets induced tip vortex structure on the performance of subsonic wings. Aerosp. Sci. Technol. 2016, 58, 328–340. [Google Scholar] [CrossRef]
- Yousefi, K.; Razeghi, A. Determination of the critical reynolds number for flow over symmetric NACA airfoils. In Proceedings of the AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; Volume 210059, pp. 1–11. [Google Scholar] [CrossRef]
- Anderson, J.D.; Degroote, J.; Degrez, G.; Dick, E.; Grundmann, R.; Vierendeels, J. Computational Fluid Dynamics an Introduction, 3rd ed.; Wendt, J.F., Ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Jeong, W.; Seong, J. Comparison of effects on technical variances of computational fluid dynamics (CFD) software based on finite element and finite volume methods. Int. J. Mech. Sci. 2014, 78, 19–26. [Google Scholar] [CrossRef]
- Siemens Digital Industries Software. Introductory Guide to Overset Simulations 2020. Available online: https://community.sw.siemens.com/s/article/Introductory-Guide-to-Overset-Simulations (accessed on 4 July 2024).
- Jain, S.; Sitaram, N.; Krishnaswamy, S. Computational Investigations on the Effects of Gurney Flap on Airfoil Aerodynamics. Int. Sch. Res. Not. 2015, 2015, 402358. [Google Scholar] [CrossRef] [PubMed]
- Kanife, P.O. Computer Aided Virtual Manufacturing Using Creo Parametric: Easy to Learn Step by Step Guide; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Mo, J.O.; Rho, B.S. Characteristics and effects of laminar separation bubbles on NREL S809 airfoil using the γ-ReΘ transition model. Appl. Sci. 2020, 10, 6095. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Açıkel, H.H.; Çağdaş, M.; Bodur, T.M. Identification of flow phenomena over NACA 4412 wind turbine airfoil at low Reynolds numbers and role of laminar separation bubble on flow evolution. Energy 2018, 144, 750–764. [Google Scholar] [CrossRef]
- Knight, J.; Fels, S.; Beazley, B.; Haritos, G.; Lewis, A. Fluid–Structure Interaction of Symmetrical and Cambered Spring-Mounted Wings Using Various Spring Preloads and Pivot Point Locations. Appl. Mech. 2021, 2, 591–612. [Google Scholar] [CrossRef]









| Parameter | Symbol | Value |
|---|---|---|
| Centre of gravity | CoG | 0.0424 m |
| Centre of rotation | CoR | 0.01 m |
| Chord length | 0.1 m | |
| Coefficient of drag | CD | CFD data 1 |
| Coefficient of lift | CL | CFD data 1 |
| Density of air | 1.226 kg/m3 | |
| Drag | D | CFD data 1 |
| Freestream velocity | 4–15 m/s | |
| Incidence | α | 0–12 degrees 1 |
| Lift | L | CFD data 1 |
| Mass moment of inertia | I | 1.862991 × 10−4 kgm2 |
| Mass of airfoil | m | 0.1193 kg |
| Reynolds number | Re | 27,000–103,000 |
| Torsional spring constant | K | 0.1638 Nmm/degree |
| Torsional spring preload | θ | 296.7 to 536.7 degrees |
| Viscosity of air | 1.784 × 10−5 kg/ms | |
| Wing area | A | 0.0228 m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knight, J.; Patel, J.; Prouse-Edwards, H.; Fels, S.; Montalvao, D.; Lewis, A. Preliminary Numerical Modelling of a Dynamic Spring-Mounted Wing System to Reduce the Drag of Vehicles at Higher Speeds. Dynamics 2024, 4, 592-608. https://doi.org/10.3390/dynamics4030031
Knight J, Patel J, Prouse-Edwards H, Fels S, Montalvao D, Lewis A. Preliminary Numerical Modelling of a Dynamic Spring-Mounted Wing System to Reduce the Drag of Vehicles at Higher Speeds. Dynamics. 2024; 4(3):592-608. https://doi.org/10.3390/dynamics4030031
Chicago/Turabian StyleKnight, Jason, Jay Patel, Harry Prouse-Edwards, Simon Fels, Diogo Montalvao, and Andrew Lewis. 2024. "Preliminary Numerical Modelling of a Dynamic Spring-Mounted Wing System to Reduce the Drag of Vehicles at Higher Speeds" Dynamics 4, no. 3: 592-608. https://doi.org/10.3390/dynamics4030031
APA StyleKnight, J., Patel, J., Prouse-Edwards, H., Fels, S., Montalvao, D., & Lewis, A. (2024). Preliminary Numerical Modelling of a Dynamic Spring-Mounted Wing System to Reduce the Drag of Vehicles at Higher Speeds. Dynamics, 4(3), 592-608. https://doi.org/10.3390/dynamics4030031








