Vertical and Lateral Dynamics of 4L Freight Bogie
Abstract
1. Introduction
1.1. Current Design of Freight Bogies
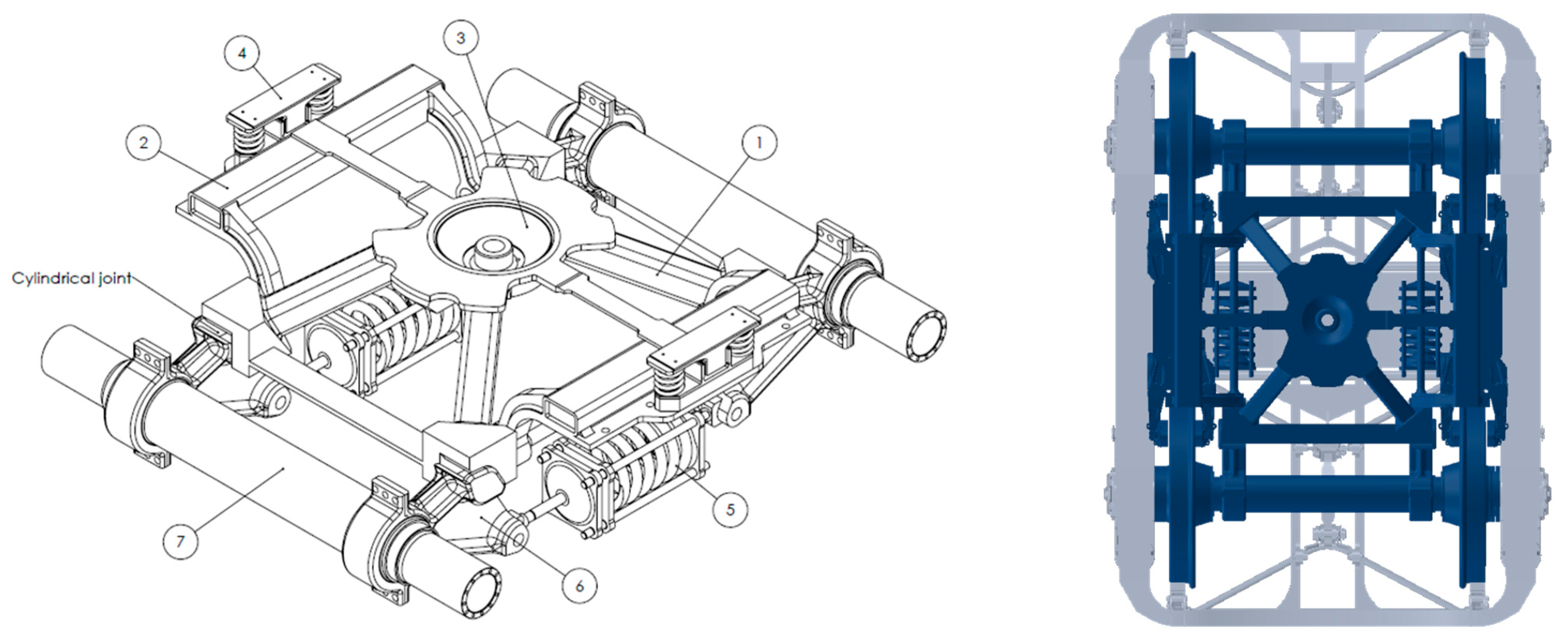
1.2. Description of the Innovative Freight Bogie
- If the track irregularity has a wavelength such that the front and rear wheels of each side of the bogie move in phase, the swinging arms rotate in the opposite direction, and the spring is stretched equally in both directions with respect to its middle plane. In this case, the dynamic apparent stiffness is half of the nominal spring stiffness.
- If track irregularity has a wavelength such that the front and rear wheels move in counter phase, the swinging arms rotate in the same direction and the spring is not stretched, showing a dynamic apparent stiffness equal to zero.
2. Material and Methods
2.1. Finite Element Model
2.2. Vehicle and Track Models
3. Results
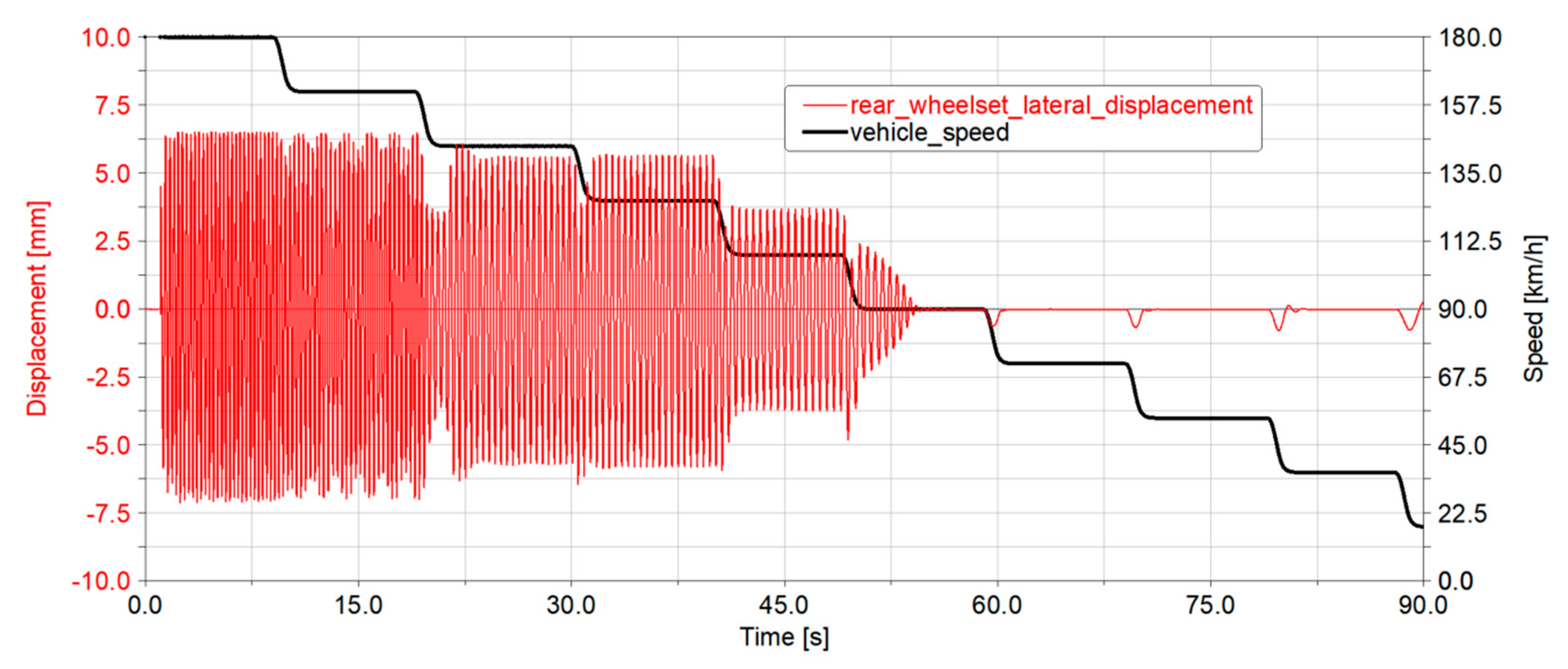
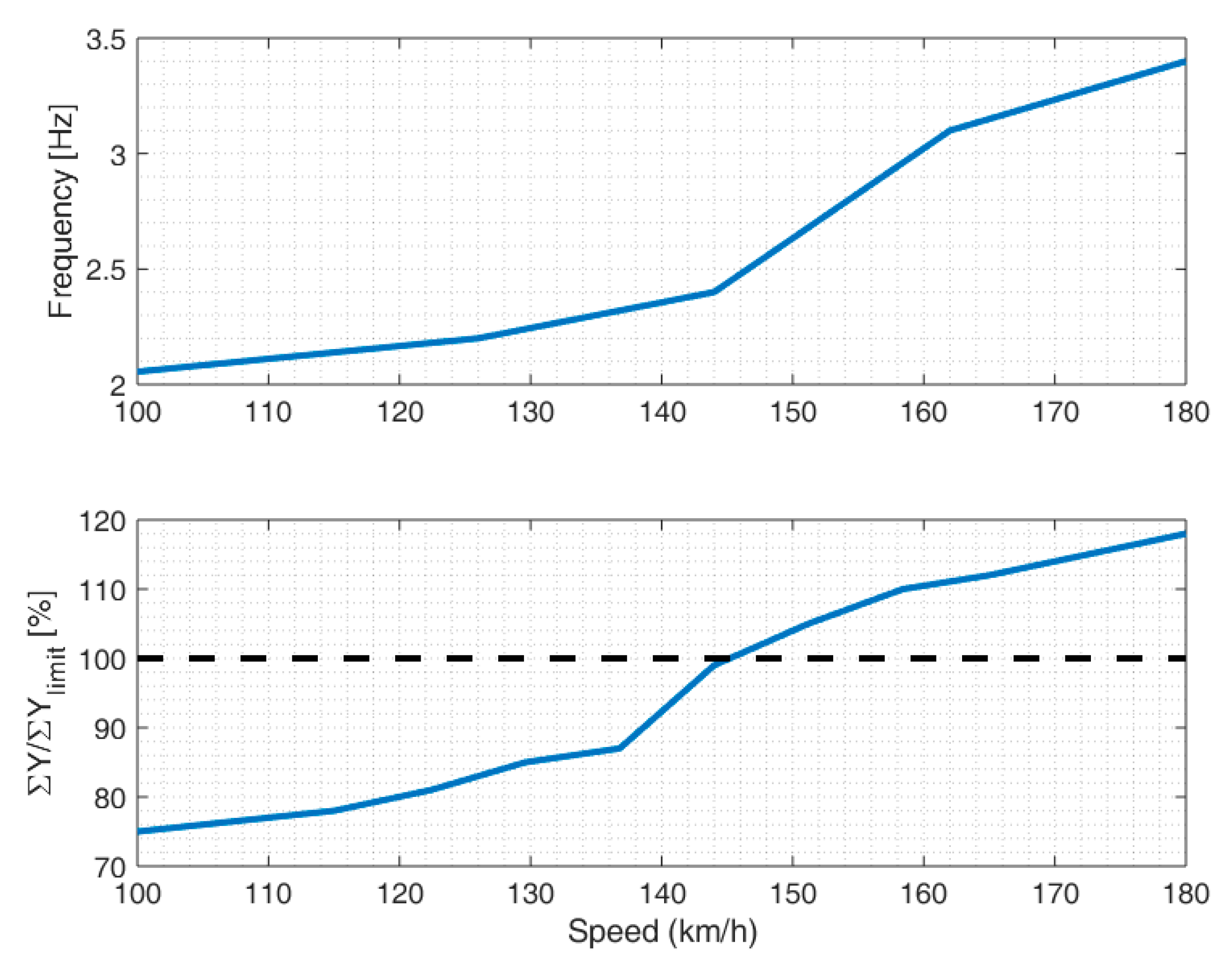
3.1. Lateral Dynamics on Straight Track
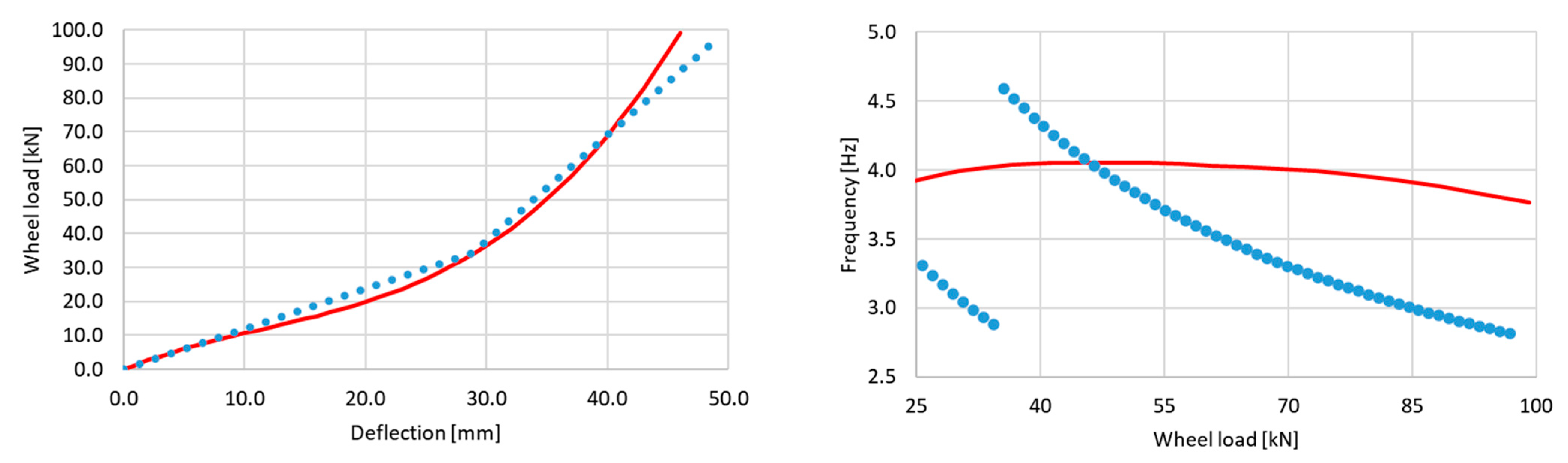
3.2. Vertical Dynamics on Sinusoidal Track Irregularities
3.3. Vertical Dynamics on Random PSD Irregularities
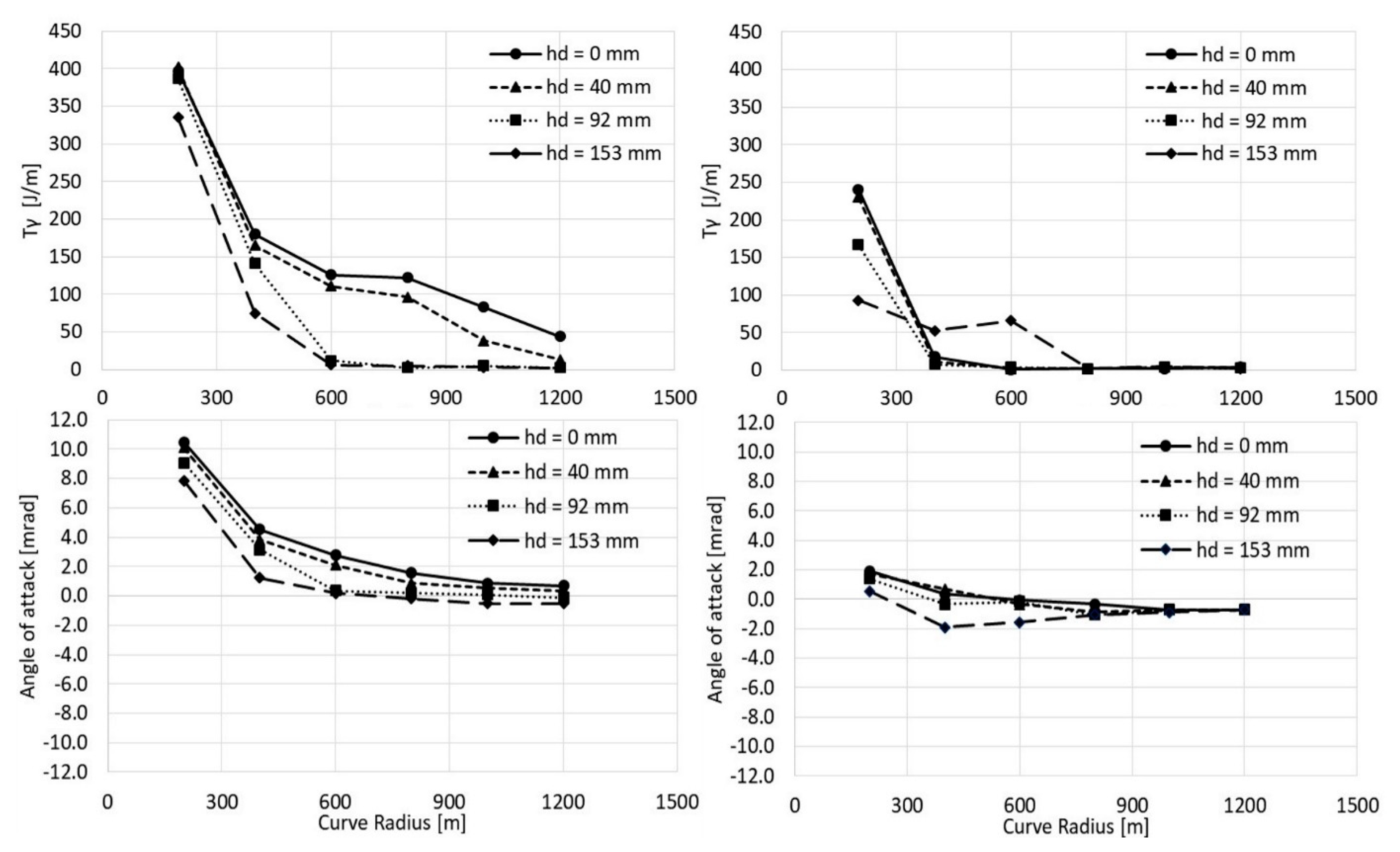
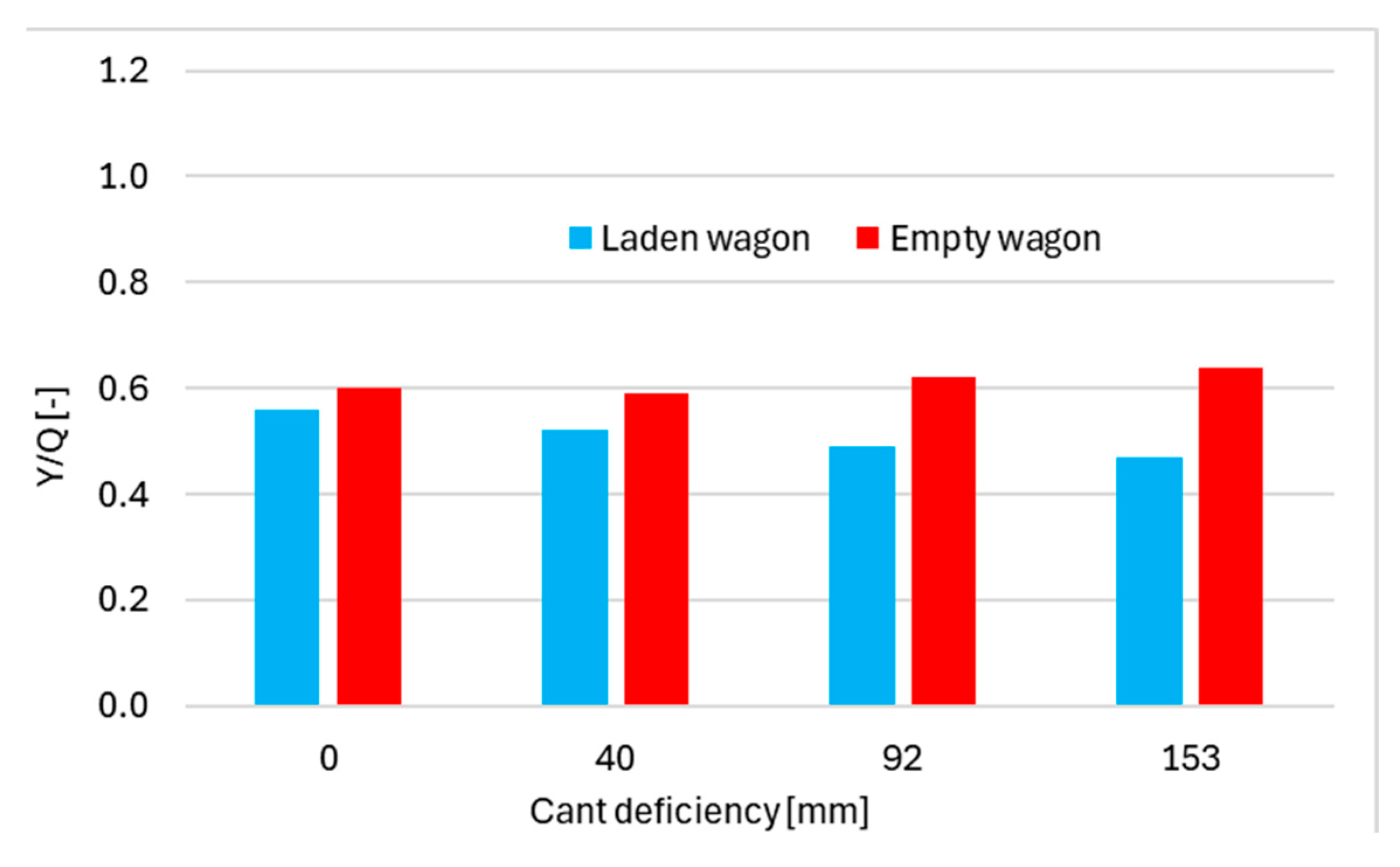
3.4. Steady State Curving Behaviour
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
List of Symbols
| Symbol | Description | Physical Unit |
| Tγ | Wear number at the wheel rail contact | J/m |
| K | Stiffness of the primary suspension | N/m |
| Q | Vertical wheel load | N |
| g | Gravitational acceleration | m/s2 |
| ΔQ | Variation of the wheel vertical load | N |
| Fz | Vertical load on the centre bowl of the bogie | N |
| a | Longitudinal length of the swinging arm | m |
| b | Vertical length of the swinging arm | m |
| X | Yaw resistance of the bogie | - |
| Mz | Frictional torque around the vertical axis | N/m |
| 2a+ | Bogie wheelbase | m |
| P0 | Vertical axle load | N |
| L | Wavelength of Klingel motion | m |
| R | Wheel radius | m |
| s | Distance between rolling radius circles | m |
| γ | Conicity of the wheels | - |
| γeq | Equivalent conicity for actual wheel/rail contact | - |
| f0 | Instability frequency | Hz |
| ΣY | Sum of the guiding (lateral) wheelset forces | N |
| λ | Wavelength of irregularities | m |
| P1 | Ride force coefficient | kN/mm |
| P2 | Ride force constant | kN |
| hd | Cant deficiency | mm |
| anc * | Non-compensated acceleration | m/s2 |
| Y | Guiding (lateral) wheel load | N |
| Y/Q | Derailment quotient | - |
| * Cant deficiency and non-compensated acceleration are related by the equation anc = hd(g/s) | ||
References
- Hecht, M. European freight vehicle running gear: Today’s position and future demands. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2001, 215, 1–11. [Google Scholar] [CrossRef]
- Iwnicki, S.D.; Stichel, S.; Orlova, A.; Hecht, M. Dynamics of railway freight vehicles. Veh. Syst. Dyn. 2015, 53, 995–1033. [Google Scholar] [CrossRef]
- SUSTRAIL Project. Concluding Technical Report. Available online: www.sustrail.eu/IMG/pdf/sustrail_final_book_web.pdf (accessed on 15 May 2024).
- 5L Project. White Paper Innovative Rail Freight Wagon 2030. Available online: https://www.schienenfzg.tu-berlin.de/fileadmin/fg62/pdf/White_Paper_Innovative_Rail_Freight_Wagon_2030_01.pdf (accessed on 15 May 2024).
- Greenbrier Europe. Products Catalogue. Available online: https://www.greenbrier-europe.com/products/product/ (accessed on 15 May 2024).
- Scoldan, D.; Gabriel, N.; Kik, W. RC25NT—A new track friendly bogie for the heavy freight transport. ZEVrail Glas. Ann. 2011, 135, 252–260. [Google Scholar]
- Tatravagonka Poprad. Track-Friendly Bogies. Available online: https://tatravagonka.sk/bogies_tax/track-friendly-bogies/?lang=en (accessed on 15 May 2024).
- TF25 Bogie. Available online: https://railway-news.com/download/wabtec-axiom-tf25-bogie-family/ (accessed on 15 May 2024).
- DRRS Bogie. Available online: https://www.railwaypro.com/wp/drrsss-y-bogie-for-rapid-freight-trains-in-germany/ (accessed on 15 May 2024).
- Searancke, E.J. The B5000 bogie development. In Wheels and Axles Cost-Effective Engineering; IMechE Seminar Publication; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Hecht, M. Wear and energy-saving freight bogie designs with rubber primary springs: Principles and experiences. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 227, 105–110. [Google Scholar] [CrossRef]
- Bracciali, A.; Megna, G. Contact mechanics issues of a vehicle equipped with partially independently rotating wheelsets. Wear 2016, 366–367, 233–240. [Google Scholar] [CrossRef]
- Ihme, J. Schienenfahrzeugtechnik; Springer: Berlin/Heidelberg, Germany, 2016; pp. 183–184. [Google Scholar]
- EN 13749:2021+A1:2023; Railway Applications—Wheelsets and Bogies—Method of Specifying the Structural Requirements of Bogie Frames. The European Committee for Standardization (CEN): Brussels, Belgium, 2023.
- DVS1612:2014; Design and Endurance Strength Analysis of Steel Welded Joints in Rail-Vehicle Construction. German Welding Society: Düsseldorf, Germany, 2014.
- Vi-Grade Engineering Software & Service; Vi-Rail 18.0 Documentation; Vi-Grade GmbH: Darmstadt, Germany, 2017.
- EN16235:2023; Railway Application—Testing for the Acceptance of Running Characteristics of Railway Vehicles—Freight Wagons—Conditions for Dispensation of Freight Wagons with Defined Characteristics from on-Track Tests according to EN 14363. The European Committee for Standardization (CEN): Brussels, Belgium, 2023.
- TENMAT. Advance Materials. Available online: https://www.tenmat.com/wear-parts-bearings/rail/ (accessed on 15 May 2024).
- EN 14363:2016+A2:2022; Railway Applications—Testing and Simulation for the Acceptance of Running Characteristics of Railway Vehicles—Running Behaviour and Stationary Tests. The European Committee for Standardization (CEN): Brussels, Belgium, 2022.
- Iwnicki, S. The results of Manchester benchmark. In The Manchester Benchmarks for Rail Vehicle Simulations, 1st ed.; Iwnicki, S., Ed.; Tailor & Francis: New York, NY, USA, 1999; pp. 2–12. [Google Scholar]
- True, H. Multiple attractors and critical parameters and how to find them numerically: The right, the wrong and the gambling way. Veh. Syst. Dyn. 2013, 51, 443–459. [Google Scholar] [CrossRef]
- Krishna, V.V.; Casanueva, C.; Hossein-Nia, S.; Stichel, S. FR8RAIL Y25 running gear for high tonnage and speed. In Proceedings of the International Heavy Haul Association Sts Conference (IHHA 2019), Narvik, Norway, 12–14 June 2019. [Google Scholar]
- Molatefi, H.; Hecht, M.; Kadivar, M.H. Critical speed and limit cycles in the empty Y25-freight wagon. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2006, 220, 347–359. [Google Scholar] [CrossRef]
- EN 15302:2021; Wheel-Rail Contact Geometry Parameters—Definitions and Methods for Evaluation. The European Committee for Standardization (CEN): Brussels, Belgium, 2021.
- CEN/TR 17039; Railway Applications—Technical Report about the Revision of EN 14363. The European Committee for Standardization (CEN): Brussels, Belgium, 2017.
- ERRI B176 RP1; Bogies with Steered or Steering Wheelsets, Report No. 1, Specifications and Preliminary Studies, Volume 2, Specifications for a Bogie with Improved Curving Characteristics. Office for Research and Experiments of the International Union of Railways: Utrecht, The Nederland, 1989.
- Network Rail. RFCpro Workshop. Available online: https://www.networkrail.co.uk/wp-content/uploads/2017/02/RFCpro-workshop-slides.pdf (accessed on 15 May 2024).
- Shackleton, P.; Bezin, Y.; Crosbee, D. Development of a new running gear for the Spectrum intermodal vehicle. In The Dynamics of Vehicles on Roads and Tracks, 1st ed.; Rosenberger, M., Plöchl, M., Six, K., Edelmann, J., Eds.; CRC Press: London, UK, 2016. [Google Scholar]
- Megna, G.; Bracciali, A. Gearless Track-Friendly Metro with Guided Independently Rotating Wheels. Urban Rail Transit 2021, 7, 285–300. [Google Scholar] [CrossRef]
- Tunna, J.; Urban, C. A parametric study of the effects of freight vehicles on rolling contact fatigue of rail. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 141–151. [Google Scholar] [CrossRef]
- Burstow, M. Whole Life Rail Model Application and Development for RSSB—Development of an RCF Damage Parameter; Rail Safety & Standards Board: London, UK, 2003. [Google Scholar]
- Öberg, J.; Andersson, E. Determining Deterioration Cost for Railway Tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 121–129. [Google Scholar] [CrossRef]
- Network Rail. VTAC Calculator: Guidance Note for Determining Tγ Values. Available online: https://www.networkrail.co.uk/wp-content/uploads/2016/12/VTAC-calculator-Guidance-note-for-determining-Tgamma-values.pdf (accessed on 15 May 2024).











| Bogie Type | Speed [km/h] | SD Mean Value [-] Tare | SD Mean Value [-] Laden |
|---|---|---|---|
| Y25 | 120 | 0.238 | 0.102 |
| 4L | 120 | 0.127 | 0.052 |
| 145 | 0.162 | 0.072 | |
| 160 | - | 0.085 | |
| Spectrum | 160 | 0.148 | 0.083 |
| Bogie Type (Empty Wagon) | Speed [km/h] | RFC [-] | Band | Discount Factor [-] |
|---|---|---|---|---|
| Y25 | 120 | 680–715 | 2 | 1.058 |
| 4L | 120 | 489 | 6 | 0.898 |
| 145 | 631 | 4 | 0.978 | |
| Spectrum | 160 | 465–564 | 6 | 0.898 |
| Bogie Type (Laden Wagon) | Speed [km/h] | RFC [-] | Band | Discount Factor [-] |
| Y25 | 120 | >1650 | 1 | 1.098 |
| 4L | 120 | 1029 | 6 | 0.898 |
| 145 | 1438 | 4 | 0.978 | |
| 160 | 1689 | 1 | 1.098 | |
| Spectrum | 160 | >1650 | 1 | 1.098 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megna, G. Vertical and Lateral Dynamics of 4L Freight Bogie. Dynamics 2024, 4, 554-571. https://doi.org/10.3390/dynamics4030029
Megna G. Vertical and Lateral Dynamics of 4L Freight Bogie. Dynamics. 2024; 4(3):554-571. https://doi.org/10.3390/dynamics4030029
Chicago/Turabian StyleMegna, Gianluca. 2024. "Vertical and Lateral Dynamics of 4L Freight Bogie" Dynamics 4, no. 3: 554-571. https://doi.org/10.3390/dynamics4030029
APA StyleMegna, G. (2024). Vertical and Lateral Dynamics of 4L Freight Bogie. Dynamics, 4(3), 554-571. https://doi.org/10.3390/dynamics4030029






