Dynamics and Stability of Double-Walled Carbon Nanotube Cantilevers Conveying Fluid in an Elastic Medium

Abstract

The paper concerns the dynamics and stability of double-walled carbon nanotubes conveying fluid. The equations of motion adopted in the current study to describe the dynamics of such nano-pipes stem from the classical Bernoulli–Euler beam theory. Several additional terms are included in the basic equations in order to take into account the influence of the conveyed fluid, the impact of the surrounding medium and the effect of the van der Waals interaction between the inner and outer single-walled carbon nanotubes constituting a double-walled one. In the present work, the flow-induced vibrations of the considered nano-pipes are studied for different values of the length of the pipe, its inner radius, the characteristics of the ambient medium and the velocity of the fluid flow, which is assumed to be constant. The critical fluid flow velocities are obtained at which such a cantilevered double-walled carbon nanotube embedded in an elastic medium loses stability.

1. Introduction

Scientific and technological progress in the last thirty years has led to the rapid development and study of mathematical models outlining the path to creating micro- and nanoelectromechanical systems (MEMS/NEMS) using various carbon allotropic forms: graphene, fullerenes and carbon nanotubes (see, e.g., [1,2,3,4,5,6,7]). All these objects are nano-sized, but the use of continuum mechanics in modelling their mechanical behaviour is surprisingly efficient, although, as noted by Yakobson et al. [8], “its relevance for a covalent bonded system of only a few atoms in diameter is far from obvious”. Among others, different types of models based on continuum mechanics have been proposed and used to describe the dynamic behaviour of structural components of nano-devices such as carbon nanotubes (CNTs) conveying fluids—the nanomechanical systems whose dynamic behaviour (vibration and stability) is the main subject of study in the present paper.

The investigation of the effects of fluid transport in CNTs is recognised to be of significant interest both for designing nanofluidic devices or CNT-based water purification membranes [9,10,11] and for testing, at the nanoscale, classical one- or two-dimensional continuum mechanics models concerning the dynamics of the investigated structures. Notably, the fluid flow rates in CNTs have been found to be extraordinarily fast, four to five orders of magnitude faster than that observed in classical pipe systems [12,13,14]. As pointed out in [9], when designing nano-devices incorporating CNT components conveying fluid (liquid or gas), the motion of both the fluid and the tube must be taken into account since the fluid–structure interaction greatly affects the dynamics of the entire mechanical system. Therefore, regardless of whether a particular model of such a mechanical system is based on one or another rod or shell theory, it necessarily takes into account the influence of the fluid flow inside a single- or multi-walled carbon nanotube (MWCNT) and the van der Waals interactions between the individual single-walled carbon nanotubes (SWCNTs) composing a multi-walled one (see, e.g., [15,16,17,18,19,20,21,22,23,24,25,26,27,28]).

Here, among the plethora of beam-like and shell-like models proposed and developed for describing the dynamics of CNTs conveying fluid, we focus on those based on the classical Bernoulli–Euler beam theory. They belong to the most popular, acknowledged and well-studied mathematical models used in structural mechanics, where the vibration of pipes conveying fluids has been extensively studied in the past 80 years after the seminal works by Bourrières [29], Niordson [30], Benjamin [31] and Gregory and Païdoussis [32]. The interested reader can find more details on this research in the comprehensive books by Païdoussis [33,34].

To the best of our knowledge, Yoon, Ru and Mioduchowski [15,16] were the first to apply such a model to describe the vibration and instability of a nano-sized pipe—a single-walled carbon nanotube conveying fluid in an elastic medium. They considered cases in which such a fluid-conveying carbon nanotube is simply supported (pinned), clamped at both ends [15] or cantilevered [16]. Using the same governing equation in which, however, the influence of the ambient medium is neglected, Reddy et al. [17,18] studied the effect of fluid flow on the free vibration (natural frequencies) and instability of fluid-conveying SWCNTs. They estimated the mass flow rate of the fluid into SWCNTs and the elastic, Coriolis and centrifugal forces generated by the flow during the vibration. The critical fluid flow velocities for clamped boundary conditions were obtained, too.

Later on, in 2008, Wang, Ni and Li [19] proposed, extending the approach developed by Ru, Yoon and Mioduchowski [15,16,35,36], a model describing the dynamic behaviour of DWCNTs conveying fluid, which is studied in the current work (see Section 2). The suggested model was built on the basis of the linear Bernoulli–Euler beam theory and takes into account the influence of the surrounding medium in the simplest possible way—as a Winkler-like elastic foundation characterised by a relevant spring constant. In their paper, the authors investigate the natural frequencies of a pipe under the assumption that it is simply supported at both ends, i.e., pinned–pinned. Analysing the corresponding dispersion relations for different values of the slenderness ratio and spring constant, they obtain the critical fluid flow velocities at which buckling instability occurs.

Within the framework of the model introduced in [19], in the subsequent two articles, He et al. [20] and Lolov and Lilkova-Markova [37] study the stability, respectively, of DWCNTs conveying fluid that are clamped at both ends and simply supported. In [20], the critical flow velocities of a nano-pipe clamped at both ends are found to increase very fast with a decrease in the ratio of the length of the tube to its outer radius. The van der Waals interaction between SWCNTs constituting a DWCNT is found to stabilise the system. The results presented in [37] show that the critical fluid flow velocity reduces when the density of the fluid increases and that longer pipes are less stable. Comparing the pipes of different cross-sections investigated in their study, the most stable among them is that with the largest inner radii of the two SWCNTs forming the respective DWCNT. Notably, all the critical velocities obtained in this paper correspond to the loss of stability of the tube not through flutter, i.e., by performing oscillations of increasing amplitude, but through divergence. Let us recall that divergence instability (or static bifurcation) means that the structure passes from stability to instability at zero frequency or, in other words, through a static solution of the respective equations of motion (see [16,38] for a detailed explanation of this matter). It should be remarked that the boundary-value problems investigated in [20,37] are solved using Galerkin’s method.

In the context of the present study, it is worth mentioning another model, quite similar to that presented in [19] as far as the respective equations of motion are concerned. It was developed, based on the classical Bernoulli–Euler beam theory by Elaikh et al. [39] to describe the free vibration and stability of two micro pipes conveying fluid that are coupled continuously via elastic springs. The stability analysis of such mechanical structures subject to cantilever boundary conditions is performed utilising Galerkin’s method in [39] and in the subsequent work by Lolov and Lilkova-Markova [40] where the interconnection between the tubes is modelled as Pasternak’s elastic foundation.

Finally, let us also remark that L. Wang [21] and Tounsi et al. [22] extended, using the nonlocal elasticity theory, the model of Ref. [19] to take into account small-scale effects. An important conclusion drawn in Wang’s paper [21] is that the local theory provides a reliable estimation of the critical fluid flow velocities of the pipe, i.e., in this aspect, the small-scale effects can be neglected. It is beyond the scope of the current article to review the models accounting for the effects of nonlocal elasticity. For a more detailed discussion of models of this type used in fluid-conveying CNTs, the interested reader is referred to the recent review [28].

As already mentioned, in the present paper, we focus on the mathematical model introduced in Ref. [19]. The corresponding equations of motion and boundary conditions are given in Section 2. Then, in Section 3, we describe the specific Galerkin procedure used to solve the investigated boundary-value problem. Some important peculiarities of the numerical implementation of the suggested approach are discussed in Section 4. In the following Section 5, we first specify the geometric, material and van der Waals interaction characteristics of the considered DWCNTs, and then, present the main results of the study. Section 6 contains some concluding remarks.

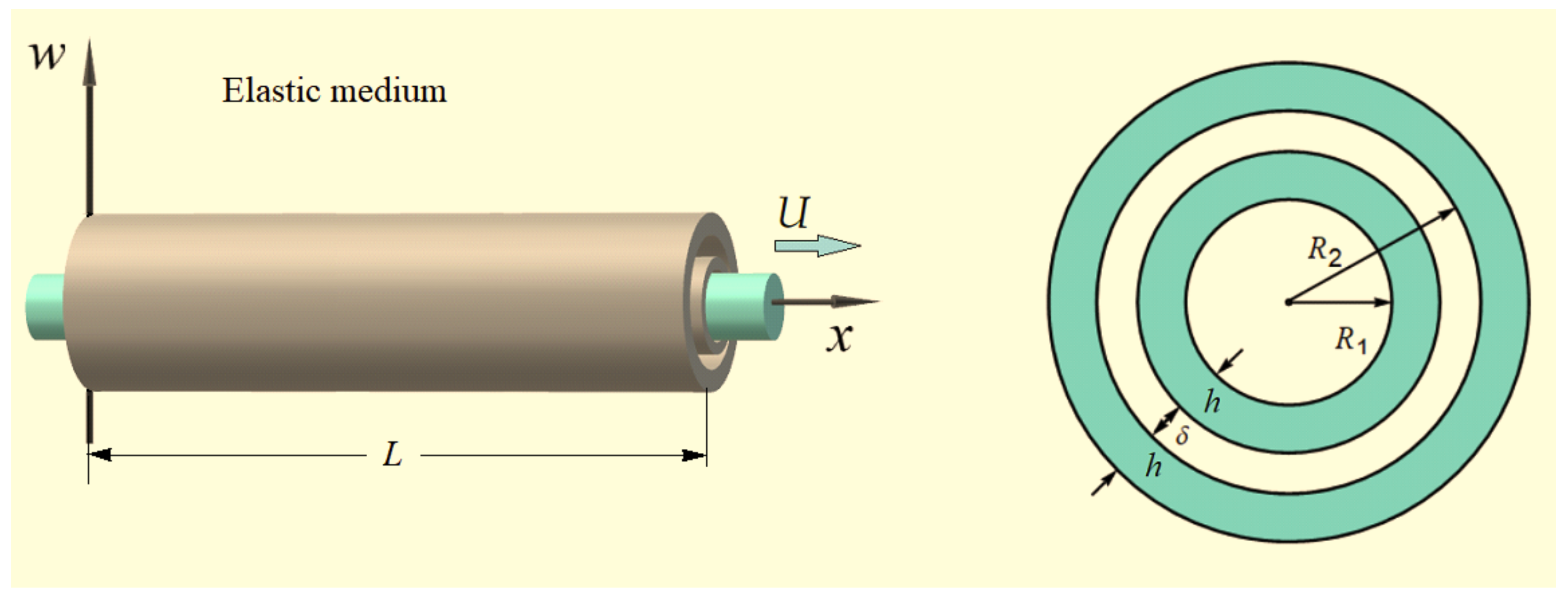
2. Equations of Motion and Boundary Conditions

In the model proposed in [19], a DWCNT is assumed to consist of two SWCNTs, with one nested into the other. The inner tube is assumed to convey an inviscid ideal fluid flowing with constant mean velocity U, while the outer tube is in contact with the surrounding elastic medium (see Figure 1). The corresponding equations of motion of such an initially straight nano-pipe read as follows:

$$\begin{array}{cc}\hfill & E{I}_1\frac{{\partial }^4{w}_1}{\partial x^4}+M{U}^2\frac{{\partial }^2{w}_1}{\partial x^2}+2MU\frac{{\partial }^2{w}_1}{\partial x\partial t}+(M+\rho A_1)\frac{{\partial }^2{w}_1}{\partial t^2}-c\left(w_2-w_1\right)=0,\hfill \\ \hfill & E{I}_2\frac{{\partial }^4{w}_2}{\partial x^4}+\rho A_2\frac{{\partial }^2{w}_2}{\partial t^2}+k{w}_2+c\left(w_2-w_1\right)=0,\hfill \end{array}$$

(1)

where E and $\rho$ are the Young’s modulus and mass density of the tubes, respectively, which are assumed to be identical for both nanotubes; M is the mass density of the fluid; c is the intertube interaction coefficient due to the van der Waals interaction between the tubes; k is a Winkler-like spring constant determined by the material properties of the surrounding elastic medium; x is the axial coordinate; t is the time; $I_{\alpha }$, $A_{\alpha }$ and $w_{\alpha }$ ($\alpha =1,2$) are the moments of inertia (let us remark that in engineering, moment of inertia commonly refers to the area moment of inertia; see [41]), the cross-section areas and the transverse displacements of the inner ($\alpha =1$) and the outer ($\alpha =2$) tube, respectively.

Upon introducing the dimensionless variables

$$z=\frac{x}{L},\tau =\frac{t}{L^2}\sqrt{\frac{E{I}_1}{M+\rho A_1}},u_1=\frac{1}{L}{w}_1,u_2=\frac{1}{L}{w}_2,$$

(2)

and parameters

$$v=UL\sqrt{\frac{M}{E{I}_1}},{\beta }_1=\frac{M}{\rho A_1+M},{\beta }_2=\frac{\rho A_2}{\rho A_1+M}\frac{I_1}{I_2},{\gamma }_1=\frac{L^4}{E{I}_1}c,{\gamma }_2=\frac{L^4}{E{I}_2}c,\kappa =\frac{L^4}{E{I}_2}k,$$

(3)

where L is the length of the tube, the system of Equation (1) takes the dimensionless form

$$\begin{array}{cc}\hfill & \frac{{\partial }^4{u}_1}{\partial z^4}+v^2\frac{{\partial }^2{u}_1}{\partial z^2}+2v\sqrt{{\beta }_1}\frac{{\partial }^2{u}_1}{\partial z\partial \tau }+\frac{{\partial }^2{u}_1}{\partial {\tau }^2}-{\gamma }_1\left(u_2-u_1\right)=0,\hfill \\ \hfill & \frac{{\partial }^4{u}_2}{\partial z^4}+{\beta }_2\frac{{\partial }^2{u}_2}{\partial {\tau }^2}+\kappa u_2+{\gamma }_2\left(u_2-u_1\right)=0.\hfill \end{array}$$

(4)

In what follows, the investigated DWCNTs are assumed to be of the cantilever type (clamped at $z=0$ and free at the other end $z=1$), i.e.,

$$u_{\alpha }(0,\tau )=\frac{\partial u_{\alpha }(0,\tau )}{\partial z}=0,\frac{{\partial }^2{u}_{\alpha }(1,\tau )}{\partial z^2}=\frac{{\partial }^3{u}_{\alpha }(1,\tau )}{\partial z^3}=0,(\alpha =1,2).$$

(5)

3. Approximate Solutions

In this study, we utilise Galerkin’s method to analyse the dynamic behaviour of the investigated nano-pipes (for more details about this approach, see, e.g., [42]). The application of Galerkin’s method enables us to determine sufficiently well the natural frequencies of the investigated system, which fully characterise its free vibration, and to draw reliable conclusions about its stability/instability.

Approximate solutions to the boundary-value problem (4), (5) are sought in the form

$$u_1={\delta }_{ij}{W}_i\left(z\right)T_j\left(\tau \right),u_2={\delta }_{ij}{W}_i\left(z\right)Q_j\left(\tau \right).$$

(6)

Here and in what follows, ${\delta }_{ij}$ is the Kronecker delta symbol, Latin indices have the range $1,2,\dots ,N$, where N is a given natural number, and the usual summation convention over repeated indices is assumed, unless explicitly stated otherwise. The functions

$$W_i\left(z\right)=A_i\left[\sin {\mu }_{i}z-\sinh {\mu }_{i}z-\frac{\sin {\mu }_i+\sinh {\mu }_i}{\cos {\mu }_i+\cosh {\mu }_i}\left(\cos {\mu }_{i}z-\cosh {\mu }_{i}z\right)\right],A_i,{\mu }_i\in \mathbf{R}$$

(7)

(no summation is assumed over the repeated index i here) are used as trial/test functions in Galerkin’s procedure. They are solutions to the equation

$$\frac{d^4{W}_i}{d{z}^4}-{\mu }_i{W}_i=0,$$

(8)

and meet the clamped–free boundary conditions

$$W_i\left(0\right)=\frac{d{W}_i\left(0\right)}{dz}=0,\frac{d^2{W}_i\left(1\right)}{d{z}^2}=\frac{d^3{W}_i\left(1\right)}{d{z}^3}=0,$$

(9)

provided that

$$\cos {\mu }_i\cosh {\mu }_i+1=0.$$

(10)

The constants $A_i$ are assumed to be such that

$$\left(W_i,W_j\right)={\delta }_{ij}.$$

(11)

Hereafter, $\left(f,g\right)$ denotes the inner product in the vector space V of real-valued smooth functions whose domain of definition is the closed interval $[0,1]$, which is determined here as usually occurring in the following manner

$$\left(f,g\right)=\underset{0}{\overset{1}{\int }}f\left(z\right)g\left(z\right)dz,f,g\in V.$$

(12)

Substituting the expressions (6) into the left-hand sides of the Equation (4) one obtains the residual functions

$$\begin{array}{c}{R}_1={\delta }_{ij}{W}_i{\ddot{T}}_j+2v\sqrt{{\beta }_1}{\delta }_{ij}{W}_i^{\prime }{\dot{T}}_j+{\delta }_{ij}\left(W_i^{\prime \prime \prime \prime }+v^2{W}_i^{\prime \prime }+{\gamma }_1{W}_i\right)T_j-{\gamma }_1{\delta }_{ij}{W}_i{Q}_j,\hfill \end{array}$$

(13)

$$\begin{array}{c}{R}_2={\beta }_2{\delta }_{ij}{W}_i{\ddot{Q}}_j+{\delta }_{ij}\left[W_i^{\prime \prime \prime \prime }+\left(\kappa +{\gamma }_2\right)W_i\right]Q_j-{\gamma }_2{\delta }_{ij}{W}_i{T}_j,\hfill \end{array}$$

(14)

where the primes and the dots indicate differentiation with respect to the variables z and t, respectively. Then, taking into account the relations (11), it is easy to see that

$$\begin{array}{c}\left(R_1,W_k\right)={\ddot{T}}_k+2v\sqrt{{\beta }_1}{a}_{kj}{\dot{T}}_j+c_{kj}{T}_j+v^2{b}_{kj}{T}_j+{\gamma }_1{T}_k-{\gamma }_1{Q}_k,\hfill \end{array}$$

(15)

$$\begin{array}{c}\left(R_2,W_k\right)={\beta }_2{\ddot{Q}}_k+c_{ki}{Q}_i+\left(\kappa +{\gamma }_2\right)Q_k-{\gamma }_2{T}_k,\hfill \end{array}$$

(16)

where

$$a_{kj}=\left(W_k,W_j^{\prime }\right),b_{kj}=\left(W_k,W_j^{\prime \prime }\right),c_{kj}=\left(W_k,W_j^{\prime \prime \prime \prime }\right).$$

(17)

According to the standard Galerkin’s procedure, the unknown functions $T_i\left(\tau \right)$ and $Q_i\left(\tau \right)$ are to be determined from the equations

$$\left(R_1,W_k\right)=0,\left(R_2,W_k\right)=0.$$

(18)

Now, from the Equation (15), one can express the functions $Q_i$ trough the functions $T_i$ and their derivatives as follows:

$$Q_i={\gamma }_1^{-1}\left({\ddot{T}}_i+2v\sqrt{{\beta }_1}{a}_{ij}{\dot{T}}_j+c_{ij}{T}_j+v^2{b}_{ij}{T}_j+{\gamma }_1{T}_i\right).$$

(19)

After that, upon substituting the relations (19) into the Equation (16), one obtains the following system of equations for the functions $T_j$:

$$\begin{array}{c}{\beta }_2{\delta }_{ij}{\stackrel{⃜}{T}}_j+2v\sqrt{{\beta }_1}{\beta }_2{a}_{ij}{\stackrel{⃛}{T}}_j\hfill \\ \hspace{1em}+\left[\left({\beta }_2+1\right)c_{ij}+v^2{\beta }_2{b}_{ij}+\left(\kappa +{\gamma }_1{\beta }_2+{\gamma }_2\right){\delta }_{ij}\right]{\ddot{T}}_j+2v\sqrt{{\beta }_1}\left[c_{ik}{a}_{kj}+\left(\kappa +{\gamma }_2\right)a_{ij}\right]{\dot{T}}_j\\ \hfill +\left[c_{ik}\left(c_{kj}+v^2{b}_{kj}\right)+\left(\kappa +{\gamma }_1+{\gamma }_2\right)c_{ij}+\left(\kappa +{\gamma }_2\right)v^2{b}_{ij}+\kappa {\gamma }_1{\delta }_{ij}\right]T_j=0.\end{array}$$

(20)

Thus, given an initially straight nano-pipe whose dynamic behaviour is described by the system (4), its small transverse vibration obeying the boundary conditions (5) is approximated by the functions of form (6), where $W_i\left(z\right)$ are of the form (7), $T_i\left(\tau \right)$ are the solutions of the system (20), and $Q_i\left(\tau \right)$ are determined via the relations (19). The convergence of this approximation to the exact solution when N tends to infinity is guaranteed since, as is well known (see [43]), the trial functions ${\left\{W_i\left(x\right)\right\}}_{i=1}^{\infty }$ form a complete set of orthonormal functions in the space of smooth functions of z in the interval $[0,1]$, which satisfy the boundary conditions (9).

Once the number N is chosen, an N-term Galerkin approximation of the considered problem is obtained. In this case, (20) becomes a system of N fourth-order linear ordinary differential equations of constant coefficients. Therefore, its general solution is expressed in terms of the roots ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{4N}$ of the characteristic polynomial $P\left[\lambda \right]=\det \left({\chi }_{ij}\right)$ of the characteristic $\lambda$-matrix

$$\begin{array}{c}{\chi }_{ij}={\beta }_2{\delta }_{ij}{\lambda }^4+2v\sqrt{{\beta }_1}{\beta }_2{a}_{ij}{\lambda }^3\hfill \\ \hspace{1em}+\left[\left({\beta }_2+1\right)c_{ij}+v^2{\beta }_2{b}_{ij}+\left(\kappa +{\gamma }_1{\beta }_2+{\gamma }_2\right){\delta }_{ij}\right]{\lambda }^2+2v\sqrt{{\beta }_1}\left[c_{ik}{a}_{kj}+\left(\kappa +{\gamma }_2\right)a_{ij}\right]\lambda \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left[c_{ik}\left(c_{kj}+v^2{b}_{kj}\right)+\left(\kappa +{\gamma }_1+{\gamma }_2\right)c_{ij}+\left(\kappa +{\gamma }_2\right)v^2{b}_{ij}+\kappa {\gamma }_1{\delta }_{ij}\right]\hfill \end{array}$$

(21)

associated with the system (20).

Knowledge of the natural frequencies of the investigated mechanical structure, i.e., the roots ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{4N}$ of the characteristic polynomial of the system (20), is sufficient for the stability analysis of the considered nano-pipe. Namely, if for a certain set of parameters, v, ${\beta }_1$, ${\beta }_2$, ${\gamma }_1$, ${\gamma }_2$, and $\kappa$, the polynomial $P\left[\lambda \right]$ has multiple roots or a root with a non-negative real part, then the system (20) has at least one non-trivial solution that is either time-independent (static), periodic or constantly increasing with time, and hence, the respective pipe is unstable; otherwise, the pipe is stable. In the first of the cases mentioned above, the system loses stability through divergence, while in the other two cases, the loss of stability is through flutter.

4. Numerical Implementation

The procedure for the determination of N-term approximate solutions of the investigated boundary-value problem (4), (5) was implemented analytically and numerically for $N=20$ using Mathematica^® [44]. It should be noted that a vast number of preliminary calculations led us to the conclusion that the 20-term Galerkin approximation gives reliable results in the sense that the differences between the critical flow velocities obtained using $N-1$ and N-term approximations are sufficiently small. At this relatively high level of approximation, these differences are less than $3\%$.

Once the level of approximation was fixed, the first 20 solutions of Equation (10), the coefficients $A_i$ in (7) and the values of $a_{ij}$, $b_{ij}$ and $c_{ij}$ in (17) were computed numerically using the routines $\mathtt{FindRoot}$ and $\mathtt{NIntegrate}$, with the $\mathtt{WorkingPrecision}$ set to 200 digits; otherwise, the functions $W_1,\dots ,W_{20}$ did not meet the boundary conditions (5) sufficiently well and the numerical values of the coefficients of the characteristic polynomial $P\left[\lambda \right]$, which, in this case, was of the 80th degree, were not computed precisely enough for the upcoming calculation of its roots. For similar reasons, the roots of the characteristic polynomial $P\left[\lambda \right]$, i.e., the natural frequencies of the pipe, corresponding to a given set of values of the parameters v, ${\beta }_1$, ${\beta }_2$, ${\gamma }_1$, ${\gamma }_2$ and $\kappa$ were calculated by numerically solving the equation

$$P\left[\lambda \right]=\det \left({\chi }_{ij}\right)=0.$$

(22)

using the routine $\mathtt{NSolve}$ with the same $\mathtt{WorkingPrecision}\to 200$.

5. Results and Discussion

In the present work, we limited our study to cantilevered DWCNTs with the following characteristics.

5.1. Geometric and Intertube Interaction Characteristics

• Wall thickness of the tubes h: $0.34$ nm = $0.34\times {10}^{-9}$ m;
• Initial distance between the tubes $\delta$: $0.34$ nm = $0.34\times {10}^{-9}$ m;
• Inside radius of the inner tube $R_1$: $5.00$ nm = $5.00\times {10}^{-9}$ m;
• Inside radius of the outer tube $R_2$: $5.68$ nm = $5.68\times {10}^{-9}$ m;
• Length of the tubes L: ${10}^{-8}$ m ÷$2\times {10}^{-7}$ m.

The cross-section areas $A_1$ and $A_2$ of the inner and outer tubes, respectively, are given by the formulas

$$A_1=\pi {\left(R_1+h\right)}^2-\pi R_1^2\mathrm{and}{A}_2=\pi {\left(R_2+h\right)}^2-\pi R_2^2.$$

(23)

The area moments of inertia $I_1$ and $I_2$ of the inner and outer tubes, respectively, are determined as follows:

$$I_1=\frac{\pi }{4}\left[{\left(R_1+h\right)}^4-R_1^4\right]\mathrm{and}{I}_2=\frac{\pi }{4}\left[{\left(R_2+h\right)}^4-R_2^4\right].$$

(24)

For a DWCNT of inner radius $R_1=5$ nm, such as those considered here, the value of the van der Waals interaction coefficient c is evaluated to be 1 TPa (see [35]). Valuable comments about the ways of determining this parameter as related to the vibrations of DWCNTs can be found in the recent paper by Strozzi [45].

5.2. Material Characteristics

• Young’s modulus of the SWCNTs E: 1 TPa ÷ 4 TPa;
• Mass density of the SWCNTs $\rho$: $2.3\times {10}^3$ kg/m³;
• Mass density of the fluid M: ${10}^3$ kg/m³.

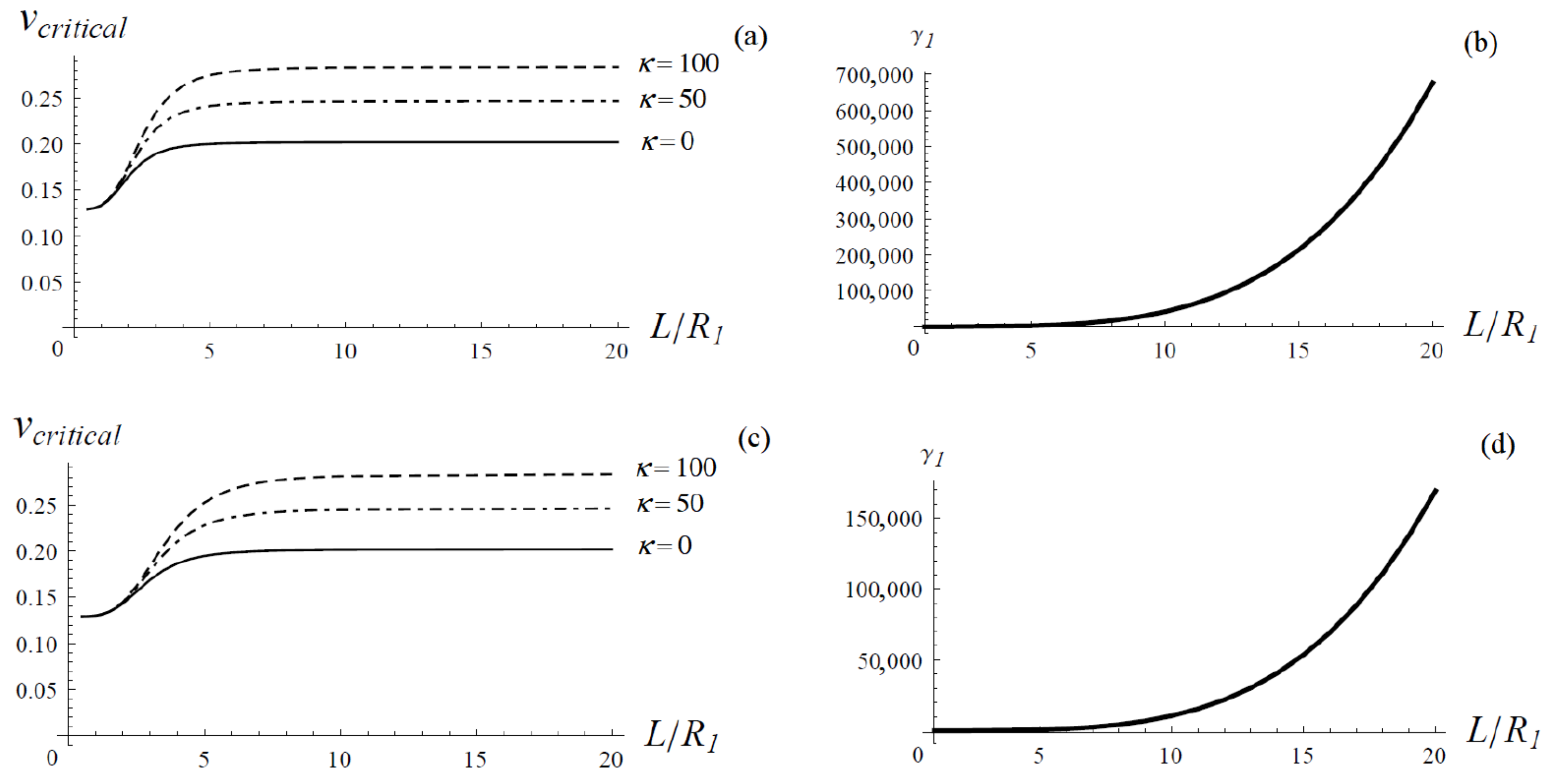
5.3. Critical Flow Velocity versus the Ratio of the Tube Length L to Its Inner Radius R₁

The assumptions presented above about the geometric and material characteristics of the investigated DWCNT conveying fluid entirely determine the values of the parameters $I_1$ and $I_2$ via the Formula (24) as well as ${\beta }_1$ and ${\beta }_2$ through the Equation (23) and the respective relations in the Equation (3). The latter equations also imply that ${\gamma }_2={\gamma }_1(I_1/I_2)$. Moreover, the expression for ${\gamma }_1$ in the Equation (3) implies that this parameter depends only on the pipe length L and Young’s modulus E, since the value of the parameter c is fixed at 1 TPa. Thus, only four parameters are free. These are L, v, E and $\kappa$.

In the current study, for three values, 0, 50 and 100, of the spring constant $\kappa$ characterising the impact of the surrounding elastic medium, and two values, 1 TPa and 4 TPa, of Young’s modulus E, we vary the length of the nano-pipe L from ${10}^{-8}\mathrm{m}$ to $2\times {10}^{-7}\mathrm{m}$ and look for the corresponding critical fluid flow velocities. The latter are obtained as the lowest values of the parameter v at which the respective characteristic polynomial $P\left[\lambda \right]$ has multiple roots or a root with a non-negative real part.

The results of our computations are plotted in Figure 2. In both cases, $E=1$ TPa and $E=4$ TPa, and for all the considered values of the parameter $\kappa$, it is observed (see Figure 2a,c) that as the length of the nano-pipe L increases, so does the critical flow velocity, although upon reasoning through analogy with the conventional pipe theory [33], one expects just the opposite to occur. The explanation for this circumstance is that as this parameter increases, the parameter ${\gamma }_1$ also increases very fast—see Figure 2b,d. Since the effect of the van der Waals interaction between the inner and the outer tubes is similar to the effect of an elastic Winkler foundation, it is not surprising that the increase in the parameter ${\gamma }_1$ stabilises the system and, actually, this is what is observed. In the context of the results obtained in structural mechanics [33], it is not surprising that the critical fluid flow velocity also rises with the rise in the spring constant, as can be seen in Figure 2a,c.

Here, we should remark that the values 50 and 100 of the (dimensionless) spring constant $\kappa$ are chosen to illustrate more clearly the tendency arising as this parameter increases rather than to accurately reflect a realistic physical situation. Actually, they correspond to a very stiff elastic medium. Thus, for instance, the value of the Winkler constant of a polymer matrix is estimated to be $k=1$ G Pa (see [15]). Bearing in mind that $\kappa =\left(L^4/E{I}_2\right)k$ and taking into account the characteristics of the CNTs considered, this means that, in this case, $\kappa$ barely differs from zero.

The profiles of the critical flow velocities of a fluid-conveying DWCNT cantilever with Young’s modulus $E=1$ TPa and one with Young’s modulus $E=4$ TPa are depicted in Figure 3 by solid and dashed lines, respectively, for two values of the spring constant $\kappa$, namely $\kappa =0$ (left) and $\kappa =100$ (right). The comparison between the respective profiles shows that the pipe with a higher Young’s modulus loses stability at a smaller critical flow velocity. However, for $L/R_1>20$, the difference between the compared critical velocities becomes negligible.

Our numerical simulations also reveal that the critical fluid flow velocity almost does not change for $L/R_1>20$ in all considered cases. Thus, for instance, in the case when $E=1$ TPa and $\kappa =0$, the difference between the critical fluid flow velocities corresponding to $L/R_1=20$ and $L/R_1=100$ is about ${10}^{-6}$. It is worth noting that similar results are reported in [20] for clamped (at both ends) DWCNTs conveying fluid whose dynamic behaviour is governed by the same equations of motion (4). All these findings demand reasonable elucidation. However, despite our best efforts, we have not yet found a satisfactory explanation for such behaviour.

6. Concluding Remarks

In the present paper, we analysed the stability of double-walled carbon nanotube cantilevers conveying fluid in an elastic medium. It is assumed that the dynamic behaviour of the investigated nano-pipes is described by the system of equations of motion (4) subjected to boundary conditions (5). It should be noted that until now, this boundary-value problem has not been studied in the current literature on the subject. Here, for that purpose, we use Galerkin’s method. The method of its implementation is described in detail in Section 3 and Section 4.

Critical fluid flow velocities are obtained at which a cantilevered nano-pipe with the characteristics given in Section 5 loses stability. The results of the numerical simulations are depicted in Figure 2. In all the considered cases, we observe the following: (1) the pipe losses stability through divergence; (2) the critical fluid flow velocity increases with an increase in the length L of the pipe; (3) pipes with a higher Young’s modulus lose stability at smaller critical flow velocities; (4) the critical fluid flow velocity almost does not change for $L/R_1>20$.

Finally, we should note that models derived via the Bernoulli–Euler beam theory, such as the one considered here, are only suitable for describing the dynamics of beams with relatively large length-to-diameter ratios. Moreover, they neglect to account for the effects of the transverse shear deformation and rotary inertia of the beams. As a first step toward more adequate modelling, these shortcomings are overcome partly by using Timoshenko’s beam theory. Probably, the earliest attempts in this direction were made by Yoon, Ru and Mioduchowski [46] and Wang et al. [47] as far as the dynamics of CNT-based structures is concerned. In the light of the above remarks, we intend to extend the current research by including double Timoshenko beam models (local and nonlocal) and, following the approaches of Liu et al. [48,49], to deepen our research in the field of the dynamics and stability of cantilevered DWCNT pipes embedded in an elastic medium.