The Classical Action as a Tool to Visualise the Phase Space of Hamiltonian Systems

Abstract

In this paper, we analyse the classical action as a tool to reveal the phase space structure of Hamiltonian systems simply and intuitively. We construct a scalar field using the values of the action along the trajectories to analyse the phase space. The different behaviours of the trajectories around important geometrical objects like normally hyperbolic invariant manifolds, their stable and unstable manifolds, and KAM structures generate characteristic patterns in the scalar field generated by the action. Also, we present a simple argument based on the conservation of energy and the behaviour of the trajectories to understand the origin of the patterns in this scalar field. As examples, we study the phase space of open Hamiltonian systems with two and three degrees of freedom.

1. Introduction

The study of phase space structure is a fundamental problem in dynamical systems. It is essential to understand the behaviour of the trajectories from a theoretical and practical perspective. The traditional tools to visualise the phase space structure like the Poincaré maps or projection of the trajectories in a plane are very useful to visualise and understand diverse properties of the phase space with three dimensions. However, the study of the phase space structure of multidimensional systems remains a challenging open problem due to the difficulty of its visualisation.

Two basic approaches have been developed to study the multidimensional phase space from two different and complementary perspectives: the statistical and geometrical approaches. Some remarkable examples of the statistical approach based on time series analysis are Renormalization Group [1], Mutual Information [2,3], and Multifractal Metrics [4,5]. In the geometrical approach, new tools have been developed to study the phase space structure of multidimensional systems like Fast Lyapunov Exponents [6,7], Mean Exponential Growth Factor of Nearby Orbits [8], Smaller Alignment Indices, generalised Alignment Indices [9,10], Determinant of Scattering Functions [11,12], Delay Time [13], Shannon Entropy [14], Birkhof Averages [15], and based on Geometric properties of Hamiltonian systems [16,17]. Those phase space structure indicators are scalar fields constructed with the trajectories of the system. The differences in the values of the scalar fields give us information about the phase space objects that intersect the set of trajectories considered.

A kind of phase space structure indicators recently developed is the Lagrangian descriptors [18,19,20]. Some recent examples of systems analysed with this method can be found in [21,22,23,24,25,26,27]. The most intuitive Lagrangian descriptors are based on trajectories’ arc length. The differences in the arc length of the trajectories with nearby initial conditions give us information about the phase space around them. In this work, we consider the Maupertuis’ action S that defines a natural arc length for Hamiltonian systems. With the action S, it is possible to construct a Lagrangian descriptor to reveal the phase space structure of this kind of system.

In Section 2, we explain in detail the principle behind the detection of phase space objects in the phase space using the differences of arc length of nearby trajectories and the construction of the Lagrangian descriptor based on the action. In Section 3, we study the Lagrangian descriptor based on the action analytically and its behaviour when the trajectories are close to the hyperbolic periodic orbit of the quadratic normal form Hamiltonian with two degrees of freedom (dof). We also explain this result using an intuitive argument based on the conservation of the energy E and the behaviour of the trajectories around the unstable hyperbolic periodic orbit. In Section 4, we explore the phase space of a three-dof system with unbounded phase space. This system has a multidimensional generalisation of a hyperbolic periodic orbit, a normally hyperbolic invariant manifold (NHIM). Finally, in Section 5, we summarise our conclusions and remarks.

2. Relation between Lagrangian Descriptors and Classical Action $\mathit{S}$

The Lagrangian descriptors, like other phase space structure indicators, are scalar fields constructed with the trajectories in the phase space. To calculate the trajectories, usually, we take a set of initial conditions with one or two dimensions to visualise the intersections of important objects in the phase space with the set of initial conditions. The scalar field’s values are determined by the behaviour of the trajectories that cross the set of initial conditions. In the next subsections, we review briefly: the ideas about the detection of invariant objects in the phase space using scalar fields constructed with trajectories, the definition of Lagrangian descriptors, and an important result to calculate the action S using only the kinetic energy for some types of Hamiltonian systems.

2.1. Detection of Invariant Manifolds in the Phase Space Using Scalar Fields Constructed with Trajectories

To understand the basic principle behind the detection of objects in the phase space, first, let us consider an unstable hyperbolic periodic orbit $\mathsf{\Gamma }$ in the phase space of a two-dof Hamiltonian system. Two remarkable invariant surfaces intersect at $\mathsf{\Gamma }$ [28,29,30]. These two-dimensional surfaces are called stable and unstable manifolds of the unstable hyperbolic periodic orbit $\mathsf{\Gamma }$. The invariance under the flow generated by the equations of motion means that the trajectories starting on an invariant surface remain on the same surface forever. The definition of the stable and unstable manifolds $W^{s/u}\left(\mathsf{\Gamma }\right)$ is the following:

$$W^{s/u}\left(\mathsf{\Gamma }\right)=\left\{\mathbf{X}\right|\mathbf{X}\left(t\right)\to \mathsf{\Gamma },t\to \pm \infty \}.$$

(1)

This means that the stable manifold $W^s\left(\mathsf{\Gamma }\right)$ is the union of all the trajectories that converge to the periodic orbit $\mathsf{\Gamma }$ as the time t goes to $+\infty$. The definition of the unstable manifold $W^u\left(\mathsf{\Gamma }\right)$ is analogous. The unstable manifold is the set of trajectories converging to the periodic orbit as the time t goes to $-\infty$.

The phase space of a two-dof Hamiltonian system has four dimensions. For each fixed value of the energy E, we can represent its dynamics in a three-dimensional constant energy manifold. The stable and unstable manifolds $W^{s/u}\left(\mathsf{\Gamma }\right)$ have two dimensions and form impenetrable barriers that divide the constant energy manifold [31,32,33]. If a stable manifold $W^s\left(\mathsf{\Gamma }\right)$ and an unstable manifold $W^u\left(\mathsf{\Gamma }\right)$ intersect transversely at one point, then there is an infinite number of transversal intersections between them. The structure generated by the stable and unstable manifolds is called a chaotic tangle and defines tubes that direct the dynamics in the phase space. A remarkable property of the dynamics is that the trajectories in a tube never cross the boundaries of the tube. This essential fact is a consequence of the uniqueness of the ODE solution and the codimension one of the stable and unstable manifolds $W^{s/u}\left(\mathsf{\Gamma }\right)$ relative to the constant energy manifold.

The trajectories very close to the stable manifold $W^s\left(\mathsf{\Gamma }\right)$ have similar behaviour to the trajectories contained in $W^s\left(\mathsf{\Gamma }\right)$ just for some finite time interval. However, those trajectories diverge from the hyperbolic periodic orbit $\mathsf{\Gamma }$ after a while. This is a characteristic property of the trajectories in a neighbourhood of an unstable hyperbolic periodic orbit. The arc length of the trajectories on the stable manifold $W^s\left(\mathsf{\Gamma }\right)$ grows like the periodic orbit’s arc length when the trajectories are close to the unstable periodic orbit $\mathsf{\Gamma }$. For the other trajectories near $W^s\left(\mathsf{\Gamma }\right)$, the arc length grows similar only when the trajectories approach the unstable periodic orbit $\mathsf{\Gamma }$. After the transit close to the unstable periodic orbit $\mathsf{\Gamma }$, the arc length grows differently. This difference makes it possible to find the boundaries of phase space objects like stable and unstable manifolds of unstable hyperbolic orbits.

Now, let us consider a trajectory near the boundary of an invariant KAM island. For some time, the trajectory is similar to the trajectories contained in the KAM island, but after that interval, it moves away from the neighbourhood of the KAM island. This different behaviour between trajectories is manifested in a difference in their arc length that we can visualise easily.

In practice, to visualise the different behaviour of the trajectories in the phase space, we usually consider a set of initial conditions like a two-dimensional plane and construct a scalar field with the arc length of the trajectories that cross the set of initial conditions. The abrupt changes in the behaviour of the trajectories generate abrupt changes in the scalar field of the arc length that we can identify with objects in the phase space. For example, the intersection of the stable manifold $W^s\left(\mathsf{\Gamma }\right)$ with the plane of initial conditions is a segment of a curve. We can appreciate the same line in the scalar field of the arc length evaluated on the plane. Similar considerations follow for the boundary of a KAM island that gives us a closed curve.

When we analyse a multidimensional Hamiltonian system with n-dof we can apply the same principle to visualise objects in the phase space. We can consider a set of initial conditions with two dimensions, calculate the trajectories that cross that set of initial conditions, and construct a scalar field with the arc lengths of the trajectories. The intersections of the multidimensional objects with the set of initial conditions are reflected in abrupt changes in the scalar field defined in the two-dimensional set of initial conditions.

In order to obtain insights into the phase space of systems with a large number of degrees of freedom using a scalar field, from the practical point of view, we just need to be able to integrate the equations of motion for enough points in the two-dimensional set of initial conditions to distinguish the characteristic patterns corresponding to important phase space objects in the scalar field constructed. An example with a large number of degrees of freedom is in the reference [34]. In that example, the phase space of a two-dof Hamiltonian system coupled with a large thermal bath of oscillators is studied with a Lagrangian descriptor technique.

2.2. Definition of Lagrangian Descriptors

Now, we review a definition of the Lagrangian descriptors. Let us consider a system of ordinary differential equations given by

$$\frac{d\mathbf{X}\left(t\right)}{dt}=\mathbf{V}\left(\mathbf{X}\left(t\right)\right),\mathbf{X}\in {\mathbb{R}}^n,t\in \mathbb{R},$$

(2)

where the vector field $\mathbf{V}\left(\mathbf{X}\right)\in C^k$ ($k\ge 1$) at the point $\mathbf{X}$. The values of the Lagrangian descriptor depend on the initial condition ${\mathbf{X}}_0=\mathbf{X}\left(t_0\right)$ and on the integration time interval $[t_0+{\tau }_{-},t_0+{\tau }_{+}]$. The Lagrangian descriptor M is defined by two integrals as

$$\begin{array}{ccc}\hfill M({\mathbf{X}}_0,t_0,{\tau }_{+},{\tau }_{-})& =& M_{+}({\mathbf{X}}_0,t_0,{\tau }_{+})+M_{-}({\mathbf{X}}_0,t_0,{\tau }_{-})\hfill \\ & =& {\displaystyle {\int }_{t_0}^{t_0+{\tau }_{+}}F\left(\mathbf{X}\left(t\right)\right)dt+{\int }_{t_0+{\tau }_{-}}^{t_0}F\left(\mathbf{X}\left(t\right)\right)dt,}\hfill \end{array}$$

(3)

where, the function F is any positive function evaluated on the solutions $\mathbf{X}\left(t\right)$, $\mathbf{X}\left(t_0\right)={\mathbf{X}}_0$, and the extremes of the interval of integration ${\tau }_{+}$ and ${\tau }_{-}$. The integration time can change between different initial conditions and allow us to stop the calculations once a trajectory leaves a defined region in the phase space. In this manner, it is possible to reveal only the phase space objects contained in the particular region considered.

The function F is chosen as positive defined to accumulate the effects of the trajectories’ behaviour as the integration time is increased. A natural choice for the function F is the infinitesimal arc length of the trajectories in the phase space. Let us notice that the first integral in the Lagrangian descriptor’s definition is calculated with trajectories forward in time. Then, it shows the presence of the phase space objects in the set of initial conditions like stable manifolds. Meanwhile, the second integral is calculated with the backward time and reveals objects like unstable manifolds.

In some situations, it is convenient to stop the calculation of the trajectories when the trajectories leave one particular region in the phase space to avoid large values of the integrals that define the Lagrangian descriptor $M({\mathbf{X}}_0,t_0,{\tau }_{+},{\tau }_{-})$. In this way, the Lagrangian descriptor $M({\mathbf{X}}_0,t_0,{\tau }_{+},{\tau }_{-})$ reveals only the phase space structure in one particular region. It is important to consider that stop of the calculation of the trajectories to interpret correctly the abrupt changes in Lagrangian descriptors plots.

For the detection of phase space invariant objects like stable and unstable manifolds of NHIMs or KAM structures, it is possible to use any scalar field generated by the trajectories of the system like the final points of the trajectories in phase space or other quantities related. For example, in scattering systems, the final asymptotic quantities, like final scattering angle or momentum, are a natural choice to find invariant chaotic sets [11,35,36]. However, for general systems, some quantities are easy to interpret like the arch length of trajectories.

Motivated by both ideas, the arc length and the final coordinate as phase space structure indicators, we consider the action S of the trajectories a natural option to visualise the phase space of Hamiltonian systems.

2.3. Maupertuis’ Action for Hamiltonian Systems

Let us consider a system of n-dof with a Lagrangian function

$$\begin{array}{ccc}\hfill L(q_1,\dots ,q_n,{\dot{q}}_1,\dots ,{\dot{q}}_n)& =& T(q_1,\dots ,q_n,{\dot{q}}_1,\dots ,{\dot{q}}_n)-V(q_1,\dots ,q_n)\hfill \\ & =& \sum _{i,j=1}^n{\displaystyle \frac{m_{ij}(q_1,\dots ,q_n)}{2}}\frac{d{q}_i}{dt}\frac{d{q}_j}{dt}-V(q_1,\dots ,q_n),\hfill \end{array}$$

(4)

where T is the kinetic energy and V is the potential energy.

The action S for the Hamiltonian $H(q_1,\dots ,q_n,p_1,\dots ,p_n)$ function is defined as

$$S={\int }_{q_0}^{q_f}\sum _{i=1}^n{p}_{i}d{q}_i,$$

(5)

where the momentum $p_i$ is defined in terms of the Lagrangian L as usual

$$p_i\equiv \frac{\partial L}{\partial \dot{q_i}}.$$

(6)

Substituting this definition of momentum $p_i$ in the definition of S and using a change of variable in the integration, it is possible to write the action S in terms of the kinetic energy T as

$$S={\int }_{q_0}^{q_f}\sum _{i=1}^n\frac{\partial L}{\partial {\dot{q}}_i}{\dot{q}}_{i}dt=2{\int }_{t_0}^{t_f}Tdt.$$

(7)

Now, let us consider briefly the geometrical framework of Hamiltonian dynamics. Using the conservation of the energy E and the definition of the momentum in terms of the generalised velocities $\dot{q_i}$, we can write the kinetic energy as

$$T=\sqrt{(E-V)\sum _{i=1}^n\frac{m_{ij}}{2}\frac{d{q}_i}{dt}\frac{d{q}_j}{dt}}.$$

(8)

Then, the action S is defined by the infinitesimal arc length $ds$ given by

$$d{s}^2=2(E-V)\sum _{i,j=1}^n{m}_{ij}d{q}_{i}d{q}_j,$$

(9)

where the trajectories of the system are geodesics of the Riemannian manifold defined by the metric corresponding to this arc length when the action S is minimal for the trajectories.

Taking all these considerations, we can consider the action S as a Lagrangian descriptor. Using the expression for the action in terms of the kinetic energy, the definition for the Lagrangian descriptor based on the action $M_S$ is given by

$$\begin{array}{ccc}\hfill M_S({\mathbf{x}}_0,t_0,{\tau }_{+},{\tau }_{-})& =& {\displaystyle 2{\int }_{t_0}^{t_0+{\tau }_{+}}Tdt+2{\int }_{t_0+{\tau }_{-}}^{t_0}Tdt}\hfill \\ & =& S_{+}+S_{-},\hfill \end{array}$$

(10)

where, $S_{+}$ is the action forward and $S_{-}$ the action backward. At this point, the reader may ask: Why is it convenient to consider the action S in terms of the kinetic energy T to visualise the phase space? To answer this question, there are two main reasons:

I.

We can interpret the results using the conservation of the energy and the geometry of the potential energy V. In this way, it is possible to find signatures of the presence of some fundamental objects in the phase space like KAM tori and NHIMs.

II.

Using the kinetic T energy, is simple to calculate the action S numerically. When we calculate the solutions of the Hamiltonian equations of motion, we just need to solve simultaneously the integral of T with respect to the time t to calculate the action S. Then, we only need to add this differential equation to the total ODE system to solve numerically.

More details about the algorithm to calculate the Lagrangian descriptor based on the action S and the visualisation of the multidimensional phase space are in Appendix A.

3. Phase Space Analysis of the Quadratic Normal Hamiltonian form Using ${\mathit{M}}_{\mathit{S}}$

An important question for the study of phase space is the detection of hyperbolic periodic orbits and their stable and unstable invariant manifolds. They constitute a fundamental component of the phase space. In this section, we study the Lagrangian descriptor’s behaviour evaluated on a set of initial conditions around the stable and unstable manifolds of an unstable hyperbolic periodic orbit. The next calculations are similar to the calculations in [37] for a family of Lagrangian descriptors based on different norms. Let us consider the most simple integrable two-dof Hamiltonian system as the first case for the analysis of the Lagrangian descriptor based on action $M_S$. 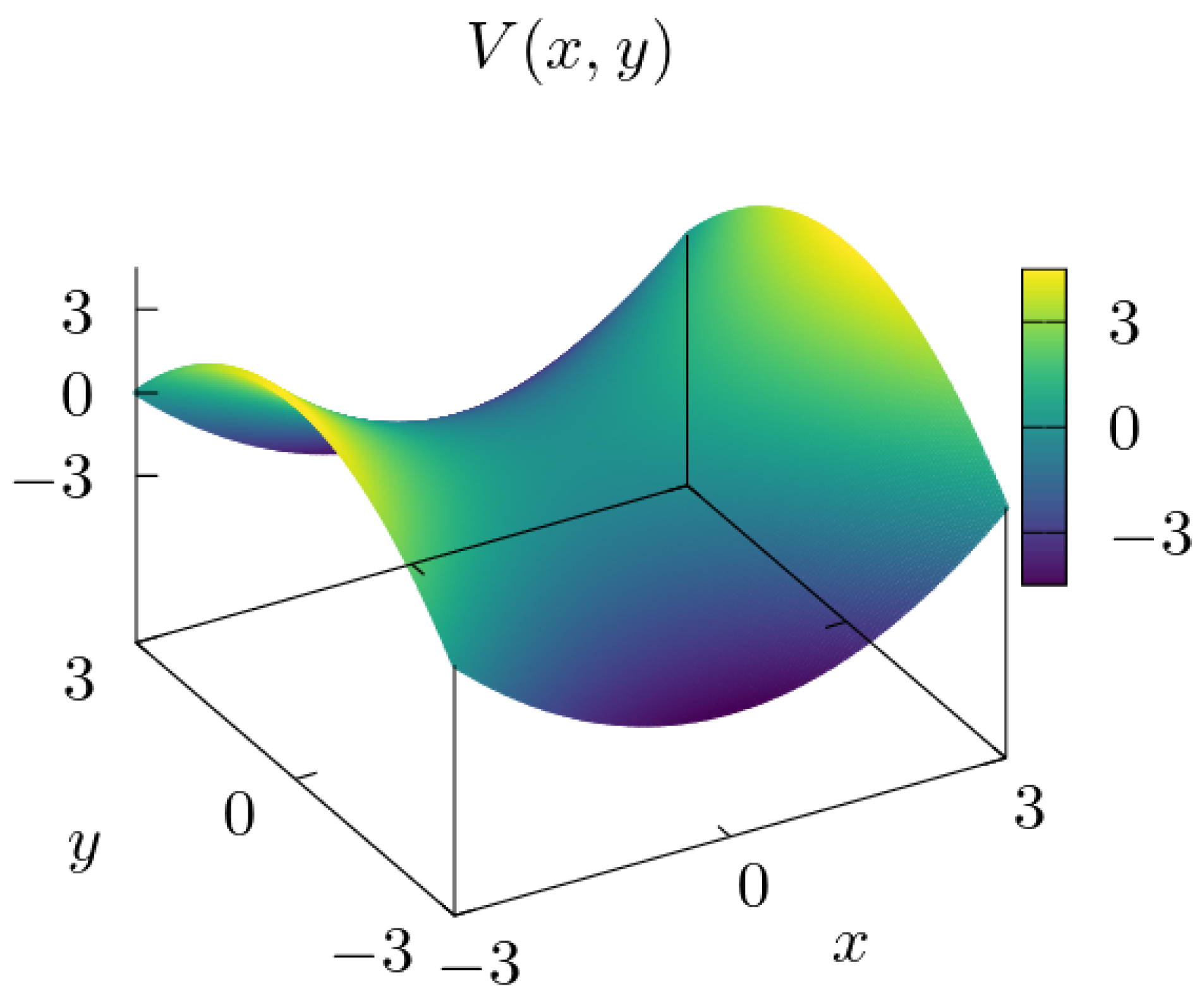The two-dof quadratic normal form Hamiltonian is given by

$$\begin{array}{ccc}\hfill H(x,y,p_x,p_y)& =& T(p_x,p_y)+V(x,y)\hfill \\ & =& \frac{\omega }{2}(p_x^2+x^2)+\frac{\lambda }{2}(p_y^2-y^2).\hfill \end{array}$$

(11)

The potential energy surface $V(x,y)$ has an index-one saddle with an unstable equilibrium point at the origin, see Figure 1 and Figure 2.

The motion in the x–component is oscillatory meanwhile the motion in the y–component is unbounded. For this two-dof system exists only one unstable hyperbolic periodic orbit $\mathsf{\Gamma }$ that oscillates on the x–direction on the line $y=0$ for each value of the energy $E>0$. The orbit $\mathsf{\Gamma }$ is a Normally Hyperbolic Invariant Manifold (NHIM) and has stable and unstable invariant manifolds. The periodic orbit $\mathsf{\Gamma }$ is given by

$$\mathsf{\Gamma }=\{(x,y,p_x,p_y)\in {\mathbb{R}}^4|y=p_y=0,E=\frac{\omega }{2}(p_x^2+x^2)\}.$$

(12)

In this integrable case, the unstable and stable invariant manifolds of the unstable hyperbolic periodic orbit $\mathsf{\Gamma }$ are given by the analytical expressions:

$$\begin{array}{ccc}\hfill W^s\left(\mathsf{\Gamma }\right)& =& \{(x,y,p_x,p_y)\in {\mathbb{R}}^4|y=-p_y,E=\frac{\omega }{2}(p_x^2+x^2)\},\hfill \\ \hfill W^u\left(\mathsf{\Gamma }\right)& =& \{(x,y,p_x,p_y)\in {\mathbb{R}}^4|y=p_y,E=\frac{\omega }{2}(p_x^2+x^2)\}.\hfill \end{array}$$

(13)

The Lagrangian descriptor based on the action $M_S$ for this two-dof separable system is

$$\begin{array}{ccc}\hfill M_S& =& M_S^x(x_0,p_{x_0},{\tau }_{+})+M_S^y(y_0,p_{y_0},{\tau }_{+})\hfill \\ & =& S_{+}^x+S_{-}^x+S_{+}^y+S_{-}^y,\hfill \end{array}$$

(14)

where the terms $M_S^x$ and $M_S^y$ are Lagrangian descriptors corresponding to the motion in x and y directions respectively. In this two-dof integrable system, $M_S^x$ is the Lagrangian descriptor associated with the elliptic motion and $M_S^y$ is the Lagrangian descriptor associated with the hyperbolic motion. Meanwhile, $S_{+}^x$, $S_{-}^x$, $S_{+}^y$, and $S_{-}^y$ are the actions that form those Lagrangian descriptors, like in the Equation (10). For the sake of simplicity, we consider the extremes of the integration interval $t_0=0$ and ${\tau }_{-}=0$ for the next analytical calculations.

Let us start the analytical calculations for the Lagrangian descriptor $M_S^y$. The solutions of the equations of motion for y and $p_y$ are

$$\begin{array}{c}\hfill y\left(t\right)=\frac{p_{y_0}}{2}(e^{\lambda t}+e^{-\lambda t})+\frac{y_0}{2}(e^{\lambda t}-e^{-\lambda t}),\\ \hfill p_y\left(t\right)=\frac{p_{y_0}}{2}(e^{\lambda t}-e^{-\lambda t})+\frac{y_0}{2}(e^{\lambda t}+e^{-\lambda t}).\end{array}$$

(15)

In this example, the integral corresponding to action is

$$\begin{array}{ccc}\hfill S_{+}^y& =& {\int }_0^{{\tau }_{+}}\frac{\lambda }{2}{p}_y^{2}dt\hfill \\ & =& {\int }_0^{{\tau }_{+}}\frac{\lambda }{2}{\left(\frac{p_{y_0}}{2}(e^{\lambda t}-e^{-\lambda t})+\frac{y_0}{2}(e^{\lambda t}+e^{-\lambda t})\right)}^{2}dt\hfill \\ & =& \frac{\lambda }{2}({\tau }_{+}(y_0^2-p_{y_0}^2)+{(p_{y_0}-y_0)}^2(e^{2\lambda {\tau }_{+}}-1)+{(p_{y_0}+y_0)}^2(e^{-2\lambda {\tau }_{+}}-1)).\hfill \end{array}$$

(16)

From the last expression, it is easy to appreciate the exponential growth of $S_{+}^y$ as t is increased. This integral has a minimum that converges to the initial conditions on the stable manifold $W^s\left(\mathsf{\Gamma }\right)$ when ${\tau }_{+}\to \infty$.

$$\begin{array}{c}\hfill \left(\frac{\partial S_{+}^y}{\partial x_0},\frac{\partial S_{+}^y}{\partial y_0}\right)(x_{0c},y_{0c})=0\Rightarrow \underset{{\tau }_{+}\to \infty }{\lim }{x}_{0c}=-y_{0c}.\end{array}$$

(17)

An analogous result follows for the integration backwards on time and the initial condition on the unstable manifold $W^u\left(\mathsf{\Gamma }\right)$.

Now we calculate the contribution associated with the motion in the x direction, the elliptic part of the Lagrangian descriptor $M_S^x$. The solutions of the equations of motion for harmonic oscillators are

$$\begin{array}{c}\hfill x\left(t\right)=p_{x_0}\sin \left(\omega t\right)+x_0\cos \left(\omega t\right),\\ \hfill p_x\left(t\right)=p_{x_0}\cos \left(\omega t\right)-x_0\sin \left(\omega t\right).\end{array}$$

(18)

Substituting this solution in the corresponding action, we obtain

$$\begin{array}{ccc}\hfill S_{+}^x& =& {\int }_0^{{\tau }_{+}}\frac{\omega }{2}{p}_x^{2}dt\hfill \\ & =& {\int }_0^{{\tau }_{+}}\frac{\omega }{2}{(p_{x_0}\cos \left(\omega t\right)-x_0\sin \left(\omega t\right))}^{2}dt.\hfill \end{array}$$

(19)

Without loss of generality, we calculate the integral starting on the initial condition $p_{x_0}=0$ and $x_0=\sqrt{2E_x/\omega }$. If we consider that $p_x$ has period $2\pi /\omega$, then ${\tau }_{+}=2N\pi /\omega +r$, where N is an integer and $r\in [0,2\pi /\omega ]$. This gives us

$$\begin{array}{ccc}\hfill S_{+}^x& =& N{E}_x{\int }_0^{2\pi }{\sin }^{2}udu+{\int }_0^r\frac{\omega }{2}{p}_x^{2}dt\hfill \\ \hfill & =& 2\pi N{E}_x+{\int }_0^r\frac{\omega }{2}{p}_x^{2}dt.\hfill \end{array}$$

(20)

From the above equation, we see that the elliptic part $M_S^x$ accumulates the same value of action every oscillation period. In contrast, the hyperbolic component $M_S^y$ grows exponentially with the time.

Considering the results for the hyperbolic and elliptic components of the Lagrangian descriptor based on the action, $M_S^x$ and $M_S^y$, we conclude that $M_S$ has a minimum on the stable and unstable manifolds $W^{s/u}\left(\mathsf{\Gamma }\right)$ of the hyperbolic periodic orbit $\mathsf{\Gamma }$. Then, the Lagrangian descriptor $M_S$ attains a global minimum on the periodic orbit $\mathsf{\Gamma }$. We can generalise this result to the neighbourhood of other nonintegrable systems with index-one saddles of potential energies due to Moser’s theorem for nonlinear systems [38].

Intuitively, we understand this result considering the geometry of the potential energy $V(x,y)$ around the index-one saddle point. For energies $E>0$, the unstable hyperbolic periodic orbit $\mathsf{\Gamma }$ oscillates on x-direction, and its kinetic energy is a periodic function of the time t. Almost any trajectory in a neighbourhood of $\mathsf{\Gamma }$ separate from it and its kinetic energy grows due to the shape of $V(x,y)$ on the y-direction and the conservation of E, see Figure 2 and Figure 3. However, the trajectories in the stable manifold $W^s\left(\mathsf{\Gamma }\right)$ converge to the periodic orbit $\mathsf{\Gamma }$ and remain bounded. Thus, their kinetic energy T converges to a periodic function and the action $S_{+}$, is minimum for the trajectories on $W^s\left(\mathsf{\Gamma }\right)$. As a result, the Lagrangian descriptor has a minimum in the stable and unstable invariant manifolds, and the global minimum that reveals the position of their intersection at $\mathsf{\Gamma }$, see Figure 4. To avoid divergences of the $M_S$, the calculation of the trajectories stops when integration time is completed or when the particle reaches circumference in the configuration space with radius $r=10$ with the centre at the origin, see Figure 5.

We can generalise the previous result for systems with a multidimensional index-one saddle point in the potential energy hypersurface. In that case, the phase space of the system has generalisation of a hyperbolic periodic orbit, a Normally Hyperbolic Invariant Manifold (NHIM) associated with the index-one saddle point in the potential energy hypersurface [31,33]. The Lagrangian descriptor based on the action $M_S$ has a minimum in the stable and unstable manifolds of the NHIM, and a global minimum at the NHIM [37]. The proof of this result is a direct consequence of the previous one. We just need to add more oscillatory degrees of freedom in the construction of the argument.

4. Exploring the Phase Space of a Three-Dof Open System Using ${\mathit{M}}_{\mathit{S}}$

In this section, we consider a three-dof Hamiltonian model as a nonlinear example. The phase space of this model has a NHIM and KAM structures. We visualise these objects in phase space using the Lagrangian descriptor based on the action $M_S$. The model is an extension of a two-dof model proposed to study the yield of products in an ultra-cold exothermic reaction [39] and studied from the phase space perspective with detain using the action S in [40]. More examples of the action S as a phase space structure indicator for two-dof chaotic closed systems can be found in the references [41,42,43].

Two features determine the dynamics of this model: a van der Waals force and a short-range force associated with the many-body interactions. Random Gaussian bumps have been added to the van der Waals potential energy to simulate the short-range effects between the particles close to the minimum of the van der Waals potential energy. The phase space of the system has a KAM tori close to the minimum of the van der Waals potential and the stable and unstable manifolds of the NHIM are associated with the maximum of the effective potential energy.

The model considers two-body interactions. The dominant interaction related to the asymptotic motion is a van der Waals force. The potential energy associated with the van der Waals force is given by

$$V_0\left(\mathbf{r}\right)=-\frac{C}{{(\beta {\left|\mathbf{r}\right|}^2+\alpha )}^3},$$

(21)

where $\mathbf{r}=(x,y,z)$ is the position from the origin, and the numerical values of the constants in this example are $\alpha =110$ a.u, $\beta =2.9$ a.u, and $C=16,130$ a.u. The potential energy function $V_0\left(\mathbf{r}\right)$ is negative defined and approaches 0 asymptotically. For $E<0$, the phase space is bounded and the particles are confined. Meanwhile, for $E>0$, the phase space is unbounded, and some particles can escape to infinity.

Due to the rotational symmetry of $V_0\left(\mathbf{r}\right)$, the dynamics is integrable and it is possible to reduce the dynamics and decompose the motion in radial and angular motion. The effective potential energy as a function of the radio r parameterised by the constant magnitude of the angular momentum L given by

$$V_{eff}(r,L)=V_0\left(r\right)+\frac{L}{2m{r}^2}.$$

(22)

Figure 6 shows the effective potential $V_{eff}(r,L)$ for $L\approx 109$. For each maximum of $V_{eff}(r,L)$, there exists an unstable fixed point for the dynamics in r-direction. Associated with this unstable fixed point there is a circular unstable hyperbolic periodic orbit ${\mathsf{\Gamma }}_L$ with radius equal to the critical radius corresponding to the maximum of $V_{eff}(r,L)$ and energy E equal to the maximum. For every direction in the configuration space, the system has a periodic orbit like ${\mathsf{\Gamma }}_L$. If we consider the union of all those periodic orbits, we can construct a NHIM ${\mathcal{M}}_E$ defined as

$${\mathcal{M}}_E=\bigcup _{\theta ,\varphi }{\mathsf{\Gamma }}_L,$$

(23)

where the angles $\theta ,\varphi$ parametrise the sphere in the configuration space. It is clear that ${\mathcal{M}}_E$ is a three-dimensional sphere $S^3$ by construction. This type of NHIM is characteristic of three-dof Hamiltonian systems with a maximum in its effective potential $V_{eff}(r,L)$.

Analogously, we can construct the stable and unstable manifolds of the NHIM ${\mathcal{M}}_E$ taking the union of the stable and unstable manifolds of the hyperbolic periodic orbit ${\mathsf{\Gamma }}_L$.

$$W^{s/u}\left({\mathcal{M}}_E\right)=\bigcup _{\theta ,\varphi }{W}^{s/u}\left({\mathsf{\Gamma }}_L\right).$$

(24)

Each of these invariant manifolds is a four-dimensional spherical cylinder $S^3\times \mathbb{R}$ and can divide the five-dimensional constant energy manifold. In this integrable case, $W^{s/u}\left({\mathcal{M}}_E\right)$ form a multidimensional homoclinic connection.

For the nonintegrable case, the short-range interactions act close to the minimum of the potential $V_0\left(\mathbf{r}\right)$. In [39], a force to mimic the many-body interaction breaking the rotational symmetry is proposed. This proposal consists of adding to the potential $V_0\left(\mathbf{r}\right)$ some random Gaussian bumps scattered inside around the minimum of $V_0\left(\mathbf{r}\right)$. In this numerical example, the bumps have $r<5$. This kind of perturbation has been used in closed quantum systems to break the degeneracy in the energy spectrum associated with the rotational symmetry [44,45]. In this case, the potential energy for the perturbed model is

$$V\left(\mathbf{r}\right)=V_0\left(\mathbf{r}\right)+\sum _{i=1}^{n}A{e}^{-B{\left|\mathbf{r}-{\mathbf{r}}_{\mathbf{i}}\right|}^2},$$

(25)

where A and $B=10$ are the coefficients that define the Gaussian bumps, and ${\mathbf{r}}_{\mathbf{i}}$ are the position of their centres. The height of the bumps defined by A is the perturbation parameter in this numerical example.

We calculate the Lagrangian descriptor $M_S$ for two different values of the parameter perturbation $A=0,0.005$ for the same energy $E=14$, see Figure 7. For the first case, $A=0$, the system is integrable and we can see the regularity in the KAM structure, in yellow and green, bound by the stable and unstable manifolds $W^{s/u}\left({\mathcal{M}}_E\right)$. The intersection of the NHIM ${\mathcal{M}}_E$ with the set of initial conditions is around $r_0=15$ and $p_{r_0}=0$, see Figure 8a. In the second case, the system is not integrable and the dynamics becomes chaotic. However, the NHIM ${\mathcal{M}}_E$ and its invariant manifolds $W^{s/u}\left({\mathcal{M}}_E\right)$ are robust under perturbations due to the persistence theorem [31,46].

The stable and unstable manifolds $W^{s/u}\left({\mathcal{M}}_E\right)$ intersect transversally and form a complicated pattern, see Figure 7b and Figure 8b. This structure is a homoclinic tangle of ${\mathcal{M}}_E$ and is a generalisation of the two-dimentional Smale horseshoes. Like in the two-dof this geometrical structure generates a complicated behaviour for the trajectories that escape to infinity. This behaviour is an example of transient chaos. More details about transient chaos and examples are in the references [47,48,49].

Figure 8. Magnification of the Lagrangian descriptor $M_S$ plots in Figure 7. Panel (a) shows a point in the NHIM ${\mathcal{M}}_E$ at the corner of the dark blue triangle around $(r_0=15,p_{r_0}=0)$ for the spherically symmetric integrable system. In panel (b), the Lagrangian descriptor shows the transversal intersections between $W^{s/u}\left({\mathcal{M}}_E\right)$ that originates transient chaos. Due to the numerical instabilities of this model, we calculate the solutions using a Taylor integrator order 25 implemented in Julia programming language [50,51].

Figure 8. Magnification of the Lagrangian descriptor $M_S$ plots in Figure 7. Panel (a) shows a point in the NHIM ${\mathcal{M}}_E$ at the corner of the dark blue triangle around $(r_0=15,p_{r_0}=0)$ for the spherically symmetric integrable system. In panel (b), the Lagrangian descriptor shows the transversal intersections between $W^{s/u}\left({\mathcal{M}}_E\right)$ that originates transient chaos. Due to the numerical instabilities of this model, we calculate the solutions using a Taylor integrator order 25 implemented in Julia programming language [50,51].

Also, we appreciate a region with large values of $M_S$ in yellow and green in Figure 9, which contains a KAM structure associated with the minimum of V, where the values of kinetic energy T of the trajectories are bigger than in the regions with bigger values of V. In panel (a), we can appreciate the regular concentric KAM tori. Meanwhile, in panel (b), we see how the KAM structure is deformed due to the perturbation and a chaotic sea created around it. For the three-dof Hamiltonian systems, the KAM torus does not have the necessary dimension to divide the phase space. For this system, the dimension of a KAM torus is three, but the constant energy manifold has five dimensions. However, the time necessary to escape to infinity is usually very large, that phenomenon is called Arnold diffusion. This is an important difference between the two-dof and three-dof Hamiltonian systems. Nevertheless, we can find the KAM structure in the phase space because of the different behaviours of the trajectories in the chaotic sea around it, and we can appreciate a complicated chaotic tangle around the KAM structure.

5. Conclusions and Remarks

We construct a natural phase space structure indicator for multidimensional Hamiltonian systems based on action S. An easy way to calculate this Lagrangian descriptor $M_S$ is with the integral of the kinetic energy T with respect to the time of the trajectories. It is possible to generalise this result when the kinetic energy is a quadratic function of the generalised velocities, and its potential energy is only a function of the generalised coordinates.

The Lagrangian descriptor $M_S$ is a convenient tool for studying the phase space of open Hamiltonian systems. Using the conservation of the energy, we can easily interpret the values of $M_S$ and link them with the geometry potential energy V in an intuitive way. The trajectories that spend time in regions with large values of V have smaller $M_S$ than trajectories that spend time in regions with smaller values of V.

Using $M_S$ it is possible to identify regular regions, unbounded regions, KAM structures and the transient chaotic sea around them formed by homoclinic and heteroclinic tangles. For the KAM islands, where the dynamics is confined to a finite region on the phase space, the values of $M_S$ change very smoothly for large integration times. Nevertheless, is its always possible to find stable periodic orbits on the KAM islands’ centres using the Poincaré map. The Lagrangian descriptors and the Poincaré maps are complementary tools to reveal the phase space structure.

Let us notice that we can apply this method to Hamiltonian systems with a large number of degrees of freedom. The only necessary condition is to be able to solve Hamilton’s equations of motion for a grid of initial conditions dense enough to find the boundary of the intersection of the objects in the phase space with the set of initial conditions. In this way, we can visualise those objects in the multidimensional phase space.

We find that $M_S$ has a minimum value on their stable and unstable manifolds of the hyperbolic periodic orbits. On the other hand, this Lagrangian descriptor has a maximal value for the stable and unstable manifolds for the inverse hyperbolic periodic orbits, see [41]. These results are intuitive considering the conservation of the energy and the trajectories’ behaviour in the neighbourhood of the periodic orbits. It is possible to generalise immediately these results for NHIMs and their stable and unstable manifolds in systems with more dimensions just by adding more oscillatory degrees of freedom and considering its contribution to $M_S$.

The classical action S has a fundamental role in the path integral formulation the quantum mechanics. Considering the stationary phase approximation of the Feynman path integral and the phase space of the classical system associated, the results presented here about the action S should have consequences for the evolution of wave packets near the stable and unstable manifolds of NHIMs and centres of KAM structures.

In the case that we want to visualise the phase space of more general systems that are not Hamiltonian, we can use an analogous algorithm. We replace the Hamilton equations of motion for the ODE system that we want to analyse and also replace the differential equation for the derivative with respect to the time of the action S with the equation for the infinitesimal arc length in the phase space. In this way, we can construct a scalar field that contains information about the trajectories that intersect the set of initial conditions.