Coexistence of Thread and Sheet Chaotic Attractors for Three-Dimensional Lozi Map
Abstract
1. Introduction
2. The Lozi Map
2.1. History
2.1.1. Initial Definition
2.1.2. Chaotic Properties of the Dissipative Map (|b| < 1)
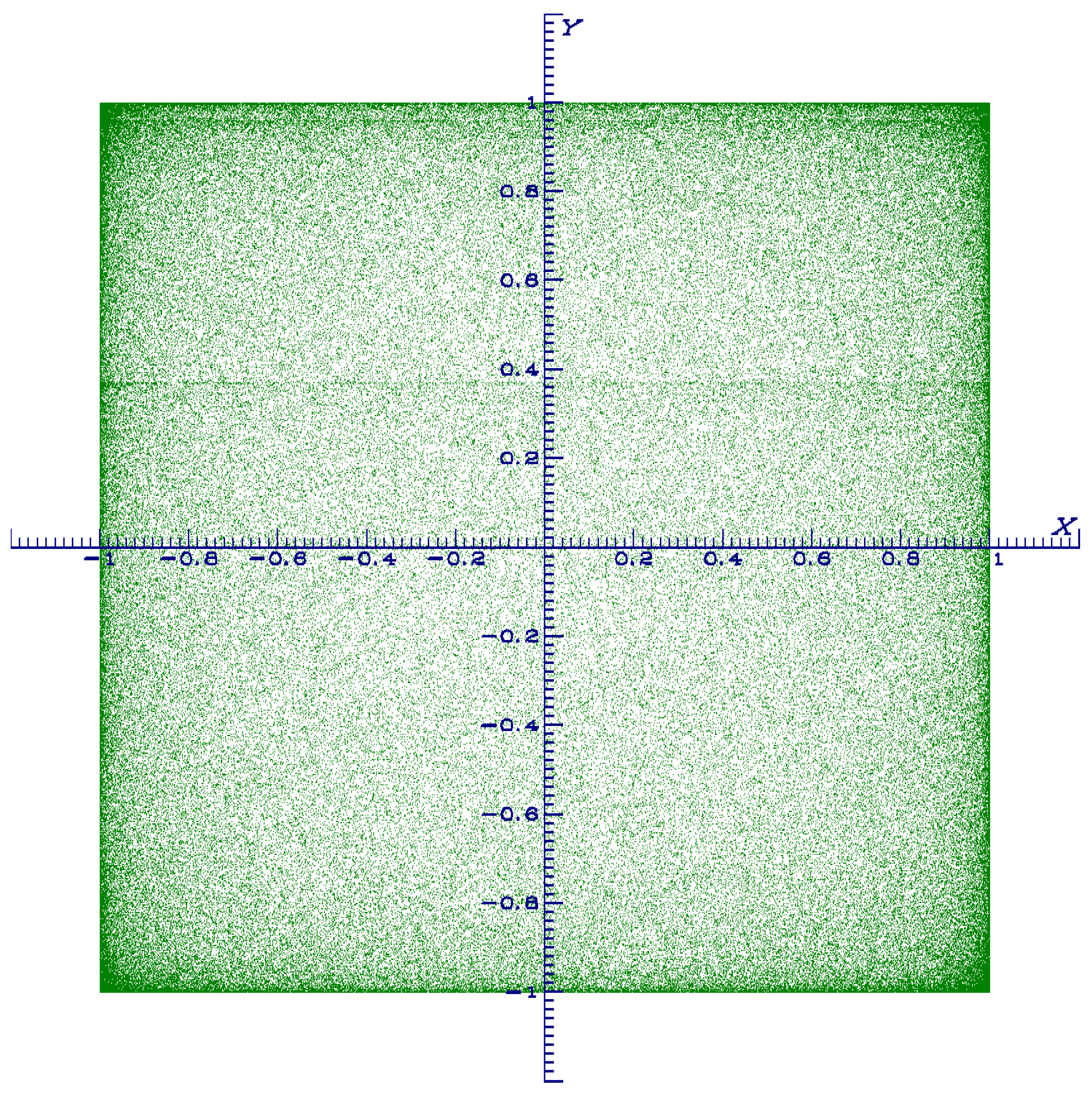
2.1.3. Fixed Points, Invariant Manifolds and Basin of Attraction
2.1.4. Other Dynamical Properties of the Dissipative Map (|b| < 1)
- -
- The union of the transversal homoclinic points and weak transversal homoclinic points is dense in ;
- -
- All periodic points are hyperbolic;
- -
- The set of periodic points forms a dense set in ;
- -
- Any two hyperbolic points form a transversal heteroclinic cycle or a weak transversal heteroclinic cycle.
2.1.5. Chaotic Properties of the Conservative Map (|b| = 1)
2.2. Generalizations
2.2.1. Topological Generalizations: Lozi-like Maps
2.2.2. Geometrical Generalization: Lozi-Type Map
2.2.3. Formulas Generalization
- (i)
- All solutions converge toward the equilibrium point . Moreover, for a large value of and , they prove that, if , then the solution converges toward the equilibrium point ;
- (ii)
- If , then the solution converges toward the periodic solution of period 5.
2.2.4. Fractal Mappings
2.2.5. Fractal Mappings
2.2.6. Network of Chaotic Maps and Chimera
- (i)
- Clustering. A dynamical cluster is defined as a subset of elements that are synchronized among themselves. In a clustered state, the elements in the system segregate into K distinct subsets that evolve in time, i.e., in the th cluster with .
- (ii)
- A chimera state consists of the coexistence of one or more clusters and a subset of desynchronized elements.
- (iii)
- A desynchronized or incoherent state occurs when .
3. Three-Dimensional Hyperchaotic Attractors
3.1. Rössler Hyperchaotic Attractors
3.1.1. The “Noodle” Attractor
3.1.2. The Folded “Curtain” Attractor
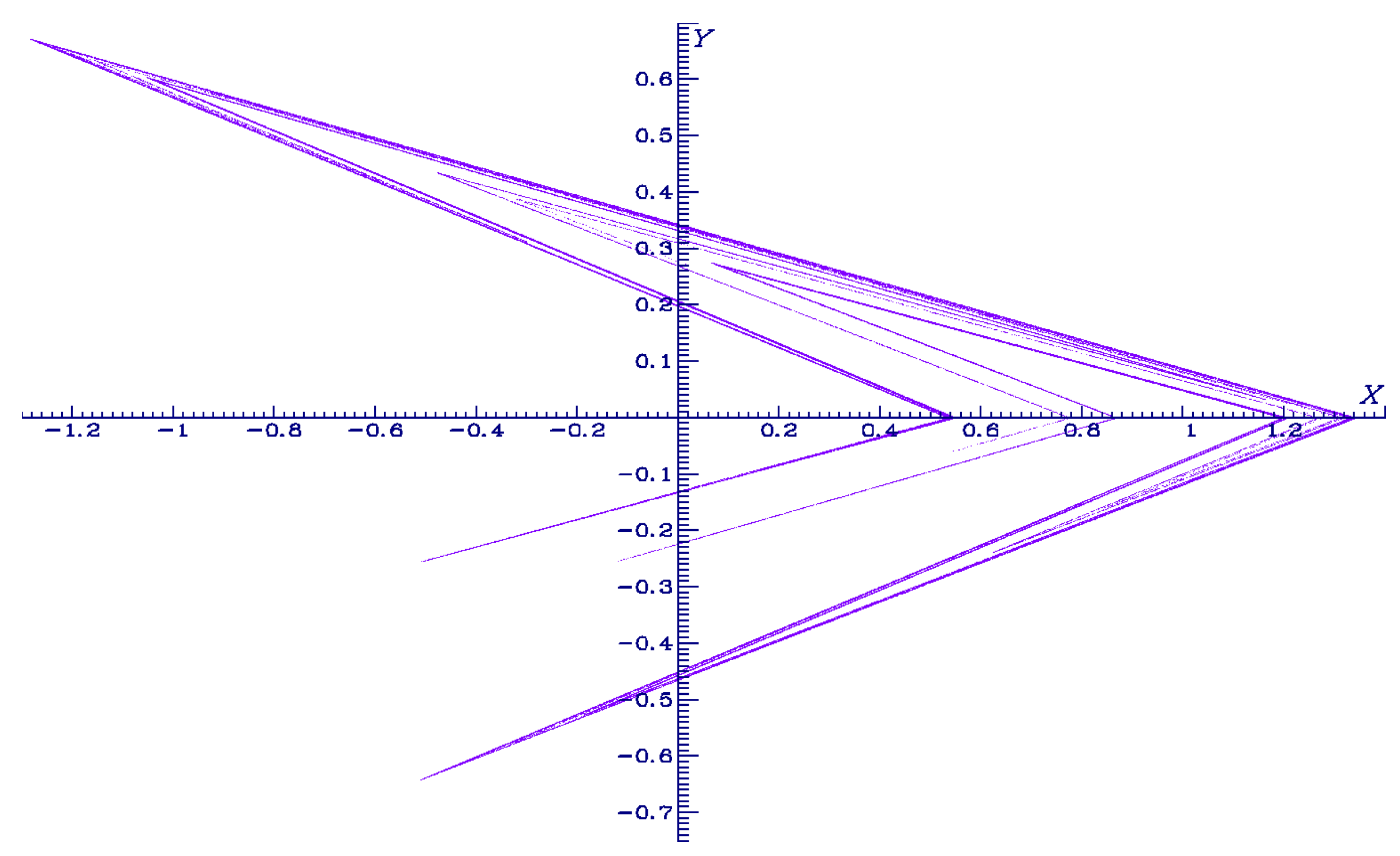
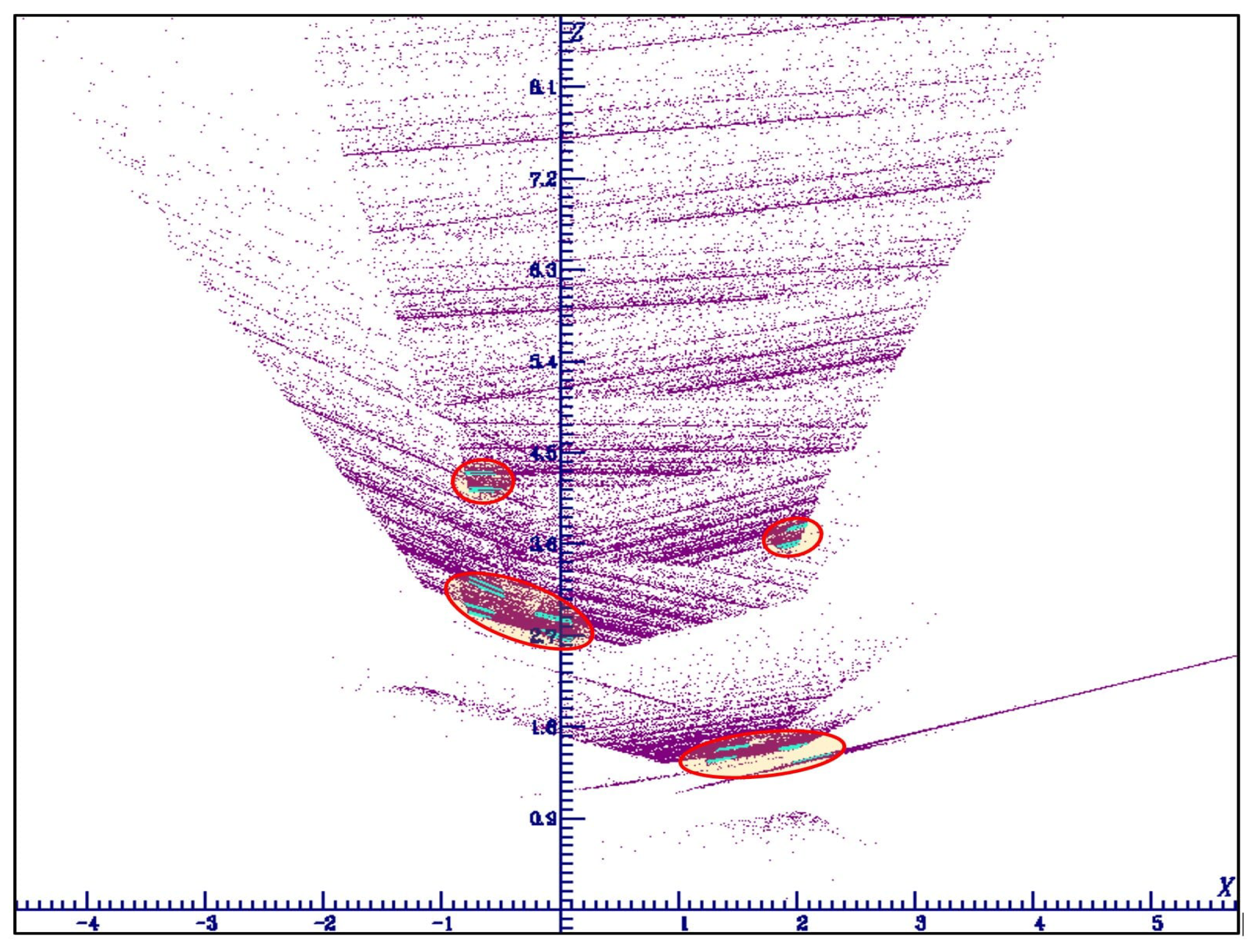
3.2. Three-Dimensional Lozi Map with Coexistence of Thread and Sheet Hyperchaotic Attractor
4. Properties of Thread–Sheet Hyperchaotic Attractor
4.1. Basic Properties: Jacobian and Symmetry
4.2. The Thread-Attractor
4.3. Fixed Points and Period-Two Orbits
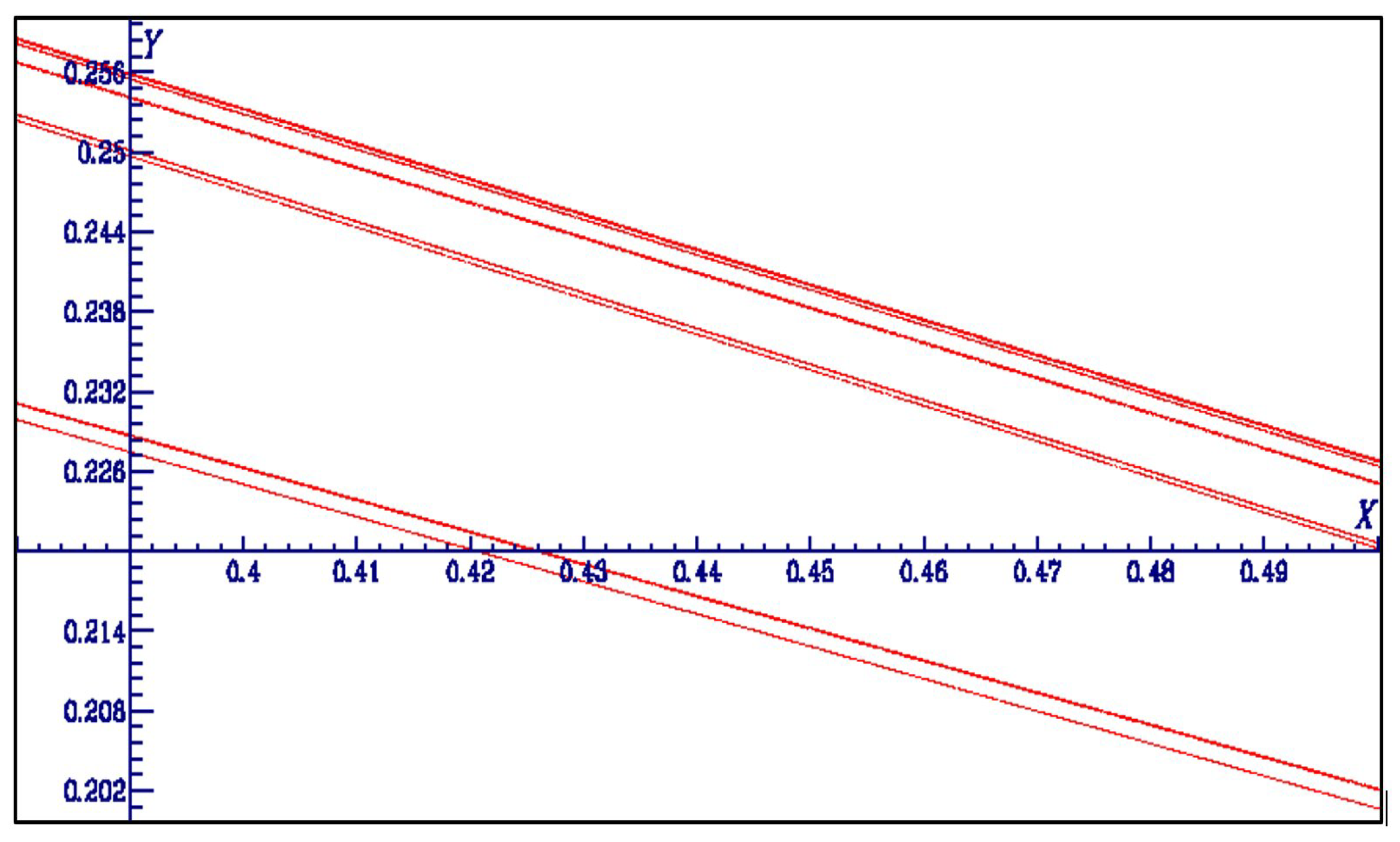
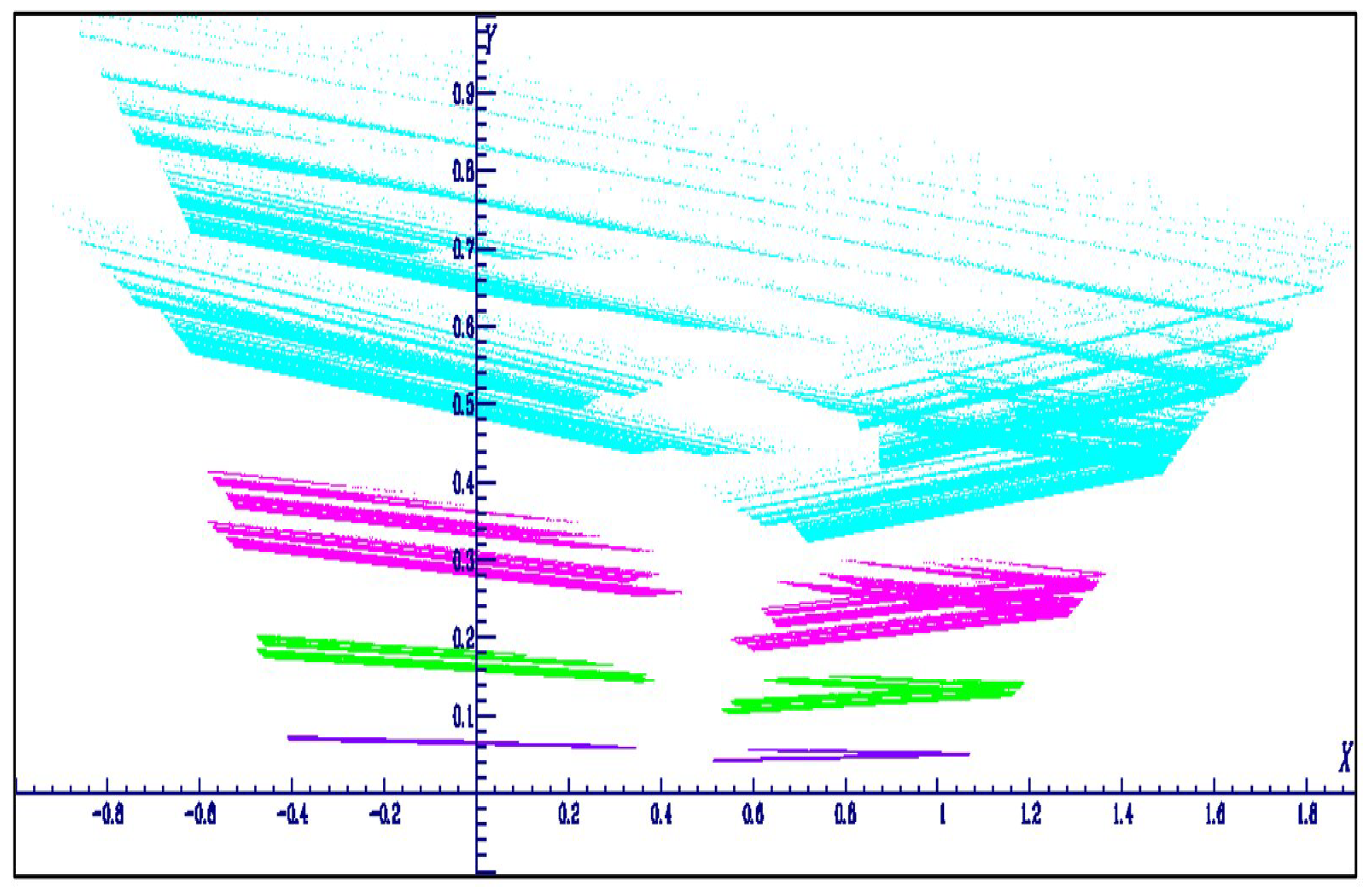
4.4. Numerical Examples
4.4.1. Case a = −1.25, b = 0.1, c = −1.25, One-Piece Chaotic Attractor, Two-Piece Hyperchaotic Attractor
4.4.2. Case Multi-Pieces Chaotic and Hyperchaotic Attractor
4.4.3. Case , Connected Hyperchaotic Attractor
4.4.4. Case and , Blow up of the Attractor versus the Parameter a
4.4.5. Case to , Blow up of the Attractor versus the Parameter b
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeraoulia, E. Lozi Mappings—Theory and Applications; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2013; 309p. [Google Scholar]
- Letellier, C.; Abraham, R.; Shepelyansky, D.L.; Rössler, O.E.; Holmes, P.; Lozi, R.; Glass, L.; Pikovsky, A.; Olsen, L.F.; Tsuda, I.; et al. Some elements for a history of the dynamical systems theory. Chaos 2021, 31, 053110. [Google Scholar] [CrossRef] [PubMed]
- Ruelle, D. Dynamical systems with turbulent behavior. In Mathematical Problems in Theoretical Physics, Lecture Notes in Physics; Dell’Antonio, G., Doplicher, S., Jona-Lasinio, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1978; Volume 80, pp. 341–360, International Mathematics Physics Conference, Roma, 1977. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Hénon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Smale, S. Differentiable dynamical systems. I Diffeormorphisms. Bull. Am. Math. Soc. 1967, 73, 747–817. [Google Scholar] [CrossRef]
- Lozi, R. Un attracteur étrange (?) du type attracteur de Hénon. J. Phys. 1978, 39, C5-9–C5-10. [Google Scholar] [CrossRef]
- Misiurewicz, M. Strange attractors for the Lozi mappings. Ann. N. Y. Acad. Sci. 1980, 357, 348–358. [Google Scholar] [CrossRef]
- Misiurewicz, M.; Stimac, S. Symbolic dynamics for Lozi maps. Nonlinearity 2016, 29, 3031–3046. [Google Scholar] [CrossRef]
- Kucharski, P. Strange attractors for the family of orientation preserving Lozi Maps. arXiv 2022, arXiv:2211.10296v1. [Google Scholar]
- Baptista, D.; Severino, R.; Vinagre, S. The basin of attraction of Lozi Mappings. Int. J. Bifurc. Chaos 2009, 19, 1043–1049. [Google Scholar] [CrossRef]
- Ishii, Y. Towards a kneading theory for Lozi mappings I: A solution of the pruning front conjecture and the first tangency problem. Nonlinearity 1997, 10, 731–747. [Google Scholar] [CrossRef]
- Boroński, J.P.; Kucharski, P.; Ou, D.-S. Lozi Maps with Periodic Points of All Periods n > 13. 2022. Available online: https://www.researchgate.net/publication/366740872_Lozi_maps_with_periodic_points_of_all_periods_n_13 (accessed on 27 April 2023).
- Botella-Soler, V.; Castelo, J.M.; Oteo, J.A.; Ros, J. Bifurcations in the Lozi map. J. Phys. A Math. Theor. 2011, 44, 305101. [Google Scholar] [CrossRef]
- Sushko, I.; Avrutin, V.; Gardini, L. Center Bifurcation in the Lozi Map. Int. J. Bifurc. Chaos 2021, 31, 2130046. [Google Scholar] [CrossRef]
- Glendinning, P.A.; Simpson, D.J.W. Chaos in the border-collision normal form: A computer-assisted proof using induced maps and invariant expanding cones. Appl. Math. Comput. 2022, 434, 127357. [Google Scholar] [CrossRef]
- Collet, P.; Levy, Y. Ergodic properties of the Lozi mappings. Commun. Math. Phys. 1984, 93, 461–482. [Google Scholar] [CrossRef]
- Rychlik, M. Invariant Measures and the Variational Principle for Lozi Mappings. In The Theory of Chaotic Attractors; Hunt, B.R., Li, T.Y., Kennedy, J.A., Nusse, H.E., Eds.; Springer: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, Z. The Geometric Structure of Strange Attractors in the Lozi Map. Commun. Nonlinear Sci. Numer. Simul. 1998, 3, 119–123. [Google Scholar] [CrossRef]
- Afraimovich, V.S.; Chernov, N.I.; Sataev, E.A. Statistical properties of 2-D generalized hyperbolic attractors. Chaos 1995, 5, 238–252. [Google Scholar] [CrossRef]
- Zheng, W.-M. Symbolic Dynamics for the Lozi Map. Chaos Solitons Fractals 1991, 1, 243–248. [Google Scholar] [CrossRef]
- Ishii, Y. Towards a kneading theory for Lozi mappings II: Monotonicity of the Topological Entropy and Hausdorff Dimension of Attractors. Commun. Math. Phys. 1997, 190, 375–394. [Google Scholar] [CrossRef]
- Ishii, Y.; Sands., D. Monotonicity of the Lozi family near the tent-maps. Comm. Math. Phys. 1998, 198, 397–406. [Google Scholar] [CrossRef]
- De Carvalho, A.; Hall, T. How to prune a horseshoe. Nonlinearity 2002, 15, R19–R68. [Google Scholar] [CrossRef]
- Li, H.; Li, K.; Chen, M.; Bao, B. Coexisting Infinite Orbits in an Area-Preserving Lozi Map. Entropy 2020, 22, 1119. [Google Scholar] [CrossRef] [PubMed]
- Natiq, H.; Banerjee, S.; Ariffin, M.R.K.; Said, M.R.M. Can hyperchaotic maps with high complexity produce multistability? Chaos 2019, 29, 011103. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E. Multistability and hidden attractors in a multilevel DC/DC converter. Math. Comput. Simul. 2015, 109, 32–45. [Google Scholar] [CrossRef]
- Bao, B.C.; Li, H.Z.; Zhu, L.; Zhang, X.; Chen, M. Initial-switched boosting bifurcations in 2D hyperchaotic map. Chaos 2020, 30, 033107. [Google Scholar] [CrossRef]
- Zhang, L.-P.; Liu, Y.; Wei, Z.-C.; Jiang, H.-B.; Bi, Q.-S. A novel class of two-dimensional chaotic maps with infinitely many coexisting attractors. Chin. Phys. B 2020, 29, 060501. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.Y.; Wang, N.; Zhu, L.; Chen, M.; Bao, B.C. Initials-boosted coexisting chaos in a 2D Sine map and its hardware implementation. IEEE Trans. Ind. Inform. 2021, 17, 1132–1140. [Google Scholar] [CrossRef]
- Lopesino, C.; Balibrea, F.; Wiggins, S.R.; Mancho, A.M. The Chaotic Saddle in the Lozi Map, Autonomous and Nonautonomous Versions. Int. J. Bifurc. Chaos 2015, 25, 1550184. [Google Scholar] [CrossRef]
- Richter, H. The generalized Henon maps: Examples for higher-dimensional chaos. Int. J. Bifurc. Chaos 2002, 12, 1371–1384. [Google Scholar] [CrossRef]
- Young, L.-S. A Bowen-Ruelle measure for certain piecewise hyperbolic maps. Trans. Am. Math. Soc. 1985, 287, 41–48. [Google Scholar] [CrossRef]
- Misiurewicz, M.; Stimac, S. Lozi-like maps. Discret. Contin. Dyn. Syst. 2018, 38, 2965–2985. [Google Scholar] [CrossRef]
- Juang, J.; Chang, Y.-C. Boundary influence on the entropy of a Lozi-type map. J. Math. Anal. Appl. 2010, 371, 728–740. [Google Scholar] [CrossRef]
- Sakurai, A. Orbit shifted shadowing property of generalized Lozi map. Taiwan. J. Math. 2010, 14, 1609–1621. Available online: https://www.jstor.org/stable/43834956 (accessed on 4 May 2023). [CrossRef]
- Boronski, J.; Stimac, S. Densely branching trees as models for Hénon-like and Lozi-like attractors. arXiv 2022, arXiv:2104.14780v2. [Google Scholar]
- Kucharski, P. Strange attractors and densely branching trees for the generalized Lozi-like family. arXiv 2023, arXiv:2302.04641. [Google Scholar]
- Aiewcharoen, B.; Boonklurb, R.; Konglawan, N. Global and Local Behavior of the System of Piecewise Linear Difference Equations xn + 1 = xn − yn − b and yn + 1 = xn − yn + 1 Where b ≥ 4. Mathematics 2021, 9, 1390. [Google Scholar] [CrossRef]
- Mammeri, M.; Kina, N.E. Dynamical properties of solutions in a 3-D Lozi map. In Proceedings of the 6th International Arab Conference on Mathematics and Computations (IACMC2019), Zarqa University. Zarqa, Jordan, 24–26 April 2019; pp. 27–33. [Google Scholar]
- Joshi, Y.; Blackmore, D.; Rahman, A. Generalized Attracting Horseshoes and Chaotic Strange Attractors. arXiv 2020, arXiv:1611.04133v2. [Google Scholar]
- Bilal, S.; Ramaswamy, R. A higher-dimensional generalization of the Lozi map: Bifurcations and dynamics. J. Differ. Equations Appl. 2022, 1–12. [Google Scholar] [CrossRef]
- Lozi, R. Strange attractors: A class of mapping of R2 which leaves some Cantor sets invariant. In Intrinsic Stochasticity in Plasmas; Laval, G., Gresillon, D., Eds.; Les Editions de Physique; Orsay: Cargese, France, 1979; pp. 373–381. [Google Scholar]
- Chutani, M.; Rao, N.; Nirmal Thyagu, N.; Gupte, N. Characterizing the complexity of time series networks of dynamical systems: A simplicial approach. Chaos 2020, 30, 013109. [Google Scholar] [CrossRef]
- Khennaoui, A.-A.; Ouannas, A.; Bendoukha, S.; Grassi, G.; Lozi, R.; Pham, V.-T. On fractional–order discrete-time systems: Chaos, stabilization and synchronization. Chaos Solitons Fractals 2019, 119, 150–162. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Baleanu, D. Global stability of local fractional Hénon-Lozi map using fixed point theory. AIMS Math. 2022, 7, 11399–11416. [Google Scholar] [CrossRef]
- Aliwi, B.H.; Ajeena, R.K.K. A performed knapsack problem on the fuzzy chaos cryptosystem with cosine Lozi chaotic map. AIP Conf. Proc. 2023, 2414, 040047. [Google Scholar] [CrossRef]
- Aliwi, B.H.; Ajeena, R.K.K. On Fuzzy Sine Chaotic Based Model in Security Communications. J. Posit. Sch. Psychol. 2022, 6, 8127–8133. Available online: https://journalppw.com/index.php/jpsp/article/view/5169 (accessed on 4 May 2023).
- Cano, A.V.; Cosenza, M.G. Chimeras and clusters in networks of hyperbolic chaotic oscillators. Phys. Rev. E 2017, 95, 030202(R). [Google Scholar] [CrossRef] [PubMed]
- Semenova, N.; Vadivasova, T.; Anishchenko, V. Mechanism of solitary state appearance in an ensemble of nonlocally coupled Lozi maps. Eur. Phys. J. Spec. Top. 2018, 227, 1173–1183. [Google Scholar] [CrossRef]
- Anishchenko, V.; Rybalova, E.; Semenova, N. Chimera States in two coupled ensembles of Henon and Lozi maps. Controlling chimera states. AIP Conf. Proc. 2018, 1978, 470013-1–470013-4. [Google Scholar] [CrossRef]
- Rössler, O.E.; Hudson, J.L.; Farmer, J.D. Noodle-map chaos: A simple example. In Stochastic Phenomena and Chaotic Behaviour in Complex Systems; Schuster, P., Ed.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 1984; Volume 21. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for hyperchaos. Phys. Lett. 1979, 71A, 155–157. [Google Scholar] [CrossRef]
- Anosov, D.V. Dynamical Systems IX: Dynamical Systems with Hyperbolic Behaviour. In Encyclopedia of Mathematical Sciences: Vol. 9; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar] [CrossRef]
- Elhadj, Z.; Sprott, J.C. Robust Chaos and Its Applications; World Scientific Series on Nonlinear Science Series A; World Scientific: Singapore, 2011; Volume 79. [Google Scholar] [CrossRef]
- Kuznetsov, S.P. Some lattice models with hyperbolic chaotic attractors. Russ. J. Nonlinear Dyn. 2020, 16, 13–21. [Google Scholar] [CrossRef]
- Kilassa Kvaternik, K. Tangential Homoclinic Points Locus of the Lozi Maps. Doctoral Thesis, University of Zagreb, Zagreb, Croatia, 2022; 110p. Available online: https://repozitorij.pmf.unizg.hr/islandora/object/pmf:11546 (accessed on 27 April 2023).
















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozi, R. Coexistence of Thread and Sheet Chaotic Attractors for Three-Dimensional Lozi Map. Dynamics 2023, 3, 315-344. https://doi.org/10.3390/dynamics3020019
Lozi R. Coexistence of Thread and Sheet Chaotic Attractors for Three-Dimensional Lozi Map. Dynamics. 2023; 3(2):315-344. https://doi.org/10.3390/dynamics3020019
Chicago/Turabian StyleLozi, René. 2023. "Coexistence of Thread and Sheet Chaotic Attractors for Three-Dimensional Lozi Map" Dynamics 3, no. 2: 315-344. https://doi.org/10.3390/dynamics3020019
APA StyleLozi, R. (2023). Coexistence of Thread and Sheet Chaotic Attractors for Three-Dimensional Lozi Map. Dynamics, 3(2), 315-344. https://doi.org/10.3390/dynamics3020019





