A Simple Transient Poiseuille-Based Approach to Mimic the Womersley Function and to Model Pulsatile Blood Flow
Abstract
:1. Introduction
2. Womersley and Poiseuille Velocity Profile for a Pulsatile Blood Flow
3. Approximation Method and Validation Model
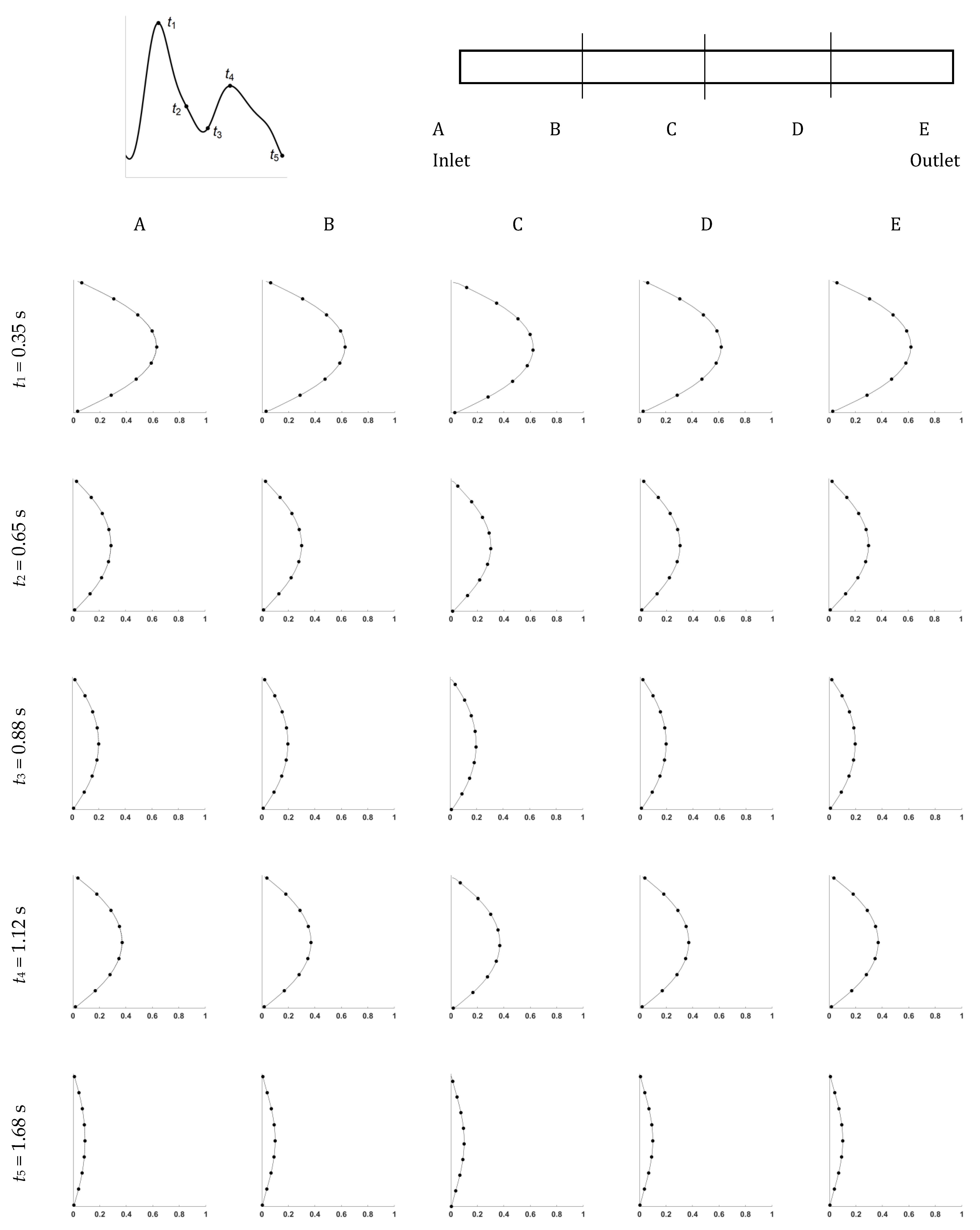
4. Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef]
- Armour, C.H.; Guo, B.; Pirola, S.; Saitta, S.; Liu, Y.; Dong, Z.; Xu, X.Y. The influence of inlet velocity profile on predicted flow in type B aortic dissection. Biomech. Model. Mechanobiol. 2021, 20, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhuang, J.; Wu, Y. The effect of Womersley number and particle radius on the accumulation of lipoproteins in the human aorta. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 571–584. [Google Scholar] [CrossRef] [PubMed]
- Bit, A.; Alblawi, A.; Chattopadhyay, H.; Quais, Q.A.; Benim, A.C.; Rahimi-Gorji, M.; Do, H.-T. Three dimensional numerical analysis of hemodynamic of stenosed artery considering realistic outlet boundary conditions. Comput. Methods Programs Biomed. 2020, 185, 105163. [Google Scholar] [CrossRef] [PubMed]
- Vimmr, J.; Jonasova, A.; Bublik, O. Effects of three geometrical parameters on pulsatile blood flow in complete idealised coronary bypasses. Comput. Fluids 2012, 69, 147–171. [Google Scholar] [CrossRef]
- Barbour, M.C.; Chassagne, F.; Chivukula, V.K.; Machicoane, N.; Kim, L.J.; Levitt, M.R.; Aliseda, A. The effect of Dean, Reynolds and Womersley numbers on the flow in a spherical cavity on a curved round pipe. Part 2. The haemodynamics of intracranial aneurysms treated with flow-diverting stents. J. Fluid Mech. 2021, 915. [Google Scholar] [CrossRef]
- Kok, F.; Myose, R.; Hoffmann, K.A. Effects of planar and nonplanar curved flow paths on the hemodynamics of helical conduits for coronary artery bypass grafting: A numerical study. Int. J. Heat Fluid Flow 2020, 86, 108690. [Google Scholar] [CrossRef]
- Carpinlioglu, M.O. A comment on unsteady-periodic flow friction factor: An analysis on experimental data gathered in pulsatile pipe flows. J. Therm. Eng. 2020, 6, 16–27. [Google Scholar] [CrossRef]
- Wei, Z.A.; Huddleston, C.; Trusty, P.M.; Singh-Gryzbon, S.; Fogel, M.A.; Veneziani, A.; Yoganathan, A.P. Analysis of Inlet Velocity Profiles in Numerical Assessment of Fontan Hemodynamics. Ann. Biomed. Eng. 2019, 47, 2258–2270. [Google Scholar] [CrossRef] [PubMed]
- Shehada, R.E.N.; Cobbold, R.S.C.; Johnston, K.W.; Aarnink, R. Three-dimensional display of calculated velocity profiles for physiological flow waveforms. J. Vasc. Surg. 1993, 17, 656–660. [Google Scholar] [CrossRef] [Green Version]
- Loudon, C.; Tordesillas, A. The use of the dimensionless Womersley number to characterize the unsteady nature of internal flow. J. Theor. Biol. 1998, 191, 63–78. [Google Scholar] [CrossRef] [PubMed]
- Thambiraj, G.; Gandhi, U.; Mangalanathan, U.; Maria Jose, V.J.; Anand, M. Investigation on the effect of Womersley number, ECG and PPG features for cuff less blood pressure estimation using machine learning. Biomed. Signal Process. Control 2020, 60, 101942. [Google Scholar] [CrossRef]
- Rohlf, K.; Tenti, G. The role of the Womersley number in pulsatile blood flow a theoretical study of the Casson model. J. Biomech. 2001, 34, 141–148. [Google Scholar] [CrossRef]
- Mingalev, S.V.; Lyubimova, T.P.; Filippov, L.O. Flow rate in a channel with small-amplitude pulsating walls. Eur. J. Mech. B/Fluids 2015, 51, 1–7. [Google Scholar] [CrossRef]
- Pfitzner, J. Poiseuille and his law. Anaesthesia 1976, 31, 273–275. [Google Scholar] [CrossRef] [PubMed]
- Womersley, J.R. Oscillatory flow in arteries: The constrained elastic tube as a model of arterial flow and pulse transmission. Phys. Med. Biol. 1957, 2, 178–187. [Google Scholar] [CrossRef]
- Hale, J.F.; McDonald, D.A.; Womersley, J.R. Velocity profiles of oscillating arterial flow, with some calculations of viscous drag and the Reynolds number. J. Physiol. 1955, 3, 629–640. [Google Scholar] [CrossRef]
- Azer, K.; Peskin, C.S. A one-dimensional model of blood flow in arteries with friction and convection based on the Womersley velocity profile. Cardiovasc. Eng. 2007, 7, 51–73. [Google Scholar] [CrossRef] [PubMed]
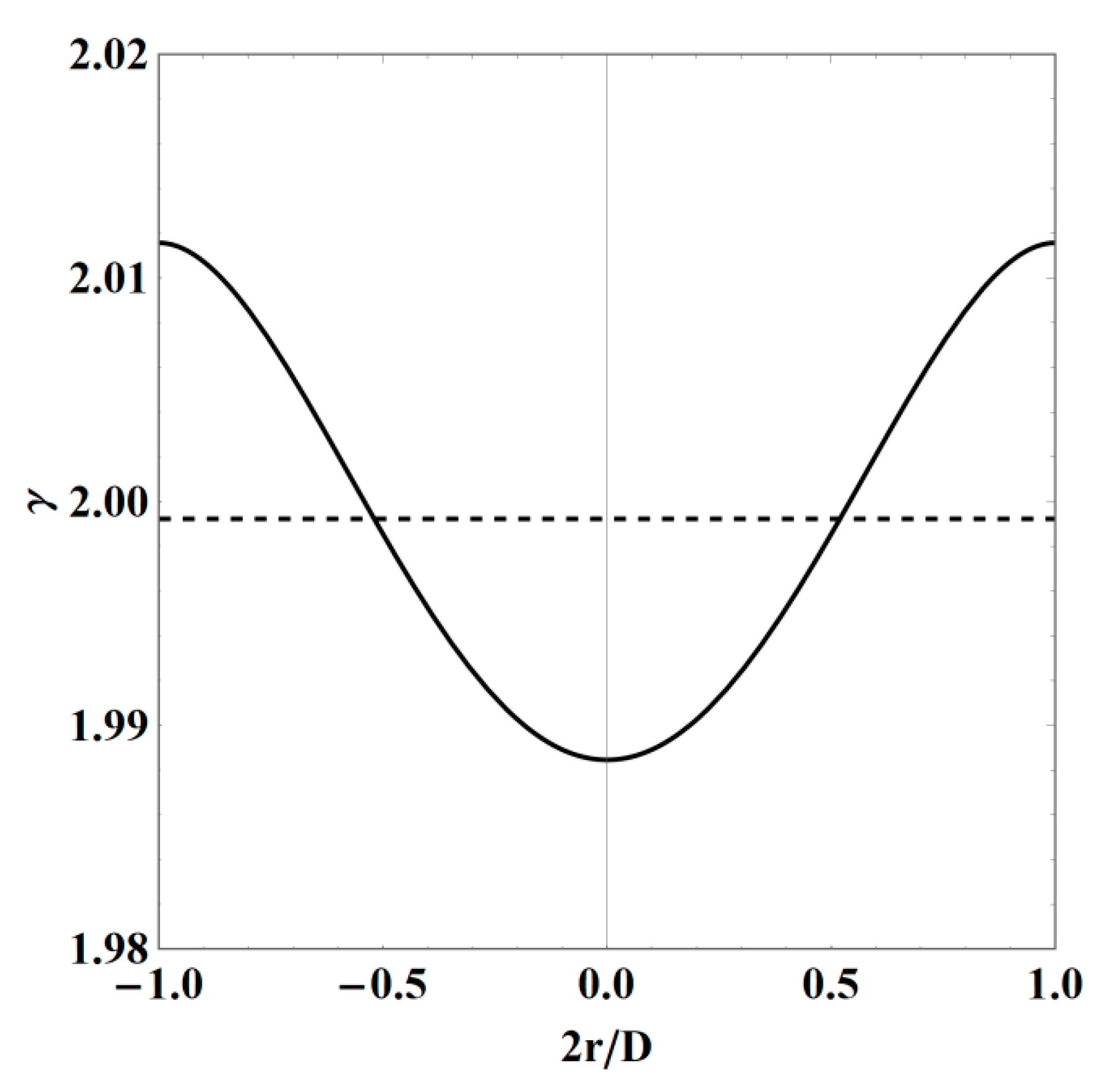


| 2r/D | f(2r/D) | vP(2r/D) | ε% | 2r/D | f(2r/D) | vP(2r/D) | ε% |
|---|---|---|---|---|---|---|---|
| 0.00 | 1.98845 | 1.99923 | 0.542061 | 0.55 | 1.39521 | 1.39446 | 0.053681 |
| 0.05 | 1.98360 | 1.99423 | 0.536241 | 0.60 | 1.28133 | 1.27951 | 0.142441 |
| 0.10 | 1.96902 | 1.97924 | 0.518870 | 0.65 | 1.15722 | 1.15456 | 0.230149 |
| 0.15 | 1.94472 | 1.95425 | 0.490221 | 0.70 | 1.02283 | 1.01961 | 0.314656 |
| 0.20 | 1.91065 | 1.91926 | 0.450745 | 0.75 | 0.87812 | 0.87466 | 0.393649 |
| 0.25 | 1.86679 | 1.87428 | 0.401073 | 0.80 | 0.72308 | 0.71972 | 0.464652 |
| 0.30 | 1.81310 | 1.81930 | 0.342012 | 0.85 | 0.55772 | 0.55479 | 0.525025 |
| 0.35 | 1.74952 | 1.75433 | 0.274547 | 0.90 | 0.38204 | 0.37985 | 0.571956 |
| 0.40 | 1.67601 | 1.67936 | 0.199834 | 0.95 | 0.19611 | 0.19493 | 0.602458 |
| 0.45 | 1.59249 | 1.59439 | 0.119200 | 1.00 | 0.00000 | 0.00000 | - |
| 0.50 | 1.49891 | 1.49942 | 0.034141 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Impiombato, A.N.; La Civita, G.; Orlandi, F.; Franceschini Zinani, F.S.; Oliveira Rocha, L.A.; Biserni, C. A Simple Transient Poiseuille-Based Approach to Mimic the Womersley Function and to Model Pulsatile Blood Flow. Dynamics 2021, 1, 9-17. https://doi.org/10.3390/dynamics1010002
Impiombato AN, La Civita G, Orlandi F, Franceschini Zinani FS, Oliveira Rocha LA, Biserni C. A Simple Transient Poiseuille-Based Approach to Mimic the Womersley Function and to Model Pulsatile Blood Flow. Dynamics. 2021; 1(1):9-17. https://doi.org/10.3390/dynamics1010002
Chicago/Turabian StyleImpiombato, Andrea Natale, Giorgio La Civita, Francesco Orlandi, Flavia Schwarz Franceschini Zinani, Luiz Alberto Oliveira Rocha, and Cesare Biserni. 2021. "A Simple Transient Poiseuille-Based Approach to Mimic the Womersley Function and to Model Pulsatile Blood Flow" Dynamics 1, no. 1: 9-17. https://doi.org/10.3390/dynamics1010002
APA StyleImpiombato, A. N., La Civita, G., Orlandi, F., Franceschini Zinani, F. S., Oliveira Rocha, L. A., & Biserni, C. (2021). A Simple Transient Poiseuille-Based Approach to Mimic the Womersley Function and to Model Pulsatile Blood Flow. Dynamics, 1(1), 9-17. https://doi.org/10.3390/dynamics1010002







