Transient Analysis of a Finite Queueing System with Bulk Arrivals in IoT-Based Edge Computing Systems
Abstract
1. Introduction
- Under the coronavirus pandemic environment, in a college library or bookstore, the number of entering students (either individual or student group) will be restricted after the number of students in the building is balanced, where the arrival students should wait in a queue in front of the door until a college staff allows a certain number of them to enter after the same number of students leave. In other words, when one student leaves, the head of line student in the queue will enter; when two students leave, the first two students in the queue will enter; and so on.
- In a doctor’s clinic, the number of daily appointments and patient companions (i.e., visitors arriving at the same time) will be restricted due to the limited space.
- In transportation processes involving buses, airplanes, trains, ships, and elevators, where customers do not arrive singly, but in groups or bulk.
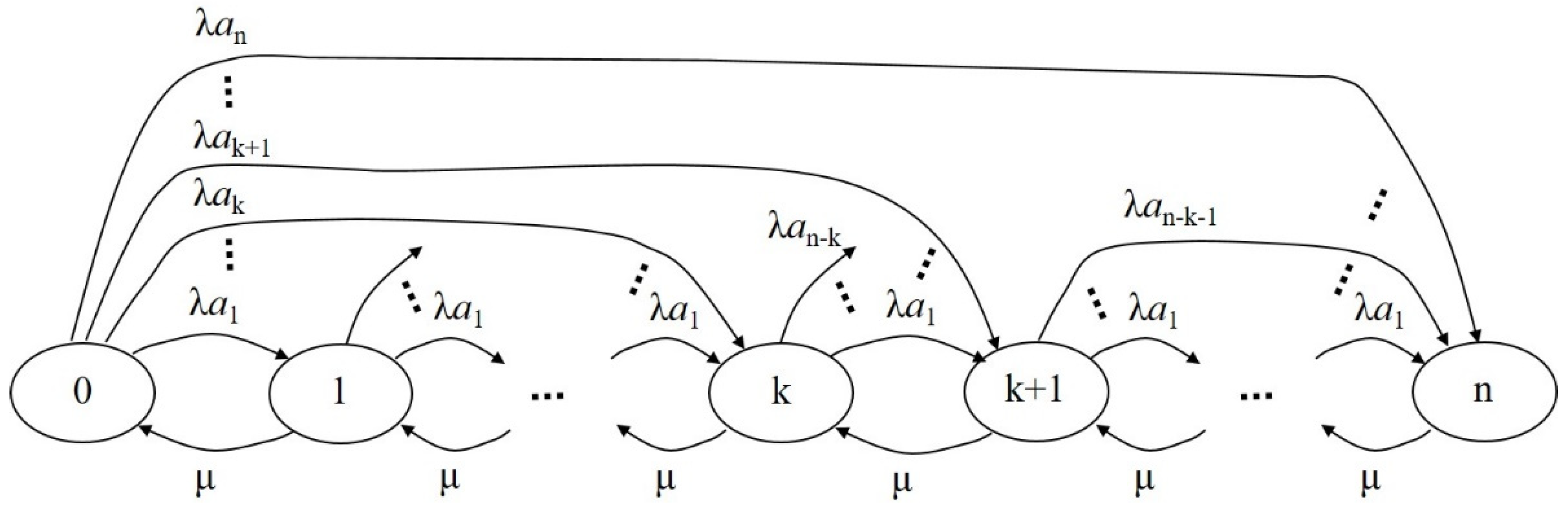
2. Stochastic Queueing Model
- (i)
- The single-server queueing system is finite with capacity of n. That is, the queue length or the maximum number of waiting places is n − 1.
- (ii)
- The customers arrive at a service facility in batches in accordance with a Poisson process with mean arrival rate λ.
- (iii)
- The number of arrivals may be either individuals or groups with random size, described by a random variable X with distribution given by ai = P(X = i), i ≥ 1, where i is the number of customers in a group. If the group of customers arriving in the system finds j customers there, the whole group will enter the system when i ≤ n − j; and leave the system when i > n − j.
- (iv)
- The service time of customers is a random variable with negative exponential distribution with parameter μ.
- (v)
- The queue discipline is first come first served (FCFS) by the arrivals and random inside the group.
- (vi)
- The arrivals, service times and batch sizes are mutually independent.
3. Model Analysis and Solutions
4. Case Study
5. Performance Metrics
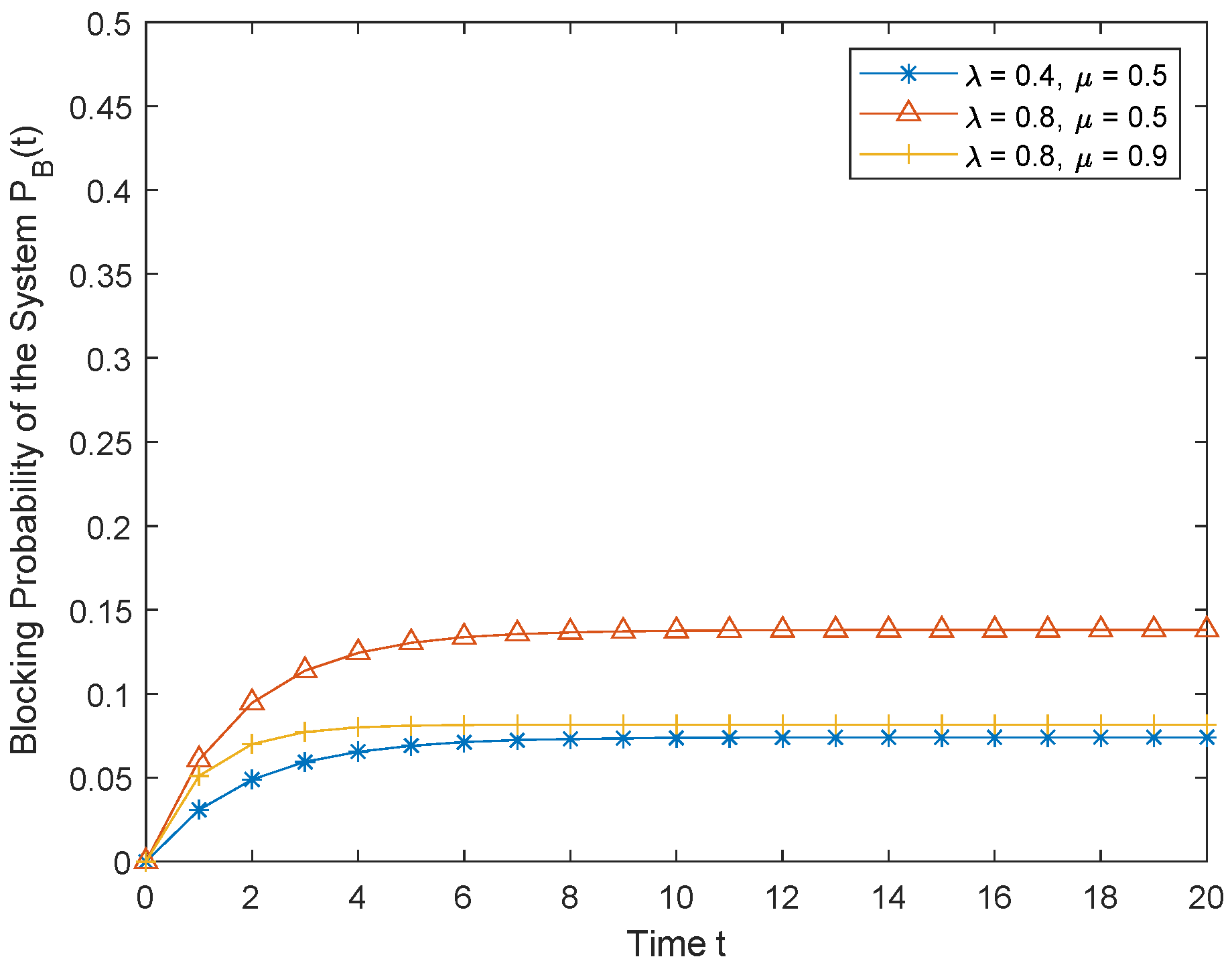
5.1. Blocking Probability of the System
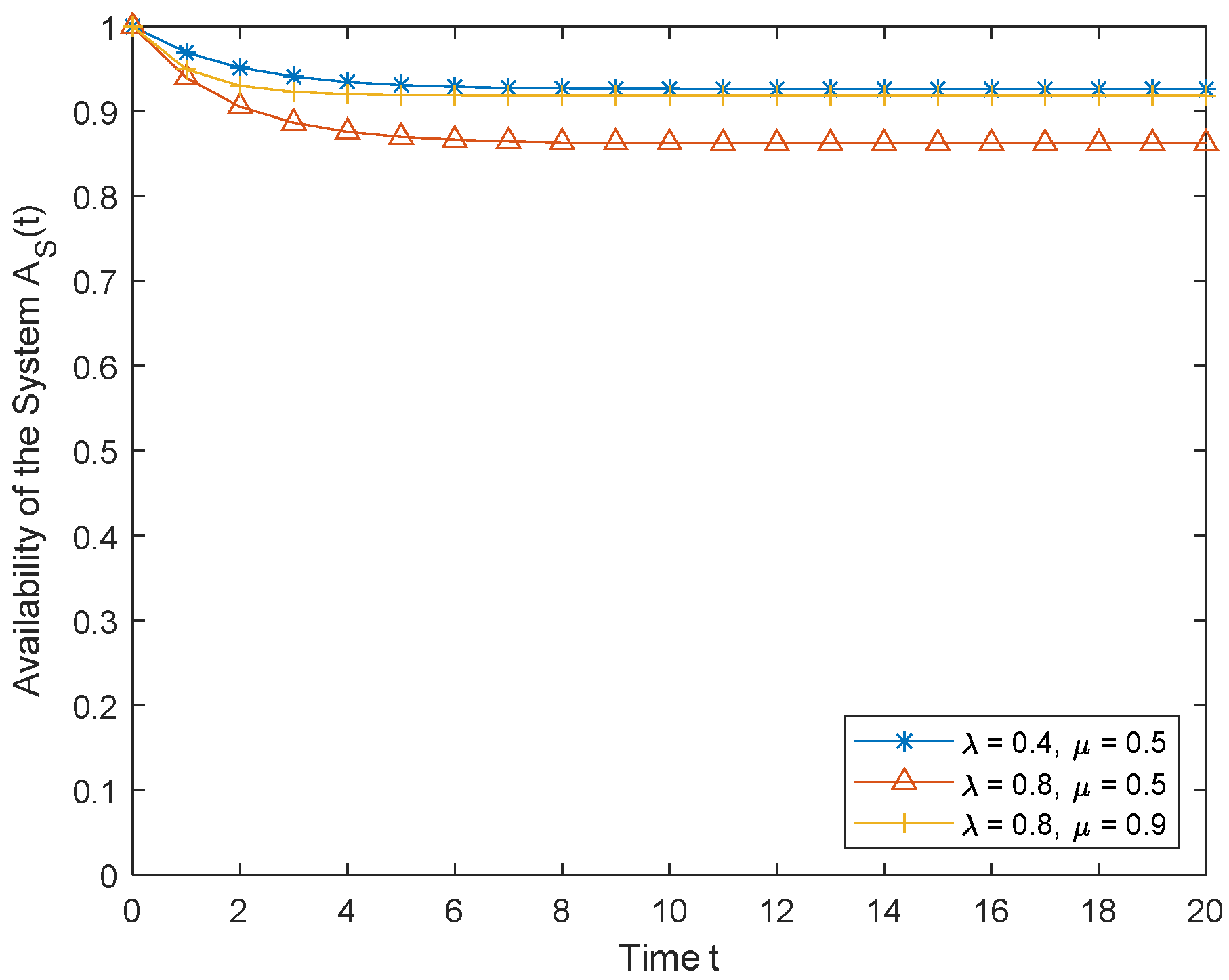
5.2. Availability of the System
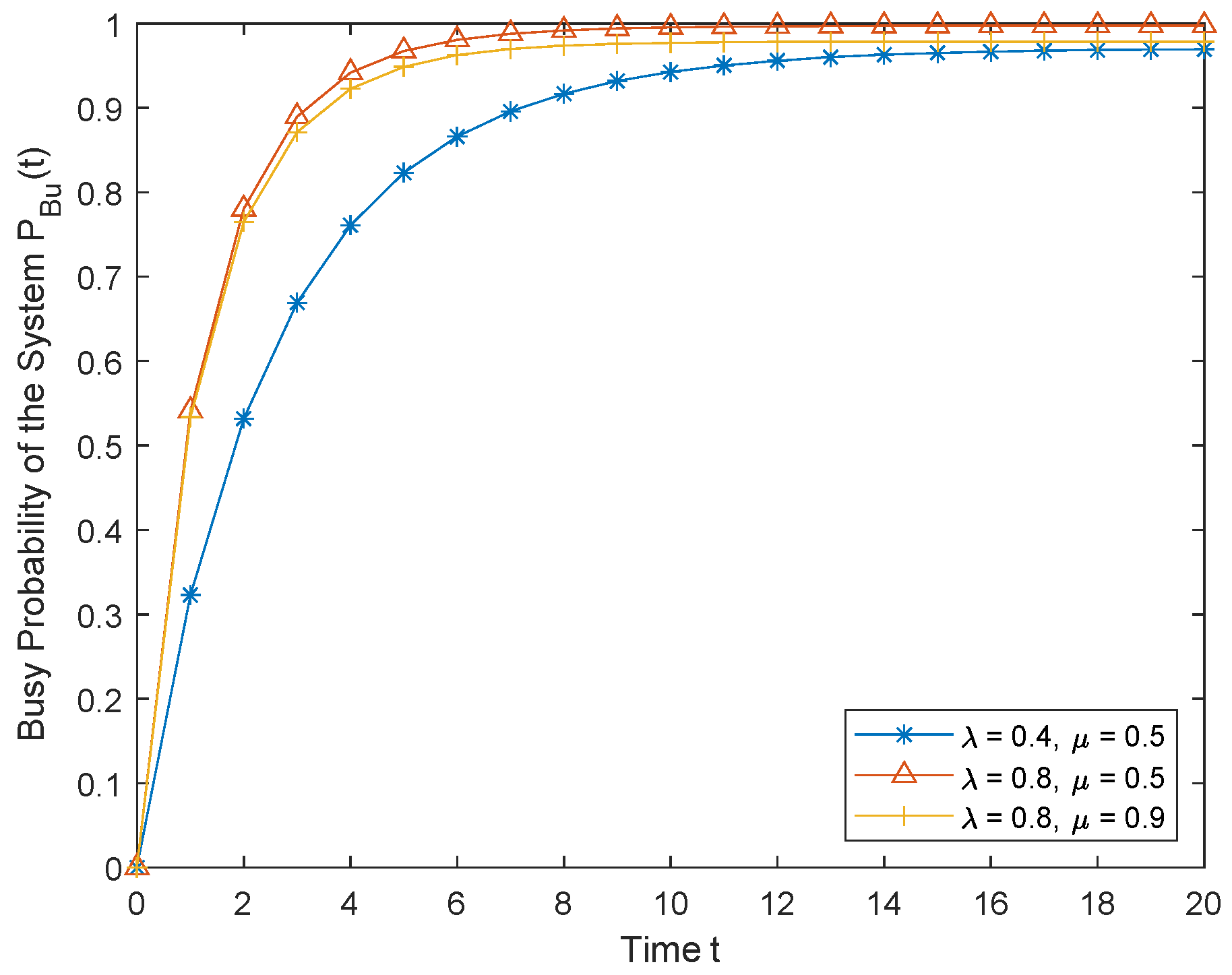
5.3. Idle and Busy Probabilities of the System
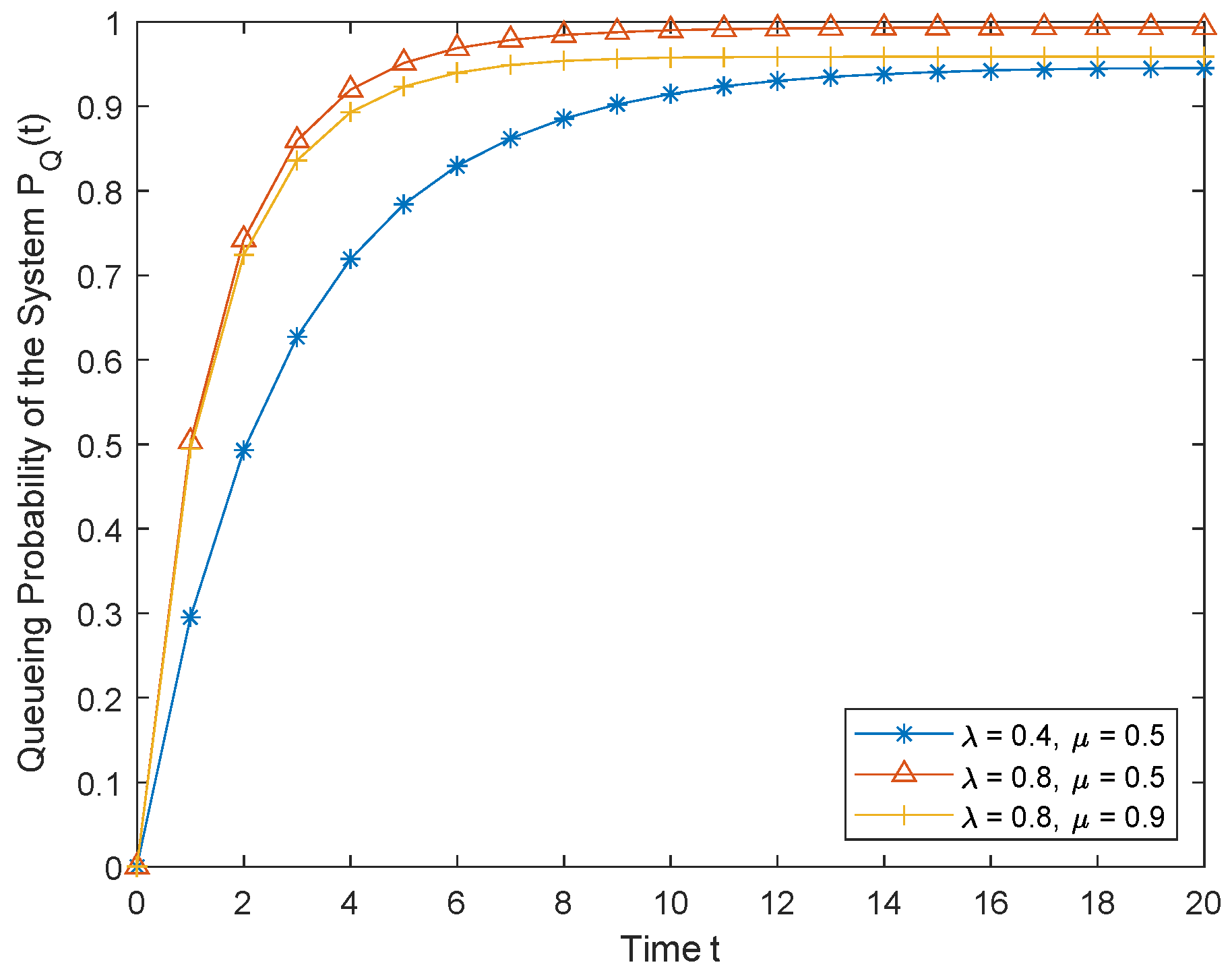
5.4. Queueing Probability of the System
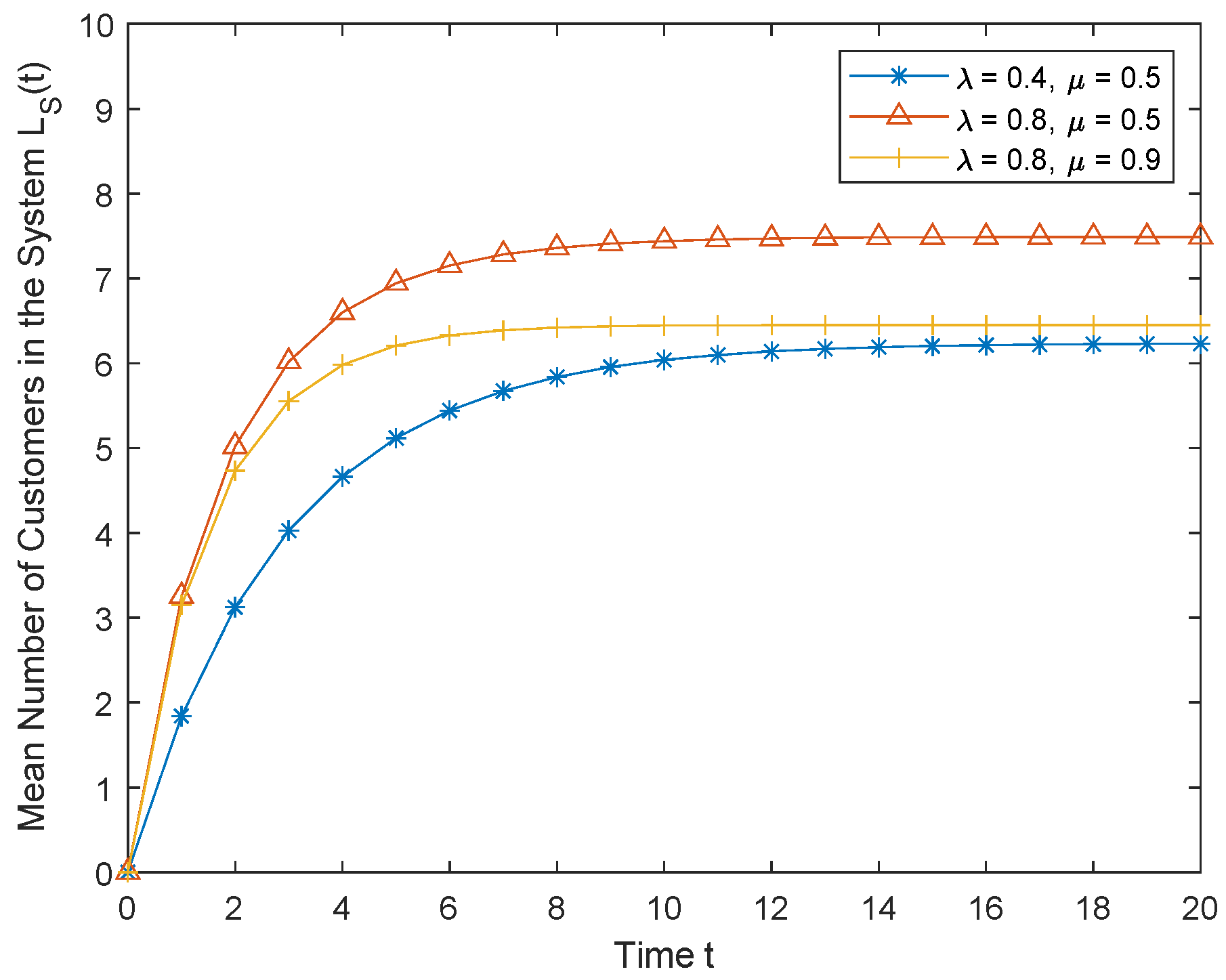
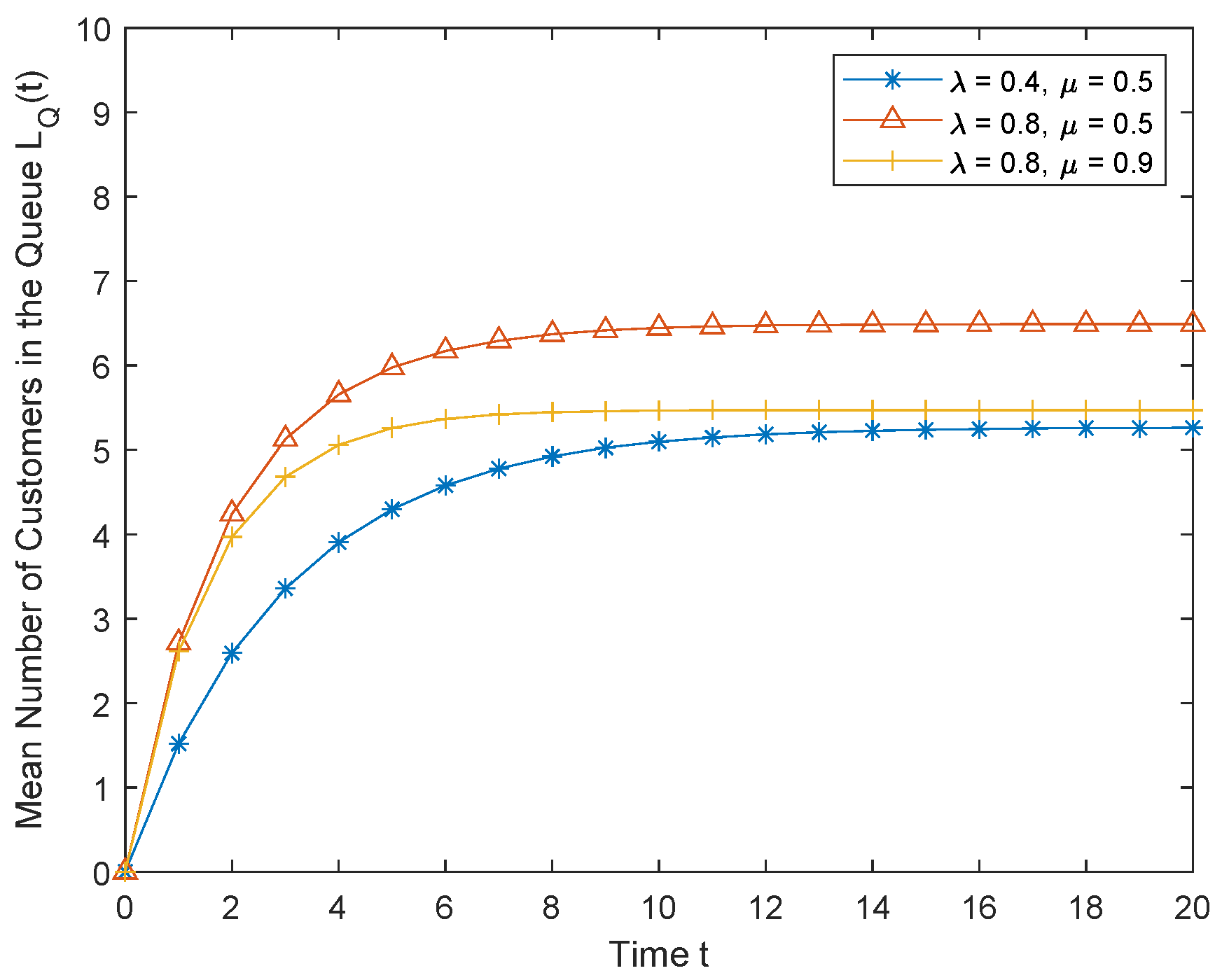
5.5. Mean Number of Customers in the System and Queue
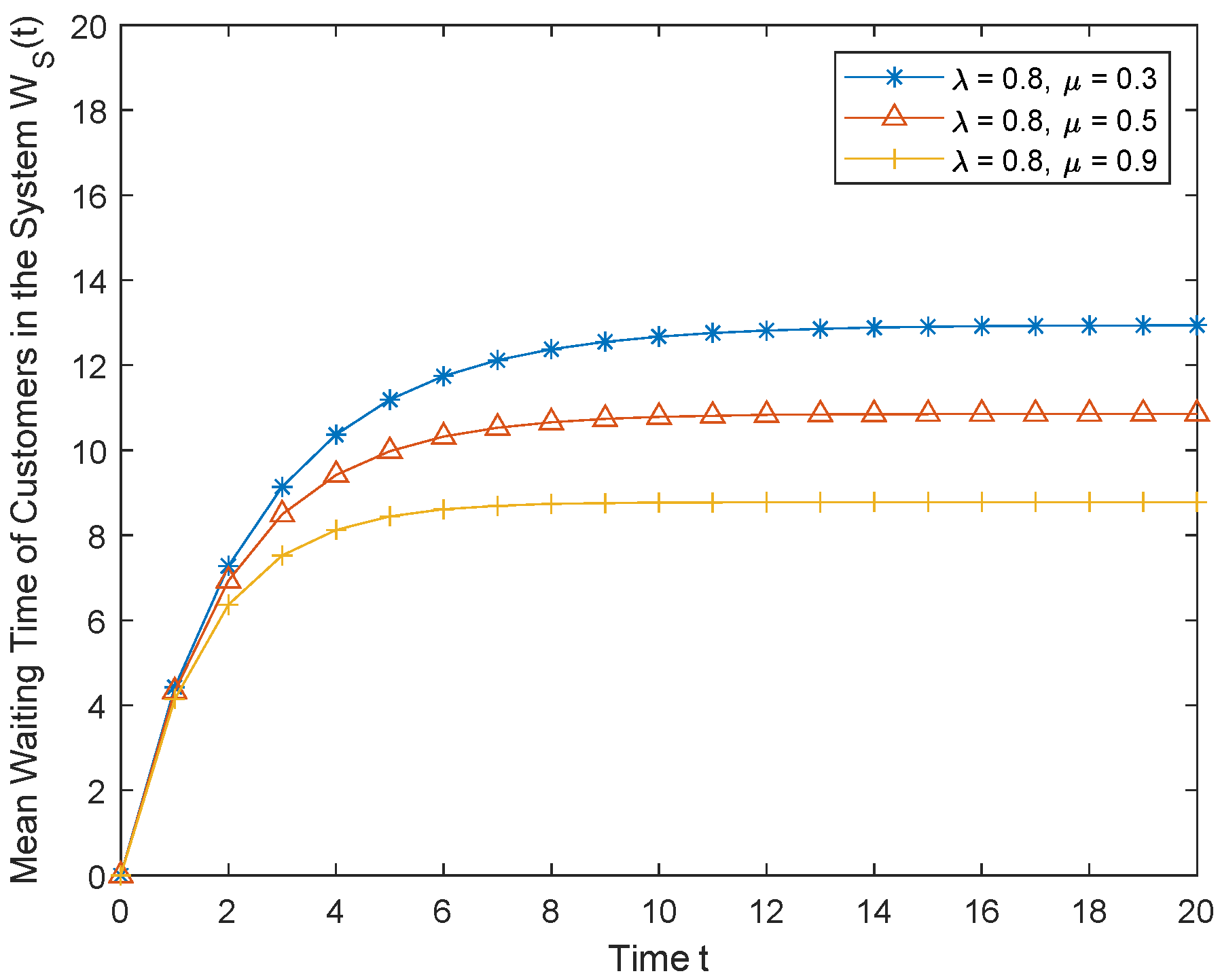
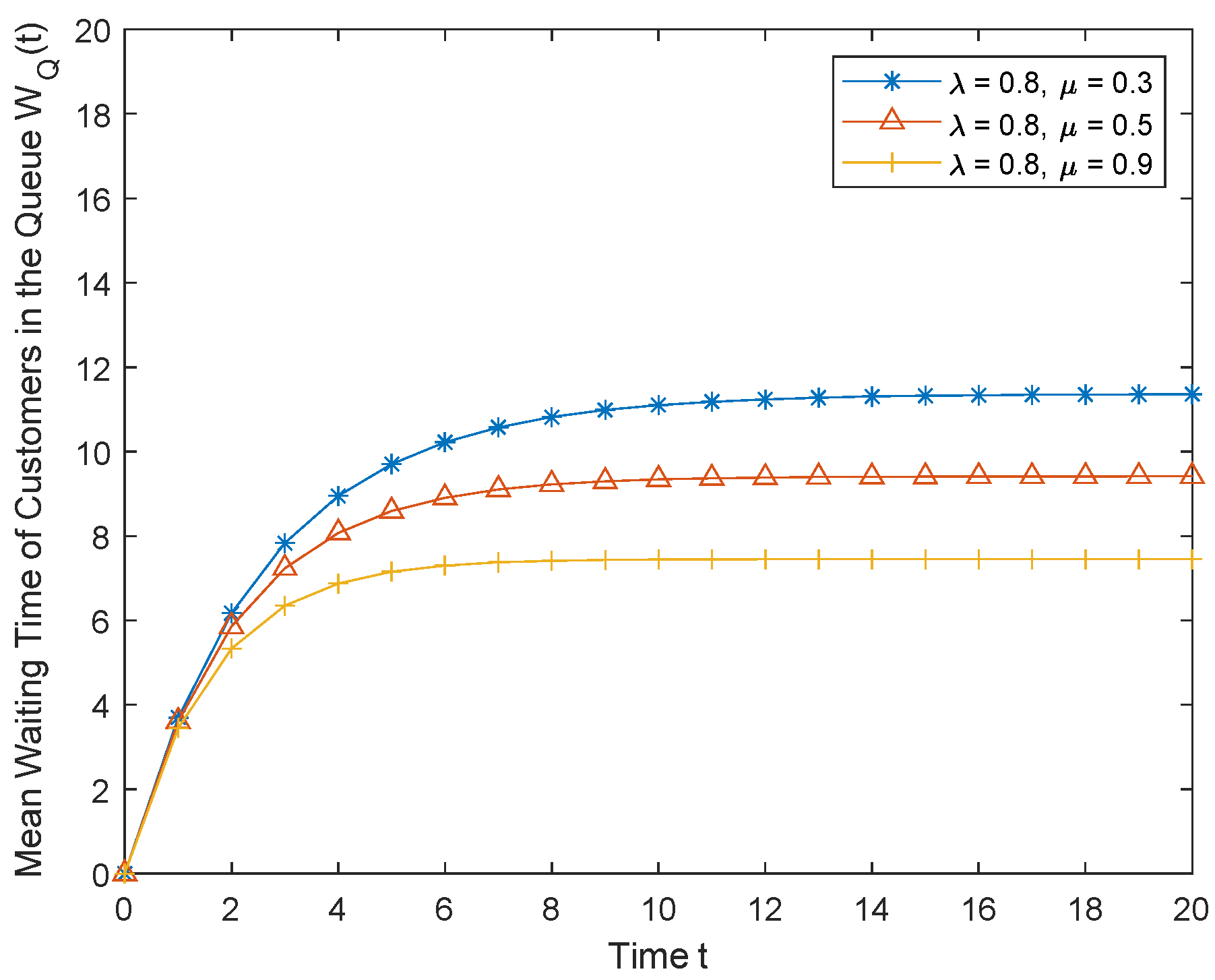
5.6. Mean Waiting Time of Customers in the System and Queue
6. Numerical Results
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| n | The total number of customers in the system. |
| k, 0 ≤ k ≤ n | The current number of customers in the system (i.e., the system state). |
| λ | The mean arrival rate of the bulk arrivals. |
| μ | The mean service rate of the single server system. |
| X | The random variable used to describe the number of arrivals in a group (i.e., batch size). |
| ai, 1≤ i ≤ n | The probability distribution of batch size, ai = P(X = i). |
| a | The probability of the batch size when the batch size X is a uniform random variable. |
| pk(t), 0 ≤ k ≤ n | The probability that k customers are present in the system at time t. |
| C(k, i) | The coefficients of the solution to the ODEs. |
| λ′ | The effective arrival rate. |
| PB(t) | The blocking probability of the system. |
| AS(t) | The system availability. |
| PId(t) | The system idle probability. |
| PBu(t) | The system busy probability. |
| PQ(t) | The system queueing probability. |
| LS(t) | The mean number of customers in the system. |
| LQ(t) | The mean number of customers in the queue. |
| WS(t) | The mean waiting time of customers in the system. |
| WQ(t) | The mean waiting time of customers in the queue. |
References
- Kleinrock, L. Queueing Systems, Volume 1: Theory, 1st ed.; Wiley-Interscience: Hoboken, NJ, USA, 1975. [Google Scholar]
- Chaudhry, M.L.; Templeton, J.G.C. A First Course in Bulk Queues; John Wiley & Sons: Hoboken, NJ, USA, 1983; ISBN 978-0471862604. [Google Scholar]
- Pegden, C.D.; Rosenshine, M. Some New Results for the M/M/1 Queue. Manag. Sci. 1982, 28, 821–828. [Google Scholar] [CrossRef]
- Lopez-Herrero, M.J. Distribution of the Number of Customers Served in an M/G/1 Retrial Queue. J. Appl. Probab. 2002, 39, 407–412. [Google Scholar] [CrossRef]
- Conolly, B.W. Queueing at a Single Serving Point with Group Arrival. J. R. Stat. Soc. Ser. B 1960, 22, 285–298. [Google Scholar] [CrossRef]
- Shanbhag, D.N. On Infinite Server Queues with Batch Arrivals. J. Appl. Probab. 1966, 3, 274–279. [Google Scholar] [CrossRef]
- Sharma, S.D. On a Continuous/Discrete Time Queueing System with Arrivals in Batches of Variable Size and Correlated Departures. J. Appl. Probab. 1975, 12, 115–129. [Google Scholar] [CrossRef]
- Alfa, A.S. A Numerical Method for Evaluating Delay to a Customer in a Time-Inhomogeneous, Single Server Queue with Batch Arrivals. J. Oper. Res. Soc. 1979, 30, 665–667. [Google Scholar] [CrossRef]
- van Dijk, N.M. An LCFS Finite Buffer Model with Finite Source Batch Input. J. Appl. Probab. 1989, 26, 372–380. [Google Scholar] [CrossRef]
- Choi, B.D.; Park, K.K. The Mk/m/∞ Queue with Heterogeneous Customers in a Batch. J. Appl. Probab. 1992, 29, 477–481. [Google Scholar]
- Chen, S.-P. A bulk arrival queueing model with fuzzy parameters and varying batch sizes. Appl. Math. Model. 2006, 30, 920–929. [Google Scholar] [CrossRef]
- Baruah, M.; Madan, K.C.; Eldabi, T. A Batch Arrival Single Server Queue with Server Providing General Service in Two Fluctuating Modes and Reneging during Vacation and Breakdowns. J. Probab. Stat. 2014, 2014, 319318. [Google Scholar] [CrossRef]
- Niranjan, S.P.; Indhira, K.; Chandrasekaran, V.M. Analysis of bulk arrival queueing system with batch size dependent service and working vacation. AIP Conf. Proc. 2018, 1952, 020061. [Google Scholar] [CrossRef]
- Laslett, G.M. Characterising the Finite Capacity GI/M/1 Queue with Renewal Output. Manag. Sci. 1975, 22, 106–110. [Google Scholar] [CrossRef]
- Chao, X. On the Departure Processes of M/M/1/N and GI/G/1/N Queues. Adv. Appl. Probab. 1992, 24, 751–754. [Google Scholar] [CrossRef][Green Version]
- Kaczynski, W.H.; Leemis, L.M.; Drew, J.H. Transient Queueing Analysis. INFORMS J. Comput. 2012, 24, 10–28. [Google Scholar] [CrossRef]
- Kelton, W.D.; Law, A.M. The Transient Behavior of the M/M/s Queue, with Implications for Steady-State Simulation. Oper. Res. 1985, 33, 378–396. [Google Scholar] [CrossRef]
- Sharma, O.P.; Gupta, U.C. Transient Behaviour of an M/M/1/N queue. Stoch. Process. Appl. 1982, 13, 327–331. [Google Scholar] [CrossRef]
- Leguesdron, P.; Pellaumail, J.; Rubino, G.; Sericola, B. Transient Analysis of the M/M/1 Queue. Adv. Appl. Probab. 1993, 25, 702–713. [Google Scholar] [CrossRef]
- Sharmaand, O.P.; Tarabia, A.M.K. A Simple Transient Analysis of an M/M/1/N Queue. Sankhyā Indian J. Stat. Ser. A 2000, 62, 273–281. [Google Scholar]
- Garcia, J.-M.; Brun, O.; Gauchard, D. Transient Analytical Solution of M/D/1/N Queues. J. Appl. Probab. 2002, 39, 853–864. [Google Scholar] [CrossRef]
- Kaczynski, W.; Leemis, L.; Drew, J. Modeling and analyzing transient military air traffic control. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010; pp. 1395–1406. [Google Scholar] [CrossRef]
- Chydzinski, A.; Adamczyk, B. Transient and Stationary Losses in a Finite-Buffer Queue with Batch Arrivals. Math. Probl. Eng. 2012, 2012, 326830. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; Wiley: Hoboken, NJ, USA, 2020; ISBN 978-1119455929. [Google Scholar]
| Parameters | Value | Unit | Description |
|---|---|---|---|
| t | [0, 30] | General time units | time |
| λ | 0.4, 0.9 | Customers/unit time | arrival rate |
| μ | 0.5, 1.0 | Customers/unit time | service rate |
| n | 10 | Number of customers | system capacity |
| ai = a, i ≤ n | 0.1 | Prob. distribution of bulk arrivals |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S. Transient Analysis of a Finite Queueing System with Bulk Arrivals in IoT-Based Edge Computing Systems. IoT 2022, 3, 435-449. https://doi.org/10.3390/iot3040023
Tang S. Transient Analysis of a Finite Queueing System with Bulk Arrivals in IoT-Based Edge Computing Systems. IoT. 2022; 3(4):435-449. https://doi.org/10.3390/iot3040023
Chicago/Turabian StyleTang, Shensheng. 2022. "Transient Analysis of a Finite Queueing System with Bulk Arrivals in IoT-Based Edge Computing Systems" IoT 3, no. 4: 435-449. https://doi.org/10.3390/iot3040023
APA StyleTang, S. (2022). Transient Analysis of a Finite Queueing System with Bulk Arrivals in IoT-Based Edge Computing Systems. IoT, 3(4), 435-449. https://doi.org/10.3390/iot3040023






