Assessing Feature Representations for Instance-Based Cross-Domain Anomaly Detection in Cloud Services Univariate Time Series Data
Abstract
:1. Introduction
- A comprehensive analysis of the multiple feature time-series feature sets for anomaly detection across a number of cross-domain time-series datasets;
- Identifying a feature set that outperforms the other representations by a statistically significant margin on the task of cross-domain anomaly detection;
- Elaborating feature importance in the top performing representation.
2. Related Work on Feature Engineering for Time-Series Analysis and Anomaly Detection
3. Feature Sets under Test
- A list of candidate periods are extracted from the time series using the periodogram method, and
- The candidate periods are then ranked using an autocorrelation method ACF.
- Spectral Residual (SR) is the concept borrowed from the visual computing world which is based on Fast Fourier Transform (FFT). Spectral residual is unsupervised and has proven its efficacy in visual saliency detection applications. In anomaly detection tasks, the anomalies in the time series have similar characteristics to saliency detection, i.e., they both visually stand out from the normal distribution.
- Skewness is the measurement of the symmetry in a frequency distribution. Skewness is very sensitive to outlier values because the calculation of skewness depends on the cubed distance between a value and the mean. Hence, we believe that the presence of any outlier may affect the skewness of a distribution within a time window, and so skewness might be helpful in anomaly detection tasks. Indeed, the authors of [36] propose an approach to anomaly detection based on skewness.
- Kurtosis is often described as the extent to which the peak of a probability distribution deviates from the shape of a normal distribution, i.e., whether the shape is too peaked or too flat to be normally distributed. This feature can be used as a complementary feature with the skewness in case of distributions that are symmetrical but are too peaked or too flat to be normally distributed. In fact, it has been mathematically proven in the context of dimensionality reduction techniques for anomaly detection that the optimal directions of projection of a time series into a reduced dimensionality are those that maximize or minimize the kurtosis coefficient of the project time series (see [37,38]), and [39] is an example of recent work that proposes an approach to anomaly detection in time-series data based on kurtosis.
- Raw (window size = 15),
- HAD
- catch22,
- catch23 (catch22 + Spectral Residual),
- catch24 (catch22 + Mean + Variance),
- catch25 (catch22 + SR + Mean + Variance).
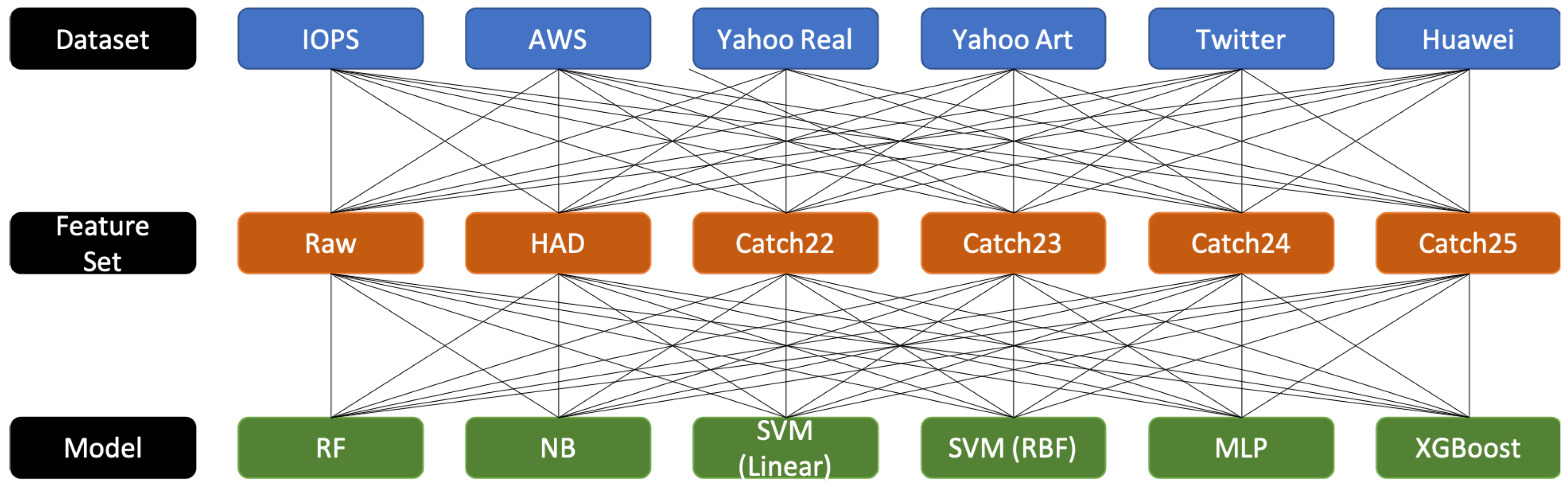
4. Experimental Design
- Naïve bayes: Model parameters are inferred from training data.
- Random forest: 200 estimators, , no max depth, two samples as minimum number of samples required to split an internal node, one as minimum number of samples in newly created leaves, with bootstrapping, using out-of-bag samples to estimate the generalization error.
- Xgboost: gbtree booster, step size shrinkage of , 0 Minimum loss reduction required to make a further partition on a leaf node of the tree, 6 maximum depth of a tree,
- Multi-layer perceptron: 1 hidden layer with 100 ReLU units per layer with a single logistic unit in the output layer, adam as the solver, using L2 penalty of 0.0001, batch size of 200, constant learning rate, 0.001 step-size in updating the weights, max iterations set to 200, no early stopping, 0.9 as exponential decay rate for estimates of first moment vector, and 0.999 as exponential decay rate for estimates of second moment vector, 1 × 10 for numerical stability.
- SVC: rbf kernel, regularization parameter of 1.0, scaled kernel coefficient on data set variance, and vector length.
- SVC linear: linear kernel, and regularization parameter of 0.25.
- -
- Other SVC parameters: shrinking heuristic, no probability estimates, 1 × 10 tolerance for stopping criterion, 200 MB kernel cache, no class weights, no limit on number of iterations, and one-vs.-rest decision function.
- NAB (AWS and Twitter) is a benchmark for evaluating anomaly detection algorithms in streaming, real-time applications. It is composed of over 50 labeled real-world and artificial time series. We focus on two of the real-world datasets: (i) web monitoring statistics from AWS and (ii) Twitter tweet volumes. The AWS time series are taken from different server metrics such as CPU utilization, network traffic, and disk write bytes. The Twitter dataset is the number of Twitter mentions of publicly-traded companies such as Google and IBM. The value represents the number of mentions for a given ticker symbol in every five windows.
- Yahoo Anomaly Detection Dataset is a publicly available collection of datasets released by Yahoo for benchmarking anomaly detection algorithms. The dataset has four sets of time series: one is collected from production traffic to yahoo services, which is labelled by editors manually, whereas the others are synthesized with anomalies that are embedded artificially. We use the real data and synthesised data but not the “A3” and “A4” datasets.
- IOPS KPI dataset is a collection of time series datasets provided by Alibaba, Tencent, Baidu, eBay, and Sogou. The dataset is from real traffic on web services and was published as part of a series of anomaly detection competitions.
- Huawei dataset is the dataset obtained from the anomaly detection hackathon organised by Huawei (Details of the Hackathon competition are available at: https://huawei-euchallenge.bemyapp.com/ireland (accessed on 2 December 2020)). The selected time series contains different KPI values, and each datapoint is labelled as either anomaly or not anomaly.
| Algorithm 1: Structure of Experimental Design |
 |
5. Results
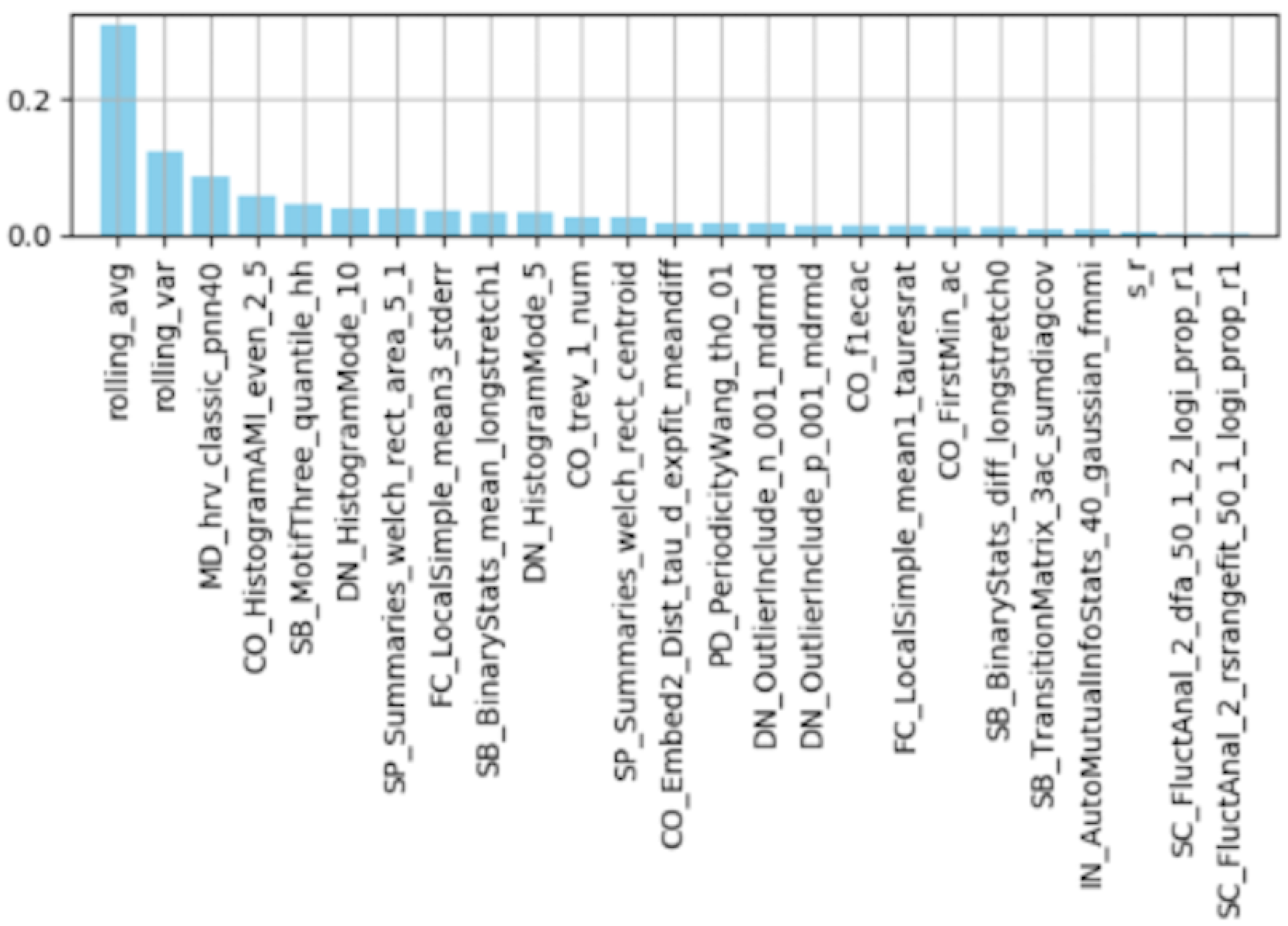
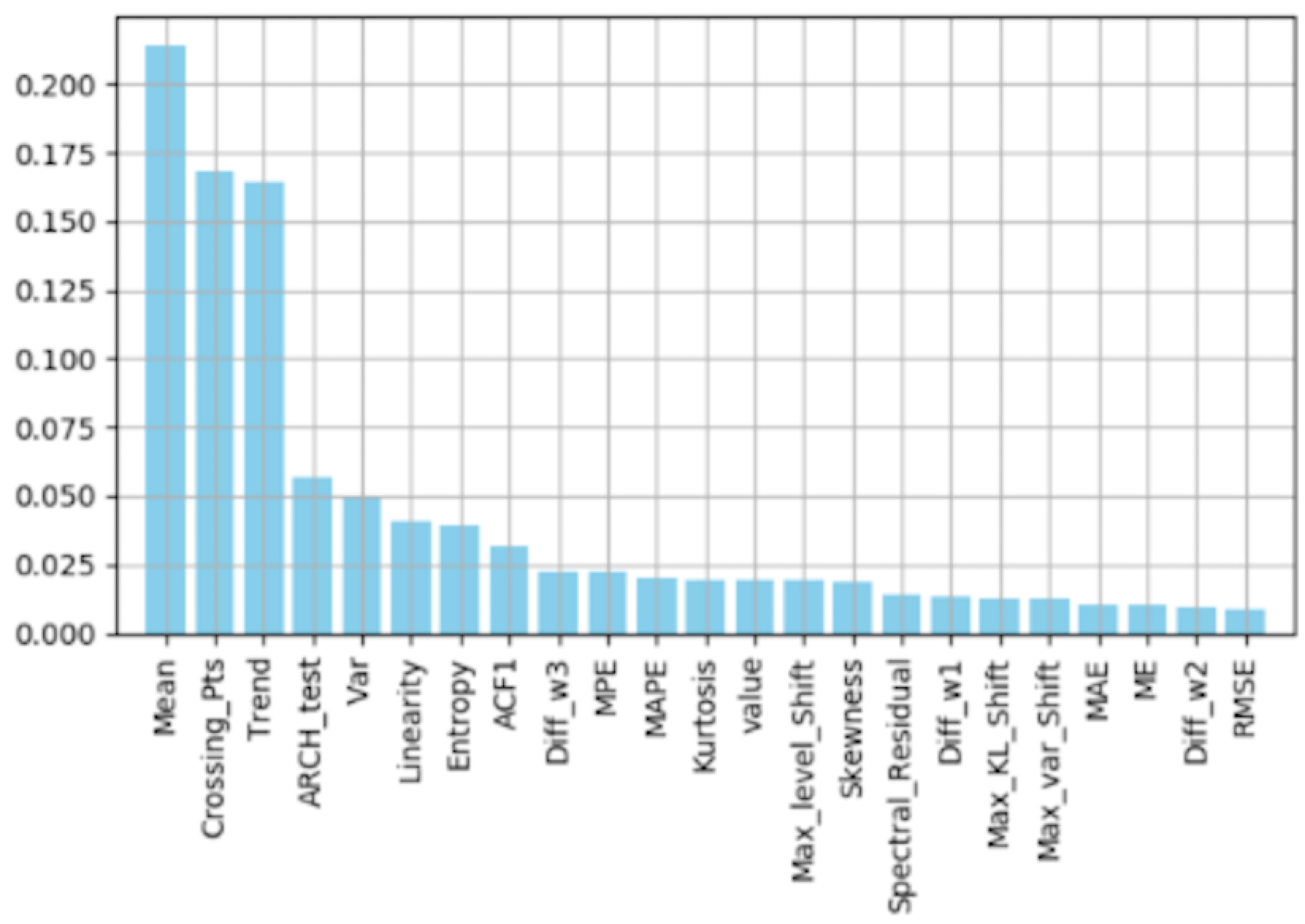
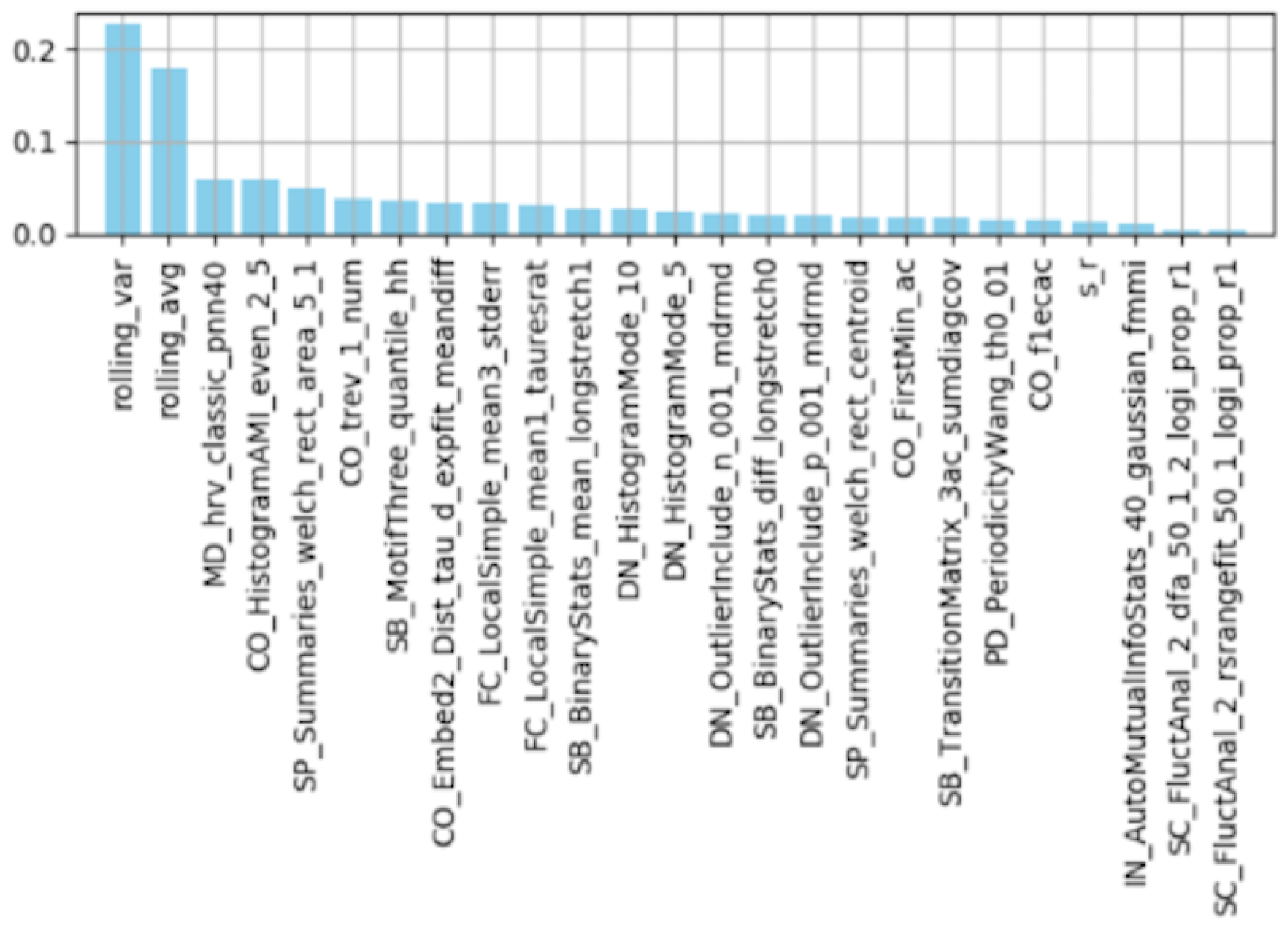
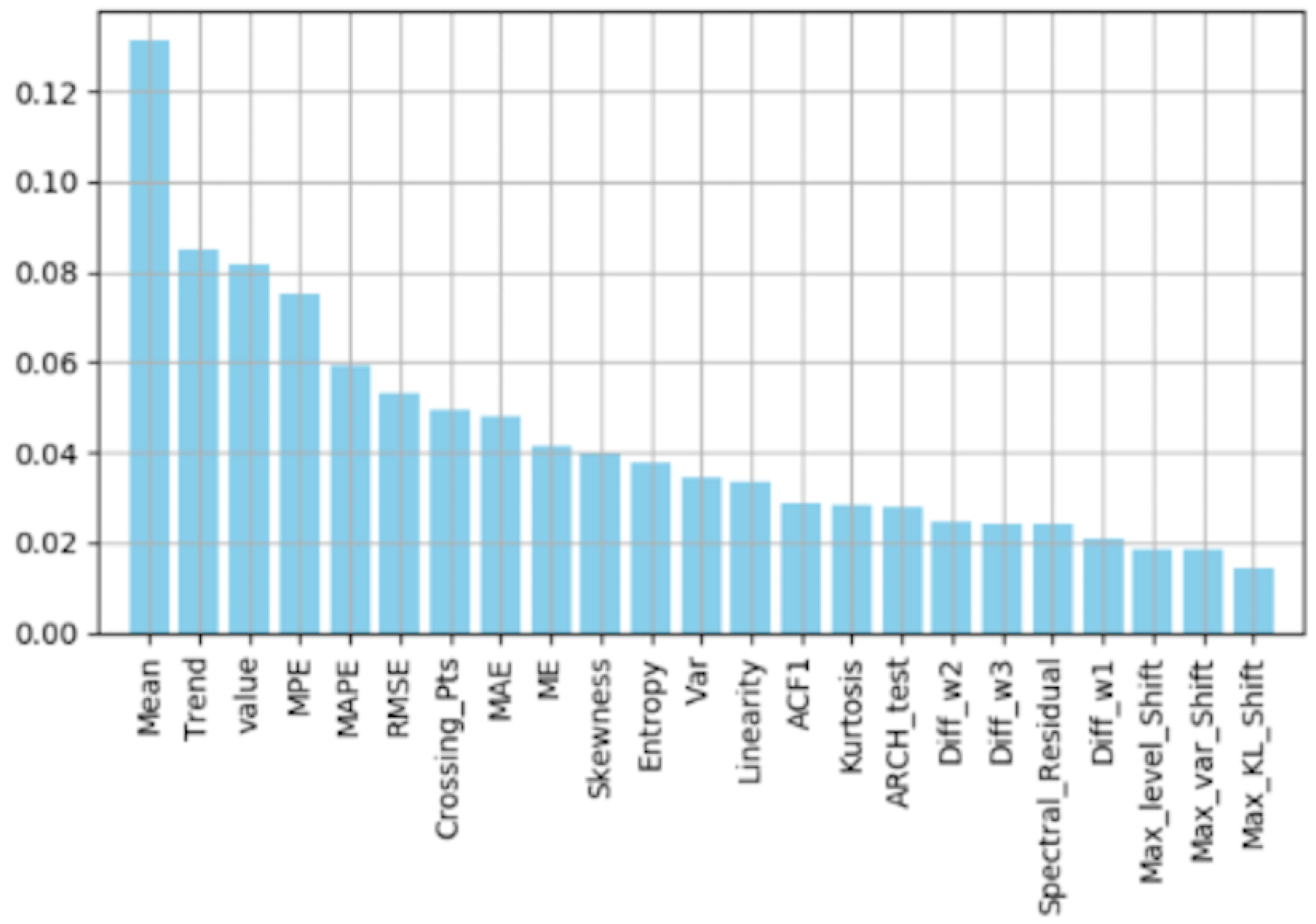
Feature Importance by Random Forest
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Feature | Description |
|---|---|
| DN HistogramMode 5 | Mode of z-scored distribution (5-bin histogram) |
| DN HistogramMode 10 | Mode of z-scored distribution (10-bin histogram) |
| SB BinaryStats mean longstretch1 | Longest period of consecutive values above the mean |
| DN OutlierInclude p 001 mdrmd | Time intervals between successive extreme event above the mean |
| DN OutlierInclude n 001 mdrmd | Time intervals between successive extreme events below the mean |
| CO f1ecac | First 1/e crossing of autocorrelation function |
| CO FirstMin ac | First minimum of autocorrelation function |
| SP Summaries welch rect area 5 1 | Total power in lowest fifth of frequencies in the Fourier power spectrum |
| SP Summaries welch rect centroid | Centroid of the Fourier power spectrum |
| FC LocalSimple mean3 stderr | Mean error from a rolling 3-sample mean |
| IN AutoMutualInfoStats 40 gaussian fmmi | First minimum of the automutual information function |
| CO HistogramAMI even 2 5 | Automutual information, |
| CO trev 1 num | Time-reversibility statistic, |
| MD hrv classic pnn40 | Proportion of successive differences exceeding |
| SB BinaryStats diff longstretch0 | Longest period of successive incremental decreases |
| SB MotifThree quantile hh | Shannon entropy of two successive letters in equiprobable 3 letter symbolization |
| FC LocalSimple mean1 tauresrat | Change in correlation length after iterative differencing |
| CO Embed2 Dist tau d expfit meandiff | Exponential fit to successive distances in 2-d embedding space |
| SC FluctAnal 2 dfa 50 1 2 logi prop r1 | Proportion of slower time scale fluctuations that scale with DFA ( sampling) |
| SC FluctAnal 2 rsrangefit 50 1 logi prop r1 | Proportion of slower time scale fluctuations that scale with linearly rescaled range fit |
| 5SB TransitionMatrix 3ac sumdiagcov | Trace of covariance of transition matrix between symbols in 3-letter alphabet |
| PD PeriodicityWang th0 01 | Periodicity |
| Feature | Description |
|---|---|
| ACF1 | First order of autocorrelation |
| ACF Remainder | Autocorrelation of remainder |
| Mean | Rolling mean |
| Variance | Rolling variance |
| Entropy | Spectral entropy |
| Linearity | Strength of linearity |
| Trend | Strength trend |
| Crossing Point | number of crossing points |
| ARCHtest | p value of Lagrange Multiplier (LM) test for ARCH model |
| Curvature | Strength of curvature computed on Trend of STL decomposition |
| GARCHtest.p | p value of Lagrange Multiplier |
| Feature | Formula | Description |
|---|---|---|
| RMSE | Root mean square error | |
| ME | Mean error | |
| MAE | Mean absolute error | |
| MPE | Mean percentage error | |
| MAPE | Mean absolute percentage error |
| Feature | Description |
|---|---|
| Max level shift | Max trimmed mean between two consecutive windows |
| Max var shift | Max variance shift between two consecutive windows |
| Max KL shift | Max shift in Kullback–Leibler divergence between two consecutive windows |
| Diff-w | The differences between the current value and the w-th previous value |
| Lumpiness | Changing variance in remainder |
| Flatspots | Discretize time series value into ten equal sized interval, find maximum run length within the same bucket |
References
- Nielsen, A. Practical Time Series Analysis: Prediction with Statistics and Machine Learning; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Kelleher, J.D.; Tierney, B. Data Science; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Qiu, J.; Du, Q.; Qian, C. Kpi-tsad: A time-series anomaly detector for kpi monitoring in cloud applications. Symmetry 2019, 11, 1350. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Lin, Q.; Xu, Y.; Qin, S.; Zhang, H.; Qiao, B.; Dang, Y.; Yang, X.; Cheng, Q.; Chintalapati, M.; et al. Cross-dataset Time Series Anomaly Detection for Cloud Systems. In Proceedings of the 2019 USENIX Annual Technical Conference (USENIX ATC 19), Renton, WA, USA, 10–12 July 2019; USENIX Association: Renton, WA, USA, 2019; pp. 1063–1076. [Google Scholar]
- Laptev, N.; Amizadeh, S.; Flint, I. Generic and scalable framework for automated time-series anomaly detection. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1939–1947. [Google Scholar]
- Liu, D.; Zhao, Y.; Xu, H.; Sun, Y.; Pei, D.; Luo, J.; Jing, X.; Feng, M. Opprentice: Towards practical and automatic anomaly detection through machine learning. In Proceedings of the 2015 Internet Measurement Conference, Tokyo, Japan, 28–30 October 2015; pp. 211–224. [Google Scholar]
- Ahmad, S.; Lavin, A.; Purdy, S.; Agha, Z. Unsupervised real-time anomaly detection for streaming data. Neurocomputing 2017, 262, 134–147. [Google Scholar] [CrossRef]
- Terzi, D.S.; Terzi, R.; Sagiroglu, S. Big data analytics for network anomaly detection from netflow data. In Proceedings of the 2017 International Conference on Computer Science and Engineering (UBMK), Antalya, Turkey, 5–8 October 2017; pp. 592–597. [Google Scholar]
- Xu, H.; Chen, W.; Zhao, N.; Li, Z.; Bu, J.; Li, Z.; Liu, Y.; Zhao, Y.; Pei, D.; Feng, Y.; et al. Unsupervised anomaly detection via variational auto-encoder for seasonal KPIs in web applications. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 187–196. [Google Scholar]
- Chalapathy, R.; Chawla, S. Deep learning for anomaly detection: A survey. arXiv 2019, arXiv:1901.03407. [Google Scholar]
- Görnitz, N.; Kloft, M.; Rieck, K.; Brefeld, U. Toward supervised anomaly detection. J. Artif. Intell. Res. 2013, 46, 235–262. [Google Scholar] [CrossRef]
- Kelleher, J.D. Deep Learning; MIT Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Verner, A. LSTM Networks for Detection and Classification of Anomalies in Raw Sensor Data. Ph.D. Thesis, College of Engineering and Computing, Nova Southeastern University, Fort Lauderdale, FL, USA, 2019. [Google Scholar]
- Gal, Y.; Islam, R.; Ghahramani, Z. Deep bayesian active learning with image data. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1183–1192. [Google Scholar]
- Kirsch, A.; Van Amersfoort, J.; Gal, Y. Batchbald: Efficient and diverse batch acquisition for deep bayesian active learning. Adv. Neural Inf. Process. Syst. 2019, 32, 7026–7037. [Google Scholar]
- Hyndman, R.J.; Wang, E.; Laptev, N. Large-scale unusual time series detection. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; pp. 1616–1619. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications with R Examples, 4th ed.; Springer Texts in Statistics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Chatfield, C.; Xing, H. The Analysis of Time Series: An Introduction with R, 7th ed.; Texts in Statistical Science; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Melbourne, Australia, 2021. [Google Scholar]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econom. J. Econom. Soc. 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef] [Green Version]
- Fulcher, B.D.; Little, M.A.; Jones, N.S. Highly comparative time-series analysis: The empirical structure of time series and their methods. J. R. Soc. Interface 2013, 10, 20130048. [Google Scholar] [CrossRef]
- Fulcher, B.D.; Jones, N.S. Highly comparative feature-based time-series classification. IEEE Trans. Knowl. Data Eng. 2014, 26, 3026–3037. [Google Scholar] [CrossRef] [Green Version]
- Fulcher, B.D.; Jones, N.S. hctsa: A computational framework for automated time-series phenotyping using massive feature extraction. Cell Syst. 2017, 5, 527–531. [Google Scholar] [CrossRef]
- O’Hara-Wild, M.; Hyndman, R.; Wang, E.; Cook, D.; Talagala, T.; Chhay, L. Feasts: Feature Extraction and Statistics for Time Series (0.2.1). 2021. Available online: https://CRAN.R-project.org/package=feasts (accessed on 17 October 2021).
- Hyndman, R.; Kang, Y.; Montero-Manso, P.; Talagala, T.; Wang, E.; Yang, Y.; O’Hara-Wild, M. Tsfeatures: Time Series Feature Extraction (1.0.2). 2020. Available online: https://CRAN.R-project.org/package=tsfeatures (accessed on 9 November 2021).
- Facebook. Kats. 2021. Available online: https://facebookresearch.github.io/Kats/ (accessed on 9 November 2021).
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time Series FeatuRe Extraction on basis of Scalable Hypothesis tests (tsfresh—A Python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Barandas, M.; Folgado, D.; Fernandes, L.; Santos, S.; Abreu, M.; Bota, P.; Liu, H.; Schultz, T.; Gamboa, H. TSFEL: Time Series Feature Extraction Library. SoftwareX 2020, 11, 100456. [Google Scholar] [CrossRef]
- Lubba, C.H.; Sethi, S.S.; Knaute, P.; Schultz, S.R.; Fulcher, B.D.; Jones, N.S. catch22: CAnonical Time-series CHaracteristics. Data Min. Knowl. Discov. 2019, 33, 1821–1852. [Google Scholar] [CrossRef] [Green Version]
- Cleveland, R.; Cleveland, W.; McRae, J.E.; Terpinning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Henderson, T.; Fulcher, B.D. An Empirical Evaluation of Time-Series Feature Sets. arXiv 2021, arXiv:2110.10914. [Google Scholar]
- Ren, H.; Xu, B.; Wang, Y.; Yi, C.; Huang, C.; Kou, X.; Xing, T.; Yang, M.; Tong, J.; Zhang, Q. Time-series anomaly detection service at Microsoft. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 3009–3017. [Google Scholar]
- Hou, X.; Zhang, L. Saliency detection: A spectral residual approach. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Vlachos, M.; Yu, P.; Castelli, V. On periodicity detection and structural periodic similarity. In Proceedings of the 2005 SIAM International Conference on Data Mining, Newport Beach, CA, USA, 21–23 April 2005; pp. 449–460. [Google Scholar]
- Heymann, S.; Latapy, M.; Magnien, C. Outskewer: Using skewness to spot outliers in samples and time series. In Proceedings of the 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Istanbul, Turkey, 26–29 August 2012; pp. 527–534. [Google Scholar]
- Galeano, P.; Peña, D.; Tsay, R.S. Outlier detection in multivariate time series by projection pursuit. J. Am. Stat. Assoc. 2006, 101, 654–669. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A Review on outlier/Anomaly Detection in Time Series Data. ACM Comput. Surv. (CSUR) 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Loperfido, N. Kurtosis-based projection pursuit for outlier detection in financial time series. Eur. J. Financ. 2020, 26, 142–164. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lavin, A.; Ahmad, S. Evaluating real-time anomaly detection algorithms–the Numenta anomaly benchmark. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 38–44. [Google Scholar]
- Cauteruccio, F.; Cinelli, L.; Corradini, E.; Terracina, G.; Ursino, D.; Virgili, L.; Savaglio, C.; Liotta, A.; Fortino, G. A framework for anomaly detection and classification in Multiple IoT scenarios. Future Gener. Comput. Syst. 2021, 114, 322–335. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Zhao, Y.; Philip, S.Y. Outlier detection in graph streams. In Proceedings of the 2011 IEEE 27th International Conference on Data Engineering, Hannover, Germany, 11–16 April 2011; pp. 399–409. [Google Scholar]
- Vanerio, J.; Casas, P. Ensemble-Learning Approaches for Network Security and Anomaly Detection. In Proceedings of the Workshop on Big Data Analytics and Machine Learning for Data Communication Networks, Los Angeles, CA, USA, 21 August 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Nesa, N.; Ghosh, T.; Banerjee, I. Non-parametric sequence-based learning approach for outlier detection in IoT. Future Gener. Comput. Syst. 2018, 82, 412–421. [Google Scholar] [CrossRef]
- Pajouh, H.H.; Javidan, R.; Khayami, R.; Dehghantanha, A.; Choo, K.K.R. A Two-Layer Dimension Reduction and Two-Tier Classification Model for Anomaly-Based Intrusion Detection in IoT Backbone Networks. IEEE Trans. Emerg. Top. Comput. 2019, 7, 314–323. [Google Scholar] [CrossRef]
- Cauteruccio, F.; Fortino, G.; Guerrieri, A.; Liotta, A.; Mocanu, D.C.; Perra, C.; Terracina, G.; Vega, M.T. Short-long term anomaly detection in wireless sensor networks based on machine learning and multi-parameterized edit distance. Inf. Fusion 2019, 52, 13–30. [Google Scholar] [CrossRef] [Green Version]
- Aljawarneh, S.A.; Vangipuram, R. GARUDA: Gaussian dissimilarity measure for feature representation and anomaly detection in Internet of things. J. Supercomput. 2020, 76, 4376–4413. [Google Scholar] [CrossRef]
- Garg, S.; Kaur, K.; Batra, S.; Kaddoum, G.; Kumar, N.; Boukerche, A. A multi-stage anomaly detection scheme for augmenting the security in IoT-enabled applications. Future Gener. Comput. Syst. 2020, 104, 105–118. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, Q.; Geng, Y. A survey of anomaly detection methods in networks. In Proceedings of the 2009 International Symposium on Computer Network and Multimedia Technology, Wuhan, China, 18–20 January 2009; pp. 1–3. [Google Scholar]
- Bhuyan, M.H.; Bhattacharyya, D.K.; Kalita, J.K. Network anomaly detection: Methods, systems and tools. IEEE Commun. Surv. Tutor. 2013, 16, 303–336. [Google Scholar] [CrossRef]
- Akoglu, L.; Tong, H.; Koutra, D. Graph based anomaly detection and description: A survey. Data Min. Knowl. Discov. 2015, 29, 626–688. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.; Mahmood, A.N.; Hu, J. A survey of network anomaly detection techniques. J. Netw. Comput. Appl. 2016, 60, 19–31. [Google Scholar] [CrossRef]
- Akoglu, L.; McGlohon, M.; Faloutsos, C. Oddball: Spotting anomalies in weighted graphs. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2010; pp. 410–421. [Google Scholar]
- Kovanen, L.; Karsai, M.; Kaski, K.; Kertész, J.; Saramäki, J. Temporal motifs in time-dependent networks. J. Stat. Mech. Theory Exp. 2011, 2011, P11005. [Google Scholar] [CrossRef]
- Li, W.; Tug, S.; Meng, W.; Wang, Y. Designing collaborative blockchained signature-based intrusion detection in IoT environments. Future Gener. Comput. Syst. 2019, 96, 481–489. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G.; Nitti, M. The social internet of things (siot)–when social networks meet the internet of things: Concept, architecture and network characterization. Comput. Netw. 2012, 56, 3594–3608. [Google Scholar] [CrossRef]
- Baldassarre, G.; Lo Giudice, P.; Musarella, L.; Ursino, D. The MIoT paradigm: Main features and an “ad-hoc” crawler. Future Gener. Comput. Syst. 2019, 92, 29–42. [Google Scholar] [CrossRef]
- Savage, D.; Zhang, X.; Yu, X.; Chou, P.; Wang, Q. Anomaly detection in online social networks. Soc. Netw. 2014, 39, 62–70. [Google Scholar] [CrossRef] [Green Version]
- Bindu, P.; Thilagam, P.S.; Ahuja, D. Discovering suspicious behavior in multilayer social networks. Comput. Hum. Behav. 2017, 73, 568–582. [Google Scholar] [CrossRef]
- Sharma, V.; You, I.; Kumar, R. ISMA: Intelligent Sensing Model for Anomalies Detection in Cross Platform OSNs With a Case Study on IoT. IEEE Access 2017, 5, 3284–3301. [Google Scholar] [CrossRef]
- Can, U.; Alatas, B. A new direction in social network analysis: Online social network analysis problems and applications. Phys. A Stat. Mech. Its Appl. 2019, 535, 122372. [Google Scholar] [CrossRef]
- Osanaiye, O.; Choo, K.K.R.; Dlodlo, M. Distributed denial of service (DDoS) resilience in cloud: Review and conceptual cloud DDoS mitigation framework. J. Netw. Comput. Appl. 2016, 67, 147–165. [Google Scholar] [CrossRef]
| Feature | Description |
|---|---|
| ACF1 | First order of autocorrelation |
| ACF Remainder | Autocorrelation of remainder |
| Mean | Mean of the rolling time series window |
| Variance | Variance of the rolling time series window |
| Entropy | Spectral entropy (see [16]) |
| Linearity | Strength of linearity computed on the trend of STL decomposition (see [16]) |
| Trend | Strength of trend |
| Crossing Point | Number of crossing points (see [16]) |
| ARCHtest.p | P value of Lagrange Multiplier (LM) test for ARCH model (see [20]) |
| Curvature | Strength of curvature computed on Trend of STL decomposition (from [16]) |
| RMSE | Root mean square error |
| ME | Mean error |
| MAE | Mean absolute error |
| MPE | Mean percentage error |
| MAPE | Mean absolute percentage error |
| Max level shift | Max trimmed mean between two consecutive windows |
| Max var shift | Max variance shift between two consecutive windows |
| Max KL shift | Max shift in Kullback–Leibler divergence between two consecutive windows |
| Diff-w | The differences between the current value and the w-th previous value |
| SR | For time point i the value calculated from the SR transformed time series: |
| Skewness | Skewness coefficient of the rolling time series window : |
| Kurtosis | Kurtosis coefficient of the rolling time series window : |
| Dataset | Number of Points | % Anomalies | Number of Time Series | Mean Length |
|---|---|---|---|---|
| Yahoo Real | 91 K | 1.76% | 64 | 1415 |
| Yahoo Art | 140 K | 1.76% | 100 | 1415 |
| IOPS | 3 M | 2.26% | 29 | 105,985 |
| AWS | 67 K | 4.57% | 17 | 67,740 |
| 142 K | 0.15% | 10 | 142,765 | |
| Huawei | 54 K | 4.19% | 6 | 9056 |
| F1 | Recall | Precision | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Avg | Conf | Range | Avg | Conf | Range | Avg | Conf | Range | |
| Raw (ws = 15) | 0.2558 | ±0.0390 | 0.2168 0.2948 | 0.2263 | ±0.0389 | 0.1873 0.2652 | 0.5604 | ±0.0565 | 0.5039 0.6169 |
| HAD | 0.6481 | ±0.0464 | 0.6016 0.6945 | 0.6297 | ±0.0465 | 0.5833 0.6762 | 0.7818 | ±0.0460 | 0.7358 0.8278 |
| catch22 | 0.5537 | ±0.0528 | 0.5009 0.6066 | 0.5132 | ±0.0516 | 0.4617 0.5648 | 0.6993 | ±0.0541 | 0.6452 0.7534 |
| catch23 | 0.5506 | ±0.0525 | 0.4980 0.6031 | 0.509 | ±0.0511 | 0.4579 0.5601 | 0.699 | ±0.0542 | 0.6447 0.7532 |
| catch24 | 0.5889 | ±0.0614 | 0.5275 0.6503 | 0.5407 | ±0.0608 | 0.4799 0.6015 | 0.7826 | ±0.0507 | 0.7319 0.8333 |
| catch25 | 0.5825 | ±0.0612 | 0.5213 0.6436 | 0.532 | ±0.0608 | 0.4712 0.5928 | 0.7812 | ±0.0504 | 0.7308 0.8316 |
| Average | Confidence | ||
|---|---|---|---|
| Data | F1 | (Error Margin) | Range |
| AWS | 0.3963 | ±0.0549 | 0.3414 0.4512 |
| Huawei | 0.5830 | ±0.0553 | 0.5278 0.6383 |
| IOPS | 0.5693 | ±0.0513 | 0.5180 0.6206 |
| 0.3729 | ±0.0476 | 0.3253 0.4205 | |
| Yahoo Artificial | 0.7724 | ±0.0392 | 0.7333 0.8116 |
| Yahoo Real | 0.4958 | ±0.0593 | 0.4365 0.5551 |
| Average | Confidence | ||
|---|---|---|---|
| Data | F1 | (Error Margin) | Range |
| Multi-Layer Perceptron | 0.6129 | ±0.0451 | 0.5677 0.6580 |
| Naïve Bayes | 0.2386 | ±0.0242 | 0.2144 0.2627 |
| Random Forest | 0.8279 | ±0.03110 | 0.7967 0.8590 |
| SVC | 0.3259 | ±0.04680 | 0.2791 0.3727 |
| SVC Linear | 0.2233 | ±0.0710 | 0.1524 0.2943 |
| Xgboost | 0.8082 | ±0.0322 | 0.7760 0.8404 |
| F1 | Recall | Precision | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Avg | Conf | Range | Avg | Conf | Range | Avg | Conf | Range | |
| Raw (ws = 15) | 0.4253 | ±0.0700 | 0.3553 0.4954 | 0.3236 | ±0.0693 | 0.2543 0.3930 | 0.7800 | ±0.0445 | 0.7355 0.8245 |
| HAD | 0.8675 | ±0.0269 | 0.8406 0.8944 | 0.8030 | ±0.0378 | 0.7652 0.8408 | 0.9556 | ±0.0144 | 0.9412 0.9700 |
| catch22 | 0.8434 | ±0.0315 | 0.8119 0.8749 | 0.7610 | ±0.0419 | 0.7191 0.8029 | 0.9598 | ±0.0120 | 0.9478 0.9718 |
| catch23 | 0.8360 | ±0.0313 | 0.8047 0.8673 | 0.7495 | ±0.0413 | 0.7082 0.7909 | 0.9587 | ±0.0123 | 0.9464 0.9710 |
| catch24 | 0.9167 | ±0.0196 | 0.8971 0.9364 | 0.8678 | ±0.0283 | 0.8395 0.8960 | 0.9766 | ±0.0070 | 0.9696 0.9835 |
| catch25 | 0.9161 | ±0.0198 | 0.8964 0.9359 | 0.8671 | ±0.0284 | 0.8387 0.8954 | 0.9760 | ±0.0073 | 0.9687 0.9832 |
| Huawei | IOPS | |||||
|---|---|---|---|---|---|---|
| Prec. | Recall | F1 | Prec. | Recall | F1 | |
| catch25 | 0.9940 | 0.9465 | 0.9697 | 0.9908 | 0.8957 | 0.9409 |
| HAD | 0.9881 | 0.8759 | 0.9287 | 0.9897 | 0.9069 | 0.9465 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agrahari, R.; Nicholson, M.; Conran, C.; Assem, H.; Kelleher, J.D. Assessing Feature Representations for Instance-Based Cross-Domain Anomaly Detection in Cloud Services Univariate Time Series Data. IoT 2022, 3, 123-144. https://doi.org/10.3390/iot3010008
Agrahari R, Nicholson M, Conran C, Assem H, Kelleher JD. Assessing Feature Representations for Instance-Based Cross-Domain Anomaly Detection in Cloud Services Univariate Time Series Data. IoT. 2022; 3(1):123-144. https://doi.org/10.3390/iot3010008
Chicago/Turabian StyleAgrahari, Rahul, Matthew Nicholson, Clare Conran, Haytham Assem, and John D. Kelleher. 2022. "Assessing Feature Representations for Instance-Based Cross-Domain Anomaly Detection in Cloud Services Univariate Time Series Data" IoT 3, no. 1: 123-144. https://doi.org/10.3390/iot3010008
APA StyleAgrahari, R., Nicholson, M., Conran, C., Assem, H., & Kelleher, J. D. (2022). Assessing Feature Representations for Instance-Based Cross-Domain Anomaly Detection in Cloud Services Univariate Time Series Data. IoT, 3(1), 123-144. https://doi.org/10.3390/iot3010008






