Robust Parameter Designs Constructed from Hadamard Matrices

Abstract

The primary objective of robust parameter design (RPD) is to determine the optimal settings of control factors in a system to minimize response variance while achieving a desirable mean response. This article investigates fractional factorial designs constructed from Hadamard matrices of orders 12, 16, and 20 to meet RPD requirements with minimal runs. For various combinations of control and noise factors, rather than recommending a single “best” design, up to the top ten good candidate designs are identified. All listed designs permit the estimation of all control-by-noise interactions and the main effects of both control and noise factors. Additionally, some nonregular RPDs allow for the estimation of one or two control-by-control interactions, which may be critical for achieving optimal mean response. These results provide practical options for efficient, resource-constrained experiments with economical run sizes.

1. Introduction

Robust parameter design (RPD), introduced by Taguchi [1], provides an effective strategy for improving the quality of a system (whether a product or a process). In RPD, two types of factors influence quality: control factors and noise factors. Control factor levels remain fixed once set, whereas noise factor levels vary randomly and are typically uncontrollable under normal operating conditions. Common examples of noise factors include changes in environmental conditions (e.g., temperature and humidity), variations in raw material batches or from different suppliers, consumer usage, etc. In experimental settings, the levels of noise factors can be intentionally varied, such as by controlling temperature and humidity in a laboratory, to facilitate data collection. The goal of RPD is to identify optimal settings of the control factors that make quality performance as insensitive as possible to random fluctuations in the noise factors, while keeping the mean response close to the target. RPD has been widely applied in the industry, especially since around the year 2000 (page 5 of [2]). We refer to [3,4] for examples of recent developments in RPD, along with their references.

Two-level fractional factorial designs (FFDs) are widely used to plan factorial experiments, particularly for screening a large number of factors in industrial settings. FFDs fall into two broad categories: regular and nonregular. A regular FFD is defined by its defining relations, which determine the alias structure so that factorial effects are either orthogonal (independent) or fully aliased (confounded). This structural simplicity makes regular FFDs easy to construct and analyze, and they have been most commonly used in both Taguchi’s original crossed-array [1] and more recent single-array RPDs in [5,6,7,8]. However, regular FFDs require run sizes that are powers of two, which can be costly, and in highly fractionated designs, some important effects may become completely aliased and non-estimable.

Nonregular FFDs, by contrast, allow run sizes that are multiples of four and offer greater flexibility. They lack defining relations, and their alias structure is more complex: a factorial effect may be partially aliased with many others. For example, in the 12-run Plackett–Burman design with 11 factors, the main effect of any factor is partially aliased with all 45 two-factor interactions that do not involve that factor, each with a correlation coefficient of $\pm 1/3$. Similarly, any two-factor interaction is partially aliased with all 36 two-factor interactions that do not involve those two factors, again with a correlation coefficient of $\pm 1/3$. This contrasts with regular FFDs, where such correlations can only be 0 (orthogonal) or 1 (fully aliased).

Although the complex alias structure of nonregular FFDs poses challenges, it also creates opportunities: it allows joint estimation of interaction effects that would be completely missed if regular FFDs had been used. Moreover, nonregular designs often possess superior statistical properties, such as higher generalized resolution [9], greater projectivity [10], and the hidden projection property [11,12]. Consequently, well-constructed nonregular FFDs reduce the severity of confounding and enable the joint estimation of critical factorial effects, making them efficient and versatile candidates for RPD. We refer to [13] for an excellent review and to [14,15,16] for examples of recent developments in nonregular FFDs, along with their references.

Among the various approaches to constructing nonregular FFDs, one of the most important classes is based on Hadamard matrices. In this article, we focus on constructing two-level nonregular FFDs from Hadamard matrices for single-array RPDs (referred to hereafter simply as RPDs). A Hadamard matrix $H_n$ of order n is an $n\times n$ matrix with entries of $\pm 1$, in which any two columns of $H_n$ are orthogonal and n must be a multiple of four. By normalizing $H_n$ so that all entries in its first column are $+1$, and labeling the columns as 0, 1, 2, ⋯, n−1, a nonregular FFD can be constructed by selecting k columns from 1, 2, ⋯, n−1.

In RPD, the most critical effects are control-by-noise (CN) interactions and the main effects of both control and noise factors. Control-by-control (CC) interactions are generally of secondary importance, while noise-by-noise interactions and higher-order interactions are the least important [8]. Assuming two levels per factor and ignoring three-factor or higher-order interactions, the response can be expressed in a linear model that includes main effects, CN interactions, and CC interactions, plus an error term. The objective of RPD is to choose control settings that bring the mean response close to the target while minimizing its variance. At a minimum, a good RPD should permit estimation of all main effects and CN interactions.

Prior research has examined nonregular FFDs for RPDs from different perspectives. Loeppky et al. [17] evaluated such designs using the extended word length pattern (EWLP), ranking them and identifying the minimum aberration RPDs for each combination of control and noise factors in 12-, 16-, and 20-run experiments. Evangelaras et al. [18] constructed nonregular FFDs from Hadamard matrices for RPDs that allowed estimation of all the main effects and all CN interactions. For each combination of control and noise factors in 12-, 16-, and 20-run experiments, they reported the single design with the highest design efficiency.

Design efficiency used in [18] and also in this article is derived from the concept of D-efficiency in the field of experimental design, which measures how well a design enables the estimation of model parameters. Let X denote the model matrix, with columns that correspond to all effects included in the model, which in our case, are all main effects and all CN interactions. Design efficiency is defined as $D_{eff}=\left[det{\left(X^{t}X\right)}^{1/p}\right]/n$ (same as in [12]), where p is the number of estimable parameters and n is the number of runs. For two-level fractional factorial designs, $0\le D_{eff}\le 1$. If the information matrix $X^{t}X$ is singular, then $D_{eff}=0$, indicating that at least one effect in the model cannot be estimated. If $X^{t}X$ is nonsingular, then $D_{eff}>0$, meaning all model effects are estimable. When $0<D_{eff}<1$, the columns of X are not all orthogonal, so some effects are partially aliased. If $D_{eff}=1$, all columns of X are mutually orthogonal, with no aliasing among the estimable effects. In general, a design with high design efficiency provides greater assurance of obtaining reliable estimates, since the true set of significant effects is often unknown.

Building on this work, our goal is not to identify a single “best” RPD for each combination of control and noise factors, but rather to provide a ranked list of top good candidate designs. These designs are evaluated not only by design efficiency but also by their ability to estimate CC interactions, which can contribute significantly to optimizing the mean response.

To illustrate the value of considering multiple candidate designs, suppose an experiment involves five control factors and one noise factor but is limited to 16 runs. Under Taguchi’s crossed-array approach, a regular $2^{5-2}$ would serve as the inner array for control factors and a $2^1$ as the outer array for the noise factor. If a single-array approach is used instead, the best regular design would be resolution IV with maximum design efficiency 1; however, in this case, all CC interactions will be fully aliased with one another. By contrast, a suitable nonregular design may achieve slightly lower design efficiency but permit estimation of nearly any three CC interactions, in addition to all main effects and CN interactions. This additional estimability is valuable, as CC interactions can be critical for achieving the optimal mean response [19], particularly since their importance is typically unknown in advance. It is important to note that the design efficiency metric used in this article is based solely on the estimation of main effects and CN interactions, since all listed designs are capable of estimating them. However, when CC interactions are also included in the model, nonregular designs often yield higher average design efficiency (over models) than regular designs, even though they may appear less efficient under the narrower criterion restricted to main effects and CN interactions.

Rather than recommending a single design with the highest design efficiency for each case, we provide up to ten top-ranked good designs. The ranking considers design efficiency, ability to estimate additional CC interactions, and the confounding frequency vector. This broader set of options enables practitioners to select the design that best suits their experimental needs. For example, if two or three CC interactions are suspected to be important in the above case of five control factors and one noise factor, one might select the seventh-ranked design in

Table A1. Robust parameter designs constructed from Hadamard matrices of order 16.

C + N	C + N Columns								HM	${\mathit{D}}_{\mathit{e}\mathit{f}\mathit{f}}$	CC a	${\mathit{F}}_3$;		${\mathit{F}}_4$;		${\mathit{F}}_5$ b
C5 N1	1	2	3	4	6			8	I	1	0.4	0	0;	3	0;	0	0
	2	3	4	5	6			10	IV	1	0.6	0	4;	1	4;	0	0
	1	2	3	4	5			7	I	1	0.4	1	0;	1	0;	1	0
	1	2	3	4	6			10	IV	1	0.6	1	2;	0	4;	0	2
	1	2	3	8	10			4	I	1	0.4	2	0;	1	0;	0	0
	4	5	6	8	12			7	II	0.949	0.6	0	4;	1	0;	0	4
	2	6	8	10	12			3	IV	0.9007	2.975	0	6;	0	4;	0	2
	1	2	4	7	8			12	II	0.8816	1.8	0	2;	1	4;	0	2
	1	2	4	8	9			10	V	0.8367	1.978	0	6;	0	4;	0	2
	2	4	8	12	14			11	III	0.7376	2.933	0	8;	0	4;	0	0
C4 N2	2	4	8	12			1	10	III	0.8203	0.5	0	4;	0	6;	0	2
	1	4	8	12			6	11	II	0.7807	0.333	0	4;	0	4;	1	0
	2	4	6	8			9	12	IV	0.673	1	0	6;	0	4;	0	2
	2	4	6	8			3	10	IV	0.6593	0.5	0	7;	0	3;	0	1
	1	2	4	6			8	12	IV	0.6404	0.833	0	4;	0	6;	0	2
	2	8	10	12			4	15	III	0.6095	0.5	0	8;	0	4;	0	0
C3 N3	1	2	3			4	7	8	I	1	na c	1	0;	1	0;	1	0
	1	2	3			4	8	12	II	1	na	1	1;	0	3;	0	3
	1	2	13			3	4	15	I	1	na	2	0;	0	0;	0	0
	1	2	4			7	8	12	II	0.8312	na	0	2;	1	4;	0	2
	1	2	8			4	10	12	III	0.691	na	0	4;	0	6;	0	2
	2	8	10			4	9	12	III	0.63	na	0	7;	0	3;	0	1
C2 N4	1	8			2	4	10	14	III	0.8312	1	0	4;	0	6;	0	2
	4	8			1	6	11	12	II	0.7579	1	0	4;	0	4;	1	0
	2	8			1	4	10	12	III	0.63	1	0	4;	0	6;	0	2
C6 N1	1	2	3	4	6	8		9	I	1	0.2	0	0;	7	0;	0	0
	2	3	4	5	6	10		11	IV	1	0.333	0	4;	3	8;	0	4
	4	5	8	9	12	13		2	II	1	0.2	0	8;	3	8;	0	0
	1	2	3	4	5	6		8	I	1	0.2	2	0;	3	0;	2	0
	1	4	5	8	9	12		2	II	1	0.333	2	4;	1	8;	0	4
	1	2	3	8	10	13		4	I	1	0.2	4	0;	3	0;	0	0
	1	2	4	8	11	12		14	V	0.8757	1.924	0	9;	0	12;	0	6
	1	2	4	8	9	10		12	V	0.8	1.771	0	10;	0	10;	0	6
	1	2	4	6	8	10		12	IV	0.773	1.848	0	8;	0	14;	0	6
	1	2	4	8	9	10		13	V	0.7114	1.743	0	11;	0	10;	0	4
C7 N1	1	2	3	4	6	8	9	12	I	1	na c	0	0;	14	0;	0	0
	1	4	6	8	10	12	14	3	II	1	na	0	8;	6	16;	0	8
	2	4	6	8	10	12	14	1	III	1	na	1	12;	1	24;	0	12
	1	4	5	8	9	12	14	3	II	1	na	2	8;	2	16;	2	8
	1	2	3	4	5	6	12	8	I	1	na	3	0;	7	0;	4	0
	1	4	5	8	9	12	13	2	II	1	na	3	8;	3	16;	0	8
	1	2	3	4	5	6	11	8	I	1	na	4	0;	6	0;	4	0
	1	2	3	8	10	13	14	4	I	1	na	7	0;	7	0;	0	0
	1	2	4	8	10	12	15	7	V	0.8312	na	0	12;	1	24;	0	16
	1	2	3	4	8	9	10	12	V	0.7699	na	1	13;	0	21;	0	14

^a The g values in the column CC: the integer part ($f=\left[g\right]$) indicates the number of f CC interactions that the RPD can fully accommodate, while the decimal part represents the proportion of models with $f+1$ CC interactions that are estimable. ^b $CFV=[F_3;F_4;F_5]$, where $F_h$ represents the respective frequencies of $J_h=16$ and $J_h=8$, $3\le h\le 5$. ^c na: no degrees of freedom available to estimate CC interactions.

, which permits estimation of nearly all sets of three CC interactions. In this case, 117 out of the 120 possible models, including all main effects, all CN interactions, and three CC interactions, are estimable.

In this article, we construct RPDs from Hadamard matrices of orders 12, 16, and 20. Because different situations may call for different designs, we provide a list of top good candidates rather than a single “optimal” RPD for each combination of control and noise factors as in [17,18]. This approach gives practitioners greater flexibility in selecting a design that best meets their needs. Section 2 describes the construction methods and the assessment criteria, Section 3 presents the resulting RPDs, and Section 4 discusses their practical usefulness.

2. Materials and Methods

An RPD uses the same design matrix structure as a regular or nonregular FFD but distinguishes between two types of factors: control and noise. An $n\times k$ matrix of $+1$ and $-1$ is used here to represent an RPD with n runs and k two-level factors, listing C control factors first, followed by N noise factors, where $k=C+N$. For a given combination of C control and N noise factors, the minimum requirement for a good RPD in this article is its ability to estimate all $C·N$ CN interactions and all $C+N$ main effects.

For simplicity, we present RPDs with $C\ge N$, since designs with larger N can be obtained simply by relabeling the control and noise factors. This equivalence holds only when CC interactions are excluded from the model.

Two two-level design matrices are isomorphic if one can be obtained from the other by permuting rows, permuting columns, switching the signs of entire columns, or by a combination of these operations. Isomorphic designs share identical statistical properties and belong to the same equivalence class. In other words, they are essentially the same design, and they differ only by relabeling runs, reordering factors, or flipping the coding of factor levels. Conversely, any two designs that differ in their properties (such as $CFV$ or design efficiency) are considered non-isomorphic. In this article, we use non-isomorphic Hadamard matrices reported in [20,21,22]; see also [23]. These are labeled H12; H16-I through H16-V; and H20-Q, H20-P, and H20-N, corresponding to orders 12, 16, and 20.

For a given combination of control and noise factors, we first select C columns from 1, 2, ⋯, n−1 of a Hadamard matrix of order n to represent the control factors, and then choose N columns from the remaining ones for the noise factors. The model matrix X (excluding the column of $+1$ for computational simplicity) consists of $k=C+N$ columns of the design matrix and all $C·N$ CN interactions. Thus, it is an $n\times p$ matrix, where $p=k+C·N$. To ensure that this model is estimable, at least $p+1$ runs are required, i.e., $p+1\le n$.

If the information matrix $X^{t}X$ of the resulting design is non-singular, meaning all main effects and all CN interactions are estimable, design efficiency $D_{eff}$ is calculated. We then compute the confounding frequency vector ($CFV$) on the design matrix (same as [23]) and assess the ability to estimate one or more CC interactions whenever sufficient degrees of freedom are available. Finally, all good RPDs derived from Hadamard matrices of the same order are combined and ranked by $D_{eff}$, ability to estimate CC interactions, and $CFV$.

For any h columns $c_1,c_2,\cdots ,c_h$ in an orthogonal design D with k factors ($h\le k$) and n runs, define $j_h$ as the sum of all entries in the column corresponding to h-factor interaction $c_1·c_2·\cdots ·c_h$. Then, set $J_h=\left|j_h\right|$. The frequency distribution of $J_h$ over all such h-factor interaction columns is denoted by $F_h$. Since D is orthogonal, $J_1=J_2=0$. For a regular design, $J_h$ must equal either 0 or n, with 0 corresponding to orthogonality and n to full aliasing. If $J_h=n$, the h columns form a word of length h in the defining relation. For a nonregular design, however, $J_h$ can take values strictly between 0 and n, corresponding to partial aliasing. In general, the values of $J_h$ follow specific patterns. For example, if n is a multiple of 8, then $J_h$ is also a multiple of 8 (see Proposition 1, page 175 of [23]). The $CFV$ of a design D is defined as $CFV\left(D\right)=[F_3\left(D\right),F_4\left(D\right)\cdots ,F_k\left(D\right)]$. To compare two designs, say, $D_1$ and $D_2$, based on their $CFV$s, we first compare $F_3\left(D_1\right)$ and $F_3\left(D_2\right)$ element-wise and sequentially. A design with the smaller frequency is preferred. If $F_3\left(D_1\right)=F_3\left(D_2\right)$, the comparison continues with $F_4\left(D_1\right)$ and $F_4\left(D_2\right)$, and so on.

The $CFV$ is often used to rank FFDs [23] under the assumption that effects of the same order are equally important, an assumption that does not strictly hold in RPDs. Nonetheless, $CFV$ remains useful as a secondary criterion for distinguishing designs with the same $D_{eff}$. For example, consider three RPDs constructed from H16-I with $D_{eff}=1$ for the case $C=5$ and $N=1$, and denoted as $D_1,D_3$ and $D_5$. In this case with $n=16$, $J_i$ must equal 16, 8, or 0, where $i=3,4,5$. Since frequencies of $J_i=16$, $J_i=8$, and $J_i=0$ always sum to the number of i-factor interactions (i.e., the combinations of selecting i columns out of six), we omit recording the frequency of $J_i=0$ in $F_i\left(D\right)$. The resulting $CFV$s are $CFV\left(D_1\right)=[[0,0];[3,0];[0,0]],CFV\left(D_3\right)=[[1,0];[1,0];[1,0]]$, and $CFV\left(D_5\right)=[[2,0];[1,0];[0,0]]$. Here, $F_i\left(D\right)=[a,b]$ for $i=3,4,5$, where a is the frequency of $J_i=16$ and b is the frequency of $J_i=8$. These $CFV$s reduce to the word-length patterns $W\left(D_1\right)=(0,3,0),W\left(D_3\right)=(1,1,1)$, and $W\left(D_5\right)=(2,1,0)$. Here, $W\left(D\right)=(u,v,w)$ denotes $u,v$, and w words of length 3, 4, and 5, respectively. After renaming the columns of each design as 1, 2, 3, 4, 5, and 6, these correspond to three regular designs, and their defining relations are $\mathbf{I}=\mathbf{1236}=\mathbf{1245}=\mathbf{3456}$, $\mathbf{I}=-\mathbf{145}=\mathbf{2356}=-\mathbf{12346}$, and $\mathbf{I}=-\mathbf{135}=-\mathbf{245}=\mathbf{1234}$. Clearly, $D_1$ is a resolution IV design, while $D_3$ and $D_5$ are resolution III designs. Although all three designs have $D_{eff}=1$ and are capable of estimating all five CN interactions and six main effects, $D_1$ is preferable as an RPD because its main effects are not aliased with any two-factor interactions, thereby reducing confounding. This example illustrates the usefulness of $CFV$ as a secondary criterion for distinguishing RPDs with the same design efficiency.

For each combination of control and noise factors, a ranked list of top good candidate RPDs is provided, with designs having larger $D_{eff}$ placed first. When multiple candidates have the same $D_{eff}$, preference is given to those with lower confounding through $CFV$, and when applicable, to those with higher estimability of CC interactions. For comparison, all regular FFDs achieving the maximum design efficiency of 1 are also included.

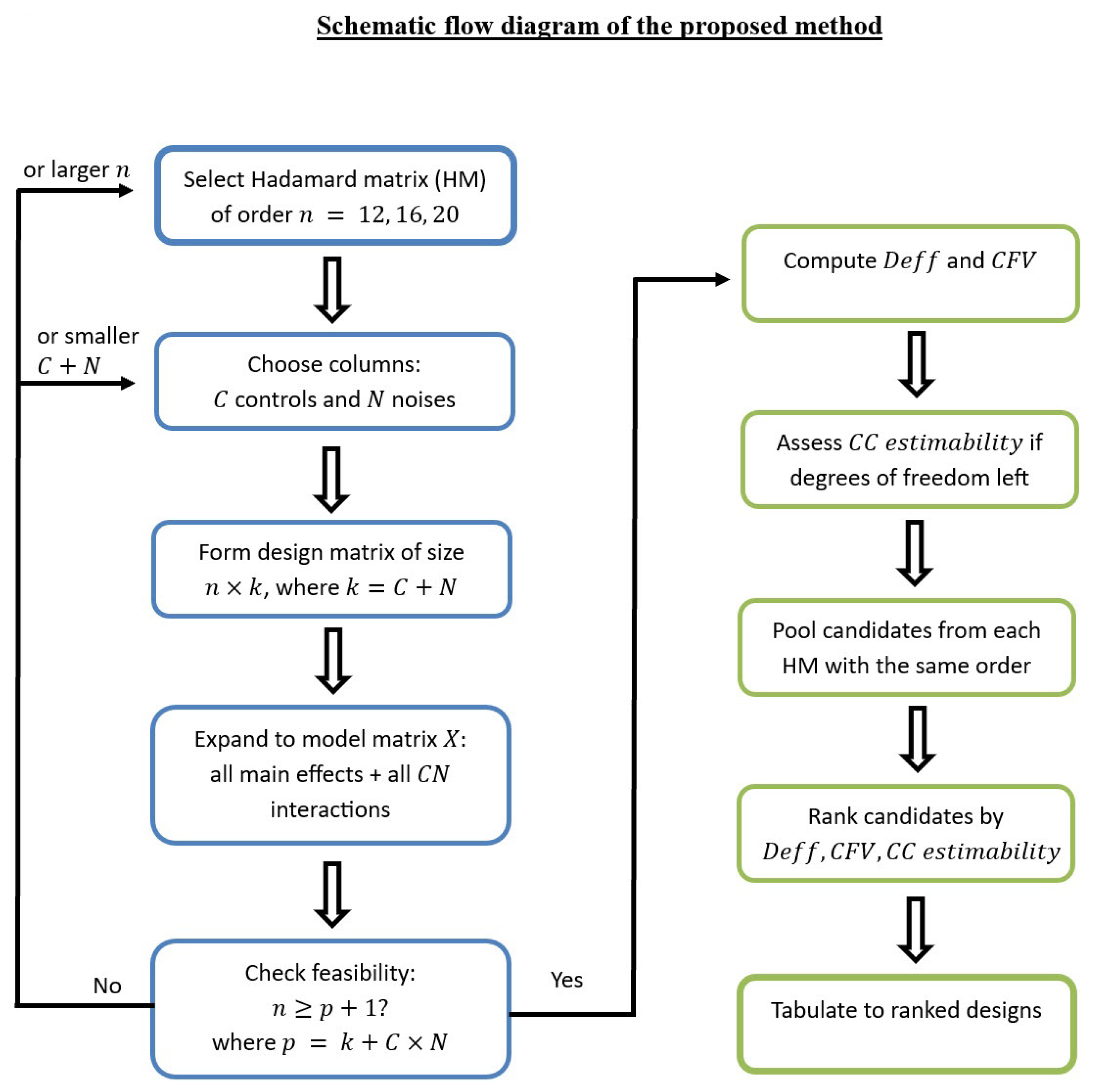
To aid understanding construction process, we include a schematic flow diagram (see Appendix B) that summarizes the steps of our method. The process begins by selecting a Hadamard matrix of order n. From this matrix, we first choose C columns to represent control factors, followed by N columns to represent noise factors. The resulting design is then expanded into the model matrix X, which includes all main effects and all CN interactions. We check whether the run size satisfies $n\ge p+1$, where p is the number of model parameters. If so, we compute design efficiency $D_{eff}$ and CFV. When degrees of freedom remain, we also assess the estimability of CC interactions. Candidate designs from each Hadamard matrix are then pooled together, ranked according to $D_{eff}$, CFV, and CC estimability, and finally summarized in tabular form. This schematic highlights the logical sequence of steps and clarifies how our evaluation criteria are applied systematically to identify top-ranked RPDs.

There is only one non-isomorphic design with four factors constructed from H12 [11]. Any projection onto four columns of a nonregular FFD permits estimation of its four main effects and six two-factor interactions, provided the run size is not a multiple of 8 [24]. Consequently, any four columns from H12 can serve as an RPD with a total of four control and noise factors. Therefore, we construct RPDs starting with $C+N=5$ as well as $C=5$ and $N=1$ from H12; $C+N=6$, as well as $C=6$ and $N=1$ and $C=7$ and $N=1$ from H16-I through H16-V; and $C+N=7$ from H20-Q to H20-N. These results complement the findings in [17,18], where only a single RPD was provided for each combination of control and noise factors.

3. Results

In this section, we present top good candidates for RPDs at possible minimal runs obtained using the methods described in Section 2. All designs presented in this section meet the minimum requirements for a good RPD: they can accommodate all CN interactions and all main effects of both control and noise factors. $D_{eff}$ is calculated based on the model matrix only consisting of $k=C+N$ main effects and all CN interactions.

If there are d degrees of freedom remaining after estimation of all CN interactions and all main effects, the ability of an RPD to estimate $f(\le d)$ CC interactions is evaluated. Let g denote the CC field value in Table A1 and

Table A2. Robust parameter designs constructed from Hadamard matrices of order 20.

C + N	C + N Columns								HM	${\mathit{D}}_{\mathit{eff}}$	CC a	${\mathit{F}}_3$; ${\mathit{F}}_4$; ${\mathit{F}}_5$ b
C5 N2	1	2	3	7	16		5	13	Q	0.7879	1.978	2;	2;	7
	1	2	3	7	18		5	14	Q	0.7831	1.978	1;	3;	7
	1	2	3	6	16		10	15	Q	0.7669	2	1;	2;	9
	1	2	3	4	13		7	11	Q	0.7639	2	0;	3;	9
	5	8	14	17	19		7	16	P	0.7477	2	1;	2;	9
	1	2	3	14	17		4	6	Q	0.7415	2	0;	3;	7
	1	2	5	10	18		7	17	P	0.7309	2	1;	2;	7
	1	2	5	6	12		10	17	P	0.724	1.978	2;	2;	5
	1	2	3	5	6		4	10	Q	0.7142	1.956	0;	4;	7
	1	2	4	6	15		3	5	Q	0.6986	2	0;	3;	9
C4 N3	1	2	6	9		5	10	19	Q	0.7234	na c	1;	2;	9
	1	2	3	18		7	11	15	Q	0.7162	na	1;	2;	7
	1	2	4	15		7	10	18	Q	0.7083	na	0;	3;	9
	1	2	3	6		5	10	15	Q	0.6995	na	1;	2;	9
	1	2	3	7		4	14	17	Q	0.6871	na	0;	3;	7
	1	2	3	12		5	14	15	Q	0.6787	na	1;	2;	7
	1	2	4	11		3	7	19	P	0.6725	na	1;	3;	7
	1	2	3	6		4	11	15	Q	0.6584	na	1;	2;	9
	1	2	3	5		7	11	19	Q	0.6503	na	0;	3;	9
	1	2	3	5		4	11	13	Q	0.6412	na	0;	4;	7
C2 N5	1	2		4	6	11	13	17	P	0.7773	1	1;	2;	7
	1	2		3	7	11	13	19	Q	0.766	1	0;	3;	9
	1	2		3	5	7	13	14	Q	0.7629	1	0;	4;	7
	1	2		8	10	11	13	18	P	0.7533	1	1;	2;	7
	1	2		3	9	11	13	19	Q	0.737	1	0;	3;	7
	1	2		3	6	8	10	17	Q	0.7272	1	0;	4;	5
	1	2		4	5	6	13	15	Q	0.719	1	0;	3;	9
	1	6		4	8	11	13	17	N	0.7131	1	0;	5;	3
	1	2		3	4	7	11	15	Q	0.7027	1	0;	3;	9
	1	6		3	8	11	12	15	N	0.6948	1	0;	3;	7

^a The g values in the column CC: the integer part ($f=\left[g\right]$) indicates the number of f CC interactions that the RPD can fully accommodate, while the decimal part represents the proportion of models with $f+1$ CC interactions that are estimable. ^b $CFV=[F_3;F_4;F_5]$, where $F_3$ ($F_4$) represents the frequency of $J_3=12$ ($J_4=12$), and $F_5$ the frequency of $J_5=8$. ^c na: no degrees of freedom available to estimate CC interactions.

. Its integer part ($f=\left[g\right]$) is the number f CC interactions guaranteed estimable (in addition to all main effects and CN). The fractional part is the proportion of models with $f+1$ CC interactions that are estimable.

The $CFV$ is computed based on the design matrix that includes only the control and noise factors. Here, we use a simplified version of $CFV$, defined as $CFV=[F_3;F_4;F_5]$. In Table A1, $F_3$, $F_4$, and $F_5$ represent the frequencies of $J_3$, $J_4$, and $J_5$ equal to 16 and 8, respectively. In Table A2, $F_3$ and $F_4$ ($F_5$) indicate the frequencies of $J_3$ and $J_4$ ($J_5$) equal to 12 (8).

3.1. RPDs from the Hadamard Matrix of Order 12

There is only one non-isomorphic Hadamard matrix of order 12 [22], and it corresponds to the 12-run Plackett–Burman design after removing the first column of $+1$. It is well-known that there are only two non-isomorphic designs with $k=5$ or 6 factors constructed from H12 for screening purposes [11,12].

For $C=4$ and $N=1$, only one $12\times 5$ design, for example, columns 1, 2, 3, 4, and 5, qualifies as a good candidate for an RPD. This design can estimate all four CN interactions, as well as all five main effects, with $D_{eff}=0.8135$. It has $CFV=[0;0;0]$, indicating no occurrences with $J_3=12$, $J_4=12$, and $J_5=8$; no full aliasing between main effects and two-factor interactions or among two-factor interactions. Additionally, this RPD can estimate any $f=1$ CC interaction, and 9 out of 15 models with two CC interactions are estimable. The other $12\times 5$ design, such as columns 1, 2, 3, 4, and 10, does not meet the minimum requirements for a good RPD and has $CFV=[0;0;1]$.

For $C=3$ and $N=2$, no $12\times 5$ design constructed from H12 can meet the minimum requirements of a good RPD to accommodate six CN interactions and five main effects.

For $C=5$ and $N=1$, two $12\times 6$ designs are suitable for RPDs, for example, columns 1, 2, 3, 4, 5, and 7; or columns 1, 2, 3, 4, 10, and 5. Both designs have the same $D_{eff}=0.7446$. However, the first design has $CFV=[0;0;0]$, while the second one has $CFV=[0;0;1]$.

3.2. RPDs from the Hadamard Matrices of Order 16

There are exactly five non-isomorphic Hadamard matrices of order 16 [20], commonly labeled as H16-I, H16-II, H16-III, H16-IV, and H16-V. The Hadamard matrix H16-I is a regular FFD, corresponding to the Plackett–Burman design. Any candidate from H16-I either meets the minimum requirements of a good RPD with $D_{eff}=1$ or fails to estimate all CN interactions and all main effects.

We did not explore $C+N=5$ designs from Hadamard matrices of order 16 for RPDs, as a resolution V design, $2_V^{5-1}$, would be the best choice in this case.

Reconsider $C=5$ and $N=1$ in 16 runs. We obtained 3, 14, 23, 20, and 20 non-isomorphic designs from H16-I through H16-V, resulting in a total of 45 non-isomorphic designs. Five of these designs have $D_{eff}=1$, including one resolution IV design and two resolution III designs. The remaining 40 designs have eight distinct $D_{eff}$ values (0.9490, 0.9007, 0.8816, 0.8367, 0.8094, 0.7772, 0.7376, and 0.6852), along with various $CFV$s. Each of the four nonregular Hadamard matrices also includes the three regular designs constructed from H16-I. From H16-II, we obtained designs capable of estimating any $f=1$ CC interaction. However, five designs constructed from H16-III through H16-V (with $D_{eff}$ = 0.9007 or 0.7376, and different $CFV$s) can accommodate any $f=2$ CC interactions. No design constructed from Hadamard matrices of order 16 can fully estimate any $f=3$ CC interactions, despite having sufficient degrees of freedom.

For $C=4$ and $N=2$, no $16\times 6$ design from H16-I meets the minimum requirements for a good RPD. We obtained 31 non-isomorphic designs from pools of 2, 16, 19, and 17 designs, respectively, from H16-II through H16-V. Fourteen of these designs have six distinct $D_{eff}$ values (0.8203, 0.7807, 0.6730, 0.6593, 0.6404, and 0.6095), while the remaining 17 designs have $D_{eff}<0.1$. We identified one design constructed from H16-IV that accommodates any $f=1$ CC interaction.

For $C=3$ and $N=3$, 13 non-isomorphic designs were identified from pools of 2, 6, 12, 9, and 9 designs, respectively, from H16-I through H16-V. Three of these designs have $D_{eff}=1$, including two resolution III designs. Another five designs have three distinct $D_{eff}$ values (0.8312, 0.6910, and 0.6300), while the remaining five designs have $D_{eff}<0.1$.

For $C=2$ and $N=4$, we focused on designs that meet the minimum requirements of a good RPD and can also estimate the only $f=1$ CC interaction. No design from H16-I meets this requirement. 17 non-isomorphic designs result in from pools of 1, 12, 10, and 12 designs from H16-II through H16-V. Six of these designs have three distinct $D_{eff}$ values (0.8312, 0.7579, and 0.63), while the remaining 11 designs have $D_{eff}<0.1$.

For $C=6$ and $N=1$, 66 non-isomorphic designs were identified from pools of 3, 18, 39, 18, and 26 designs from H16-I through H16-V. Among these, six designs have $D_{eff}=1$, including one resolution IV design and two resolution III designs. The remaining 60 designs have ten distinct values (0.8989, 0.8757, 0.8599, 0.8079, 0.8000, 0.7730, 0.7262, 0.7114, 0.6528, and 0.6245), along with various $CFV$s. In addition to six designs with $D_{eff}=1$, four additional designs capable of estimating any $f=1$ CC interaction are reported in Table A1.

For $C=7$ and $N=1$, a total of 58 non-isomorphic designs were identified from pools of 4, 17, 44, 15, and 22 designs from H16-I through H16-V. Eight of these designs have $D_{eff}=1$, including one resolution IV design and three resolution III designs. The remaining 50 designs have four distinct values (0.8312, 0.7699, 0.6910, and 0.5743), along with various $CFV$s.

3.3. RPDs from the Hadamard Matrices of Order 20

There are exactly three non-isomorphic Hadamard matrices of order 20 [21], labeled as H20-Q, H20-P, and H20-N. H20-Q is isomorphic to the Plackett–Burman design.

For $C=5$ and $N=2$, a total of 2,437 non-isomorphic designs were identified from pools of 1216, 1094, and 1021 designs from H20-Q, H20-P, and H20-N, respectively. Among these designs, 2426 designs have $D_{eff}>0.5$, two designs have $D_{eff}=0.4969$, and nine designs have $D_{eff}<0.1$. Overall, there are 958 distinct $D_{eff}$ values, ranging from 0.7879 to 0.0648. Additionally, six of these designs can accommodate any $f=2$ CC interactions.

For $C=4$ and $N=3$, a total of 260 non-isomorphic designs were identified from pools of 135, 123, and 102 designs from H20-Q, H20-P, and H20-N, respectively. Among these designs, 88 designs have $D_{eff}>0.5$, distributed across 30 distinct $D_{eff}$ values, ranging from 0.7234 to 0.5225. Seven designs have the same $D_{eff}=0.4857$ but different $CFV$s, while one design has $D_{eff}=0.1020$. The remaining 164 designs have $D_{eff}<0.1$.

For $C=2$ and $N=5$, we focused on designs that meet the minimum requirements of a good RPD and can also estimate the only $f=1$ CC interaction. A total of 689 non-isomorphic designs were identified from pools of 285, 299, and 327 designs from H20-Q, H20-P, and H20-N, respectively. Among these designs, 649 designs have $D_{eff}>0.5$, distributed across 289 distinct $D_{eff}$ values, ranging from 0.7773 to 0.5103. Three designs have the same $D_{eff}=0.491$ but different $CFV$s. The remaining 37 designs have $D_{eff}<0.1$.

4. Examples and Discussion

We use examples to discuss the potential usefulness of the top good candidates in Table A1 and Table A2 for RPDs.

4.1. Illustrative Examples

4.1.1. Example 1: Case of $C=5$ and $N=2$

Choice 1: A minimum of 32 runs is required for a regular design in this case. If the cost of 32 runs is affordable, the regular resolution IV design $2_{IV}^{7-2}$, with the defining relation $\mathbf{I}=\mathbf{1236}=\mathbf{12457}=\mathbf{34567}$ (page 254 of [8]), is an excellent choice. This design, with five control factors (1, 2, 3, 4, and 6) and two noise factors (5 and 7), has fifteen distinct two-factor interactions that are not fully aliased with any main effects or with one another, including ten CN interactions, four CC interactions (14, 24, 34, and 46), and one noise-by-noise interaction (57) under assumption that three-factor and higher order interactions are negligible. It certainly has $D_{eff}=1$.

Choice 2: If 32 runs, however, are not affordable, the 20-run nonregular design from Table A2, with five control factors (1, 2, 3, 6, and 16) and two noise factors (10 and 15) from H20-Q, can meet the minimum requirement and also enable the estimation of any two CC interactions. This design, with $D_{eff}=0.7669$, is not as effective as the design $2_{IV}^{7-2}$ mentioned above, but it gets the job done while saving 12 runs, a significant reduction in resources, especially if each run (experiment) is time-consuming or expensive.

4.1.2. Example 2: Case of $C=5$ and $N=1$

Choice 1: The regular resolution IV design from Table A1, with five control factors (1, 2, 3, 4, and 6) and one noise factor (8) from H16-I, has $D_{eff}=1$. In this design, no main effect is fully confounded with any two-factor interactions, and CN interactions are fully confounded with one or two CC interactions. Four out of ten models with one CC interaction in this design are estimable.

Choice 2: The nonregular design with five control factors (2, 3, 4, 5, and 6) and one noise factor (10) from H16-IV has $D_{eff}=1$. The four instances of partial confounding ($J_3=8$) involve only control factors. Specifically, the three-factor-interaction columns 2-4-6, 2-5-6, 3-4-6, and 3-5-6 result in $J_3=8$ but do not involve any important CN interactions. The single instance of full confounding ($J_4=16$) involves the four-factor-interaction column 2-3-4-5, which also does not include any important CN interactions. Compared to the resolution IV design in Choice 1, the confounding among important factorial effects is less severe in this nonregular design. This design can estimate 6 out of 10 models containing one CC interaction, and it could be a good choice for $C=5$ and $N=1$.

Choice 3: The nonregular design with five control factors (2, 6, 8, 10, and 12) and one noise factor (3) from H16-IV has $D_{eff}=0.9007$. Only partial confounding occurs among factorial effects. Specifically, six three-factor-interactions (2-6-12, 2-8-10, 6-8-10, 6-10-12, 6-12-3, and 8-10-3) lead to $J_3=8$, and four four-factor-interactions (2-6-8-12, 2-8-10-12, 6-8-12-3, and 8-10-12-3) lead to $J_4=8$. The confounding is much less severe compared to other designs mentioned above. This design has enhanced capabilities in terms of estimation. It can estimate any 2 CC interactions while meeting the minimum requirements of a good RPD. If a model contains three CC interactions, then 117 out of 120 models are estimable with this design. Therefore, if it is suspected that a couple of CC interactions might be significant, this design could be an excellent choice for $C=5$ and $N=1$.

4.1.3. Example 3: Adjusting for Prior Knowledge from Subject Experts

Imagine an extreme case where a practitioner knows one particular control factor does not interact with all noise factors. For example, in a chemical process, certain type of catalyst (control factor) may not interact with ambient humidity (noise factor). However, the practitioner wants to include this control factor in the study to improve quality (e.g., by maximizing the response mean).

Case 1: $C=3$ and $N=3$. A regular resolution III design from H16-I, using control factors (1, 2, and 3) and noise factors (4, 7, and 8), certainly meets the minimum requirements of a good RPD. However, if it is known that one particular control factor will not interact with three noise factors, an alternative design with control factors (1, 2, and 8) and noise (4, 10, and 12) from H16-III in Table A1 could be a better choice. In this case, assign the control factor that does not interact with noise factor to the column 1 to ensure appropriate placement, the resulting design can accommodate all three CC interactions, six (2-4, 2-10, 2-12, 8-4, 8-10, and 8-12) CN interactions, and six main effects.

Case 2: $C=4$ and $N=3$. A nonregular design from H20-Q, using control factors (1, 2, 4, and 15) and noise factors (7, 10, and 18), may be a better choice if one control factor does not interact with the three noise factors. In this case, assign the control factor that does not interact with the noise factors to column 15, the resulting design can accommodate any three CC interactions, nine CN interactions (1-7, 1-10, 1-18, 2-7, 2-10, 2-18, 4-7, 4-10, and 4-18), and all seven main effects.

4.2. Discussion

4.2.1. Comparison with Previous Work

The authors in [17] have classified RPDs constructed from Hadamard matrices using the extended word-length pattern. Their results are very similar to those of [18] and to our top-ranked designs, provided their RPDs meet our minimum requirements, i.e., able to estimate all main effects and all CN interactions. For example, their cases with $C+N=5$ ($C=5,N=1$ from $H_{12}$, and $C=6,N=1$ and $C=7,N=1$ from $H_{16}$) match our results. However, their approach has not required designs to estimate all main effects and all CN interactions. For instance, Table 3 of [17] lists RPDs with 7 to 11 factors in 12 runs, while we require at least 14 runs to ensure estimability of seven main effects and fix CN interactions in the case of $C=6,N=1$, not to mention 8 to 11 factors. In addition, the RPDs in [17] do not consider any CC interactions.

We have also compared our RPDs with those reported in [18] and found that their $D_{eff}$ values are very similar to our top-ranked designs in Table A1 and Table A2. For example, in the case of $C=5$ and $N=1$, ref. [18] recommended design D, which has $D_{eff}=1$. This is the same as our #1 RPD in Table A1, a regular resolution IV design. Its advantage is that all main effects can be estimated independently, assuming three-factor or higher-order interactions are negligible. For practitioners who do not need to include CC interactions, this design is the best choice.

However, if one or two CC interactions are suspected to be important, the recommended design from [18] is inadequate. Because it is a regular resolution IV design, some two-factor interactions are confounded. In fact, six of ten models with one CC interaction are not estimable. Our work extends that of [18] by providing additional nonregular alternatives. For the same case ($C=5$, $N=1$), our design #7, although it has a slightly lower $D_{eff}=0.9007$, can estimate any two CC interactions as well as all main effects and CN interactions. Among 120 models with three CC interactions included, only three are not estimable. Its CFV is $F_3=[0,6]$, showing that aliasing is limited (only six $J_3=8$, the rest $J_3=0$).

In addition, the authors in [18] studied RPDs constructed from two Plackett–Burman designs, which are special cases of Hadamard matrices of orders 24 and 28. Specifically, the 24-run Plackett–Burman design corresponds to Hadamard matrix $H{24}_{60}$, and the 28-run Plackett–Burman design corresponds to Hadamard matrix $H{28}_{487}$. For the case of $C=4$ and $N=3$, they reported a 20-run design J and a 24-run design K, with reported $D_{eff}$ values of 0.735 and 0.838, respectively. However, our preliminary study shows that these results follow the same argument. For example, if we select columns 1, 13, 18, and 22 from $H{24}_{38}$ as controls and then select columns 2, 10, and 16 as noise factors, the resulting RPD has $D_{eff}=0.859$ and can estimate all CC interactions, in addition to all main effects and CN interactions. By contrast, their design K can only estimate a single CC interaction and cannot estimate any two CC interactions.

4.2.2. Limitations of the Proposed Approach

Our proposed method follows a straightforward procedure: select columns from a Hadamard matrix to represent control factors, select noise factors from the remaining columns, and then evaluate each candidate design based on D-efficiency, the estimability of CC interactions, and $CFV$. This exhaustive search strategy works well for small to moderate numbers of factors and yields many useful designs. However, as the number of control and noise factors increases, the computational burden grows exponentially and quickly becomes prohibitive.

For example, consider a case with five control factors and three noise factors. To estimate one overall mean, eight main effects, and fifteen CN interactions, we need 24 degrees of freedom. Using a Hadamard matrix of order 24, there are over 27 million possible candidate designs (selecting 5 out of 23 columns for controls and then 3 out of 18 for noise). Moreover, there are 60 non-isomorphic Hadamard matrices of this order, further multiplying the search space. Designs constructed in this way can estimate all main effects and CN interactions, but if we also wish to estimate even a small number of CC interactions, larger matrices are required. For instance, with order 28 matrices, there are 487 non-isomorphic Hadamard matrices, and for each, more than 124 million candidate designs exist. In addition, since only four degrees of freedom remain for CC interactions, there are 210 possible models containing four out of ten CC interactions (for five control factors). Altogether, evaluating all possibilities would require over 1.27 trillion computations, each requiring the calculation of a $28\times 28$ information matrix from the model matrix and its determinant.

In practice, such exhaustive searches are infeasible for large numbers of factors, highlighting the need for alternative strategies when addressing higher-dimensional RPD problems. This challenge is the focus of our ongoing research, and we have obtained some promising preliminary results.

5. Conclusions

In this article, we investigated fractional factorial designs constructed from Hadamard matrices of orders 12, 16, and 20 for robust parameter designs. These nonregular designs not only meet the minimum requirements of a good RPD, i.e., estimating all control-by-noise interactions and the main effects of both control and noise factors, but also save experimental runs and often provide better estimation of other potentially important factorial effects. The examples in Section 4 illustrate potential applications of the top good candidates presented in Table A1 and Table A2. Practitioners can refer to these tables to compare and select designs that are most suitable for their specific experimental needs. The list of top good candidates is particularly valuable in resource-limited situations, where the ability to also estimate one or two control-by-control interactions may also be critical. Further research is needed for higher-dimensional RPD problems, since the computational cost grows dramatically as the number of factors increases.