Analysis of the Truncated XLindley Distribution Using Bayesian Robustness
Abstract
1. Introduction
2. Model’s Origins
3. The Robustness of Bayesian Models
3.1. Basic Quadratic Loss Function
3.1.1. Stability for in Bayesian Models
3.1.2. Stability for β in Bayesian Models
3.2. Generalized Quadratic Loss Function
3.2.1. Bayesian Stability for α
3.2.2. Bayesian Stability for β
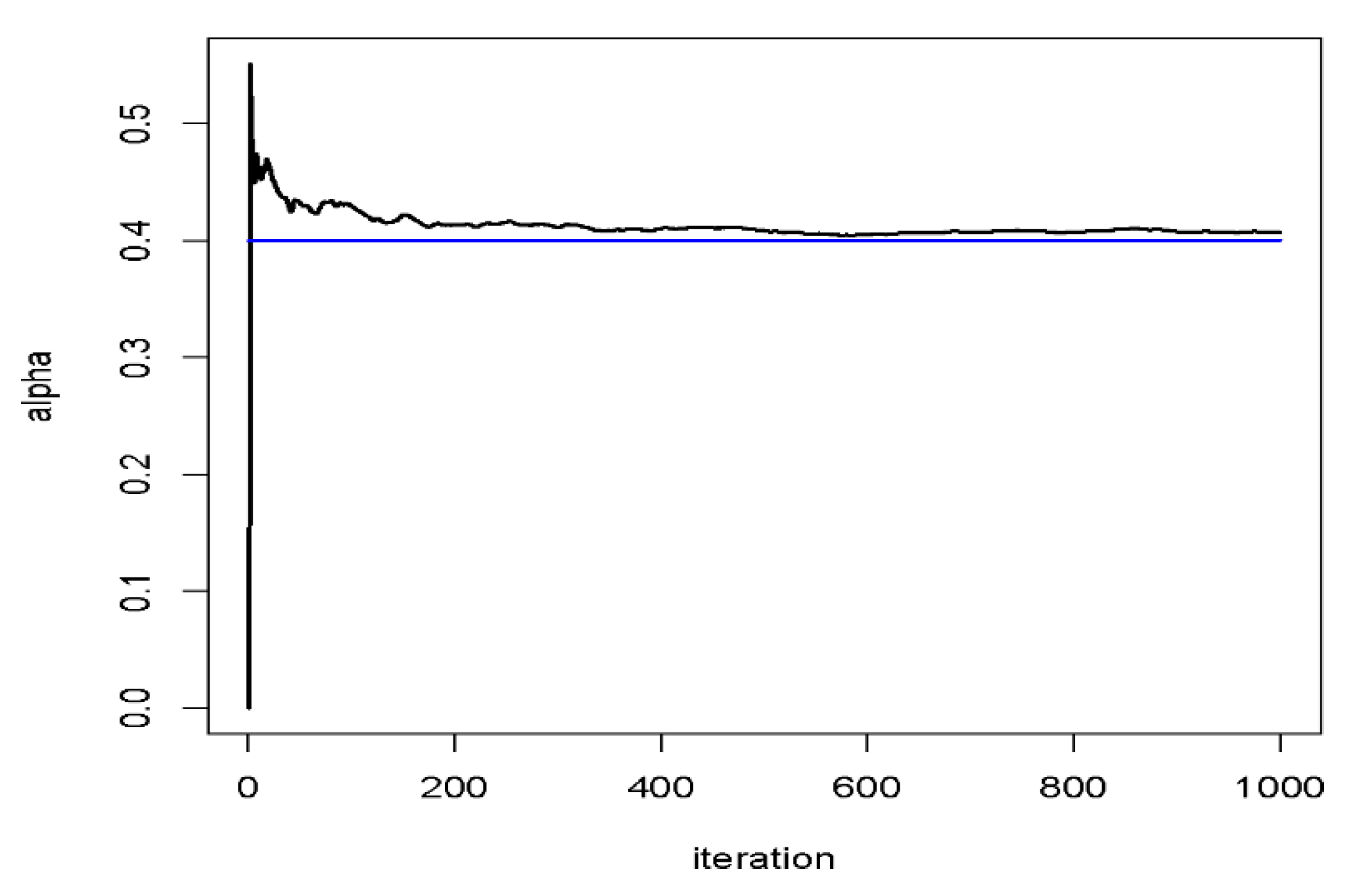
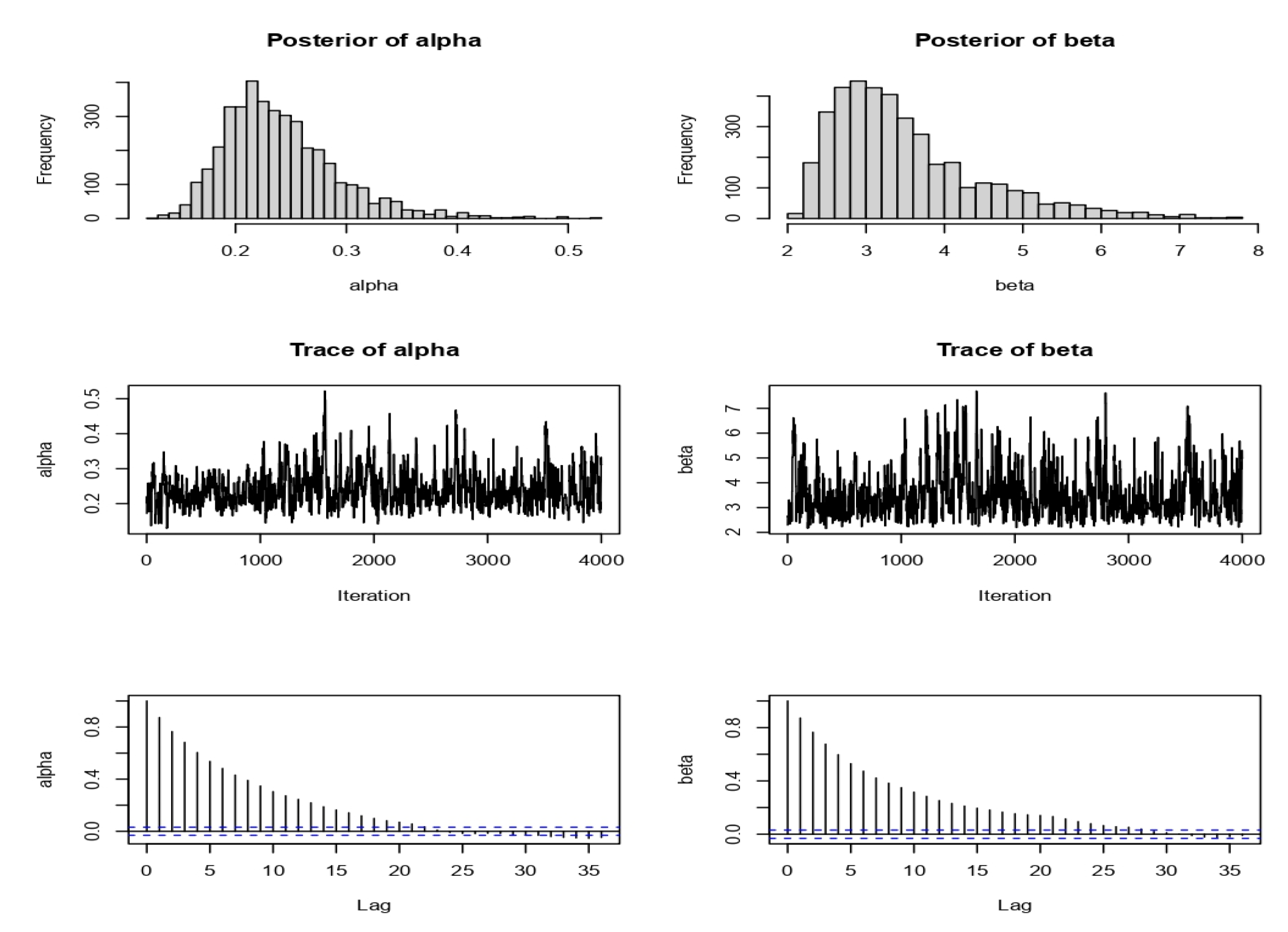
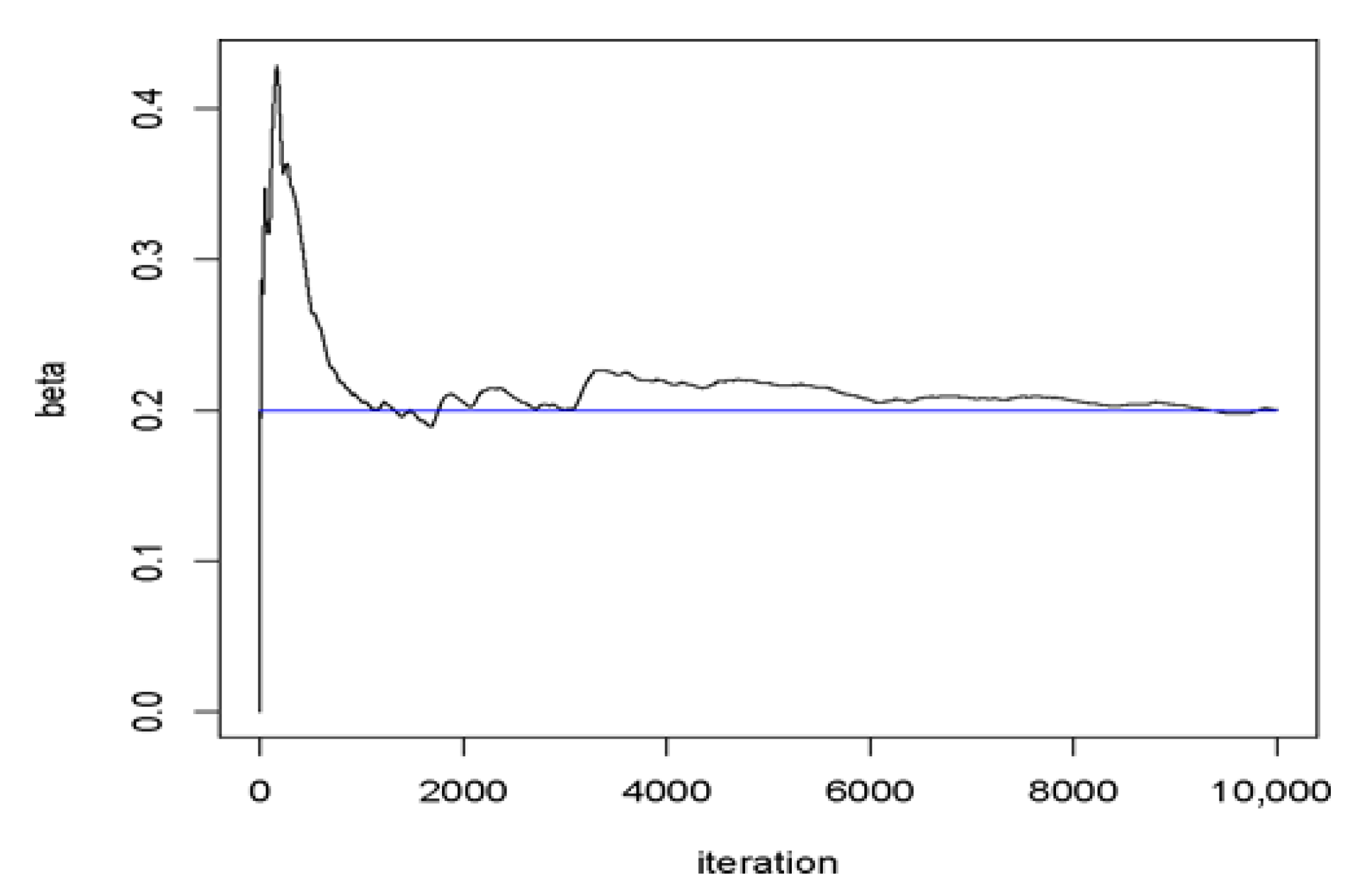
4. Monte Carlo Study
4.1. Bayesian Stability for
Example
- (i)
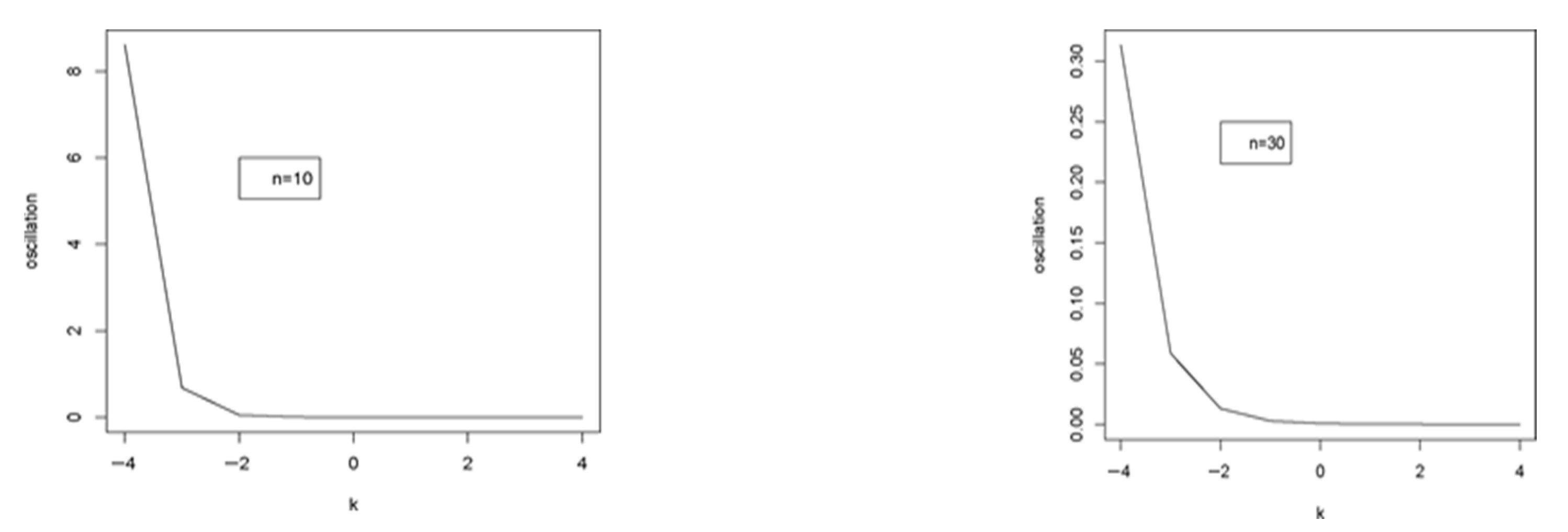
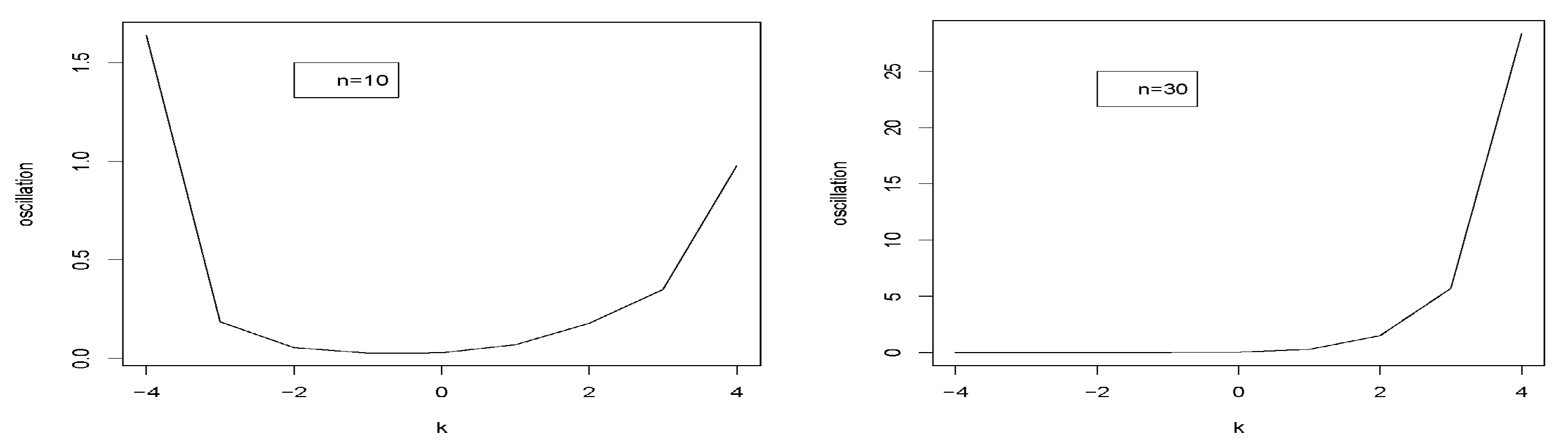
- When k increases for n = 10, 30, 50, the oscillation diminishes for = 0.2 (refer to Figure 3).
- (ii)
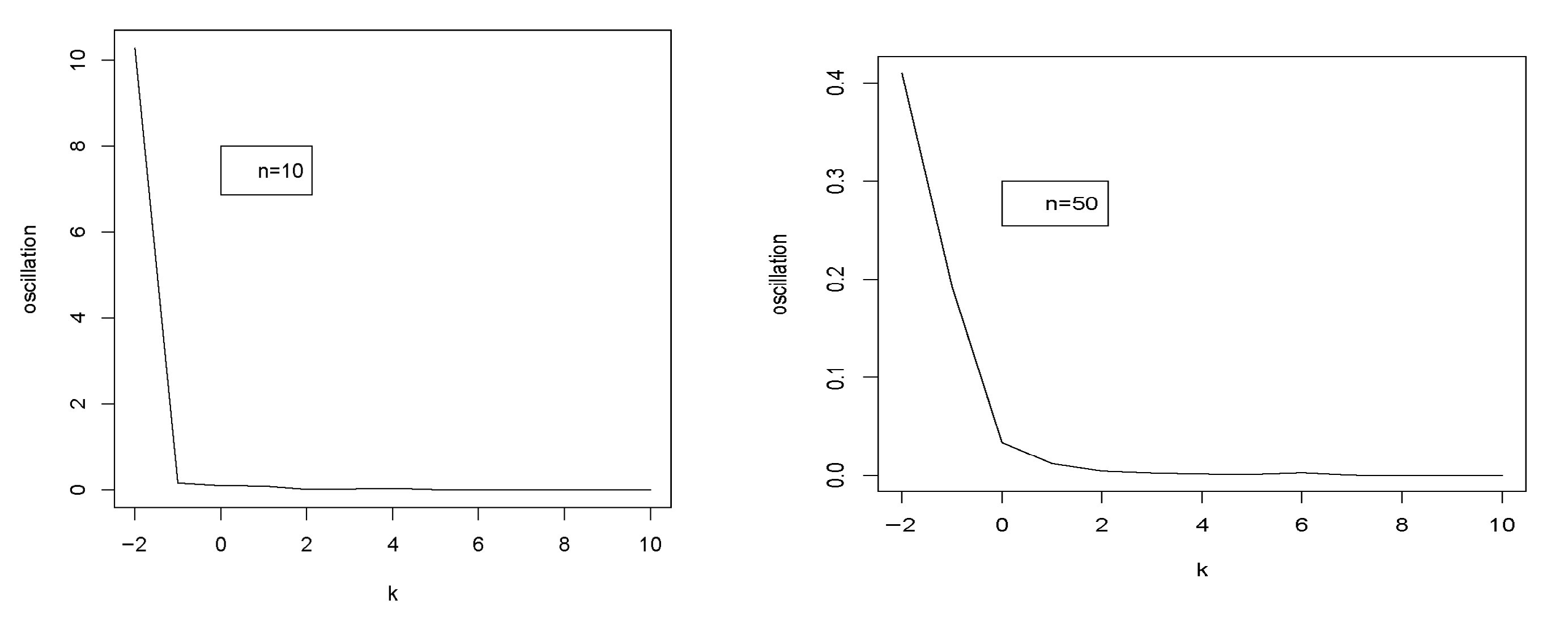
- The oscillation values for = 0.4 fall to a specific value k0, after which they increase for n = 10, 30, and 50 (refer to Figure 4).
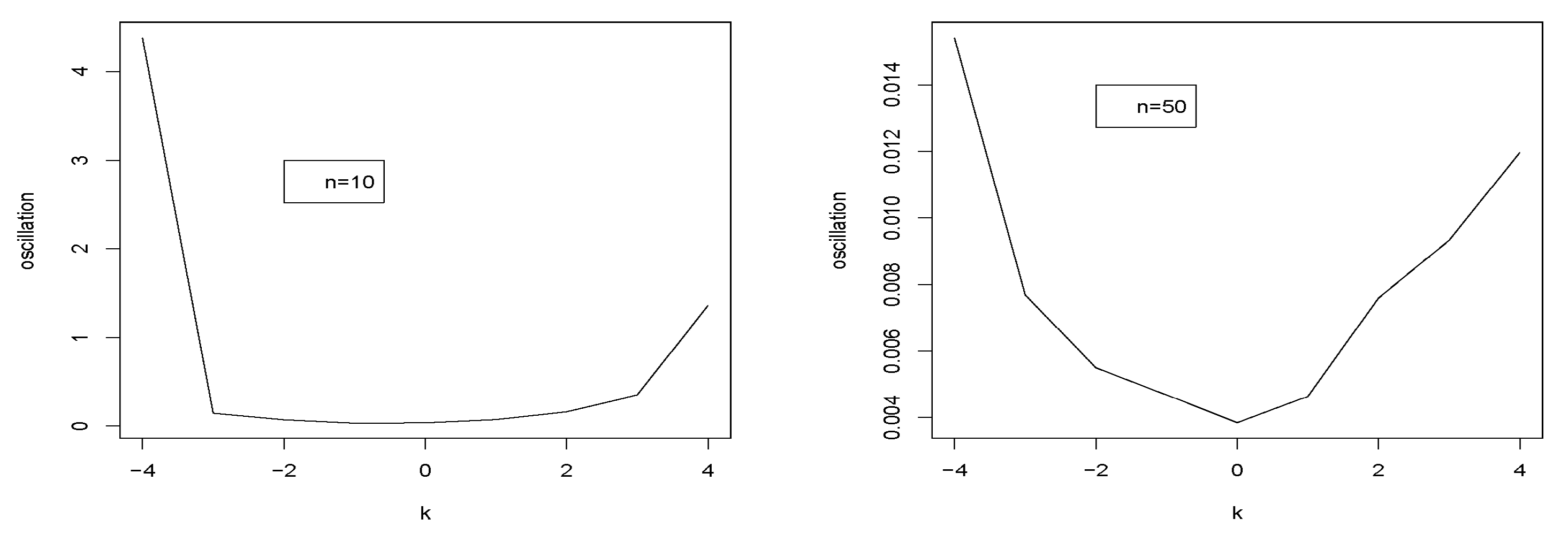
- (iii)
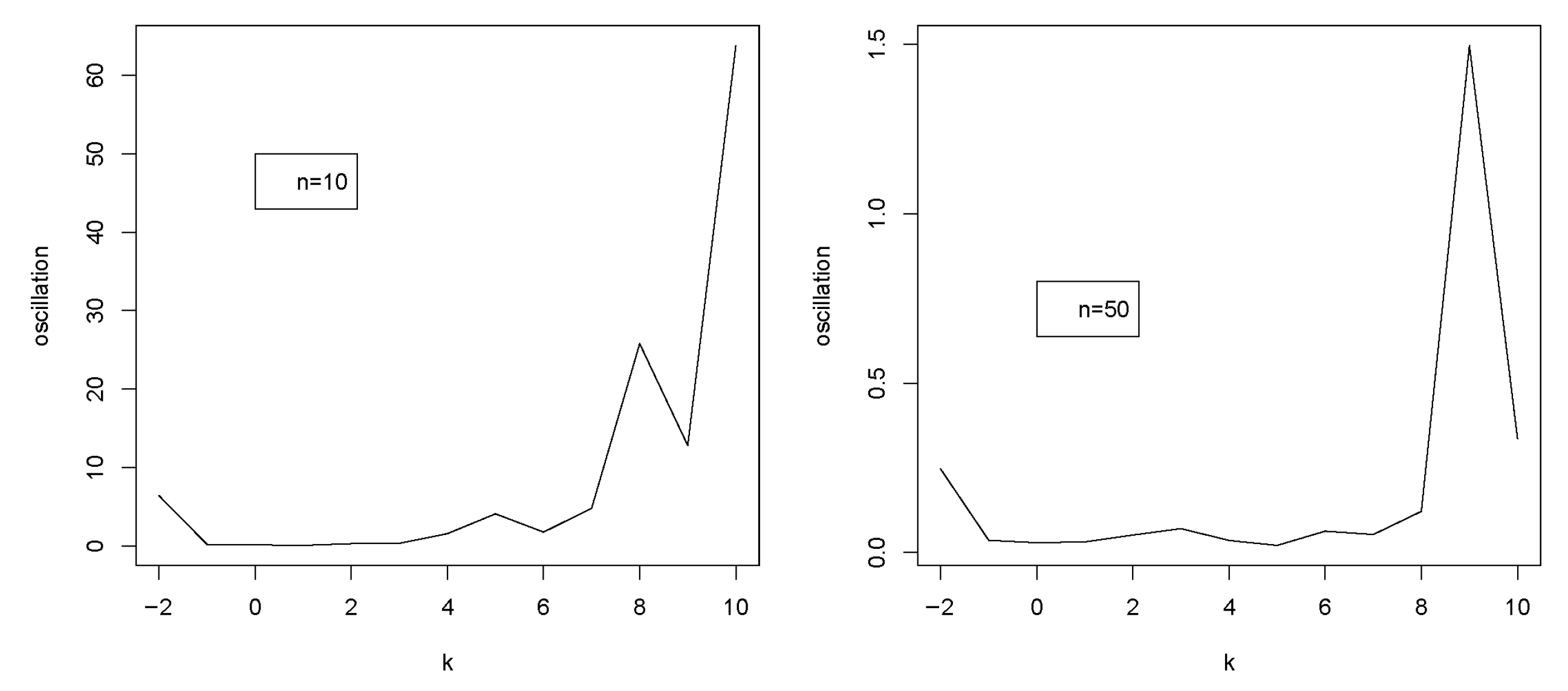
- When = 1, the oscillation increases for k = 30, 50 and then reduces until a certain value at which point it grows (refer to Figure 5).
4.2. Bayesian Stability of β
Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bantan, R.A.R.; Jamal, F.; Chesneau, C.; Elgarhy, M. Truncated Inverted Kumaraswamy Generated Family of Distributions with Applications. Entropy 2019, 21, 1089. [Google Scholar] [CrossRef]
- Aldahlan, M.A.; Jamal, F.; Chesneau, C.; Elgarhy, M.; Elbatal, I. The Truncated Cauchy Power Family of Distributions with Inference and Applications. Entropy 2020, 22, 346. [Google Scholar] [CrossRef]
- Mansour, M.M.; Butt, N.S.; Yousof, H.; Ansari, S.I.; Ibrahim, M. A Generalization of Reciprocal Exponential Model: Clayton Copula, Statistical Properties and Modeling Skewed and Symmetric Real Data Sets: A Generalization of Reciprocal Exponential Model. Pak. J. Stat. Oper. Res. 2020, 16, 373–386. [Google Scholar] [CrossRef]
- Singh, B.; Tyagi, S.; Singh, R.P.; Tyagi, A. Modified Topp-Leone Distribution: Properties, Classical and Bayesian Estimation with Application to COVID-19 and Reliability Data. Thail. Stat. 2025, 23, 72–96. [Google Scholar]
- Elshahhat, A.; Abo-Kasem, O.E.; Mohammed, H.S. The Inverted Hjorth Distribution and Its Applications in Environmental and Pharmaceutical Sciences. Symmetry 2025, 17, 1327. [Google Scholar] [CrossRef]
- Khodja, N.; Aiachi, H.; Talhi, H.; Benatallah, I.N. The truncated XLindley distribution with classic and Bayesian inference under censored data. Adv. Math. Sci. J. 2021, 10, 1191–1207. [Google Scholar]
- Ghitany, M.E.; Al-Mutairi, D.K.; Nadarajah, S. Zero-truncated Poisson–Lindley distribution and its application. Math. Comput. Simul. 2008, 79, 279–287. [Google Scholar] [CrossRef]
- Zeghdoudi, H.; Chouia, S. The XLindley Distribution: Properties and Application. J. Stat. Theory Appl. 2021, 20, 318–327. [Google Scholar] [CrossRef]
- Talhi, H.; Aiachi, H. On Truncated Zeghdoudi Distribution: Posterior Analysis under Different Loss Functions for Type II Censored Data. Pak. J. Stat. Oper. Res. 2021, 17, 497–508. [Google Scholar] [CrossRef]
- Mȩczarski, M.; Zieliński, R. Stability of the Bayesian estimator of the Poisson mean under the inexactly specified gamma prior. Statist. Probab. Lett. 1991, 12, 329–333. [Google Scholar] [CrossRef]
- Chadli, A.; Talhi, H.; Fellag, H. Comparison of the Maximum Likelihood and Bayes Estimators of the parameters and mean Time Between Failure for bivariate exponential Distribution under different loss functions. Afr. Stat. 2013, 8, 499–514. [Google Scholar]
- Berger, J.O.; Rios Insua, D.; Ruggeri, F. Bayesian robustness. In Robust Bayesian Analysis; Insua, D.R., Ruggeri, F., Eds.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Micheas, A.C. A Unified Approach to Prior and Loss Robustness. Comm. Statist. Theory Methods 2006, 35, 309–323. [Google Scholar] [CrossRef]
- Gilks, W.R.; Richardson, S.; Spiegelhalter, D.J. Introducing Markov Chain Monte Carlo. In Markov Chain Monte Carlo in Practice; CRC Press: Boca Raton, FL, USA, 1995; pp. 1–17. [Google Scholar]
- Larbi, L.; Fellag, H. Robust bayesian analysis of an autoregressive model with exponential innovations. Afr. Stat. 2016, 11, 955–964. [Google Scholar] [CrossRef]

| β | n | |||
|---|---|---|---|---|
| 10 | 30 | 50 | ||
| 0.2 | 0.1646 (0.0025) | 0.2312 (0.0028) | 0.2234 (0.0015) | |
| 0.2 | 1 | 0.1867 (0.0041) | 0.2002 (0.0017) | 0.21208 (0.0012) |
| 5 | 0.1423 (0.0020) | 0.2062 (0.0018) | 0.2869 (0.0025) | |
| 20 | 0.3213 (0.0113) | 0.1853 (0.0017) | 0.2052 (0.0012) | |
| 0.2 | 0.3340 (0.0265) | 0.3032 (0.0044) | 0.3264 (0.0035) | |
| 0.4 | 1 | 0.3327 (0.0139) | 0.5600 (0.0190) | 0.4596 (0.0074) |
| 5 | 0.3505 (0.0146) | 0.4344 (0.0115) | 0.4715 (0.0089) | |
| 20 | 0.3876 (0.0189) | 0.2611 (0.0034) | 0.4063 (0.0056) | |
| 0.2 | 0.4692 (0.0325) | 0.5974 (0.0303) | 0.6318 (0.0182) | |
| 1 | 1 | 0.4955 (0.0317) | 0.7672 (0.0466) | 0.7225 (0.0264) |
| 5 | 0.4199 (0.0249) | 0.5528 (0.0198) | 0.6288 (0.0165) | |
| 20 | 0.43611 (0.0463) | 0.5718 (0.0217) | 0.5940 (0.0146) | |
| 0.2 | 1.1850 (0.1388) | 3.4193 (0.3725) | 5.6590 (0.6387) | |
| 20 | 1 | 1.2088 (0.1401) | 0.9099 (0.1030) | 1.2388 (0.1325) |
| 5 | 0.8152 (0.0879) | 0.8236 (0.1358) | 1.2353 (0.3469) | |
| 20 | 0.7521 (0.0571) | 0. 9499 (0.0787) | 1.7520 (0.1229) | |
| β | n | |||
|---|---|---|---|---|
| 10 | 30 | 50 | ||
| 0.2 | 0.2 | 0.0009 | 0.0015 | 0.0009 |
| 1 | 0.0019 | 0.0014 | 0.0002 | |
| 5 | 0.0018 | 0.0004 | 0.0004 | |
| 20 | 0.0051 | 0.0005 | 0.00007 | |
| 0.2 | 0.0277 | 0.0006 | 0.0005 | |
| 0.4 | 1 | 0.0089 | 0.0088 | 0.0010 |
| 5 | 0.0452 | 0.0081 | 0.0034 | |
| 20 | 0.0146 | 0.0008 | 0.0007 | |
| 0.2 | 0.0079 | 0.0058 | 0.0031 | |
| 1 | 1 | 0.0140 | 0.0070 | 0.0040 |
| 5 | 0.0023 | 0.0026 | 0.0024 | |
| 20 | 0.0167 | 0.0026 | 0.0019 | |
| 0.2 | 0.0333 | 0.0864 | 0.1383 | |
| 20 | 1 | 0.0375 | 0.3669 | 0.3928 |
| 5 | 0.1754 | 0.4066 | 0.3588 | |
| 20 | 0.0599 | 0.2178 | 0.5529 | |
| β | n | |||
|---|---|---|---|---|
| 10 | 30 | 50 | ||
| 0.2 | 0.2 | 0.1696 (0.0212) | 0.1096 (0.0050) | 0.1825 (0.0251) |
| 1 | 0.0831 (0.0089) | 0.2009 (0.0150) | 0.1129 (0.0020) | |
| 5 | 0.16022 (0.0197) | 0.1500 (0.0273) | 0.1920 (0.0286) | |
| 10 | 0.1805 (0.0264) | 0.2128 (0.0319) | 0.2615 (0.0965) | |
| 0.2 | 0.1530 (0.0207) | 0.1958 (0.0223) | 0.2729 (0.0207) | |
| 0.4 | 1 | 0.2817 (0.0382) | 0.2730 (0.0212) | 0.2864 (0.0202) |
| 5 | 0.2004 (0.0222) | 0.2813 (0.0337) | 0.3828 (0.0474) | |
| 10 | 0.2120 (0.0316) | 0.2288 (0.0327) | 0.2710 (0.0230) | |
| 0.2 | 0.2919 (0.0489) | 0.3670 (0.0748) | 0.6435 (0.0671) | |
| 1 | 1 | 0.2221 (0.0334) | 0.4716 (0.0506) | 0.5565 (0.0565) |
| 5 | 0.1857 (0.0354) | 0.4122 (0.0344) | 0.6075 (0.0589) | |
| 10 | 0.2620 (0.0417) | 0.2775 (0.0296) | 0.4035 (0.0471) | |
| 0.2 | 0.3519 (0.0929) | 0.6078 (0.0838) | 1.0438 (0.1725) | |
| 20 | 1 | 0.4933 (0.0745) | 1.3863 (0.0312) | 1.8561 (0.4235) |
| 5 | 0.3925 (0.0934) | 1.0965 (0.2054) | 1.5682 (0.2850) | |
| 10 | 0.4321 (0.0429) | 0.7656 (0.1948) | 1.3402 (0.2297) | |
| β | n | |||
|---|---|---|---|---|
| 10 | 30 | 50 | ||
| 0.2 | 0.2 | 0.0783 | 0.0049 | 0.0321 |
| 1 | 0.0253 | 0.0254 | 0.0213 | |
| 5 | 0.2593 | 0.4273 | 0.3667 | |
| 10 | 0.1669 | 0.2545 | 0.1618 | |
| 0.2 | 0.0469 | 0.0370 | 0.0154 | |
| 0.4 | 1 | 0.0575 | 0.0201 | 0.0155 |
| 5 | 0.0583 | 0.0606 | 0.1287 | |
| 10 | 0.0652 | 0.1171 | 0.1121 | |
| 0.2 | 0.0625 | 0.0683 | 0.0340 | |
| 1 | 1 | 0.0628 | 0.0365 | 0.0306 |
| 5 | 0.0854 | 0.0547 | 0.0842 | |
| 10 | 0.0654 | 0.0663 | 0.0725 | |
| 0.2 | 0.3024 | 0.4366 | 0.3037 | |
| 20 | 1 | 0.2416 | 0.8071 | 0.8361 |
| 5 | 0.4973 | 0.2700 | 0.2904 | |
| 10 | 0.3819 | 0.3820 | 0.2793 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keddali, M.; Talhi, H.; Slimani, A.; Meraou, M.A. Analysis of the Truncated XLindley Distribution Using Bayesian Robustness. Stats 2025, 8, 108. https://doi.org/10.3390/stats8040108
Keddali M, Talhi H, Slimani A, Meraou MA. Analysis of the Truncated XLindley Distribution Using Bayesian Robustness. Stats. 2025; 8(4):108. https://doi.org/10.3390/stats8040108
Chicago/Turabian StyleKeddali, Meriem, Hamida Talhi, Ali Slimani, and Mohammed Amine Meraou. 2025. "Analysis of the Truncated XLindley Distribution Using Bayesian Robustness" Stats 8, no. 4: 108. https://doi.org/10.3390/stats8040108
APA StyleKeddali, M., Talhi, H., Slimani, A., & Meraou, M. A. (2025). Analysis of the Truncated XLindley Distribution Using Bayesian Robustness. Stats, 8(4), 108. https://doi.org/10.3390/stats8040108






