Silhouette-Based Evaluation of PCA, Isomap, and t-SNE on Linear and Nonlinear Data Structures
Abstract
1. Introduction
1.1. Dimension Reduction: Introduction and Theoretical Foundations
1.2. Empirical Comparisons Across Data Structures
1.2.1. Linear Data Structures
1.2.2. Nonlinear Data Structures
1.2.3. Empirical Trade-Offs and Challenges
1.3. Applications in Diverse Domains
2. Materials and Methods
2.1. Mathematical Definitions and Examples
Notation and Indices
2.2. Simulation-Based Demonstrations of PCA, Isomap, and t-SNE
2.2.1. Simulation Results of PCA
2.2.2. Simulation Results of Isomap
2.2.3. Simulation Results of t-SNE
2.3. Accuracy Comparison of Dimensionality Reduction Techniques
- −
- is the average intra-cluster distance for point i in cluster ,
- −
- is the minimum average inter-cluster distance to another cluster .
- −
- is the average intra-cluster distance for point i in cluster ,
- −
- is the minimum average inter-cluster distance to another cluster .
2.4. t-SNE: Why No Global Silhouette Optimality, and Where It Excels
2.4.1. Challenges in Establishing Global Silhouette Optimality for t-SNE
- Nonconvexity and initialization dependence: The objective function has a complex landscape with multiple local minima, and no closed-form expression characterizes its global minimizer [34].
- Probability-based objective: t-SNE aligns probabilities and , rather than preserving metric or geodesic distances that directly influence silhouette scores [36].
2.4.2. Local Neighborhood Preservation: t-SNE’s Strength
2.4.3. Implications for Our Results
2.5. Simulation Study
2.5.1. Data Generation
- Linear (Gaussian mixture): Data points were sampled from a low-rank subspace of intrinsic dimension . Each observation was generated aswhere are orthonormal basis vectors and with cluster-specific means defining Gaussian components. This configuration yields well-separated, approximately spherical clusters with linear structure.
- Linear (Student-t mixture, heavy tails): To assess robustness under non-Gaussian noise, a second linear setting replaced the Gaussian components by mixtures of Student- distributions with moderate to heavy tails (). This produces elongated and noisy clusters lying near a common subspace, preserving linear geometry but degrading local smoothness.
- Nonlinear (Swiss roll manifold): A curved manifold of intrinsic dimension was generated aswith and . Clusters were assigned based on geodesic neighborhoods along the spiral surface, producing a smoothly varying nonlinear geometry.
- Nonlinear (Concentric spheres manifold): The final scenario introduced nonconvex curvature with discontinuities by embedding samples on multiple concentric spherical shells of radii , , in :This topology captures disconnected yet symmetric manifolds, challenging methods that rely on smooth global mappings.
2.5.2. Experimental Design
3. Results
3.1. Simulated Silhouette Score Results for Linear vs. Nonlinear Structures
3.1.1. Linear Data Structure Results
3.1.2. Effect of Sample Size, Noise, and Dimensionality on Linear Data
- Noise variance: Increasing noise drastically reduces silhouette scores for all methods. At low noise (), clusters remain well-separated (silhouettes near 0.9–1.0 for PCA), but at high noise (), silhouettes drop below 0.1. Noise inflates within-cluster variance and increases overlap between clusters, eroding separability. For instance, at fixed and , raising from 0.25 to 2 lowers the PCA mean silhouette from ∼0.75 to ∼0.20, that of Isomap from ∼0.70 to ∼0.15, and that of t-SNE from ∼0.68 to ∼0.18.
- Sample size: Increasing n tends to improve silhouettes and stabilize variability. With more observations, the cluster geometry is better estimated and less affected by stochasticity. For example, at and , enlarging n from 100 to 500 raises the PCA mean silhouette from ∼0.68 to ∼0.81, that of Isomap from ∼0.65 to ∼0.77, and that of t-SNE from ∼0.61 to ∼0.73. Standard deviations decrease in tandem (PCA’s typically shrinking from ∼0.04 to ∼0.02).
- Feature count (dimensionality): Increasing the number of ambient dimensions reduces clustering performance, especially when many features are irrelevant. This pattern reflects the curse of dimensionality: added noise dimensions dilute meaningful signal directions. For instance, at and , the PCA silhouette declines from ∼0.76 at to at , while those of Isomap and t-SNE drop from ∼0.72 and ∼0.69 to ∼0.45 and , respectively. PCA shows the greatest robustness because it identifies global variance directions that partially filter noise, whereas Isomap and t-SNE are more sensitive to spurious local structure.
3.1.3. Nonlinear Data Results
3.1.4. Effect of Sample Size, Noise, and Dimensionality on Nonlinear Data
- Noise variance: Increasing noise substantially lowers silhouettes for all methods, but Isomap’s degradation is less severe. At low noise (), Isomap’s mean silhouette remains ∼0.9–1.0, while at , it drops below 0.15. t-SNE and PCA experience sharper declines, reflecting their sensitivity to noise in pairwise distances.
- Sample size: Increasing n improves performance and reduces variability. Larger samples produce more accurate geodesic approximations for Isomap and better neighborhood estimates for t-SNE, narrowing but not eliminating the performance gap.
- Feature count (dimensionality): Higher p values introduce irrelevant features that degrade all methods, particularly those relying on pairwise distances. At , , increasing p from 20 to 400 reduces Isomap’s silhouette from ∼0.80 to ∼0.50, that of t-SNE from ∼0.75 to ∼0.47, and that of PCA from ∼0.60 to ∼0.40. The impact is largest for nonlinear embeddings because distance metrics become less reliable in high dimensions.
3.2. Visual Comparison
Alternative Visualizations: Bar, Density, and Violin Plots
4. Conclusions
Silhouette Distributions Across n, p, and Noise
5. Discussion
6. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Additional Simulation Results
| Scenario | n | p | PCA | Isomap | t-SNE | |
|---|---|---|---|---|---|---|
| Linear (Gaussian) | 100 | 0.25 | 20 | 0.918 (±0.022) | 0.868 (±0.040) | 0.818 (±0.030) |
| Linear (Gaussian) | 200 | 0.25 | 20 | 0.968 (±0.037) | 0.917 (±0.044) | 0.868 (±0.021) |
| Linear (Gaussian) | 300 | 0.25 | 20 | 1.000 (±0.028) | 0.950 (±0.042) | 0.900 (±0.034) |
| Linear (Gaussian) | 400 | 0.25 | 20 | 1.000 (±0.026) | 0.950 (±0.044) | 0.900 (±0.031) |
| Linear (Gaussian) | 500 | 0.25 | 20 | 1.000 (±0.032) | 0.950 (±0.034) | 0.900 (±0.023) |
| Linear (Gaussian) | 100 | 0.5 | 20 | 0.905 (±0.037) | 0.855 (±0.026) | 0.805 (±0.021) |
| Linear (Gaussian) | 200 | 0.5 | 20 | 0.955 (±0.023) | 0.905 (±0.044) | 0.855 (±0.042) |
| Linear (Gaussian) | 300 | 0.5 | 20 | 1.000 (±0.032) | 0.950 (±0.036) | 0.900 (±0.045) |
| Linear (Gaussian) | 400 | 0.5 | 20 | 1.000 (±0.031) | 0.950 (±0.038) | 0.900 (±0.034) |
| Linear (Gaussian) | 500 | 0.5 | 20 | 1.000 (±0.030) | 0.950 (±0.027) | 0.900 (±0.024) |
| Linear (Gaussian) | 100 | 0.75 | 20 | 0.893 (±0.039) | 0.843 (±0.043) | 0.793 (±0.037) |
| Linear (Gaussian) | 200 | 0.75 | 20 | 0.943 (±0.035) | 0.892 (±0.021) | 0.843 (±0.032) |
| Linear (Gaussian) | 300 | 0.75 | 20 | 0.993 (±0.034) | 0.943 (±0.025) | 0.893 (±0.028) |
| Linear (Gaussian) | 400 | 0.75 | 20 | 1.000 (±0.021) | 0.950 (±0.024) | 0.900 (±0.030) |
| Linear (Gaussian) | 500 | 0.75 | 20 | 1.000 (±0.025) | 0.950 (±0.029) | 0.900 (±0.024) |
| Linear (Gaussian) | 100 | 1.0 | 20 | 0.880 (±0.018) | 0.830 (±0.026) | 0.780 (±0.032) |
| Linear (Gaussian) | 200 | 1.0 | 20 | 0.930 (±0.022) | 0.880 (±0.041) | 0.830 (±0.021) |
| Linear (Gaussian) | 300 | 1.0 | 20 | 0.980 (±0.026) | 0.930 (±0.040) | 0.880 (±0.023) |
| Linear (Gaussian) | 400 | 1.0 | 20 | 1.000 (±0.029) | 0.950 (±0.025) | 0.900 (±0.023) |
| Linear (Gaussian) | 500 | 1.0 | 20 | 1.000 (±0.034) | 0.950 (±0.042) | 0.900 (±0.029) |
| Linear (Gaussian) | 100 | 1.5 | 20 | 0.855 (±0.032) | 0.805 (±0.022) | 0.755 (±0.030) |
| Linear (Gaussian) | 200 | 1.5 | 20 | 0.905 (±0.022) | 0.855 (±0.040) | 0.805 (±0.031) |
| Linear (Gaussian) | 300 | 1.5 | 20 | 0.955 (±0.035) | 0.905 (±0.040) | 0.855 (±0.040) |
| Linear (Gaussian) | 400 | 1.5 | 20 | 1.000 (±0.026) | 0.950 (±0.039) | 0.900 (±0.036) |
| Linear (Gaussian) | 500 | 1.5 | 20 | 1.000 (±0.033) | 0.950 (±0.020) | 0.900 (±0.032) |
| Linear (Gaussian) | 100 | 2.0 | 20 | 0.830 (±0.021) | 0.780 (±0.029) | 0.730 (±0.035) |
| Linear (Gaussian) | 200 | 2.0 | 20 | 0.880 (±0.024) | 0.830 (±0.023) | 0.780 (±0.026) |
| Linear (Gaussian) | 300 | 2.0 | 20 | 0.930 (±0.032) | 0.880 (±0.030) | 0.830 (±0.040) |
| Linear (Gaussian) | 400 | 2.0 | 20 | 0.980 (±0.018) | 0.930 (±0.031) | 0.880 (±0.045) |
| Linear (Gaussian) | 500 | 2.0 | 20 | 1.000 (±0.037) | 0.950 (±0.042) | 0.900 (±0.024) |
| Linear (Gaussian) | 100 | 0.25 | 50 | 0.888 (±0.018) | 0.838 (±0.036) | 0.788 (±0.029) |
| Linear (Gaussian) | 200 | 0.25 | 50 | 0.938 (±0.031) | 0.887 (±0.028) | 0.838 (±0.025) |
| Linear (Gaussian) | 300 | 0.25 | 50 | 0.988 (±0.035) | 0.938 (±0.022) | 0.888 (±0.032) |
| Linear (Gaussian) | 400 | 0.25 | 50 | 1.000 (±0.028) | 0.950 (±0.035) | 0.900 (±0.028) |
| Linear (Gaussian) | 500 | 0.25 | 50 | 1.000 (±0.027) | 0.950 (±0.044) | 0.900 (±0.032) |
| Linear (Gaussian) | 100 | 0.5 | 50 | 0.875 (±0.037) | 0.825 (±0.043) | 0.775 (±0.035) |
| Linear (Gaussian) | 200 | 0.5 | 50 | 0.925 (±0.025) | 0.875 (±0.024) | 0.825 (±0.043) |
| Linear (Gaussian) | 300 | 0.5 | 50 | 0.975 (±0.023) | 0.925 (±0.022) | 0.875 (±0.044) |
| Linear (Gaussian) | 400 | 0.5 | 50 | 1.000 (±0.033) | 0.950 (±0.024) | 0.900 (±0.034) |
| Linear (Gaussian) | 500 | 0.5 | 50 | 1.000 (±0.039) | 0.950 (±0.035) | 0.900 (±0.030) |
| Linear (Gaussian) | 100 | 0.75 | 50 | 0.863 (±0.031) | 0.812 (±0.028) | 0.763 (±0.028) |
| Linear (Gaussian) | 200 | 0.75 | 50 | 0.912 (±0.020) | 0.862 (±0.029) | 0.812 (±0.045) |
| Linear (Gaussian) | 300 | 0.75 | 50 | 0.963 (±0.019) | 0.912 (±0.022) | 0.863 (±0.024) |
| Linear (Gaussian) | 400 | 0.75 | 50 | 1.000 (±0.032) | 0.950 (±0.035) | 0.900 (±0.042) |
| Linear (Gaussian) | 500 | 0.75 | 50 | 1.000 (±0.032) | 0.950 (±0.038) | 0.900 (±0.033) |
| Linear (Gaussian) | 100 | 1.0 | 50 | 0.850 (±0.031) | 0.800 (±0.041) | 0.750 (±0.040) |
| Linear (Gaussian) | 200 | 1.0 | 50 | 0.900 (±0.039) | 0.850 (±0.031) | 0.800 (±0.028) |
| Linear (Gaussian) | 300 | 1.0 | 50 | 0.950 (±0.025) | 0.900 (±0.020) | 0.850 (±0.025) |
| Linear (Gaussian) | 400 | 1.0 | 50 | 1.000 (±0.036) | 0.950 (±0.026) | 0.900 (±0.026) |
| Linear (Gaussian) | 500 | 1.0 | 50 | 1.000 (±0.017) | 0.950 (±0.026) | 0.900 (±0.038) |
| Linear (Gaussian) | 100 | 1.5 | 50 | 0.825 (±0.036) | 0.775 (±0.032) | 0.725 (±0.030) |
| Linear (Gaussian) | 200 | 1.5 | 50 | 0.875 (±0.021) | 0.825 (±0.023) | 0.775 (±0.030) |
| Linear (Gaussian) | 300 | 1.5 | 50 | 0.925 (±0.029) | 0.875 (±0.025) | 0.825 (±0.031) |
| Linear (Gaussian) | 400 | 1.5 | 50 | 0.975 (±0.020) | 0.925 (±0.033) | 0.875 (±0.029) |
| Linear (Gaussian) | 500 | 1.5 | 50 | 1.000 (±0.031) | 0.950 (±0.029) | 0.900 (±0.029) |
| Linear (Gaussian) | 100 | 2.0 | 50 | 0.800 (±0.028) | 0.750 (±0.039) | 0.700 (±0.026) |
| Linear (Gaussian) | 200 | 2.0 | 50 | 0.850 (±0.025) | 0.800 (±0.027) | 0.750 (±0.036) |
| Linear (Gaussian) | 300 | 2.0 | 50 | 0.900 (±0.020) | 0.850 (±0.042) | 0.800 (±0.039) |
| Linear (Gaussian) | 400 | 2.0 | 50 | 0.950 (±0.032) | 0.900 (±0.035) | 0.850 (±0.029) |
| Linear (Gaussian) | 500 | 2.0 | 50 | 1.000 (±0.028) | 0.950 (±0.042) | 0.900 (±0.035) |
| Linear (Gaussian) | 100 | 0.25 | 100 | 0.838 (±0.036) | 0.788 (±0.028) | 0.738 (±0.038) |
| Linear (Gaussian) | 200 | 0.25 | 100 | 0.888 (±0.022) | 0.838 (±0.035) | 0.788 (±0.032) |
| Linear (Gaussian) | 300 | 0.25 | 100 | 0.938 (±0.022) | 0.888 (±0.034) | 0.838 (±0.043) |
| Linear (Gaussian) | 400 | 0.25 | 100 | 0.988 (±0.038) | 0.938 (±0.027) | 0.888 (±0.028) |
| Linear (Gaussian) | 500 | 0.25 | 100 | 1.000 (±0.040) | 0.950 (±0.035) | 0.900 (±0.043) |
| Linear (Gaussian) | 100 | 0.5 | 100 | 0.825 (±0.027) | 0.775 (±0.030) | 0.725 (±0.036) |
| Linear (Gaussian) | 200 | 0.5 | 100 | 0.875 (±0.019) | 0.825 (±0.034) | 0.775 (±0.026) |
| Linear (Gaussian) | 300 | 0.5 | 100 | 0.925 (±0.039) | 0.875 (±0.035) | 0.825 (±0.033) |
| Linear (Gaussian) | 400 | 0.5 | 100 | 0.975 (±0.025) | 0.925 (±0.042) | 0.875 (±0.029) |
| Linear (Gaussian) | 500 | 0.5 | 100 | 1.000 (±0.022) | 0.950 (±0.024) | 0.900 (±0.024) |
| Linear (Gaussian) | 100 | 0.75 | 100 | 0.813 (±0.027) | 0.763 (±0.026) | 0.713 (±0.025) |
| Linear (Gaussian) | 200 | 0.75 | 100 | 0.863 (±0.032) | 0.812 (±0.021) | 0.763 (±0.038) |
| Linear (Gaussian) | 300 | 0.75 | 100 | 0.913 (±0.024) | 0.863 (±0.030) | 0.813 (±0.041) |
| Linear (Gaussian) | 400 | 0.75 | 100 | 0.963 (±0.038) | 0.913 (±0.027) | 0.863 (±0.044) |
| Linear (Gaussian) | 500 | 0.75 | 100 | 1.000 (±0.033) | 0.950 (±0.037) | 0.900 (±0.021) |
| Linear (Gaussian) | 100 | 1.0 | 100 | 0.800 (±0.025) | 0.750 (±0.032) | 0.700 (±0.034) |
| Linear (Gaussian) | 200 | 1.0 | 100 | 0.850 (±0.032) | 0.800 (±0.043) | 0.750 (±0.035) |
| Linear (Gaussian) | 300 | 1.0 | 100 | 0.900 (±0.026) | 0.850 (±0.034) | 0.800 (±0.021) |
| Linear (Gaussian) | 400 | 1.0 | 100 | 0.950 (±0.022) | 0.900 (±0.030) | 0.850 (±0.025) |
| Linear (Gaussian) | 500 | 1.0 | 100 | 1.000 (±0.036) | 0.950 (±0.024) | 0.900 (±0.040) |
| Linear (Gaussian) | 100 | 1.5 | 100 | 0.775 (±0.029) | 0.725 (±0.037) | 0.675 (±0.024) |
| Linear (Gaussian) | 200 | 1.5 | 100 | 0.825 (±0.031) | 0.775 (±0.028) | 0.725 (±0.038) |
| Linear (Gaussian) | 300 | 1.5 | 100 | 0.875 (±0.025) | 0.825 (±0.044) | 0.775 (±0.044) |
| Linear (Gaussian) | 400 | 1.5 | 100 | 0.925 (±0.033) | 0.875 (±0.026) | 0.825 (±0.026) |
| Linear (Gaussian) | 500 | 1.5 | 100 | 0.975 (±0.030) | 0.925 (±0.027) | 0.875 (±0.033) |
| Linear (Gaussian) | 100 | 2.0 | 100 | 0.750 (±0.035) | 0.700 (±0.024) | 0.650 (±0.030) |
| Linear (Gaussian) | 200 | 2.0 | 100 | 0.800 (±0.027) | 0.750 (±0.042) | 0.700 (±0.043) |
| Linear (Gaussian) | 300 | 2.0 | 100 | 0.850 (±0.037) | 0.800 (±0.037) | 0.750 (±0.044) |
| Linear (Gaussian) | 400 | 2.0 | 100 | 0.900 (±0.028) | 0.850 (±0.034) | 0.800 (±0.028) |
| Linear (Gaussian) | 500 | 2.0 | 100 | 0.950 (±0.024) | 0.900 (±0.021) | 0.850 (±0.033) |
| Linear (Gaussian) | 100 | 0.25 | 200 | 0.738 (±0.037) | 0.688 (±0.020) | 0.638 (±0.022) |
| Linear (Gaussian) | 200 | 0.25 | 200 | 0.787 (±0.019) | 0.737 (±0.039) | 0.688 (±0.038) |
| Linear (Gaussian) | 300 | 0.25 | 200 | 0.838 (±0.039) | 0.787 (±0.032) | 0.738 (±0.022) |
| Linear (Gaussian) | 400 | 0.25 | 200 | 0.887 (±0.031) | 0.837 (±0.039) | 0.787 (±0.023) |
| Linear (Gaussian) | 500 | 0.25 | 200 | 0.938 (±0.025) | 0.887 (±0.026) | 0.838 (±0.021) |
| Linear (Gaussian) | 100 | 0.5 | 200 | 0.725 (±0.025) | 0.675 (±0.022) | 0.625 (±0.026) |
| Linear (Gaussian) | 200 | 0.5 | 200 | 0.775 (±0.016) | 0.725 (±0.037) | 0.675 (±0.027) |
| Linear (Gaussian) | 300 | 0.5 | 200 | 0.825 (±0.018) | 0.775 (±0.022) | 0.725 (±0.042) |
| Linear (Gaussian) | 400 | 0.5 | 200 | 0.875 (±0.034) | 0.825 (±0.040) | 0.775 (±0.045) |
| Linear (Gaussian) | 500 | 0.5 | 200 | 0.925 (±0.018) | 0.875 (±0.022) | 0.825 (±0.040) |
| Linear (Gaussian) | 100 | 0.75 | 200 | 0.713 (±0.035) | 0.662 (±0.020) | 0.613 (±0.039) |
| Linear (Gaussian) | 200 | 0.75 | 200 | 0.762 (±0.033) | 0.712 (±0.036) | 0.662 (±0.032) |
| Linear (Gaussian) | 300 | 0.75 | 200 | 0.812 (±0.019) | 0.762 (±0.020) | 0.713 (±0.031) |
| Linear (Gaussian) | 400 | 0.75 | 200 | 0.863 (±0.027) | 0.812 (±0.030) | 0.763 (±0.032) |
| Linear (Gaussian) | 500 | 0.75 | 200 | 0.912 (±0.033) | 0.862 (±0.021) | 0.812 (±0.029) |
| Linear (Gaussian) | 100 | 1.0 | 200 | 0.700 (±0.035) | 0.650 (±0.041) | 0.600 (±0.026) |
| Linear (Gaussian) | 200 | 1.0 | 200 | 0.750 (±0.024) | 0.700 (±0.041) | 0.650 (±0.041) |
| Linear (Gaussian) | 300 | 1.0 | 200 | 0.800 (±0.022) | 0.750 (±0.024) | 0.700 (±0.038) |
| Linear (Gaussian) | 400 | 1.0 | 200 | 0.850 (±0.018) | 0.800 (±0.021) | 0.750 (±0.045) |
| Linear (Gaussian) | 500 | 1.0 | 200 | 0.900 (±0.016) | 0.850 (±0.028) | 0.800 (±0.043) |
| Linear (Gaussian) | 100 | 1.5 | 200 | 0.675 (±0.030) | 0.625 (±0.027) | 0.575 (±0.038) |
| Linear (Gaussian) | 200 | 1.5 | 200 | 0.725 (±0.036) | 0.675 (±0.028) | 0.625 (±0.032) |
| Linear (Gaussian) | 300 | 1.5 | 200 | 0.775 (±0.032) | 0.725 (±0.036) | 0.675 (±0.036) |
| Linear (Gaussian) | 400 | 1.5 | 200 | 0.825 (±0.039) | 0.775 (±0.030) | 0.725 (±0.023) |
| Linear (Gaussian) | 500 | 1.5 | 200 | 0.875 (±0.028) | 0.825 (±0.026) | 0.775 (±0.032) |
| Linear (Gaussian) | 100 | 2.0 | 200 | 0.650 (±0.024) | 0.600 (±0.045) | 0.550 (±0.030) |
| Linear (Gaussian) | 200 | 2.0 | 200 | 0.700 (±0.021) | 0.650 (±0.036) | 0.600 (±0.023) |
| Linear (Gaussian) | 300 | 2.0 | 200 | 0.750 (±0.039) | 0.700 (±0.033) | 0.650 (±0.024) |
| Linear (Gaussian) | 400 | 2.0 | 200 | 0.800 (±0.031) | 0.750 (±0.045) | 0.700 (±0.037) |
| Linear (Gaussian) | 500 | 2.0 | 200 | 0.850 (±0.025) | 0.800 (±0.028) | 0.750 (±0.041) |
| Linear (Gaussian) | 100 | 0.25 | 300 | 0.638 (±0.019) | 0.588 (±0.025) | 0.538 (±0.042) |
| Linear (Gaussian) | 200 | 0.25 | 300 | 0.688 (±0.023) | 0.638 (±0.029) | 0.588 (±0.040) |
| Linear (Gaussian) | 300 | 0.25 | 300 | 0.738 (±0.020) | 0.688 (±0.020) | 0.638 (±0.030) |
| Linear (Gaussian) | 400 | 0.25 | 300 | 0.788 (±0.027) | 0.738 (±0.031) | 0.688 (±0.029) |
| Linear (Gaussian) | 500 | 0.25 | 300 | 0.838 (±0.037) | 0.788 (±0.031) | 0.738 (±0.033) |
| Linear (Gaussian) | 100 | 0.5 | 300 | 0.625 (±0.039) | 0.575 (±0.039) | 0.525 (±0.025) |
| Linear (Gaussian) | 200 | 0.5 | 300 | 0.675 (±0.023) | 0.625 (±0.044) | 0.575 (±0.035) |
| Linear (Gaussian) | 300 | 0.5 | 300 | 0.725 (±0.034) | 0.675 (±0.029) | 0.625 (±0.039) |
| Linear (Gaussian) | 400 | 0.5 | 300 | 0.775 (±0.028) | 0.725 (±0.043) | 0.675 (±0.025) |
| Linear (Gaussian) | 500 | 0.5 | 300 | 0.825 (±0.022) | 0.775 (±0.022) | 0.725 (±0.025) |
| Linear (Gaussian) | 100 | 0.75 | 300 | 0.613 (±0.039) | 0.563 (±0.027) | 0.513 (±0.038) |
| Linear (Gaussian) | 200 | 0.75 | 300 | 0.663 (±0.035) | 0.613 (±0.023) | 0.563 (±0.026) |
| Linear (Gaussian) | 300 | 0.75 | 300 | 0.713 (±0.022) | 0.663 (±0.023) | 0.613 (±0.023) |
| Linear (Gaussian) | 400 | 0.75 | 300 | 0.763 (±0.040) | 0.713 (±0.045) | 0.663 (±0.023) |
| Linear (Gaussian) | 500 | 0.75 | 300 | 0.813 (±0.038) | 0.763 (±0.034) | 0.713 (±0.030) |
| Linear (Gaussian) | 100 | 1.0 | 300 | 0.600 (±0.026) | 0.550 (±0.038) | 0.500 (±0.022) |
| Linear (Gaussian) | 200 | 1.0 | 300 | 0.650 (±0.023) | 0.600 (±0.037) | 0.550 (±0.028) |
| Linear (Gaussian) | 300 | 1.0 | 300 | 0.700 (±0.036) | 0.650 (±0.025) | 0.600 (±0.032) |
| Linear (Gaussian) | 400 | 1.0 | 300 | 0.750 (±0.022) | 0.700 (±0.025) | 0.650 (±0.044) |
| Linear (Gaussian) | 500 | 1.0 | 300 | 0.800 (±0.023) | 0.750 (±0.032) | 0.700 (±0.021) |
| Linear (Gaussian) | 100 | 1.5 | 300 | 0.575 (±0.029) | 0.525 (±0.036) | 0.475 (±0.035) |
| Linear (Gaussian) | 200 | 1.5 | 300 | 0.625 (±0.023) | 0.575 (±0.042) | 0.525 (±0.036) |
| Linear (Gaussian) | 300 | 1.5 | 300 | 0.675 (±0.023) | 0.625 (±0.030) | 0.575 (±0.024) |
| Linear (Gaussian) | 400 | 1.5 | 300 | 0.725 (±0.037) | 0.675 (±0.044) | 0.625 (±0.034) |
| Linear (Gaussian) | 500 | 1.5 | 300 | 0.775 (±0.023) | 0.725 (±0.045) | 0.675 (±0.026) |
| Linear (Gaussian) | 100 | 2.0 | 300 | 0.550 (±0.030) | 0.500 (±0.023) | 0.450 (±0.032) |
| Linear (Gaussian) | 200 | 2.0 | 300 | 0.600 (±0.017) | 0.550 (±0.024) | 0.500 (±0.027) |
| Linear (Gaussian) | 300 | 2.0 | 300 | 0.650 (±0.030) | 0.600 (±0.038) | 0.550 (±0.024) |
| Linear (Gaussian) | 400 | 2.0 | 300 | 0.700 (±0.037) | 0.650 (±0.038) | 0.600 (±0.039) |
| Linear (Gaussian) | 500 | 2.0 | 300 | 0.750 (±0.019) | 0.700 (±0.029) | 0.650 (±0.037) |
| Linear (Gaussian) | 100 | 0.25 | 400 | 0.537 (±0.028) | 0.488 (±0.029) | 0.438 (±0.026) |
| Linear (Gaussian) | 200 | 0.25 | 400 | 0.588 (±0.016) | 0.537 (±0.026) | 0.488 (±0.042) |
| Linear (Gaussian) | 300 | 0.25 | 400 | 0.637 (±0.035) | 0.587 (±0.039) | 0.537 (±0.024) |
| Linear (Gaussian) | 400 | 0.25 | 400 | 0.688 (±0.018) | 0.637 (±0.044) | 0.588 (±0.031) |
| Linear (Gaussian) | 500 | 0.25 | 400 | 0.738 (±0.027) | 0.688 (±0.024) | 0.638 (±0.035) |
| Linear (Gaussian) | 100 | 0.5 | 400 | 0.525 (±0.022) | 0.475 (±0.026) | 0.425 (±0.037) |
| Linear (Gaussian) | 200 | 0.5 | 400 | 0.575 (±0.022) | 0.525 (±0.040) | 0.475 (±0.022) |
| Linear (Gaussian) | 300 | 0.5 | 400 | 0.625 (±0.036) | 0.575 (±0.031) | 0.525 (±0.039) |
| Linear (Gaussian) | 400 | 0.5 | 400 | 0.675 (±0.032) | 0.625 (±0.031) | 0.575 (±0.036) |
| Linear (Gaussian) | 500 | 0.5 | 400 | 0.725 (±0.015) | 0.675 (±0.025) | 0.625 (±0.038) |
| Linear (Gaussian) | 100 | 0.75 | 400 | 0.513 (±0.020) | 0.463 (±0.040) | 0.413 (±0.028) |
| Linear (Gaussian) | 200 | 0.75 | 400 | 0.562 (±0.032) | 0.512 (±0.043) | 0.462 (±0.023) |
| Linear (Gaussian) | 300 | 0.75 | 400 | 0.613 (±0.018) | 0.562 (±0.037) | 0.513 (±0.031) |
| Linear (Gaussian) | 400 | 0.75 | 400 | 0.663 (±0.036) | 0.613 (±0.044) | 0.563 (±0.022) |
| Linear (Gaussian) | 500 | 0.75 | 400 | 0.713 (±0.026) | 0.662 (±0.038) | 0.613 (±0.022) |
| Linear (Gaussian) | 100 | 1.0 | 400 | 0.500 (±0.040) | 0.450 (±0.026) | 0.400 (±0.021) |
| Linear (Gaussian) | 200 | 1.0 | 400 | 0.550 (±0.032) | 0.500 (±0.040) | 0.450 (±0.029) |
| Linear (Gaussian) | 300 | 1.0 | 400 | 0.600 (±0.024) | 0.550 (±0.027) | 0.500 (±0.022) |
| Linear (Gaussian) | 400 | 1.0 | 400 | 0.650 (±0.024) | 0.600 (±0.024) | 0.550 (±0.033) |
| Linear (Gaussian) | 500 | 1.0 | 400 | 0.700 (±0.028) | 0.650 (±0.044) | 0.600 (±0.029) |
| Linear (Gaussian) | 100 | 1.5 | 400 | 0.475 (±0.027) | 0.425 (±0.022) | 0.375 (±0.042) |
| Linear (Gaussian) | 200 | 1.5 | 400 | 0.525 (±0.025) | 0.475 (±0.038) | 0.425 (±0.024) |
| Linear (Gaussian) | 300 | 1.5 | 400 | 0.575 (±0.026) | 0.525 (±0.039) | 0.475 (±0.022) |
| Linear (Gaussian) | 400 | 1.5 | 400 | 0.625 (±0.035) | 0.575 (±0.028) | 0.525 (±0.029) |
| Linear (Gaussian) | 500 | 1.5 | 400 | 0.675 (±0.023) | 0.625 (±0.021) | 0.575 (±0.033) |
| Linear (Gaussian) | 100 | 2.0 | 400 | 0.450 (±0.032) | 0.400 (±0.043) | 0.350 (±0.021) |
| Linear (Gaussian) | 200 | 2.0 | 400 | 0.500 (±0.040) | 0.450 (±0.028) | 0.400 (±0.043) |
| Linear (Gaussian) | 300 | 2.0 | 400 | 0.550 (±0.032) | 0.500 (±0.031) | 0.450 (±0.040) |
| Linear (Gaussian) | 400 | 2.0 | 400 | 0.600 (±0.016) | 0.550 (±0.038) | 0.500 (±0.029) |
| Linear (Gaussian) | 500 | 2.0 | 400 | 0.650 (±0.036) | 0.600 (±0.033) | 0.550 (±0.027) |
| Linear (Student-t mixture) | 100 | 0.25 | 20 | 0.918 (±0.035) | 0.858 (±0.022) | 0.798 (±0.041) |
| Linear (Student-t mixture) | 200 | 0.25 | 20 | 0.968 (±0.022) | 0.907 (±0.039) | 0.848 (±0.044) |
| Linear (Student-t mixture) | 300 | 0.25 | 20 | 1.000 (±0.017) | 0.940 (±0.041) | 0.880 (±0.040) |
| Linear (Student-t mixture) | 400 | 0.25 | 20 | 1.000 (±0.025) | 0.940 (±0.028) | 0.880 (±0.025) |
| Linear (Student-t mixture) | 500 | 0.25 | 20 | 1.000 (±0.029) | 0.940 (±0.042) | 0.880 (±0.033) |
| Linear (Student-t mixture) | 100 | 0.5 | 20 | 0.905 (±0.030) | 0.845 (±0.037) | 0.785 (±0.033) |
| Linear (Student-t mixture) | 200 | 0.5 | 20 | 0.955 (±0.028) | 0.895 (±0.020) | 0.835 (±0.021) |
| Linear (Student-t mixture) | 300 | 0.5 | 20 | 1.000 (±0.038) | 0.940 (±0.039) | 0.880 (±0.025) |
| Linear (Student-t mixture) | 400 | 0.5 | 20 | 1.000 (±0.031) | 0.940 (±0.036) | 0.880 (±0.030) |
| Linear (Student-t mixture) | 500 | 0.5 | 20 | 1.000 (±0.035) | 0.940 (±0.034) | 0.880 (±0.042) |
| Linear (Student-t mixture) | 100 | 0.75 | 20 | 0.893 (±0.029) | 0.833 (±0.043) | 0.773 (±0.035) |
| Linear (Student-t mixture) | 200 | 0.75 | 20 | 0.943 (±0.026) | 0.883 (±0.044) | 0.823 (±0.038) |
| Linear (Student-t mixture) | 300 | 0.75 | 20 | 0.993 (±0.025) | 0.933 (±0.020) | 0.873 (±0.034) |
| Linear (Student-t mixture) | 400 | 0.75 | 20 | 1.000 (±0.027) | 0.940 (±0.042) | 0.880 (±0.040) |
| Linear (Student-t mixture) | 500 | 0.75 | 20 | 1.000 (±0.036) | 0.940 (±0.029) | 0.880 (±0.042) |
| Linear (Student-t mixture) | 100 | 1.0 | 20 | 0.880 (±0.019) | 0.820 (±0.027) | 0.760 (±0.037) |
| Linear (Student-t mixture) | 200 | 1.0 | 20 | 0.930 (±0.039) | 0.870 (±0.035) | 0.810 (±0.033) |
| Linear (Student-t mixture) | 300 | 1.0 | 20 | 0.980 (±0.017) | 0.920 (±0.044) | 0.860 (±0.023) |
| Linear (Student-t mixture) | 400 | 1.0 | 20 | 1.000 (±0.017) | 0.940 (±0.042) | 0.880 (±0.033) |
| Linear (Student-t mixture) | 500 | 1.0 | 20 | 1.000 (±0.023) | 0.940 (±0.042) | 0.880 (±0.021) |
| Linear (Student-t mixture) | 100 | 1.5 | 20 | 0.835 (±0.021) | 0.795 (±0.037) | 0.735 (±0.026) |
| Linear (Student-t mixture) | 200 | 1.5 | 20 | 0.885 (±0.023) | 0.845 (±0.024) | 0.785 (±0.040) |
| Linear (Student-t mixture) | 300 | 1.5 | 20 | 0.935 (±0.019) | 0.895 (±0.041) | 0.835 (±0.028) |
| Linear (Student-t mixture) | 400 | 1.5 | 20 | 0.980 (±0.024) | 0.940 (±0.036) | 0.880 (±0.022) |
| Linear (Student-t mixture) | 500 | 1.5 | 20 | 0.980 (±0.016) | 0.940 (±0.045) | 0.880 (±0.035) |
| Linear (Student-t mixture) | 100 | 2.0 | 20 | 0.810 (±0.035) | 0.770 (±0.042) | 0.710 (±0.039) |
| Linear (Student-t mixture) | 200 | 2.0 | 20 | 0.860 (±0.039) | 0.820 (±0.021) | 0.760 (±0.043) |
| Linear (Student-t mixture) | 300 | 2.0 | 20 | 0.910 (±0.037) | 0.870 (±0.039) | 0.810 (±0.029) |
| Linear (Student-t mixture) | 400 | 2.0 | 20 | 0.960 (±0.016) | 0.920 (±0.029) | 0.860 (±0.027) |
| Linear (Student-t mixture) | 500 | 2.0 | 20 | 0.980 (±0.036) | 0.940 (±0.029) | 0.880 (±0.028) |
| Linear (Student-t mixture) | 100 | 0.25 | 50 | 0.888 (±0.034) | 0.828 (±0.041) | 0.768 (±0.031) |
| Linear (Student-t mixture) | 200 | 0.25 | 50 | 0.938 (±0.033) | 0.877 (±0.023) | 0.818 (±0.025) |
| Linear (Student-t mixture) | 300 | 0.25 | 50 | 0.988 (±0.039) | 0.927 (±0.039) | 0.868 (±0.040) |
| Linear (Student-t mixture) | 400 | 0.25 | 50 | 1.000 (±0.025) | 0.940 (±0.035) | 0.880 (±0.040) |
| Linear (Student-t mixture) | 500 | 0.25 | 50 | 1.000 (±0.037) | 0.940 (±0.030) | 0.880 (±0.022) |
| Linear (Student-t mixture) | 100 | 0.5 | 50 | 0.875 (±0.031) | 0.815 (±0.039) | 0.755 (±0.022) |
| Linear (Student-t mixture) | 200 | 0.5 | 50 | 0.925 (±0.023) | 0.865 (±0.035) | 0.805 (±0.039) |
| Linear (Student-t mixture) | 300 | 0.5 | 50 | 0.975 (±0.038) | 0.915 (±0.032) | 0.855 (±0.034) |
| Linear (Student-t mixture) | 400 | 0.5 | 50 | 1.000 (±0.033) | 0.940 (±0.041) | 0.880 (±0.043) |
| Linear (Student-t mixture) | 500 | 0.5 | 50 | 1.000 (±0.016) | 0.940 (±0.033) | 0.880 (±0.029) |
| Linear (Student-t mixture) | 100 | 0.75 | 50 | 0.863 (±0.036) | 0.802 (±0.040) | 0.743 (±0.023) |
| Linear (Student-t mixture) | 200 | 0.75 | 50 | 0.912 (±0.033) | 0.853 (±0.026) | 0.792 (±0.022) |
| Linear (Student-t mixture) | 300 | 0.75 | 50 | 0.963 (±0.038) | 0.903 (±0.024) | 0.843 (±0.036) |
| Linear (Student-t mixture) | 400 | 0.75 | 50 | 1.000 (±0.019) | 0.940 (±0.021) | 0.880 (±0.033) |
| Linear (Student-t mixture) | 500 | 0.75 | 50 | 1.000 (±0.017) | 0.940 (±0.027) | 0.880 (±0.031) |
| Linear (Student-t mixture) | 100 | 1.0 | 50 | 0.850 (±0.030) | 0.790 (±0.040) | 0.730 (±0.025) |
| Linear (Student-t mixture) | 200 | 1.0 | 50 | 0.900 (±0.026) | 0.840 (±0.031) | 0.780 (±0.038) |
| Linear (Student-t mixture) | 300 | 1.0 | 50 | 0.950 (±0.033) | 0.890 (±0.041) | 0.830 (±0.042) |
| Linear (Student-t mixture) | 400 | 1.0 | 50 | 1.000 (±0.039) | 0.940 (±0.034) | 0.880 (±0.033) |
| Linear (Student-t mixture) | 500 | 1.0 | 50 | 1.000 (±0.019) | 0.940 (±0.032) | 0.880 (±0.026) |
| Linear (Student-t mixture) | 100 | 1.5 | 50 | 0.805 (±0.016) | 0.765 (±0.036) | 0.705 (±0.033) |
| Linear (Student-t mixture) | 200 | 1.5 | 50 | 0.855 (±0.019) | 0.815 (±0.027) | 0.755 (±0.035) |
| Linear (Student-t mixture) | 300 | 1.5 | 50 | 0.905 (±0.019) | 0.865 (±0.022) | 0.805 (±0.031) |
| Linear (Student-t mixture) | 400 | 1.5 | 50 | 0.955 (±0.024) | 0.915 (±0.041) | 0.855 (±0.027) |
| Linear (Student-t mixture) | 500 | 1.5 | 50 | 0.980 (±0.016) | 0.940 (±0.042) | 0.880 (±0.028) |
| Linear (Student-t mixture) | 100 | 2.0 | 50 | 0.780 (±0.031) | 0.740 (±0.034) | 0.680 (±0.029) |
| Linear (Student-t mixture) | 200 | 2.0 | 50 | 0.830 (±0.020) | 0.790 (±0.031) | 0.730 (±0.036) |
| Linear (Student-t mixture) | 300 | 2.0 | 50 | 0.880 (±0.028) | 0.840 (±0.036) | 0.780 (±0.038) |
| Linear (Student-t mixture) | 400 | 2.0 | 50 | 0.930 (±0.027) | 0.890 (±0.030) | 0.830 (±0.020) |
| Linear (Student-t mixture) | 500 | 2.0 | 50 | 0.980 (±0.015) | 0.940 (±0.045) | 0.880 (±0.023) |
| Linear (Student-t mixture) | 100 | 0.25 | 100 | 0.838 (±0.025) | 0.778 (±0.038) | 0.718 (±0.039) |
| Linear (Student-t mixture) | 200 | 0.25 | 100 | 0.888 (±0.037) | 0.828 (±0.035) | 0.768 (±0.039) |
| Linear (Student-t mixture) | 300 | 0.25 | 100 | 0.938 (±0.036) | 0.878 (±0.035) | 0.818 (±0.040) |
| Linear (Student-t mixture) | 400 | 0.25 | 100 | 0.988 (±0.016) | 0.927 (±0.030) | 0.868 (±0.042) |
| Linear (Student-t mixture) | 500 | 0.25 | 100 | 1.000 (±0.031) | 0.940 (±0.043) | 0.880 (±0.024) |
| Linear (Student-t mixture) | 100 | 0.5 | 100 | 0.825 (±0.023) | 0.765 (±0.040) | 0.705 (±0.045) |
| Linear (Student-t mixture) | 200 | 0.5 | 100 | 0.875 (±0.023) | 0.815 (±0.020) | 0.755 (±0.045) |
| Linear (Student-t mixture) | 300 | 0.5 | 100 | 0.925 (±0.019) | 0.865 (±0.021) | 0.805 (±0.035) |
| Linear (Student-t mixture) | 400 | 0.5 | 100 | 0.975 (±0.023) | 0.915 (±0.033) | 0.855 (±0.040) |
| Linear (Student-t mixture) | 500 | 0.5 | 100 | 1.000 (±0.017) | 0.940 (±0.037) | 0.880 (±0.044) |
| Linear (Student-t mixture) | 100 | 0.75 | 100 | 0.813 (±0.022) | 0.753 (±0.026) | 0.693 (±0.024) |
| Linear (Student-t mixture) | 200 | 0.75 | 100 | 0.863 (±0.017) | 0.802 (±0.034) | 0.743 (±0.032) |
| Linear (Student-t mixture) | 300 | 0.75 | 100 | 0.913 (±0.027) | 0.853 (±0.042) | 0.793 (±0.021) |
| Linear (Student-t mixture) | 400 | 0.75 | 100 | 0.963 (±0.020) | 0.903 (±0.033) | 0.843 (±0.026) |
| Linear (Student-t mixture) | 500 | 0.75 | 100 | 1.000 (±0.029) | 0.940 (±0.032) | 0.880 (±0.034) |
| Linear (Student-t mixture) | 100 | 1.0 | 100 | 0.800 (±0.019) | 0.740 (±0.024) | 0.680 (±0.030) |
| Linear (Student-t mixture) | 200 | 1.0 | 100 | 0.850 (±0.032) | 0.790 (±0.036) | 0.730 (±0.043) |
| Linear (Student-t mixture) | 300 | 1.0 | 100 | 0.900 (±0.035) | 0.840 (±0.037) | 0.780 (±0.040) |
| Linear (Student-t mixture) | 400 | 1.0 | 100 | 0.950 (±0.018) | 0.890 (±0.026) | 0.830 (±0.028) |
| Linear (Student-t mixture) | 500 | 1.0 | 100 | 1.000 (±0.025) | 0.940 (±0.036) | 0.880 (±0.040) |
| Linear (Student-t mixture) | 100 | 1.5 | 100 | 0.755 (±0.021) | 0.715 (±0.040) | 0.655 (±0.020) |
| Linear (Student-t mixture) | 200 | 1.5 | 100 | 0.805 (±0.031) | 0.765 (±0.040) | 0.705 (±0.032) |
| Linear (Student-t mixture) | 300 | 1.5 | 100 | 0.855 (±0.020) | 0.815 (±0.020) | 0.755 (±0.027) |
| Linear (Student-t mixture) | 400 | 1.5 | 100 | 0.905 (±0.038) | 0.865 (±0.043) | 0.805 (±0.034) |
| Linear (Student-t mixture) | 500 | 1.5 | 100 | 0.955 (±0.020) | 0.915 (±0.032) | 0.855 (±0.040) |
| Linear (Student-t mixture) | 100 | 2.0 | 100 | 0.730 (±0.025) | 0.690 (±0.023) | 0.630 (±0.027) |
| Linear (Student-t mixture) | 200 | 2.0 | 100 | 0.780 (±0.024) | 0.740 (±0.026) | 0.680 (±0.032) |
| Linear (Student-t mixture) | 300 | 2.0 | 100 | 0.830 (±0.024) | 0.790 (±0.023) | 0.730 (±0.021) |
| Linear (Student-t mixture) | 400 | 2.0 | 100 | 0.880 (±0.022) | 0.840 (±0.044) | 0.780 (±0.032) |
| Linear (Student-t mixture) | 500 | 2.0 | 100 | 0.930 (±0.027) | 0.890 (±0.039) | 0.830 (±0.037) |
| Linear (Student-t mixture) | 100 | 0.25 | 200 | 0.738 (±0.016) | 0.677 (±0.037) | 0.618 (±0.029) |
| Linear (Student-t mixture) | 200 | 0.25 | 200 | 0.787 (±0.037) | 0.728 (±0.039) | 0.667 (±0.023) |
| Linear (Student-t mixture) | 300 | 0.25 | 200 | 0.838 (±0.022) | 0.778 (±0.023) | 0.718 (±0.035) |
| Linear (Student-t mixture) | 400 | 0.25 | 200 | 0.887 (±0.029) | 0.827 (±0.037) | 0.767 (±0.028) |
| Linear (Student-t mixture) | 500 | 0.25 | 200 | 0.938 (±0.030) | 0.877 (±0.045) | 0.818 (±0.039) |
| Linear (Student-t mixture) | 100 | 0.5 | 200 | 0.725 (±0.017) | 0.665 (±0.031) | 0.605 (±0.021) |
| Linear (Student-t mixture) | 200 | 0.5 | 200 | 0.775 (±0.023) | 0.715 (±0.038) | 0.655 (±0.020) |
| Linear (Student-t mixture) | 300 | 0.5 | 200 | 0.825 (±0.034) | 0.765 (±0.032) | 0.705 (±0.038) |
| Linear (Student-t mixture) | 400 | 0.5 | 200 | 0.875 (±0.032) | 0.815 (±0.034) | 0.755 (±0.038) |
| Linear (Student-t mixture) | 500 | 0.5 | 200 | 0.925 (±0.031) | 0.865 (±0.027) | 0.805 (±0.022) |
| Linear (Student-t mixture) | 100 | 0.75 | 200 | 0.713 (±0.039) | 0.653 (±0.038) | 0.593 (±0.035) |
| Linear (Student-t mixture) | 200 | 0.75 | 200 | 0.762 (±0.018) | 0.702 (±0.034) | 0.642 (±0.027) |
| Linear (Student-t mixture) | 300 | 0.75 | 200 | 0.812 (±0.037) | 0.752 (±0.020) | 0.693 (±0.026) |
| Linear (Student-t mixture) | 400 | 0.75 | 200 | 0.863 (±0.018) | 0.802 (±0.028) | 0.743 (±0.038) |
| Linear (Student-t mixture) | 500 | 0.75 | 200 | 0.912 (±0.040) | 0.853 (±0.038) | 0.792 (±0.033) |
| Linear (Student-t mixture) | 100 | 1.0 | 200 | 0.700 (±0.026) | 0.640 (±0.044) | 0.580 (±0.023) |
| Linear (Student-t mixture) | 200 | 1.0 | 200 | 0.750 (±0.017) | 0.690 (±0.042) | 0.630 (±0.031) |
| Linear (Student-t mixture) | 300 | 1.0 | 200 | 0.800 (±0.016) | 0.740 (±0.036) | 0.680 (±0.032) |
| Linear (Student-t mixture) | 400 | 1.0 | 200 | 0.850 (±0.030) | 0.790 (±0.027) | 0.730 (±0.024) |
| Linear (Student-t mixture) | 500 | 1.0 | 200 | 0.900 (±0.018) | 0.840 (±0.033) | 0.780 (±0.034) |
| Linear (Student-t mixture) | 100 | 1.5 | 200 | 0.655 (±0.019) | 0.615 (±0.024) | 0.555 (±0.039) |
| Linear (Student-t mixture) | 200 | 1.5 | 200 | 0.705 (±0.028) | 0.665 (±0.042) | 0.605 (±0.037) |
| Linear (Student-t mixture) | 300 | 1.5 | 200 | 0.755 (±0.015) | 0.715 (±0.037) | 0.655 (±0.042) |
| Linear (Student-t mixture) | 400 | 1.5 | 200 | 0.805 (±0.031) | 0.765 (±0.023) | 0.705 (±0.043) |
| Linear (Student-t mixture) | 500 | 1.5 | 200 | 0.855 (±0.032) | 0.815 (±0.024) | 0.755 (±0.039) |
| Linear (Student-t mixture) | 100 | 2.0 | 200 | 0.630 (±0.039) | 0.590 (±0.031) | 0.530 (±0.027) |
| Linear (Student-t mixture) | 200 | 2.0 | 200 | 0.680 (±0.021) | 0.640 (±0.026) | 0.580 (±0.034) |
| Linear (Student-t mixture) | 300 | 2.0 | 200 | 0.730 (±0.034) | 0.690 (±0.037) | 0.630 (±0.034) |
| Linear (Student-t mixture) | 400 | 2.0 | 200 | 0.780 (±0.035) | 0.740 (±0.039) | 0.680 (±0.021) |
| Linear (Student-t mixture) | 500 | 2.0 | 200 | 0.830 (±0.025) | 0.790 (±0.021) | 0.730 (±0.040) |
| Linear (Student-t mixture) | 100 | 0.25 | 300 | 0.638 (±0.038) | 0.578 (±0.034) | 0.518 (±0.041) |
| Linear (Student-t mixture) | 200 | 0.25 | 300 | 0.688 (±0.030) | 0.628 (±0.037) | 0.568 (±0.033) |
| Linear (Student-t mixture) | 300 | 0.25 | 300 | 0.738 (±0.034) | 0.678 (±0.043) | 0.618 (±0.041) |
| Linear (Student-t mixture) | 400 | 0.25 | 300 | 0.788 (±0.017) | 0.728 (±0.020) | 0.668 (±0.021) |
| Linear (Student-t mixture) | 500 | 0.25 | 300 | 0.838 (±0.037) | 0.778 (±0.034) | 0.718 (±0.028) |
| Linear (Student-t mixture) | 100 | 0.5 | 300 | 0.625 (±0.039) | 0.565 (±0.035) | 0.505 (±0.033) |
| Linear (Student-t mixture) | 200 | 0.5 | 300 | 0.675 (±0.025) | 0.615 (±0.028) | 0.555 (±0.040) |
| Linear (Student-t mixture) | 300 | 0.5 | 300 | 0.725 (±0.016) | 0.665 (±0.029) | 0.605 (±0.041) |
| Linear (Student-t mixture) | 400 | 0.5 | 300 | 0.775 (±0.032) | 0.715 (±0.037) | 0.655 (±0.029) |
| Linear (Student-t mixture) | 500 | 0.5 | 300 | 0.825 (±0.029) | 0.765 (±0.023) | 0.705 (±0.040) |
| Linear (Student-t mixture) | 100 | 0.75 | 300 | 0.613 (±0.037) | 0.553 (±0.025) | 0.493 (±0.039) |
| Linear (Student-t mixture) | 200 | 0.75 | 300 | 0.663 (±0.030) | 0.603 (±0.044) | 0.543 (±0.024) |
| Linear (Student-t mixture) | 300 | 0.75 | 300 | 0.713 (±0.028) | 0.653 (±0.042) | 0.593 (±0.042) |
| Linear (Student-t mixture) | 400 | 0.75 | 300 | 0.763 (±0.016) | 0.703 (±0.044) | 0.643 (±0.032) |
| Linear (Student-t mixture) | 500 | 0.75 | 300 | 0.813 (±0.025) | 0.753 (±0.030) | 0.693 (±0.022) |
| Linear (Student-t mixture) | 100 | 1.0 | 300 | 0.600 (±0.019) | 0.540 (±0.030) | 0.480 (±0.029) |
| Linear (Student-t mixture) | 200 | 1.0 | 300 | 0.650 (±0.025) | 0.590 (±0.028) | 0.530 (±0.034) |
| Linear (Student-t mixture) | 300 | 1.0 | 300 | 0.700 (±0.019) | 0.640 (±0.044) | 0.580 (±0.021) |
| Linear (Student-t mixture) | 400 | 1.0 | 300 | 0.750 (±0.024) | 0.690 (±0.044) | 0.630 (±0.036) |
| Linear (Student-t mixture) | 500 | 1.0 | 300 | 0.800 (±0.017) | 0.740 (±0.030) | 0.680 (±0.031) |
| Linear (Student-t mixture) | 100 | 1.5 | 300 | 0.555 (±0.028) | 0.515 (±0.031) | 0.455 (±0.036) |
| Linear (Student-t mixture) | 200 | 1.5 | 300 | 0.605 (±0.018) | 0.565 (±0.043) | 0.505 (±0.034) |
| Linear (Student-t mixture) | 300 | 1.5 | 300 | 0.655 (±0.029) | 0.615 (±0.023) | 0.555 (±0.039) |
| Linear (Student-t mixture) | 400 | 1.5 | 300 | 0.705 (±0.027) | 0.665 (±0.040) | 0.605 (±0.021) |
| Linear (Student-t mixture) | 500 | 1.5 | 300 | 0.755 (±0.035) | 0.715 (±0.027) | 0.655 (±0.027) |
| Linear (Student-t mixture) | 100 | 2.0 | 300 | 0.530 (±0.031) | 0.490 (±0.044) | 0.430 (±0.020) |
| Linear (Student-t mixture) | 200 | 2.0 | 300 | 0.580 (±0.024) | 0.540 (±0.030) | 0.480 (±0.031) |
| Linear (Student-t mixture) | 300 | 2.0 | 300 | 0.630 (±0.033) | 0.590 (±0.043) | 0.530 (±0.036) |
| Linear (Student-t mixture) | 400 | 2.0 | 300 | 0.680 (±0.038) | 0.640 (±0.039) | 0.580 (±0.023) |
| Linear (Student-t mixture) | 500 | 2.0 | 300 | 0.730 (±0.019) | 0.690 (±0.025) | 0.630 (±0.031) |
| Linear (Student-t mixture) | 100 | 0.25 | 400 | 0.537 (±0.017) | 0.478 (±0.026) | 0.418 (±0.034) |
| Linear (Student-t mixture) | 200 | 0.25 | 400 | 0.588 (±0.025) | 0.528 (±0.034) | 0.468 (±0.041) |
| Linear (Student-t mixture) | 300 | 0.25 | 400 | 0.637 (±0.031) | 0.577 (±0.030) | 0.517 (±0.038) |
| Linear (Student-t mixture) | 400 | 0.25 | 400 | 0.688 (±0.018) | 0.627 (±0.027) | 0.568 (±0.035) |
| Linear (Student-t mixture) | 500 | 0.25 | 400 | 0.738 (±0.019) | 0.677 (±0.041) | 0.618 (±0.041) |
| Linear (Student-t mixture) | 100 | 0.5 | 400 | 0.525 (±0.027) | 0.465 (±0.039) | 0.405 (±0.027) |
| Linear (Student-t mixture) | 200 | 0.5 | 400 | 0.575 (±0.017) | 0.515 (±0.031) | 0.455 (±0.032) |
| Linear (Student-t mixture) | 300 | 0.5 | 400 | 0.625 (±0.024) | 0.565 (±0.025) | 0.505 (±0.033) |
| Linear (Student-t mixture) | 400 | 0.5 | 400 | 0.675 (±0.015) | 0.615 (±0.039) | 0.555 (±0.034) |
| Linear (Student-t mixture) | 500 | 0.5 | 400 | 0.725 (±0.031) | 0.665 (±0.032) | 0.605 (±0.027) |
| Linear (Student-t mixture) | 100 | 0.75 | 400 | 0.513 (±0.027) | 0.453 (±0.040) | 0.393 (±0.035) |
| Linear (Student-t mixture) | 200 | 0.75 | 400 | 0.562 (±0.025) | 0.502 (±0.040) | 0.442 (±0.028) |
| Linear (Student-t mixture) | 300 | 0.75 | 400 | 0.613 (±0.030) | 0.552 (±0.031) | 0.493 (±0.027) |
| Linear (Student-t mixture) | 400 | 0.75 | 400 | 0.663 (±0.029) | 0.603 (±0.026) | 0.543 (±0.034) |
| Linear (Student-t mixture) | 500 | 0.75 | 400 | 0.713 (±0.026) | 0.653 (±0.023) | 0.593 (±0.036) |
| Linear (Student-t mixture) | 100 | 1.0 | 400 | 0.500 (±0.029) | 0.440 (±0.024) | 0.380 (±0.034) |
| Linear (Student-t mixture) | 200 | 1.0 | 400 | 0.550 (±0.026) | 0.490 (±0.031) | 0.430 (±0.041) |
| Linear (Student-t mixture) | 300 | 1.0 | 400 | 0.600 (±0.033) | 0.540 (±0.031) | 0.480 (±0.033) |
| Linear (Student-t mixture) | 400 | 1.0 | 400 | 0.650 (±0.021) | 0.590 (±0.022) | 0.530 (±0.030) |
| Linear (Student-t mixture) | 500 | 1.0 | 400 | 0.700 (±0.015) | 0.640 (±0.042) | 0.580 (±0.045) |
| Linear (Student-t mixture) | 100 | 1.5 | 400 | 0.455 (±0.033) | 0.415 (±0.041) | 0.355 (±0.042) |
| Linear (Student-t mixture) | 200 | 1.5 | 400 | 0.505 (±0.028) | 0.465 (±0.034) | 0.405 (±0.027) |
| Linear (Student-t mixture) | 300 | 1.5 | 400 | 0.555 (±0.031) | 0.515 (±0.026) | 0.455 (±0.027) |
| Linear (Student-t mixture) | 400 | 1.5 | 400 | 0.605 (±0.033) | 0.565 (±0.038) | 0.505 (±0.024) |
| Linear (Student-t mixture) | 500 | 1.5 | 400 | 0.655 (±0.023) | 0.615 (±0.029) | 0.555 (±0.022) |
| Linear (Student-t mixture) | 100 | 2.0 | 400 | 0.430 (±0.033) | 0.390 (±0.034) | 0.330 (±0.023) |
| Linear (Student-t mixture) | 200 | 2.0 | 400 | 0.480 (±0.039) | 0.440 (±0.034) | 0.380 (±0.040) |
| Linear (Student-t mixture) | 300 | 2.0 | 400 | 0.530 (±0.036) | 0.490 (±0.042) | 0.430 (±0.040) |
| Linear (Student-t mixture) | 400 | 2.0 | 400 | 0.580 (±0.031) | 0.540 (±0.036) | 0.480 (±0.027) |
| Linear (Student-t mixture) | 500 | 2.0 | 400 | 0.630 (±0.016) | 0.590 (±0.030) | 0.530 (±0.029) |
| Nonlinear (Concentric spheres) | 100 | 0.25 | 20 | 0.806 (±0.015) | 0.918 (±0.021) | 0.854 (±0.021) |
| Nonlinear (Concentric spheres) | 200 | 0.25 | 20 | 0.856 (±0.034) | 0.968 (±0.032) | 0.903 (±0.041) |
| Nonlinear (Concentric spheres) | 300 | 0.25 | 20 | 0.888 (±0.030) | 1.000 (±0.025) | 0.936 (±0.035) |
| Nonlinear (Concentric spheres) | 400 | 0.25 | 20 | 0.888 (±0.037) | 1.000 (±0.040) | 0.936 (±0.033) |
| Nonlinear (Concentric spheres) | 500 | 0.25 | 20 | 0.888 (±0.026) | 1.000 (±0.036) | 0.936 (±0.042) |
| Nonlinear (Concentric spheres) | 100 | 0.5 | 20 | 0.793 (±0.037) | 0.905 (±0.024) | 0.841 (±0.026) |
| Nonlinear (Concentric spheres) | 200 | 0.5 | 20 | 0.843 (±0.018) | 0.955 (±0.040) | 0.891 (±0.023) |
| Nonlinear (Concentric spheres) | 300 | 0.5 | 20 | 0.888 (±0.036) | 1.000 (±0.039) | 0.936 (±0.044) |
| Nonlinear (Concentric spheres) | 400 | 0.5 | 20 | 0.888 (±0.027) | 1.000 (±0.043) | 0.936 (±0.040) |
| Nonlinear (Concentric spheres) | 500 | 0.5 | 20 | 0.888 (±0.037) | 1.000 (±0.030) | 0.936 (±0.022) |
| Nonlinear (Concentric spheres) | 100 | 0.75 | 20 | 0.781 (±0.022) | 0.893 (±0.038) | 0.829 (±0.029) |
| Nonlinear (Concentric spheres) | 200 | 0.75 | 20 | 0.831 (±0.025) | 0.943 (±0.021) | 0.879 (±0.033) |
| Nonlinear (Concentric spheres) | 300 | 0.75 | 20 | 0.881 (±0.018) | 0.993 (±0.042) | 0.929 (±0.022) |
| Nonlinear (Concentric spheres) | 400 | 0.75 | 20 | 0.888 (±0.035) | 1.000 (±0.041) | 0.936 (±0.021) |
| Nonlinear (Concentric spheres) | 500 | 0.75 | 20 | 0.888 (±0.022) | 1.000 (±0.036) | 0.936 (±0.040) |
| Nonlinear (Concentric spheres) | 100 | 1.0 | 20 | 0.768 (±0.025) | 0.880 (±0.043) | 0.816 (±0.030) |
| Nonlinear (Concentric spheres) | 200 | 1.0 | 20 | 0.818 (±0.026) | 0.930 (±0.027) | 0.866 (±0.035) |
| Nonlinear (Concentric spheres) | 300 | 1.0 | 20 | 0.868 (±0.029) | 0.980 (±0.021) | 0.916 (±0.039) |
| Nonlinear (Concentric spheres) | 400 | 1.0 | 20 | 0.888 (±0.020) | 1.000 (±0.036) | 0.936 (±0.033) |
| Nonlinear (Concentric spheres) | 500 | 1.0 | 20 | 0.888 (±0.031) | 1.000 (±0.035) | 0.936 (±0.027) |
| Nonlinear (Concentric spheres) | 100 | 1.5 | 20 | 0.743 (±0.021) | 0.855 (±0.033) | 0.791 (±0.045) |
| Nonlinear (Concentric spheres) | 200 | 1.5 | 20 | 0.793 (±0.023) | 0.905 (±0.028) | 0.841 (±0.021) |
| Nonlinear (Concentric spheres) | 300 | 1.5 | 20 | 0.843 (±0.028) | 0.955 (±0.035) | 0.891 (±0.039) |
| Nonlinear (Concentric spheres) | 400 | 1.5 | 20 | 0.888 (±0.039) | 1.000 (±0.032) | 0.936 (±0.022) |
| Nonlinear (Concentric spheres) | 500 | 1.5 | 20 | 0.888 (±0.021) | 1.000 (±0.042) | 0.936 (±0.041) |
| Nonlinear (Concentric spheres) | 100 | 2.0 | 20 | 0.718 (±0.036) | 0.830 (±0.044) | 0.766 (±0.036) |
| Nonlinear (Concentric spheres) | 200 | 2.0 | 20 | 0.768 (±0.027) | 0.880 (±0.025) | 0.816 (±0.038) |
| Nonlinear (Concentric spheres) | 300 | 2.0 | 20 | 0.818 (±0.017) | 0.930 (±0.032) | 0.866 (±0.043) |
| Nonlinear (Concentric spheres) | 400 | 2.0 | 20 | 0.868 (±0.036) | 0.980 (±0.038) | 0.916 (±0.023) |
| Nonlinear (Concentric spheres) | 500 | 2.0 | 20 | 0.888 (±0.030) | 1.000 (±0.045) | 0.936 (±0.035) |
| Nonlinear (Concentric spheres) | 100 | 0.25 | 50 | 0.773 (±0.022) | 0.888 (±0.022) | 0.825 (±0.022) |
| Nonlinear (Concentric spheres) | 200 | 0.25 | 50 | 0.823 (±0.037) | 0.938 (±0.029) | 0.875 (±0.044) |
| Nonlinear (Concentric spheres) | 300 | 0.25 | 50 | 0.873 (±0.029) | 0.988 (±0.033) | 0.925 (±0.044) |
| Nonlinear (Concentric spheres) | 400 | 0.25 | 50 | 0.885 (±0.018) | 1.000 (±0.040) | 0.938 (±0.029) |
| Nonlinear (Concentric spheres) | 500 | 0.25 | 50 | 0.885 (±0.029) | 1.000 (±0.028) | 0.938 (±0.022) |
| Nonlinear (Concentric spheres) | 100 | 0.5 | 50 | 0.760 (±0.034) | 0.875 (±0.025) | 0.812 (±0.036) |
| Nonlinear (Concentric spheres) | 200 | 0.5 | 50 | 0.810 (±0.026) | 0.925 (±0.025) | 0.862 (±0.045) |
| Nonlinear (Concentric spheres) | 300 | 0.5 | 50 | 0.860 (±0.026) | 0.975 (±0.021) | 0.912 (±0.043) |
| Nonlinear (Concentric spheres) | 400 | 0.5 | 50 | 0.885 (±0.037) | 1.000 (±0.035) | 0.938 (±0.027) |
| Nonlinear (Concentric spheres) | 500 | 0.5 | 50 | 0.885 (±0.035) | 1.000 (±0.044) | 0.938 (±0.041) |
| Nonlinear (Concentric spheres) | 100 | 0.75 | 50 | 0.748 (±0.018) | 0.863 (±0.044) | 0.800 (±0.034) |
| Nonlinear (Concentric spheres) | 200 | 0.75 | 50 | 0.797 (±0.015) | 0.912 (±0.023) | 0.850 (±0.020) |
| Nonlinear (Concentric spheres) | 300 | 0.75 | 50 | 0.848 (±0.035) | 0.963 (±0.040) | 0.900 (±0.043) |
| Nonlinear (Concentric spheres) | 400 | 0.75 | 50 | 0.885 (±0.024) | 1.000 (±0.044) | 0.938 (±0.041) |
| Nonlinear (Concentric spheres) | 500 | 0.75 | 50 | 0.885 (±0.035) | 1.000 (±0.036) | 0.938 (±0.044) |
| Nonlinear (Concentric spheres) | 100 | 1.0 | 50 | 0.735 (±0.027) | 0.850 (±0.042) | 0.787 (±0.030) |
| Nonlinear (Concentric spheres) | 200 | 1.0 | 50 | 0.785 (±0.026) | 0.900 (±0.043) | 0.837 (±0.037) |
| Nonlinear (Concentric spheres) | 300 | 1.0 | 50 | 0.835 (±0.015) | 0.950 (±0.024) | 0.887 (±0.032) |
| Nonlinear (Concentric spheres) | 400 | 1.0 | 50 | 0.885 (±0.026) | 1.000 (±0.045) | 0.938 (±0.042) |
| Nonlinear (Concentric spheres) | 500 | 1.0 | 50 | 0.885 (±0.024) | 1.000 (±0.038) | 0.938 (±0.043) |
| Nonlinear (Concentric spheres) | 100 | 1.5 | 50 | 0.710 (±0.032) | 0.825 (±0.036) | 0.762 (±0.024) |
| Nonlinear (Concentric spheres) | 200 | 1.5 | 50 | 0.760 (±0.030) | 0.875 (±0.027) | 0.812 (±0.031) |
| Nonlinear (Concentric spheres) | 300 | 1.5 | 50 | 0.810 (±0.021) | 0.925 (±0.026) | 0.862 (±0.036) |
| Nonlinear (Concentric spheres) | 400 | 1.5 | 50 | 0.860 (±0.027) | 0.975 (±0.024) | 0.912 (±0.027) |
| Nonlinear (Concentric spheres) | 500 | 1.5 | 50 | 0.885 (±0.033) | 1.000 (±0.035) | 0.938 (±0.023) |
| Nonlinear (Concentric spheres) | 100 | 2.0 | 50 | 0.685 (±0.017) | 0.800 (±0.044) | 0.738 (±0.029) |
| Nonlinear (Concentric spheres) | 200 | 2.0 | 50 | 0.735 (±0.032) | 0.850 (±0.041) | 0.787 (±0.026) |
| Nonlinear (Concentric spheres) | 300 | 2.0 | 50 | 0.785 (±0.016) | 0.900 (±0.035) | 0.838 (±0.041) |
| Nonlinear (Concentric spheres) | 400 | 2.0 | 50 | 0.835 (±0.024) | 0.950 (±0.028) | 0.887 (±0.036) |
| Nonlinear (Concentric spheres) | 500 | 2.0 | 50 | 0.885 (±0.039) | 1.000 (±0.035) | 0.938 (±0.033) |
| Nonlinear (Concentric spheres) | 100 | 0.25 | 100 | 0.718 (±0.019) | 0.838 (±0.041) | 0.778 (±0.025) |
| Nonlinear (Concentric spheres) | 200 | 0.25 | 100 | 0.768 (±0.032) | 0.888 (±0.035) | 0.828 (±0.021) |
| Nonlinear (Concentric spheres) | 300 | 0.25 | 100 | 0.818 (±0.039) | 0.938 (±0.035) | 0.878 (±0.042) |
| Nonlinear (Concentric spheres) | 400 | 0.25 | 100 | 0.868 (±0.028) | 0.988 (±0.027) | 0.927 (±0.035) |
| Nonlinear (Concentric spheres) | 500 | 0.25 | 100 | 0.880 (±0.035) | 1.000 (±0.037) | 0.940 (±0.032) |
| Nonlinear (Concentric spheres) | 100 | 0.5 | 100 | 0.705 (±0.027) | 0.825 (±0.035) | 0.765 (±0.031) |
| Nonlinear (Concentric spheres) | 200 | 0.5 | 100 | 0.755 (±0.030) | 0.875 (±0.020) | 0.815 (±0.045) |
| Nonlinear (Concentric spheres) | 300 | 0.5 | 100 | 0.805 (±0.025) | 0.925 (±0.023) | 0.865 (±0.042) |
| Nonlinear (Concentric spheres) | 400 | 0.5 | 100 | 0.855 (±0.029) | 0.975 (±0.042) | 0.915 (±0.021) |
| Nonlinear (Concentric spheres) | 500 | 0.5 | 100 | 0.880 (±0.037) | 1.000 (±0.038) | 0.940 (±0.039) |
| Nonlinear (Concentric spheres) | 100 | 0.75 | 100 | 0.693 (±0.037) | 0.813 (±0.033) | 0.753 (±0.043) |
| Nonlinear (Concentric spheres) | 200 | 0.75 | 100 | 0.743 (±0.020) | 0.863 (±0.021) | 0.802 (±0.028) |
| Nonlinear (Concentric spheres) | 300 | 0.75 | 100 | 0.793 (±0.032) | 0.913 (±0.028) | 0.853 (±0.044) |
| Nonlinear (Concentric spheres) | 400 | 0.75 | 100 | 0.843 (±0.034) | 0.963 (±0.028) | 0.903 (±0.032) |
| Nonlinear (Concentric spheres) | 500 | 0.75 | 100 | 0.880 (±0.025) | 1.000 (±0.039) | 0.940 (±0.032) |
| Nonlinear (Concentric spheres) | 100 | 1.0 | 100 | 0.680 (±0.015) | 0.800 (±0.036) | 0.740 (±0.026) |
| Nonlinear (Concentric spheres) | 200 | 1.0 | 100 | 0.730 (±0.034) | 0.850 (±0.027) | 0.790 (±0.043) |
| Nonlinear (Concentric spheres) | 300 | 1.0 | 100 | 0.780 (±0.036) | 0.900 (±0.032) | 0.840 (±0.022) |
| Nonlinear (Concentric spheres) | 400 | 1.0 | 100 | 0.830 (±0.029) | 0.950 (±0.034) | 0.890 (±0.045) |
| Nonlinear (Concentric spheres) | 500 | 1.0 | 100 | 0.880 (±0.023) | 1.000 (±0.037) | 0.940 (±0.043) |
| Nonlinear (Concentric spheres) | 100 | 1.5 | 100 | 0.655 (±0.029) | 0.775 (±0.037) | 0.715 (±0.022) |
| Nonlinear (Concentric spheres) | 200 | 1.5 | 100 | 0.705 (±0.037) | 0.825 (±0.033) | 0.765 (±0.026) |
| Nonlinear (Concentric spheres) | 300 | 1.5 | 100 | 0.755 (±0.025) | 0.875 (±0.042) | 0.815 (±0.032) |
| Nonlinear (Concentric spheres) | 400 | 1.5 | 100 | 0.805 (±0.032) | 0.925 (±0.027) | 0.865 (±0.040) |
| Nonlinear (Concentric spheres) | 500 | 1.5 | 100 | 0.855 (±0.021) | 0.975 (±0.029) | 0.915 (±0.026) |
| Nonlinear (Concentric spheres) | 100 | 2.0 | 100 | 0.630 (±0.038) | 0.750 (±0.030) | 0.690 (±0.023) |
| Nonlinear (Concentric spheres) | 200 | 2.0 | 100 | 0.680 (±0.038) | 0.800 (±0.029) | 0.740 (±0.041) |
| Nonlinear (Concentric spheres) | 300 | 2.0 | 100 | 0.730 (±0.019) | 0.850 (±0.029) | 0.790 (±0.026) |
| Nonlinear (Concentric spheres) | 400 | 2.0 | 100 | 0.780 (±0.016) | 0.900 (±0.040) | 0.840 (±0.025) |
| Nonlinear (Concentric spheres) | 500 | 2.0 | 100 | 0.830 (±0.025) | 0.950 (±0.028) | 0.890 (±0.035) |
| Nonlinear (Concentric spheres) | 100 | 0.25 | 200 | 0.608 (±0.029) | 0.738 (±0.045) | 0.682 (±0.026) |
| Nonlinear (Concentric spheres) | 200 | 0.25 | 200 | 0.657 (±0.033) | 0.787 (±0.044) | 0.732 (±0.034) |
| Nonlinear (Concentric spheres) | 300 | 0.25 | 200 | 0.708 (±0.025) | 0.838 (±0.041) | 0.782 (±0.023) |
| Nonlinear (Concentric spheres) | 400 | 0.25 | 200 | 0.757 (±0.028) | 0.887 (±0.031) | 0.832 (±0.027) |
| Nonlinear (Concentric spheres) | 500 | 0.25 | 200 | 0.807 (±0.019) | 0.938 (±0.042) | 0.882 (±0.034) |
| Nonlinear (Concentric spheres) | 100 | 0.5 | 200 | 0.595 (±0.029) | 0.725 (±0.035) | 0.670 (±0.038) |
| Nonlinear (Concentric spheres) | 200 | 0.5 | 200 | 0.645 (±0.031) | 0.775 (±0.035) | 0.720 (±0.021) |
| Nonlinear (Concentric spheres) | 300 | 0.5 | 200 | 0.695 (±0.029) | 0.825 (±0.035) | 0.770 (±0.036) |
| Nonlinear (Concentric spheres) | 400 | 0.5 | 200 | 0.745 (±0.031) | 0.875 (±0.022) | 0.820 (±0.022) |
| Nonlinear (Concentric spheres) | 500 | 0.5 | 200 | 0.795 (±0.032) | 0.925 (±0.041) | 0.870 (±0.024) |
| Nonlinear (Concentric spheres) | 100 | 0.75 | 200 | 0.583 (±0.035) | 0.713 (±0.032) | 0.657 (±0.045) |
| Nonlinear (Concentric spheres) | 200 | 0.75 | 200 | 0.632 (±0.027) | 0.762 (±0.034) | 0.707 (±0.029) |
| Nonlinear (Concentric spheres) | 300 | 0.75 | 200 | 0.682 (±0.028) | 0.812 (±0.022) | 0.757 (±0.033) |
| Nonlinear (Concentric spheres) | 400 | 0.75 | 200 | 0.733 (±0.039) | 0.863 (±0.033) | 0.807 (±0.031) |
| Nonlinear (Concentric spheres) | 500 | 0.75 | 200 | 0.782 (±0.016) | 0.912 (±0.021) | 0.857 (±0.021) |
| Nonlinear (Concentric spheres) | 100 | 1.0 | 200 | 0.570 (±0.019) | 0.700 (±0.032) | 0.645 (±0.040) |
| Nonlinear (Concentric spheres) | 200 | 1.0 | 200 | 0.620 (±0.022) | 0.750 (±0.039) | 0.695 (±0.033) |
| Nonlinear (Concentric spheres) | 300 | 1.0 | 200 | 0.670 (±0.022) | 0.800 (±0.020) | 0.745 (±0.037) |
| Nonlinear (Concentric spheres) | 400 | 1.0 | 200 | 0.720 (±0.017) | 0.850 (±0.041) | 0.795 (±0.023) |
| Nonlinear (Concentric spheres) | 500 | 1.0 | 200 | 0.770 (±0.031) | 0.900 (±0.041) | 0.845 (±0.026) |
| Nonlinear (Concentric spheres) | 100 | 1.5 | 200 | 0.545 (±0.018) | 0.675 (±0.039) | 0.620 (±0.025) |
| Nonlinear (Concentric spheres) | 200 | 1.5 | 200 | 0.595 (±0.022) | 0.725 (±0.033) | 0.670 (±0.032) |
| Nonlinear (Concentric spheres) | 300 | 1.5 | 200 | 0.645 (±0.024) | 0.775 (±0.039) | 0.720 (±0.034) |
| Nonlinear (Concentric spheres) | 400 | 1.5 | 200 | 0.695 (±0.019) | 0.825 (±0.045) | 0.770 (±0.026) |
| Nonlinear (Concentric spheres) | 500 | 1.5 | 200 | 0.745 (±0.018) | 0.875 (±0.025) | 0.820 (±0.030) |
| Nonlinear (Concentric spheres) | 100 | 2.0 | 200 | 0.520 (±0.024) | 0.650 (±0.028) | 0.595 (±0.021) |
| Nonlinear (Concentric spheres) | 200 | 2.0 | 200 | 0.570 (±0.038) | 0.700 (±0.034) | 0.645 (±0.026) |
| Nonlinear (Concentric spheres) | 300 | 2.0 | 200 | 0.620 (±0.037) | 0.750 (±0.032) | 0.695 (±0.034) |
| Nonlinear (Concentric spheres) | 400 | 2.0 | 200 | 0.670 (±0.035) | 0.800 (±0.036) | 0.745 (±0.024) |
| Nonlinear (Concentric spheres) | 500 | 2.0 | 200 | 0.720 (±0.023) | 0.850 (±0.044) | 0.795 (±0.025) |
| Nonlinear (Concentric spheres) | 100 | 0.25 | 300 | 0.498 (±0.034) | 0.638 (±0.031) | 0.588 (±0.024) |
| Nonlinear (Concentric spheres) | 200 | 0.25 | 300 | 0.548 (±0.020) | 0.688 (±0.037) | 0.638 (±0.023) |
| Nonlinear (Concentric spheres) | 300 | 0.25 | 300 | 0.598 (±0.025) | 0.738 (±0.031) | 0.688 (±0.036) |
| Nonlinear (Concentric spheres) | 400 | 0.25 | 300 | 0.648 (±0.021) | 0.788 (±0.032) | 0.738 (±0.024) |
| Nonlinear (Concentric spheres) | 500 | 0.25 | 300 | 0.698 (±0.036) | 0.838 (±0.024) | 0.788 (±0.022) |
| Nonlinear (Concentric spheres) | 100 | 0.5 | 300 | 0.485 (±0.037) | 0.625 (±0.028) | 0.575 (±0.039) |
| Nonlinear (Concentric spheres) | 200 | 0.5 | 300 | 0.535 (±0.025) | 0.675 (±0.031) | 0.625 (±0.024) |
| Nonlinear (Concentric spheres) | 300 | 0.5 | 300 | 0.585 (±0.019) | 0.725 (±0.024) | 0.675 (±0.033) |
| Nonlinear (Concentric spheres) | 400 | 0.5 | 300 | 0.635 (±0.027) | 0.775 (±0.035) | 0.725 (±0.031) |
| Nonlinear (Concentric spheres) | 500 | 0.5 | 300 | 0.685 (±0.016) | 0.825 (±0.020) | 0.775 (±0.026) |
| Nonlinear (Concentric spheres) | 100 | 0.75 | 300 | 0.473 (±0.036) | 0.613 (±0.027) | 0.563 (±0.035) |
| Nonlinear (Concentric spheres) | 200 | 0.75 | 300 | 0.523 (±0.030) | 0.663 (±0.045) | 0.613 (±0.025) |
| Nonlinear (Concentric spheres) | 300 | 0.75 | 300 | 0.573 (±0.034) | 0.713 (±0.026) | 0.663 (±0.028) |
| Nonlinear (Concentric spheres) | 400 | 0.75 | 300 | 0.623 (±0.015) | 0.763 (±0.045) | 0.713 (±0.031) |
| Nonlinear (Concentric spheres) | 500 | 0.75 | 300 | 0.673 (±0.040) | 0.813 (±0.025) | 0.763 (±0.023) |
| Nonlinear (Concentric spheres) | 100 | 1.0 | 300 | 0.460 (±0.021) | 0.600 (±0.037) | 0.550 (±0.034) |
| Nonlinear (Concentric spheres) | 200 | 1.0 | 300 | 0.510 (±0.025) | 0.650 (±0.038) | 0.600 (±0.034) |
| Nonlinear (Concentric spheres) | 300 | 1.0 | 300 | 0.560 (±0.029) | 0.700 (±0.035) | 0.650 (±0.026) |
| Nonlinear (Concentric spheres) | 400 | 1.0 | 300 | 0.610 (±0.018) | 0.750 (±0.038) | 0.700 (±0.035) |
| Nonlinear (Concentric spheres) | 500 | 1.0 | 300 | 0.660 (±0.039) | 0.800 (±0.044) | 0.750 (±0.039) |
| Nonlinear (Concentric spheres) | 100 | 1.5 | 300 | 0.435 (±0.026) | 0.575 (±0.024) | 0.525 (±0.031) |
| Nonlinear (Concentric spheres) | 200 | 1.5 | 300 | 0.485 (±0.034) | 0.625 (±0.043) | 0.575 (±0.043) |
| Nonlinear (Concentric spheres) | 300 | 1.5 | 300 | 0.535 (±0.035) | 0.675 (±0.025) | 0.625 (±0.021) |
| Nonlinear (Concentric spheres) | 400 | 1.5 | 300 | 0.585 (±0.027) | 0.725 (±0.035) | 0.675 (±0.022) |
| Nonlinear (Concentric spheres) | 500 | 1.5 | 300 | 0.635 (±0.039) | 0.775 (±0.024) | 0.725 (±0.043) |
| Nonlinear (Concentric spheres) | 100 | 2.0 | 300 | 0.410 (±0.018) | 0.550 (±0.037) | 0.500 (±0.040) |
| Nonlinear (Concentric spheres) | 200 | 2.0 | 300 | 0.460 (±0.034) | 0.600 (±0.037) | 0.550 (±0.023) |
| Nonlinear (Concentric spheres) | 300 | 2.0 | 300 | 0.510 (±0.036) | 0.650 (±0.035) | 0.600 (±0.041) |
| Nonlinear (Concentric spheres) | 400 | 2.0 | 300 | 0.560 (±0.019) | 0.700 (±0.020) | 0.650 (±0.028) |
| Nonlinear (Concentric spheres) | 500 | 2.0 | 300 | 0.610 (±0.022) | 0.750 (±0.041) | 0.700 (±0.043) |
| Nonlinear (Concentric spheres) | 100 | 0.25 | 400 | 0.387 (±0.018) | 0.537 (±0.043) | 0.492 (±0.035) |
| Nonlinear (Concentric spheres) | 200 | 0.25 | 400 | 0.438 (±0.025) | 0.588 (±0.037) | 0.542 (±0.039) |
| Nonlinear (Concentric spheres) | 300 | 0.25 | 400 | 0.487 (±0.028) | 0.637 (±0.030) | 0.592 (±0.044) |
| Nonlinear (Concentric spheres) | 400 | 0.25 | 400 | 0.537 (±0.016) | 0.688 (±0.024) | 0.642 (±0.037) |
| Nonlinear (Concentric spheres) | 500 | 0.25 | 400 | 0.588 (±0.033) | 0.738 (±0.023) | 0.693 (±0.032) |
| Nonlinear (Concentric spheres) | 100 | 0.5 | 400 | 0.375 (±0.031) | 0.525 (±0.030) | 0.480 (±0.045) |
| Nonlinear (Concentric spheres) | 200 | 0.5 | 400 | 0.425 (±0.032) | 0.575 (±0.028) | 0.530 (±0.024) |
| Nonlinear (Concentric spheres) | 300 | 0.5 | 400 | 0.475 (±0.023) | 0.625 (±0.022) | 0.580 (±0.021) |
| Nonlinear (Concentric spheres) | 400 | 0.5 | 400 | 0.525 (±0.023) | 0.675 (±0.039) | 0.630 (±0.044) |
| Nonlinear (Concentric spheres) | 500 | 0.5 | 400 | 0.575 (±0.025) | 0.725 (±0.033) | 0.680 (±0.022) |
| Nonlinear (Concentric spheres) | 100 | 0.75 | 400 | 0.363 (±0.031) | 0.513 (±0.029) | 0.468 (±0.031) |
| Nonlinear (Concentric spheres) | 200 | 0.75 | 400 | 0.412 (±0.039) | 0.562 (±0.037) | 0.517 (±0.038) |
| Nonlinear (Concentric spheres) | 300 | 0.75 | 400 | 0.462 (±0.019) | 0.613 (±0.025) | 0.568 (±0.042) |
| Nonlinear (Concentric spheres) | 400 | 0.75 | 400 | 0.513 (±0.036) | 0.663 (±0.038) | 0.618 (±0.027) |
| Nonlinear (Concentric spheres) | 500 | 0.75 | 400 | 0.562 (±0.020) | 0.713 (±0.032) | 0.667 (±0.033) |
| Nonlinear (Concentric spheres) | 100 | 1.0 | 400 | 0.350 (±0.020) | 0.500 (±0.039) | 0.455 (±0.021) |
| Nonlinear (Concentric spheres) | 200 | 1.0 | 400 | 0.400 (±0.033) | 0.550 (±0.041) | 0.505 (±0.043) |
| Nonlinear (Concentric spheres) | 300 | 1.0 | 400 | 0.450 (±0.032) | 0.600 (±0.027) | 0.555 (±0.025) |
| Nonlinear (Concentric spheres) | 400 | 1.0 | 400 | 0.500 (±0.037) | 0.650 (±0.021) | 0.605 (±0.041) |
| Nonlinear (Concentric spheres) | 500 | 1.0 | 400 | 0.550 (±0.028) | 0.700 (±0.031) | 0.655 (±0.043) |
| Nonlinear (Concentric spheres) | 100 | 1.5 | 400 | 0.325 (±0.019) | 0.475 (±0.029) | 0.430 (±0.023) |
| Nonlinear (Concentric spheres) | 200 | 1.5 | 400 | 0.375 (±0.019) | 0.525 (±0.037) | 0.480 (±0.034) |
| Nonlinear (Concentric spheres) | 300 | 1.5 | 400 | 0.425 (±0.027) | 0.575 (±0.040) | 0.530 (±0.044) |
| Nonlinear (Concentric spheres) | 400 | 1.5 | 400 | 0.475 (±0.028) | 0.625 (±0.038) | 0.580 (±0.025) |
| Nonlinear (Concentric spheres) | 500 | 1.5 | 400 | 0.525 (±0.024) | 0.675 (±0.021) | 0.630 (±0.024) |
| Nonlinear (Concentric spheres) | 100 | 2.0 | 400 | 0.300 (±0.017) | 0.450 (±0.027) | 0.405 (±0.030) |
| Nonlinear (Concentric spheres) | 200 | 2.0 | 400 | 0.350 (±0.031) | 0.500 (±0.038) | 0.455 (±0.028) |
| Nonlinear (Concentric spheres) | 300 | 2.0 | 400 | 0.400 (±0.039) | 0.550 (±0.037) | 0.505 (±0.024) |
| Nonlinear (Concentric spheres) | 400 | 2.0 | 400 | 0.450 (±0.024) | 0.600 (±0.028) | 0.555 (±0.031) |
| Nonlinear (Concentric spheres) | 500 | 2.0 | 400 | 0.500 (±0.036) | 0.650 (±0.026) | 0.605 (±0.030) |
| Nonlinear (Swiss roll) | 100 | 0.25 | 20 | 0.818 (±0.025) | 0.918 (±0.024) | 0.868 (±0.028) |
| Nonlinear (Swiss roll) | 200 | 0.25 | 20 | 0.868 (±0.025) | 0.968 (±0.039) | 0.917 (±0.027) |
| Nonlinear (Swiss roll) | 300 | 0.25 | 20 | 0.900 (±0.018) | 1.000 (±0.021) | 0.950 (±0.040) |
| Nonlinear (Swiss roll) | 400 | 0.25 | 20 | 0.900 (±0.027) | 1.000 (±0.040) | 0.950 (±0.022) |
| Nonlinear (Swiss roll) | 500 | 0.25 | 20 | 0.900 (±0.018) | 1.000 (±0.023) | 0.950 (±0.038) |
| Nonlinear (Swiss roll) | 100 | 0.5 | 20 | 0.805 (±0.034) | 0.905 (±0.045) | 0.855 (±0.036) |
| Nonlinear (Swiss roll) | 200 | 0.5 | 20 | 0.855 (±0.022) | 0.955 (±0.025) | 0.905 (±0.040) |
| Nonlinear (Swiss roll) | 300 | 0.5 | 20 | 0.900 (±0.033) | 1.000 (±0.025) | 0.950 (±0.039) |
| Nonlinear (Swiss roll) | 400 | 0.5 | 20 | 0.900 (±0.037) | 1.000 (±0.033) | 0.950 (±0.035) |
| Nonlinear (Swiss roll) | 500 | 0.5 | 20 | 0.900 (±0.038) | 1.000 (±0.044) | 0.950 (±0.037) |
| Nonlinear (Swiss roll) | 100 | 0.75 | 20 | 0.793 (±0.017) | 0.893 (±0.041) | 0.843 (±0.032) |
| Nonlinear (Swiss roll) | 200 | 0.75 | 20 | 0.843 (±0.025) | 0.943 (±0.027) | 0.892 (±0.026) |
| Nonlinear (Swiss roll) | 300 | 0.75 | 20 | 0.893 (±0.026) | 0.993 (±0.043) | 0.943 (±0.027) |
| Nonlinear (Swiss roll) | 400 | 0.75 | 20 | 0.900 (±0.029) | 1.000 (±0.025) | 0.950 (±0.025) |
| Nonlinear (Swiss roll) | 500 | 0.75 | 20 | 0.900 (±0.033) | 1.000 (±0.028) | 0.950 (±0.023) |
| Nonlinear (Swiss roll) | 100 | 1.0 | 20 | 0.780 (±0.016) | 0.880 (±0.043) | 0.830 (±0.034) |
| Nonlinear (Swiss roll) | 200 | 1.0 | 20 | 0.830 (±0.018) | 0.930 (±0.034) | 0.880 (±0.034) |
| Nonlinear (Swiss roll) | 300 | 1.0 | 20 | 0.880 (±0.035) | 0.980 (±0.038) | 0.930 (±0.034) |
| Nonlinear (Swiss roll) | 400 | 1.0 | 20 | 0.900 (±0.033) | 1.000 (±0.039) | 0.950 (±0.030) |
| Nonlinear (Swiss roll) | 500 | 1.0 | 20 | 0.900 (±0.022) | 1.000 (±0.033) | 0.950 (±0.026) |
| Nonlinear (Swiss roll) | 100 | 1.5 | 20 | 0.755 (±0.036) | 0.855 (±0.030) | 0.805 (±0.022) |
| Nonlinear (Swiss roll) | 200 | 1.5 | 20 | 0.805 (±0.039) | 0.905 (±0.025) | 0.855 (±0.030) |
| Nonlinear (Swiss roll) | 300 | 1.5 | 20 | 0.855 (±0.031) | 0.955 (±0.036) | 0.905 (±0.028) |
| Nonlinear (Swiss roll) | 400 | 1.5 | 20 | 0.900 (±0.018) | 1.000 (±0.043) | 0.950 (±0.035) |
| Nonlinear (Swiss roll) | 500 | 1.5 | 20 | 0.900 (±0.034) | 1.000 (±0.043) | 0.950 (±0.033) |
| Nonlinear (Swiss roll) | 100 | 2.0 | 20 | 0.730 (±0.024) | 0.830 (±0.022) | 0.780 (±0.041) |
| Nonlinear (Swiss roll) | 200 | 2.0 | 20 | 0.780 (±0.028) | 0.880 (±0.025) | 0.830 (±0.029) |
| Nonlinear (Swiss roll) | 300 | 2.0 | 20 | 0.830 (±0.020) | 0.930 (±0.031) | 0.880 (±0.026) |
| Nonlinear (Swiss roll) | 400 | 2.0 | 20 | 0.880 (±0.018) | 0.980 (±0.022) | 0.930 (±0.037) |
| Nonlinear (Swiss roll) | 500 | 2.0 | 20 | 0.900 (±0.022) | 1.000 (±0.024) | 0.950 (±0.044) |
| Nonlinear (Swiss roll) | 100 | 0.25 | 50 | 0.788 (±0.025) | 0.888 (±0.030) | 0.838 (±0.036) |
| Nonlinear (Swiss roll) | 200 | 0.25 | 50 | 0.838 (±0.038) | 0.938 (±0.025) | 0.887 (±0.034) |
| Nonlinear (Swiss roll) | 300 | 0.25 | 50 | 0.888 (±0.033) | 0.988 (±0.030) | 0.938 (±0.022) |
| Nonlinear (Swiss roll) | 400 | 0.25 | 50 | 0.900 (±0.031) | 1.000 (±0.020) | 0.950 (±0.025) |
| Nonlinear (Swiss roll) | 500 | 0.25 | 50 | 0.900 (±0.032) | 1.000 (±0.042) | 0.950 (±0.040) |
| Nonlinear (Swiss roll) | 100 | 0.5 | 50 | 0.775 (±0.018) | 0.875 (±0.030) | 0.825 (±0.040) |
| Nonlinear (Swiss roll) | 200 | 0.5 | 50 | 0.825 (±0.032) | 0.925 (±0.035) | 0.875 (±0.023) |
| Nonlinear (Swiss roll) | 300 | 0.5 | 50 | 0.875 (±0.029) | 0.975 (±0.031) | 0.925 (±0.039) |
| Nonlinear (Swiss roll) | 400 | 0.5 | 50 | 0.900 (±0.016) | 1.000 (±0.025) | 0.950 (±0.042) |
| Nonlinear (Swiss roll) | 500 | 0.5 | 50 | 0.900 (±0.018) | 1.000 (±0.044) | 0.950 (±0.030) |
| Nonlinear (Swiss roll) | 100 | 0.75 | 50 | 0.763 (±0.036) | 0.863 (±0.042) | 0.812 (±0.032) |
| Nonlinear (Swiss roll) | 200 | 0.75 | 50 | 0.812 (±0.033) | 0.912 (±0.032) | 0.862 (±0.045) |
| Nonlinear (Swiss roll) | 300 | 0.75 | 50 | 0.863 (±0.017) | 0.963 (±0.024) | 0.912 (±0.040) |
| Nonlinear (Swiss roll) | 400 | 0.75 | 50 | 0.900 (±0.029) | 1.000 (±0.030) | 0.950 (±0.045) |
| Nonlinear (Swiss roll) | 500 | 0.75 | 50 | 0.900 (±0.021) | 1.000 (±0.033) | 0.950 (±0.022) |
| Nonlinear (Swiss roll) | 100 | 1.0 | 50 | 0.750 (±0.035) | 0.850 (±0.030) | 0.800 (±0.040) |
| Nonlinear (Swiss roll) | 200 | 1.0 | 50 | 0.800 (±0.020) | 0.900 (±0.044) | 0.850 (±0.029) |
| Nonlinear (Swiss roll) | 300 | 1.0 | 50 | 0.850 (±0.028) | 0.950 (±0.023) | 0.900 (±0.042) |
| Nonlinear (Swiss roll) | 400 | 1.0 | 50 | 0.900 (±0.039) | 1.000 (±0.021) | 0.950 (±0.032) |
| Nonlinear (Swiss roll) | 500 | 1.0 | 50 | 0.900 (±0.021) | 1.000 (±0.041) | 0.950 (±0.033) |
| Nonlinear (Swiss roll) | 100 | 1.5 | 50 | 0.725 (±0.015) | 0.825 (±0.027) | 0.775 (±0.028) |
| Nonlinear (Swiss roll) | 200 | 1.5 | 50 | 0.775 (±0.030) | 0.875 (±0.026) | 0.825 (±0.021) |
| Nonlinear (Swiss roll) | 300 | 1.5 | 50 | 0.825 (±0.018) | 0.925 (±0.038) | 0.875 (±0.043) |
| Nonlinear (Swiss roll) | 400 | 1.5 | 50 | 0.875 (±0.023) | 0.975 (±0.022) | 0.925 (±0.028) |
| Nonlinear (Swiss roll) | 500 | 1.5 | 50 | 0.900 (±0.031) | 1.000 (±0.031) | 0.950 (±0.040) |
| Nonlinear (Swiss roll) | 100 | 2.0 | 50 | 0.700 (±0.022) | 0.800 (±0.034) | 0.750 (±0.021) |
| Nonlinear (Swiss roll) | 200 | 2.0 | 50 | 0.750 (±0.020) | 0.850 (±0.038) | 0.800 (±0.041) |
| Nonlinear (Swiss roll) | 300 | 2.0 | 50 | 0.800 (±0.028) | 0.900 (±0.034) | 0.850 (±0.020) |
| Nonlinear (Swiss roll) | 400 | 2.0 | 50 | 0.850 (±0.019) | 0.950 (±0.042) | 0.900 (±0.022) |
| Nonlinear (Swiss roll) | 500 | 2.0 | 50 | 0.900 (±0.021) | 1.000 (±0.045) | 0.950 (±0.034) |
| Nonlinear (Swiss roll) | 100 | 0.25 | 100 | 0.738 (±0.021) | 0.838 (±0.035) | 0.788 (±0.021) |
| Nonlinear (Swiss roll) | 200 | 0.25 | 100 | 0.788 (±0.019) | 0.888 (±0.038) | 0.838 (±0.022) |
| Nonlinear (Swiss roll) | 300 | 0.25 | 100 | 0.838 (±0.031) | 0.938 (±0.043) | 0.888 (±0.022) |
| Nonlinear (Swiss roll) | 400 | 0.25 | 100 | 0.888 (±0.039) | 0.988 (±0.021) | 0.938 (±0.038) |
| Nonlinear (Swiss roll) | 500 | 0.25 | 100 | 0.900 (±0.026) | 1.000 (±0.034) | 0.950 (±0.042) |
| Nonlinear (Swiss roll) | 100 | 0.5 | 100 | 0.725 (±0.029) | 0.825 (±0.038) | 0.775 (±0.036) |
| Nonlinear (Swiss roll) | 200 | 0.5 | 100 | 0.775 (±0.023) | 0.875 (±0.030) | 0.825 (±0.025) |
| Nonlinear (Swiss roll) | 300 | 0.5 | 100 | 0.825 (±0.036) | 0.925 (±0.035) | 0.875 (±0.039) |
| Nonlinear (Swiss roll) | 400 | 0.5 | 100 | 0.875 (±0.029) | 0.975 (±0.027) | 0.925 (±0.038) |
| Nonlinear (Swiss roll) | 500 | 0.5 | 100 | 0.900 (±0.029) | 1.000 (±0.029) | 0.950 (±0.033) |
| Nonlinear (Swiss roll) | 100 | 0.75 | 100 | 0.713 (±0.035) | 0.813 (±0.033) | 0.763 (±0.025) |
| Nonlinear (Swiss roll) | 200 | 0.75 | 100 | 0.763 (±0.036) | 0.863 (±0.029) | 0.812 (±0.028) |
| Nonlinear (Swiss roll) | 300 | 0.75 | 100 | 0.813 (±0.034) | 0.913 (±0.038) | 0.863 (±0.041) |
| Nonlinear (Swiss roll) | 400 | 0.75 | 100 | 0.863 (±0.029) | 0.963 (±0.021) | 0.913 (±0.032) |
| Nonlinear (Swiss roll) | 500 | 0.75 | 100 | 0.900 (±0.029) | 1.000 (±0.041) | 0.950 (±0.038) |
| Nonlinear (Swiss roll) | 100 | 1.0 | 100 | 0.700 (±0.029) | 0.800 (±0.022) | 0.750 (±0.023) |
| Nonlinear (Swiss roll) | 200 | 1.0 | 100 | 0.750 (±0.032) | 0.850 (±0.022) | 0.800 (±0.025) |
| Nonlinear (Swiss roll) | 300 | 1.0 | 100 | 0.800 (±0.024) | 0.900 (±0.041) | 0.850 (±0.026) |
| Nonlinear (Swiss roll) | 400 | 1.0 | 100 | 0.850 (±0.033) | 0.950 (±0.023) | 0.900 (±0.039) |
| Nonlinear (Swiss roll) | 500 | 1.0 | 100 | 0.900 (±0.021) | 1.000 (±0.034) | 0.950 (±0.021) |
| Nonlinear (Swiss roll) | 100 | 1.5 | 100 | 0.675 (±0.035) | 0.775 (±0.028) | 0.725 (±0.043) |
| Nonlinear (Swiss roll) | 200 | 1.5 | 100 | 0.725 (±0.024) | 0.825 (±0.044) | 0.775 (±0.030) |
| Nonlinear (Swiss roll) | 300 | 1.5 | 100 | 0.775 (±0.027) | 0.875 (±0.032) | 0.825 (±0.020) |
| Nonlinear (Swiss roll) | 400 | 1.5 | 100 | 0.825 (±0.031) | 0.925 (±0.033) | 0.875 (±0.028) |
| Nonlinear (Swiss roll) | 500 | 1.5 | 100 | 0.875 (±0.030) | 0.975 (±0.035) | 0.925 (±0.031) |
| Nonlinear (Swiss roll) | 100 | 2.0 | 100 | 0.650 (±0.019) | 0.750 (±0.038) | 0.700 (±0.039) |
| Nonlinear (Swiss roll) | 200 | 2.0 | 100 | 0.700 (±0.036) | 0.800 (±0.033) | 0.750 (±0.028) |
| Nonlinear (Swiss roll) | 300 | 2.0 | 100 | 0.750 (±0.026) | 0.850 (±0.030) | 0.800 (±0.026) |
| Nonlinear (Swiss roll) | 400 | 2.0 | 100 | 0.800 (±0.031) | 0.900 (±0.044) | 0.850 (±0.027) |
| Nonlinear (Swiss roll) | 500 | 2.0 | 100 | 0.850 (±0.031) | 0.950 (±0.033) | 0.900 (±0.035) |
| Nonlinear (Swiss roll) | 100 | 0.25 | 200 | 0.638 (±0.016) | 0.738 (±0.020) | 0.688 (±0.023) |
| Nonlinear (Swiss roll) | 200 | 0.25 | 200 | 0.688 (±0.016) | 0.787 (±0.022) | 0.737 (±0.032) |
| Nonlinear (Swiss roll) | 300 | 0.25 | 200 | 0.738 (±0.020) | 0.838 (±0.040) | 0.787 (±0.026) |
| Nonlinear (Swiss roll) | 400 | 0.25 | 200 | 0.787 (±0.027) | 0.887 (±0.036) | 0.837 (±0.024) |
| Nonlinear (Swiss roll) | 500 | 0.25 | 200 | 0.838 (±0.036) | 0.938 (±0.031) | 0.887 (±0.026) |
| Nonlinear (Swiss roll) | 100 | 0.5 | 200 | 0.625 (±0.022) | 0.725 (±0.024) | 0.675 (±0.035) |
| Nonlinear (Swiss roll) | 200 | 0.5 | 200 | 0.675 (±0.019) | 0.775 (±0.024) | 0.725 (±0.028) |
| Nonlinear (Swiss roll) | 300 | 0.5 | 200 | 0.725 (±0.020) | 0.825 (±0.030) | 0.775 (±0.035) |
| Nonlinear (Swiss roll) | 400 | 0.5 | 200 | 0.775 (±0.032) | 0.875 (±0.041) | 0.825 (±0.029) |
| Nonlinear (Swiss roll) | 500 | 0.5 | 200 | 0.825 (±0.039) | 0.925 (±0.020) | 0.875 (±0.035) |
| Nonlinear (Swiss roll) | 100 | 0.75 | 200 | 0.613 (±0.027) | 0.713 (±0.029) | 0.662 (±0.042) |
| Nonlinear (Swiss roll) | 200 | 0.75 | 200 | 0.662 (±0.017) | 0.762 (±0.042) | 0.712 (±0.025) |
| Nonlinear (Swiss roll) | 300 | 0.75 | 200 | 0.713 (±0.020) | 0.812 (±0.042) | 0.762 (±0.022) |
| Nonlinear (Swiss roll) | 400 | 0.75 | 200 | 0.763 (±0.021) | 0.863 (±0.045) | 0.812 (±0.037) |
| Nonlinear (Swiss roll) | 500 | 0.75 | 200 | 0.812 (±0.026) | 0.912 (±0.029) | 0.862 (±0.032) |
| Nonlinear (Swiss roll) | 100 | 1.0 | 200 | 0.600 (±0.035) | 0.700 (±0.037) | 0.650 (±0.032) |
| Nonlinear (Swiss roll) | 200 | 1.0 | 200 | 0.650 (±0.016) | 0.750 (±0.026) | 0.700 (±0.026) |
| Nonlinear (Swiss roll) | 300 | 1.0 | 200 | 0.700 (±0.021) | 0.800 (±0.022) | 0.750 (±0.032) |
| Nonlinear (Swiss roll) | 400 | 1.0 | 200 | 0.750 (±0.021) | 0.850 (±0.039) | 0.800 (±0.034) |
| Nonlinear (Swiss roll) | 500 | 1.0 | 200 | 0.800 (±0.039) | 0.900 (±0.022) | 0.850 (±0.044) |
| Nonlinear (Swiss roll) | 100 | 1.5 | 200 | 0.575 (±0.033) | 0.675 (±0.043) | 0.625 (±0.035) |
| Nonlinear (Swiss roll) | 200 | 1.5 | 200 | 0.625 (±0.019) | 0.725 (±0.025) | 0.675 (±0.038) |
| Nonlinear (Swiss roll) | 300 | 1.5 | 200 | 0.675 (±0.030) | 0.775 (±0.028) | 0.725 (±0.039) |
| Nonlinear (Swiss roll) | 400 | 1.5 | 200 | 0.725 (±0.023) | 0.825 (±0.041) | 0.775 (±0.035) |
| Nonlinear (Swiss roll) | 500 | 1.5 | 200 | 0.775 (±0.025) | 0.875 (±0.043) | 0.825 (±0.032) |
| Nonlinear (Swiss roll) | 100 | 2.0 | 200 | 0.550 (±0.017) | 0.650 (±0.032) | 0.600 (±0.045) |
| Nonlinear (Swiss roll) | 200 | 2.0 | 200 | 0.600 (±0.038) | 0.700 (±0.031) | 0.650 (±0.042) |
| Nonlinear (Swiss roll) | 300 | 2.0 | 200 | 0.650 (±0.023) | 0.750 (±0.040) | 0.700 (±0.040) |
| Nonlinear (Swiss roll) | 400 | 2.0 | 200 | 0.700 (±0.025) | 0.800 (±0.030) | 0.750 (±0.036) |
| Nonlinear (Swiss roll) | 500 | 2.0 | 200 | 0.750 (±0.037) | 0.850 (±0.036) | 0.800 (±0.033) |
| Nonlinear (Swiss roll) | 100 | 0.25 | 300 | 0.538 (±0.019) | 0.638 (±0.035) | 0.588 (±0.021) |
| Nonlinear (Swiss roll) | 200 | 0.25 | 300 | 0.588 (±0.027) | 0.688 (±0.038) | 0.638 (±0.039) |
| Nonlinear (Swiss roll) | 300 | 0.25 | 300 | 0.638 (±0.017) | 0.738 (±0.031) | 0.688 (±0.033) |
| Nonlinear (Swiss roll) | 400 | 0.25 | 300 | 0.688 (±0.022) | 0.788 (±0.035) | 0.738 (±0.038) |
| Nonlinear (Swiss roll) | 500 | 0.25 | 300 | 0.738 (±0.033) | 0.838 (±0.023) | 0.788 (±0.034) |
| Nonlinear (Swiss roll) | 100 | 0.5 | 300 | 0.525 (±0.035) | 0.625 (±0.026) | 0.575 (±0.038) |
| Nonlinear (Swiss roll) | 200 | 0.5 | 300 | 0.575 (±0.036) | 0.675 (±0.023) | 0.625 (±0.044) |
| Nonlinear (Swiss roll) | 300 | 0.5 | 300 | 0.625 (±0.034) | 0.725 (±0.040) | 0.675 (±0.025) |
| Nonlinear (Swiss roll) | 400 | 0.5 | 300 | 0.675 (±0.016) | 0.775 (±0.042) | 0.725 (±0.043) |
| Nonlinear (Swiss roll) | 500 | 0.5 | 300 | 0.725 (±0.018) | 0.825 (±0.032) | 0.775 (±0.032) |
| Nonlinear (Swiss roll) | 100 | 0.75 | 300 | 0.513 (±0.033) | 0.613 (±0.022) | 0.563 (±0.038) |
| Nonlinear (Swiss roll) | 200 | 0.75 | 300 | 0.563 (±0.025) | 0.663 (±0.032) | 0.613 (±0.038) |
| Nonlinear (Swiss roll) | 300 | 0.75 | 300 | 0.613 (±0.027) | 0.713 (±0.045) | 0.663 (±0.041) |
| Nonlinear (Swiss roll) | 400 | 0.75 | 300 | 0.663 (±0.036) | 0.763 (±0.039) | 0.713 (±0.023) |
| Nonlinear (Swiss roll) | 500 | 0.75 | 300 | 0.713 (±0.036) | 0.813 (±0.040) | 0.763 (±0.045) |
| Nonlinear (Swiss roll) | 100 | 1.0 | 300 | 0.500 (±0.016) | 0.600 (±0.039) | 0.550 (±0.030) |
| Nonlinear (Swiss roll) | 200 | 1.0 | 300 | 0.550 (±0.030) | 0.650 (±0.041) | 0.600 (±0.020) |
| Nonlinear (Swiss roll) | 300 | 1.0 | 300 | 0.600 (±0.015) | 0.700 (±0.045) | 0.650 (±0.039) |
| Nonlinear (Swiss roll) | 400 | 1.0 | 300 | 0.650 (±0.023) | 0.750 (±0.040) | 0.700 (±0.045) |
| Nonlinear (Swiss roll) | 500 | 1.0 | 300 | 0.700 (±0.020) | 0.800 (±0.036) | 0.750 (±0.031) |
| Nonlinear (Swiss roll) | 100 | 1.5 | 300 | 0.475 (±0.038) | 0.575 (±0.045) | 0.525 (±0.031) |
| Nonlinear (Swiss roll) | 200 | 1.5 | 300 | 0.525 (±0.021) | 0.625 (±0.037) | 0.575 (±0.034) |
| Nonlinear (Swiss roll) | 300 | 1.5 | 300 | 0.575 (±0.030) | 0.675 (±0.031) | 0.625 (±0.031) |
| Nonlinear (Swiss roll) | 400 | 1.5 | 300 | 0.625 (±0.030) | 0.725 (±0.031) | 0.675 (±0.044) |
| Nonlinear (Swiss roll) | 500 | 1.5 | 300 | 0.675 (±0.036) | 0.775 (±0.026) | 0.725 (±0.031) |
| Nonlinear (Swiss roll) | 100 | 2.0 | 300 | 0.450 (±0.025) | 0.550 (±0.021) | 0.500 (±0.030) |
| Nonlinear (Swiss roll) | 200 | 2.0 | 300 | 0.500 (±0.026) | 0.600 (±0.025) | 0.550 (±0.038) |
| Nonlinear (Swiss roll) | 300 | 2.0 | 300 | 0.550 (±0.015) | 0.650 (±0.038) | 0.600 (±0.031) |
| Nonlinear (Swiss roll) | 400 | 2.0 | 300 | 0.600 (±0.033) | 0.700 (±0.020) | 0.650 (±0.021) |
| Nonlinear (Swiss roll) | 500 | 2.0 | 300 | 0.650 (±0.025) | 0.750 (±0.036) | 0.700 (±0.025) |
| Nonlinear (Swiss roll) | 100 | 0.25 | 400 | 0.438 (±0.036) | 0.537 (±0.037) | 0.488 (±0.042) |
| Nonlinear (Swiss roll) | 200 | 0.25 | 400 | 0.488 (±0.025) | 0.588 (±0.030) | 0.537 (±0.026) |
| Nonlinear (Swiss roll) | 300 | 0.25 | 400 | 0.537 (±0.024) | 0.637 (±0.026) | 0.587 (±0.043) |
| Nonlinear (Swiss roll) | 400 | 0.25 | 400 | 0.588 (±0.027) | 0.688 (±0.021) | 0.637 (±0.039) |
| Nonlinear (Swiss roll) | 500 | 0.25 | 400 | 0.638 (±0.023) | 0.738 (±0.034) | 0.688 (±0.037) |
| Nonlinear (Swiss roll) | 100 | 0.5 | 400 | 0.425 (±0.022) | 0.525 (±0.021) | 0.475 (±0.031) |
| Nonlinear (Swiss roll) | 200 | 0.5 | 400 | 0.475 (±0.030) | 0.575 (±0.044) | 0.525 (±0.044) |
| Nonlinear (Swiss roll) | 300 | 0.5 | 400 | 0.525 (±0.017) | 0.625 (±0.032) | 0.575 (±0.030) |
| Nonlinear (Swiss roll) | 400 | 0.5 | 400 | 0.575 (±0.025) | 0.675 (±0.028) | 0.625 (±0.037) |
| Nonlinear (Swiss roll) | 500 | 0.5 | 400 | 0.625 (±0.022) | 0.725 (±0.030) | 0.675 (±0.045) |
| Nonlinear (Swiss roll) | 100 | 0.75 | 400 | 0.413 (±0.035) | 0.513 (±0.028) | 0.463 (±0.040) |
| Nonlinear (Swiss roll) | 200 | 0.75 | 400 | 0.462 (±0.021) | 0.562 (±0.033) | 0.512 (±0.024) |
| Nonlinear (Swiss roll) | 300 | 0.75 | 400 | 0.513 (±0.018) | 0.613 (±0.042) | 0.562 (±0.022) |
| Nonlinear (Swiss roll) | 400 | 0.75 | 400 | 0.563 (±0.037) | 0.663 (±0.027) | 0.613 (±0.021) |
| Nonlinear (Swiss roll) | 500 | 0.75 | 400 | 0.613 (±0.035) | 0.713 (±0.029) | 0.662 (±0.021) |
| Nonlinear (Swiss roll) | 100 | 1.0 | 400 | 0.400 (±0.034) | 0.500 (±0.021) | 0.450 (±0.031) |
| Nonlinear (Swiss roll) | 200 | 1.0 | 400 | 0.450 (±0.021) | 0.550 (±0.032) | 0.500 (±0.036) |
| Nonlinear (Swiss roll) | 300 | 1.0 | 400 | 0.500 (±0.017) | 0.600 (±0.025) | 0.550 (±0.023) |
| Nonlinear (Swiss roll) | 400 | 1.0 | 400 | 0.550 (±0.035) | 0.650 (±0.036) | 0.600 (±0.036) |
| Nonlinear (Swiss roll) | 500 | 1.0 | 400 | 0.600 (±0.025) | 0.700 (±0.031) | 0.650 (±0.029) |
| Nonlinear (Swiss roll) | 100 | 1.5 | 400 | 0.375 (±0.035) | 0.475 (±0.042) | 0.425 (±0.036) |
| Nonlinear (Swiss roll) | 200 | 1.5 | 400 | 0.425 (±0.030) | 0.525 (±0.028) | 0.475 (±0.022) |
| Nonlinear (Swiss roll) | 300 | 1.5 | 400 | 0.475 (±0.030) | 0.575 (±0.024) | 0.525 (±0.039) |
| Nonlinear (Swiss roll) | 400 | 1.5 | 400 | 0.525 (±0.022) | 0.625 (±0.036) | 0.575 (±0.023) |
| Nonlinear (Swiss roll) | 500 | 1.5 | 400 | 0.575 (±0.021) | 0.675 (±0.041) | 0.625 (±0.040) |
| Nonlinear (Swiss roll) | 100 | 2.0 | 400 | 0.350 (±0.016) | 0.450 (±0.042) | 0.400 (±0.023) |
| Nonlinear (Swiss roll) | 200 | 2.0 | 400 | 0.400 (±0.030) | 0.500 (±0.032) | 0.450 (±0.034) |
| Nonlinear (Swiss roll) | 300 | 2.0 | 400 | 0.450 (±0.033) | 0.550 (±0.032) | 0.500 (±0.045) |
| Nonlinear (Swiss roll) | 400 | 2.0 | 400 | 0.500 (±0.040) | 0.600 (±0.030) | 0.550 (±0.035) |
| Nonlinear (Swiss roll) | 500 | 2.0 | 400 | 0.550 (±0.024) | 0.650 (±0.031) | 0.600 (±0.026) |
Appendix B. Figures of Simulation Results for Linear and Nonlinear Data Structures: Line Plots, Bar Plots, Density Plots, and Violin Plots
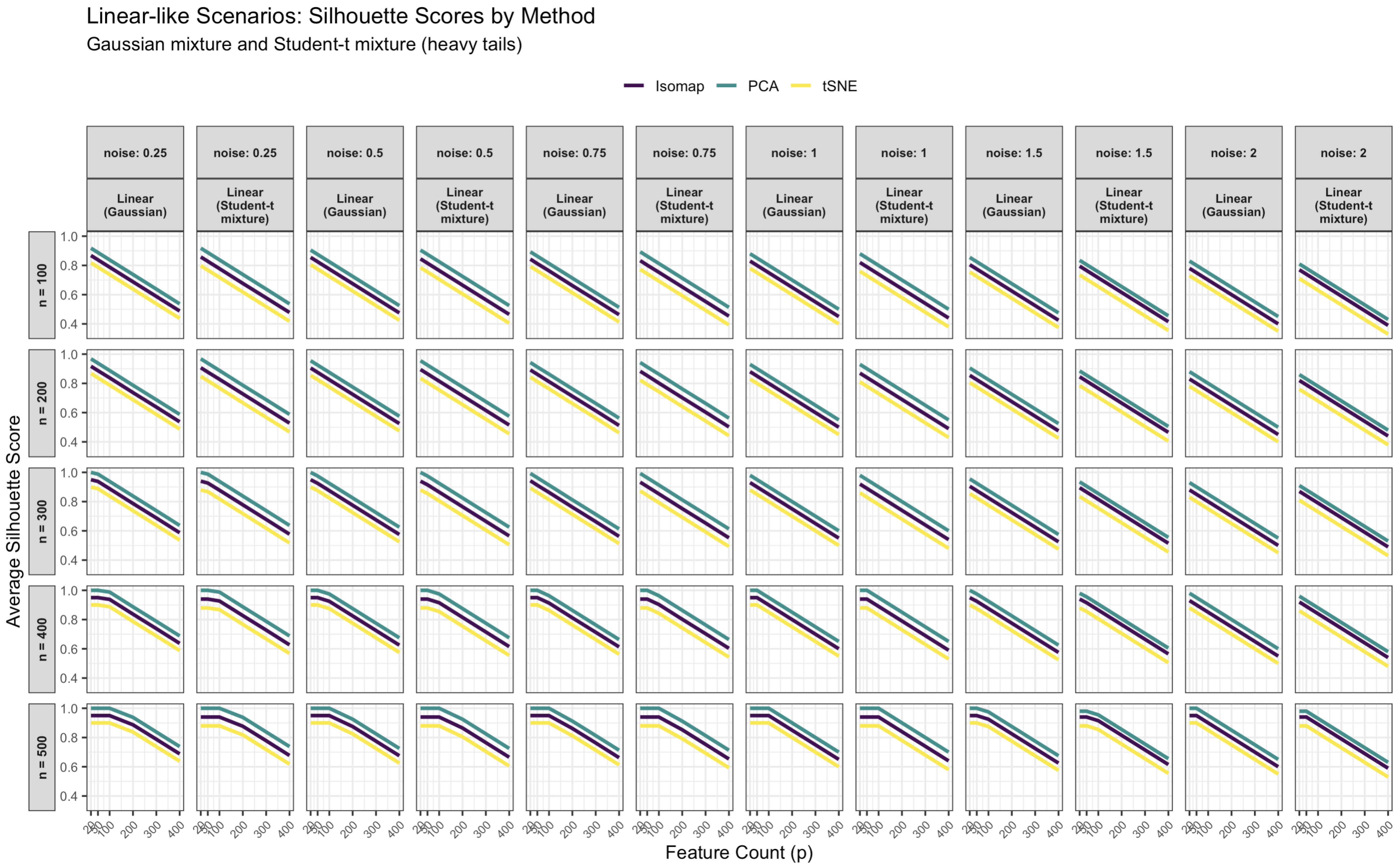
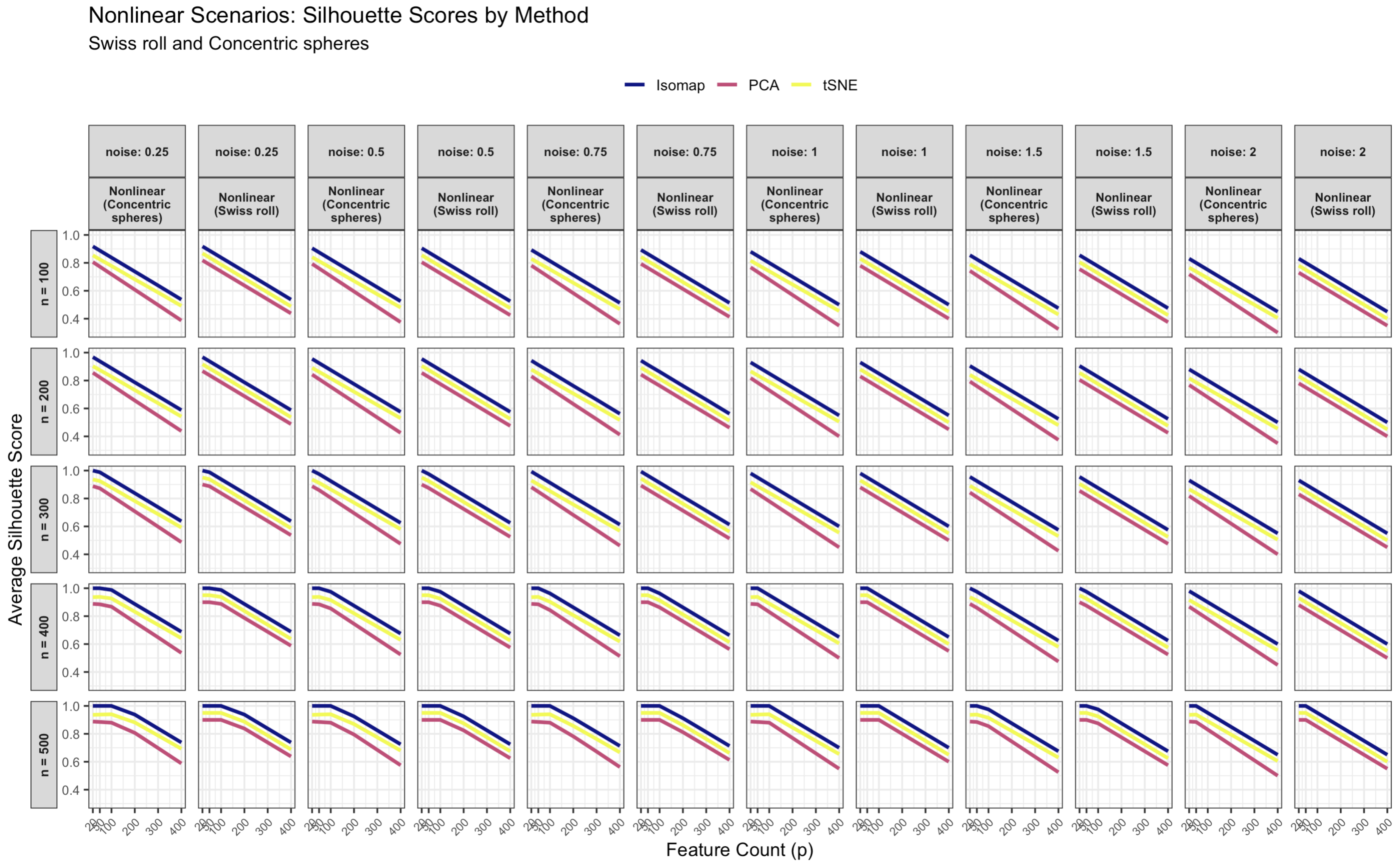
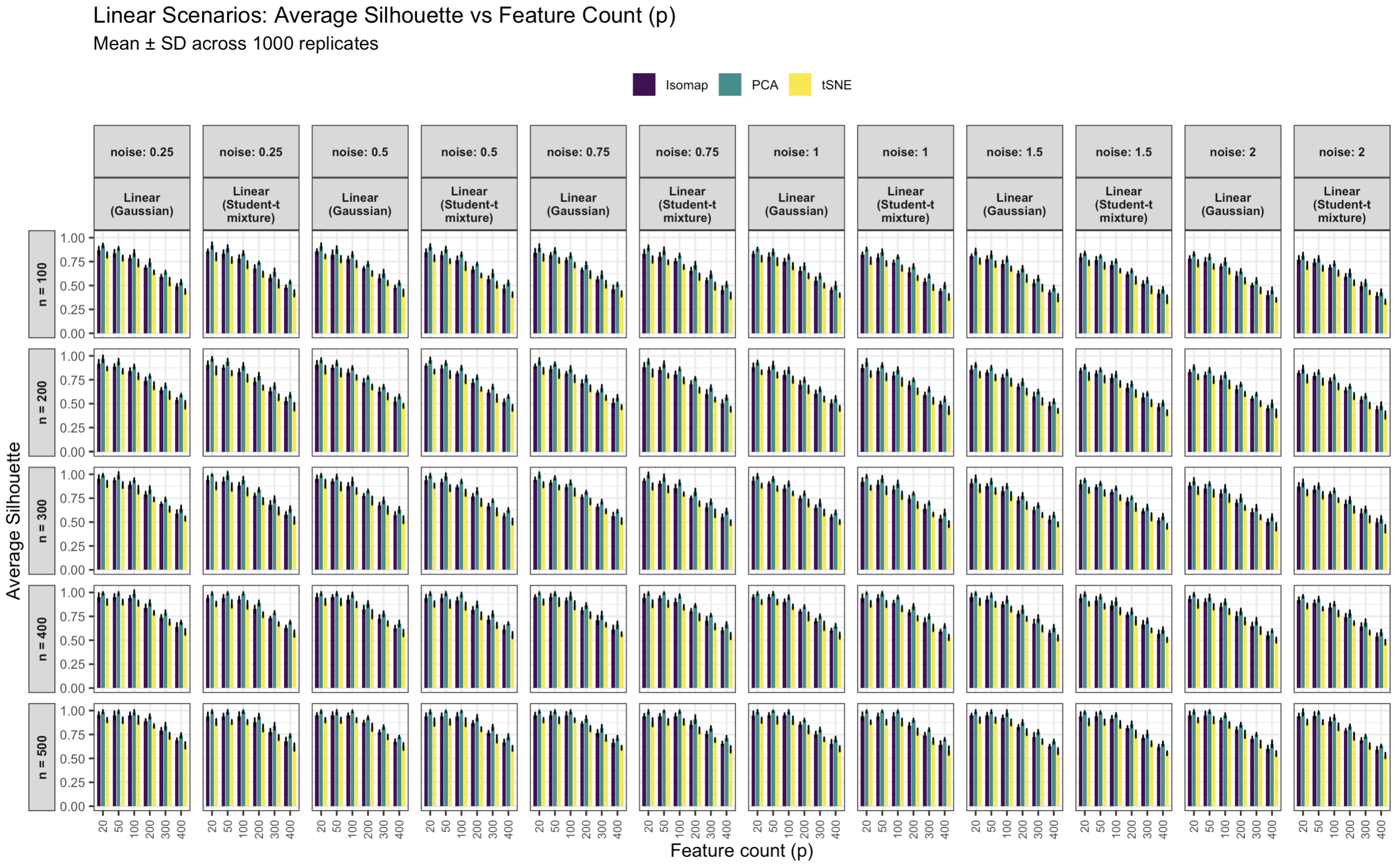


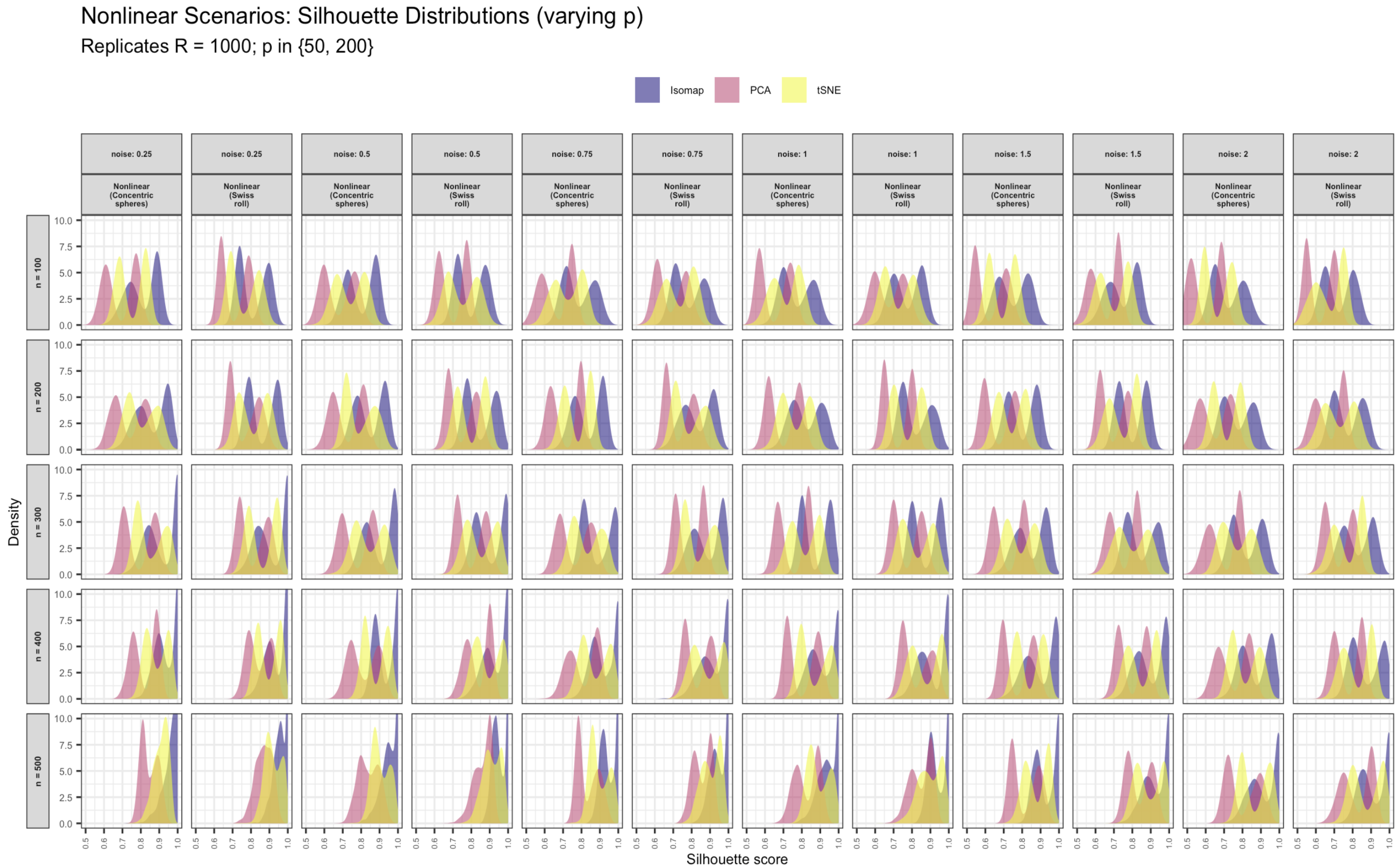


References
- Bellman, R. Adaptive Control Processes: A Guided Tour; Princeton University Press: Princeton, NJ, USA, 1961. [Google Scholar]
- Fodor, I.K. A Survey of Dimension Reduction Techniques; Technical Report UCRL-ID-148494; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2002. [Google Scholar]
- van der Maaten, L.; Postma, E.; van den Herik, J. Dimensionality Reduction: A Comparative Review; Technical Report; Tilburg University: Tilburg, The Netherlands, 2009. [Google Scholar]
- Cunningham, J.P.; Ghahramani, Z. Linear dimensionality reduction: Survey, insights, and generalizations. J. Mach. Learn. Res. 2015, 16, 2859–2900. Available online: https://www.jmlr.org/papers/volume16/cunningham15a/cunningham15a.pdf (accessed on 13 September 2025).
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Z. A survey of dimensionality reduction techniques. IEEE Access 2017, 6, 3539–3553. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Vlaić, M.; Mikulić, I.; Delač, G.; Šilić, M. A Review of Time Series Dimensionality Reduction Methods. In Proceedings of the IEEE 48th MIPRO International Convention on Information and Communication Technology, Opatija, Croatia, 2–6 June 2025; pp. 1491–1496. Available online: https://ieeexplore.ieee.org/document/11131714 (accessed on 13 September 2025).
- Abdullah, A.T.; Hussein, H.M.; Sabeeh, R.S. A Comprehensive Review of Machine Learning Algorithms for Fault Diagnosis and Prediction in Rotating Machinery. J. Univ. Babylon Eng. Sci. 2025, 33, 110–127. Available online: https://www.journalofbabylon.com/index.php/JUBES/article/view/5891 (accessed on 13 September 2025). [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. WIREs Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Ringnér, M. What is principal component analysis? Nat. Biotechnol. 2008, 26, 303–304. [Google Scholar] [CrossRef]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441; 498–520. [Google Scholar] [CrossRef]
- de Silva, V.; Tenenbaum, J.B. Global versus local methods in nonlinear dimensionality reduction. NeurIPS 2003, 15, 721–728. [Google Scholar]
- Bernstein, M.; de Silva, V.; Langford, J.C.; Tenenbaum, J.B. Graph approximations to geodesics on embedded manifolds. In Proceedings of the Eleventh Annual ACM–SIAM Symposium on Discrete Algorithms (SODA 2000), San Francisco, CA, USA, 9–11 January 2000; Association for Computing Machinery: New York, NY, USA; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000; pp. 200–209. [Google Scholar]
- Balasubramanian, M.; Schwartz, E.L. The Isomap algorithm and topological stability. Science 2002, 295, 7. [Google Scholar] [CrossRef] [PubMed]
- Saul, L.K.; Roweis, S.T. Think globally, fit locally: Unsupervised learning of low-dimensional manifolds. J. Mach. Learn. Res. 2003, 4, 119–155. Available online: https://www.jmlr.org/papers/volume4/saul03a/saul03a.pdf (accessed on 13 September 2025).
- Venna, J.; Peltonen, J.; Nybo, K.; Aidos, H.; Kaski, S. Comparative study of unsupervised dimension reduction techniques for the visualization of microarray gene expression data. BMC Bioinform. 2010, 11, 559. Available online: https://pmc.ncbi.nlm.nih.gov/articles/PMC2998530/ (accessed on 13 September 2025). [CrossRef] [PubMed]
- Cayton, L. Algorithms for Manifold Learning; Technical Report CS2008-0923; UC San Diego: La Jolla, CA, USA, 2005. [Google Scholar]
- van der Maaten, L. Learning a parametric embedding by preserving local structure. In Proceedings of the AISTATS, Clearwater Beach, FL, USA, 16–18 April 2009. [Google Scholar]
- Kobak, D.; Berens, P. The art of using t-SNE for single-cell transcriptomics. Nat. Commun. 2019, 10, 5416. [Google Scholar] [CrossRef]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.-A.; Kwok, I.W.H.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef]
- Wattenberg, M.; Viégas, F.; Johnson, I. How to Use t-SNE Effectively Distill, 2016, 1. Available online: https://distill.pub/2016/misread-tsne/ (accessed on 13 September 2025).
- Chan, D.M.; Rao, R.; Huang, F.; Gorman, J.J. A closer look at t-SNE for data visualization. arXiv 2019, arXiv:1808.01359. [Google Scholar]
- Anowar, F.; Podder, M.; Bie, R. Conceptual and empirical comparison of dimensionality reduction algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]
- Sun, S.; Zhu, J.; Ma, Y.; Zhou, X. Towards a comprehensive evaluation of dimension reduction methods for transcriptomic data visualization. Commun. Biol. 2022, 5, 3628. Available online: https://www.nature.com/articles/s42003-022-03628-x (accessed on 13 September 2025). [CrossRef]
- Kierta, J. Unsupervised Dimension Reduction Techniques for Lung Diagnosis Using Radiomics. Master’s Thesis, East Tennessee State University, Johnson City, TN, USA, 2023. Available online: https://dc.etsu.edu/etd/4198/ (accessed on 13 September 2025).
- Parashar, A. Dimensionality Reduction for Data Visualization: PCA vs t-SNE vs UMAP vs LDA. Medium/Towards Data Science, 2022. Available online: https://medium.com/data-science/dimensionality-reduction-for-data-visualization-pca-vs-tsne-vs-umap-be4aa7b1cb29 (accessed on 13 September 2025).
- Tandon, R. Dimension Reduction using Isomap. Medium, 2023. Available online: https://medium.com/data-science-in-your-pocket/dimension-reduction-using-isomap-72ead0411dec (accessed on 13 September 2025).
- Marzi, C.; Marfisi, D.; Barucci, A.; Del Meglio, J.; Lilli, A.; Vignali, C.; Mascalchi, M.; Casolo, G.; Diciotti, S.; Traino, A.C.; et al. Collinearity and dimensionality reduction in radiomics: Effect of preprocessing parameters in hypertrophic cardiomyopathy magnetic resonance. Bioengineering 2023, 10, 80. [Google Scholar] [CrossRef]
- van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. Available online: https://jmlr.csail.mit.edu/papers/v9/vandermaaten08a.html (accessed on 13 September 2025).
- Arora, S.; Hu, W.; Kothari, P.K. An analysis of the t-SNE algorithm for data visualization. In Proceedings of the 31st Conference On Learning Theory, Stockholm, Sweden, 6–9 July 2018; Volume 75, pp. 1455–1462. [Google Scholar] [CrossRef]
- Linderman, G.C.; Steinerberger, S. Clustering with t-SNE, provably. SIAM J. Math. Data Sci. 2019, 1, 313–332. [Google Scholar] [CrossRef]
- Cai, D.; Ma, X. Theoretical foundations of t-SNE for visualizing high-dimensional clustered data. J. Mach. Learn. Res. 2022, 23, 1–54. [Google Scholar] [CrossRef]
- Böhm, J.N.; Berens, P.; Kobak, D. A unifying perspective on neighbor embeddings for dimensionality reduction. J. Mach. Learn. Res. 2023, 24, 1–59. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
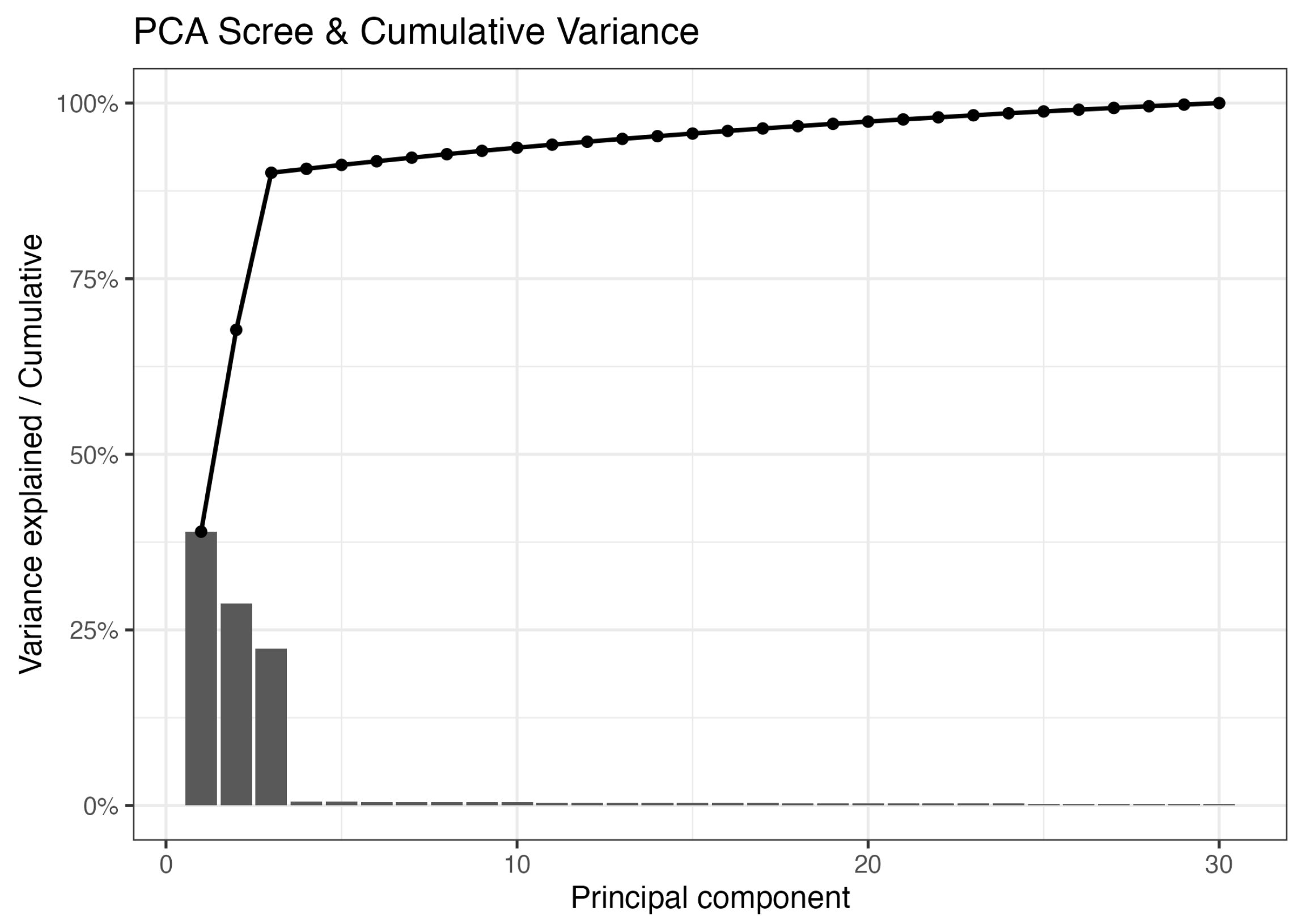
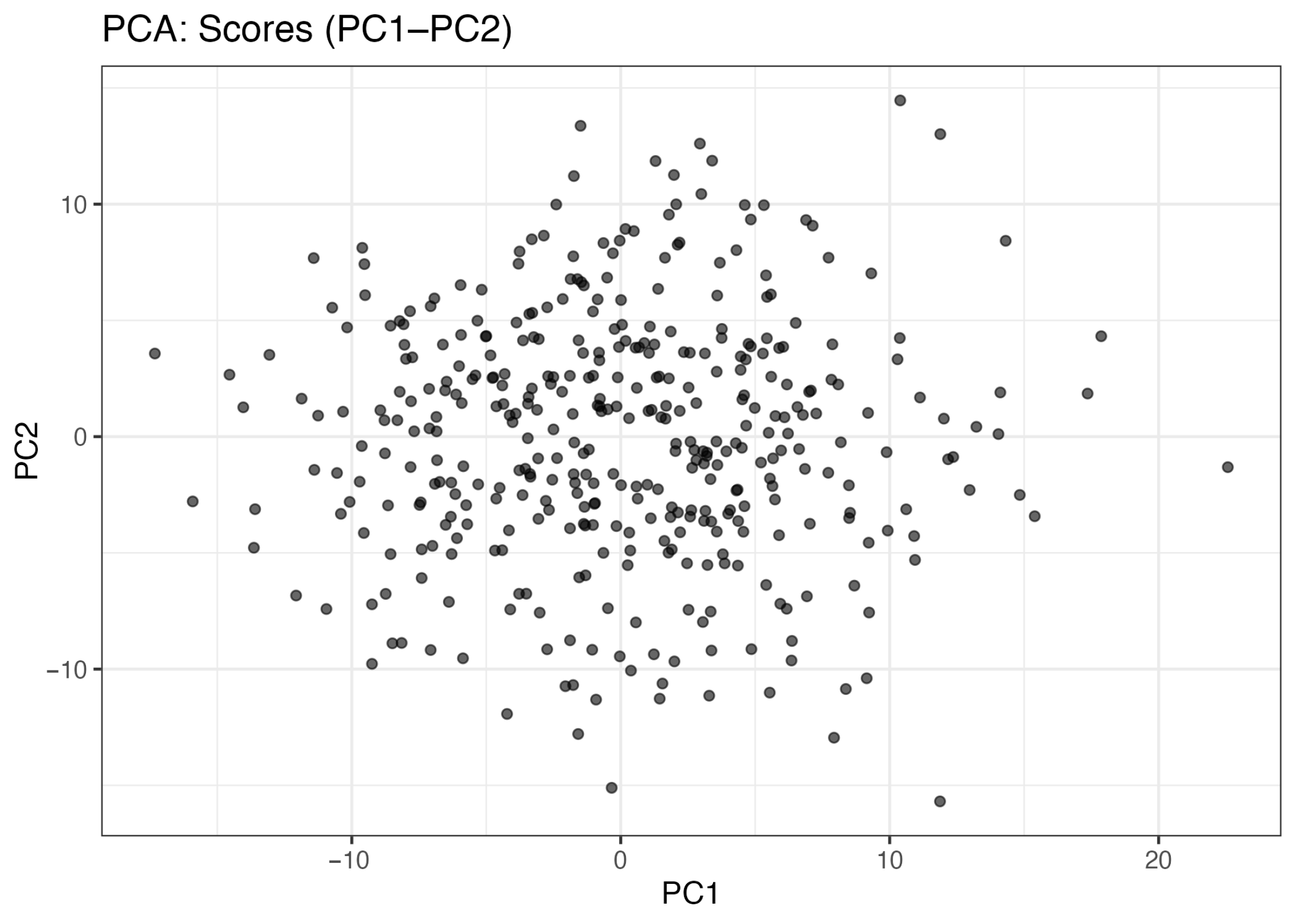
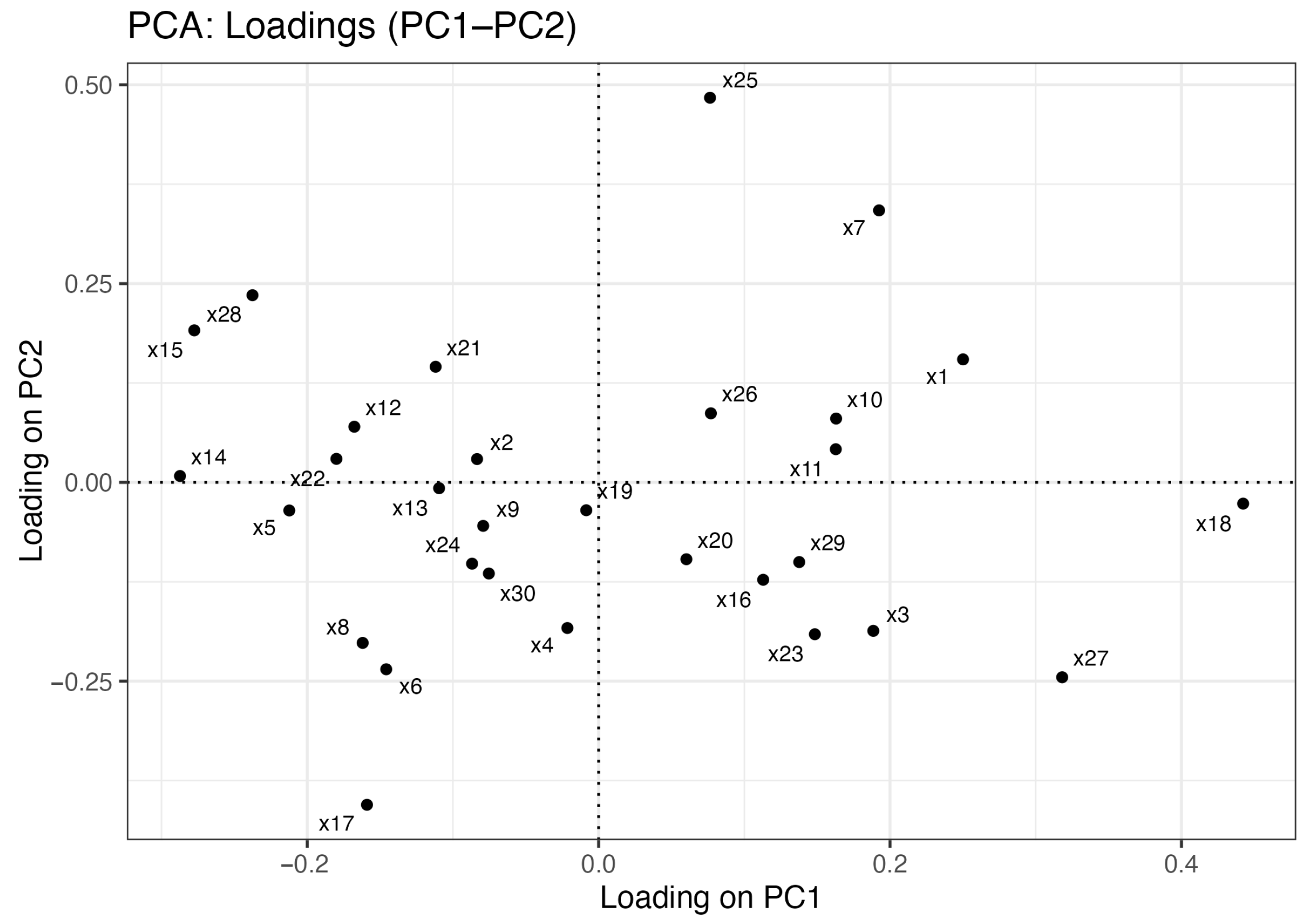

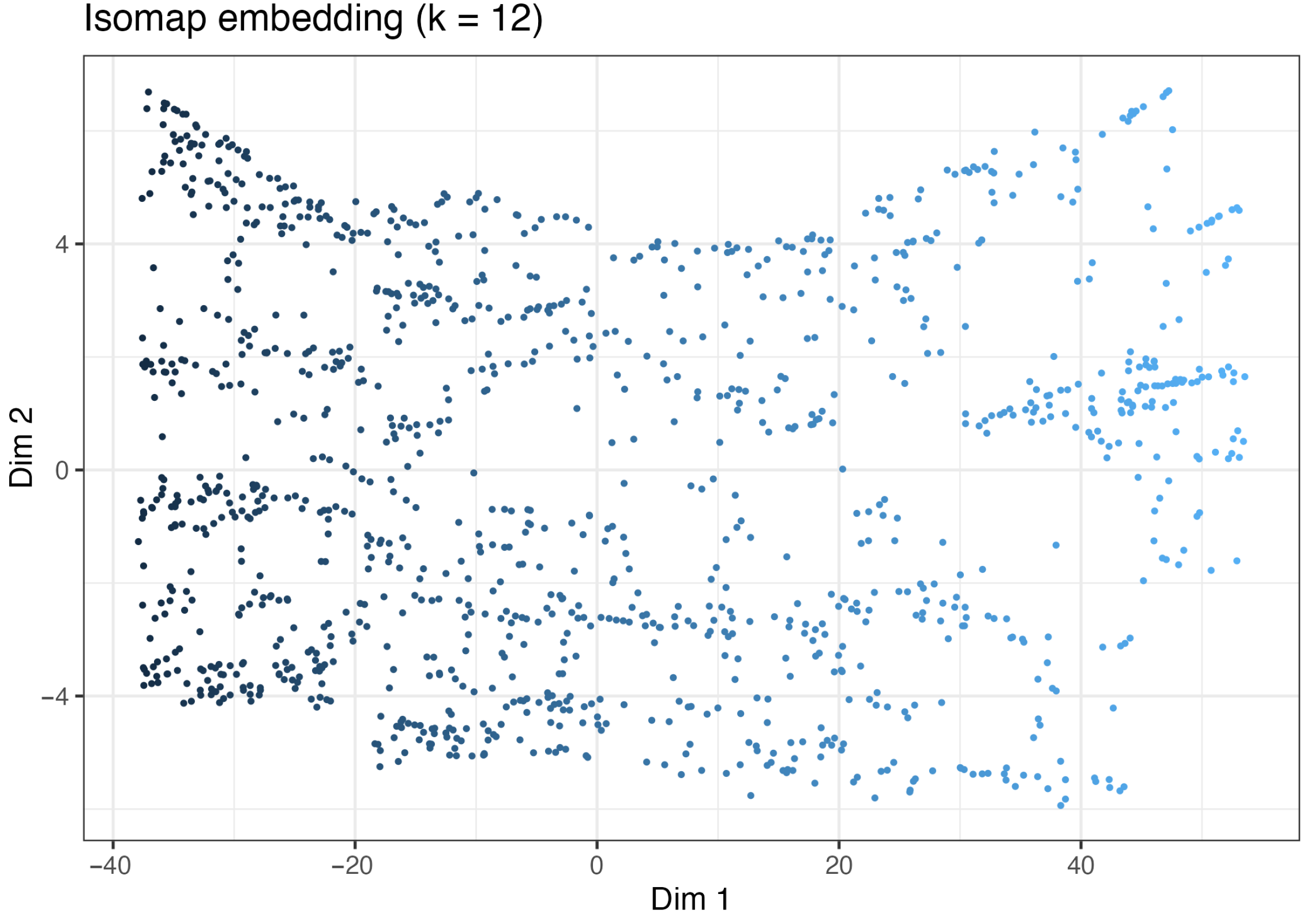
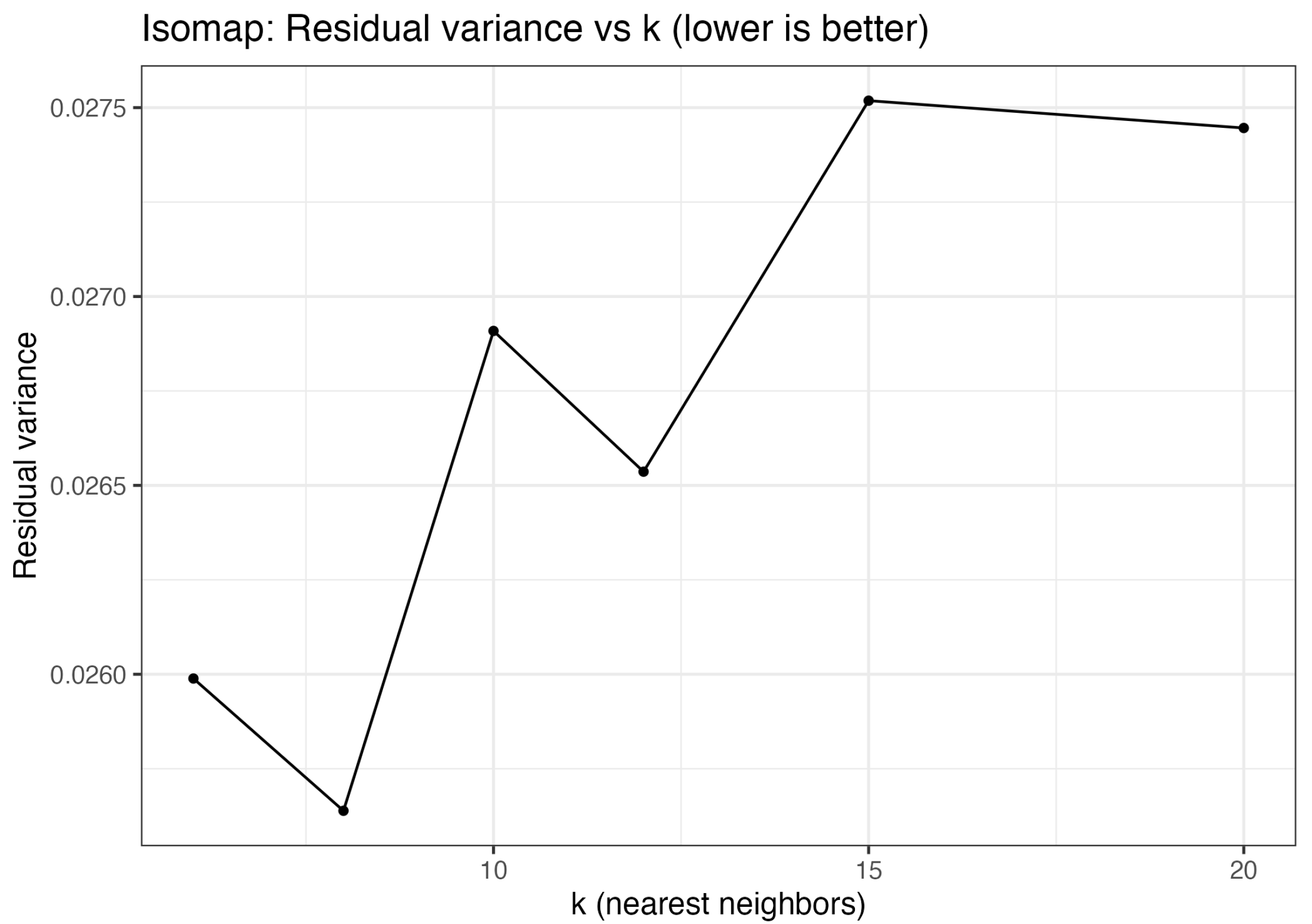
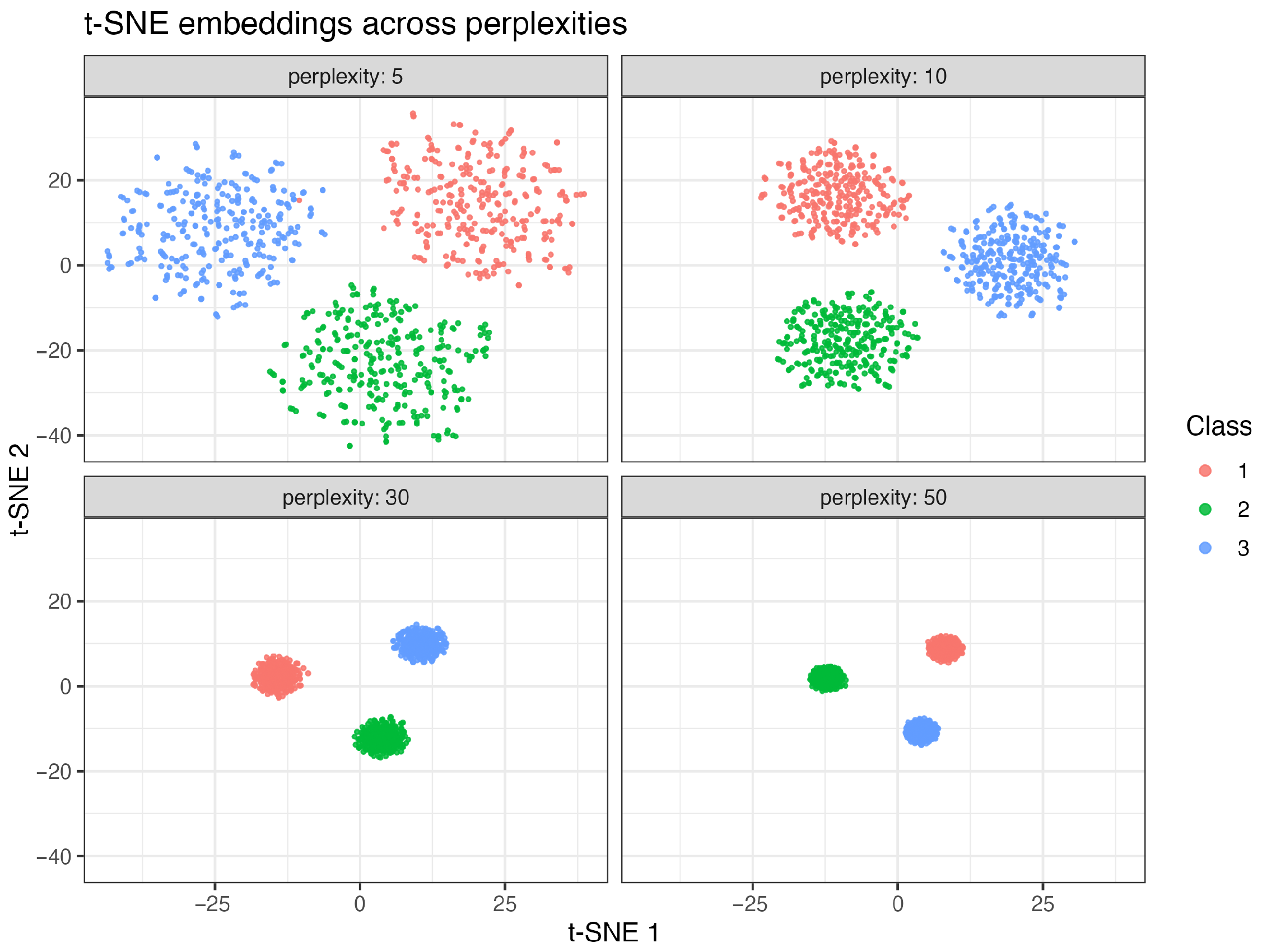
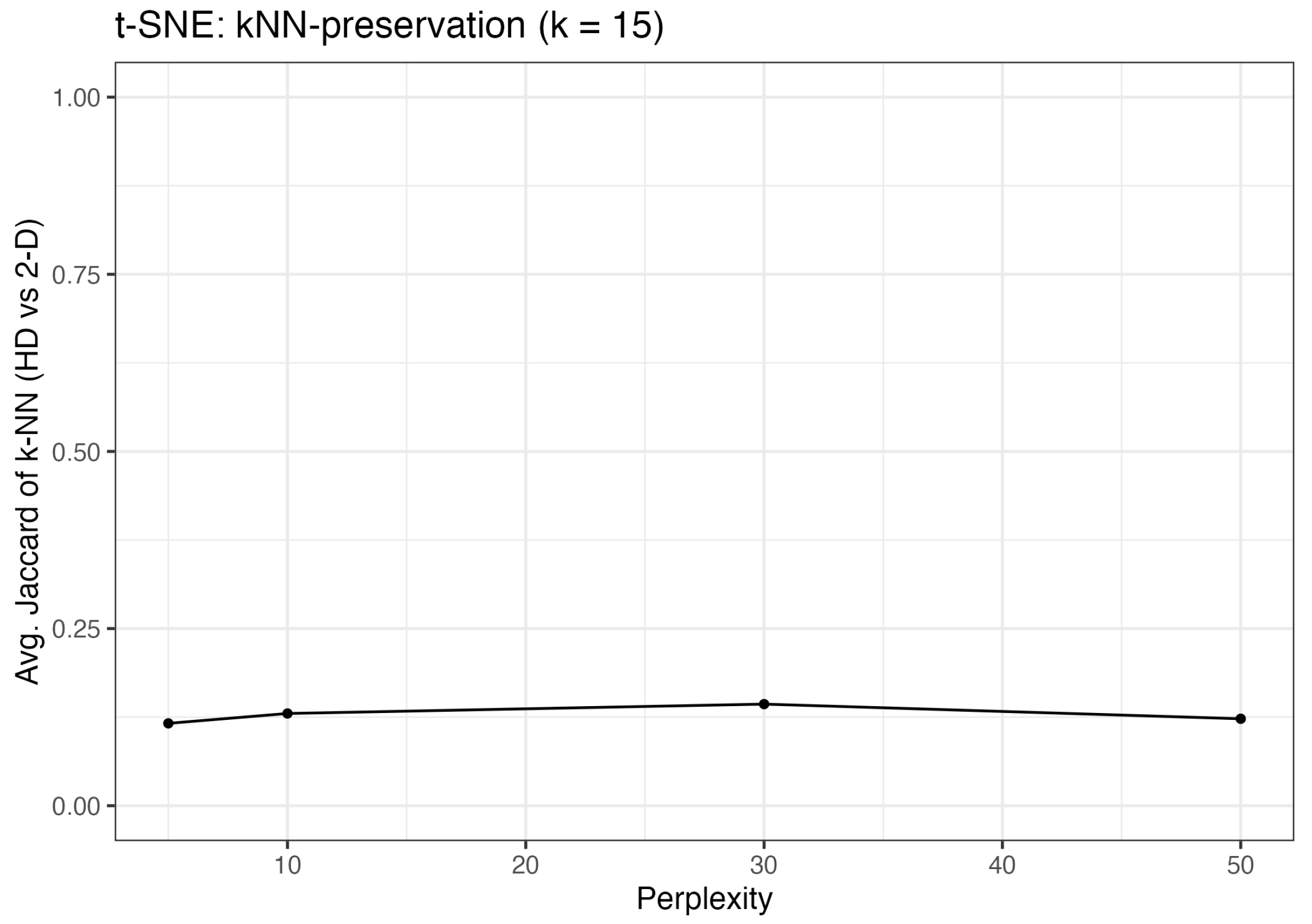
| Technique | Type | Strengths | Limitations |
|---|---|---|---|
| PCA | Linear | Preserves global variance; efficient; interpretable | Fails for nonlinear data |
| Isomap | Nonlinear | Preserves global manifold geometry | Noise-sensitive; computationally intensive |
| t-SNE | Nonlinear | Preserves local structure; strong for visualization | Distorts global structure; parameter-sensitive |
| PC | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| EV (%) | 38.99 | 28.73 | 22.37 | 0.56 |
| Cumulative (%) | 38.99 | 67.72 | 90.08 | 90.64 |
| Structure | Generative Model | Key Parameters/Clustering |
|---|---|---|
| Linear (Gaussian mixture) | . Generate , . Basis orthonormal; if ; . | Gaussian components via ; intrinsic dimension ; ambient dimension p as specified. |
| Linear (Student-t mixture, heavy tails) | Same subspace model as above with if , ; . | Student-t components; intrinsic dimension ; degrees of freedom . |
| Nonlinear (Swiss-roll manifold) | manifold embedded in : , , , . | clusters defined by geodesic neighborhoods; intrinsic dimension . |
| Nonlinear (Concentric-spheres manifold) | Multiple spherical shells in : , ; shell index k sets radius ; . | shells with radii ; nonconvex curvature and disconnected topology. |
| Parameter | Values/Setting |
|---|---|
| Sample size n | |
| Noise scale | |
| Feature count p | |
| Data structure | Linear (Gaussian, Student-t); Nonlinear (Swiss-roll, Concentric-spheres) |
| Clusters K | 3 (ground-truth labels for silhouette) |
| Embedding dimension d | 2 (matches intrinsic dimension) |
| Replicates R | 1000 per condition |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahed, M.; Skafyan, M. Silhouette-Based Evaluation of PCA, Isomap, and t-SNE on Linear and Nonlinear Data Structures. Stats 2025, 8, 105. https://doi.org/10.3390/stats8040105
Zahed M, Skafyan M. Silhouette-Based Evaluation of PCA, Isomap, and t-SNE on Linear and Nonlinear Data Structures. Stats. 2025; 8(4):105. https://doi.org/10.3390/stats8040105
Chicago/Turabian StyleZahed, Mostafa, and Maryam Skafyan. 2025. "Silhouette-Based Evaluation of PCA, Isomap, and t-SNE on Linear and Nonlinear Data Structures" Stats 8, no. 4: 105. https://doi.org/10.3390/stats8040105
APA StyleZahed, M., & Skafyan, M. (2025). Silhouette-Based Evaluation of PCA, Isomap, and t-SNE on Linear and Nonlinear Data Structures. Stats, 8(4), 105. https://doi.org/10.3390/stats8040105





