Abstract
Issues related to the duration of university studies have attracted the interest of many researchers from different scientific fields, as far back as the middle of the 20th century. In this study, a Survival Analysis methodology and, more specifically, a Cox Proportional hazards model, has been proposed to evaluate a theoretical framework/model that relates the risk a student might face either graduating on time or having a late graduation, with a number of observed and latent factors that have been proposed in the literature as the main determinants of time to degree completion. The major findings of the analysis suggest that the factors contributing to reducing the duration of studies include high academic achievements at early stages, positive motivation, expectations, attitudes, and beliefs regarding studies. On the contrary, external situations, negative academic experiences, and some individual characteristics of the students contribute to an extended duration of studies.
1. Introduction
Phenomena regarding quitting studies and late graduation were made noticeable since 1939, mainly in the U.S.A. [1]. Essentially, such phenomena reflect the academic outcomes when it does not conform to “on time graduation”, that is, obtaining their degree as determined by the regulations of an established educational system or institution. Similar phenomena were beginning to appear outside the United States as education became more massive. These terms often reflect the local character of the phenomenon. Student mortality, attrition, late graduation, dropout, voluntary withdrawal, and delayed college progress are some of those terms (see, among others [1,2,3,4]). The systematic study of these phenomena and the risk of extending or dropping out of studies, and the factors associated with them, has aroused the interest of many researchers, also given that the volume of students who deal with that risk reaches a significant size [5,6,7]. This interest has to do with the operational planning of tertiary education, such as human resource planning at the national or regional level. Furthermore, the corresponding research results could be useful in educational policy decision-making as they could be used as KPIs. Various theories or approaches have been proposed to understand and explain the aforementioned phenomena. These approaches can be broadly categorized into the following categories [6].
1.1. Psychological Perspective—“Students’ Involvement Theory”
The psychological perspective, proposed by Astin [8], is based on the theory of student involvement, and it can be summarized as follows: student persistence depends on the amount of physical and psychological energy they devote to the academic experience. Astin focuses on the effects of student characteristics (e.g., gender, age, and place of residence) as well as institutional characteristics (e.g., type, location, and selectivity) on student retention.
1.2. Sociological Perspective—“Integration Model”
From a sociological standpoint, one of the most widely referenced models is Tinto’s theory of student integration [2]. This framework explores the ways in which academic and social structures within the university interact to influence a student’s likelihood of persisting in their studies. Tinto posits that a student’s retention is strongly linked to their level of academic and social integration within the institution. These levels of integration are, in turn, shaped by various pre-university attributes, including socioeconomic background, prior academic achievement, ethnicity, and gender.
1.3. Organizational/Economic Perspectives—“Attrition Model”
The organizational approach, on the other hand, uses concepts of management in order to investigate the withdrawal of students from universities. The main exponent of this approach was Bean, whose study of job satisfaction was extended to the study of student attrition. His proposed model of student attrition explores the relationship between universities’ organizational structures and student retention, based on students’ perceived satisfaction with their studies [9].
1.4. Integrated Perspective—“Combination of Theories”
Lastly, integrative approaches synthesize components from the previously discussed theoretical models to offer a more holistic understanding of the phenomenon. Through a comparative examination of Tinto’s [2] student integration framework and Bean’s [9] model of student attrition, Cabrera, Nora, and Castaneda [10] demonstrated that the two perspectives are not contradictory but instead offer complementary insights.
Within this context, several statistical methodologies have been proposed for the application of the aforementioned theories to real cases. These methodologies vary from simple descriptive methods to multidimensional methods, for example, ordinary and logistic regression [11] as well as structural equation models [12] and survival analysis methods (see, among others, refs. [5,7,13,14,15,16,17,18,19]).
In the framework of the Greek higher education, there are findings concerning the distribution of the duration of studies in a university oriented to social and political sciences given the condition that there is a lower time limit for graduation but there is no upper limit (this is a rule that covers university studies in Greece). This distribution is studied using survival analysis methods [14]. In particular, the distribution of the duration of studies has been studied by means of the survival function (see Section 3), reflecting the probability that an individual student will “survive at the university” or, speaking in terms of graduation, will not graduate up to a given point in time t. The results show that there are three clear categories of students: those who graduate just after the threshold, those who graduate at a later time, and those who may have a very late graduation or will not graduate at all.
In this paper, an analysis of such determinants is performed by means of a Cox Proportional Hazard Model (see Section 3), in order to investigate factors associated with or causing the aforementioned distribution of duration of studies. More specifically, building on Kalamatianou and McClean’s [14] study, the objective of this paper is to evaluate a conceptual model (see Section 2), which draws on the model of Tinto [2] and Bean [9], that associates time to degree (or the previously mentioned distribution of the duration of studies) with a number of observed and latent variables, related to students’ prior academic achievement, motives, expectation and preparedness. These variables or factors have been proposed in the literature as the main determinants of students’ academic success and degree completion.
Building on Tinto’s [2] model of student attrition, the university is understood as a distinct social environment governed by its own norms and structures. Within this environment operate two interdependent subsystems, academic and social, which interact continuously. This foundational premise is incorporated into the present study.
Likewise, Bean’s [9] student retention framework suggests that low levels of satisfaction with academic life, along with various external pressures, contribute to student attrition. This study refines that premise by proposing that academic satisfaction, external encouragement, and the absence of disruptive external conditions foster timely degree completion, whereas dissatisfaction, lack of support, and negative external influences tend to delay graduation.
In addition, the conceptual approach employed here draws on Cabrera, Nora, and Castaneda’s [10] synthesis of the Tinto and Bean models into a unified theoretical structure for examining the determinants of time to degree.
Accordingly, the framework proposed in this research assumes that students enter higher education with specific academic and personal attributes that serve as the foundation for their educational journey. These individual characteristics affect the duration of studies, as illustrated in Figure 1.
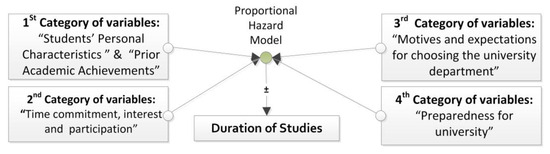
Figure 1.
Graphical representation of the conceptual model.
The empirical findings presented in Section 4 support the robustness of the conceptual model and its statistical application, while also offering key insights into the variables associated with study duration within the university under investigation.
2. Materials and Methods
2.1. Participants
The sample consists of 1236 graduates and students. Data were collected in two ways. (a) Regarding the dates of enrolment and graduation which were necessary for the calculation of the dependent variable, as well as for the independent variables X1, X3, X4, X5, X6, X16, (see below) data came from the student register maintained in the computerization department of the university involved in the study. (b) The remaining data were collected between January and April 2024 using telephone interviews with a stratified simple random sample of students through collaboration with the administrative offices of the university involved in the study.
The research conducted in this study received ethical approval from the PGR AOC Ethics Committee (Approval Code: PGR-AOC-2023-09D23, Approval Date: 13 September 2023), ensuring that the study adhered to ethical standards in research involving human participants, maintained the integrity of the research process, and safeguarded the well-being of the participants.
2.2. The Conceptual Model, the Variables, and the Data
This paper supposes that the duration of studies, considered as the dependent variable, is related to four categories of variables, as briefly shown in Figure 1. For the sake of brevity, the variables included in each category, along with the coding of their values, are described below.
Dependent variable: Duration of studies, our dependent time variable includes: (a) complete observations (graduates) corresponding to students that obtained their degrees during the follow-up period, which lasted until the end of June 2018 (so that, by 2024, every student in the sample had at least 6 opportunities to complete their studies), and for whom the duration of study was calculated as the time between their first enrolment in the university and their graduation date and (b) right censored observations (non- graduates) corresponding to students who did not obtain their degrees at the end of the follow-up period (for details see [15]).
Specifically, the dependent variable reflects the length of time, in months, between a student’s first enrolment at the university and their eventual graduation, applying the method outlined by Kalamatianou and McClean [14]. In the context of Greek public universities, which offer four-year undergraduate degrees, students are eligible to graduate at one of three examination sessions held annually—typically after the June, October, or February exam periods. As a result, the shortest possible time to graduation is 46 months. Students who complete the required coursework and meet graduation criteria within this period may graduate precisely at the 46-month mark. Those who do not fulfill the requirements by that point may continue participating in subsequent examination cycles, without a defined upper limit, until all academic obligations are met. Thus, the values taken by the dependent variable are discrete and follow the structure 46 + 4i months, where i (i = 0, 1, 2, …) denotes the number of additional examination sessions needed.
Explanatory variables/Covariates: We considered four categories of observed and latent covariates, which were assumed to be time-independent. In order to compose latent variables, we used Gutman’s Accumulative Scale of methodology of latent summation score.
The first category represents Students’ Personal Characteristics as well as Prior Academic Achievements corresponding to six observed variables:
- X1.
- Gender: (1, male; 0, female);
- X2.
- Place of Origin: (1, Athens; 0, other);
- X3.
- Students’ Age at the time of university enrolment: (Age of each individual at the time of enrolment at the university);
- X4.
- Secondary school grades: (the score ranges from a 10-minimum grade required for admission to university to 20);
- X5.
- University access score: (it is the mean grade achieved at the university entrance examinations);
- X6.
- Way of admission to the university: (1, General examination; 0, other).
The second category represents Time Commitment, interests, and participation and includes 10 observed and one latent covariate:
- X7.
- Study habits: (1, Studying throughout the semester; 0, not at all or during examination period);
- X8.
- Attendance: (1, continuously; 0, sometimes or less);
- X9.
- Class participation: (1, Yes; 0, No);
- X10.
- Prior interest in field of studies (1, Yes; 0, No);
- X11.
- Satisfaction derived from the curriculum: (1, Yes; 0, No);
- X12.
- Satisfaction derived from the course (1, Yes; 0, No);
- X13.
- Order of preference of the Department of Studies;
- X14.
- Work during studies (1, Had a job during studies; 0, otherwise);
- X15.
- Unforeseen factors during studies (1, Yes; 0, No);
- X16.
- Academic performance: Average score of the first two semesters of studies (the score ranges from 0 to 10).
In addition to this second category of variables, one more latent covariate is included:
- X17.
- Academic adjustment (Cronbach’s a = 0.71). To capture academic adjustment, five observed variables were scored. These correspond to: Participation to the university events, Participation to students’ parties and other political events, Participation in students’ election activities, “Hanging out” with classmates, and Living in University Campus.
The third category represents students’ Motives for choosing the particular university department and expectations from it, and includes four observed and one latent covariate as below:
- X18.
- Vocational rehabilitation (1, Yes; 0, No);
- X19.
- Skills and qualifications required by the labor market (1, Yes; 0, No);
- X20.
- Prestige that is expected to be gained from the specific curriculum (1, Yes; 0, No);
- X21.
- Knowledge acquisition on the specific field of science;
- X22.
- Parental socioeconomic status (SES), which is a latent variable measured on the base of parental educational, occupational, and income level (1, High SES; 0, Low SES).
The fourth category corresponds to students’ preparedness for entering the university and includes two latent covariates:
- X23.
- The influence on the decision of the student to be admitted to university (Cronbach’s a = 0.73), was assessed based on the following variables: the extent to which the selection of a specific field of study was driven by the students’ desire for education (measured on a Likert scale from 1 to 5); the extent to which the choice reflected the students’ personal preferences (Likert scale, 1 to 5); and the degree of parental interest in the students’ academic progress throughout their studies (Likert scale, 1 to 5).
- X24.
- The reasons which led the students to pursue university studies (Cronbach’s a = 0.74), were evaluated through the following variables: the pursuit of social advancement (Likert scale, 1 to 5); the aspiration for social recognition (Likert scale, 1 to 5); personal development (Likert scale, 1 to 5); the desire for social mobility (Likert scale, 1 to 5); the perception that attending university is an expected norm within Greek society (Likert scale, 1 to 5); the wish for independence from the family environment (Likert scale, 1 to 5); the acquisition of general knowledge (Likert scale, 1 to 5); the pursuit of prestige associated with being a university graduate (Likert scale, 1 to 5); meeting parental expectations (Likert scale, 1 to 5); and experiencing “student life” (Likert scale, 1 to 5).
In order to test the applicability of the above model to the Greek context, data were collected in a period of 18 months (from September 2016 until February 2018), using a questionnaire on a sample of 1236 cases. The sample derives from a population that amounts to 20,892 observations, which represent study times (In months) of students who entered different departments of a certain Greek University, from the academic year 1983–1984 to 2005–2006 (i.e., 23 consecutive cohorts). The sample was collected using finite population sample techniques for censored data [20], and it was a proportionally stratified sample for gender and academic department [21]. Subsequently, data were analyzed using a Cox proportional hazards model as described in the next section.
2.3. The Statistical Model
Survival analysis is a frequently used method for observing the duration between events. The basic concepts and terminology of survival analysis are as follows: We consider as a random variable that represents survival time, in our case, the duration of studies. Then, the survival distributions of can be described by four functions, which for the purposes of this study express graduation probabilities, as follows: We define as the graduation probability density function and F(t) as the cumulative graduation density function. The survivor function is , defined in our context as the probability that a student has not graduated, immediately past time t. Then, we define the hazard function as as the instantaneous graduation rate or, (see Figure 2) in other words, as a measure of the likelihood that a student graduates at time t, given that the specific student has been studying at university until time [22].
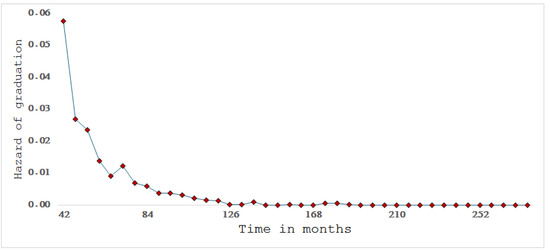
Figure 2.
Hazard function is an instantaneous graduation rate for the total sample.
In the context of survival analysis, various methods have been proposed to examine the relationship of survival distributions with a number of independent variables (commonly known as covariates). Cox Proportional Hazard Model or Cox Model is a method proposed by Cox [23] in order to examine how specified covariates influence the rate of a particular event happening. This rate is commonly referred to as the hazard rate. The Cox model expressed the hazard function by the following equation:
where represents the survival time, is the hazard function determined by a set of covariates , and the coefficients measure the impact of the covariates. The term corresponds to the value of the hazard if all are equal to zero and it is called the baseline hazard, while the “” in denotes that the risk may change over time. Finally, the quantities are called hazard ratios (HR). A value of HR greater than one, or, equivalently, a hazard ratio greater than one, indicates that as the value of the covariate increases, the event hazard increases and, thus, the length of survival decreases.
Note that, in the Cox model, the dependent variable is not the time variable per se, but the hazard function . Thus, the Cox model is semi-parametric and can be applied in the case of discrete time variables, as it does not require assumptions about the underlying distribution of survival times. In addition, the effects of the covariates over are assumed to be constant over time.
2.4. The Empirical Model
The Cox proportional hazards model is used in this study because it serves the investigation of the relationship between the duration of study-dependent time variable that includes discrete censored values, and a number of covariates/independent variables.
More specifically, it is considered that the random variable Yt represents the duration of studies for each one of the 1236 students, members of the sample, as described in Section 2. It is also considered that the dependent variable is associated with 24 covariates/independent variables, four latent and 20 observed (as it is described in Section 2), on the basis of the Cox proportional hazards model described by the following equation:
where i denotes each one of the i = 1, 2, …, n students (members of the sample); in our case, n = 1236, is the hazard function, represents the duration of studies for each of the above students, enotes each one of the covariates and symbolizes each one of the coefficients. It is considered that the above model (Figure 1 and Equation (2)) can adequately describe the factors affecting time until graduation in the case of Greek higher education. Subsequently, the above model was applied in real cases, while goodness of fit tests was applied to check the applicabbility of the model to the empirical sample data, (see Appendix A and Figure A1), using the SPSSv26 statistical package and the Backward Stepwise method for variable selection, and the results are described in Section 3.
3. Results
Figure 3 represents the estimates of the significant regression coefficients eβi of the model described in Equation (2). Based on these results, one could argue the following: Study habits, vocational rehabilitation, academic performance, unforeseen factors, and work during studies, as well as gender, age at admission in the university, and finally the reasons which led the students to pursue university education appear to have a significant impact on the duration of studies.
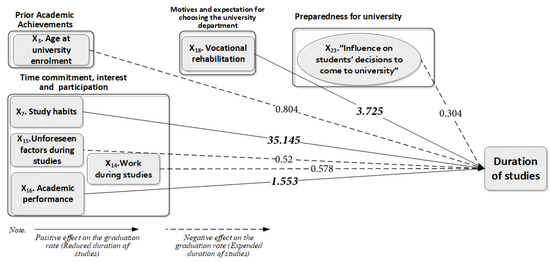
Figure 3.
Graphical representation of the statistically significant covariates.
The first three of the above covariates have a positive effect on the graduation rate in the sense that they reduce the duration of studies. In particular, students studying throughout the semester (i.e., variable Study Habits) tend to graduate faster than those who study during the examination period or less. Quoting that for these students exp (β) is bigger than one (eβ7 = 35.145, 95% CI [32.8, 37.5]), it follows that the hazard of graduating for students who study throughout the semester is 35 times higher, compared to those who do not study throughout the semester. Vocational rehabilitation expectations from studies accelerate the graduation time, as well. Again, students who have the above expectations are almost four times more likely to graduate faster (eβ18 = 3.725, 95% CI [1.38, 11.1]) than those who do not. Another factor that contributes to faster graduation is academic performance. In fact, as the average score achieved at the end of the first two semesters increases by one unit, the graduation rate increases by one and a half times (eβ16 = 1.553, 95% CI [1.3, 1.9]).
The remaining covariates have a negative effect on the graduation rate in the sense that they extend the duration of studies. More specifically, it is clear that students’ conjunctures during their studies, such as illness and work, are key factors that tend to increase the time to graduation. Indeed, the hazard of graduation for students who experience unforeseen factors during their studies (eβ15 = 0.52, 95% CI [0.3, 0.8]) is 48.2% lower than those who do not (100 × (1 − 0.52) = 48.2%); similarly, the hazard of graduation for those who work during their studies (eβ14 = 0.578, 95% CI [0.4, 0.8]) is less than half (42%) compared to those who do not work during their studies (100 × (1 − 0.578) = 42.2%). Also, it seems that students who have enrolled at the university at an older age than usual, and students whose decision to pursue university studies was influenced by others, are more likely to graduate later (eβ3 = 0.804, 95% CI [0.7, 0.9]). In fact, the hazard of graduation for students who enroll at the university at an older age is 20% (100× (1 − 0.804) = 19.6) compared to those who enroll at the university at the usual age. And finally, students whose decision to be admitted to university was influenced by others (eβ23 = 0.304, 95% CI [0.1, 0.9] are less likely to graduate compared to those whose decision was not influenced (100 × (1 − 0.304) = 69.6%).
4. Conclusions
In this study, Cox’s Proportional Hazards Model was used to evaluate a theoretical model for the factors affecting time to degree. In the above framework, a conceptual model was developed, through which the duration of studies is associated with specific observed and latent factors/covariates. These factors either pre-exist students’ enrolment at the university or are formulated later during their studies. Following that, a Cox Proportional Hazards Model was employed to test the applicability of the above theoretical model on real data. The results indicate that Cox’s Proportional Hazards Model proved suitable in approaching and interpreting factors associated with academic success in higher education, measured in terms of time to graduation. Overall, the first conclusion from the proportional hazards model developed here is that the students who study throughout the semester, expect vocational rehabilitation, and achieve high average scores by the end of the first two semesters of their studies, tend to graduate faster.
Author Contributions
Conceptualization, D.K. and L.M.; methodology, D.K.; validation, D.K.; formal analysis, D.K.; investigation, D.K., L.M. and F.N.; data curation, D.K.; writing—original draft preparation, D.K.; writing—review and editing, L.M. and F.N.; visualization, D.K.; supervision, L.M. and F.N.; project administration, L.M.; funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study protocol was approved by the Ethics Committee of PGR AOC (protocol code PGR-AOC-2023-09D23, date of approval 13 September 2023).
Informed Consent Statement
The Committee confirms that the proposed research meets the ethical standards required for studies involving human participants. The study design ensures voluntary participation, anonymity, informed consent, and safeguards the rights and well-being of participants throughout the study and the process.
Data Availability Statement
There are no data available for this article as the general research it is part of is still ongoing and the authors do not want their data to be made public yet.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Goodness of Fit Test
To assess the goodness of fit of our model, we rely on the most common metric, Harrell’s C statistic (C-index), which is defined as the percentage of congruent pairs, i.e., pairs of individuals for which the expected event times are predicted in the correct order, divided by the total number of possible pairs to evaluate. The closer to one, the more accurate the Cox model is. We support the index C with a further evaluation by looking for the graphical validation of the proportional hazards assumption (see table and diagrams below).
| Maximum likelihood for the baseline model (when the effect of all covariates is set to zero) | ||||
| 2642.904. | ||||
| Maximum likelihood for the final model | df. | p | Step * | |
| 2515.444 | 117.717 | 13 | 0.000 | 29 |
| Harrell’s C statistic = 0.797 | ||||
- * The method used is Backward Stepwise, which was completed in k steps.
| Correlations among numeric Covariates | |||||
| (X3) Students’ Age at the time of university enrolment | X4. Secondary school grades: (the score ranges from 10, the minimum grade required for admission to university, to 20), | X5. University access score: | (X16) Academic performance: Average score of the first two semesters of studies | ||
| (X3) Students’ Age at the time of university enrolment | Pearson Correlation | 1 | −0.252 | −0.549 | −0.044 |
| Sig. (2-tailed) | 0.000 | 0.000 | 0.123 | ||
| X4. Secondary school grades: (the score ranges from 10, the minimum grade required for admission to university, to 20), | Pearson Correlation | −0.252 | 1 | 0.252 | 0.267 |
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | ||
| X5. University access score: | Pearson Correlation | −0.549 | 0.252 | 1 | 0.223 |
| Sig. (2-tailed) | 0.000 | 0.000 | 0.000 | ||
| (X16) Academic performance: Average score of the first two semesters of studies | Pearson Correlation | −0.044 | 0.267 | 0.223 | 1 |
| Sig. (2-tailed) | 0.123 | 0.000 | 0.000 | 0.000 | |
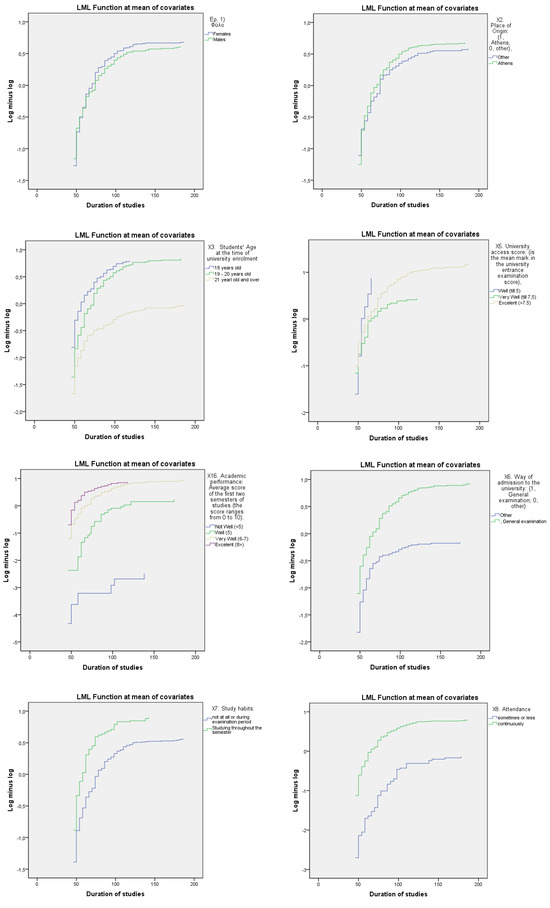
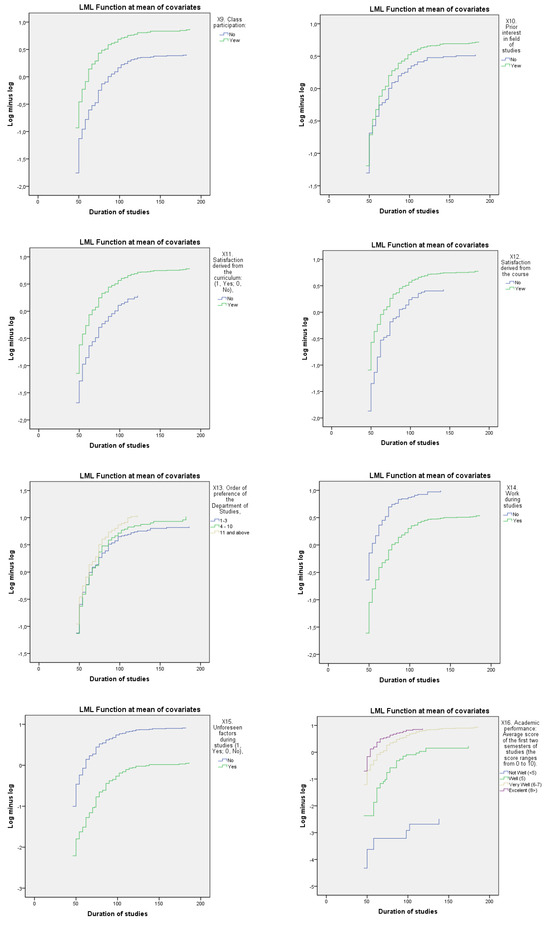
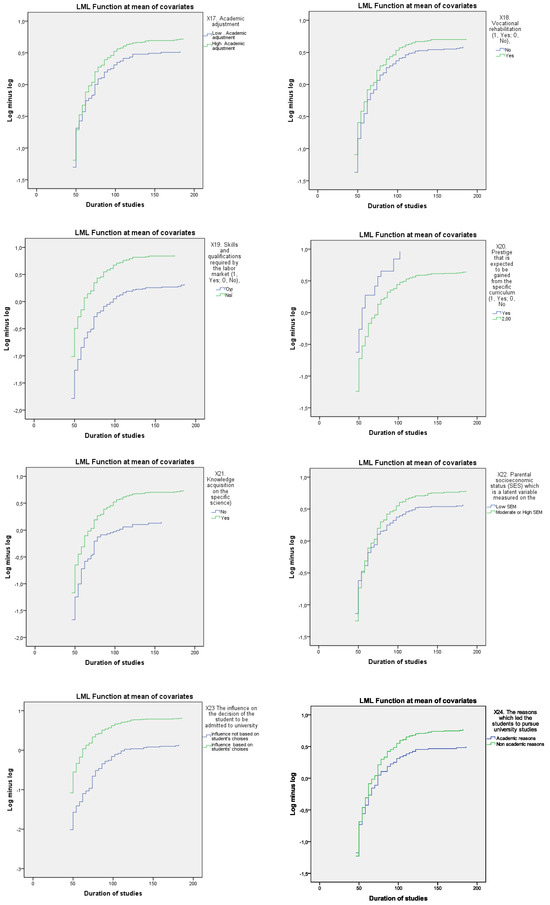
Figure A1.
Graphical representation of the graphical validation of the proportional hazards assumption.
References
- Mcneely, J. College Student Mortality; United States Government Printing Office: Washington, DC, USA, 1938. [Google Scholar]
- Tinto, V. Dropout from Higher Education: A Theoretical Synthesis of Recent Research. Rev. Educ. Res. 1975, 45, 89–125. [Google Scholar] [CrossRef]
- Bayer, A.E.; Astin, A.W.; Bauman, K.E.; Schoenfeldt, L.F. Personal and Environmental Factors Associated with College Dropouts Among High Aptitude Students. J. Educ. Psychol. 1966, 55, 219. [Google Scholar]
- Spady, W.G. Dropouts from Higher Education: Toward an Empirical Model. Interchange 1971, 2, 38–62. [Google Scholar] [CrossRef]
- Aina, C. Parental Background and College Drop Out. Evidence from Italy. Higher Educ. 2005, 65, 1–22. [Google Scholar]
- Vander Schee, B.A. College Student Retention: Formula for Student Success (review). J. Coll. Stud. Dev. 2007, 48, 360–362. [Google Scholar] [CrossRef]
- Reason, R.D. Student Variables that Predict Retention: Recent Research and New Developments. NASPA J. 2009, 46, 482–501. [Google Scholar] [CrossRef]
- Astin, A.W. Student Involvement: A Developmental Theory for Higher Education. J. Coll. Stud. Development. 1999, 40, 518. [Google Scholar]
- Bean, J.P. Dropouts and Turnover: The Synthesis and Test of a Causal Model of Student Attrition. Res. High. Educ. 1980, 12, 155–187. [Google Scholar] [CrossRef]
- Cabrera, A.F.; Nora, A.; Castaneda, M.B. College Persistence: Structural Equations Modeling Test of an Integrated Model of Student Retention. J. High. Education. 1993, 64, 123–139. [Google Scholar] [CrossRef]
- Smith, J.P.; Naylor, R.A. Dropping out of university: A statistical analysis of the probability of withdrawal for UK university students. J. R. Stat. Soc. Ser. A Stat. Soc. 2001, 164, 389–405. [Google Scholar] [CrossRef]
- Voelkle, M.C.; Sander, N. University Dropout: A Structural Equation Approach to Discrete-Time Survival Analysis. J. Individ. Differ. 2008, 29, 134–147. [Google Scholar] [CrossRef]
- Booth, A.L.; Satchell, S.E.; Bootht, A.L. The Hazards of Doing a PhD: An Analysis of Completion and Withdrawal Rates of British PhD Students in the 1980s. J. R. Stat. Soc. Ser. A Stat. Soc. 1995, 158, 297–318. [Google Scholar] [CrossRef]
- Kalamatianou, A.G.; McClean, S. The Perpetual Student: Modeling Duration of Undergraduate Studies Based on Lifetime-Type Educational Data. Lifetime Data Anal. 2003, 9, 311–330. [Google Scholar] [CrossRef] [PubMed]
- Arulampalam, W.; Naylor, R.; Smith, J. Factors affecting the probability of first year medical student dropout in the UK: A logistic analysis for the intake cohorts of 1980–1992. Med. Educ. 2004, 38, 492–503. [Google Scholar] [CrossRef] [PubMed]
- Nikolaidis, P.; Ismail, M.; Shuib, L.; Khan, S.; Dhiman, G. Predicting Student Attrition in Higher Education through the Determinants of Learning Progress: A Structural Equation Modelling Approach. Sustainability 2022, 14, 13584. [Google Scholar] [CrossRef]
- Thies, T.; Falk, S. Article Which Factors Drive Major Change and University Dropout? An Analysis on International Degree-Seeking Students at German Universities. J. Int. Stud. 2024, 14, 326–346. [Google Scholar]
- Visser, M.S.; Luwel, M.; Moed, H.F. The attainment of doctoral degrees at Flemish Universities: A survival analysis. High. Educ. 2007, 54, 741–757. [Google Scholar] [CrossRef]
- Marshall, A.H.; Zenga, M. Simulating Coxian phase-type distributions for patient survival. Int. Trans. Oper. Res. 2009, 16, 213–226. [Google Scholar] [CrossRef]
- Marc, E.B.; Maurice, J.S.; Richard, J.S. Cancer Clinical Trials Methods and Practice; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 8th ed.; State University Press: Ames, IA, USA, 1989. [Google Scholar]
- Chimka, J.R.; Reed-Rhoads, T.; Barker, K. Proportional hazards models of graduation. J. Coll. Stud. Ret. 2007, 9, 221–232. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life tables (with discussion). J. R. Stat. Soc. Ser. B 1972, 34, 187–220. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).