The New Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X-G Family of Distributions with Properties and Applications
Abstract
1. Introduction
2. The New Family of Distributions
Sub-Families
- When we obtain the new Marshall–Olkin–type II half-logistic-G–odd Burr X-G (MO-TIIHL-OBX-G) family of distributions, with the cdf given byfor , and parameter vector .
- If , we obtain the type II exponentiated half-logistic-G odd Burrr X-G (TIIEHL-OBX-G) with the cdf given byfor , and parameter vector . This is a new family of distributions.
- When we obtain the Marshall–Olkin–type II exponentiated half-logistic-G–odd Rayleigh-G (MO-TIIEHL-OR-G) family of distributions, with the cdf given byfor , and parameter vector . This is a new family of distributions.
- When we obtain the Marshall–Olkin–type II half-logistic-G–odd Rayleigh-G (MO-TIIHL-OR-G) family of distributions, with the cdf given byfor and parameter vector . This is a new family of distributions.
- When we obtain the type II half-logistic-G odd Burrr X-G (TIIHL-OBX-G) family of distributions, with the cdf given byfor and parameter vector . This is a new family of distributions.
- When we obtain the type II exponentiated half-logistic-G Odd Rayleigh-G (TIIEHL-OR-G) family of distributions, with the cdf given byfor and parameter vector . This is a new family of distributions.
- When we obtain the type II half-logistic-G Odd Rayleigh-G (TIIHL-OR-G) family of distributions, with the cdf given bywith parameter vector . This is a new family of distributions.There are several generalized distributions that can be readily obtained by specifying the baseline cdf G.
3. Some Statistical Properties
3.1. Linear Representation of the Density
3.2. Quantile Function
3.3. Moments and Probability-Weighted Moments
3.4. Distribution of Order Statistics
3.5. Rényi Entropy
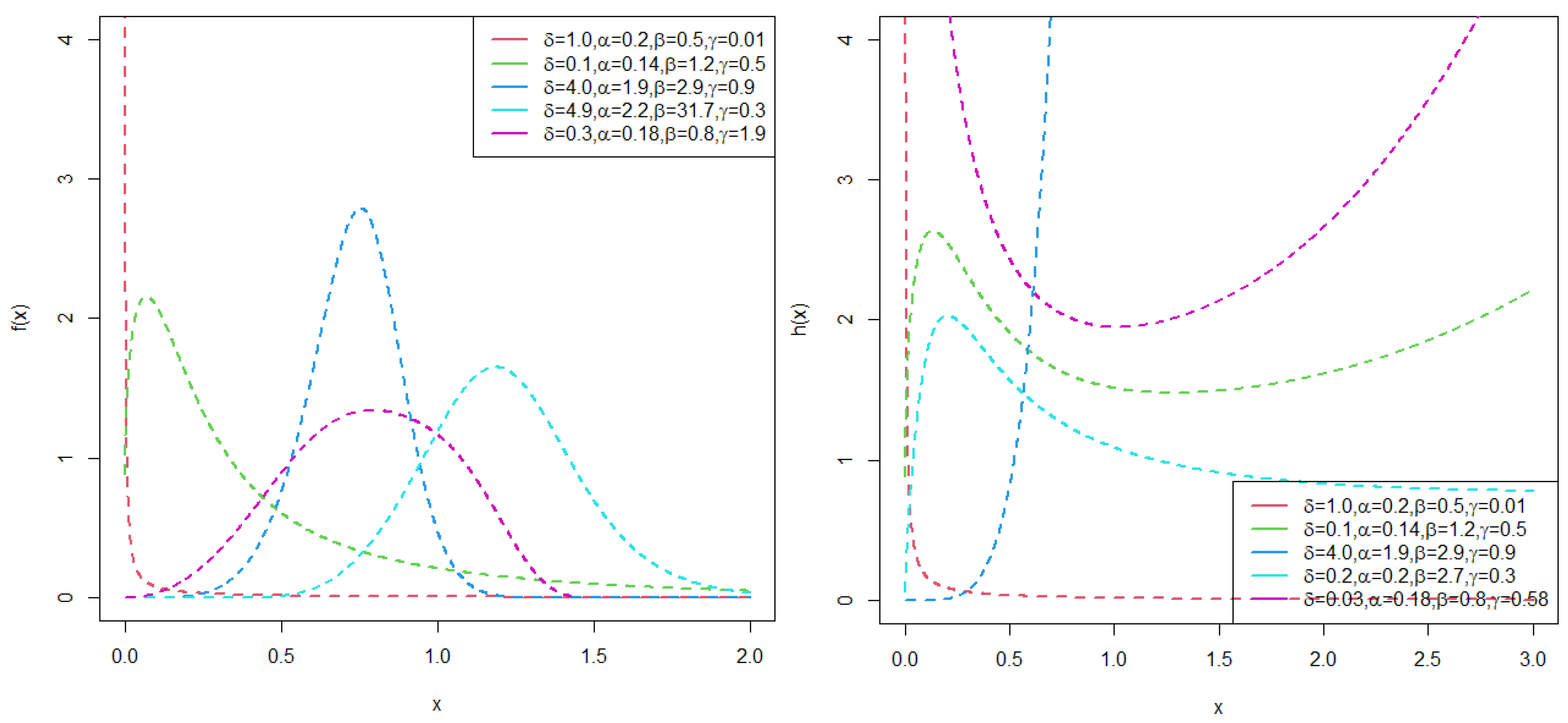
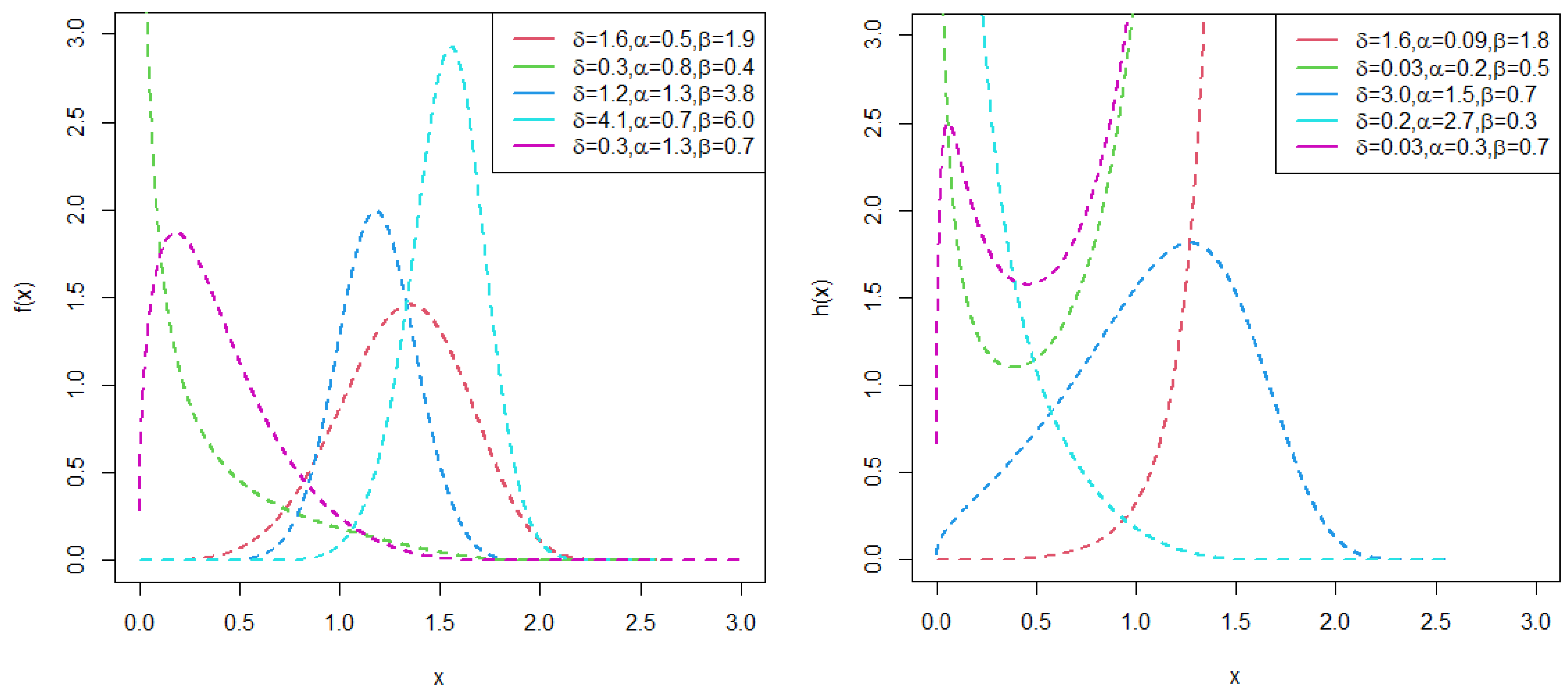
4. Some Special Models
4.1. Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X–Weibull (MO-TIIEHL-OBX-W) Distribution
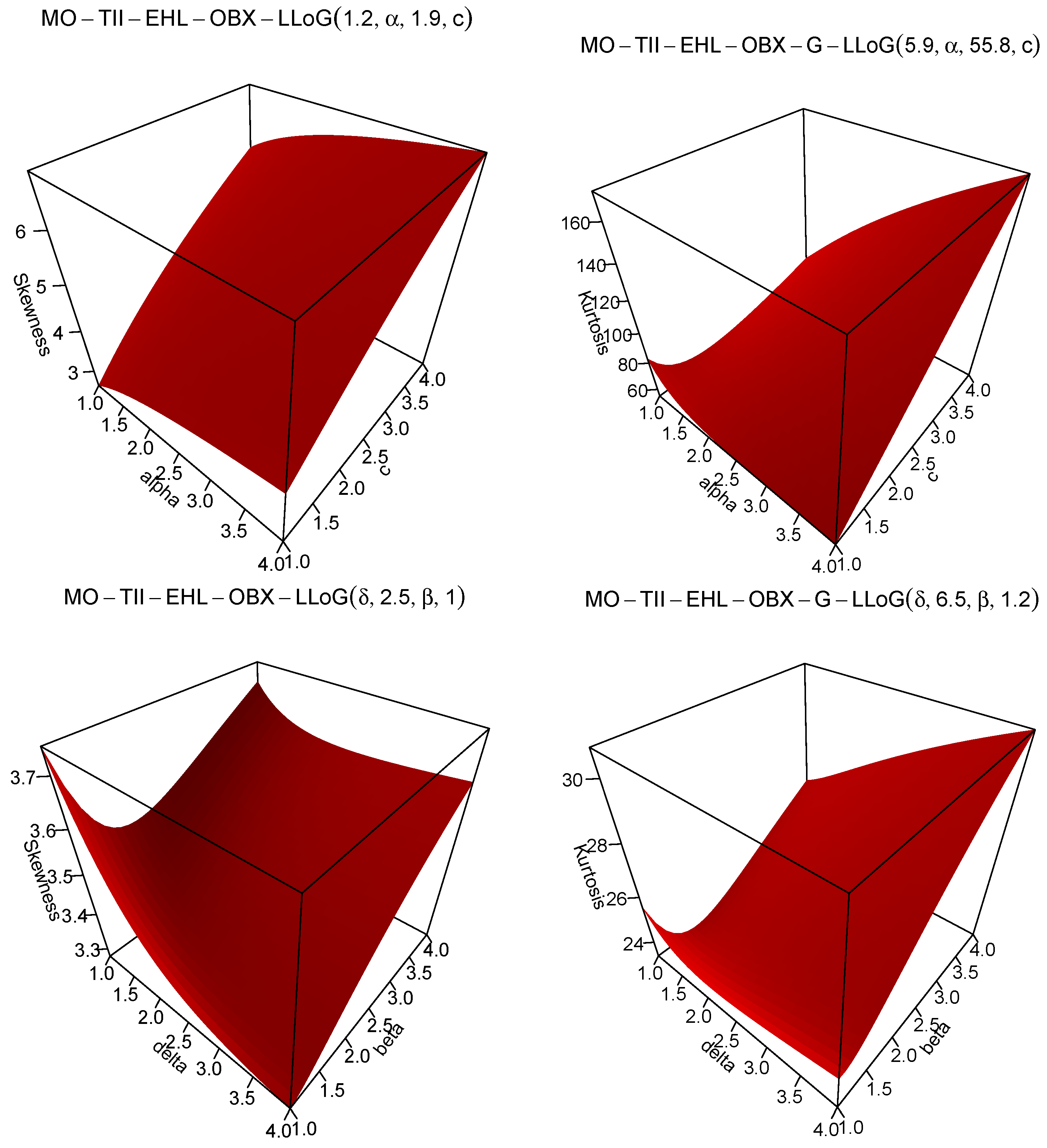
4.2. Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X–Log-Logistic (MO-TIIEHL-OBX-LLoG) Distribution
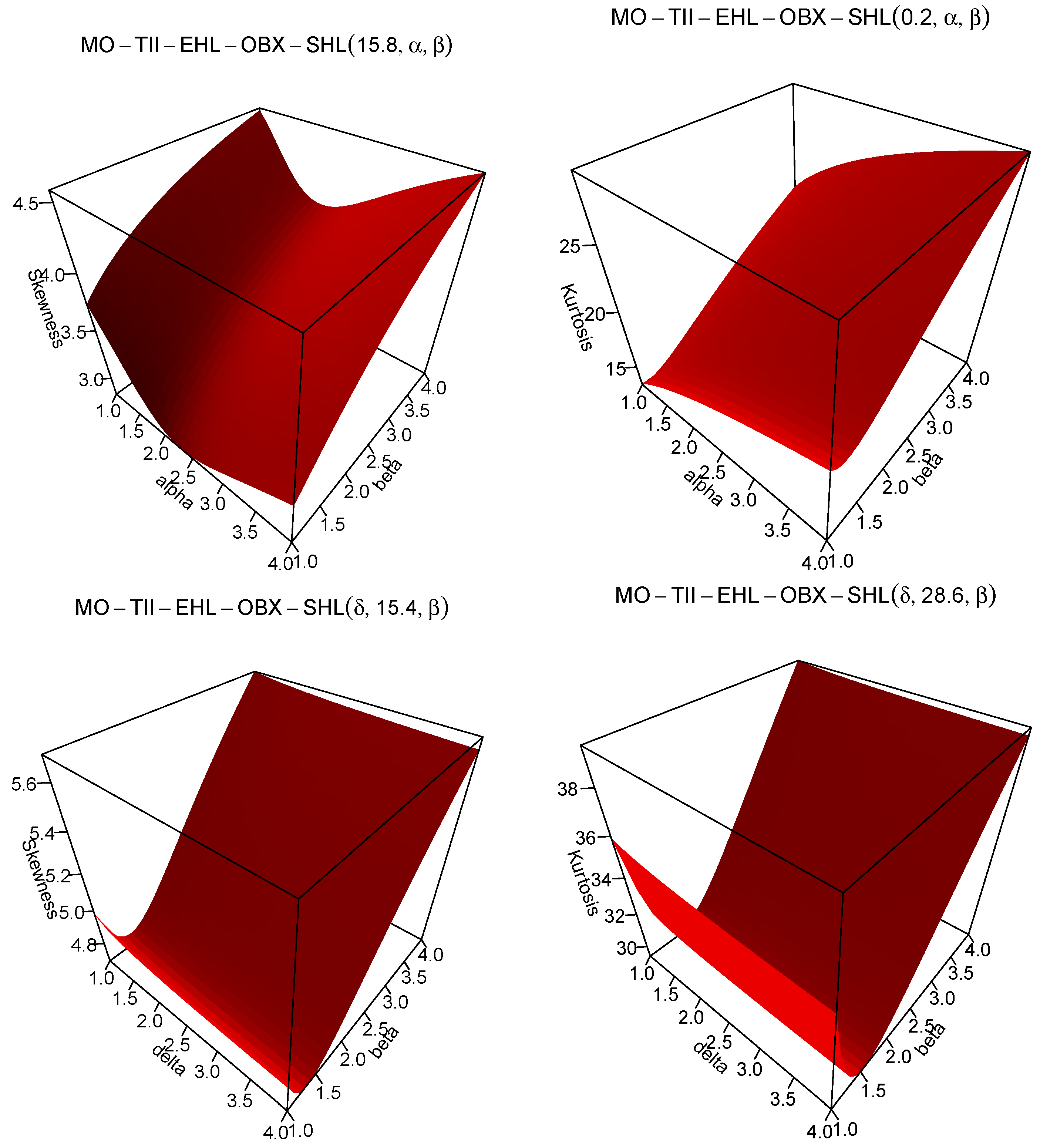
4.3. Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X–Standard Half-Logistic (MO-TIIEHL-OBX-SHL) Distribution
5. Simulation Study
6. Risk Measures
6.1. Value at Risk
6.2. Tail Value at Risk
6.3. Tail Variance
6.4. Tail Variance Premium
6.5. Numerical Study for the Risk Measures
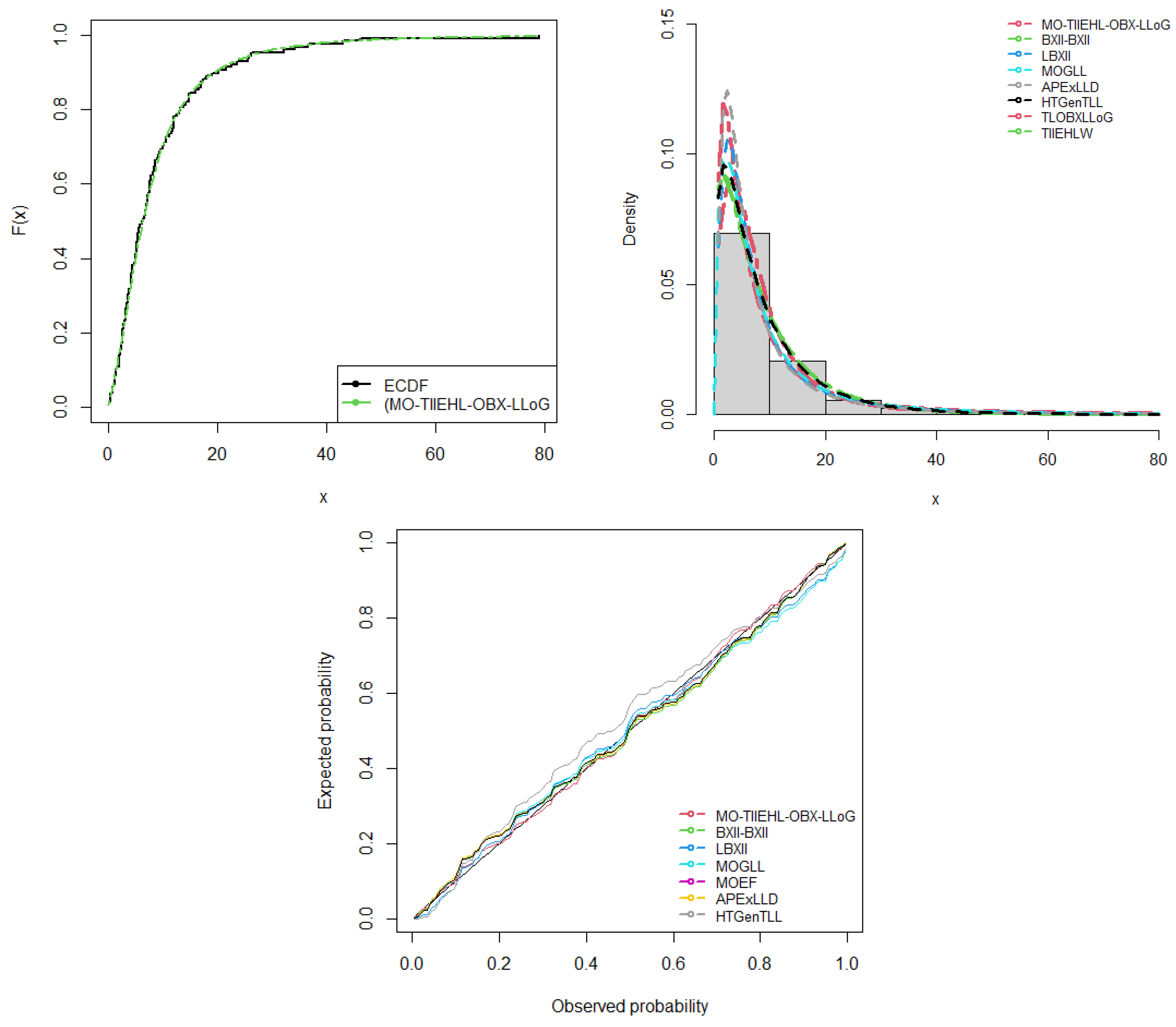
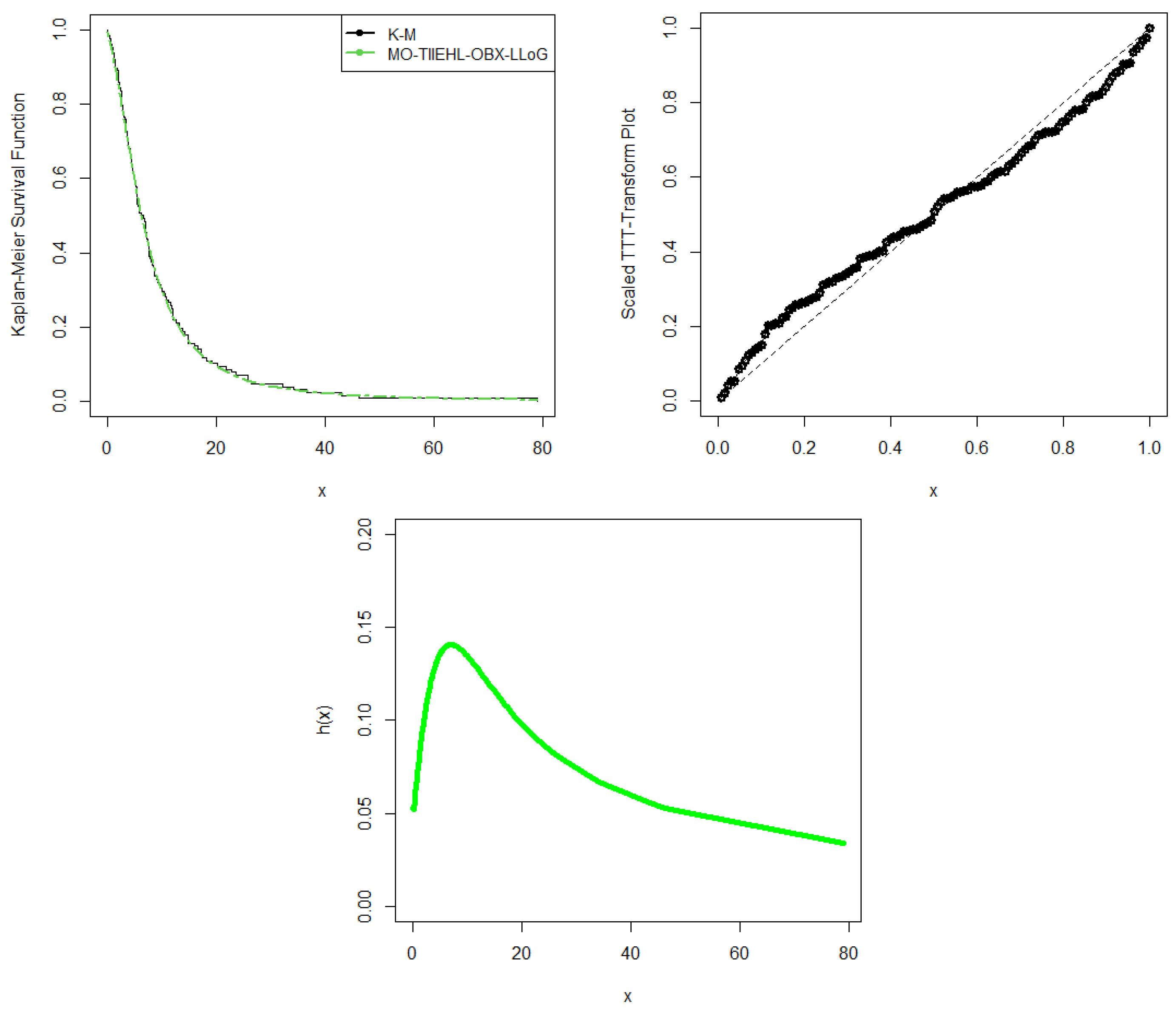
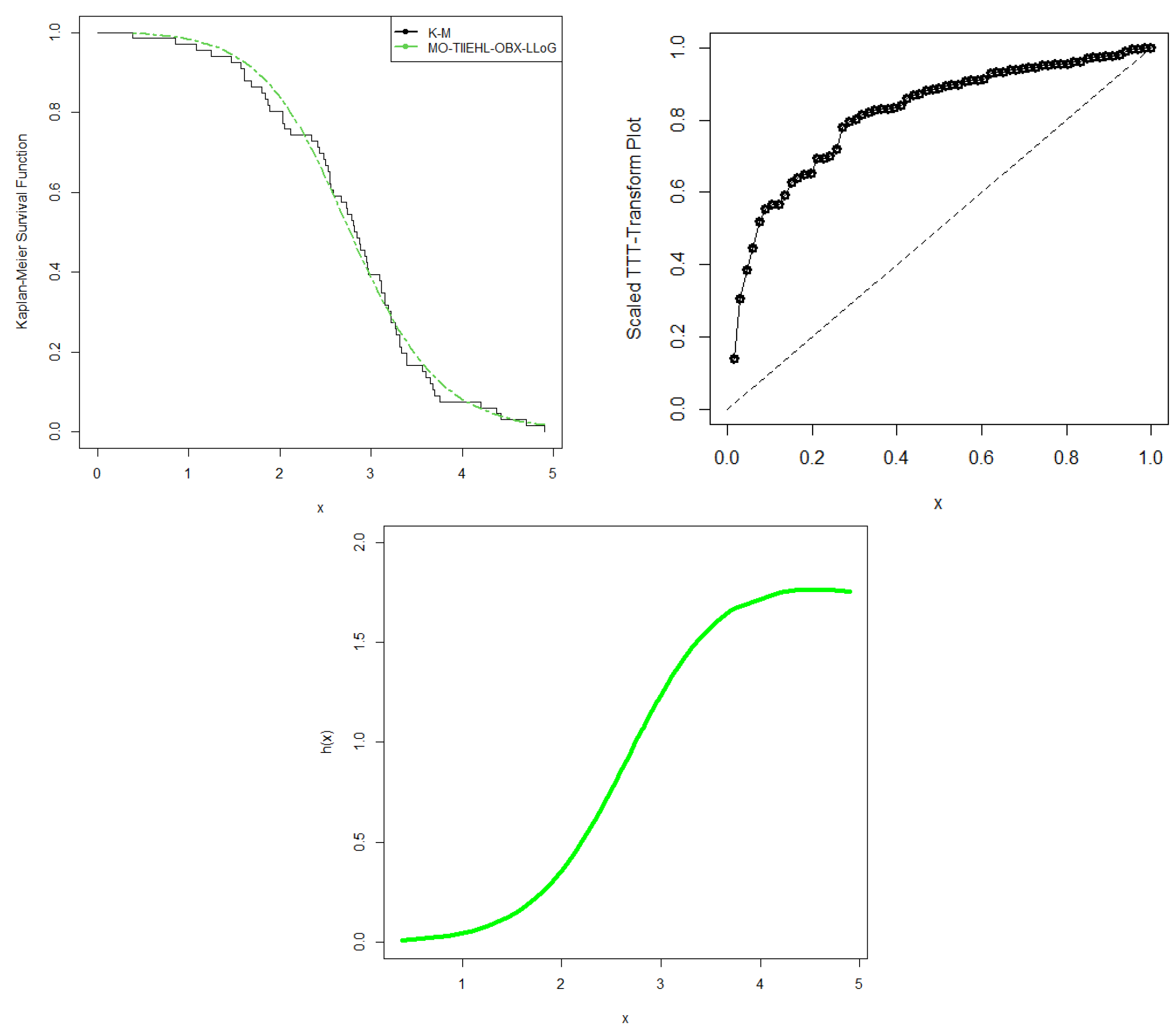
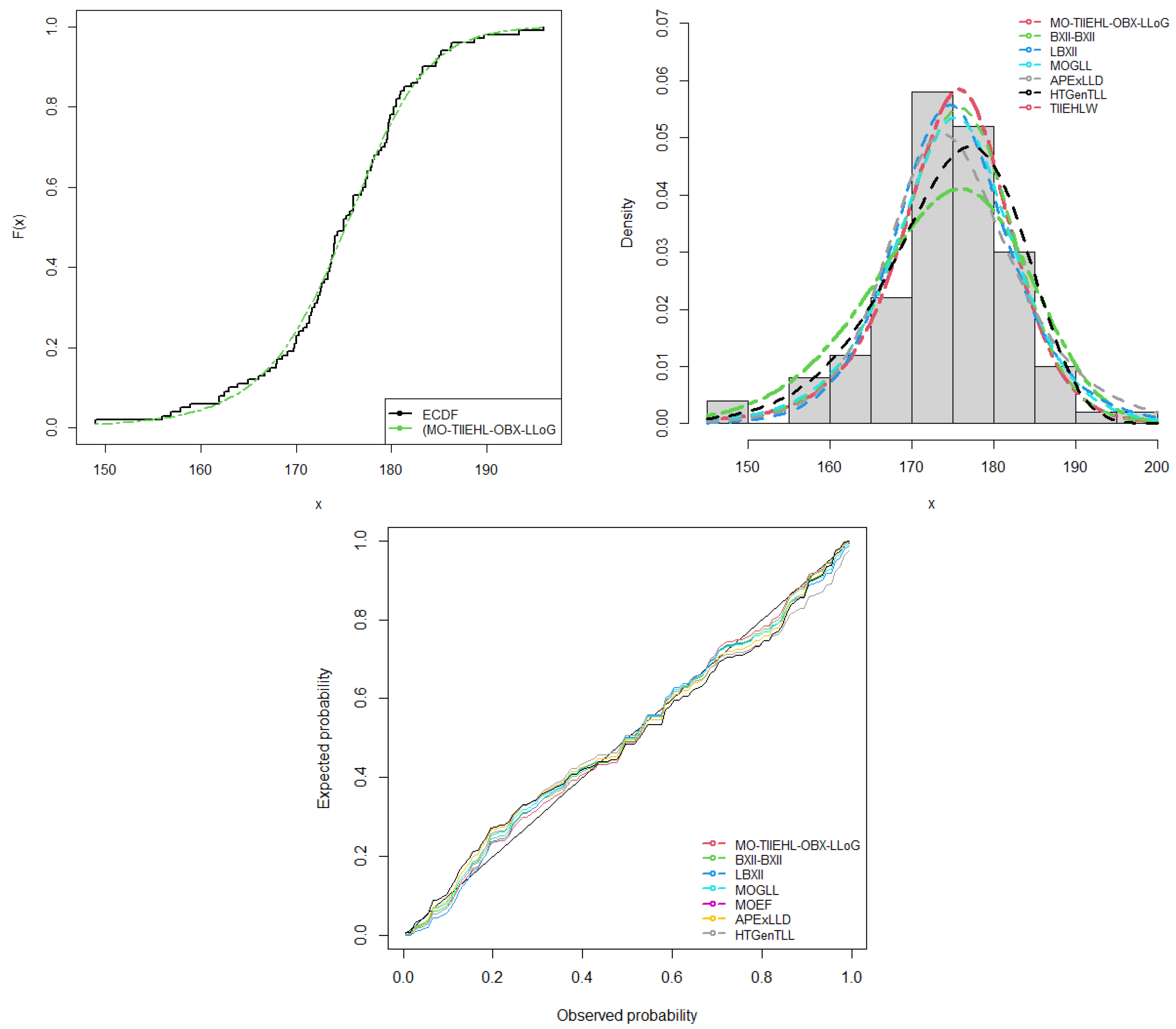
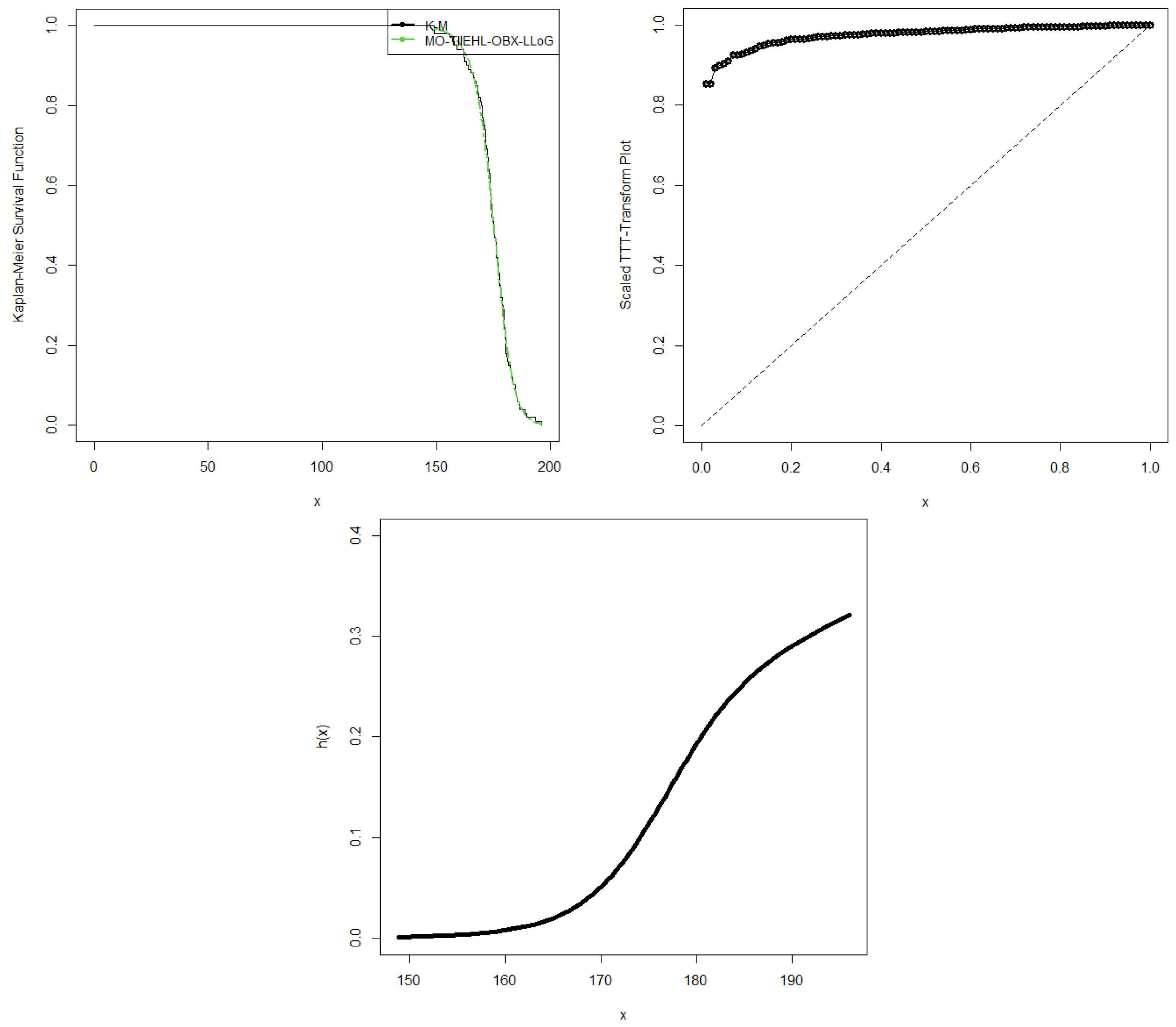
7. Applications
7.1. Remission Time of Cancer Data
7.2. Carbon Fiber Data
7.3. Height Data
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Competing Models
Application Data Sets
- x<-c(0.08, 4.98, 25.74, 3.7, 10.06, 2.69, 7.62, 1.26, 7.87, 4.4,
- 2.02, 21.73, 2.09, 6.97, 0.5, 5.17, 14.77, 4.18, 10.75, 2.83,
- 11.64, 5.85, 3.31, 2.07, 3.48, 9.02, 2.46, 7.28, 32.15, 5.34,
- 16.62, 4.33, 17.36, 8.26, 4.51, 3.36, 4.87, 13.29, 3.64, 9.74,
- 2.64, 7.59, 43.01, 5.49, 1.4, 11.98, 6.54, 6.93, 6.94, 0.4, 5.09,
- 14.76, 3.88, 10.66, 1.19, 7.66, 3.02, 19.13, 8.53, 8.65, 8.66,
- 2.26 ,7.26 ,26.31, 5.32, 15.96, 2.75, 11.25, 4.34, 1.76, 12.03,
- 12.63, 13.11, 3.57, 9.47, 0.81, 7.39, 36.66, 4.26, 17.14, 5.71,
- 3.25, 20.28, 22.69, 23.63, 5.06, 14.24, 2.62, 10.34, 1.05, 5.41,
- 79.05, 7.93, 4.5, 2.02, 0.2 ,7.09, 25.82, 3.82, 14.83, 2.69, 7.63,
- 1.35, 11.79, 6.25, 3.36, 2.23, 9.22, 0.51, 5.32, 34.26 ,4.23, 17.12,
- 2.87, 18.1, 8.37, 6.76 ,3.52, 13.8, 2.54, 7.32 ,0.9 ,5.41, 46.12,
- 5.62, 1.46, 12.02 ,12.07
- )
- ## MO-TIIEHL-OBX-LLoG
- fMOTIIEHLOBXLLoG<-function(delta ,alpha ,beta ,c)
- {
- −sum(log(4∗delta∗alpha∗beta∗(c∗((1+x^c)^(−2))∗(x^(c−1)))∗
- ((1−(1+x^c)^(−1))/((1+x^c)^(−1))^3)∗
- (exp(−((1−(1+x^c)^(−1))/((1+x^c)^(−1)))^2))∗
- ((1−exp(−((1−(1+x^c)^(−1))/((1+x^c)^(−1)))^2))^(beta−1))
- ∗((1+(1−exp(−((1−(1+x^c)^(−1))/((1+x^c)
- ^(−1)))^2))^beta)^(−(alpha+1)))∗((1−(1−exp(−((1−(1+x^c)^(−1))
- /((1+x^c)^(−1)))^2))^beta)^(alpha−1))
- ∗((1−(1−delta)∗((1−(1−exp(−((1−(1+x^c)
- ^(−1))/((1+x^c)^(−1)))^2))^beta)
- /(1+(1−exp(−((1−(1+x^c)^(−1))/((1+x^c)^(−1)))^2))^beta))
- ^alpha))^(−2)
- ))
- }
- MOTIIEHLOBXLLoG.result<-mle2(fMOTIIEHLOBXLLoG, hessian = NULL,
- start=list(delta=939.8992, alpha=91.96, beta=11.099, c=.088),
- optimizer="nlminb" ,lower=0)
- summary(MOTIIEHLOBXLLoG.result)
Goodness-of-Fit Test
- library(AdequacyModel)
- data=c(0.08, 4.98, 25.74, 3.7, 10.06, 2.69, 7.62, 1.26, 7.87, 4.4,
- 2.02, 21.73, 2.09, 6.97, 0.5, 5.17, 14.77, 4.18, 10.75, 2.83,
- 11.64, 5.85, 3.31, 2.07, 3.48, 9.02, 2.46, 7.28, 32.15, 5.34,
- 16.62, 4.33, 17.36, 8.26, 4.51, 3.36, 4.87, 13.29, 3.64, 9.74,
- 2.64, 7.59, 43.01, 5.49, 1.4, 11.98, 6.54, 6.93, 6.94, 0.4, 5.09,
- 14.76, 3.88, 10.66, 1.19, 7.66, 3.02, 19.13, 8.53, 8.65, 8.66,
- 2.26 ,7.26 ,26.31, 5.32, 15.96, 2.75, 11.25, 4.34, 1.76, 12.03,
- 12.63, 13.11, 3.57, 9.47, 0.81, 7.39, 36.66, 4.26, 17.14, 5.71,
- 3.25, 20.28, 22.69, 23.63, 5.06, 14.24, 2.62, 10.34, 1.05, 5.41,
- 79.05, 7.93, 4.5, 2.02, 0.2 ,7.09, 25.82, 3.82, 14.83, 2.69, 7.63,
- 1.35, 11.79, 6.25, 3.36, 2.23, 9.22, 0.51, 5.32, 34.26 ,4.23, 17.12,
- 2.87, 18.1, 8.37, 6.76 ,3.52, 13.8, 2.54, 7.32 ,0.9 ,5.41, 46.12,
- 5.62, 1.46, 12.02 ,12.07
- )
- MOTIIEHLOBXLLoG_pdf<-function(par,x){
- delta=par[1]
- alpha=par[2]
- beta=par[3]
- c=par[4]
- 4∗delta∗alpha∗beta∗(c∗((1+x^c)^(−2))∗(x^(c−1)))∗((1−(1+x^c)^(−1))
- /((1+x^c)^(−1))^3)∗(exp(−((1−(1+x^c)^(−1))/((1+x^c)^(−1)))^2))
- ∗((1−exp(−((1−(1+x^c)^(−1))/((1+x^c)^(−1)))^2))^(beta−1))
- ∗((1+(1−exp(−((1−(1+x^c)^(−1))/((1+x^c)^(−1)))^2))^beta)
- ^(−(alpha+1)))∗((1−(1−exp(−((1−(1+x^c)^(−1))/((1+x^c)^(−1)))^2))
- ^beta)^(alpha−1))∗((1−(1−delta)∗((1−(1−exp(−((1−(1+x^c)^(−1))
- /((1+x^c)^(−1)))^2))^beta)/(1+(1−exp(−((1−(1+x^c)^(−1))
- /((1+x^c)^(−1)))^2))^beta))^alpha))^(−2)
- }
- MOTIIEHLOBXLLoG_cdf<-function(par,x){
- delta=par[1]
- alpha=par[2]
- beta=par[3]
- c=par[4]
- 1-(delta∗((1-(1-exp(-((1-(1+x^c)^(-1))/((1+x^c)^(-1)))^2))^beta)
- /(1+(1-exp(-((1-(1+x^c)^(-1))/((1+x^c)^(-1)))^2))^beta)
- )^alpha)/(1-(1-delta)∗((1-(1-exp(-((1-(1+x^c)^(-1))
- /((1+x^c)^(-1)))^2))^beta)/(1+(1-exp(-((1-(1+x^c)^(-1))
- /((1+x^c)^(-1)))^2))^beta)
- )^alpha)}
- goodness.fit(pdf=MOTIIEHLOBXLLoG_pdf, cdf=MOTIIEHLOBXLLoG_cdf,
- mle=c( 9.6978e+02 , 1.1338e+01 , 3.7292e+00 , 6.5701e-02 ),
- data = data,method = "BFGS",
- domain = c(0,Inf), lim_inf = c(0,0,0,0),
- lim_sup = c(10000000000000000,100000000000000,
- 10000000000000000,10000000000000000))
References
- Marshall, A.W.; Olkin, I. A new method for adding a parameter to a family of distributions with application to the exponential and Weibull families. Biometrika 1997, 83, 641–652. [Google Scholar] [CrossRef]
- Yousof, H.M.; Afify, A.Z.; Hamedani, G.; Aryal, G.R. The Burr X generator of distributions for lifetime data. J. Stat. Theory Appl. 2017, 16, 288–305. [Google Scholar] [CrossRef]
- Al-Shomrani, A.; Arif, O.; Shawku, K.; Harif, S.; Shahbaz, M.Q. Topp-Leone family of distributions: Some properties and applications. Pak. J. Stat. Oper. Res. 2016, 12, 443–451. [Google Scholar] [CrossRef]
- Hassan, A.S.; Elgarhy, M.; Shakil, M. Type II half-logistic family of distributions with applications. Pak. J. Stat. Oper. Res. 2017, 13, 245–264. [Google Scholar]
- Al-Mofleh, H.; Elgarhy, M.; Afify, A.Z.; Zannon, M.S. Type II exponentiated half-logistic generated family of distributions with applications. Electron. J. Appl. Stat. Anal. 2020, 13, 536–561. [Google Scholar]
- Zografos, K.; Balakrishnan, N. On families of Beta and generalized gamma-generated distributions and associated inference. Stat. Methodol. 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Ristić, M.M.; Balakrishnan, N. The gamma-exponentiated exponential distribution. J. Stat. Comput. Simul. 2012, 82, 1191–1206. [Google Scholar] [CrossRef]
- Khaleel, M.A.; Oguntunde, P.E.; Al Abbasi, J.N.; Ibrahim, N.A.; Abujarad, M.H. The Marshall–Olkin Topp–Leone-G family of distributions with applications. Sci. Afr. 2020, 8, e00470. [Google Scholar]
- Al-Saiari, A.Y.; Baharith, L.A.; Mousa, S.A. Marshall-Olkin extended Burr type XII distribution. Int. J. Stat. Probab. 2014, 3, 78–84. [Google Scholar] [CrossRef]
- Yousof, H.M.; Afify, A.Z.; Nadarajah, S.; Hamedani, G.; Aryal, G.R. The Marshall-Olkin gerenalized-G family of distributions with applications. Statistica 2018, 78, 273–295. [Google Scholar]
- Krishna, E.; Jose, K.K.; Alice, T.; Ristić, M.M. The Marshall-Olkin Fréchet distribution. Commun. Stat.-Theory Methods 2013, 42, 4091–4107. [Google Scholar] [CrossRef]
- Ristić, M.M.; Kundu, D. Marshall-Olkin generalized exponential distribution. Metron 2015, 73, 317–333. [Google Scholar] [CrossRef]
- Almetwall, E.M.; Sabry, M.A.H.; Alharbi, R.; Alnagar, D.; Mubarak, S.A.M.; Hafez, E.H. Marshall-Olkin Alpha power Weibull distribution: Different methods of estimation based on type-I and type-II censoring. Complexity 2021, 1, 5533799. [Google Scholar] [CrossRef]
- Basheer, A.M. Marshall-Olkin alpha power inverse exponential distribution: Properties and aplications. Ann. Data Sci. 2022, 9, 301–313. [Google Scholar] [CrossRef]
- Mansoor, M.; Tahir, M.H.; Cordeiro, G.M.; Provost, S.B.; Alzaatreh, A. The Marshall-Olkin logistic exponential distribution. Commun. Stat.-Theory Methods 2019, 48, 220–234. [Google Scholar] [CrossRef]
- Dingalo, N.; Oluyede, B.; Chipepa, F. The type II exponentiated half logistic-odd Burr X-G power series class of distributions with applications. Heliyon 2023, 9, e22402. [Google Scholar] [CrossRef]
- Oluyede, B.; Tlhaloganyang, B.P.; Sengweni, W. The Topp-Leone odd Burr X-G family of distributions: Properties and applications. Stat. Optim. Inf. Comput. 2024, 12, 109–132. [Google Scholar] [CrossRef]
- Raghav, Y.S.; Ahmadini, A.A.H.; Mahnashi, A.M.; Rather, K.U.I. Enhancing estimation efficiency with proposed estimator: A comparative analysis of Poisson regression-based mean estimators. Kuwait J. Sci. 2025, 52, 100282. [Google Scholar] [CrossRef]
- Mishra, R.; Singh, R.; Raghav, Y.S. On combining ratio and product type estimators for estimation of finite population mean in adaptive cluster sampling design. Braz. J. Biom. 2024, 42, 412–420. [Google Scholar] [CrossRef]
- Rényi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; Volume 1, pp. 547–561. [Google Scholar]
- Mead, M.E.; Cordeiro, G.M.; Afify, A.Z.; Al-Mofleh, H. The Alpha power transformation family: Properties and applications. Pak. J. Stat. Oper. Res. 2019, 15, 525–545. [Google Scholar] [CrossRef]
- Moakofi, T.; Oluyede, B.; Tlhaloganyang, B.; Puoetsile, A. A new family of heavy-tailed generalized Topp-Leone-G distributions with application. Pak. J. Stat. Oper. Res. 2024, 20, 233–260. [Google Scholar] [CrossRef]
- Gad, A.M.; Hamedani, G.G.; Salehabadi, S.M.; Yousof, H.M. The Burr XII-Burr XII distribution: Mathematical properties and characterizations. Pak. J. Stat. 2019, 35, 229–248. [Google Scholar]
- Guerra, R.; Peña-Ramírez, F.A.; Cordeiro, G.M. The logistic Burr XII distribution: Properties and applications to income data. Stats 2023, 6, 1260–1279. [Google Scholar] [CrossRef]
- Niyoyunguruza, A.; Odongo, L.; Nyarige, E.; Habaneza, A.; Muse, A. Marshall-Olkin exponentiated Fréchet distribution. J. Data Anal. Inf. Process. 2023, 11, 262–292. [Google Scholar]
- Lee, E.T.; Wang, J. Statistical Methods For Survival Data Analysis; John Wiley and Sons: Hoboken, NJ, USA, 2003; Volume 476. [Google Scholar]
- Telee, L.B.S.; Kumar, V. Some properties and applications of half-Cauchy exponential extension distribution. Int. J. Stat. Appl. Math. 2022, 7, 91–101. [Google Scholar] [CrossRef]
- Mustafa, A.; Khan, M.I. Length biased extended Rayleigh distribution and its applications. J. Mod. Appl. Stat. Methods 2023, 22. [Google Scholar]


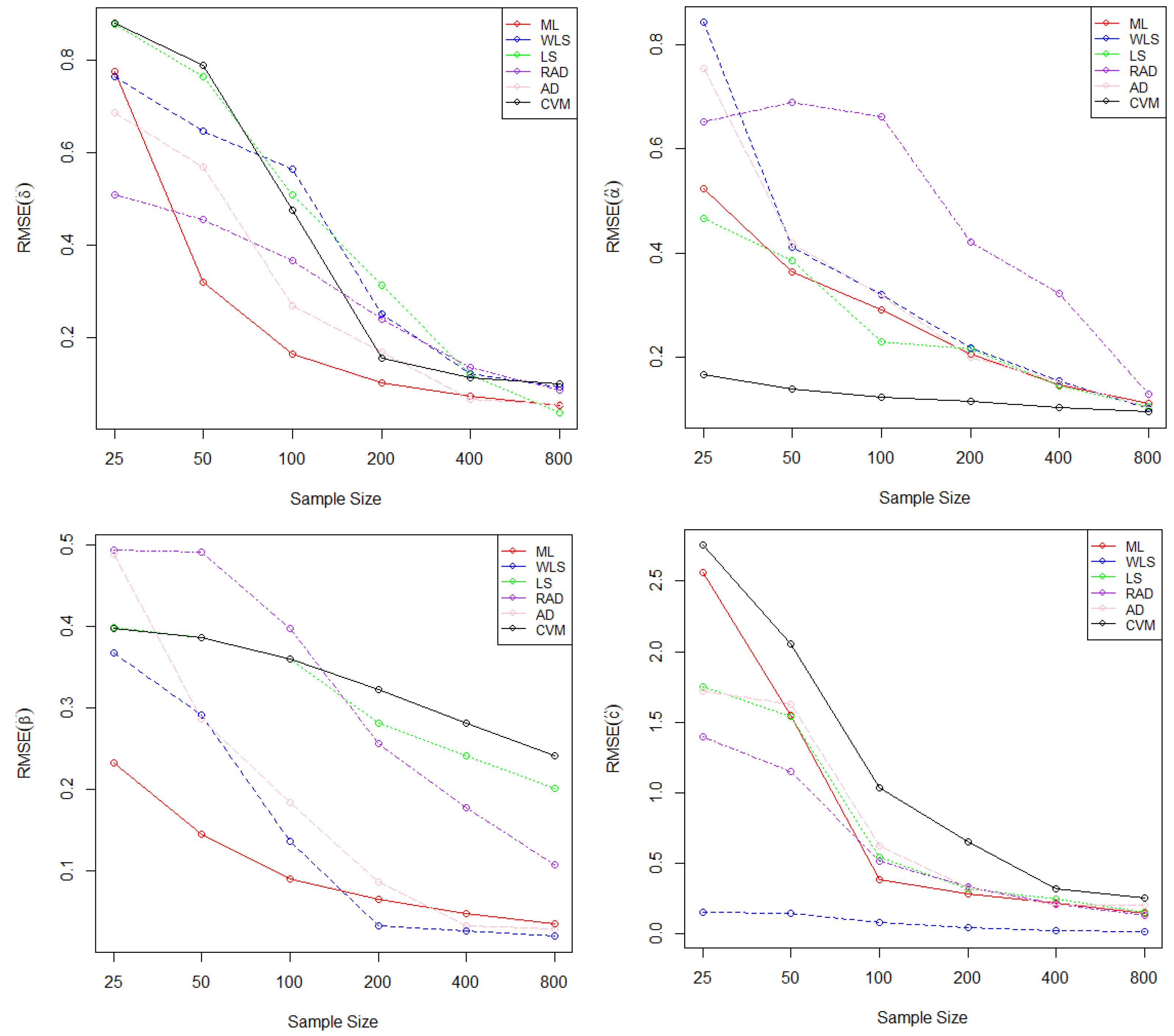
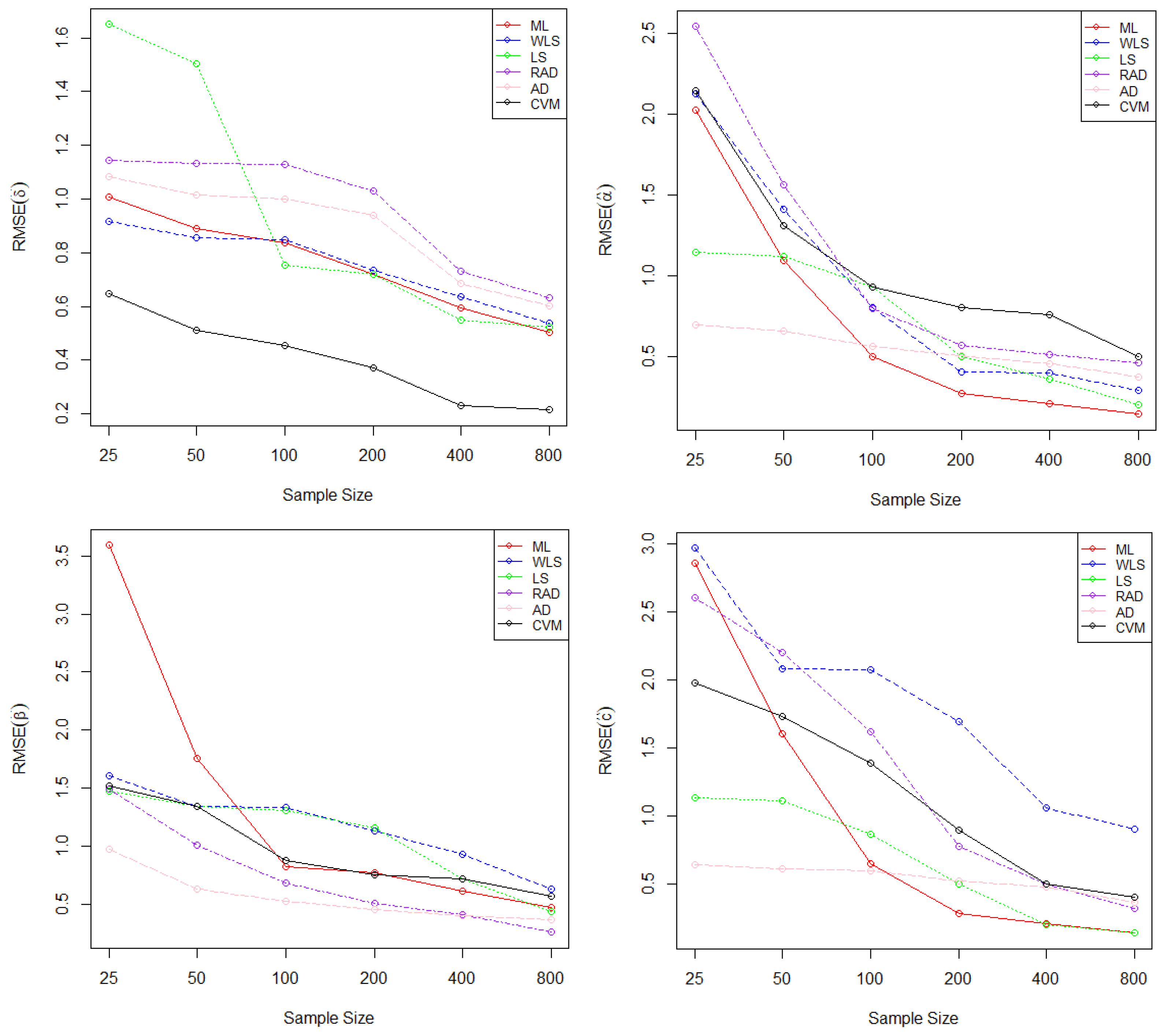

| (0.3, 1.4, 0.6, 2.2) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Sample Size (n) | Estimate | Parameter | ML | WLS | LS | RAD | AD | CVM |
| 25 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 20 | 25 | 34 | 33 | 22 | 33 | ||
| 50 | Abias | |||||||
| - | ||||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 14 | 21 | 33 | 37 | 24 | 35 | ||
| 100 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 12 | 25 | 37 | 36 | 22 | 34 | ||
| 200 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 13 | 23 | 36 | 38 | 22 | 35 | ||
| 400 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 18 | 25 | 29 | 38 | 17 | 36 | ||
| 800 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 23 | 20 | 28 | 33.5 | 24 | 39.5 | ||
| (1.4, 2.2, 1.4, 2.2) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Sample Size (n) | Estimate | Parameter | ML | WLS | LS | RAD | AD | CVM |
| 25 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 24 | 38 | 23 | 38 | 17 | 28 | ||
| 50 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 19 | 33 | 30 | 36 | 19 | 31 | ||
| 100 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 13 | 38 | 29 | 34 | 23 | 31 | ||
| 200 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 13 | 25 | 25 | 36 | 26 | 34 | ||
| 400 | Abias | |||||||
| - | ||||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 13 | 38 | 20 | 34 | 29 | 33 | ||
| 800 | Abias | |||||||
| c | ||||||||
| RMSE | ||||||||
| c | ||||||||
| Sum of the ranks | 14 | 34 | 22 | 32 | 32 | 34 | ||
| Parameters | n | ML | WLS | LS | RAD | AD | CVM |
|---|---|---|---|---|---|---|---|
| 25 | 1 | 3 | 6 | 4.5 | 2 | 4.5 | |
| 50 | 1 | 2 | 4 | 6 | 3 | 5 | |
| 100 | 1 | 3 | 6 | 5 | 2 | 4 | |
| 200 | 1 | 3 | 5 | 6 | 2 | 4 | |
| 400 | 2 | 3 | 4 | 6 | 1 | 5 | |
| 800 | 2 | 1 | 4 | 5 | 3 | 6 | |
| 25 | 3 | 5.5 | 2 | 5.5 | 1 | 4 | |
| 50 | 1.5 | 5 | 3 | 6 | 1.5 | 4 | |
| 100 | 1 | 6 | 3 | 5 | 2 | 4 | |
| 200 | 1 | 2.5 | 2.5 | 6 | 4 | 5 | |
| 400 | 1 | 6 | 2 | 5 | 3 | 4 | |
| 800 | 1 | 5.5 | 2 | 3.5 | 3.5 | 5.5 | |
| ∑ ranks | 16.5 | 45.5 | 43.5 | 63.5 | 28 | 55 | |
| Overall rank | 1 | 4 | 3 | 6 | 2 | 5 | |
| Significance Level | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 | |
|---|---|---|---|---|---|---|---|
| MO-TIIEHL-OBX-LLoG () | VaR | 2.1124 | 2.2503 | 2.4140 | 2.6182 | 2.8953 | 3.3454 |
| TVaR | 1.9689 | 2.2814 | 2.7358 | 3.4637 | 4.8428 | 8.6341 | |
| TV | 76.5335 | 91.1101 | 112.6387 | 147.7041 | 215.1270 | 399.3349 | |
| TVP | 55.5424 | 70.6139 | 92.8467 | 129.0122 | 198.4572 | 388.0023 | |
| MO-TIIEHL-OBX-LLoG () | VaR | 2.0091 | 2.1085 | 2.2264 | 2.3736 | 2.5744 | 2.9037 |
| TVaR | 1.7200 | 1.9960 | 2.3985 | 3.0451 | 4.2748 | 7.6771 | |
| TV | 22.2368 | 26.1101 | 31.6559 | 40.2540 | 55.2919 | 85.8062 | |
| TVP | 17.2858 | 21.5787 | 27.7232 | 37.2610 | 54.0375 | 89.1931 | |
| MO-TIIEHL-OBX-LLoG () | VaR | 1.2636 | 1.3617 | 2.0774 | 2.2131 | 2.8168 | 3.1372 |
| TVaR | 0.7460 | 0.8606 | 1.0271 | 1.2935 | 1.7966 | 3.1723 | |
| TV | 7.1450 | 8.3766 | 10.1435 | 12.8951 | 17.7657 | 28.2292 | |
| TVP | 5.7475 | 7.1431 | 9.1420 | 12.2544 | 17.7858 | 29.9901 | |
| MO-TIIEHL-OBX-LLoG () | VaR | 1.6813 | 1.7574 | 1.8464 | 1.9554 | 2.1003 | 2.3285 |
| TVaR | 1.7622 | 2.0546 | 2.4841 | 3.1812 | 4.5267 | 8.3453 | |
| TV | 17.1972 | 19.8867 | 23.5344 | 28.6380 | 35.4242 | 30.9662 | |
| TVP | 13.8003 | 16.9696 | 21.3117 | 27.5236 | 36.4085 | 37.7633 | |
| MO-TIIEHL-OBX-LLoG () | VaR | 1.6788 | 1.7337 | 1.7978 | 1.8765 | 1.9814 | 2.1486 |
| TVaR | 0.9592 | 1.1081 | 1.3255 | 1.6756 | 2.3431 | 4.2007 | |
| TV | 2.8928 | 3.2448 | 3.6748 | 4.1516 | 4.2952 | 5.8521 | |
| TVP | 2.9842 | 3.5417 | 4.2654 | 5.2044 | 6.2088 | 3.3912 | |
| APExLLD () | VaR | 0.5417 | 0.6815 | 0.8652 | 1.1226 | 1.5288 | 2.3797 |
| TVaR | 1.7497 | 1.9779 | 2.2802 | 2.7117 | 3.4139 | 4.9413 | |
| TV | 7.8451 | 9.0645 | 10.8087 | 13.5354 | 18.4869 | 30.8310 | |
| TVP | 7.2413 | 8.7764 | 10.9272 | 14.2169 | 20.0521 | 34.2308 | |
| HTGenTLL () | VaR | 1.2015 | 1.3140 | 1.4520 | 1.6321 | 1.8938 | 2.3720 |
| TVaR | 1.8703 | 1.9931 | 2.1463 | 2.3492 | 2.6472 | 3.1926 | |
| TV | 0.7327 | 0.7863 | 0.8622 | 0.9793 | 1.1913 | 1.7483 | |
| TVP | 2.3832 | 2.5829 | 2.8360 | 3.1816 | 3.7195 | 4.8536 |
| Estimates | Statistics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | c | p-value | SS | ||||||||||
| MO-TIIEHL-OBX-LLoG | 9.6978 | 1.1338 | 3.7292 | 6.5701 | 819.2223 | 827.2223 | 827.5475 | 838.6304 | 0.0175 | 0.1019 | 0.0307 | 0.9997 | 0.0151 |
| (5.4183 ) | (2.0601 ) | (1.1030 ) | (4.2346 ) | ||||||||||
| TLOBXLLoG | 20.4950 | 0.9898 | 0.1528 | 832.2939 | 838.2939 | 838.4874 | 846.8500 | 0.1465 | 0.9796 | 0.0739 | 0.4862 | 0.1803 | |
| (23.7196) | (0.6755) | (0.0099) | |||||||||||
| a | |||||||||||||
| TIIEHLW | 9.3869 | 1.7964 | 2.9019 | 4.3135 | 822.9009 | 830.9060 | 831.2312 | 842.3141 | 0.0685 | 0.4256 | 0.0539 | 0.8515 | 0.0673 |
| (2.1942 ) | (1.2065 ) | (2.2305 ) | (2.7661 ) | ||||||||||
| a | b | ||||||||||||
| BXII-BXII | 5.0574 | 9.9973 | 3.6341 | 9.9147 | 822.1404 | 830.1404 | 830.4656 | 841.5486 | 0.0570 | 0.3605 | 0.0509 | 0.8942 | 0.0552 |
| (3.6205 ) | (1.2000 ) | (1.6190) | (1.5951 ) | ||||||||||
| d | c | s | |||||||||||
| LBXII | 13.9233 | 0.4357 | 0.2974 | 0.0038 | 829.0201 | 837.0201 | 837.3453 | 848.4282 | 0.1012 | 0.6998 | 0.0483 | 0.9265 | 0.0535 |
| (0.0047) | (0.1491) | (0.0723) | (0.0052) | ||||||||||
| a | |||||||||||||
| MOGLL | 3.1630 | 3.7785 | 3.0537 | 3.9977 | 825.9789 | 833.9788 | 834.3040 | 845.3869 | 0.0475 | 0.3423 | 0.0550 | 0.8342 | 0.0911 |
| (4.6045 ) | (4.2102 ) | (3.4285 ) | (2.2651 ) | ||||||||||
| MOEF | 6.6142 | 1.5844 | 1.0986 | 1.1521 | 822.1622 | 830.1622 | 830.4875 | 841.5704 | 0.0538 | 0.3500 | 0.0517 | 0.8832 | 0.0502 |
| (2.5092 ) | (5.2148 ) | (4.9159 ) | (7.5640 ) | ||||||||||
| a | b | c | |||||||||||
| APExLLD | 3.8295 | 4.8498 | 3.4902 | 8.7071 | 846.592 | 854.5916 | 854.9168 | 865.9997 | 0.2627 | 1.7289 | 0.0799 | 0.3873 | 0.1904 |
| (1.4896 ) | (8.2971 ) | (2.9078 ) | (5.2280 ) | ||||||||||
| b | c | ||||||||||||
| HTGenTLL | 2.5660 | 4.3961 | 1.7472 | 5.2477 | 821.7432 | 829.7432 | 830.0684 | 841.1513 | 0.0471 | 0.3120 | 0.0480 | 0.9294 | 0.0417 |
| (1.6923 ) | (1.3474 ) | (1.7736 ) | (1.3997 ) | ||||||||||
| Estimates | Statistics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | c | p-value | SS | ||||||||||
| MO-TIIEHL-OBX-LLoG | 7.9960 | 7.9156 | 1.3883 | 5.6589 | 171.5707 | 179.5711 | 180.2269 | 188.3297 | 0.0812 | 0.4362 | 0.0657 | 0.9380 | 0.0616 |
| (2.1640 ) | (7.3497 ) | (2.6932 ) | (5.9267 ) | ||||||||||
| TLOBXLLoG | 0.4149 | 23.3458 | 0.4524 | 184.5695 | 190.3248 | 190.7119 | 196.8937 | 0.2655 | 1.4483 | 0.1506 | 0.1001 | 0.3200 | |
| (0.1873) | (9.6571) | (0.0266) | |||||||||||
| a | |||||||||||||
| TIIEHLW | 2.6668 | 1.8559 | 4.1681 | 1.8892 | 172.21 | 180.2273 | 180.8830 | 188.9859 | 0.0949 | 0.5327 | 0.0823 | 0.7629 | 0.0812 |
| (9.0535 ) | (6.0362 ) | (7.2830 ) | (5.7951 ) | ||||||||||
| a | b | ||||||||||||
| BXII-BXII | 9.9332 | 8.1871 | 3.6819 | 4.2860 | 172.1631 | 180.1631 | 180.8189 | 188.9218 | 0.0935 | 0.5281 | 0.0826 | 0.7589 | 0.0811 |
| (9.8805 ) | (7.3219 ) | (6.1847 ) | (3.0345 ) | ||||||||||
| d | c | s | |||||||||||
| LBXII | 4.7440 | 2.4782 | 1.0322 | 5.2642 | 183.2949 | 191.2949 | 191.9507 | 200.0536 | 0.2592 | 1.3925 | 0.0939 | 0.6054 | 0.1537 |
| (4.9621 ) | (1.2187 ) | (5.8405 ) | (5.9123 ) | ||||||||||
| a | |||||||||||||
| MOGLL | 1.9647 | 9.9580 | 3.5448 | 4.8817 | 183.3055 | 191.3055 | 191.9612 | 200.0641 | 0.2682 | 1.4462 | 0.0949 | 0.5924 | 0.1570 |
| (1.0408 ) | (7.6149 ) | (5.6133 ) | (4.0673 ) | ||||||||||
| MOEF | 3.9383 | 2.5347 | 7.3102 | 9.4078 | 175.4444 | 183.4444 | 184.1001 | 192.2030 | 0.1436 | 0.7753 | 0.1050 | 0.4606 | 0.137 |
| (3.1272 ) | (2.2964 ) | (1.4974 ) | (4.3489 ) | ||||||||||
| a | b | c | |||||||||||
| APExLLD | 6.5148 | 4.0874 | 2.2649 | 2.7501 | 183.2165 | 191.2164 | 191.8722 | 199.9751 | 0.2596 | 1.3781 | 0.1147 | 0.3504 | 0.230 |
| (5.6474 ) | (6.9509 ) | (3.7404 ) | (1.2474 ) | ||||||||||
| b | c | ||||||||||||
| HTGenTLL | 7.7041 | 1.8951 | 1.5163 | 2.1003 | 173.4224 | 181.4224 | 182.0781 | 190.181 | 0.1136 | 0.6218 | 0.0925 | 0.6244 | 0.1027 |
| (1.6220) | (5.8707 ) | (1.3597 ) | (2.6600 ) | ||||||||||
| Estimates | Statistics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | c | p-value | SS | ||||||||||
| MO-TIIEHL-OBX-LLoG | 2.9017 | 2.8657 | 2.9446 | 1.3981 | 696.8013 | 704.8026 | 705.2236 | 715.2233 | 0.0313 | 0.2033 | 0.0432 | 0.9923 | 0.0275 |
| (2.3347 ) | (1.9910 ) | (8.4166 ) | (1.1369 ) | ||||||||||
| TLOBXLLoG | 3.5687 | 7.4386 | 2.4035 | 772.1108 | 778.1111 | 778.3611 | 785.9266 | 0.4891 | 2.8872 | 0.2608 | <0.001 | 1.8830 | |
| (5.3580 ) | (2.4618) | (2.7587 ) | |||||||||||
| a | |||||||||||||
| TIIEHLW | 2.1326 | 2.7418 | 5.0848 | 8.3401 | 707.9298 | 715.9301 | 716.3512 | 726.3508 | 0.0994 | 0.6209 | 0.1341 | 0.05483 | 0.3828 |
| (1.0112 ) | (4.9965 ) | (1.9763 ) | (7.4975 ) | ||||||||||
| a | b | ||||||||||||
| BXII-BXII | 1.3434 | 9.9308 | 1.2136 | 2.1236 | 697.7634 | 705.7637 | 706.1848 | 716.1844 | 0.0538 | 0.3430 | 0.0545 | 0.9282 | 0.0425 |
| (1.8424 ) | (1.3605 ) | (2.7630 ) | (5.1861 ) | ||||||||||
| d | c | s | |||||||||||
| LBXII | 8.6948 | 1.7098 | 2.6223 | 1.8805 | 702.0292 | 710.0306 | 710.4516 | 720.4512 | 0.1093 | 0.7120 | 0.0514 | 0.9543 | 0.0574 |
| (5.3659 ) | (1.4258 ) | (1.8488 ) | (5.4088 ) | ||||||||||
| a | |||||||||||||
| MOGLL | 1.1053 | 3.7152 | 3.2956 | 2.6875 | 698.0007 | 706.0015 | 706.4225 | 716.4222 | 0.0470 | 0.3100 | 0.0635 | 0.8149 | 0.0641 |
| (8.8650 ) | (3.7622 ) | (1.1214 ) | (4.1052 ) | ||||||||||
| MOEF | 562.9600 | 3.7090 | 292.2274 | 1.0160 | 701.2151 | 709.2151 | 709.6362 | 719.6358 | 0.1033 | 0.6445 | 0.0766 | 0.6003 | 0.0971 |
| (0.6906) | (0.4051) | (11.9099) | (0.8383) | ||||||||||
| a | b | c | |||||||||||
| APExLLD | 43.9590 | 30.6073 | 166.8402 | 0.9114 | 705.5595 | 713.5595 | 713.9806 | 723.9802 | 0.1414 | 0.9084 | 0.0779 | 0.5786 | 0.1409 |
| (77.6731) | (4.7926) | (5.0830) | (0.6220) | ||||||||||
| b | c | ||||||||||||
| HTGenTLL | 3.1367 | 8.1214 | 7.2348 | 2.4561 | 703.0059 | 711.0059 | 711.4270 | 721.4266 | 0.1099 | 0.6799 | 0.0824 | 0.5059 | 0.1336 |
| (1.9221 ) | (9.0667 ) | (6.1750 ) | (1.4828 ) | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oluyede, B.; Moakofi, T.; Lekono, G. The New Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X-G Family of Distributions with Properties and Applications. Stats 2025, 8, 26. https://doi.org/10.3390/stats8020026
Oluyede B, Moakofi T, Lekono G. The New Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X-G Family of Distributions with Properties and Applications. Stats. 2025; 8(2):26. https://doi.org/10.3390/stats8020026
Chicago/Turabian StyleOluyede, Broderick, Thatayaone Moakofi, and Gomolemo Lekono. 2025. "The New Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X-G Family of Distributions with Properties and Applications" Stats 8, no. 2: 26. https://doi.org/10.3390/stats8020026
APA StyleOluyede, B., Moakofi, T., & Lekono, G. (2025). The New Marshall–Olkin–Type II Exponentiated Half-Logistic–Odd Burr X-G Family of Distributions with Properties and Applications. Stats, 8(2), 26. https://doi.org/10.3390/stats8020026






