Optimal ANOVA-Based Emulators of Models With(out) Derivatives
Abstract
1. Introduction
- We designed adequate structures of emulators based on information gathered from global and derivative-based sensitivity analysis, such as unbiased orders of truncations and the selection of relevant ANOVA components (inputs and interactions);
- We constructed derivative-based or derivative-free global emulators that are easy to fit and compute and can cope with every distribution of continuous input variables;
- We examined the convergence analysis of our emulators, with a particular focus on the (i) dimension-free upper bounds of the biases and MSEs; (ii) the parametric rates of convergence (i.e., ); and (iii) the number of model runs needed to obtain the stability and accuracy of our estimations.
General Notation
2. New Insight into Derivative-Based ANOVA and Emulators
2.1. Full Derivative-Based Emulators
2.2. Adequate Structures of Emulators and Truncations
- implies that using leads to unbiased truncations;
- implies that using leads to unbiased truncations;
- If there exists an integer, α, such that and , then leads to unbiased truncations.
- or implies removing all cross-partial derivatives or interactions involving ;
- and suggest removing the first-order terms, corresponding to ;
- or, equivalently, and implies keeping only and .
3. Derivative-Free Emulators of Models
3.1. Stochastic Surrogates of Functions Using Db-ANOVA
3.2. Statistical Properties of Our Emulators
3.2.1. Biases of the Proposed Emulators
3.2.2. Mean Squared Errors
- (i)
- If , then .
- (ii)
- If with , then
3.2.3. Mean Squared Errors for Every Distribution of Inputs
4. Illustrations
- ;
- if L is odd and ; otherwise, .
4.1. Test Functions
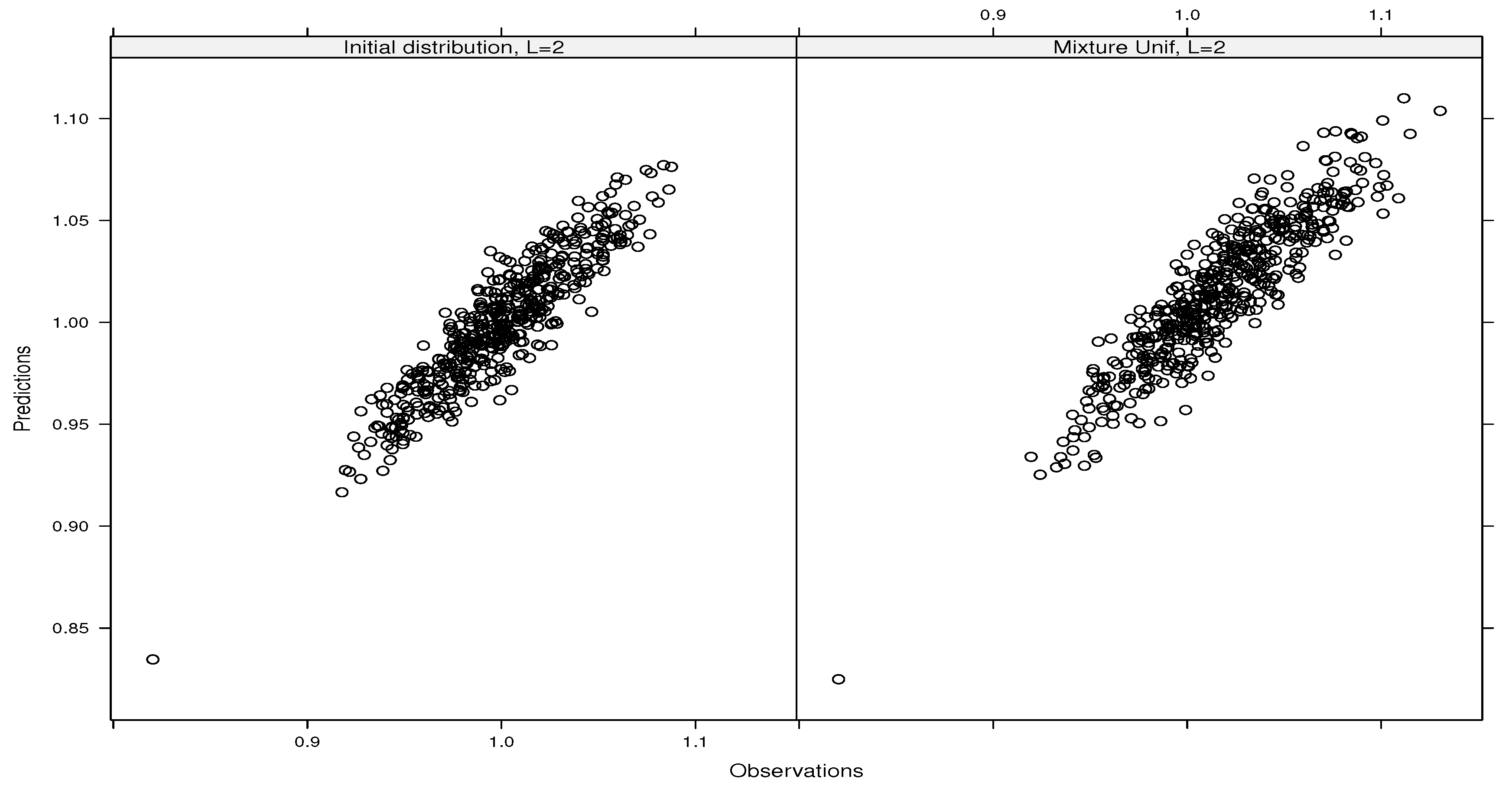
4.1.1. Ishigami’s Function ()
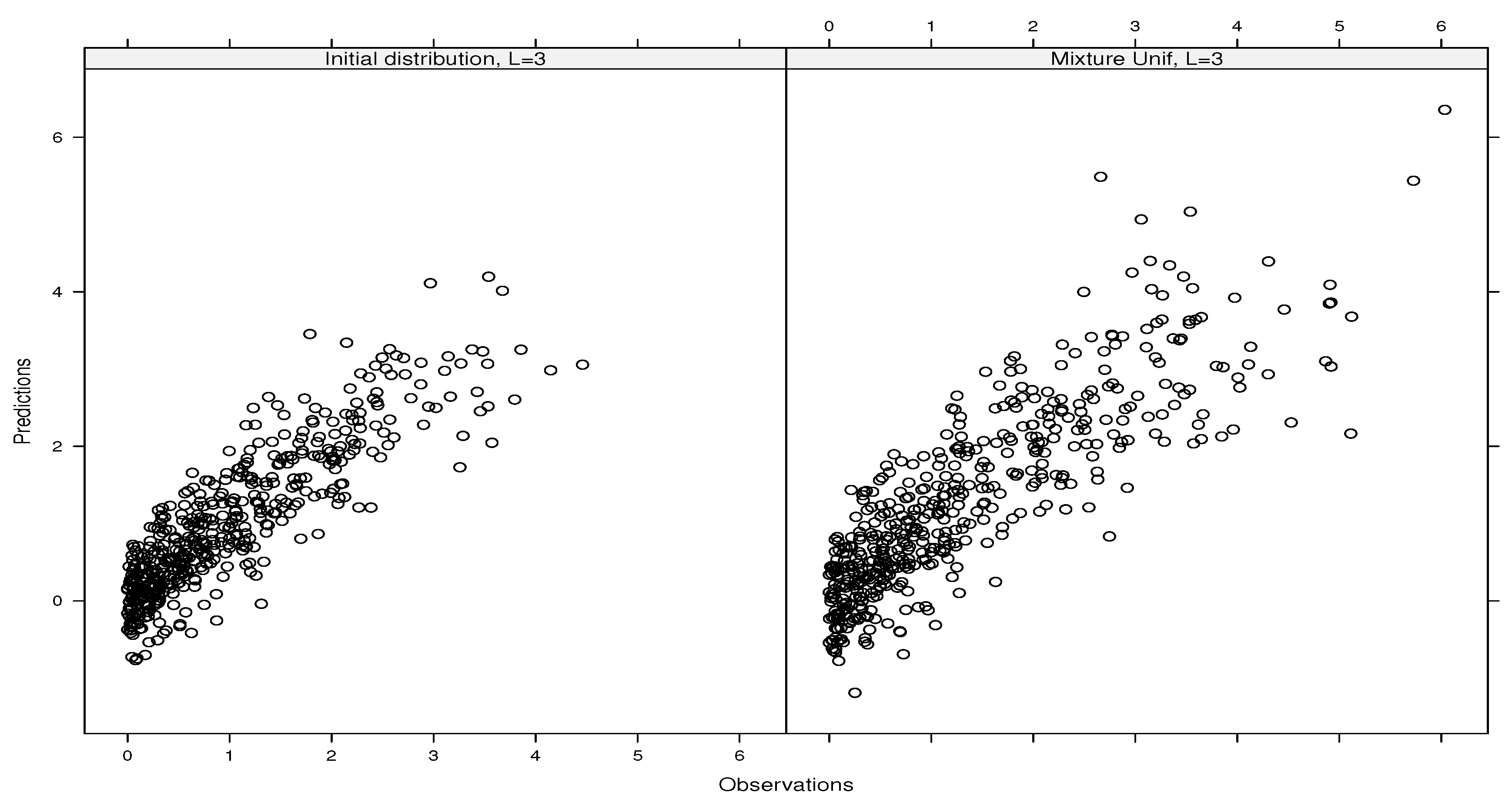
4.1.2. Sobol’s g-Function ()
- If (i.e., type A), we have , , , , and , . We have , as . Moreover, we have , suggesting that we should only include and in our emulator;
- If (i.e., type B), we have and , leading to ;
- If (i.e., type C), we have and , , and we can check that and that all the inputs are important. Thus, we have to include a lot of ANOVA components in our emulator with small effective effects since the variance of that function is fixed. More information is needed to design the structure of this function better.
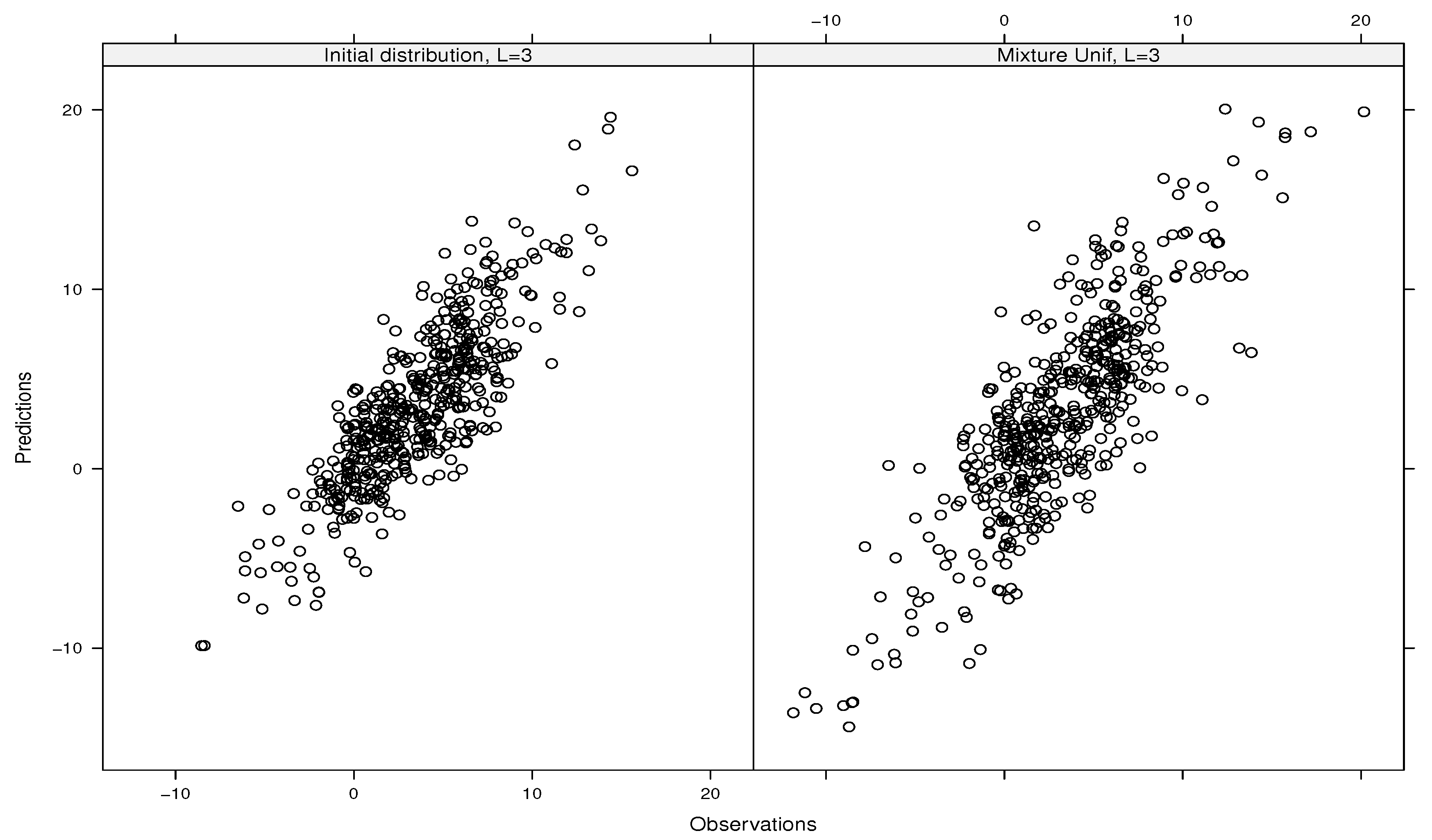
5. Application: Heat Diffusion Models with Stochastic Initial Conditions
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivations of Unbiased Truncations (Proposition 1)
Appendix B. Proof of Theorem 1
Appendix C. Proof of Lemma 1
Appendix D. Proof of Theorem 2
Appendix E. Proof of Corollary 1
Appendix F. Proof of Corollary 2
Appendix G. Proof of Theorem 3
Appendix H. Proof of Corollary 3
Appendix I. Proof of Corollary 5
Appendix J. Proof of Corollary 6
References
- Max, D.; Morris, T.J.M.; Ylvisaker, D. Bayesian Design and Analysis of Computer Experiments: Use of Derivatives in Surface Prediction. Technometrics 1993, 35, 243–255. [Google Scholar]
- Solak, E.; Murray-Smith, R.; Leithead, W.; Leith, D.; Rasmussen, C. Derivative observations in Gaussian process models of dynamic systems. Adv. Neural Inf. Process. Syst. 2002, 15, 1–8. [Google Scholar]
- Le Dimet, F.X.; Talagrand, O. Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects. Tellus A Dyn. Meteorol. Oceanogr. 1986, 38, 97–110. [Google Scholar] [CrossRef]
- Le Dimet, F.X.; Ngodock, H.E.; Luong, B.; Verron, J. Sensitivity analysis in variational data assimilation. J. Meteorol. Soc. Jpn. 1997, 75, 245–255. [Google Scholar] [CrossRef]
- Cacuci, D.G. Sensitivity and Uncertainty Analysis—Theory; Chapman & Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Gunzburger, M.D. Perspectives in Flow Control and Optimization; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Borzi, A.; Schulz, V. Computational Optimization of Systems Governed by Partial Differential Equations; SIAM: Philadelphia, PA, USA, 2012. [Google Scholar]
- Ghanem, R.; Higdon, D.; Owhadi, H. Handbook of Uncertainty Quantification; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Agarwal, A.; Dekel, O.; Xiao, L. Optimal Algorithms for Online Convex Optimization with Multi-Point Bandit Feedback. In Proceedings of the COLT, Haifa, Israel, 27–29 June 2010; Citeseer: Princeton, NJ, USA, 2010; pp. 28–40. [Google Scholar]
- Bach, F.; Perchet, V. Highly-Smooth Zero-th Order Online Optimization. In Proceedings of the 29th Annual Conference on Learning Theory, New York, NY, USA, 23–26 June 2016; Volume 49, pp. 257–283. [Google Scholar]
- Akhavan, A.; Pontil, M.; Tsybakov, A.B. Exploiting higher order smoothness in derivative-free optimization and continuous bandits. In Proceedings of the NIPS ’20: Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020. [Google Scholar]
- Lamboni, M. Optimal and Efficient Approximations of Gradients of Functions with Nonindependent Variables. Axioms 2024, 13, 426. [Google Scholar] [CrossRef]
- Lamboni, M. Optimal Estimators of Cross-Partial Derivatives and Surrogates of Functions. Stats 2024, 7, 1–22. [Google Scholar] [CrossRef]
- Chkifa, A.; Cohen, A.; DeVore, R.; Schwab, C. Sparse adaptive Taylor approximation algorithms for parametric and stochastic elliptic PDEs. ESAIM Math. Model. Numer. Anal. 2013, 47, 253–280. [Google Scholar] [CrossRef]
- Patil, P.; Babaee, H. Reduced-Order Modeling with Time-Dependent Bases for PDEs with Stochastic Boundary Conditions. SIAM/ASA J. Uncertain. Quantif. 2023, 11, 727–756. [Google Scholar] [CrossRef]
- Sobol, I.M.; Kucherenko, S. Derivative based global sensitivity measures and the link with global sensitivity indices. Math. Comput. Simul. 2009, 79, 3009–3017. [Google Scholar] [CrossRef]
- Kucherenko, S.; Rodriguez-Fernandez, M.; Pantelides, C.; Shah, N. Monte Carlo evaluation of derivative-based global sensitivity measures. Reliab. Eng. Syst. Saf. 2009, 94, 1135–1148. [Google Scholar] [CrossRef]
- Lamboni, M.; Iooss, B.; Popelin, A.L.; Gamboa, F. Derivative-based global sensitivity measures: General links with Sobol’ indices and numerical tests. Math. Comput. Simul. 2013, 87, 45–54. [Google Scholar] [CrossRef]
- Roustant, O.; Fruth, J.; Iooss, B.; Kuhnt, S. Crossed-derivative based sensitivity measures for interaction screening. Math. Comput. Simul. 2014, 105, 105–118. [Google Scholar] [CrossRef]
- Roustant, O.; Barthe, F.; Iooss, B. Poincar inequalities on intervals—Application to sensitivity analysis. Electron. J. Statist. 2017, 11, 3081–3119. [Google Scholar] [CrossRef]
- Lamboni, M. Derivative-based integral equalities and inequality: A proxy-measure for sensitivity analysis. Math. Comput. Simul. 2021, 179, 137–161. [Google Scholar] [CrossRef]
- Lamboni, M. Weak derivative-based expansion of functions: ANOVA and some inequalities. Math. Comput. Simul. 2022, 194, 691–718. [Google Scholar] [CrossRef]
- Lamboni, M.; Kucherenko, S. Multivariate sensitivity analysis and derivative-based global sensitivity measures with dependent variables. Reliab. Eng. Syst. Saf. 2021, 212, 107519. [Google Scholar] [CrossRef]
- Krige, D.G. A Statistical Approaches to Some Basic Mine Valuation Problems on the Witwatersrand. J. Chem. Metall. Soc. S. Afr. 1951, 52, 119–139. [Google Scholar]
- Currin, C.; Mitchell, T.; Morris, M.; Ylvisaker, D. Bayesian Prediction of Deterministic Functions, with Applications to the Design and Analysis of Computer Experiments. J. Am. Stat. Assoc. 1991, 86, 953–963. [Google Scholar] [CrossRef]
- Oakley, J.E.; O’Hagan, A. Probabilistic sensitivity analysis of complex models: A Bayesian approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2004, 66, 751–769. [Google Scholar] [CrossRef]
- Conti, S.; O’Hagan, A. Bayesian emulation of complex multi-output and dynamic computer models. J. Stat. Plan. Inference 2010, 140, 640–651. [Google Scholar] [CrossRef]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G. The Wiener-Askey polynomial chaos for stochastic di eren-tial equations. Siam J. Sci. Comput. 2002, 24. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991; pp. 1–214. [Google Scholar]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1990. [Google Scholar] [CrossRef]
- Wong, R.K.W.; Storlie, C.B.; Lee, T.C.M. A Frequentist Approach to Computer Model Calibration. J. R. Stat. Soc. Ser. B Stat. Methodol. 2016, 79, 635–648. [Google Scholar] [CrossRef]
- Friedman, J.H.; Popescu, B.E. Predictive learning via rule ensembles. Ann. Appl. Stat. 2008, 2, 916–954. [Google Scholar] [CrossRef]
- Horiguchi, A.; Pratola, M.T. Estimating Shapley Effects in Big-Data Emulation and Regression Settings using Bayesian Additive Regression Trees. arXiv 2024, arXiv:2304.03809. [Google Scholar]
- Migliorati, G.; Nobile, F.; Schwerin, E.; Tempone, R. Analysis of Discrete L2 Projection on Polynomial Spaces with Random Evaluations. Found. Comput. Math. 2014, 14, 419–456. [Google Scholar]
- Hampton, J.; Doostan, A. Coherence motivated sampling and convergence analysis of least squares polynomial Chaos regression. Comput. Methods Appl. Mech. Eng. 2015, 290, 73–97. [Google Scholar] [CrossRef]
- Cohen, A.; Davenport, M.A.; Leviatan, D. On the stability and accuracy of least squares approximations. arXiv 2018, arXiv:math.NA/1111.4422. [Google Scholar] [CrossRef]
- Tsybakov, A. Introduction to Nonparametric Estimation; Springer: New York, NY, USA, 2009. [Google Scholar]
- Zemanian, A. Distribution Theory and Transform Analysis: An Introduction to Generalized Functions, with Applications; Dover Books on Advanced Mathematics; Dover Publications: Garden City, NY, USA, 1987. [Google Scholar]
- Strichartz, R. A Guide to Distribution Theory and Fourier Transforms; Studies in advanced mathematics; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Caflisch, R.E.; Morokoff, W.J.; Owen, A.B. Valuation of mortgage-backed securities using Brownian bridges to reduce effective dimension. J. Comput. Financ. 1997, 1, 27–46. [Google Scholar] [CrossRef]
- Owen, A. The dimension distribution and quadrature test functions. Stat. Sin. 2003, 13, 1–17. [Google Scholar]
- Rabitz, H. General foundations of high dimensional model representations. J. Math. Chem. 1999, 25, 197–233. [Google Scholar] [CrossRef]
- Kuo, F.; Sloan, I.; Wasilkowski, G.; Woźniakowski, H. On decompositions of multivariate functions. Math. Comput. 2010, 79, 953–966. [Google Scholar] [CrossRef]
- Alatawi, M.S.; Martinucci, B. On the Elementary Symmetric Polynomials and the Zeros of Legendre Polynomials. J. Math. 2022, 1–9. [Google Scholar] [CrossRef]
- Arafat, A.; El-Mikkawy, M. A Fast Novel Recursive Algorithm for Computing the Inverse of a Generalized Vandermonde Matrix. Axioms 2023, 12, 27. [Google Scholar] [CrossRef]
- Rawashdeh, E. A simple method for finding the inverse matrix of Vandermonde matrix. Mathematiqki Vesnik 2019, 71, 207–213. [Google Scholar]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamboni, M. Optimal ANOVA-Based Emulators of Models With(out) Derivatives. Stats 2025, 8, 24. https://doi.org/10.3390/stats8010024
Lamboni M. Optimal ANOVA-Based Emulators of Models With(out) Derivatives. Stats. 2025; 8(1):24. https://doi.org/10.3390/stats8010024
Chicago/Turabian StyleLamboni, Matieyendou. 2025. "Optimal ANOVA-Based Emulators of Models With(out) Derivatives" Stats 8, no. 1: 24. https://doi.org/10.3390/stats8010024
APA StyleLamboni, M. (2025). Optimal ANOVA-Based Emulators of Models With(out) Derivatives. Stats, 8(1), 24. https://doi.org/10.3390/stats8010024



