Factor Analysis of Ordinal Items: Old Questions, Modern Solutions?
Abstract
1. Introduction
1.1. Factor Analysis
1.2. Stanley Stevens and the Scales of Measurement
Is It Permissible to Do Factor Analysis with Ordinal Items?
2. Other Methods to Analyze Ordinal Items
2.1. The Spearman Correlation Coefficient
2.2. The Polychoric Correlation Coefficient
3. Results
3.1. Case Study 1: Exploratory Factor Analysis of Ordinal Items with 3 Points
3.2. Case Study 2: Confirmatory Factor Analysis of Ordinal Items with 5 Points
3.3. Case Study 3: Confirmatory Factor Analysis of Ordinal Items—Artificial Results?
4. Simulation Studies
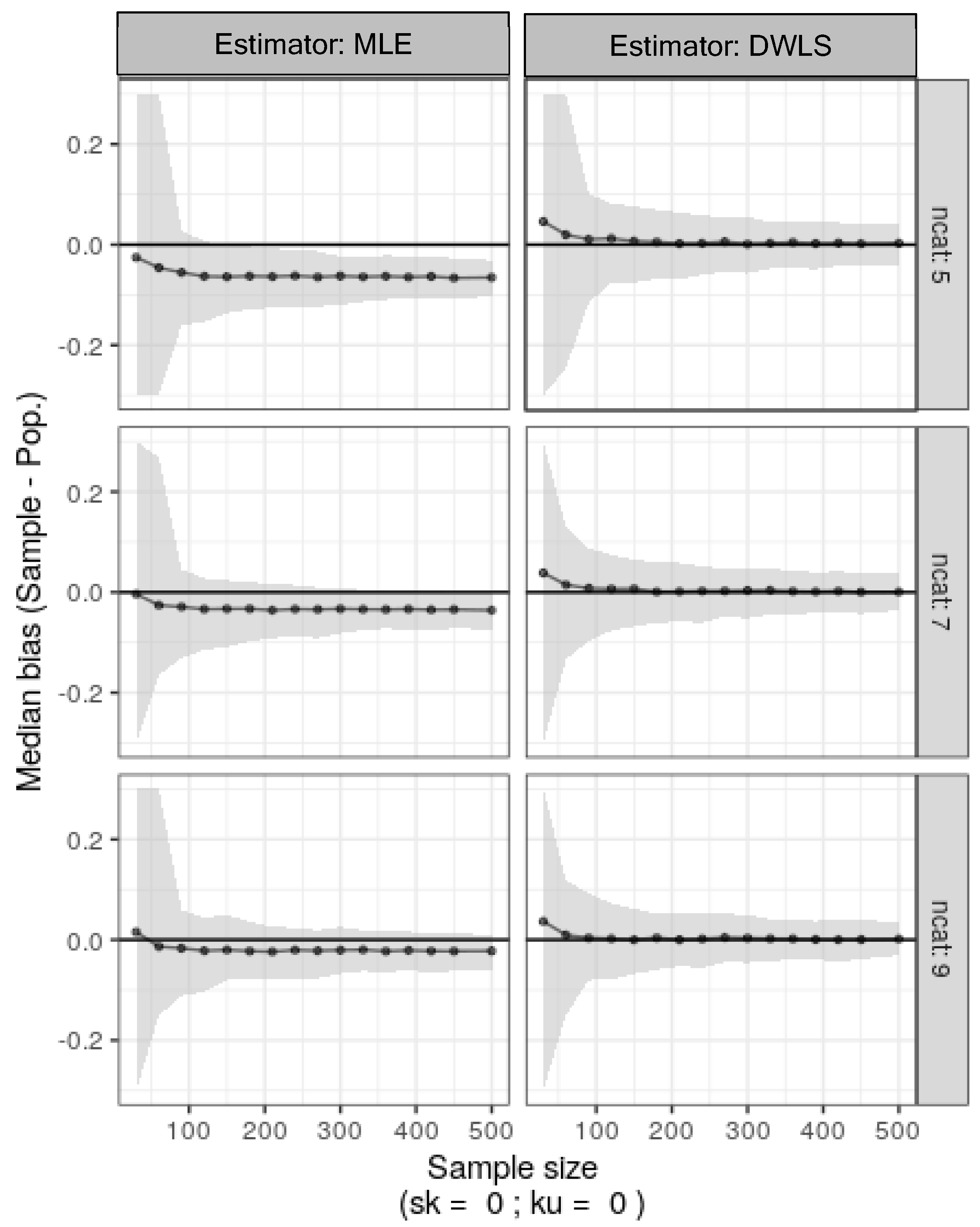
4.1. Simulation 1: Symmetrical Ordinal Data Generated from Normal Continuous Data
4.2. Simulation 2: Symmetrical Ordinal Data Generated from Nonnormal Continuous Data
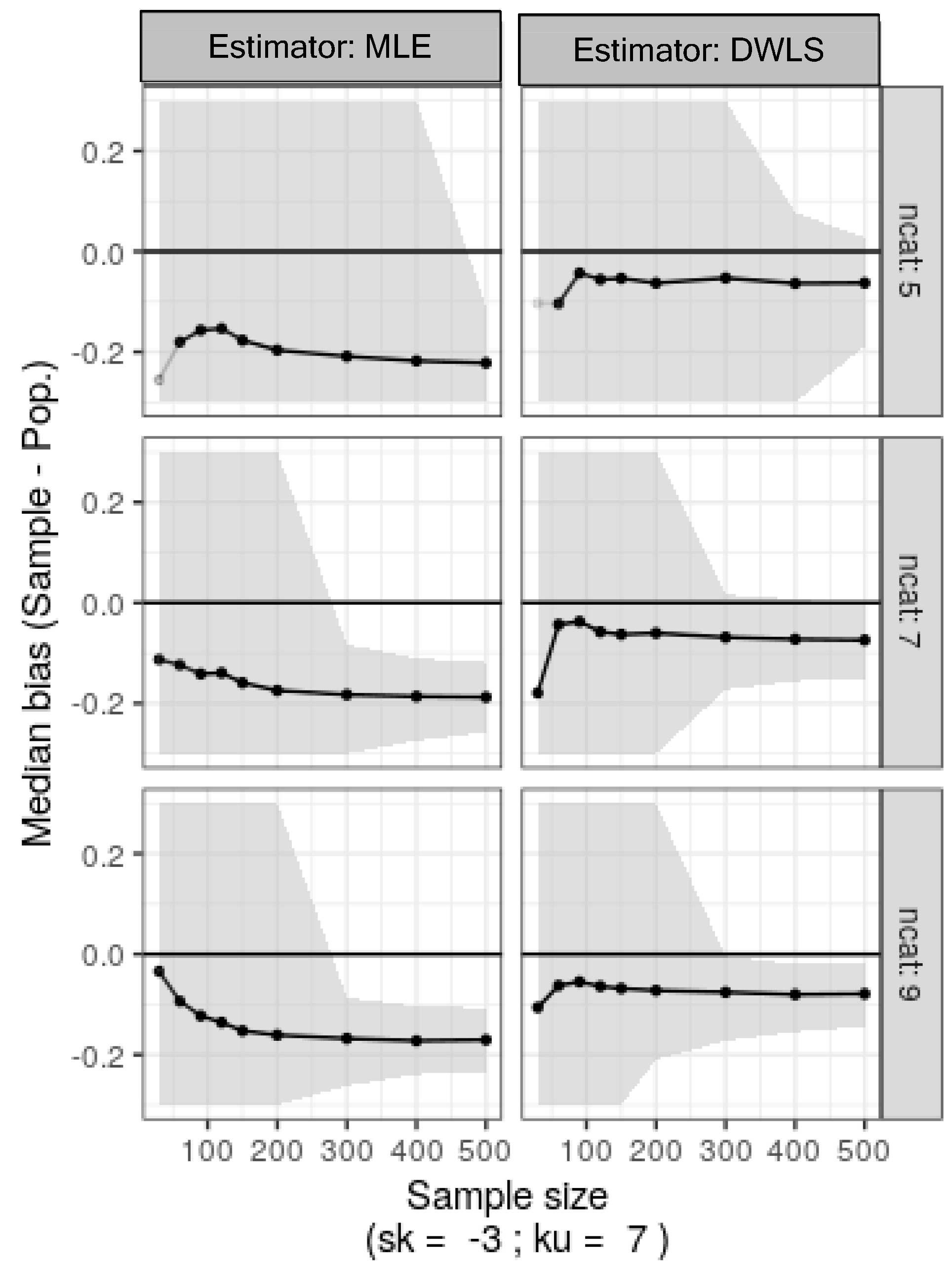
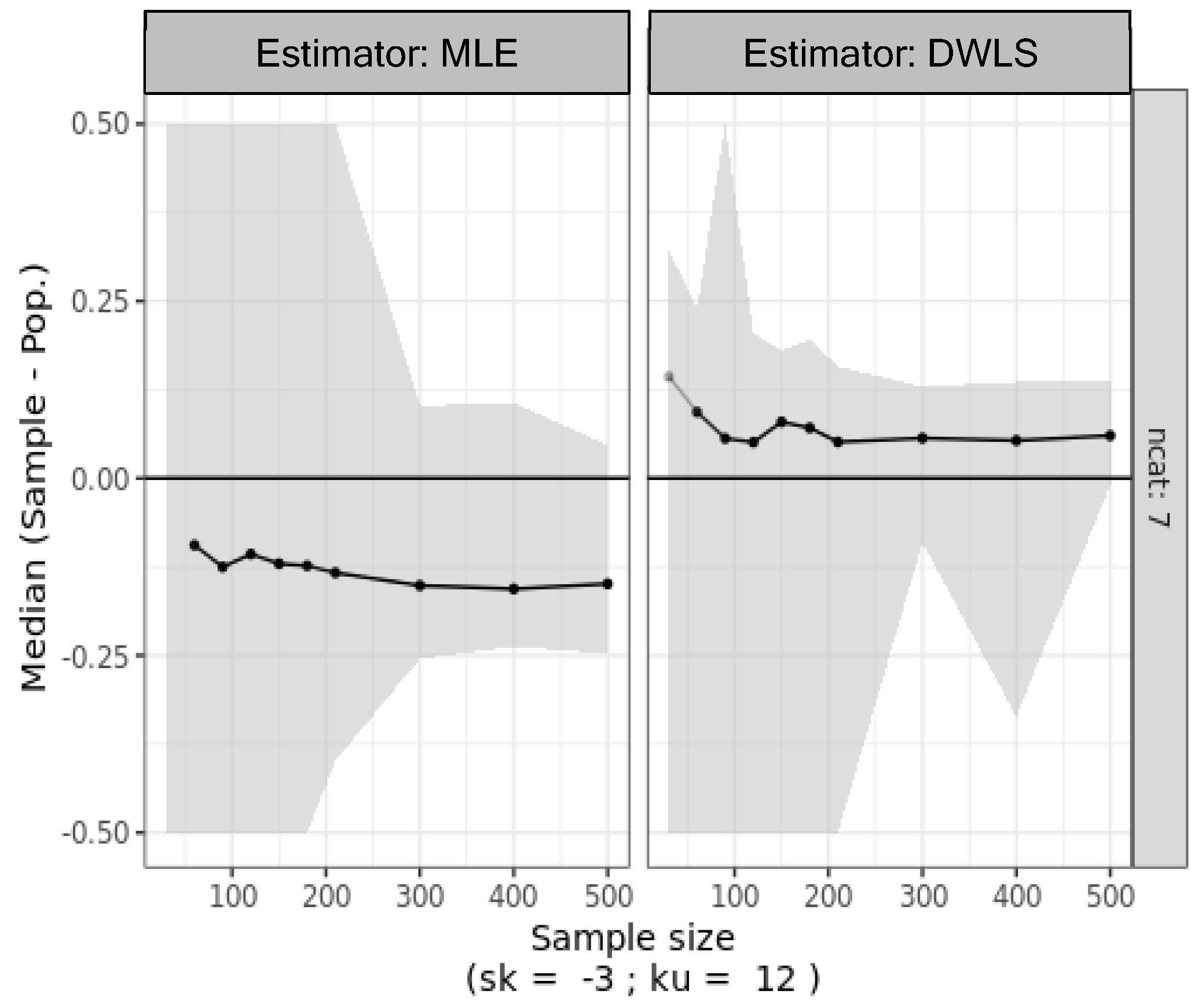
4.3. Simulation 3: Asymmetrical Ordinal Data Generated from Biased Sampling of Normal Ordinal Data
5. Discussion
6. Concluding Remarks
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Spearman, C. General Intelligence, Objectively Determined and Measured. Am. J. Psychol. 1904, 15, 201. [Google Scholar] [CrossRef]
- Thomson, G.H. A Hierarchy Without a General Factor. Br. J. Psychol. 1916, 8, 271–281. [Google Scholar] [CrossRef]
- Thurstone, L.L. Primary Mental Abilities; University of Chicago Press: Chicago, IL, USA, 1938; Available online: http://catalog.hathitrust.org/api/volumes/oclc/2471740.html (accessed on 1 August 2024).
- Likert, R. A Technique for the Measurement of Attitudes. Arch. Psychol. 1932, 22, 55. [Google Scholar]
- Muthén, B.; Kaplan, D. A comparison of some methodologies for the factor analysis of non-normal Likert variables. Br. J. Math. Stat. Psychol. 1985, 38, 171–189. [Google Scholar] [CrossRef]
- Li, C.H. The performance of ML, DWLS, and ULS estimation with robust corrections in structural equation models with ordinal variables. Psychol. Methods 2016, 21, 369–387. [Google Scholar] [CrossRef] [PubMed]
- Li, C.H. Confirmatory factor analysis with ordinal data: Comparing robust maximum likelihood and diagonally weighted least squares. Behav. Res. 2015, 48, 936–949. [Google Scholar] [CrossRef]
- Rhemtulla, M.; Brosseau-Liard, P.É.; Savalei, V. When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions. Psychol. Methods 2012, 17, 354–373. [Google Scholar] [CrossRef]
- Liddell, T.M.; Kruschke, J.K. Analyzing ordinal data with metric models: What could possibly go wrong? J. Exp. Soc. Psychol. 2018, 79, 328–348. [Google Scholar] [CrossRef]
- Foldnes, N.; Grønneberg, S. Pernicious Polychorics: The Impact and Detection of Underlying Non-normality. Struct. Equ. Model. 2020, 27, 525–543. [Google Scholar] [CrossRef]
- Cattell, R.B. The measurement of adult intelligence. Psychol. Bull. 1943, 40, 153–193. [Google Scholar] [CrossRef]
- Bartholomew, D.J. Three Faces of Factor Analysis. In Factor Analysis at 100: Historical Developments and Future Directions; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 2007; pp. 9–21. [Google Scholar]
- de Winter, J.C.F.; Dodou, D. Factor Recovery by Principal Axis Factoring and Maximum Likelihood Factor Analysis as a Function of Factor Pattern and Sample Size. J. Appl. Stat. 2011, 39, 695–710. [Google Scholar] [CrossRef]
- Lawley, D.N.; Maxwell, A.E. Factor Analysis as a Statistical Method. Stat 1962, 12, 209. [Google Scholar] [CrossRef]
- Jöreskog, K.G. Factor Analysis and Its Extensions. In Factor Analysis at 100: Historical Developments and Future Directions; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 2007; pp. 47–77. [Google Scholar]
- Marôco, J. Análise de Equações Estruturais: Fundamentos Teóricos, Software & Aplicações, 3rd ed.; ReportNumber: Pêro Pinheiro, Portugal, 2014; ISBN 9789899676367. [Google Scholar]
- Arbuckle, J. Amos, Version 4.0. [Computer Software]; SPSS: Chicago, IL, USA, 2006.
- Li, C.-H. The Performance of MLR, USLMV, and WLSMV Estimation in Structural Regression Models with Ordinal Variables. J. Chem. Inf. Model. 2014, 53, 1689–1699. [Google Scholar] [CrossRef]
- Finney, S.J.; DiStefano, C. Nonnormal and Categorical Data in Structural Equation Modeling. In A Second Course in Structural Equation Modeling, 2nd ed.; Hancock, G.R., Mueller, R.O., Eds.; Information Age: Charlotte, NC, USA, 2013. [Google Scholar]
- Muthén, B. A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika 1984, 49, 115–132. [Google Scholar] [CrossRef]
- Stevens, S.S. On the theory of scales of measurement. Science 1946, 103, 677–680. [Google Scholar] [CrossRef]
- Lord, F.M. On the statistical treatment of football numbers. Am. Psychol. 1953, 8, 750–751. [Google Scholar] [CrossRef]
- Velleman, P.F.; Wilkinson, L. Nominal, ordinal, interval, and ratio typologies are misleading. Am. Stat. 1993, 47, 65–72. [Google Scholar] [CrossRef]
- Feuerstahler, L. Scale Type Revisited: Some Misconceptions, Misinterpretations, and Recommendations. Psych 2023, 5, 234–248. [Google Scholar] [CrossRef]
- Jamieson, S. Likert scales: How to (ab)use them. Med. Educ. 2004, 38, 1217–1218. [Google Scholar] [CrossRef]
- Babakus, E.; Ferguson, C.E.; Joreskog, K.G. The Sensitivity of Confirmatory Maximum Likelihood Factor Analysis to Violations of Measurement Scale and Distributional Assumptions. J. Mark. Res. 1987, 24, 222–228. [Google Scholar] [CrossRef]
- Bollen, K.A. Structural Equations with Latent Variables; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Spearman, C. The Proof and Measurement of Association between Two Things. Am. J. Psychol. 1904, 15, 72. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical Contributions to the Theory of Evolution. VII. On the Correlation of Characters Not Quantitatively Measurable. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1900, 195, 1–47. [Google Scholar]
- Finney, S.J.; DiStefano, C.; Kopp, J.P. Overview of estimation methods and preconditions for their application with structural equation modeling. In Principles and Methods of Test Construction: Standards and Recent Advances; Schweizer, E.K., DiStefano, C., Eds.; Hogrefe Publishing: Boston, MA, USA, 2016; pp. 135–165. ISBN 9780889374492. [Google Scholar]
- Holgado-Tello, F.P.; Chacón-Moscoso, S.; Barbero-García, I.; Vila-Abad, E. Polychoric versus Pearson correlations in exploratory and confirmatory factor analysis of ordinal variables. Qual. Quant. 2009, 44, 153–166. [Google Scholar] [CrossRef]
- Drasgow, F. Polychoric and Polyserial Correlations. In Encyclopedia of Statistical Sciences; Samuel, E.K., Balakrishnan, N., Read, C.B., Vidakovic, B., Johnson, N.L., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1986; pp. 68–74. [Google Scholar]
- Jöreskog, K.G. On the estimation of polychoric correlations and their asymptotic covariance matrix. Psychometrika 1994, 59, 381–389. [Google Scholar] [CrossRef]
- Olsson, U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika 1979, 44, 443–460. [Google Scholar] [CrossRef]
- Grønneberg, S.; Foldnes, N. Factor Analyzing Ordinal Items Requires Substantive Knowledge of Response Marginals. Psychol. Methods 2024, 29, 65–87. [Google Scholar] [CrossRef]
- Rigdon, E.E.; Ferguson, C.E. The Performance of the Polychoric Correlation Coefficient and Selected Fitting Functions in Confirmatory Factor Analysis with Ordinal Data. J. Mark. Res. 2006, 28, 491. [Google Scholar] [CrossRef]
- Yung, Y.-F.; Bentler, P.M. Bootstrap-corrected ADF test statistics in covariance structure analysis. Br. J. Math. Stat. Psychol. 1994, 47, 63–84. [Google Scholar] [CrossRef]
- Ekström, J. A Generalized Definition of the Polychoric Correlation Coefficient; Department of Statistics, UCLA: Los Angeles, CA, USA, 2011; pp. 1–24. [Google Scholar]
- Robitzsch, A.A. Why Ordinal Variables Can (Almost) Always Be Treated as Continuous Variables: Clarifying Assumptions of Robust Continuous and Ordinal Factor Analysis Estimation Methods. Front. Educ. 2020, 5, 177. [Google Scholar] [CrossRef]
- Robitzsch, A.A. On the Bias in Confirmatory Factor Analysis When Treating Discrete Variables as Ordinal Instead of Continuous. Axioms 2022, 11, 162. [Google Scholar] [CrossRef]
- Marôco, J.P. Statistical Analysis with SPSS Statistics, 8th ed.; ReportNumber: Pêro Pinheiro, Portugal, 2021; ISBN 978-989-96763-7-4. [Google Scholar]
- Fox, J. Polycor: Polychoric and Polyserial Correlations. R Package Version 0.7-9. 2016. Available online: https://cran.r-project.org/package=polycor (accessed on 1 August 2024).
- Maroco, J.; Maroco, A.L.; Bonini Campos, J.A.D.; Fredricks, J.A. University student’s engagement: Development of the University Student Engagement Inventory (USEI). Psicol. Reflex. E Crit. 2016, 29, 21. [Google Scholar] [CrossRef]
- Rosseel, Y. Lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–21. [Google Scholar] [CrossRef]
- Saur, A.M.; Sinval, J.; Marôco, J.P.; Bettiol, H. Psychometric Properties of the Postpartum Bonding Questionnaire for Brazil: Preliminary Data. In Proceedings of the 10th International Test Comission Conference, Vancouver, BC, Canada, 1–4 July 2016. [Google Scholar]
- Flora, D.B.; Curran, P.J. An Empirical Evaluation of Alternative Methods of Estimation for Confirmatory Factor Analysis with Ordinal Data. Psychol. Methods 2004, 9, 466–491. [Google Scholar] [CrossRef]
 ), Spearman’s (
), Spearman’s ( ) and the polychoric (
) and the polychoric ( ) correlation matrices.
) correlation matrices.
 ), Spearman’s (
), Spearman’s ( ) and the polychoric (
) and the polychoric ( ) correlation matrices.
) correlation matrices.

| (A) Correlation types and Correlation Coefficients | |||||
| WithoutVoice | Complex | Desinter | Contact | Parties | |
| WithoutVoice | 1 | Pearson | Pearson | Pearson | Pearson |
| Complex | 0.829 | 1 | Pearson | Pearson | Pearson |
| Desinter | 0.338 | 0.0523 | 1 | Pearson | Pearson |
| Contact | 0.386 | 0.288 | 0.655 | 1 | Pearson |
| Parties | 0.268 | 0.196 | 0.473 | 0.628 | 1 |
| (B) Correlation types and Correlation Coefficients | |||||
| WithoutVoice | Complex | Desinter | Contact | Parties | |
| WithoutVoice | 1 | Spearman | Spearman | Spearman | Spearman |
| Complex | 0.828 | 1 | Spearman | Spearman | Spearman |
| Desinter | 0.310 | 0.0156 | 1 | Spearman | Spearman |
| Contact | 0.377 | 0.283 | 0.661 | 1 | Spearman |
| Parties | 0.234 | 0.150 | 0.458 | 0.588 | 1 |
| (C) Correlation types and Correlation Coefficients | |||||
| WithoutVoice | Complex | Desinter | Contact | Parties | |
| WithoutVoice | 1 | Polychoric | Polychoric | Polychoric | Polychoric |
| Complex | 0.932 | 1 | Polychoric | Polychoric | Polychoric |
| Desinter | 0.386 | 0.0601 | 1 | Polychoric | Polychoric |
| Contact | 0.495 | 0.345 | 0.783 | 1 | Polychoric |
| Parties | 0.333 | 0.228 | 0.599 | 0.753 | 1 |
| Items | Pearson Correlation | Spearman Correlation | Polychoric Correlation | |||
|---|---|---|---|---|---|---|
| Factor Loadings | ||||||
| F1 | F2 | F1 | F2 | F1 | F2 | |
| WithoutVoice | 0.256 | 0.918 | 0.242 | 0.921 | 0.292 | 0.939 |
| Complex | 0.048 | 0.968 | 0.027 | 0.969 | 0.056 | 0.994 |
| Desinter | 0.849 | 0.049 | 0.857 | 0.030 | 0.901 | 0.052 |
| Contact | 0.867 | 0.235 | 0.859 | 0.248 | 0.903 | 0.283 |
| Parties | 0.801 | 0.123 | 0.787 | 0.092 | 0.849 | 0.146 |
| Extracted Variance (%) | 53.3 | 27.4 | 51.7 | 28.5 | 59.9 | 28.2 |
| Factor | Items | AFC on the Pearson Correlation Matrix with MLE | AFC on the Polychoric Correlation Matrix with DWLS | Difference | ||
|---|---|---|---|---|---|---|
| λMLE | p | λDWLS | p | λMLE − λDWLS | ||
| Ecp | ECP1 | 0.582 | 0.018 | 0.654 | 0.007 | −0.072 |
| ECP3 | 0.431 | 0.020 | 0.474 | 0.008 | −0.043 | |
| ECP4 | 0.530 | 0.018 | 0.559 | 0.007 | −0.029 | |
| ECP5 | 0.574 | 0.018 | 0.624 | 0.007 | −0.050 | |
| ECP6 | 0.555 | 0.018 | 0.664 | 0.009 | −0.109 | |
| EAt | EE14r | 0.480 | <0.001 | 0.513 | <0.001 | −0.033 |
| EE15 | 0.794 | <0.001 | 0.845 | <0.001 | −0.051 | |
| EE16 | 0.778 | <0.001 | 0.812 | <0.001 | −0.034 | |
| EE17 | 0.878 | <0.001 | 0.935 | <0.001 | −0.057 | |
| EE19 | 0.662 | <0.001 | 0.722 | <0.001 | −0.060 | |
| ECn | ECC22 | 0.537 | <0.001 | 0.596 | <0.001 | −0.059 |
| ECC25 | 0.484 | <0.001 | 0.557 | <0.001 | −0.073 | |
| ECC26 | 0.614 | <0.001 | 0.670 | <0.001 | −0.056 | |
| ECC28 | 0.769 | <0.001 | 0.848 | <0.001 | −0.079 | |
| ECC32 | 0.698 | <0.001 | 0.749 | <0.001 | −0.051 | |
| ENG | ECp | 0.948 | <0.001 | 0.947 | 00.014 | 0.001 |
| EAt | 0.646 | <0.001 | 0.662 | <0.001 | −0.016 | |
| ECn | 0.726 | <0.001 | 0.726 | <0.001 | 0.000 | |
| Factor | Items | AFC in Cov Matrix with MLE | AFC in Poly Matrix with WLSMV | Difference | ||
|---|---|---|---|---|---|---|
| λML | p | λWLSMV | p | λMLE − λWLSMV | ||
| F1 | PBQ.1 | 0.346 | <0.001 | 0.542 | <0.001 | −0.196 |
| PBQ.2.Inv | 0.431 | <0.001 | 0.536 | <0.001 | −0.105 | |
| PBQ.6.Inv | 0.238 | <0.001 | 0.43 | <0.001 | −0.192 | |
| PBQ.7.Inv | 0.418 | <0.001 | 0.481 | <0.001 | −0.063 | |
| PBQ.8 | 0.254 | <0.001 | 0.623 | <0.001 | −0.369 | |
| PBQ.9 | 0.246 | <0.001 | 0.635 | <0.001 | −0.389 | |
| PBQ.10.Inv | 0.541 | <0.001 | 0.593 | <0.001 | −0.052 | |
| PBQ.12.Inv | 0.378 | <0.001 | 0.403 | <0.001 | −0.025 | |
| PBQ.13.Inv | 0.584 | <0.001 | 0.662 | <0.001 | −0.078 | |
| PBQ.15.Inv | 0.24 | <0.001 | 0.587 | <0.001 | −0.347 | |
| PBQ.16 | 0.256 | <0.001 | 0.547 | <0.001 | −0.291 | |
| PBQ.17.Inv | 0.185 | <0.001 | 0.567 | <0.001 | −0.382 | |
| F2 | PBQ.3.Inv | 0.346 | <0.001 | 0.499 | <0.001 | −0.153 |
| PBQ.4 | 0.367 | <0.001 | 0.638 | <0.001 | −0.271 | |
| PBQ.5.Inv | 0.398 | <0.001 | 0.691 | <0.001 | −0.293 | |
| PBQ.11 | 0.446 | <0.001 | 0.636 | <0.001 | −0.190 | |
| PBQ.14.Inv | 0.609 | <0.001 | 0.682 | <0.001 | −0.073 | |
| PBQ.21.Inv | 0.614 | <0.001 | 0.692 | <0.001 | −0.078 | |
| PBQ.23.Inv | 0.320 | <0.001 | 0.519 | <0.001 | −0.199 | |
| F3 | PBQ.19.Inv | 0.429 | <0.001 | 0.504 | <0.001 | −0.075 |
| PBQ.20.Inv | 0.348 | <0.001 | 0.601 | <0.001 | −0.253 | |
| PBQ.22 | 0.378 | <0.001 | 0.629 | <0.001 | −0.251 | |
| PBQ.25 | 0.358 | <0.001 | 0.464 | <0.001 | −0.106 | |
| F4 | PBQ.18.Inv | 0.411 | <0.001 | 0.622 | <0.001 | −0.211 |
| PBQ.24.Inv | 0.396 | <0.001 | 0.82 | <0.001 | −0.424 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marôco, J. Factor Analysis of Ordinal Items: Old Questions, Modern Solutions? Stats 2024, 7, 984-1001. https://doi.org/10.3390/stats7030060
Marôco J. Factor Analysis of Ordinal Items: Old Questions, Modern Solutions? Stats. 2024; 7(3):984-1001. https://doi.org/10.3390/stats7030060
Chicago/Turabian StyleMarôco, João. 2024. "Factor Analysis of Ordinal Items: Old Questions, Modern Solutions?" Stats 7, no. 3: 984-1001. https://doi.org/10.3390/stats7030060
APA StyleMarôco, J. (2024). Factor Analysis of Ordinal Items: Old Questions, Modern Solutions? Stats, 7(3), 984-1001. https://doi.org/10.3390/stats7030060






