Active Learning for Stacking and AdaBoost-Related Models
Abstract
1. Introduction
2. Ensemble Learning: A Brief Review
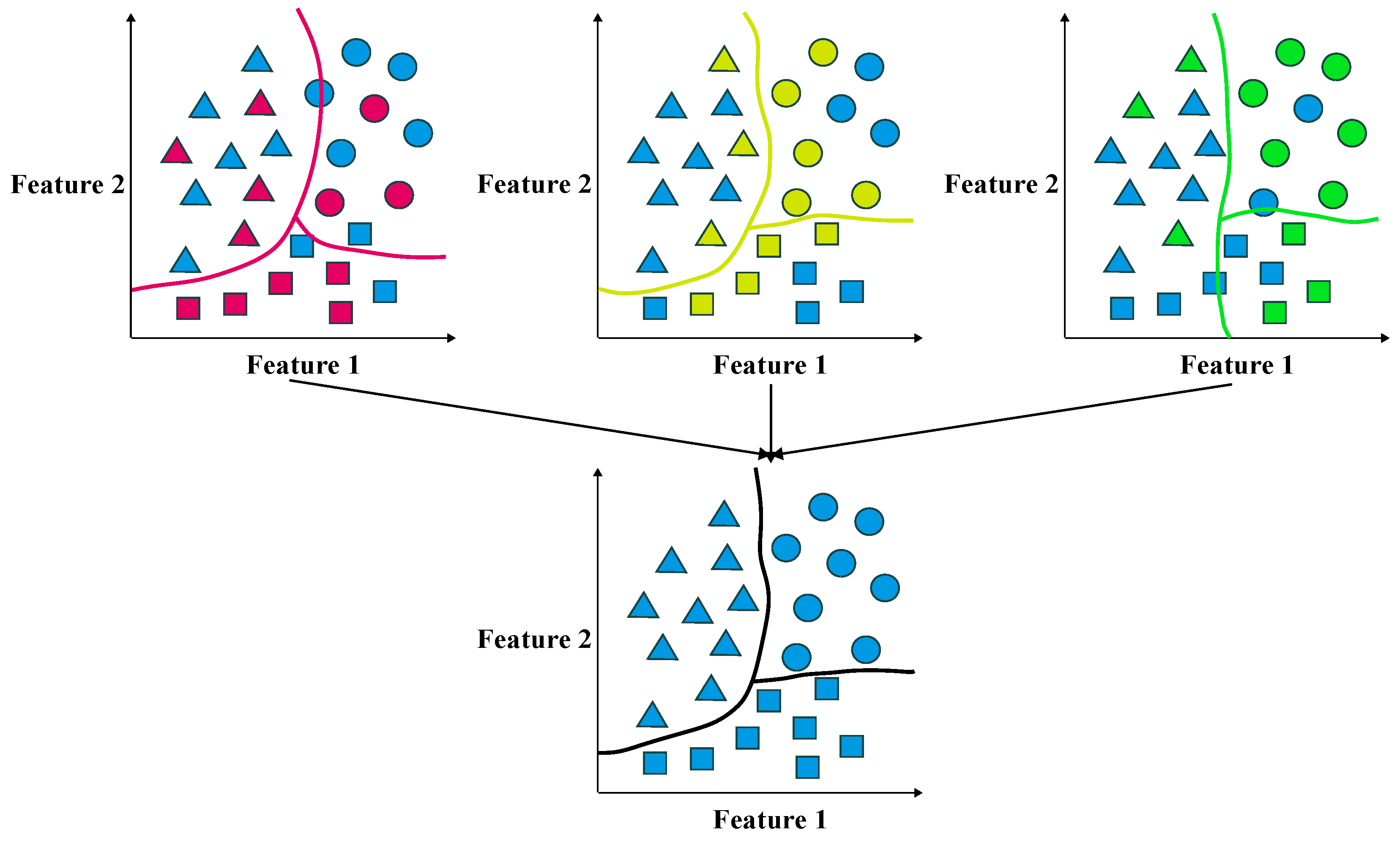
2.1. Boosting
| Algorithm 1 AdaBoost Algorithm |
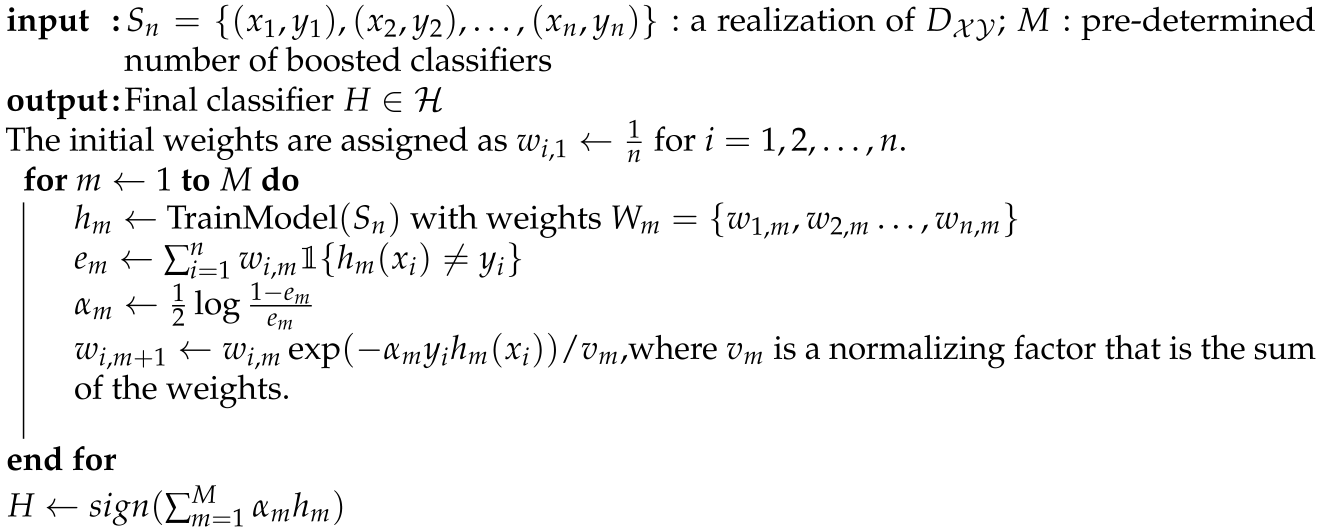 |
2.2. Parallel Ensemble Learning
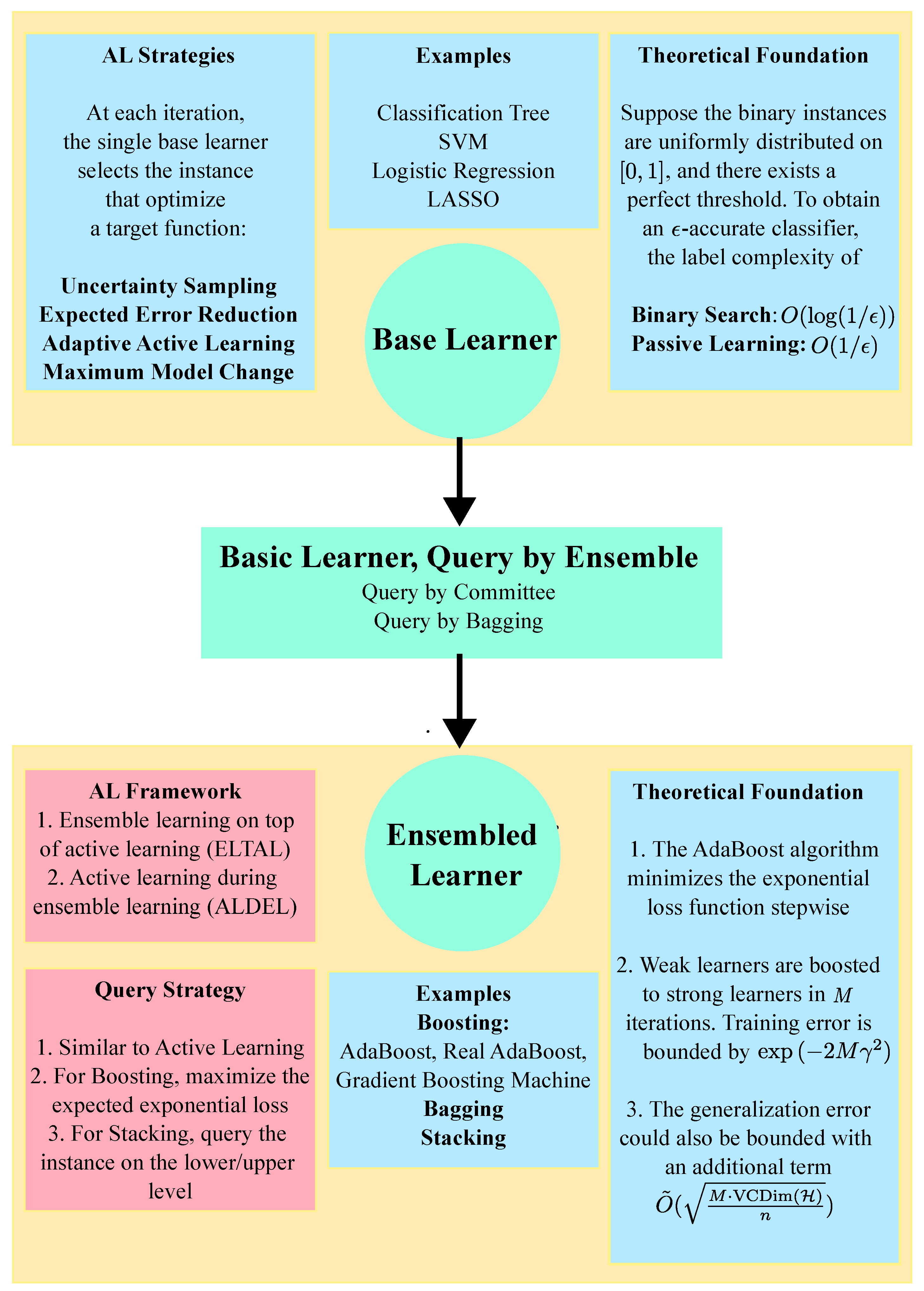
3. Active Learning for Ensemble Learning: A Brief Review
4. Active Learning in Boosting
4.1. ELTAL in Boosting
| Algorithm 2 Ensemble Learning on top of Active Learning (ELTAL) in Boosting |
 |
- Expected Error Reduction [10]:where is the probability that an instance x belongs to the class u when the hypothesis is trained on . The notation is the extended labeled dataset when the instance is labeled as u and added to .
4.2. ALDEL in Boosting
| Algorithm 3 Active Learning During Ensemble Learning (ALDEL) in Boosting |
 |
- Expected Exponential Loss Maximization (EELM): The proposed querying strategy aims to select the instance that maximizes the expected exponential loss over all unlabeled data. Within the Real AdaBoost framework, the hypothesis is a transformation of the weighted probability estimates. The training and transformation steps of Real AdaBoost are identical to those of Discrete AdaBoost, with the objective of approximately optimizing in a stage-wise manner. The selection criterion could be described asIt is important to note that the expected exponential loss in (9) can be expressed as a weighted conditional expectation on . For ease of presentation, we continue to denote as the weighted conditional probability. The selection criterion can also be viewed from an active learning perspective. By substituting the expression of , the expected exponential loss reduces to , which is directly proportional to the standard deviation of . Therefore, the selected instance has the highest variance among all instances in . This aligns with the principle of uncertainty sampling [8].
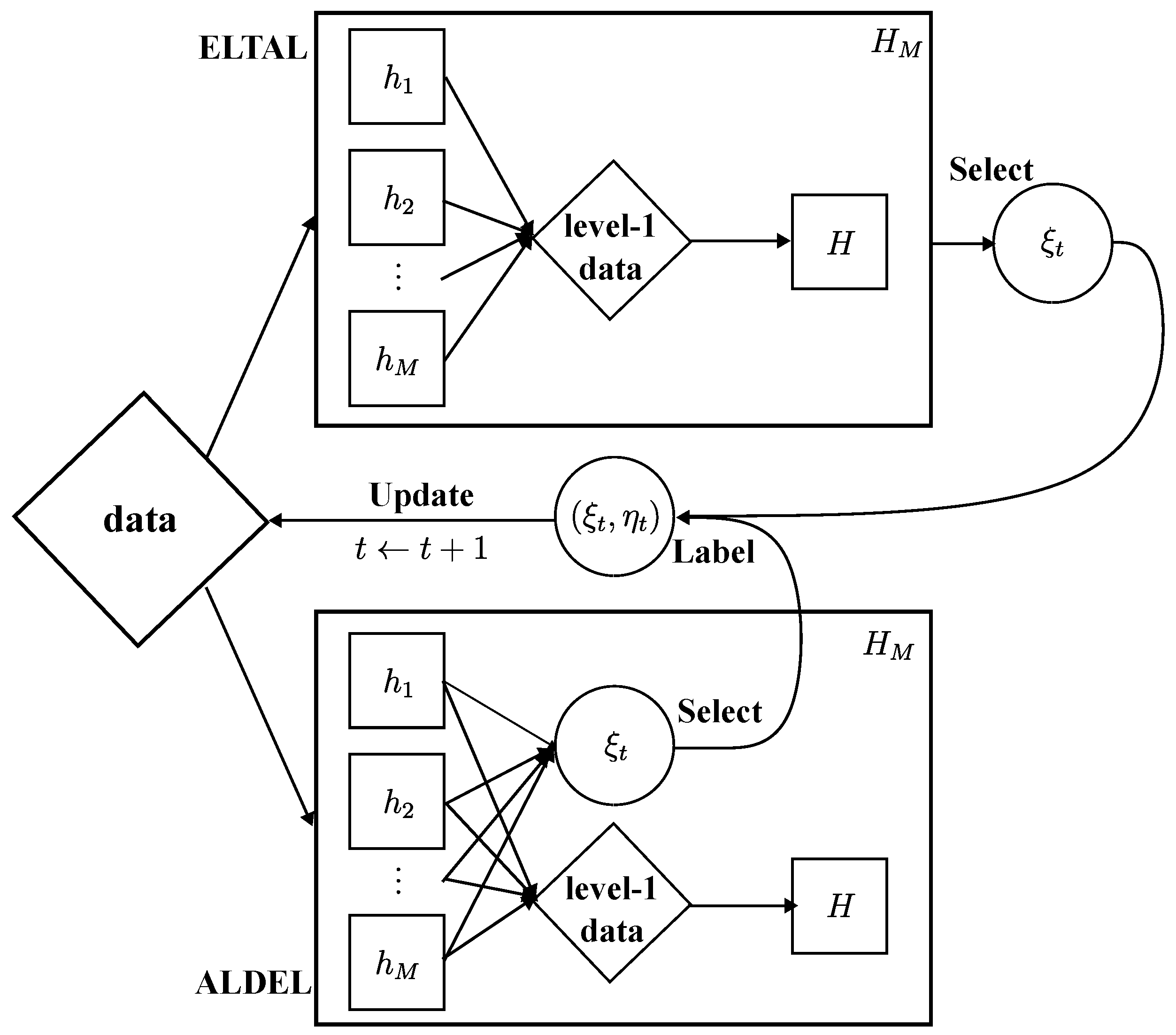
5. Active Learning in Stacking
5.1. ELTAL in Stacking
| Algorithm 4 Ensemble Learning on top of Active Learning (ELTAL) in Stacking |
 |
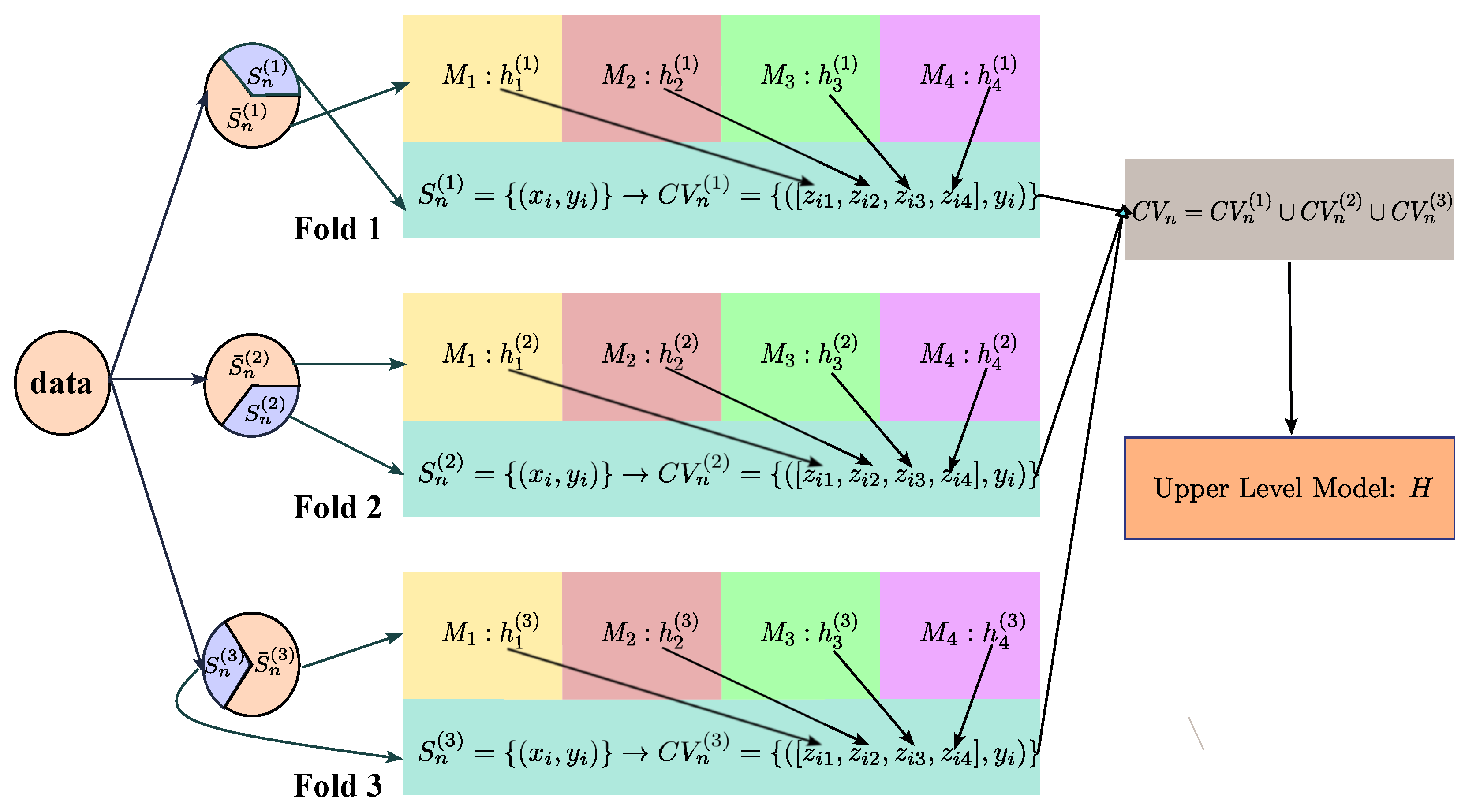
5.2. Two-Level Selection for ALDEL in Stacking
- How to determine the appropriate selection criterion for each lower-level model. As the lower-level models are heterogeneous, it is reasonable to assume that their selection functions will differ.
- How should the selected M instances be combined or integrated if each learner selects only one instance per iteration.
- How to implement the active learning framework in the context of cross-validation.
| Algorithm 5 Active Learning During Ensemble Learning (ALDEL) in Stacking |
 |
5.3. Direct Selection from the Lower-Level
6. Numerical Illustrations
6.1. Simulated Datasets
- Comparison of applying the same active learning selection criterion to the weak learner, the boosted learner and the stacked learner. For instance, SVM-ENTROPY vs. ELTALB-ENTROPY vs. ELTALS-ENTROPY.
- Comparison of different SVM-related and BOOST-related active learning algorithms with the vanilla SVM model, i.e., SVM-UNIF vs. SVM-ENTROPY vs. ELTALB-UNIF vs. ELTALB-ENTROPY vs. ALDEL-EELM.
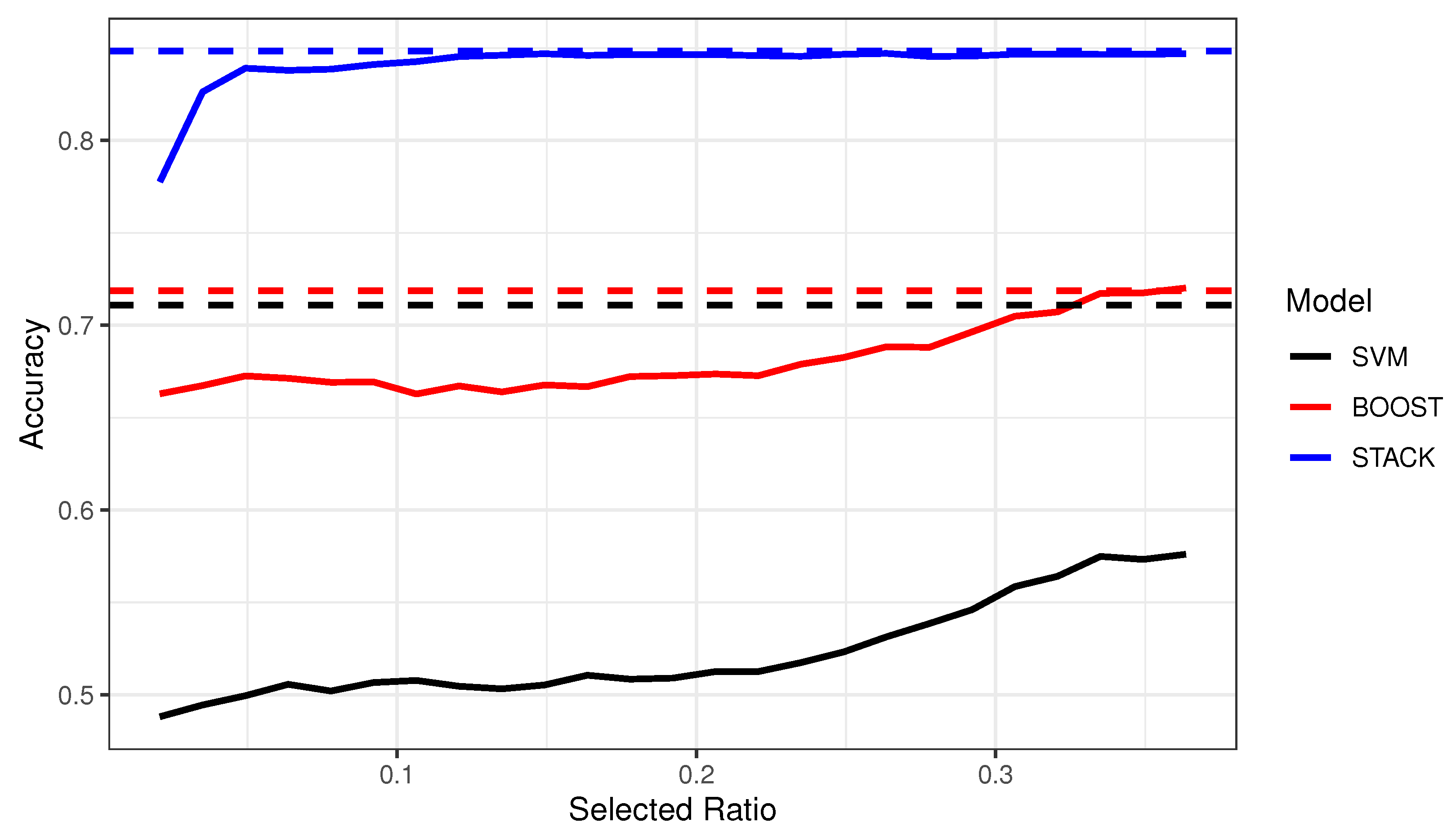
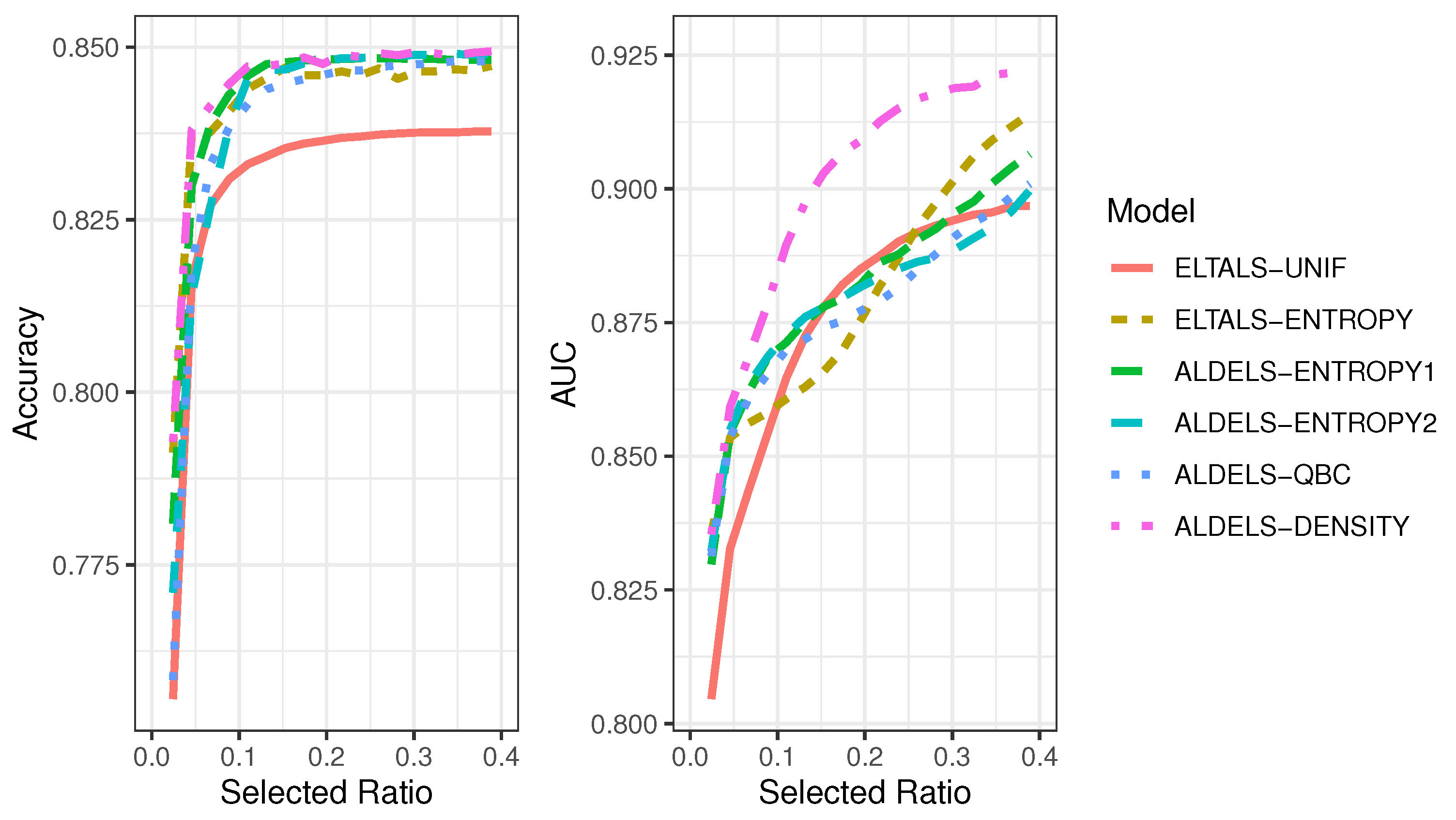
- Comparison of different stacking-related active learning algorithms with the vanilla stacking model, i.e., STACK vs. ELTALS-UNIF vs. ELTALS-ENTROPY vs. ALDELS-ENTROPY1 vs. ALDEL-ENTROPY2 vs. ALDELS-QBC vs. ALDELS-DENSITY.
6.2. Real Data Application
7. Discussion and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. Experiments with a new boosting algorithm. ICML 1996, 96, 148–156. [Google Scholar]
- Freund, Y.; Schapire, R.E. Game theory, on-line prediction and boosting. In Proceedings of the Ninth Annual Conference on Computational Learning Theory, Desenzano del Garda, Italy, 28 June–1 July 1996; pp. 325–332. [Google Scholar]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef]
- Lewis, D.D.; Gale, W.A. A sequential algorithm for training text classifiers. In Proceedings of the SIGIR’94, Dublin, Ireland, 3–6 July 1994; pp. 3–12. [Google Scholar]
- Settles, B. Active Learning Literature Survey; University of Wisconsin-Madison Department of Computer Sciences: Madison, WI, USA, 2009. [Google Scholar]
- Roy, N.; McCallum, A. Toward optimal active learning through sampling estimation of error reduction. Int. Conf. Mach. Learn. 2001, 441–448. [Google Scholar]
- Müller, B.; Reinhardt, J.; Strickland, M.T. Neural Networks: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Ren, P.; Xiao, Y.; Chang, X.; Huang, P.Y.; Li, Z.; Gupta, B.B.; Chen, X.; Wang, X. A survey of deep active learning. ACM Comput. Surv. (CSUR) 2021, 54, 1–40. [Google Scholar] [CrossRef]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Gal, Y.; Islam, R.; Ghahramani, Z. Deep bayesian active learning with image data. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1183–1192. [Google Scholar]
- Beluch, W.H.; Genewein, T.; Nürnberger, A.; Köhler, J.M. The power of ensembles for active learning in image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9368–9377. [Google Scholar]
- Sener, O.; Savarese, S. A geometric approach to active learning for convolutional neural networks. arXiv 2017, arXiv:1708.00489. [Google Scholar]
- Pop, R.; Fulop, P. Deep ensemble bayesian active learning: Addressing the mode collapse issue in monte carlo dropout via ensembles. arXiv 2018, arXiv:1811.03897. [Google Scholar]
- Valiant, L.G. A theory of the learnable. Commun. ACM 1984, 27, 1134–1142. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, B. Boosting with early stopping: Convergence and consistency. Ann. Stat. 2005, 1538. [Google Scholar] [CrossRef]
- Mease, D.; Wyner, A. Evidence Contrary to the Statistical View of Boosting. J. Mach. Learn. Res. 2008, 9, 131–156. [Google Scholar]
- Schapire, R.E.; Singer, Y. Improved boosting algorithms using confidence-rated predictions. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 80–91. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 1–34. [Google Scholar]
- Raftery, A.E.; Madigan, D.; Hoeting, J.A. Bayesian model averaging for linear regression models. J. Am. Stat. Assoc. 1997, 92, 179–191. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial (with comments by M. Clyde, David Draper and EI George, and a rejoinder by the authors. Stat. Sci. 1999, 14, 382–417. [Google Scholar] [CrossRef]
- Wasserman, L. Bayesian model selection and model averaging. J. Math. Psychol. 2000, 44, 92–107. [Google Scholar] [CrossRef]
- Clarke, B. Comparing Bayes model averaging and stacking when model approximation error cannot be ignored. J. Mach. Learn. Res. 2003, 4, 683–712. [Google Scholar]
- Zhou, Z.H. Machine Learning; Springer Nature: Singapore, 2021. [Google Scholar]
- Seung, H.S.; Opper, M.; Sompolinsky, H. Query by committee. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 287–294. [Google Scholar]
- Kumar, P.; Gupta, A. Active learning query strategies for classification, regression, and clustering: A survey. J. Comput. Sci. Technol. 2020, 35, 913–945. [Google Scholar] [CrossRef]
- Settles, B.; Craven, M.; Ray, S. Multiple-instance active learning. Adv. Neural Inf. Process. Syst. 2007, 20, 1289–1296. [Google Scholar]
- Fu, Y.; Zhu, X.; Li, B. A survey on instance selection for active learning. Knowl. Inf. Syst. 2013, 35, 249–283. [Google Scholar] [CrossRef]
- Wu, Y.; Kozintsev, I.; Bouguet, J.Y.; Dulong, C. Sampling strategies for active learning in personal photo retrieval. In Proceedings of the 2006 IEEE International Conference on Multimedia and Expo, Toronto, ON, Canada, 9–12 July 2006; pp. 529–532. [Google Scholar]
- Li, X.; Guo, Y. Adaptive active learning for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 859–866. [Google Scholar]
- Yang, Y.; Loog, M. A variance maximization criterion for active learning. Pattern Recognit. 2018, 78, 358–370. [Google Scholar] [CrossRef]
- Wang, L.M.; Yuan, S.M.; Li, L.; Li, H.J. Boosting Naïve Bayes by active learning. In Proceedings of the 2004 International Conference on Machine Learning and Cybernetics (IEEE Cat. No. 04EX826), Shanghai, China, 26–29 August 2004; Volume 3, pp. 1383–1386. [Google Scholar]
- Abe, N. Query learning strategies using boosting and bagging. In Proceedings of the Fifteenth International Conference on Machine Learning, San Francisco, CA, USA, 24–27 July 1998; pp. 1–9. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Menéndez, M.; Pardo, J.; Pardo, L.; Pardo, M. The jensen-shannon divergence. J. Frankl. Inst. 1997, 334, 307–318. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Platt, J. Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods. Adv. Large Margin Classif. 2000, 10, 61–74. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]



| Name | Description | Active Learning Selection Criterion | Hyperparameters |
|---|---|---|---|
| SVM | Support Vector Machine with Radial Basis Function (RBF) kernel | N/A | kernel parameter , regularization constant C |
| SVM-UNIF | Same as SVM | Random selection | |
| SVM-Entropy | Same as SVM | Entropy variant in (6) | |
| BOOST | Real AdaBoost Algorithm. The basic learner is taken as SVM. | N/A | Basic setup is the same as SVM; SVM is boosted for times |
| ELTALB-UNIF | ELTAL in Boosting using Real AdaBoost The basic learner is taken as SVM. | Random selection | |
| ELTALB-Entropy | ELTAL in Boosting using Real AdaBoost The basic learner is taken as SVM. | Entropy variant in (6) | |
| ALDEL-EELM | ALDEL in Boosting using Real AdaBoost The basic learner is taken as SVM. | EELM in (9) | |
| STACK | A Stacking Model. Lower-level models are taken as SVM, Random Forest, Artificial Neural Networks (ANN) and Gradient Boosting Machine (GBM). The upper-level model is a logistic regression model. | N/A | SVM: same as above Random Forest: number of trees: 100, number of variables used for splitting ANN: number of units, weight decay GBM: max depth, learning rate, minimum number of observations in each node, number of trees: 100 |
| ELTALS-UNIF | ELTAL in Stacking, Models on both levels are the same as STACK. | Random selection | |
| ELTALS-ENTROPY | ELTAL in Stacking, Models on both levels are the same as STACK. | Entropy variant in uncertainty sampling | |
| ALDELS-ENTROPY1 | ALDEL in Stacking, Models on both levels are the same as STACK. | Lower-level selection is based on entropy Upper-level selection is implemented using | |
| ALDELS-ENTROPY2 | ALDEL in Stacking, Models on both levels are the same as STACK. | Lower-level selection is based on entropy Upper-level selection is implemented using | |
| ALDELS-QBC | ALDEL in Stacking, Models on both levels are the same as STACK. | Apply QBC to lower-level models. KL divergence as the disagreement measure | |
| ALDELS-DENSITY | ALDEL in Stacking, Models on both levels are the same as STACK. | Apply Information Density AL on . Information entropy is taken as . Cosine similarity is used Set |
| 5% | 10% | 25% | 50% | |||||
|---|---|---|---|---|---|---|---|---|
| Time |
vs. UNIF vs. Full | Time |
vs. UNIF
vs. Full | Time |
vs. UNIF vs. Full | Time |
vs. UNIF
vs. Full | |
| SVM | 0.006 | 0.711 | 0.007 | 0.711 | 0.016 | 0.711 | 0.040 | 0.711 |
| SVM- ENTROPY | 0.017 | 0.071 | 0.019 | 0.032 | 0.028 | 0.009 | 0.043 | 0.02 |
| −0.218 | −0.211 | −0.204 | −0.180 | |||||
| ALDELB- EELM | 0.028 | 0.130 | 0.031 | 0.069 | 0.047 | 0.035 | 0.084 | 0.031 |
| −0.165 | −0.181 | −0.185 | −0.181 | |||||
| BOOST | 0.332 | 0.719 | 0.420 | 0.719 | 0.924 | 0.719 | 2.349 | 0.719 |
| ELTALB- ENTROPY | 0.669 | 0.032 | 0.809 | 0.034 | 1.327 | 0.029 | 2.042 | 0.042 |
| −0.052 | −0.049 | −0.048 | −0.020 | |||||
| STACK | 2.162 | 0.848 | 2.220 | 0.848 | 2.797 | 0.848 | 4.287 | 0.848 |
| ELTALS- ENTROPY | 0.596 | 0.030 | 0.633 | 0.019 | 0.757 | 0.014 | 0.892 | 0.011 |
| −0.037 | −0.021 | −0.009 | −0.005 | |||||
| ALDELS- ENTROPY1 | 1.375 | 0.021 | 1.451 | 0.016 | 1.877 | 0.013 | 2.689 | 0.012 |
| −0.047 | −0.024 | −0.009 | −0.004 | |||||
| ALDELS- ENTROPY2 | 1.703 | 0.008 | 1.806 | 0.005 | 2.242 | 0.009 | 3.245 | 0.010 |
| −0.059 | −0.035 | −0.013 | −0.006 | |||||
| ALDELS- QBC | 0.599 | 0.002 | 0.644 | 0.005 | 0.749 | 0.008 | 0.878 | 0.009 |
| −0.066 | −0.035 | −0.015 | −0.007 | |||||
| ALDELS- DENSITY | 44.16 | 0.033 | 41.97 | 0.022 | 39.01 | 0.016 | 35.04 | 0.013 |
| −0.035 | −0.018 | −0.007 | −0.003 | |||||
| Accuracy | F1 Score | |||||||
|---|---|---|---|---|---|---|---|---|
| Selected Ratio | 20% | 30% | 50% | 100% | 20% | 30% | 50% | 100% |
| SVM-UNIF | 79.64 (0.24) | 80.17 (0.23) | 79.61 (0.17) | 80.20 | 76.68 (0.43) | 77.78 (0.45) | 77.36 (0.29) | 77.89 |
| SVM-ENTROPY | 75.50 (1.46) | 70.16 (2.22) | 73.42 (1.01) | 80.20 | 72.82 (2.76) | 60.26 (5.29) | 73.00 (1.98) | 77.89 |
| ELTALB-UNIF | 85.16 (0.54) | 87.33 (0.63) | 87.91 (0.85) | 96.23 | 82.95 (1.45) | 86.11 (1.61) | 87.36 (2.00) | 96.79 |
| ELTALB-ENTROPY | 89.60 (0.62) | 91.97 (1.01) | 93.51 (0.61) | 96.23 | 87.60 (1.93) | 91.64 (2.07) | 93.75 (1.09) | 96.79 |
| ALDELB-EELM | 75.73 (1.72) | 80.10 (1.61) | 79.92 (1.66) | 80.20 | 77.58 (2.89) | 81.60 (3.09) | 62.80 (3.73) | 77.89 |
| ELTALS-UNIF | 80.45 (0.68) | 83.49 (0.53) | 85.86 (0.69) | 94.08 | 77.04 (1.14) | 80.00 (1.31) | 83.94 (1.12) | 93.38 |
| ELTALS-ENTROPY | 87.01 (0.68) | 90.94 (0.70) | 92.80 (0.50) | 94.08 | 87.35 (0.62) | 90.13 (1.19) | 92.51 (0.13) | 93.38 |
| ALDELS-ENTROPY1 | 82.05 (0.63) | 87.62 (1.11) | 91.31 (0.89) | 94.08 | 82.14 (2.11) | 88.47 (1.23) | 90.99 (1.17) | 93.38 |
| ALDELS-ENTROPY2 | 82.15 (1.27) | 86.97 (1.34) | 90.87 (0.90) | 94.08 | 84.73 (1.12) | 87.08 (1.85) | 90.19 (1.63) | 93.38 |
| ALDELS-QBC | 80.73 (1.00) | 86.30 (0.62) | 90.83 (0.42) | 94.08 | 78.96 (1.92) | 84.11 (1.50) | 89.54 (0.56) | 93.38 |
| ALDELS-DENSITY | 86.31 (0.33) | 90.79 (0.23) | 92.02 (0.28) | 94.08 | 85.04 (0.58) | 89.90 (0.38) | 91.73 (0.43) | 93.38 |
| Accuracy | F1 Score | |||||||
|---|---|---|---|---|---|---|---|---|
| Selected Ratio | 5% | 10% | 25% | 100% | 5% | 10% | 25% | 100% |
| SVM-UNIF | 88.66 (0.28) | 88.94 (0.28) | 89.64 (0.17) | 89.79 | 89.21 (0.27) | 89.50 (0.29) | 90.18 (0.19) | 90.26 |
| SVM-ENTROPY | 83.99 (3.05) | 89.36 (1.21) | 86.88 (1.52) | 89.79 | 83.41 (3.16) | 89.42 (1.57) | 85.80 (2.31) | 90.26 |
| ELTALB-UNIF | 89.03 (2.15) | 91.23 (1.43) | 92.87 (0.72) | 95.05 | 86.17 (3.63) | 91.87 (2.04) | 93.49 (0.50) | 95.25 |
| ELTALB-ENTROPY | 89.34 (2.95) | 94.66 (1.98) | 92.57 (2.32) | 95.05 | 85.43 (4.31) | 94.45 (2.34) | 90.87 (3.29) | 95.25 |
| ALDELB-EELM | 71.78 (3.47) | 65.19 (2.92) | 59.75 (2.85) | 89.79 | 63.61 (5.12) | 65.47 (3.72) | 62.85 (3.95) | 90.26 |
| ELTALS-UNIF | 98.60 (0.10) | 99.05 (0.06) | 99.53 (0.04) | 99.70 | 98.69 (0.10) | 99.15 (0.05) | 99.58 (0.03) | 99.70 |
| ELTALS-ENTROPY | 99.87 (0.01) | 99.71 (0.01) | 99.71 (0.01) | 99.70 | 99.86 (0.01) | 99.71 (0.01) | 99.71 (0.01) | 99.70 |
| ALDELS-ENTROPY1 | 99.85 (0.02) | 99.77 (0.02) | 99.69 (0.01) | 99.70 | 99.88 (0.01) | 99.76 (0.01) | 99.69 (0.01) | 99.70 |
| ALDELS-ENTROPY2 | 99.87 (0.01) | 99.72 (0.01) | 99.71 (0.01) | 99.70 | 99.87 (0.01) | 99.73 (0.01) | 99.71 (0.01) | 99.70 |
| ALDELS-QBC | 97.78 (0.26) | 98.15 (0.17) | 98.16 (0.22) | 99.70 | 99.73 (0.27) | 98.13 (0.15) | 98.15 (0.20) | 99.70 |
| ALDELS-DENSITY | 99.51 (0.23) | 99.47 (0.18) | 99.52 (0.13) | 99.70 | 99.53 (0.22) | 99.48 (0.17) | 99.53 (0.12) | 99.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, Q.; Ghosh, S.K. Active Learning for Stacking and AdaBoost-Related Models. Stats 2024, 7, 110-137. https://doi.org/10.3390/stats7010008
Sui Q, Ghosh SK. Active Learning for Stacking and AdaBoost-Related Models. Stats. 2024; 7(1):110-137. https://doi.org/10.3390/stats7010008
Chicago/Turabian StyleSui, Qun, and Sujit K. Ghosh. 2024. "Active Learning for Stacking and AdaBoost-Related Models" Stats 7, no. 1: 110-137. https://doi.org/10.3390/stats7010008
APA StyleSui, Q., & Ghosh, S. K. (2024). Active Learning for Stacking and AdaBoost-Related Models. Stats, 7(1), 110-137. https://doi.org/10.3390/stats7010008







