A Bayesian One-Sample Test for Proportion
Abstract
1. Introduction
2. Inferences Using Relative Belief
3. One-Sample Bayesian Test for Proportion
3.1. The Approach
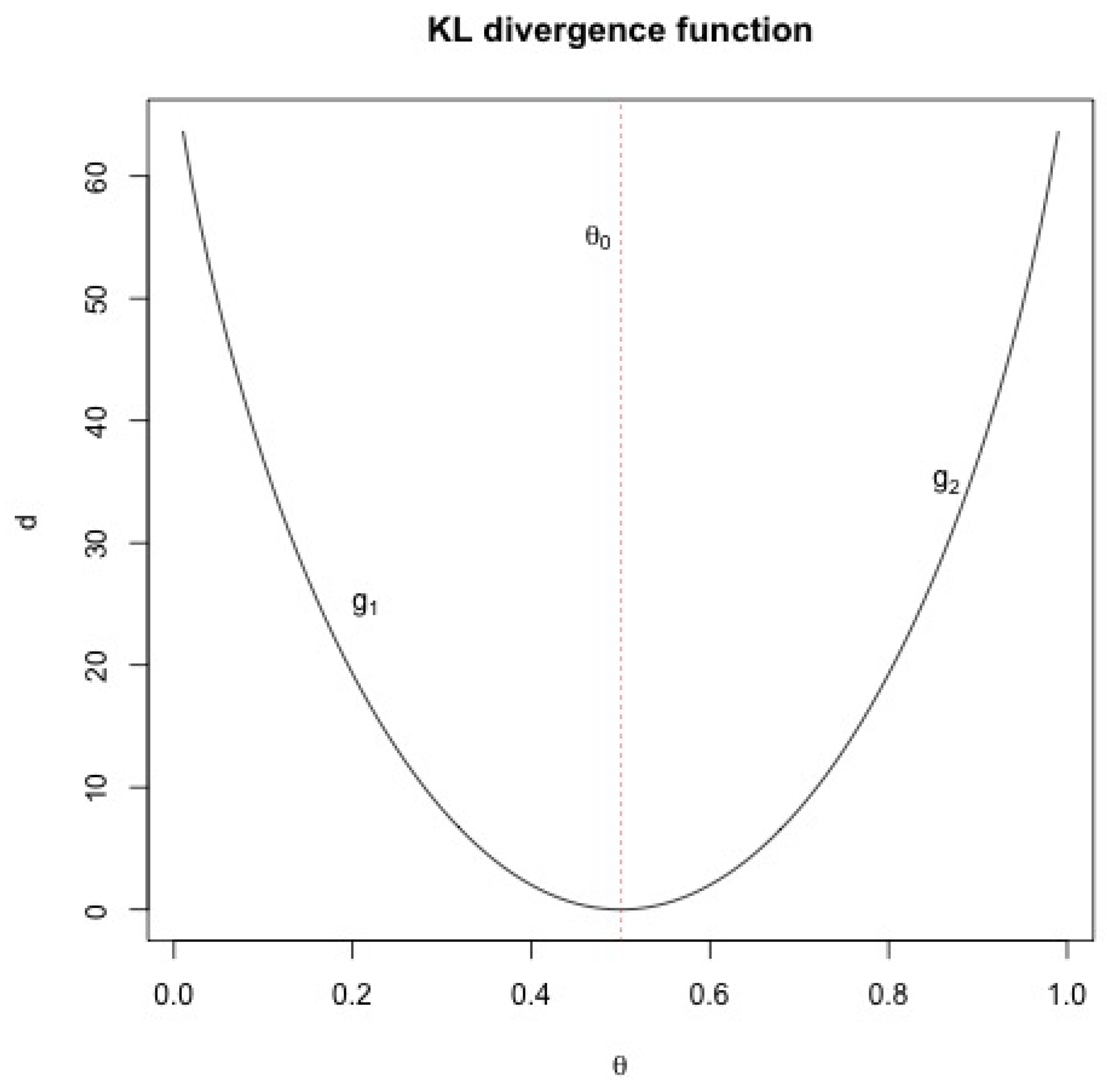
3.2. Checking for Prior-Data Conflict
- (i)
- If Beta, then
- (ii)
- If Beta, thenwhere is the digamma function.
3.3. Checking the Prior for Bias
3.4. The Algorithm
- (i)
- Generate from Beta, and compute D.
- (ii)
- Repeat Step (ii) to obtain a sample of values of D.
- (iii)
- Generate from Beta, and compute .
- (iv)
- Repeat Step (iv) to obtain a sample of values of .
- (v)
- Compute the relative belief ratio and the strength as follows:
- (a)
- Let L be a positive number. Let denote the empirical cdf of D based on the prior sample in (3), and for let be the estimate of the -prior quantile of D. Here, , and is the largest value of D. Let denote the empirical cdf based on . For , estimate bythe ratio of the estimates of the posterior and prior contents of Thus, we estimate by , where and are chosen so that is not too small (typically, .
- (b)
- Estimate the strength by the finite sum:
4. Examples
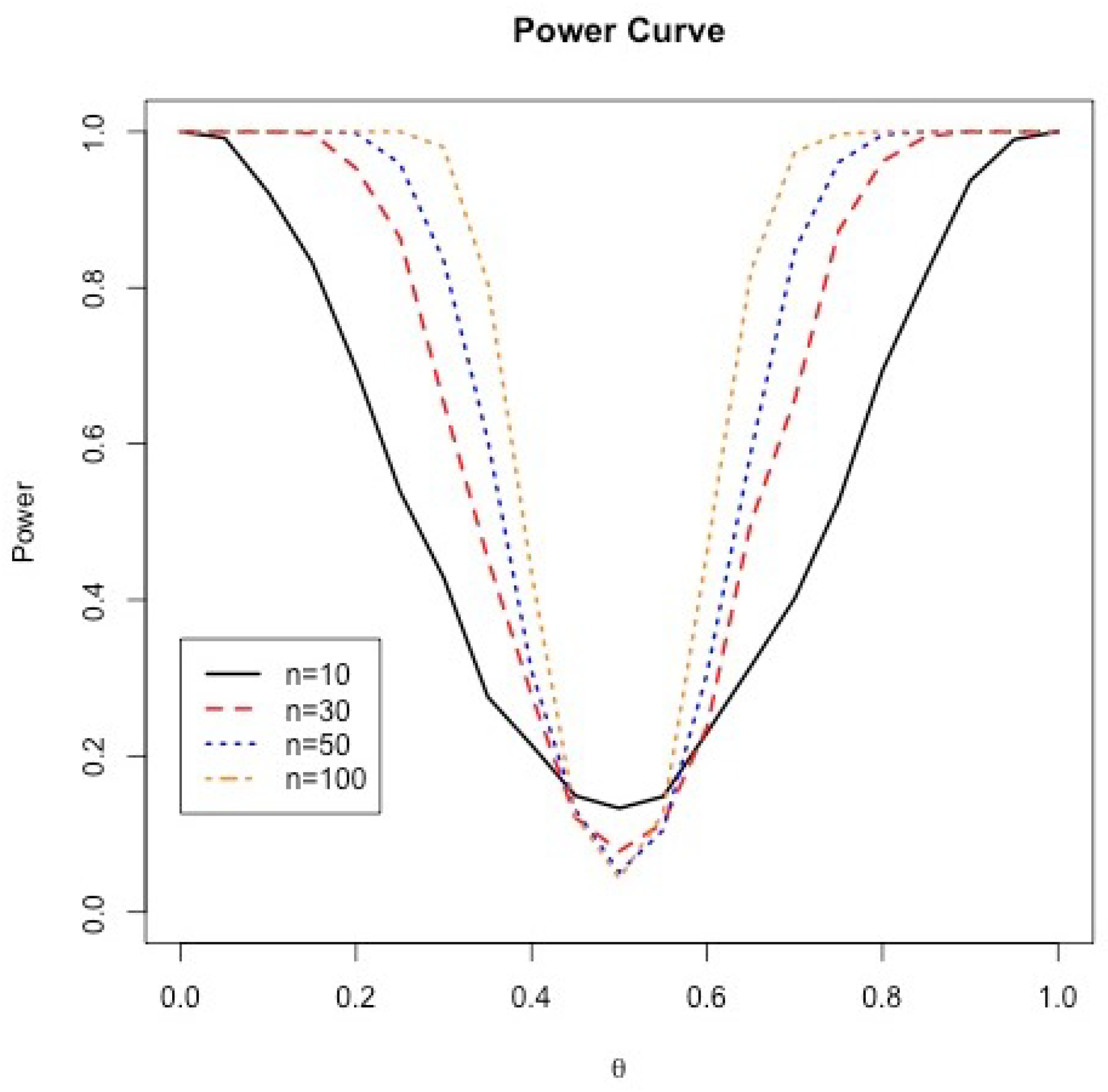
5. Simulation Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bain, L.J.; Engelhardt, M. Introduction to Probability and Mathematical Statistics; Duxbury Press: Belmont, CA, USA, 1992; Volume 4. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Rouder, J.N.; Morey, R.D.; Speckman, P.L.; Province, J.M. Default Bayes factors for ANOVA designs. J. Math. Psychol. 2012, 56, 356–374. [Google Scholar] [CrossRef]
- Kass, R.E.; Vaidyanathan, S.K. Approximate Bayes factors and orthogonal parameters, with application to testing equality of two binomial proportions. J. R. Stat. Soc. Ser. B (Methodol.) 1992, 54, 129–144. [Google Scholar] [CrossRef]
- Dablander, F.; Huth, K.; Gronau, Q.F.; Etz, A.; Wagenmakers, E.J. A puzzle of proportions: Two popular Bayesian tests can yield dramatically different conclusions. Stat. Med. 2022, 41, 1319–1333. [Google Scholar] [CrossRef] [PubMed]
- Jamil, T.; Ly, A.; Morey, R.D.; Love, J.; Marsman, M.; Wagenmakers, E.J. Default “Gunel and Dickey” Bayes factors for contingency tables. Behav. Res. Methods 2017, 49, 638–652. [Google Scholar] [CrossRef] [PubMed]
- Nieto, A.; Extremera, S.; Gómez, J. Bayesian hypothesis testing for proportions. In Paper SP08; PhUSE: Madrid, Spain, 2011; Available online: https://www.lexjansen.com/phuse/2011/sp/SP08.pdf (accessed on 1 October 2022).
- Morey, R.D.; Rouder, J.N.; Jamil, T.; Urbanek, S.; Forner, K.; Ly, A. Package ‘BayesFactor’. 2022. Available online: https://cran.rproject.org/web/packages/BayesFactor/BayesFactor.pdf (accessed on 1 October 2022).
- Evans, M. Measuring Statistical Evidence Using Relative Belief; Monographs on Statistics and Applied Probability 144; Taylor & Francis Group, CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Al-Labadi, L.; Evans, M. Optimal robustness results for relative belief inferences and the relationship to prior-data conflict. Bayesian Anal. 2017, 12, 705–728. [Google Scholar] [CrossRef]
- Abdelrazeq, I.; Al-Labadi, L.; Alzaatreh, A. On one-sample Bayesian tests for the mean. Statistics 2020, 54, 424–440. [Google Scholar] [CrossRef]
- Al-Labadi, L.; Berry, S. Bayesian estimation of extropy and goodness of fit tests. J. Appl. Stat. 2020, 49, 357–370. [Google Scholar] [CrossRef] [PubMed]
- Al-Labadi, L.; Patel, V.; Vakiloroayaei, K.; Wan, C. Kullback–Leibler divergence for Bayesian nonparametric model checking. J. Korean Stat. Soc. 2020, 50, 272–289. [Google Scholar] [CrossRef]
- Al-Labadi, L. The two-sample problem via relative belief ratio. Comput. Stat. 2021, 36, 1791–1808. [Google Scholar] [CrossRef]
- Baskurt, Z.; Evans, M. Hypothesis assessment and inequalities for Bayes factors and relative belief ratios. Bayesian Anal. 2013, 8, 569–590. [Google Scholar] [CrossRef]
- Evans, M.; Moshonov, H. Checking for prior-data conflict. Bayesian Anal. 2006, 1, 893–914. [Google Scholar] [CrossRef]
- Nott, D.J.; Seah, M.; Al-Labadi, L.; Evans, M.; Ng, H.K.; Englert, B. Using prior expansion for prior-data conflict checking. Bayesian Anal. 2021, 16, 203–231. [Google Scholar] [CrossRef]
- Al-Labadi, L.; Asl, F.F. On robustness of the relative belief ratio and the strength of its evidence with respect to the geometric contamination prior. J. Korean Stat. Soc. 2022, 1–15. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Al-Labadi, L.; Evans, M. Prior-based model checking. Can. J. Stat. 2018, 46, 380–398. [Google Scholar] [CrossRef]
- Rouder, J.; Speckman, P.; Sun, D.; Morey, R.; Iverson, G. Bayesian t tests for accepting and rejecting the null hypothesis. Psychon. Bull. Rev. 2009, 16, 225–237. [Google Scholar] [CrossRef] [PubMed]
- Jeffreys, H. Theory Probability; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Raftery, A.E. Bayesian model selection in social research. Sociol. Methodol. 1995, 25, 111–164. [Google Scholar] [CrossRef]
- McClave, J.; Sincich, T. Statistics, 13th ed.; Person: Boston, MA, USA, 2017. [Google Scholar]
- Wackerly, D.; Mendenhall, W.; Scheaffer, R.L. Mathematical Atatistics with Applications; Cengage Learning: Belmont, CA, USA, 2014. [Google Scholar]
| Test | Values | Decision |
|---|---|---|
| RB (strength) | 0.0400 (0.0021) | Strong evidence to reject |
| RB (strength) using (15) | 0.0166 (0.0002) | Strong evidence to reject |
| BF | 167.8429 | Extreme evidence to reject |
| p-value (exact) | 0.0003 | Reject |
| p-value (approximate) | 0.0012 | Reject |
| Test | Values | Decision |
|---|---|---|
| RB (strength) | 4.094 (0.406) | Moderate evidence in favor of |
| RB (strength) using (15) | 2.790 (0.1177) | Moderate/weak evidence in favor of |
| BF | 0.9567 | Anecdotal evidence for |
| p-value (exact) | 0.0962 | Fail to reject |
| p-value (approximate) | 0.1336 | Fail to reject |
| n = 10 | ||||
|---|---|---|---|---|
| Proportion | Exact Test | z-Test | ||
| 0.922 | 0.984 | 0.719 | 0.835 | |
| 0.832 | 0.934 | 0.535 | 0.689 | |
| 0.696 | 0.869 | 0.368 | 0.530 | |
| 0.539 | 0.772 | 0.236 | 0.381 | |
| 0.428 | 0.654 | 0.150 | 0.256 | |
| 0.276 | 0.534 | 0.081 | 0.161 | |
| 0.214 | 0.437 | 0.044 | 0.098 | |
| 0.149 | 0.351 | 0.029 | 0.062 | |
| 0.133 | 0.341 | 0.021 | 0.050 | |
| 0.148 | 0.382 | 0.034 | 0.062 | |
| 0.230 | 0.441 | 0.06 | 0.098 | |
| 0.315 | 0.530 | 0.088 | 0.161 | |
| 0.402 | 0.663 | 0.139 | 0.256 | |
| 0.526 | 0.771 | 0.240 | 0.381 | |
| 0.694 | 0.887 | 0.390 | 0.530 | |
| 0.818 | 0.950 | 0.551 | 0.689 | |
| 0.937 | 0.988 | 0.704 | 0.835 | |
| 0.990 | 0.998 | 0.906 | 0.943 | |
| n = 30 | ||||
| 1 | 1 | 1 | 0.999 | |
| 0.998 | 0.999 | 0.993 | 0.989 | |
| 0.953 | 0.974 | 0.929 | 0.941 | |
| 0.864 | 0.884 | 0.791 | 0.818 | |
| 0.652 | 0.712 | 0.574 | 0.615 | |
| 0.453 | 0.502 | 0.352 | 0.386 | |
| 0.278 | 0.297 | 0.188 | 0.197 | |
| 0.121 | 0.153 | 0.079 | 0.085 | |
| 0.078 | 0.101 | 0.037 | 0.050 | |
| 0.114 | 0.152 | 0.072 | 0.085 | |
| 0.237 | 0.297 | 0.184 | 0.197 | |
| 0.499 | 0.489 | 0.337 | 0.386 | |
| 0.657 | 0.721 | 0.572 | 0.616 | |
| 0.873 | 0.891 | 0.801 | 0.818 | |
| 0.962 | 0.979 | 0.952 | 0.941 | |
| 0.994 | 0.998 | 0.993 | 0.989 | |
| 1 | 1 | 1 | 0.999 | |
| 1 | 1 | 1 | 1 | |
| n = 50 | ||||
|---|---|---|---|---|
| Proportion | Exact Test | z-Test | ||
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 0.998 | 1 | |
| 0.998 | 0.997 | 0.988 | 0.995 | |
| 0.959 | 0.983 | 0.940 | 0.959 | |
| 0.834 | 0.902 | 0.770 | 0.829 | |
| 0.605 | 0.720 | 0.499 | 0.577 | |
| 0.309 | 0.422 | 0.226 | 0.296 | |
| 0.131 | 0.208 | 0.071 | 0.109 | |
| 0.051 | 0.129 | 0.034 | 0.050 | |
| 0.105 | 0.218 | 0.089 | 0.109 | |
| 0.306 | 0.449 | 0.242 | 0.296 | |
| 0.589 | 0.741 | 0.514 | 0.577 | |
| 0.848 | 0.913 | 0.779 | 0.829 | |
| 0.961 | 0.989 | 0.946 | 0.959 | |
| 0.996 | 1 | 0.995 | 0.995 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| n = 100 | ||||
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 0.999 | 0.999 | |
| 0.980 | 0.99 | 0.977 | 0.984 | |
| 0.806 | 0.91 | 0.838 | 0.861 | |
| 0.434 | 0.629 | 0.478 | 0.521 | |
| 0.124 | 0.230 | 0.133 | 0.170 | |
| 0.043 | 0.092 | 0.039 | 0.050 | |
| 0.126 | 0.248 | 0.133 | 0.170 | |
| 0.461 | 0.633 | 0.469 | 0.521 | |
| 0.821 | 0.907 | 0.833 | 0.861 | |
| 0.974 | 0.989 | 0.970 | 0.984 | |
| 0.997 | 1 | 1 | 0.999 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Labadi, L.; Cheng, Y.; Fazeli-Asl, F.; Lim, K.; Weng, Y. A Bayesian One-Sample Test for Proportion. Stats 2022, 5, 1242-1253. https://doi.org/10.3390/stats5040075
Al-Labadi L, Cheng Y, Fazeli-Asl F, Lim K, Weng Y. A Bayesian One-Sample Test for Proportion. Stats. 2022; 5(4):1242-1253. https://doi.org/10.3390/stats5040075
Chicago/Turabian StyleAl-Labadi, Luai, Yifan Cheng, Forough Fazeli-Asl, Kyuson Lim, and Yanqing Weng. 2022. "A Bayesian One-Sample Test for Proportion" Stats 5, no. 4: 1242-1253. https://doi.org/10.3390/stats5040075
APA StyleAl-Labadi, L., Cheng, Y., Fazeli-Asl, F., Lim, K., & Weng, Y. (2022). A Bayesian One-Sample Test for Proportion. Stats, 5(4), 1242-1253. https://doi.org/10.3390/stats5040075






