Abstract
The paper shows how the linear regression depends on the selection of the reference frame. The slope of the fitted line and the corresponding Pearson’s correlation coefficient are expressed in terms of the rotation angle. The correlation coefficient is found to be maximized for a certain optimal angle, for which the slope attains a special optimal value. The optimal angle, the value of the optimal slope, and the corresponding maximum correlation coefficient were expressed in terms of the covariance matrix, but also in terms of the values of the slope, derived from the fitting at the nonrotated and right-angle-rotated axes. The potential of the new method is to improve the derived values of the fitting parameters by detecting the optimal rotation angle, that is, the one that maximizes the correlation coefficient. The presented analysis was applied to the linear regression of density and temperature measurements characterizing the proton plasma in the inner heliosheath, the outer region of our heliosphere.
1. Introduction
The fitting of a given dataset to the values of a statistical model in the domain [1,2,3,4,5] involves finding the optimal parameter value in that minimizes the sum of squared residuals, also known in physical sciences as total square deviations (TSD) between model and data,
where the inverse of variance of the data measurements is weighting the summation. In the case of the multiparametrical fitting, we consider that the statistical model depends on n independent parameters, . Then, TSD becomes (e.g., [6,7,8,9]):
or, for a biparametrical (α and β) linear regression, we have:
Minimization of TSD leads to the optimal value of the involved parameters (least-square method), that is,
The optimal fitting value of the slope β is noted as β0. The optimal value of the slope β for the inverse linear regression, that is, between (y,x), is:
where the ratio equals the correlation of these linear regressions, which is maximized for .
In this paper, we focus on the optimal fitting value of the slope β, derived from the linear regression of data expressed on the rotated Cartesian axes. The slope β and the corresponding Pearson’s correlation coefficient are calculated as a function of the rotation angle ϑ, while the optimal fitting value of the slope is derived from the maximization of the correlation coefficient. Finally, we expose an application from the discipline of space physics. In particular, the presented analysis was applied to the linear regression of density and temperature measurements characterizing the proton plasma in the inner heliosheath, the outer region of our heliosphere. Those measurements can be fitted with a line of negative slope, which gives the polytropic index of the plasma. The new statistical method improves the applied linear regression and the estimated value of the polytropic index.
2. Rotated Optimal Slope
The orthogonal Cartesian system is rotated by an angle ϑ, according to
Then, the total square deviations are given by:
Next, we express the parameter values, the slope and intercept , in terms of their values at the nonrotated system. First, we observe that the slope is transformed as follows:
hence,
In order to find the transform intercept, we consider the yellow-shaded triangle in Figure 1, where we have:
thus, we end up with:
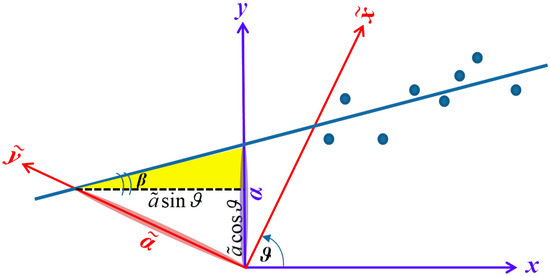
Figure 1.
Scheme of the rotated axes and the corresponding symbols. The angle noted by the symbol “))” in the yellow-shaded triangle has its tangent equal to β and is related to Equation (10).
Therefore, the total square deviations in the rotated reference frame is given by:
(with ). Hence, the minimization of TSD can be still expressed in terms of the linear parameters α and β of the nonrotated frame; namely, we first derive the normal equation with respect to α:
leading to
Next, we derive the normal equation with respect to β:
or
Hence, we have
or
We observe that for ϑ = 0 and for ϑ = 900.
Finally, we note that is the slope of the fitted curve derived from the fitting performed in the rotated frame, while is the expression of the slope in the nonrotated frame. One may find , that is, the slope expressed in the rotated frame, simply by substituting Equation (18) in Equation (9):
3. Maximized Correlation Coefficient
The Pearson’s correlation coefficient is derived as follows. First, we construct the covariance and variances, and then the correlation coefficient at the rotated reference frame. We have:
thus, we obtain:
In similar, we have:
Hence, the Pearson’s correlation coefficient for the normal and the rotated frames:
Note: While the covariance cov(x,y) or the Pearson’s correlation coefficient can be either positive or negative, their algebraic sign has no effect on the method of correlation maximization presented here. Indeed, the examined datasets may be correlated, r > 0, or anti-correlated, r < 0, but it is important to ask just how big is the correlation or anticorrelation; hence, the meaningful quantity needed to be maximized is the absolute correlation or the square of the correlation, r2. For the same reason, the sign of the covariance does not affect the presented analysis, and it is ignored. For this, we denote the covariance with the square symbol , though it may have negative sign.
We observe that
Then, we have
where we used the identity . Hence, we find the invariant:
Then, the correlation coefficient at the rotated system becomes:
or
Hence, we first calculate the right-hand side of Equation (29):
thus, Equation (29) becomes:
Using trigonometric functions of angle 4ϑ, we easily find:
This can be rewritten in a compact way:
where
Given and , we rewrite the correlation coefficient as:
Note that, as expected, for ϑ = 0 and ϑ = 900, the correlation coefficient remains the same, .
The correlation coefficient is maximized [10] for the optimal angle :
or
Given the half-tangent formula , we derive the solutions:
or
where the subscript “opt” denotes the optimal rotation angle, , for which the correlation is maximized (i.e., ). Then, from Equation (35), we derive the respective optimal correlation coefficient for each of the two solutions:
- For the (i) solution, we have a maximum of r2:
and solving in terms of :
We observe that the maximized correlation coefficient at the rotated system ranges from for X = 0 to for X→∞. The case is consistent with ϑ = 0; hence, we expect for X = 0 to have ϑ = 0. The positive root in the (i) solution gives ϑ→0 for X→0, which is consistent with . However, the negative root gives ϑ→450 for X→0; thus, the negative sign case must be rejected.
- For the (ii) solution, we have a minimum of r2:
We seek the maximum correlation, so we reject the minimum of the (ii) solution and Equation (42). Therefore, the only acceptable solution is (i):
Solving Equation (18) in terms of tanϑ, we obtain:
Therefore, the optimal value of the slope can be expressed in terms of the slope for ϑ = 0, , and ϑ = 900, . Namely,
We obtain for X→0, leading to , and for X→∞, leading to ; (see: [11]).
In general, the optimal value of the slope is given by:
4. Application to the Inner Heliosheath
Classical collisional particle systems residing in thermal equilibrium have their particle velocity/energy distribution function stabilized into a Maxwell-Boltzmann distribution. On the contrary, space and astrophysical plasmas are collisionless particle systems residing in stationary states characterized by kappa distributions [12,13,14,15]. The role of kappa distributions has become increasingly widespread across the physics of space plasma processes, describing particles in the heliosphere, from the solar wind and planetary magnetospheres to the heliosheath and beyond, the interstellar and intergalactic plasmas.
The presented statistical analysis is applied to the measurements of number density n and temperature T of the proton plasma in the inner heliosheath, the outer boundary of our heliosphere. By fitting kappa distributions to the proton energy distributions derived from the IBEX mission [16], Livadiotis et al. [17,18,19] derived the sky maps of the radially averaged values of several thermodynamic quantities in the inner heliosheath, such as the number density n, the temperature T, and the kappa indices κ0; these thermal observables parameterize the kappa distributions. The kappa index is the parameter that labels the kappa distribution, and its physical meaning is interwoven with the correlation between particles; in fact, the stronger the correlations, the smaller the kappa index [13,15,20].
The measurements of density and temperature of the inner heliosheath are anticorrelated. In particular, the logarithms of these measurements are linearly related with a negative slope, that is, the polytropic index. The polytropic behavior stands for the powe-law relationship, , where γ is the polytropic index, along a certain streamline of the plasma flow. A polytrope is a certain thermodynamic process characterized by such a relation. Typically, this is a power-law between two thermodynamic variables,
where the exponent a denotes the typical polytropic index; ν is another way of expressing the polytropic index, which corresponds to the effective degrees of freedom. While most of the space plasmas exhibit positive correlations between density and temperature, there are several plasmas with negative correlations, consistent with constant or quasi-constant thermal pressure, that were found in heliosheath [10,17,18,19,20,21] and planetary magnetosheaths (e.g., the low-latitude boundary layer at the terrestrial magnetosheath [22]; in the terrestrial central plasma sheet [23]; and in the Jovian magnetosheath, [24]). Other plasmas exhibit more complicate relationships that involves also the kappa index [17,25].
The temperature T and density n values of the proton plasma along the equatorial streamline from the heliospheric nose towards the heliotail were shown to be characterized by a negative correlation relationship [10,26,27]. More precisely, it was shown that the variations of T and n follow a near isobaric process, that is a polytropic index (or ).
Here, we examine the linear regression of the data (x,y), where x = log(n) and y = log(1/T). The slope β coincides with the quantity 1−γ, thus, the polytropic index γ can be retrieved once we estimate the slope β. The correlation coefficient r2(ϑ) and the slope β(ϑ) for a rotated reference frame are plotted in panels (a) and (b) in Figure 2, respectively. We also exclude the data points with small kappa index (as more erroneous). The plots are depicted for different thresholds, κ0min, that is, 0.1 (red), 0.25 (blue), and 0.4 (green). We observe that the larger the kappa index threshold, the more the correlation coefficient shifts to the left, to the negative values of tanϑ. This corresponds to smaller values of the slope, thus larger values of the polytropic index. The optimal value of tanϑ is the one that maximizes the correlation coefficient; this is plotted against the kappa index threshold κ0min in panel Figure 2c.
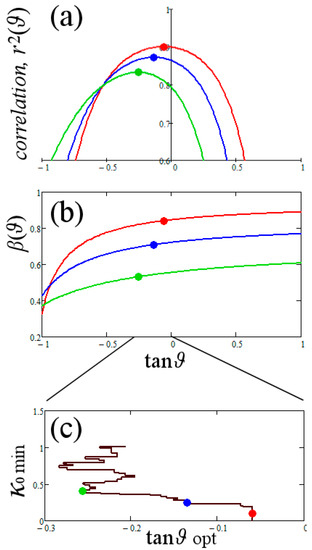
Figure 2.
(a) The Pearson’s correlation coefficient (square) r2, and (b) the slope β, both at the rotation reference frame, are plotted against the tangent of the rotation angle tanϑ. We exclude data points with small kappa index, and the plots are depicted for different thresholds (i.e., κ0min: 0.1 (red), 0.25 (blue), and 0.4 (green)). (c) The optimal tanϑ is plotted against the kappa index threshold κ0min.
5. Conclusions
The paper presented the dependence of the linear regression on the selection of the reference frame. Both the slope of the fitted line and the corresponding Pearson’s correlation coefficient were expressed in terms of the rotation angle. The correlation coefficient was found to be maximized for a certain optimal angle, for which the slope attains a special optimal value. The optimal angle, the value of the optimal slope, and the corresponding maximum correlation coefficient were expressed in terms of the covariance matrix, but also in terms of the slopes β0 and β90, namely, those derived from the nonrotated and right-angle-rotated fittings.
The presented analysis can be used as a method for improving the fitting and optimizing the derived values of the involved parameters. The analysis can be further completed for including the following cases:
- -
- the data points are given with errors , .
- -
- the statistical model is nonlinear and multiparametrical, for example, a polynomial of order M, that is, .
- -
- the estimation of the errors of the parameters, .
- -
- minimization of least deviation in Lp norm [10,11,12,28].
The presented analysis was applied in the density and temperature measurements of the proton plasma in the inner heliosheath, the outer boundary of our heliosphere. Those measurements are known to be fitted with a line with a negative slope, which is related to the polytropic index of the plasma. The application of the new statistical method improved the estimated value of this index.
Finally, Table 1 summarizes the critical equations shown in this paper.

Table 1.
Formulae of the developed method for finding the optimal rotation of maximum correlation.
Funding
This research was funded by NASA’s HGI Program, grant number NNX17AB74G.
Conflicts of Interest
The author declares no conflict of interest.
References
- Kenney, J.F.; Keeping, E.S. Linear Regression and Correlation. In Mathematics of Statistics, 3rd ed.; Van Nostrand: Princeton, NJ, USA, 1962; pp. 252–285. [Google Scholar]
- McCullagh, P. What is statistical model? Ann. Stat. 2002, 30, 1225–1310. [Google Scholar] [CrossRef]
- Adèr, H.J. Modelling. In Advising on Research Methods: A Consultant’s Companion; Adèr, H.J., Mellenbergh, G.J., Eds.; Johannes van Kessel Publishing: Huizen, The Netherlands, 2008; pp. 271–304. [Google Scholar]
- Melissinos, A.C. Experiments in Modern Physics; Academic Press Inc.: London, UK, 1966; pp. 438–464. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis; PWS Publishing Company: Boston, MA, USA, 1993; pp. 437–438. [Google Scholar]
- Livadiotis, G. Approach to general methods for fitting and their sensitivity. Physica A 2007, 375, 518–536. [Google Scholar] [CrossRef]
- Livadiotis, G. Expectation values and Variance based on Lp norms. Entropy 2012, 14, 2375–2396. [Google Scholar] [CrossRef]
- Livadiotis, G. Chi-p distribution: Characterization of the goodness of the fitting using Lp norms. J. Stat Distr. Appl. 2014, 1, 4. [Google Scholar] [CrossRef]
- Livadiotis, G.; Moussas, X. The sunspot as an autonomous dynamical system: A model for the growth and decay phases of sunspots. Physica A 2007, 379, 436–458. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Fitting method based on correlation maximization: Applications in Astrophysics. J. Geophys. Res. 2013, 118, 2863–2875. [Google Scholar] [CrossRef]
- Schmid, J., Jr. The relationship between the coefficient of correlation and the angle included between regression lines. J. Educ. Res. 1947, 41, 311–313. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa Distribution: Theory & Applications in Plasmas, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis statistical mechanics in space plasmas. J. Geophys. Res. 2009, 114, A11105. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Understanding kappa distributions: A toolbox for space science and astrophysics. Space Sci. Rev. 2013, 175, 183–214. [Google Scholar] [CrossRef]
- Livadiotis, G. Thermodynamic origin of kappa distributions. Europhys. Lett. 2018, 122, 50001. [Google Scholar] [CrossRef]
- McComas, D.J.; Allegrini, F.; Bochsler, P.; Bzowski, M.; Christian, E.R.; Crew, G.B.; DeMajistre, R.; Fahr, H.; Fichtner, H.; Frisch, P.C.; et al. Global observations of the interstellar interaction from the Interstellar Boundary Explorer (IBEX). Science 2009, 326, 959. [Google Scholar] [CrossRef] [PubMed]
- Livadiotis, G.; McComas, D.J.; Dayeh, M.A.; Funsten, H.O.; Schwadron, N.A. First sky map of the inner heliosheath temperature using IBEX spectra. Astrophys. J. 2011, 734, 1. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Randol, B.; Mӧbius, E.; Dayeh, M.A.; Frisch, P.C.; Funsten, H.O.; Schwadron, N.A.; Zank, G.P. Pick-up ion distributions and their influence on ENA spectral curvature. Astrophys. J. 2012, 751, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Schwadron, N.A.; Funsten, H.O.; Fuselier, S.A. Pressure of the proton plasma in the inner heliosheath. Astrophys. J. 2013, 762, 134. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Invariant kappa distribution in space plasmas out of equilibrium. Astrophys. J. 2011, 741, 88. [Google Scholar] [CrossRef]
- Elliott, H.A.; McComas, D.J.; Zirnstein, E.J.; Randol, B.M.; Delamere, P.A.; Livadiotis, G.; Bagenal, F.; Barnes, N.P.; Stern, S.A.; Young, L.A.; et al. Slowing of the solar wind in the outer heliosphere. Astrophys. J. 2019, in press. [Google Scholar]
- Sckopke, N.; Paschmann, G.; Haerendel, G.; Sonnerup, B.U.O.; Bame, S.J.; Forbes, T.G.; Hones, E.W., Jr.; Russell, C.T. Structure of the low-latitude boundary layer. J. Geophys. Res. 1981, 86, 2099–2110. [Google Scholar] [CrossRef]
- Pang, X.X.; Cao, J.B.; Liu, W.; Ma, Y.; Lu, H.; Yang, J.; Li, L.; Liu, X.; Wang, J.; Wang, T.; et al. Polytropic index of central plasma sheet ions based on MHD Bernoulli integral. J. Geophys. Res. 2015, 120, 4736–4747. [Google Scholar] [CrossRef]
- Nicolaou, G.; McComas, D.J.; Bagenal, F.; Elliott, H.A.; Wilson, R.J. Plasma properties in the deep Jovian magnetotail. Planet. Space Sci. 2015, 119, 222–232. [Google Scholar] [CrossRef]
- Ogasawara, K.; Angelopoulos, V.; Dayeh, M.A.; Fuselier, S.A.; Livadiotis, G.; McComas, D.J.; McFadden, J.P. Characterizing the dayside magnetosheath using ENAs: IBEX and THEMIS observations. J. Geophys. Res. 2013, 118, 3126–3137. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Non-equilibrium thermodynamic processes: Space plasmas and the inner heliosheath. Astrophys. J. 2012, 749, 11. [Google Scholar] [CrossRef]
- Livadiotis, G. Superposition of polytropes in the inner heliosheath. Astrophys. J. Suppl. Ser. 2016, 223, 13. [Google Scholar] [CrossRef]
- Livadiotis, G. Non-Euclidean-normed Statistical Mechanics. Physica A 2016, 445, 240–255. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).