Abstract
Metabolic syndrome (MS) directly increases the risk of cardiovascular diseases. Childhood and adulthood have been the most studied in MS, leaving aside the young adult population. This study aimed to compare the epidemiological probabilities between MS and different anthropometric parameters of body composition. Using a cross-sectional study with the sample of 1351 young adults, different body composition parameters were obtained such as Waist Circumference (WC), Body Mass Index (BMI), Body Fat% (BF%), Waist-to-Height Ratio (WHtR), and Waist-Hip Ratio. The Bayes Theorem was applied to estimate the conditional probability that any subject developed MS with an altered anthropometric parameter of body composition. Areas under receiver operating characteristic curves (AUCs) and adjusted odds ratios of the five parameters were analyzed in their optimal cutoffs. The conditional probability of developing MS with an altered anthropometric parameter was 17% in WHtR, WC, and Waist-hip R. Furthermore, body composition parameters were adjusted by age, BMI, and gender. Only WHtR (OR = 9.43, CI = 3.4–26.13, p < 0.0001), and BF% (OR = 3.18, CI = 1.42–7.13, p = 0.005) were significant, and the sensitivity (84%) and the AUCs (86%) was higher in WHtR than other parameters. In young adults, the WHtR was the best predictor of metabolic syndrome.
1. Introduction
Metabolic syndrome (MS) is a clinical condition that includes multiple cardiovascular disease risk factors, like obesity, high blood pressure or hypertension, dyslipidemia, and abnormal glucose metabolism, which directly increase the risk of coronary heart disease, atherosclerotic cardiovascular disease, and type 2 diabetes mellitus (DM2) [1,2]. The panel criteria III (ATP III) [3] is the most accepted criteria in the whole world for MS. People with abdominal obesity may be more prone to develop cardiometabolic alterations compared to those who present peripheral obesity [4]. The most studied populations are children (aged 6–12 years) and adults (aged > 25 years), but young adults (18–25 years) have been omitted since they may be studied in the future. It is believed that the prevalence of MS in young adults has increased, but there is no reliable data [5], and consequently, predictors have been sought that are associated in a simple way with the detection of some metabolic disorder [6].
There are several anthropometric parameters of diagnosis for MS. Among the most used is body mass index (BMI) [7], which is not considered a valid criterion because it does not reflect the distribution of body fat, although there are prediction formulas for total body fat [8]. The waist circumference (WC) is a non-invasive and straightforward measurement that has been shown to be a useful parameter to evaluate the distribution of body fat and cardiovascular risk as well as mortality from these events [9,10].
A characteristic of MS is high WC, and different medical associations consider WC as a useful tool for the early detection of MS [11]. However, recent research has doubted the usefulness of WC because it does not consider the size of the body, and that its effectiveness decreases in tall or short individuals [12,13]. Moreover, it has been shown that tests for adiposity, such as the percentage of body fat (BF%) or the body fat index (FMI), are quite sensitive to the diagnosis of MS [14].
The Waist-to-Height ratio (WHtR) is an indicator of central obesity, and evidence for it as a reasonable predictor for cardiovascular risk has been shown, considering the cut-off at 0.5 [15,16,17,18]. Most of the studies have been carried out in adults or children [19] but not in young adults.
As mentioned above, this study aimed to compare the epidemiological probabilities between MS and the different anthropometric parameters of body composition, such as WC, BMI, %BF, WHtR, and Waist–Hip Ratio. The Bayes Theorem was applied to estimate the conditional probability that a subject develops MS with an altered anthropometric parameter of body composition.
2. Methods
2.1. Study Design and Participants
This study was approved by the Ethics and Research Committee from the School of Medicine from the Benemérita Universidad Autónoma de Puebla, with the number 279. A cross-sectional study was conducted with a sample of 1351 young adults (18–22 years), from August 2015 to June 2016, from a universe of 6000 newly enrolled students from a high education institution (HEI) in the city of Puebla, Mexico. The inclusion criteria were fast of 12–14 h and ages from 18–22 years with informed consent. The excluded participants were the ones who did not meet the inclusion criteria or who had hemolyzed or lipemic samples of serum. The individuals presented themselves within the facilities of Biochemistry Department from School of Medicine from Benemérita Universidad Autónoma de Puebla for measurement of anthropometric variables (weight, size, waist and hip circumference), blood sampling, and preparation of their medical history.
2.2. Variables
2.2.1. Anthropometrical and Clinical Analysis
Anthropometry was measured by certified clinicians (ISAK 1) with standardized instruments. The participants wore light clothing. Weight measurement had an accuracy of 100 g, and height had an accuracy of 0.1 cm. WC was measured at the midpoint between the lower edge of the rib cage and the iliac crest, whereas Hip Circumference (HC) was measured in the most prominent part of the hip. BMI was calculated as weight (kg) divided by height squared (m2). WHtR was calculated as WC between height.
A standardized clinician measured the blood pressure thrice with the participant seated at five-minute intervals at the right arm using a standard mercury sphygmomanometer. The average of the last two measurements was adopted.
2.2.2. Biochemical Analysis
For the biochemical analysis, a VITROS DT60 II analyzer determined glucose, triglycerides, total cholesterol, and high-density lipoprotein cholesterol (HDL-C). The biochemical parameters were categorized according to ATP III [11], BMI, and waist–hip ratio according to WHO for adults [20] and WHtR according to Maffeis et al. 2008 [21]. The calculation of BF% was made from Deuremberg’s formula: [body fat percentage: (1.2 × BMI) + (0.23 × age in years) − (10.8 × gender) − 5.4, where gender = 0 for women and 1 for men] [8].
2.3. Metabolic Syndrome
MS was defined in accordance by ATP III [11], which requires ≥3 risk factors from the following five components: WC ≥ 80 cm in women or ≥90 cm in men; hypertension, considered as systolic blood pressure ≥ 130 mmHg or diastolic blood pressure ≥ 85 mmHg, or a prior diagnosis of hypertension with specific medication; hyperglycemia, defined as FPG ≥ 100 mg/dL (5.6 mmol/L) or a history of diabetes or anti-diabetic medication; TG ≥ 150 mg/dL (1.7 mmol/L) or relevant medication; and HDL-C < 40 mg/dL (1.0 mmol/L) in men or <50 mg/dL (1.3 mmol/L) in women or taking relevant medication.
2.4. Statistical Methods
The statistical package SPSS v.21 and GraphPad Prism v.6 (both for Windows) processed analyzes and figures. The continuous variables were shown as the mean ± standard deviation (SD), while the categorical variables as the number of cases and percentage. The normality of the variables was analyzed by Kolmogorov-Smirnov statistic and by the expected values in Q-Q graphs. To compare all quantitative variables, the parametric Student’s t-test was applied. Fisher’s exact test on contingency tables was used to compare the nonparametric results in independent categorical variables by Chi-square. The MS risk was calculated from each parameter of body composition and adjusted OR at 95% confidence intervals by logistic regression analysis; age, sex, and BMI were used as confounders for multivariate analysis.
Sensitivity and specificity of each variable of body composition for diagnosis of metabolic syndrome, as well as positive and negative predictive values and likelihood ratios, were calculated. ROC curves were plotted, and AUCs were compared to evaluate the efficacy of any anthropometric parameters to discriminate subjects with and without MS. A two-sided level of significance of 0.05 was used to reject the null hypothesis.
To estimate the conditional probability of MS in any altered anthropometric parameters of body composition, given the pretest probability, we used the Bayes’ theorem [22] according to the following formula:
Substituting
where P(A1|B) = Conditional probability of a subject with a modified anthropometric parameter of body composition developing MS. P(B|A1) = Conditional probability of an altered anthropometric parameter given the presence of MS. P(A1) = A priori probability, the probability of MS in the study population. P(B|A2) = Conditional probability of an altered anthropometric parameter given the absence of MS, and Pr(A2) = 1 − Pr(A1), probability of lack of MS in the study population.
B represents the subjects with an altered anthropometric parameter of body composition (High WC, overweight or obesity, high BF%, high WHtR or high Waist-Hip R). A1 represents the subjects with MS, and A2 represents the subjects without MS.
Conditional probability was defined as a probability of an event given that (by assumption, presumption, assertion, or evidence) another event had occurred. This fact is similar to the intersection of the probabilities of A and B (A ∩ B), between the probabilities of B, provided that the probability of B is different from zero [22].
3. Results
3.1. Participants
Of 1351, the average age ranged between 18 and 19 years for women and men, respectively (Table 1). Weight, height, WC, BMI, BF%, and Waist–Hip R were statistically different in men and women (All p < 0.0001). WHtR was identical in both genders. Regarding the prevalence of metabolic syndrome, there were no significant differences in any of the sexes.

Table 1.
Essential characteristics of the study sample by gender.
The mean age of the subjects who presented MS was 18 years, which was not statistically different from the average of those who did not show it, the weight was different (p < 0.0001) and had a significant difference, being higher in the subjects with MS. The presence of altered anthropometric parameters (WC, BMI, BF%, WHtR, and Waist–Hip R) were statistically different (Table 2) between individuals with MS and without MS. In MS (All p < 0.0001), the means of each parameter were found above the cut-off point in each one.

Table 2.
Characteristics of patient with altered anthropometric parameters according to Metabolic Syndrome (MS).
3.2. Body Composition Indexes and Metabolic Syndrome
We associated each of the body composition parameters (above the cut-off points: WC ≥ 80 cm in women or ≥ 90 cm in men, BMI ≥ 25, BF% ≥ 25 in men ≥29 in women, WHtR ≥ 0.5 in both, and Waist-hip R ≥ 0.85 in women or 1.00 in men) with the risk of MS; The WC increases 13 times the risk of MS (OR = 13.09, CI = 7.08–23.85, p < 0.0001), BMI increases 6.9 times the risk of MS (OR = 6.99, CI = 3.67–13.30, p < 0.0001), BF% increases 8.78 times the risk of MS (OR = 8.78, CI = 4.87–15.81, p < 0.0001), WHtR increases the risk of MS by 18.8 times (OR = 18.84, CI = 9.49–37.40, p < 0.0001), finally, the increase in MS risk by the Waist-Hip R is 6.39 times (OR = 6.39, CI = 3.43–11.89, p < 0.0001) (Figure 1). When all body composition parameters were adjusted for age, BMI and gender (Table 3), only WHtR (OR = 9.43, CI = 3.4–26.13, p < 0.0001), and BF% (OR = 3.18, CI = 1.42–7.13, p = 0.005), were significant.
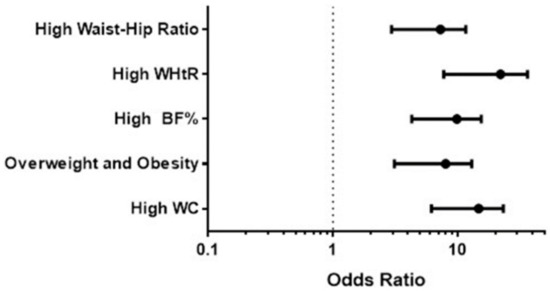
Figure 1.
Risk of metabolic syndrome from each anthropometric parameter of body composition.

Table 3.
Adjusted ORs (95% CI) for Metabolic Syndrome.
3.3. Efficacy of WHtR in the Prediction of Metabolic Syndrome
The discriminative and diagnostic efficacy of body composition parameters were determined using ROC curves (Figure 2, Table 4 and Table 5). The AUC of WHtR was superior to all other parameters (WC, BMI, BF%, Waist–Hip R) in the diagnosis of MS. The WHtR proves to be the most sensitive test, for diagnosis. But it was found that WC, BF%, and Waist–Hip R, were more specific, than the other parameters.
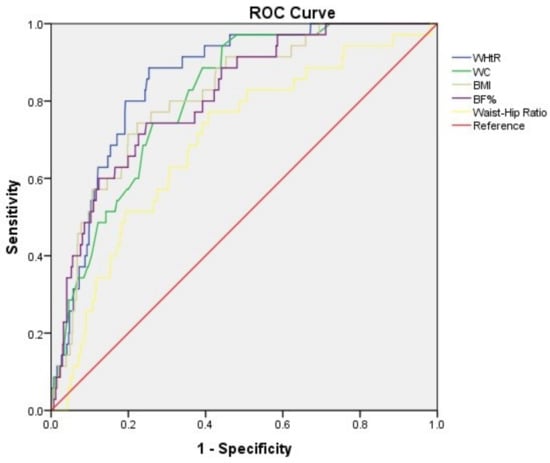
Figure 2.
Receiver operating characteristic (ROC) curve for predicting metabolic syndrome.

Table 4.
Receiver operating characteristic (ROC) curve analysis for predicting MS.

Table 5.
Sensitivity, specificity, and predictive values of different anthropometric parameters for the diagnosis of MS.
All categories were defined as mutually exclusive events to perform probable calculations. The probability to present metabolic syndrome in the study population was 4%, and the chance not show it was 96%. The likelihood of high WC was 15%, of BMI > 25 was 31%, of high BF% was 10%, of high WHtR was 18%, and high Waist–Hip R was 8%.
The conditional probability of high WC given the presence of MS was 66%, and the conditional probability of high WC given the absence of MS was 13%. Applying the Bayes’ Theorem, the conditional probability of developing MS increases from 4–17% when high WC occurs. The probabilistic notation was the following:
Regarding BMI, the conditional probability of BMI ≥ 25 given the presence of MS was 74%, and the conditional probability of high BMI ≥ 25 given the absence of MS was 29%. Applying the Bayes theorem, the conditional probability of developing MS increases only 6%, from 4–10%. The probabilistic notation was the following:
For BF%, the conditional probabilities were the following: 46% of high BF% given the presence of MS, 10% of high BF% given the absence of MS, and 16% of developing MS. The probabilistic notation was the following:
The conditional probability of high WHtR given the presence of MS was 78%, and the conditional probability of high WHtR given the absence of MS was 16%. Applying the Bayes theorem, the conditional probability of developing MS was the same as WC, which increases from 4–17% when high WHtR occurs. The probabilistic notation was the following:
Finally, the probabilities of Waist-Hip R were: 34% of conditional probability of high Waist–Hip R given the presence of MS, 7% of conditional probability of high WC given the absence of MS and 17% of conditional probability of developing MS when high Waist-Hip R occurs, the same as WC and WHtR. The probabilistic notation was the following:
4. Discussion
The age between 18 and 19 years allows us to show that the population studied was young adults. Likewise, it is necessary to point out that when the anthropometric parameters were analyzed, it was shown that all were below the cut-off points, making it appear that the population did not have any alteration in their body composition.
The findings of this study indicate that, in a population of young adults, WHtR is the most useful anthropometric parameter of body composition to diagnose and detect the presence of MS.
In the Mexican population, different parameters of body composition such as BMI, height-adjusted weight, waist circumference, hip circumference, waist–hip ratio, and waist-to-height ratio have been associated with some components of MS [23]. This association was found in an adult population, which had an age range of 35–89 years. The studies carried out on the risk of MS or its associations with these markers were mainly in the adult population or child population [21,24,25,26,27,28,29]. Research on young adult populations has been left mostly out of the question. Research in this group is of great importance since some studies have suggested that controlling some risk factors such as anthropometry could reduce the incidence of MS in similar populations by up to 93% [30]. As a result, it is necessary to find other MS biomarkers that can be used as routine diagnostic tests by clinicians.
The findings on the prediction of the MS were similar to those found by Rodea-Montero [31] that show that WHtR is a better anthropometric parameter in than BMI and WC. Also, their AUC was very similar to ours (0.737), but the sample they evaluated was small (n = 110), and although adolescents were assessed, the age range is completely different.
Two studies were conducted in young adults in the Mexican population. The study by Ramos-Jiménez A. et al. [32] performed in young adults with intellectual disabilities (aged 13–30 years) found that WC adjusted to height correlated with MS. In the research developed by Ferreira-Hermosillo A. et al. [33] in relatively young adult patients (aged 26–42 years) found evidence on the prediction of MS from the WHtR (AUC 0.71). The results were similar to ours, but the study was performed in patients with type 1 DM, and the individuals of this research, whether with or without MS, did not present a history of cardiometabolic alterations during the collection of the clinical history, assuming that they were apparently healthy.
The superiority of the WHtR in the predictions of the metabolic syndrome had been demonstrated by Asian authors [12,13]. They consider that their populations are smaller than the Caucasian ones. Thus, WHtR achieves an improved representation of the central adiposity than other anthropometric parameters; we believe this hypothesis since the Mexican population does not differ from the anthropometric characteristics (height and weight) of the Asian population.
Evidence of anthropometric parameters has been sought as predictors of MS has been sought in heterogeneous populations. It is controversial but is not far from reality, since MS is a public health problem on a global scale. Studies in North American populations [34] found that WC and BMI were equally functional parameters in the Mexican-American people for detection of MS. Other studies [35,36] have shown that WC is the best predictor. Ashweel, in a review of 21 studies [15], explained the superiority of WHtR as the best predictor for adverse events in different populations mainly those with already previous metabolic alterations and none of the healthy young adults. On the other hand, the same author, in a recently published study [37], showed the superiority of WHtR in the detection of metabolic alterations. Like her, we perform a regression to examine the different levels of risk adjusted by age, sex, and BMI, but we do it to detect the risk of MS and not metabolic alterations.
All the above suggests that, for such a heterogeneous sample of ethnic groups, different cutoff values would be required for each of the ratios. Regarding WHtR, the amount most used in research, whether in adults or children, was 0.5, which was estimated to have a specificity of 100% [15,16,17,18,37] and which was used in this study. Concerning the Mexican population, Elizondo-Montemayor et al. [38], in a study in children diagnosed with overweight or obesity, showed that the cutoff of 0.59 would have a sensitivity of 81.8% and specificity of 78.5%. In the present study, focused on young adults, we found that the cutoff point at 0.45 would have a sensitivity of 97.1% and a specificity of 67.1%, but we did not emphasize that value since this was not the purpose of this research.
This study was the first in which the predictive capacities of different anthropometric parameters of body composition were evaluated. No study had used the Bayes’ Theorem to obtain the conditional probabilities of developing MS given that there was some alteration of some parameter of body composition. This study is a pioneer in applying Bayesian statistics to obtain the conditional probabilities post-test.
WC, WHtR, and Waist–Hip Ratio showed that an alteration of these anthropometric parameters increases more than four times the probability of having MS, since the inherent probability of the population was 4%, and in those individuals who present an alteration in these anthropometric parameters, its probability was 17%.
Although the results obtained during the application of Bayesian statistics suggested that the WC, WHtR, and Waist–Hip Ratio probabilities are similar, we must analyze each element of the theorem, that is, each conditional probability. The conditional probability of having a high WHtR given that MS was higher than any other anthropometric parameters, this being the ability to detect patients who have MS. The similarity of the results was caused by the conditional probability of having an altered anthropometric parameter given that MS was not present, there. The Waist-Hip Ratio was the highest since only a conditional probability of 7% was presented, less than a half than in the other tests, the above suggests that the best way to detect MS is through WHtR, and the best way to identify an individual without MS is when the Waist–Hip Ratio is not altered.
With the analysis of all the epidemiological tests performed (risk analysis, prediction analysis, and probability analysis), we found a superior utility of WHtR in the diagnosis of MS.
In the present study, we found the association between the different anthropometric parameters of body composition and MS. Risk analyses adjusted for age, sex, and BMI showed that WHtR had an excellent prediction of MS risk. It is necessary to evaluate the association along with other types of confounding factors such as smoking, dietary intake, or family inheritance background that allow for affirming this risk. Another inherent limitation of our study is its design: being a cross-sectional study, there is a limitation in the interpretation of cause-and-effect temporality. Similarly, our population was from a single state in central Mexico, suggesting that it would not be representative for other communities, so it is necessary to perform multicenter longitudinal observational studies in which the usefulness of WHtR for diagnosis of MS can be confirmed
5. Conclusions
The findings in this study indicate that, in a population of young adults, WHtR was the best predictor of metabolic syndrome, superior to WC, BMI, BF%, or Waist–Hip Ratio. The use of the Bayes Theorem shows that WHtR, at the cut-off value of 0.5, increases up to four times the conditional probability of presenting MS in populations of Mexican young adults. Studies in different populations with larger samples can validate the utility as well as the limitations of WHtR as a marker of Metabolic Syndrome.
Author Contributions
Conceptualization, A.K., M.L.C.M.-M.; Biochemical Analysis, M.E.H.-H., A.M.O.-B.; P.L.-M., M.d.L.C.M.-M.; Anthropometrical and Clinical Analysis, M.E.H.-H., A.M.O.-B.; P.L.-M., M.d.L.C.M.-M.; Statical Analysis, A.K.; Writing, A.K.; Review & Editing, all authors.
Acknowledgments
The authors would like to thank the School of Medicine from the Benemérita Universidad Autónoma de Puebla for the support it provides to the research carried out in the Biochemistry Department, and to the editor and reviewers for the observations and recommendations to improve this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Falkner, B.; Cossrow, N. Prevalence of metabolic syndrome and obesity-associated hypertension in the racialethnic minorities of the United States. Curr. Hypertens. Rep. 2014, 16, 449. [Google Scholar] [CrossRef] [PubMed]
- Suyilaqimuge, S.U.X. Research progress of metabolic syndrome. China Mod. Med. 2016, 23, 13–16. [Google Scholar]
- Grundy, S.M.; Cleeman, J.I.; Daniels, S.R.; Donato, K.A.; Eckel, R.H.; Franklin, B.A.; Gordon, D.J.; Krauss, R.M.; Savage, P.J.; Smith, S.C., Jr.; et al. Diagnosis and management of the metabolic syndrome: An American Heart Association/National Heart, Lung, and Blood Institute Scientific Statement. Circulation 2005, 112, 2735–2752. [Google Scholar] [CrossRef] [PubMed]
- Després, J.P. Health consequences of visceral obesity. Ann. Med. 2001, 33, 534–541. [Google Scholar] [CrossRef] [PubMed]
- Instituto Nacional de Salud Pública. Encuesta Nacional de Salud y Nutrición. [Mexico’s National Health and Nutrition Survey; Instituto Nacional de Salud Pública: Cuernavaca, Mexico, 2012. [Google Scholar]
- Qiao, Q.; Nyamdorj, R. Is the association of type II diabetes with waist circumference or waist-to-hip ratio stronger than that with body mass index? Eur. J. Clin. Nutr. 2010, 64, 30–34. [Google Scholar] [CrossRef] [PubMed]
- Espinoza, M.; Ruiz, N.; Barrios, E.; Reigosa, A.; Leal, U.; Julio, H.; González, C. Perfil metabólico de riesgo cardiovascular y resistencia a la insulina según índice de masa corporal, circunferencia de cintura y cintura hipertrigliceridémica en pacientes adultos. Revista Médica de Chile 2009, 137, 1179–1186. [Google Scholar] [CrossRef]
- Deurenberg, P.; Weststrate, J.A.; Seidell, J.C. Body mass index as a measure of body fatness: Age- and sex-specific prediction formulas. Br. J. Nutr. 1991, 65, 105–114. [Google Scholar] [CrossRef] [PubMed]
- De Koning, L.; Merchant, A.T.; Pogue, J.; de Koning, L.; Merchant, A.T.; Pogue, J.; Anand, S.S. Waist circumference and waist-to-hip ratio as predictors of cardiovascular events: Meta-regression analysis of prospective studies. Eur. Heart J. 2007, 28, 850–856. [Google Scholar] [CrossRef] [PubMed]
- Cornier, M.A.; Despres, J.P.; Davis, N.; Grossniklaus, D.A.; Klein, S.; Lamarche, B.; Lopez-Jimenez, F.; Rao, G.; St-Onge, M.P.; Towfighi, A.; et al. Assessing adiposity: A scientific statement from the American Heart Association. Circulation 2011, 124, 1996–2019. [Google Scholar] [CrossRef] [PubMed]
- Alberti, K.G.; Eckel, R.H.; Grundy, S.M.; Zimmet, P.Z.; Cleeman, J.I.; Donato, K.A.; Fruchart, J.C.; James, W.P.; Loria, C.M.; Smith, S.C., Jr. Harmonizing the metabolic syndrome: A joint interim statement of the International Diabetes Federation Task Force on Epidemiology and Prevention; National Heart, Lung, and Blood Institute; American Heart Association; World Heart Federation; International Atherosclerosis Society; and International Association for the Study of Obesity. Circulation 2009, 120, 1640–1645. [Google Scholar] [PubMed]
- Misra, A.; Wasir, J.S.; Vikram, N.K. Waist circumference criteria for the diagnosis of abdominal obesity are not applicable uniformly to all populations and ethnic groups. Nutrition 2005, 21, 969–976. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.J.; Klotsche, J.; Silber, S.; Stalla, G.K.; Wittchen, H.U. Measuring abdominal obesity: Effects of height on distribution of cardiometabolic risk factors risk using waist circumference and waist-to-height ratio. Diabetes Care 2011, 34, e7. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Vélez, R.; Correa-Bautista, J.E.; Sanders-Tordecilla, A.; Ojeda-Pardo, M.L.; Cobo-Mejía, E.A.; Castellanos-Vega, R.D.P.; García-Hermoso, A.; González-Jiménez, E.; Schmidt-RioValle, J.; González-Ruíz, K.; et al. Percentage of Body Fat and Fat Mass Index as a Screening Tool for Metabolic Syndrome Prediction in Colombian University Students. Nutrients 2017, 9, 1009. [Google Scholar] [CrossRef] [PubMed]
- Ashwell, M.; Gunn, P.; Gibson, S. Waist-to-height ratio is a better screening tool than waist circumference and BMI for adult cardiometabolic risk factors: Systematic review and meta-analysis. Obes. Rev. 2012, 13, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Li, W.C.; Chen, I.C.; Chang, Y.C.; Loke, S.S.; Wang, S.H.; Hsiao, K.Y. Waist-to-height ratio, waist circumference, and body mass index as indices of cardiometabolic risk among 36,642 Taiwanese adults. Eur. J. Nutr. 2013, 52, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Li, W.; Wang, Y.; Bo, J.; Chen, H. The cut-off point and boundary values of waist-to-height ratio as an indicator for cardiovascular risk factors in Chinese Adults from the PURE study. PLoS ONE 2015, 10, e0144539. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Xin, Z.; Feng, J.P.; Yang, J.K. Waist-to-height ratio is better than body mass index and waist circumference as a screening criterion for metabolic syndrome in Han Chinese adults. Medicine 2017, 96, 8192. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Yang, M.; Yuan, Z.P.; Zhang, D.D.; Liang, L.; Wang, C.L.; Zhang, S.; Zhu, H.H.; Lai, M.D.; Zhu, Y.M. Waist-to-Height Ratio: A simple, effective and practical screening tool for childhood obesity and metabolic syndrome. Prev. Med. 2014, 67, 35–40. [Google Scholar] [CrossRef] [PubMed]
- Norma Oficial Mexicana NOM-008-SSA3-2010. Para el Tratamiento Integral del Sobrepeso y la Obesidad; Norma Oficial Mexicana: Ciudad de México, México, 2010. [Google Scholar]
- Maffeis, C.; Banzato, C.; Talamini, G. Waist to Height ratio, a useful index to identify high risk in overweight children. J. Pediatr. 2008, 152, 207–213. [Google Scholar] [CrossRef] [PubMed]
- Shott, S. Statistics for Health Professionals; Saunders: Philadelphia, PA, USA, 1990; pp. 23–41. [Google Scholar]
- Gnatiuc, L.; Alegre-Díaz, J.; Halsey, J.; Herrington, W.G.; López-Cervantes, M.; Lewington, S.; Collins, R.; Tapia-Conyer, R.; Peto, R.; Emberson, J.R. Adiposity and Blood Pressure in 110,000 Mexican Adults. Hypertension 2017, 69, 608–614. [Google Scholar] [CrossRef] [PubMed]
- López-González, D.; Miranda-Lora, A.; Klünder-Klünder, M.; Queipo-García, G.; Bustos-Esquivel, M.; Paez-Villa, M.; Villanueva-Ortega, E.; Chávez-Requena, I.; Laresgoiti-Servitje, E.; Garibay-Nieto, N. Diagnostic performance of waist circumference measurements for predicting cardiometabolic risk in Mexican children. Hypertension 2017, 69, 608–614. [Google Scholar] [CrossRef] [PubMed]
- Jayawardana, R.; Ranasinghe, P.; Sheriff, M.H.; Matthews, D.R.; Katulanda, P. Waist to height ratio: A better anthropometric marker of diabetes and cardio-metabolic risks in South Asian adults. Diabetes Res. Clin. Pract. 2013, 99, 292–299. [Google Scholar] [CrossRef] [PubMed]
- Valle-Leal, J.; Abundis-Castro, L.; Hernández-Escareño, J.; Flores-Rubio, S. Waist-to-height ratio is an indicator of metabolic risk in children. Rev. Chil. Pediatr. 2016, 87, 180–185. [Google Scholar] [CrossRef] [PubMed]
- Mokha, J.S.; Srinivasan, S.R.; DasMahapatra, P.; Fernandez, C.; Chen, W.; Xu, J.; Berenson, G.S. Utility of waist-to-height ratio in assessing the status of central obesity and related cardiometabolic risk profile among normal weight and overweight/obese children: The Bogalusa Heart Study. BMC Pediatr. 2010, 10. [Google Scholar] [CrossRef] [PubMed]
- Lo, K.; Wong, M.; Khalechelvam, P.; Tam, W. Waist-to-height ratio, body mass index and waist circumference for screening pediatric cardio-metabolic risk factors: A meta-analysis. Obes. Rev. 2016, 17, 1258–1275. [Google Scholar] [CrossRef] [PubMed]
- Khoury, M.; Manlhiot, C.; Dobbin, S.; Gibson, D.; Chahal, N.; Wong, H.; Davies, J.; Stearne, K.; Fisher, A.; McCrindle, B.W. Role of waist measures in characterizing the lipid and blood pressure assessment of adolescents classified by body mass index. Arch. Pediatr. Adolesc. Med. 2012, 166, 719–724. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Martínez-Montaño, M.L.; Blázquez-Gutiérrez, M.E.; Hernández-Hernández, M.E.; López-Moreno, P.; Ortiz-Bueno, A.; Kammar-García, A.; Calderón-Ibarra, E.; Delgado-Romero, J.; García-Cruz, S.P. Waist-Length Index: Test for cardiovascular risk assessment and diagnosis of metabolic syndrome. Revista Cubana de Medicina 2017, 56, 109–118. [Google Scholar]
- Rodea-Montero, E.R.; Evia-Viscarra, M.L.; Apolinar-Jiménez, E. Waist-to-Height Ratio Is a Better Anthropometric Index than Waist Circumference and BMI in Predicting Metabolic Syndrome among Obese Mexican Adolescents. Int. J. Endocrinol. 2014, 2014, 195407. [Google Scholar] [CrossRef] [PubMed]
- Ramos-Jiménez, A.; Hernández-Torres, R.P.; Wall-Medrano, A.; Villalobos-Molina, R. Metabolomic (anthropometric and biochemical) indexes and metabolic syndrome in adolescents and young adults with intellectual disabilities. Res. Dev. Disabil. 2014, 35, 2987–2992. [Google Scholar] [CrossRef] [PubMed]
- Ferreira-Hermosillo, A.; Ramírez-Rentería, C.; Mendoza-Zubieta, V.; Molina-Ayala, M.A. Utility of the waist-to-height ratio, waist circumference and body mass index in the screening of metabolic syndrome in adult patients with type 1 diabetes mellitus. Diabetol. Metab. Syndr. 2014, 6, 32. [Google Scholar] [CrossRef] [PubMed]
- Han, T.S.; Williams, K.; Sattar, N.; Hunt, K.J.; Lean, M.E.; Haffner, S.M. Analysis of obesity and hyperinsulinemia in the development of metabolic syndrome: San Antonio Heart Study. Obes. Res. 2002, 10, 923–931. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.J.; Klotsche, J.; Stalla, G.K.; Wittchen, H.U. Obesity and risk of myocardial infarction: The INTERHEART study. Lancet 2006, 367, 1052–1054. [Google Scholar] [CrossRef]
- Bener, A.; Yousafzai, M.T.; Darwish, S.; Al-Hamaq, A.O.; Nasralla, E.A.; Abdul-Ghani, M. Obesity index that better predict metabolic syndrome: Body mass index, waist circumference, waist hip ratio, or waist height ratio. J. Obes. 2013, 2013, 269038. [Google Scholar] [CrossRef] [PubMed]
- Ashwell, M.; Gibson, S. Waist-to-height ratio as an indicator of ‘early health risk’: Simpler and more predictive than using a ‘matrix’ based on BMI and waist circumference. BMJ Open 2016, 6, e010159. [Google Scholar] [CrossRef] [PubMed]
- Elizondo-Montemayor, L.; Serrano-González, M.; Ugalde-Casas, P.A.; Bustamante-Careaga, H.; Cuello-García, C. Waist-to-height: Cutoff matters in predicting metabolic syndrome in Mexican children. Metab. Syndr. Relat. Disord. 2011, 9, 183–190. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).