Causality between Oil Prices and Tourist Arrivals
Abstract
1. Introduction
2. Literature Review
3. Methodology of Causality Tests
3.1. Time Domain Granger Causality
- Simple Granger CausalityIf the forecast error of X based on all the information I is smaller than the forecast error of X based on the past information apart from series Y, which is denoted as , then Y is causing X. Ref. [58] stated, “if we are better able to predict X using all available information than if the information apart from Y had been used, we say that Y is causing X”.
- Feedback ModelIf the Simple Granger Causality from Y to X is donated as , then the feedback indicates that when X is causing Y and also Y is causing X, which can be represented as , can also be denoted as the following:if and , then we say .
- Instantaneous Granger CausalityInstantaneous causality is indicated if a better forecast of current value of X can be conducted when the present value of Y is also considered, rather than only considering the set of past information. This can be donated as the following: if , the instantaneous causality of is occurring.
3.2. Frequency Domain Causality
3.3. Convergent Cross Mapping (CCM)
4. Data
4.1. Descriptive Statistics
4.2. Stationarity of Data
5. Causality Results
5.1. Time Domain Granger Causality
5.2. Frequency Domain Causality
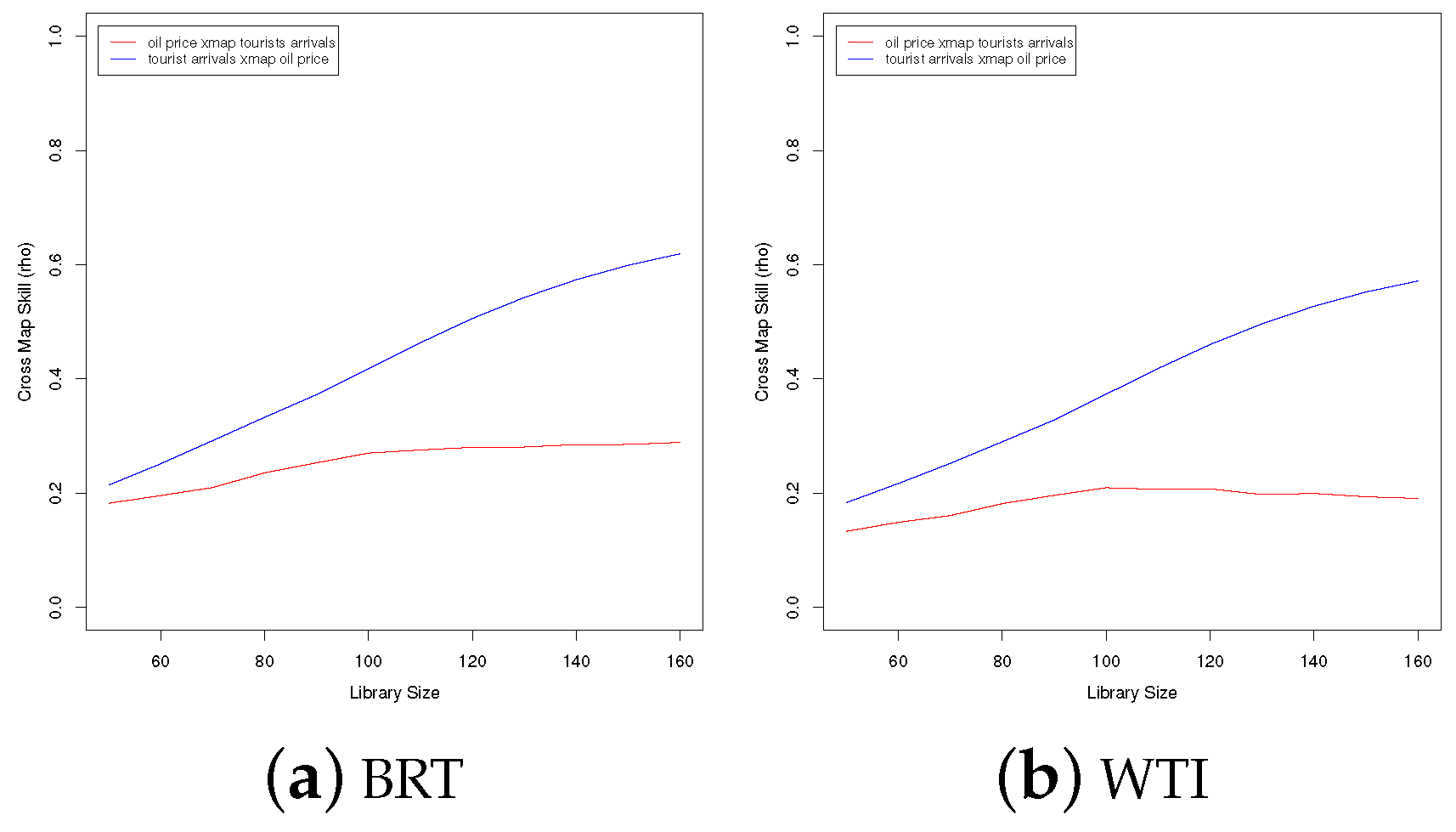
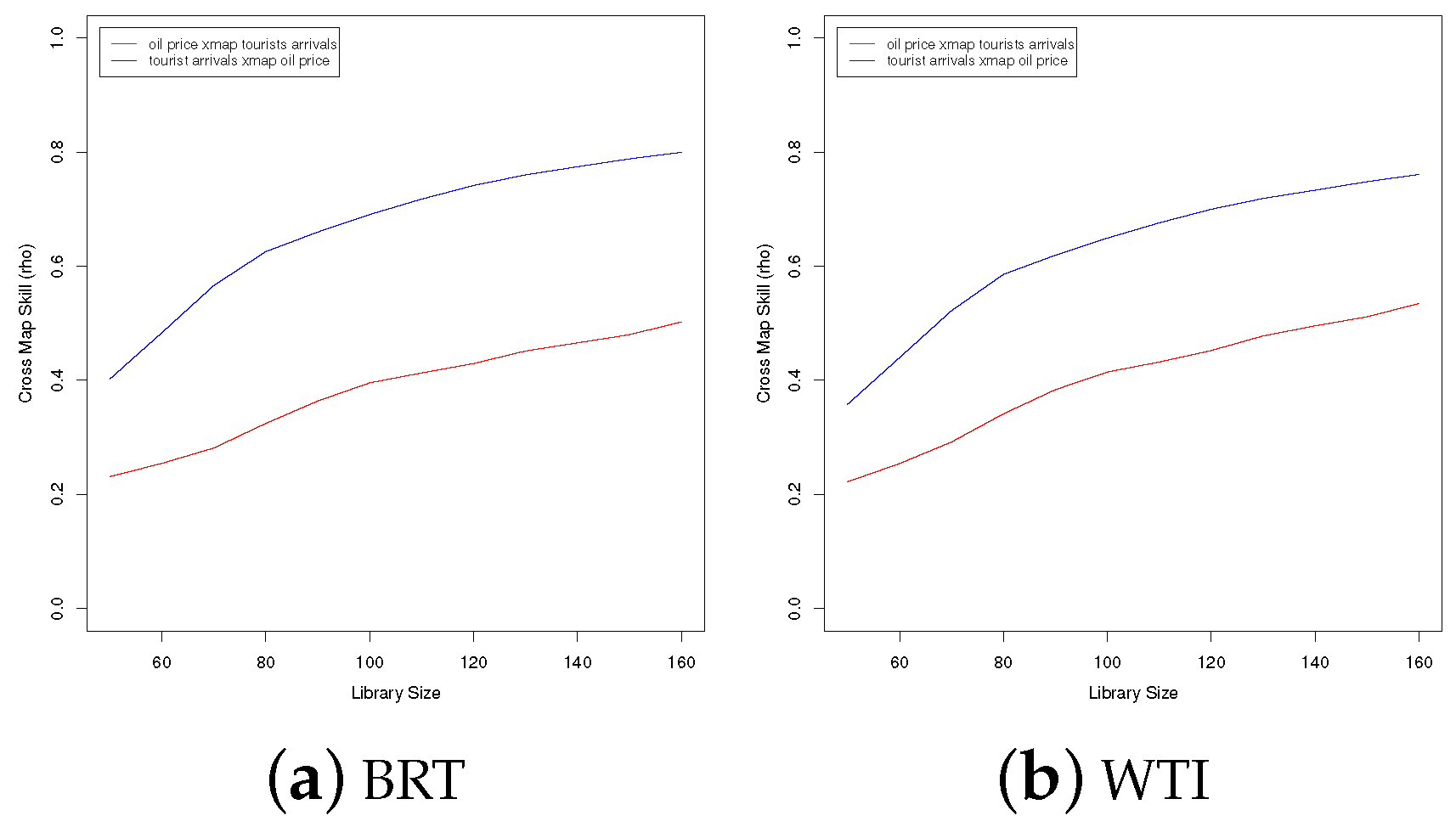
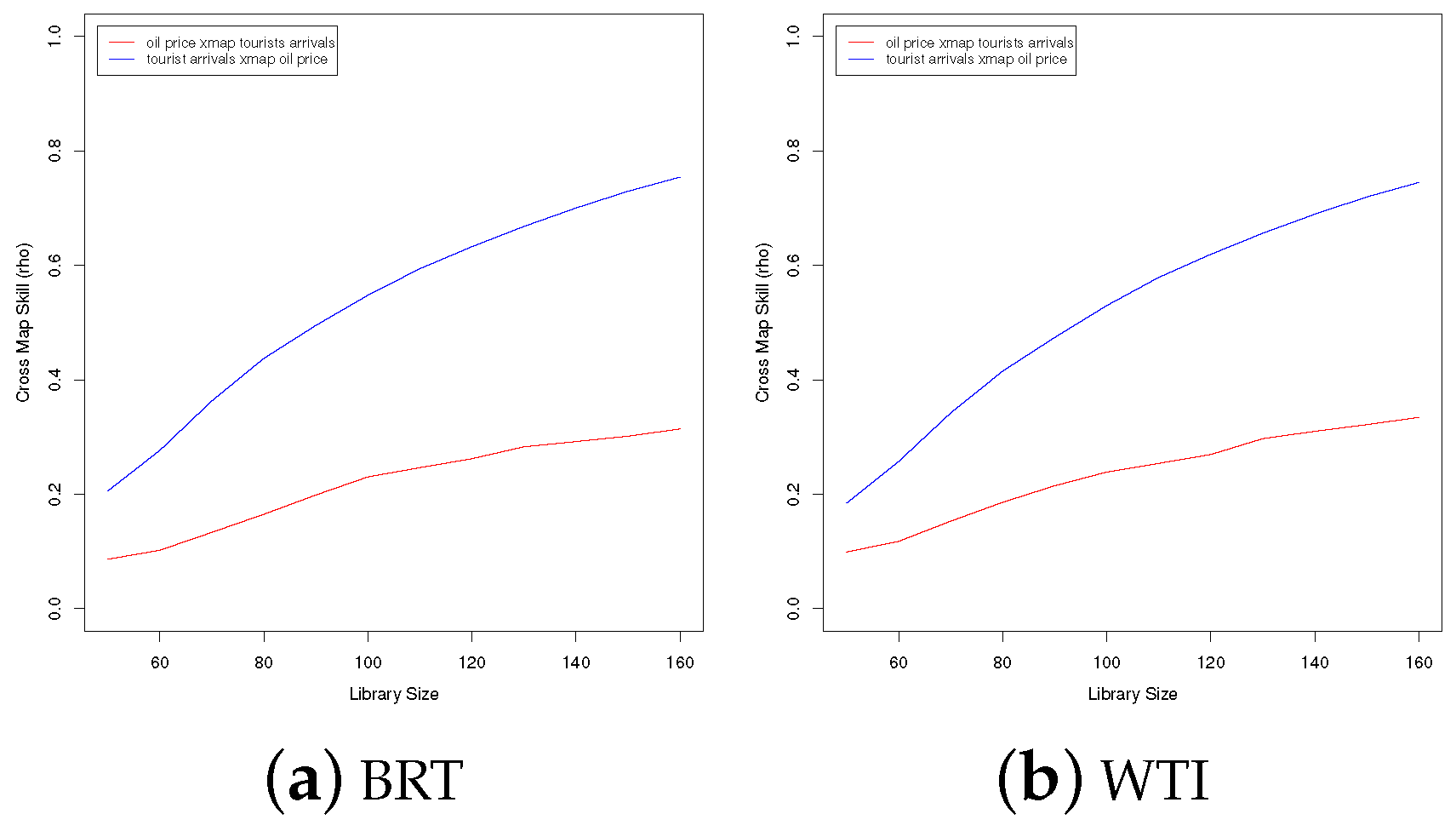
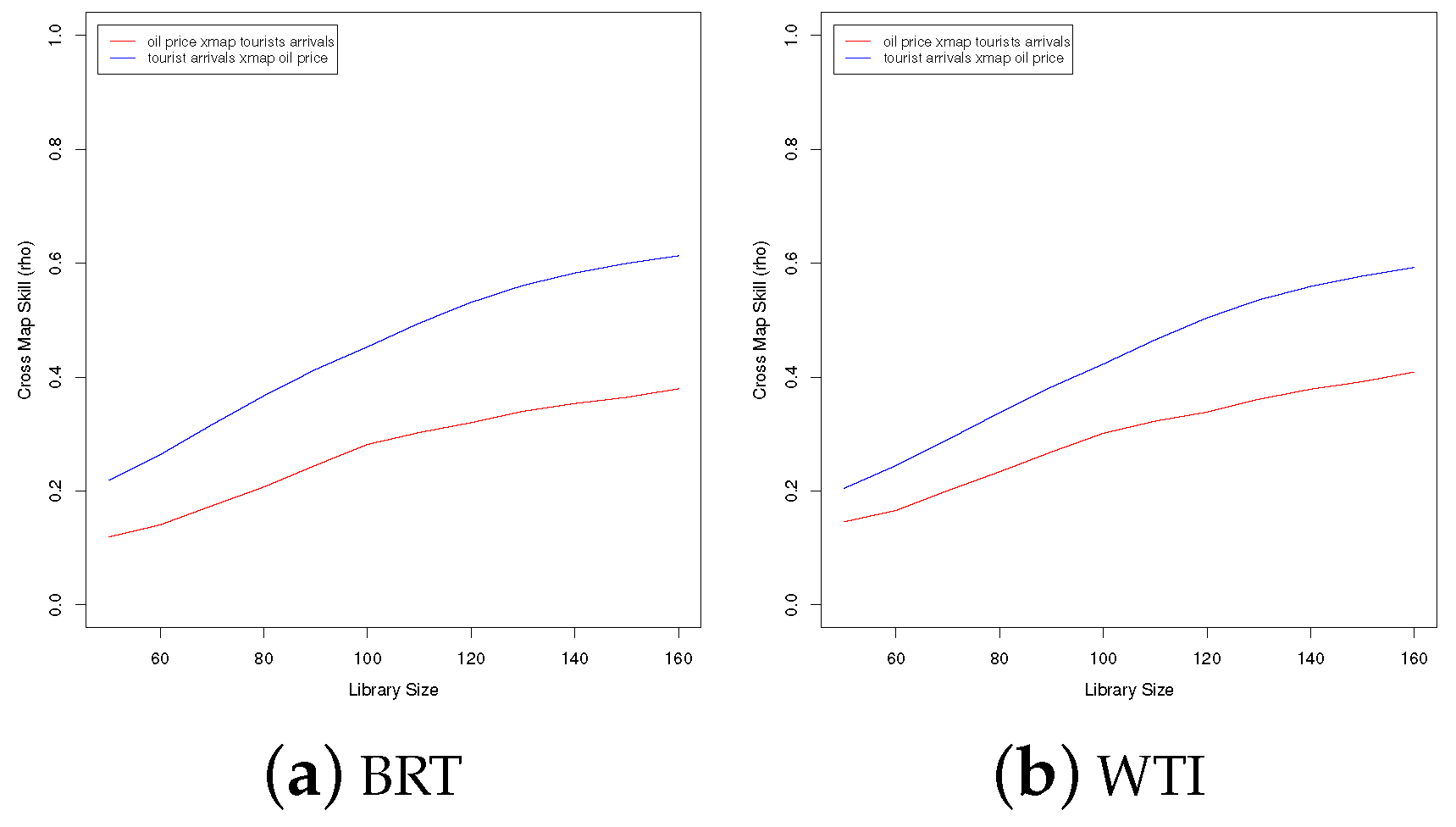
5.3. Convergent Cross Mapping (CCM)
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A





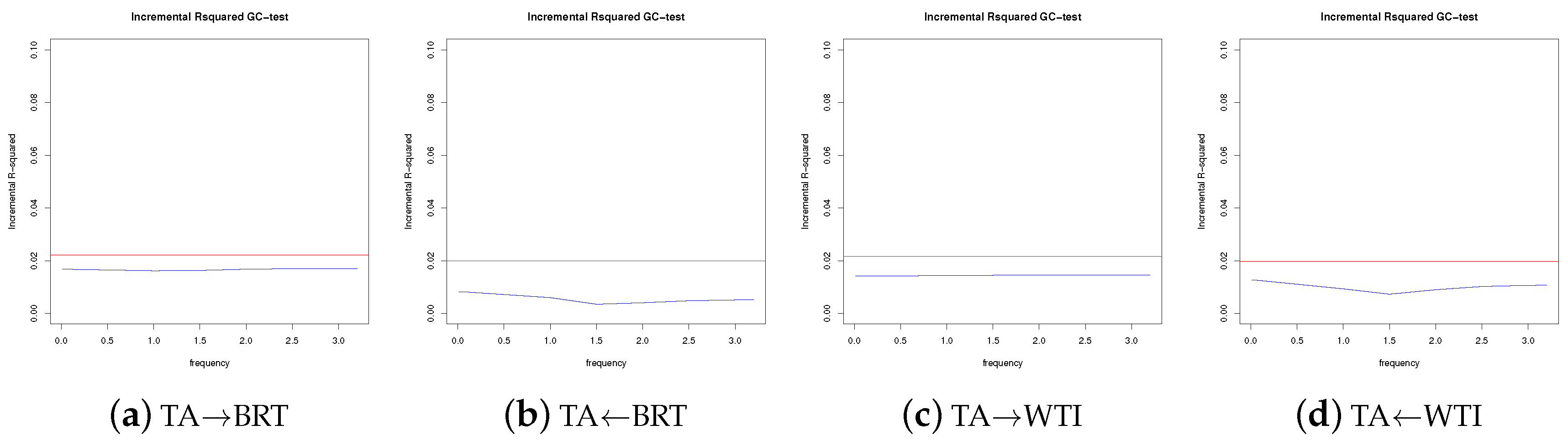


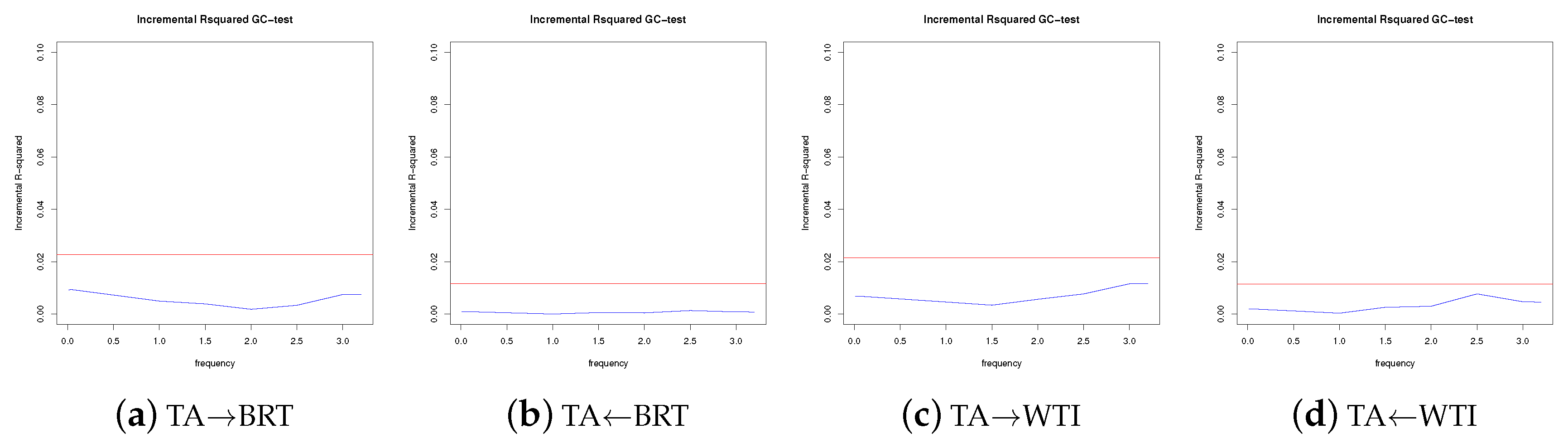
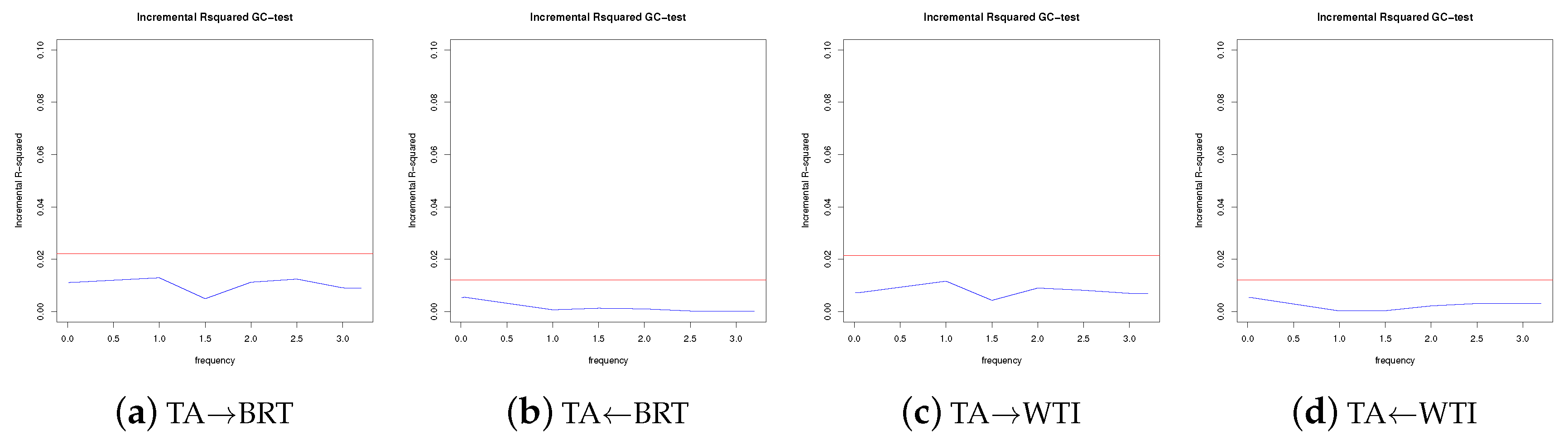
Appendix B


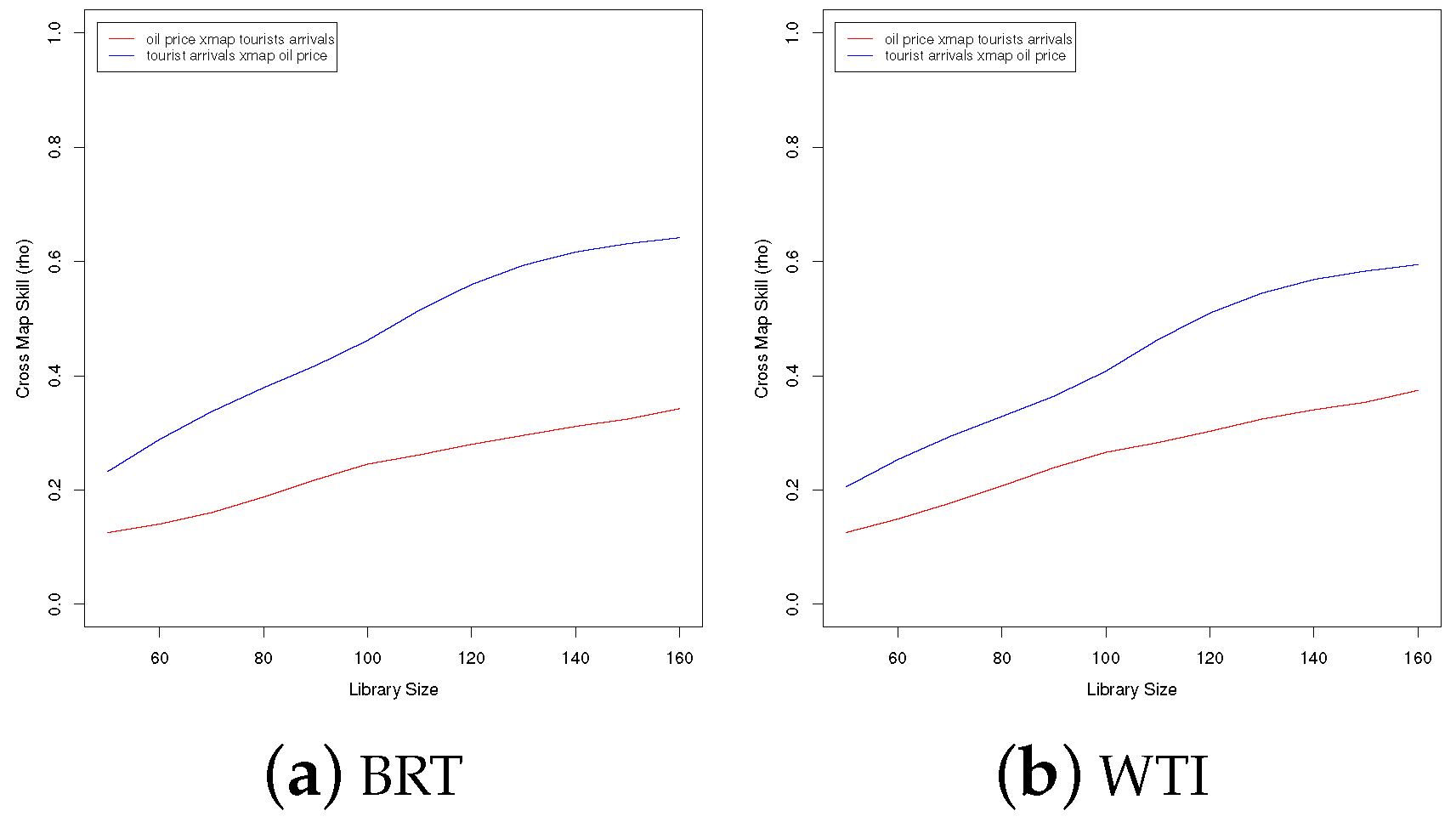



References
- Becken, S.; Lennox, J. Implications of a long-term increase in oil prices for tourism. Tour. Manag. 2012, 33, 133–142. [Google Scholar] [CrossRef]
- Becken, S. Developing indicators for managing tourism in the face of peak oil. Tour. Manag. 2008, 29, 695–705. [Google Scholar] [CrossRef]
- Chatziantoniou, I.; Filis, G.; Eeckels, B.; Apostolakis, A. Oil prices, tourism income and economic growth: A structural VAR approach for European Mediterranean countries. Tour. Manag. 2013, 36, 331–341. [Google Scholar] [CrossRef]
- Hamilton, J.D. This is what happened to the oil price-macroeconomy relationship. J. Monetary Econ. 1996, 38, 215–220. [Google Scholar] [CrossRef]
- Ferderer, J.P. Oil price volatility and the macroeconomy. J. Macroecon. 1997, 18, 1–26. [Google Scholar] [CrossRef]
- Sadorsky, P. Oil price shocks and stock market activity. Energy Econ. 1999, 21, 449–469. [Google Scholar] [CrossRef]
- Leduc, S.; Sill, K. A quantitative analysis of oil-price shocks, systematic monetary policy, and economic downturns. J. Monet. Econ. 2004, 51, 781–808. [Google Scholar]
- Huang, B.N.; Hwang, M.J.; Peng, H.P. The asymmetry of the impact of oil price shocks on economic activities: An application of the multivariate threshold model. Energy Econ. 2005, 27, 455–476. [Google Scholar] [CrossRef]
- Park, J.; Ratti, R.A. Oil price shocks and stock markets in the US and 13 European countries. Energy Econ. 2008, 30, 2587–2608. [Google Scholar] [CrossRef]
- Cong, R.G.; Wei, Y.M.; Jiao, J.L.; Fan, Y. Relationships between oil price shocks and stock market: An empirical analysis from China. Energy Policy 2008, 36, 3544–3553. [Google Scholar] [CrossRef]
- Hassani, H.; Zhigljavsky, A. Singular spectrum analysis: Methodology and application to economics data. J. Syst. Sci. Complex. 2009, 22, 372–394. [Google Scholar] [CrossRef]
- Ji, Q.; Fan, Y. How does oil price volatility affect non-energy commodity markets? Appl. Energy 2012, 89, 273–280. [Google Scholar] [CrossRef]
- Kilian, L.; Hicks, B. Did unexpectedly strong economic growth cause the oil price shock of 2003–2008? J. Forecast. 2013, 32, 385–394. [Google Scholar] [CrossRef]
- Acemoglu, D.; Finkelstein, A.; Notowidigdo, M.J. Income and health spending: Evidence from oil price shocks. Rev. Econ. Stat. 2013, 95, 1079–1095. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.; Yang, L. Oil price shocks and stock market activities: Evidence from oil-importing and oil-exporting countries. J. Comp. Econ. 2013, 41, 1220–1239. [Google Scholar] [CrossRef]
- Yeoman, I.; Lennon, J.J.; Blake, A.; Galt, M.; Greenwood, C.; McMahon-Beattie, U. Oil depletion: What does this mean for Scottish tourism? Tour. Manag. 2007, 28, 1354–1365. [Google Scholar]
- Pentelow, L.; Scott, D. The implications of climate change mitigation policy and oil price volatility for tourism arrivals to the Caribbean. Tour. Hosp. Plan. Dev. 2010, 7, 301–315. [Google Scholar] [CrossRef]
- Tang, C.F. Temporal Granger Causality and the Dynamics Relationship Between RealTourism Receipts, Real Income and RealExchange Rates in Malaysia. Int. J. Tour. Res. 2013, 15, 272–284. [Google Scholar] [CrossRef]
- Goh, C. Exploring impact of climate on tourism demand. Ann. Tour. Res. 2012, 39, 1859–1883. [Google Scholar] [CrossRef]
- Sheldon, P.J.; Var, T. Tourism forecasting: A review of empirical research. J. Forecast. 1985, 4, 183–195. [Google Scholar]
- Chou, C.-M.; Hsieh, S.F.; Tseng, H.P. The crowding-out effects of Chinese tourists on inbound tourism in Taiwan. Tour. Econ. 2014, 20, 1235–1251. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting causality in complex ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Li, G. Tourism demand modelling and forecasting: A review of recent research. Tour. Manag. 2008, 29, 203–220. [Google Scholar] [CrossRef]
- Gunter, U.; Onder, I. Forecasting international city tourism demand for Paris: Accuracy of uni- and multivariate models employing monthly data. Tour. Manag. 2015, 46, 123–135. [Google Scholar] [CrossRef]
- Becken, S. A critical review of tourism and oil. Ann. Tour. Res. 2011, 38, 359–379. [Google Scholar] [CrossRef]
- Selvanathan, S.; Selvanathan, E.A.; Viswanathan, B. Causality Between Foreign Direct Investment and Tourism: Empirical Evidence from India. Tour. Anal. 2012, 17, 91–98. [Google Scholar] [CrossRef]
- Massidda, C.; Mattana, P. A SVECM Analysis of the Relationship between International Tourism Arrivals, GDP and Trade in Italy. J. Travel Res. 2012, 52, 93–105. [Google Scholar] [CrossRef]
- Tang, C.F.; Tan, E.C. How stable is the tourism-led growth hypothesis in Malaysia? Evidence from disaggregated tourism markets. Tour. Manag. 2013, 37, 52–57. [Google Scholar] [CrossRef]
- Ghartey, E.E. Effects of tourism, economic growth, real exchange rate, structural changes and hurricanes in Jamaica. Tour. Econ. 2013, 19, 919–942. [Google Scholar] [CrossRef]
- Cellini, R.; Cuccia, T. Museum and monument attendance and tourism flow: A time series analysis approach. Appl. Econ. 2013, 45, 473–3482. [Google Scholar] [CrossRef]
- Albaladejo, I.P.; González-Martínez, M.I.; Martínez-García, M.P. Quality and endogenous tourism: An empirical approach. Tour. Manag. 2014, 41, 141–147. [Google Scholar] [CrossRef]
- Katircioğlu, S.T. Testing the tourism-induced EKC hypothesis: The case of Singapore. Econ. Model. 2014, 41, 383–391. [Google Scholar] [CrossRef]
- Katircioğlu, S.T.; Feridun, M.; Kilinc, C. Estimating tourism-induced energy consumption and CO2 emissions: The case of Cyprus. Renew. Sustain. Energy Rev. 2014, 29, 634–640. [Google Scholar] [CrossRef]
- Tang, C.F.; Abosedra, S. Small sample evidence on the tourism-led growth hypothesis in Lebanon. Curr. Issues Tour. 2014, 17, 234–246. [Google Scholar] [CrossRef]
- Fereidouni, H.G.; Al-mulali, U. The interaction between tourism and FDI in real estate in OECD countries. Curr. Issues Tour. 2014, 17, 105–113. [Google Scholar] [CrossRef]
- Solarin, S.A. Tourist arrivals and macroeconomic determinants of CO2 emissions in Malaysia. Anatolia 2014, 25, 228–241. [Google Scholar] [CrossRef]
- Antonakakis, N.; Dragouni, M.; Filis, G. Tourism and growth: The times they are a-changing. Ann. Tour. Res. 2015, 50, 165–169. [Google Scholar] [CrossRef]
- Chen, M.-H.; Lin, C.-P.; Chen, B.T. Drivers of Taiwan’s Tourism Market Cycle. J. Travel Tour. Mark. 2015, 32, 260–275. [Google Scholar] [CrossRef]
- Tang, C.F.; Tan, E.C. Does tourism effectively stimulate Malaysia’s economic growth? Tour. Manag. 2015, 46, 158–163. [Google Scholar] [CrossRef]
- Paerez-Rodríguez, J.V.; Ledesma-Rodríguez, F.; Santana-Gallego, M. Testing dependence between GDP and tourism’s growth rates. Tour. Manag. 2015, 48, 268–282. [Google Scholar] [CrossRef]
- Antonakakis, N.; Dragouni, M.; Filis, G. How strong is the linkage between tourism and economic growth in Europe? Econ. Model. 2015, 44, 142–145. [Google Scholar] [CrossRef]
- Dogan, E.; Seker, F.; Bulbul, S. Investigating the impacts of energy consumption, real GDP, tourism and trade on CO2 emissions by accounting for cross-sectional dependence: A panel study of OECD countries. Curr. Issues Tour. 2015, 20, 1701–1719. [Google Scholar] [CrossRef]
- Shahbaz, M.; Kumar, R.R.; Ivanov, S.; Loganathan, N. The nexus between tourism demand and output per capita, with the relative importance of trade openness and financial development: A study of Malaysia. Tour. Econ. 2015, 23, 168–186. [Google Scholar] [CrossRef]
- Al-Mulali, U.; Fereidouni, H.G.; Mohammed, A.H. The effect of tourism arrival on CO2 emissions from transportation sector. Anatolia 2015, 26, 230–243. [Google Scholar] [CrossRef]
- Durbarry, R.; Seetanah, B. The Impact of Long Haul Destinations on Carbon Emissions: The Case of Mauritius. J. Hosp. Mark. Manag. 2015, 24, 401–410. [Google Scholar] [CrossRef]
- Ertugrul, H.M.; Mangir, F. The tourism-led growth hypothesis: Empirical evidence from Turkey. Curr. Issues Tour. 2015, 18, 633–646. [Google Scholar] [CrossRef]
- Tang, C.F.; Tan, E.C. Tourism-Led Growth Hypothesis in Malaysia: Evidence Based Upon Regime Shift Cointegration and Time-Varying Granger Causality Techniques. Asia-Pac. J. Tour. Res. 2015, 20, 1430–1450. [Google Scholar] [CrossRef]
- Tsui, W.H.K.; Fung, M.K.Y. Causality between business travel and trade volumes: Empirical evidence from Hong Kong. Tour. Manag. 2016, 52, 395–404. [Google Scholar] [CrossRef]
- Zaman, K.; Shahbaz, M.; Loganathan, N.; Raza, S.Y. Tourism development, energy consumption and Environmental Kuznets Curve: Trivariate analysis in the panel of developed and developing countries. Tour. Manag. 2016, 54, 275–283. [Google Scholar] [CrossRef]
- Rakotondramaro, H.; Andriamasy, L. Multivariate Granger Causality among tourism, poverty and growth in Madagascar. Tour. Manag. Perspect. 2016, 20, 109–111. [Google Scholar] [CrossRef]
- Tang, C.F.; Abosedra, S. Tourism and growth in Lebanon: New evidence from bootstrap simulation and rolling causality approaches. Empir. Econ. 2016, 50, 679–696. [Google Scholar] [CrossRef]
- Toda, H.Y.; Yamamoto, T. Statistical inference in vector autoregressions with possibly integrated processes. J. Econom. 1995, 66, 225–250. [Google Scholar] [CrossRef]
- Dolado, J.J.; Lütkepohl, H. Making Wald tests work for cointegrated VAR system. Econom. Rev. 1996, 15, 369–386. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Kulendran, N. The Impact of Climate Variables on Seasonal Variation in Hong Kong Inbound Tourism Demand. J. Travel Res. 2016, 26, 94–107. [Google Scholar] [CrossRef]
- Hatemi-J, A. On the tourism-led growth hypothesis in the UAE: A bootstrap approach with leveraged adjustments. Appl. Econ. Lett. 2016, 23, 424–427. [Google Scholar] [CrossRef]
- Li, X.; Pan, B.; Law, R.; Huang, X. Forecasting tourism demand with composite search index. Tour. Manag. 2017, 59, 57–66. [Google Scholar] [CrossRef]
- Valadkhani, A.; Smyth, R.; O’Mahony, B. Asymmetric causality between Australian inbound and outbound tourism flows. Appl. Econ. 2017, 49, 33–50. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econ. J. Econ. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Sims, C.A. Money, income, and causality. Am. Econ. Rev. 1972, 62, 540–552. [Google Scholar]
- Hsiao, C. Autoregressive modelling and money-income causality detection. J. Monetary Econ. 1981, 7, 85–106. [Google Scholar] [CrossRef]
- Sims, C.A.; Stock, J.H.; Watson, M.W. Inference in linear time series models with some unit roots. Econ. J. Econ. Soc. 1990, 58, 113–144. [Google Scholar] [CrossRef]
- Toda, H.Y.; Phillips, P.C. Vector autoregressions and causality. Econ. J. Econ. Soc. 1993, 61, 1367–1393. [Google Scholar] [CrossRef]
- Pesaran, H.H.; Shin, Y. Generalized impulse response analysis in linear multivariate models. Econ. Lett. 1998, 58, 17–29. [Google Scholar] [CrossRef]
- Chen, Y.; Bressler, S.L.; Ding, M. Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J. Neurosci. Methods 2006, 150, 228–237. [Google Scholar] [CrossRef] [PubMed]
- Gow, D.W.; Segawa, J.A.; Ahlfors, S.P.; Lin, F.H. Lexical influences on speech perception: A Granger causality analysis of MEG and EEG source estimates. Neuroimage 2008, 43, 614–623. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, G.; Sathian, K.; Hu, X. Effect of hemodynamic variability on Granger causality analysis of fMRI. Neuroimage 2010, 52, 884–896. [Google Scholar] [CrossRef] [PubMed]
- Geweke, J. Measurement of linear dependence and feedback between multiple time series. J. Am. Stat. Assoc. 1982, 77, 304–324. [Google Scholar] [CrossRef]
- Ciner, C. Eurocurrency interest rate linkages: A frequency domain analysis. Rev. Econ. Financ. 2011, 20, 498–505. [Google Scholar] [CrossRef]
- Breitung, J.; Candelon, B. Testing for short- and long-run causality: A frequency-domain approach. J. Econom. 2006, 132, 363–378. [Google Scholar] [CrossRef]
- Deyle, E.; Fogarty, M.; Hsieh, C.; Kaufman, L.; MacCall, A.; Munch, S.; Perretti, C.; Ye, H.; Sugihara, G. Predicting climate effects on Pacific sardine. Proc. Natl. Acad. Sci. USA 2013, 110, 6430–6435. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.; Deyle, E.; Gilarranz, L.; Sugihara, G. Distinguishing time-delayed causal interactions using convergent cross mapping. Sci. Rep. 2015, 5, 14750. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.T.; Ye, H.; Isbell, F.; Deyle, E.; Cowles, J.; Tilman, G.; Sugihara, G. Spatial convergent cross mapping to detect causal relationships from short time series. Ecology 2015, 96, 1174–1181. [Google Scholar] [CrossRef] [PubMed]
- Sugihara, G.; May, R. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 1990, 344, 734–741. [Google Scholar] [CrossRef] [PubMed]
- Takens, F. Detecting strange attractors in turbulence Dynamical Systems and Turbulence. Dyn. Syst. Turbul. 1981, 898, 366–381. [Google Scholar]
- EIA. U.S. Energy Information Administration. 2016. Available online: http://www.eia.gov/outlooks/steo/outlook.cfm (accessed on 15 December 2016).
- Hassani, H.; Mahmoudvand, R.; Omer, H.N.; Silva, E.S. A Preliminary Investigation into the Effect of Outlier(s) on Singular Spectrum Analysis. Fluct. Noise Lett. 2014, 13, 1450029. [Google Scholar] [CrossRef]
- Akaike, H. Maximum likelihood identification of Gaussian autoregressive moving average models. Biometrika 1973, 60, 255–265. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The determination of the order of an autoregression. J. R. Stat. Soc. Ser. B-Stat. Methodol. 1979, 42, 190–195. [Google Scholar]
- Akaike, H. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math. 1969, 21, 243–247. [Google Scholar] [CrossRef]
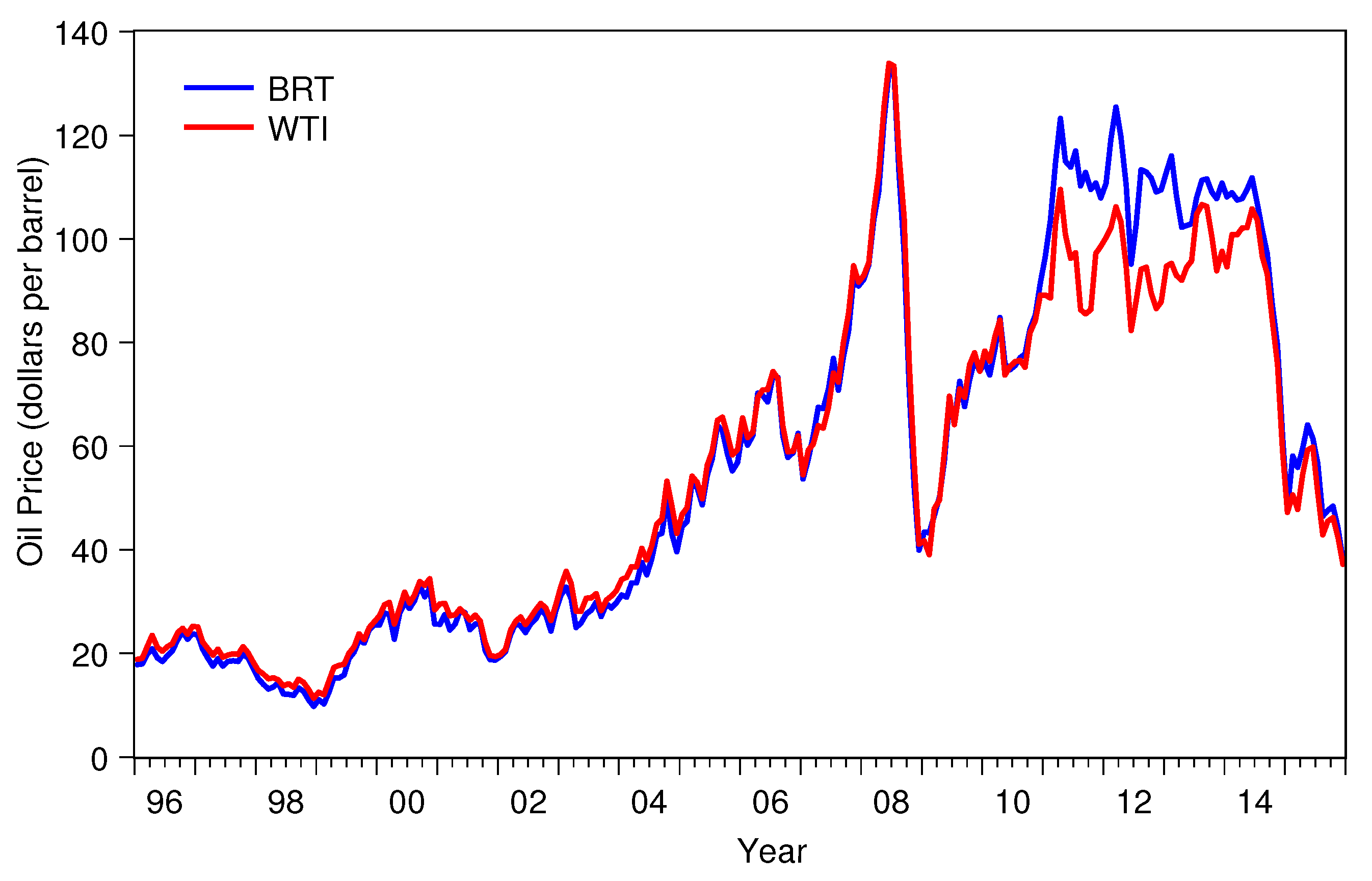

| Oil Prices | ||||||||
| Obs | Mean | Median | Max | Min | SD | Skewness | Kurtosis | |
| BRT | 240 | 56.41 | 49.22 | 132.72 | 9.82 | 35.24 | 0.47 | 1.85 |
| WTI | 240 | 54.78 | 49.06 | 133.88 | 11.35 | 31.19 | 0.40 | 1.89 |
| Tourist Arrivals | ||||||||
| Obs | Mean | Median | Max | Min | Std. Dev. | Skewness | Kurtosis | |
| Austria | 240 | 1,481,894 | 1,434,455 | 3,205,966 | 446,240 | 504,448 | 0.39 | 3.21 |
| Germany | 240 | 1,918,394 | 1,788,583 | 4,401,682 | 747,141 | 724,552 | 0.75 | 3.29 |
| Greece | 240 | 765,847 | 564,523 | 3,107,955 | 29,856 | 710,611 | 1.11 | 3.66 |
| Italy | 240 | 3,343,953 | 3,277,084 | 8,084,209 | 907,367 | 1,709,118 | 0.50 | 2.45 |
| Netherland | 240 | 870,900 | 864,200 | 1,745,779 | 275,000 | 284,180 | 0.34 | 2.79 |
| Portugal | 240 | 539,796 | 522,395 | 1,359,284 | 155,438 | 256,280 | 0.70 | 3.03 |
| Spain | 240 | 3,229,314 | 2,934,373 | 7,443,749 | 671,109 | 1,533,209 | 0.51 | 2.42 |
| Sweden | 240 | 357,927 | 239,902 | 1,428,207 | 98,357 | 289,081 | 1.93 | 5.97 |
| UK | 240 | 1,668,020 | 1,541,000 | 3,390,515 | 692,120 | 582,239 | 0.59 | 2.64 |
| US | 240 | 4,325,374 | 4,222,034 | 8,364,940 | 2,094,287 | 1,292,787 | 0.59 | 2.88 |
| Variables | Series | Methods | None | Intercept | Intercept and Trend | |||
|---|---|---|---|---|---|---|---|---|
| Level | Decision | Level | Decision | Level | Decision | |||
| Oil Prices (240 Obs) January 1996–December 2015 | BRT | KPSS | --------- | --------- | 1.675 ***(11) | I(1) | 0.139 *(11) | I(0) |
| ADF | −10.284 ***(0) | I(1) | −10.264 ***(0) | I(1) | −10.294 ***(0) | I(1) | ||
| PP | −10.279 ***(4) | I(1) | −10.258 ***(4) | I(1) | −10.283 ***(4) | I(1) | ||
| WTI | KPSS | --------- | --------- | 1.663 ***(11) | I(1) | 0.166 **(11) | I(1) | |
| ADF | −10.104 ***(0) | I(1) | −10.083 ***(0) | I(1) | −10.109 ***(0) | I(1) | ||
| PP | −10.104 ***(0) | I(1) | −10.083 ***(0) | I(1) | −10.109 ***(0) | I(1) | ||
| Tourist Arrivals (240 Obs) January 1996–December 2015 | Austria | KPSS | --------- | --------- | 1.458 ***(15) | I(1) | 0.144 *(27) | I(0) |
| ADF | −3.938 ***(14) | I(1) | −16.637 ***(11) | I(1) | −17.093 ***(11) | I(0) | ||
| PP | −49.801 ***(23) | I(1) | −9.945 ***(31) | I(0) | −10.345 ***(24) | I(0) | ||
| Germany | KPSS | --------- | --------- | 2.305 ***(9) | I(1) | 0.115(1) | I(0) | |
| ADF | −2.524 ***(13) | I(1) | −3.581 ***(13) | I(1) | −3.825 ***(13) | I(1) | ||
| PP | −12.185 ***(16) | I(1) | −4.832 ***(5) | I(0) | −5.169 ***(0) | I(0) | ||
| Greece | KPSS | --------- | --------- | 0.755 ***(3) | I(1) | 0.058(2) | I(0) | |
| ADF | −4.411 ***(11) | I(1) | −4.791 ***(11) | I(1) | −4.985 ***(11) | I(1) | ||
| PP | −4.056 ***(5) | I(0) | −5.414 ***(6) | I(0) | −5.529 ***(6) | I(0) | ||
| Italy | KPSS | --------- | --------- | 1.079 ***(5) | I(1) | 0.014(2) | I(0) | |
| ADF | −3.527 ***(13) | I(1) | −4.403 ***(13) | I(1) | −4.527 ***(13) | I(1) | ||
| PP | −2.828 ***(3) | I(0) | −6.291 ***(4) | I(0) | −6.604 ***(4) | I(0) | ||
| Netherland | KPSS | --------- | --------- | 1.744 ***(8) | I(1) | 0.084(4) | I(0) | |
| ADF | −2.976 ***(13) | I(1) | −3.496 ***(13) | I(1) | −3.503 ***(13) | I(1) | ||
| PP | −14.361 ***(3) | I(1) | −5.952 ***(2) | I(0) | −6.548 ***(1) | I(0) | ||
| Portugal | KPSS | --------- | --------- | 1.653 ***(7) | I(1) | 0.111(1) | I(0) | |
| ADF | −4.077 ***(12) | I(1) | −4.658 ***(12) | I(1) | −4.848 ***(12) | I(1) | ||
| PP | −2.101 **(6) | I(0) | −5.731 ***(5) | I(0) | −5.672 ***(6) | I(0) | ||
| Spain | KPSS | --------- | --------- | 1.991 ***(8) | I(1) | 0.071(1) | I(0) | |
| ADF | −2.353 **(12) | I(1) | −2.857 *(12) | I(0) | −3.469 **(13) | I(0) | ||
| PP | −2.306 **(4) | I(0) | −5.646 ***(4) | I(0) | −6.118 ***(5) | I(0) | ||
| Sweden | KPSS | --------- | --------- | 1.052 ***(2) | I(1) | 0.161 **(9) | I(1) | |
| ADF | −5.708 ***(13) | I(1) | −6.117 ***(13) | I(1) | −6.104 ***(13) | I(1) | ||
| PP | −3.940 ***(14) | I(0) | −5.961 ***(19) | I(0) | −5.794 ***(24) | I(0) | ||
| UK | KPSS | --------- | --------- | 0.818 ***(5) | I(1) | 0.090(3) | I(0) | |
| ADF | −4.889 ***(12) | I(1) | −4.981 ***(12) | I(1) | −5.196 ***(12) | I(1) | ||
| PP | −10.446 ***(4) | I(1) | −5.821 ***(1) | I(0) | −6.387 ***(2) | I(0) | ||
| US | KPSS | --------- | --------- | 1.825 ***(11) | I(1) | 0.392 ***(9) | I(1) | |
| ADF | −3.591 ***(12) | I(1) | −3.928 ***(12) | I(1) | −4.074 ***(12) | I(1) | ||
| PP | −19.331 ***(6) | I(1) | −3.796 ***(8) | I(0) | −7.063 ***(8) | I(0) | ||
| Country | Oil Prices | |||||||
|---|---|---|---|---|---|---|---|---|
| BRT | WTI | |||||||
| → | ← | → | ← | |||||
| p-Value | Yes/No | p-Value | Yes/No | p-Value | Yes/No | p-Value | Yes/No | |
| Austria | 0.68 | No | 0.56 | No | 0.81 | No | 0.34 | No |
| Germany | 0.52 | No | 0.27 | No | 0.29 | No | 0.17 | No |
| Greece | 0.54 | No | 0.36 | No | 0.46 | No | 0.44 | No |
| Italy | 0.60 | No | 0.98 | No | 0.67 | No | 0.74 | No |
| Netherlands | 0.30 | No | 0.83 | No | 0.29 | No | 0.65 | No |
| Portugal | 0.38 | No | 0.41 | No | 0.72 | No | 0.31 | No |
| Spain | 0.62 | No | 0.24 | No | 0.54 | No | 0.12 | No |
| Sweden | 0.21 | No | 0.55 | No | 0.14 | No | 0.93 | No |
| UK | 0.63 | No | 0.95 | No | 0.53 | No | 0.82 | No |
| US | 0.48 | No | 0.85 | No | 0.53 | No | 0.48 | No |
| Country | Oil Prices | |||
|---|---|---|---|---|
| BRT | WTI | |||
| → | ← | → | ← | |
| Austria | No | No | No | No |
| Germany | No | No | No | No |
| Greece | No | No | No | No |
| Italy | No | No | No | No |
| Netherland | No | No | No | No |
| Portugal | No | No | No | No |
| Spain | No | No | No | No |
| Sweden | No | No | No | No |
| UK | No | No | No | No |
| US | No | No | No | No |
| Country | Oil Prices | |||
|---|---|---|---|---|
| BRT | WTI | |||
| → | ← | → | ← | |
| Austria | No | Yes | No | Yes |
| Germany | No | Yes | No | Yes |
| Greece | No | Yes | No | Yes |
| Italy | No | Yes | No | Yes |
| Netherland | No | Yes | No | Yes |
| Portugal | No | Yes | No | Yes |
| Spain | No | Yes | No | Yes |
| Sweden | No | Yes | No | Yes |
| UK | No | Yes | No | Yes |
| US | No | Yes | No | Yes |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Silva, E.; Hassani, H. Causality between Oil Prices and Tourist Arrivals. Stats 2018, 1, 134-154. https://doi.org/10.3390/stats1010010
Huang X, Silva E, Hassani H. Causality between Oil Prices and Tourist Arrivals. Stats. 2018; 1(1):134-154. https://doi.org/10.3390/stats1010010
Chicago/Turabian StyleHuang, Xu, Emmanuel Silva, and Hossein Hassani. 2018. "Causality between Oil Prices and Tourist Arrivals" Stats 1, no. 1: 134-154. https://doi.org/10.3390/stats1010010
APA StyleHuang, X., Silva, E., & Hassani, H. (2018). Causality between Oil Prices and Tourist Arrivals. Stats, 1(1), 134-154. https://doi.org/10.3390/stats1010010







