A Selective Review of Multi-Level Omics Data Integration Using Variable Selection
Abstract
:1. Introduction
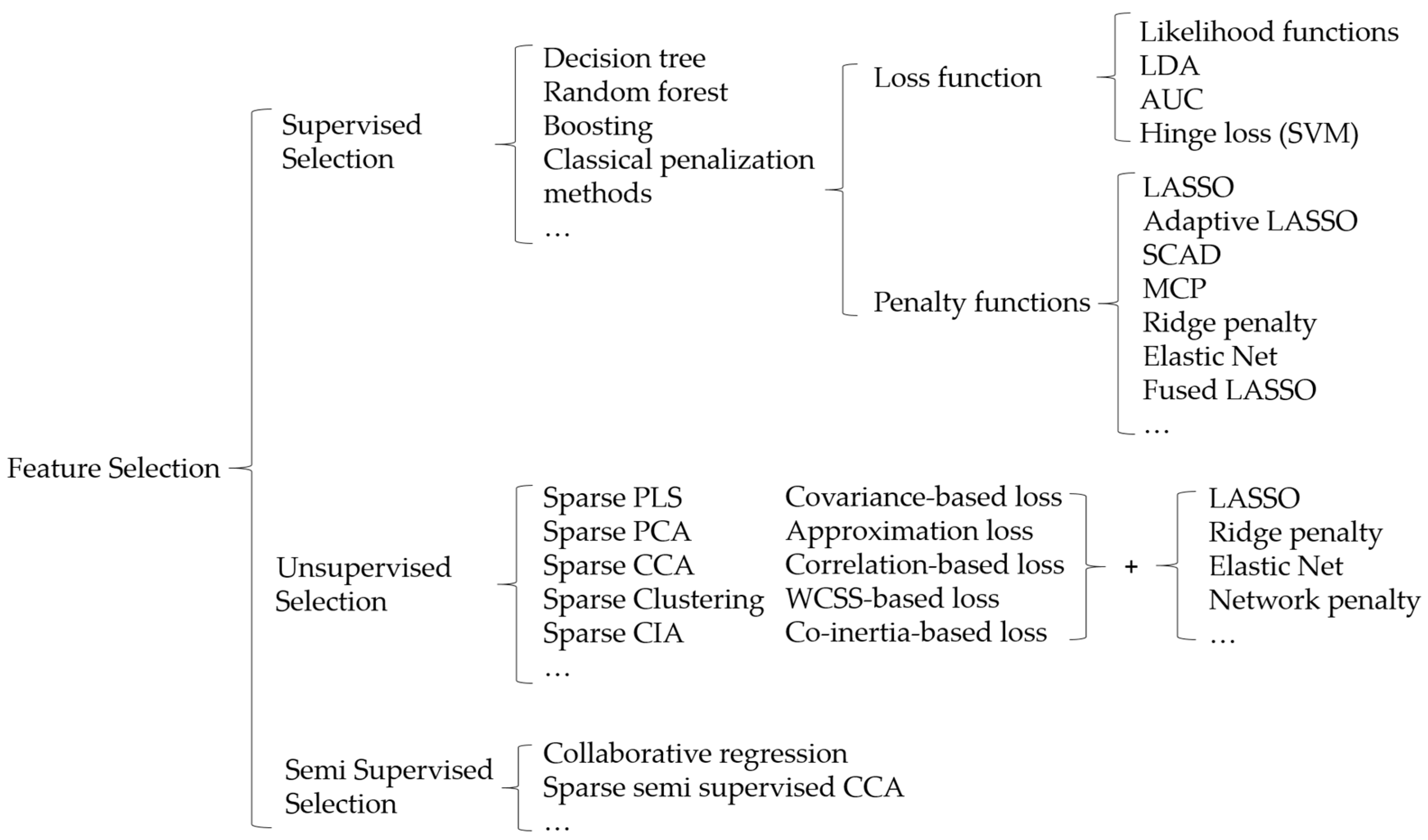
2. Statistical Methods in Integrative Analysis
2.1. Penalized Variable Selection
2.2. Bayesian Variable Selection
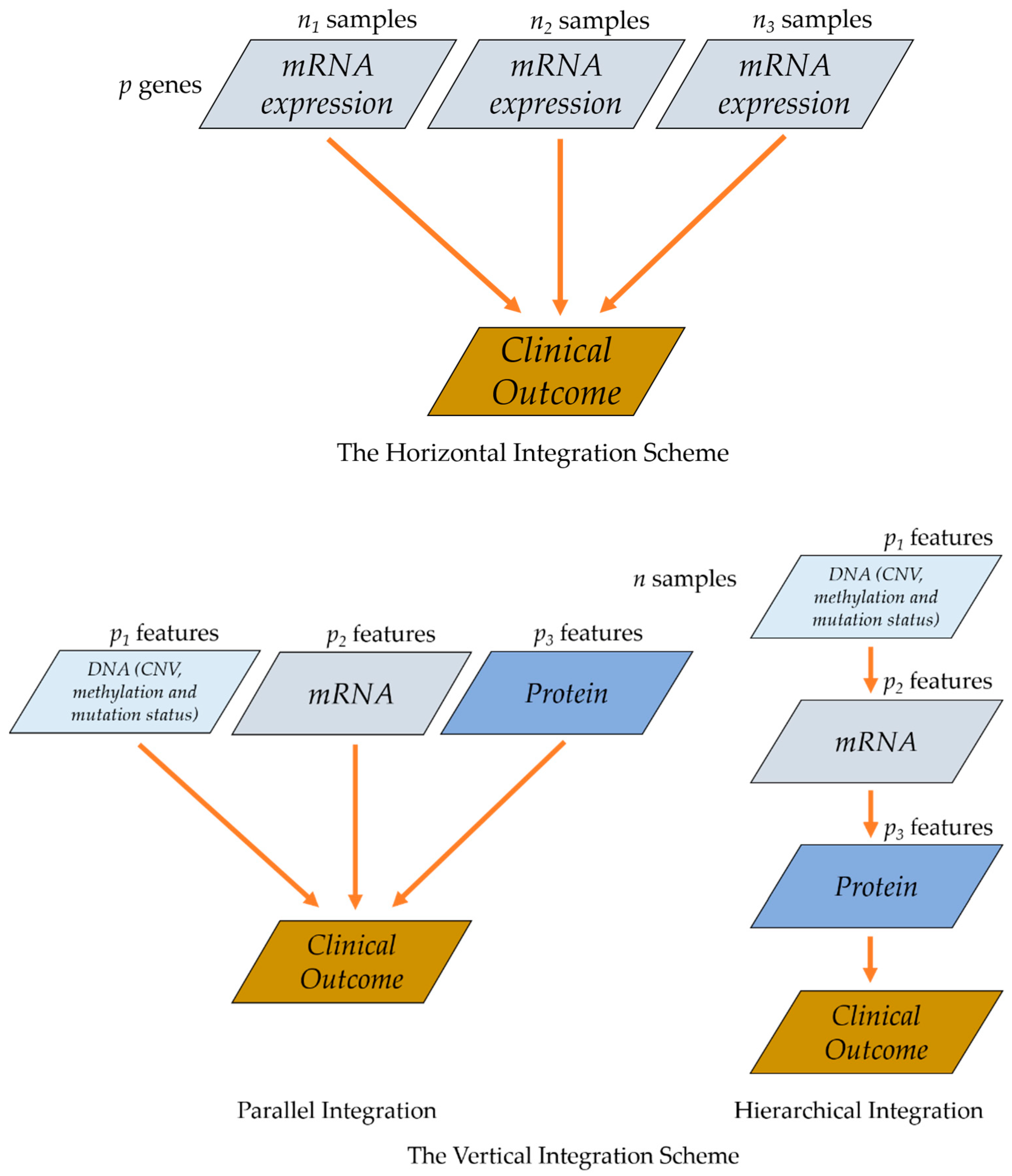
3. Multi-Omics Data Integration
3.1. Parallel Integration
3.1.1. Supervised Parallel Integration
3.1.2. Unsupervised/Semi-Supervised Parallel Integration
Correlation, Covariance and Co-Inertia Based Integration
Low Rank Approximation Based Integration
3.2. Hierarchical Integration
3.2.1. Supervised Hierarchical Integration
3.2.2. Unsupervised Hierarchical Integration
3.3. Other Methods for Integrating Multi-Omics Data
3.4. Computation Algorithms
3.5. Examples
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADMM | alternating direction method of multipliers |
| AML | acute myeloid leukemia |
| ARMI | assisted robust marker identification |
| AUC | area under the curve |
| BRCA | breast cancer dataset |
| BXD | murine liver dataset |
| CCA | canonical correlation analysis |
| CD | coordinate descent |
| CIA | co-inertia analysis |
| CNV | copy number variation |
| COAD | colon adenocarcinoma |
| EM | expectation–maximization |
| GBM | glioblastoma |
| GE | gene expression |
| GWAS | whole genome association study |
| JIVE | the joint and individual variation explained |
| KIRC | kidney renal clear cell carcinoma |
| LAD | least absolute deviation |
| LASSO | least absolute shrinkage and selection operator |
| LDA | linear discriminant analysis |
| LIHC | liver hepatocellular carcinoma |
| LPP | locality preserving projections |
| LRMs | linear regulatory modules |
| LUSC | lung squamous cell carcinoma |
| MALA | microarray logic analyzer |
| MCCA | multiple canonical correlation analysis |
| MCIA | multiple co-inertia analysis |
| MCMC | Markov chain Monte Carlo |
| MCP | minimax concave penalty |
| MDI | multiple dataset integration |
| MFA | multiple factor analysis |
| NMF | non-negative matrix factorization |
| OV | ovarian cancer |
| PCA | principle component analysis |
| PINS | perturbation clustering for data integration and disease subtyping |
| PLS | partial least squares |
| rMKL | robust multiple kernel learning |
| SARC | Sarcoma Alliance for Research through Collaboration |
| SCAD | smoothly clipped absolute deviation |
| SKCM | skin cutaneous melanoma |
| SNF | similarity network fusion |
| SNP | single nucleotide polymorphism |
| TCGA | The Cancer Genome Atlas |
References
- Cancer Genome Atlas Research Network. Comprehensive molecular profiling of lung adenocarcinoma. Nature 2014, 511, 543. [Google Scholar] [CrossRef] [PubMed]
- Cancer Genome Atlas Research Network. Comprehensive molecular characterization of gastric adenocarcinoma. Nature 2014, 513, 202. [Google Scholar] [CrossRef] [PubMed]
- Akbani, R.; Akdemir, K.C.; Aksoy, B.A.; Albert, M.; Ally, A.; Amin, S.B.; Arachchi, H.; Arora, A.; Auman, J.T.; Ayala, B. Genomic classification of cutaneous melanoma. Cell 2015, 161, 1681–1696. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Fan, J.; Lv, J. A selective overview of variable selection in high dimensional feature space. Stat. Sin. 2010, 20, 101. [Google Scholar]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principal component analysis. J. Comput. Graph. Stat. 2006, 15, 265–286. [Google Scholar] [CrossRef]
- Zhao, Q.; Shi, X.; Huang, J.; Liu, J.; Li, Y.; Ma, S. Integrative analysis of ‘-omics’ data using penalty functions. Wiley Interdiscip. Rev. Comput. Stat. 2015, 7, 99–108. [Google Scholar] [CrossRef]
- Richardson, S.; Tseng, G.C.; Sun, W. Statistical methods in integrative genomics. Annu. Rev. Stat. Appl. 2016, 3, 181–209. [Google Scholar] [CrossRef]
- Bersanelli, M.; Mosca, E.; Remondini, D.; Giampieri, E.; Sala, C.; Castellani, G.; Milanesi, L. Methods for the integration of multi-omics data: Mathematical aspects. BMC Bioinform. 2016, 17, S15. [Google Scholar] [CrossRef] [PubMed]
- Hasin, Y.; Seldin, M.; Lusis, A. Multi-omics approaches to disease. Genome Biol. 2017, 18, 83. [Google Scholar] [CrossRef]
- Huang, S.; Chaudhary, K.; Garmire, L.X. More Is Better: Recent Progress in Multi-Omics Data Integration Methods. Front. Genet. 2017, 8, 84. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wu, F.X.; Ngom, A. A review on machine learning principles for multi-view biological data integration. Brief. Bioinform. 2018, 19, 325–340. [Google Scholar] [CrossRef] [PubMed]
- Pucher, B.M.; Zeleznik, O.A.; Thallinger, G.G. Comparison and evaluation of integrative methods for the analysis of multilevel omics data: A study based on simulated and experimental cancer data. Brief. Bioinform. 2018, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.T.; Zeng, T. Integrative Analysis of Omics Big Data. Methods Mol. Biol. 2018, 1754, 109–135. [Google Scholar] [PubMed]
- Zeng, I.S.L.; Lumley, T. Review of Statistical Learning Methods in Integrated Omics Studies (An Integrated Information Science). Bioinform. Biol. Insights 2018, 12, 1–16. [Google Scholar] [CrossRef]
- Rappoport, N.; Shamir, R. Multi-omic and multi-view clustering algorithms: Review and cancer benchmark. Nucl. Acids Res. 2018, 46, 10546–10562. [Google Scholar] [CrossRef]
- Tini, G.; Marchetti, L.; Priami, C.; Scott-Boyer, M.P. Multi-omics integration-a comparison of unsupervised clustering methodologies. Brief. Bioinform. 2017, 1–11. [Google Scholar] [CrossRef]
- Chalise, P.; Koestler, D.C.; Bimali, M.; Yu, Q.; Fridley, B.L. Integrative clustering methods for high-dimensional molecular data. Transl. Cancer Res. 2014, 3, 202–216. [Google Scholar]
- Wang, D.; Gu, J. Integrative clustering methods of multi-omics data for molecule-based cancer classifications. Quant. Biol. 2016, 4, 58–67. [Google Scholar] [CrossRef] [Green Version]
- Ickstadt, K.; Schäfer, M.; Zucknick, M. Toward Integrative Bayesian Analysis in Molecular Biology. Annu. Rev. Stat. Appl. 2018, 5, 141–167. [Google Scholar] [CrossRef]
- Meng, C.; Zeleznik, O.A.; Thallinger, G.G.; Kuster, B.; Gholami, A.M.; Culhane, A.C. Dimension reduction techniques for the integrative analysis of multi-omics data. Brief. Bioinform. 2016, 17, 628–641. [Google Scholar] [CrossRef]
- Rendleman, J.; Choi, H.; Vogel, C. Integration of large-scale multi-omic datasets: A protein-centric view. Curr. Opin. Syst. Biol. 2018, 11, 74–81. [Google Scholar] [CrossRef]
- Yan, K.K.; Zhao, H.; Pang, H. A comparison of graph- and kernel-based -omics data integration algorithms for classifying complex traits. BMC Bioinform. 2017, 18, 539. [Google Scholar] [CrossRef] [PubMed]
- Witten, D.M.; Tibshirani, R.J. Extensions of sparse canonical correlation analysis with applications to genomic data. Stat. Appl. Genet. Mol. Biol. 2009, 8, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Lock, E.F.; Hoadley, K.A.; Marron, J.S.; Nobel, A.B. Joint and individual variation explained (JIVE) for integrated analysis of multiple data types. Ann. Appl. Stat. 2013, 7, 523–542. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.-H. Nearly unbiased variable selection under minimax concave penalty. Ann. Appl. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [Green Version]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused lasso. J. R. Stat. Soc. Ser. B 2005, 67, 91–108. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Huang, J. Penalized feature selection and classification in bioinformatics. Brief. Bioinform. 2008, 9, 392–403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, C.; Ma, S. A selective review of robust variable selection with applications in bioinformatics. Brief. Bioinform. 2015, 16, 873–883. [Google Scholar] [CrossRef] [PubMed]
- O’Hara, R.B.; Sillanpää, M.J. A review of Bayesian variable selection methods: What, how and which. Bayesian Anal. 2009, 4, 85–117. [Google Scholar] [CrossRef]
- Park, T.; Casella, G. The bayesian lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Carvalho, C.M.; Polson, N.G.; Scott, J.G. The horseshoe estimator for sparse signals. Biometrika 2010, 97, 465–480. [Google Scholar] [CrossRef] [Green Version]
- Polson, N.G.; Scott, J.G.; Windle, J. Bayesian inference for logistic models using Pólya–Gamma latent variables. J. Am. Stat. Assoc. 2013, 108, 1339–1349. [Google Scholar] [CrossRef]
- George, E.I.; McCulloch, R.E. Variable Selection via Gibbs Sampling. J. Am. Stat. Assoc. 1993, 88, 881–889. [Google Scholar] [CrossRef]
- George, E.I.; McCulloch, R.E. Approaches for Bayesian variable selection. Stat. Sin. 1997, 339–373. [Google Scholar]
- Ročková, V.; George, E.I. EMVS: The EM approach to Bayesian variable selection. J. Am. Stat. Assoc. 2014, 109, 828–846. [Google Scholar] [CrossRef]
- Kyung, M.; Gill, J.; Ghosh, M.; Casella, G. Penalized regression, standard errors and Bayesian lassos. Bayesian Anal. 2010, 5, 369–411. [Google Scholar] [CrossRef]
- Ročková, V.; George, E.I. The spike-and-slab lasso. J. Am. Stat. Assoc. 2018, 113, 431–444. [Google Scholar] [CrossRef]
- Zhang, L.; Baladandayuthapani, V.; Mallick, B.K.; Manyam, G.C.; Thompson, P.A.; Bondy, M.L.; Do, K.A. Bayesian hierarchical structured variable selection methods with application to molecular inversion probe studies in breast cancer. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2014, 63, 595–620. [Google Scholar] [CrossRef] [Green Version]
- Tang, Z.; Shen, Y.; Zhang, X.; Yi, N. The spike-and-slab lasso generalized linear models for prediction and associated genes detection. Genetics 2017, 205, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Huang, X.; Gan, J.; Karmaus, W.; Sabo-Attwood, T. A Two-Component $ G $-Prior for Variable Selection. Bayesian Anal. 2016, 11, 353–380. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, Y.; Du, Y.; Zhao, Y.; Ren, J.; Ma, S.; Wu, C. Identification of prognostic genes and pathways in lung adenocarcinoma using a Bayesian approach. Cancer Inform. 2017, 1, 7. [Google Scholar]
- Stingo, F.C.; Chen, Y.A.; Tadesse, M.G.; Vannucci, M. Incorporating biological information into linear models: A Bayesian approach to the selection of pathways and genes. Ann. Appl. Stat. 2011, 5. [Google Scholar] [CrossRef] [PubMed]
- Peterson, C.; Stingo, F.C.; Vannucci, M. Bayesian inference of multiple Gaussian graphical models. J. Am. Stat. Assoc. 2015, 110, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Huang, J.; Ma, S.; Li, H.; Zhang, C.-H. The sparse Laplacian shrinkage estimator for high-dimensional regression. Ann. Stat. 2011, 39, 2021. [Google Scholar] [CrossRef]
- Ren, J.; He, T.; Li, Y.; Liu, S.; Du, Y.; Jiang, Y.; Wu, C. Network-based regularization for high dimensional SNP data in the case—Control study of Type 2 diabetes. BMC Genet. 2017, 18, 44. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Du, Y.; Li, S.; Ma, S.; Jiang, Y.; Wu, C. Robust network based regularization and variable selection for high dimensional genomics data in cancer prognosis. Genet. Epidemiol. 2019. (In press) [Google Scholar]
- Hotelling, H. Relations between two sets of variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Wold, H. Partial least squares. Encycl. Stat. Sci. 2004, 9. [Google Scholar] [CrossRef]
- Witten, D.M.; Tibshirani, R. A framework for feature selection in clustering. J. Am. Stat. Assoc. 2010, 105, 713–726. [Google Scholar] [CrossRef] [PubMed]
- Lê Cao, K.-A.; Rossouw, D.; Robert-Granié, C.; Besse, P. A sparse PLS for variable selection when integrating omics data. Stat. Appl. Genet. Mol. Biol. 2008, 7. [Google Scholar] [CrossRef] [PubMed]
- Kristensen, V.N.; Lingjaerde, O.C.; Russnes, H.G.; Vollan, H.K.; Frigessi, A.; Borresen-Dale, A.L. Principles and methods of integrative genomic analyses in cancer. Nat. Rev. Cancer 2014, 14, 299–313. [Google Scholar] [CrossRef]
- Zhao, Q.; Shi, X.; Xie, Y.; Huang, J.; Shia, B.; Ma, S. Combining multidimensional genomic measurements for predicting cancer prognosis: Observations from TCGA. Brief. Bioinform. 2014, 16, 291–303. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, X.; Zhao, Q.; Krauthammer, M.; Rothberg, B.E.G.; Ma, S. Integrated analysis of multidimensional omics data on cutaneous melanoma prognosis. Genomics 2016, 107, 223–230. [Google Scholar] [CrossRef] [Green Version]
- Mankoo, P.K.; Shen, R.; Schultz, N.; Levine, D.A.; Sander, C. Time to Recurrence and Survival in Serous Ovarian Tumors Predicted from Integrated Genomic Profiles. PLoS ONE 2011, 6, e24709. [Google Scholar] [CrossRef]
- Park, M.Y.; Hastie, T. L1-regularization path algorithm for generalized linear models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2007, 69, 659–677. [Google Scholar] [CrossRef]
- Liu, J.; Zhong, W.; Li, R. A selective overview of feature screening for ultrahigh-dimensional data. Sci. China Math. 2015, 58, 1–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, R.; Lu, W.; Ma, S.; Jessie Jeng, X. Censored rank independence screening for high-dimensional survival data. Biometrika 2014, 101, 799–814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, G.; Yu, Y.; Li, R.; Buu, A. Feature screening in ultrahigh dimensional Cox’s model. Stat. Sin. 2016, 26, 881. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Kuster, B.; Culhane, A.C.; Gholami, A.M. A multivariate approach to the integration of multi-omics datasets. BMC Bioinform. 2014, 15, 162. [Google Scholar] [CrossRef] [PubMed]
- Witten, D.M.; Tibshirani, R.; Hastie, T. A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics 2009, 10, 515–534. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gross, S.M.; Tibshirani, R. Collaborative regression. Biostatistics 2014, 16, 326–338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, C.; Liu, J.; Dey, D.K.; Chen, K. Canonical variate regression. Biostatistics 2016, 17, 468–483. [Google Scholar] [CrossRef] [Green Version]
- Lê Cao, K.-A.; Martin, P.G.; Robert-Granié, C.; Besse, P. Sparse canonical methods for biological data integration: Application to a cross-platform study. BMC Bioinform. 2009, 10, 34. [Google Scholar] [CrossRef] [PubMed]
- Dolédec, S.; Chessel, D. Co-inertia analysis: An alternative method for studying species—Environment relationships. Freshw. Biol. 1994, 31, 277–294. [Google Scholar] [CrossRef]
- Min, E.J.; Safo, S.E.; Long, Q. Penalized Co-Inertia Analysis with Applications to-Omics Data. Bioinformatics 2018. [Google Scholar] [CrossRef] [PubMed]
- Shen, R.; Olshen, A.B.; Ladanyi, M. Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 2009, 25, 2906–2912. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, R.; Wang, S.; Mo, Q. Sparse integrative clustering of multiple omics data sets. Ann. Appl. Stat. 2013, 7, 269. [Google Scholar] [CrossRef] [PubMed]
- Mo, Q.; Wang, S.; Seshan, V.E.; Olshen, A.B.; Schultz, N.; Sander, C.; Powers, R.S.; Ladanyi, M.; Shen, R. Pattern discovery and cancer gene identification in integrated cancer genomic data. Proc. Natl. Acad. Sci. USA 2013, 110, 4245–4250. [Google Scholar] [CrossRef] [PubMed]
- Mo, Q.; Shen, R.; Guo, C.; Vannucci, M.; Chan, K.S.; Hilsenbeck, S.G. A fully Bayesian latent variable model for integrative clustering analysis of multi-type omics data. Biostatistics 2017, 19, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Helm, D.; Frejno, M.; Kuster, B. moCluster: Identifying Joint Patterns Across Multiple Omics Data Sets. J. Proteome Res. 2016, 15, 755–765. [Google Scholar] [CrossRef] [PubMed]
- Ray, P.; Zheng, L.; Lucas, J.; Carin, L.J.B. Bayesian joint analysis of heterogeneous genomics data. Bioinformatics 2014, 30, 1370–1376. [Google Scholar] [CrossRef] [Green Version]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Ghahramani, Z.; Griffiths, T.L. Infinite latent feature models and the Indian buffet process. In Advances in Neural Information Processing Systems; 2006; pp. 475–482. [Google Scholar]
- Paisley, J.; Carin, L. Nonparametric factor analysis with beta process priors. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 777–784. [Google Scholar]
- Thibaux, R.; Jordan, M.I. Hierarchical beta processes and the Indian buffet process. In Proceedings of the Artificial Intelligence and Statistics, San Juan, Puerto Rico, 21–24 March 2007; pp. 564–571. [Google Scholar]
- Hellton, K.H.; Thoresen, M. Integrative clustering of high-dimensional data with joint and individual clusters. Biostatistics 2016, 17, 537–548. [Google Scholar] [CrossRef] [Green Version]
- Lock, E.F.; Dunson, D.B. Bayesian consensus clustering. Bioinformatics 2013, 29, 2610–2616. [Google Scholar] [CrossRef] [Green Version]
- Tadesse, M.G.; Sha, N.; Vannucci, M. Bayesian variable selection in clustering high-dimensional data. J. Am. Stat. Assoc. 2005, 100, 602–617. [Google Scholar] [CrossRef]
- Bouveyron, C.; Brunet-Saumard, C. Model-based clustering of high-dimensional data: A review. Comput. Stat. Data Anal. 2014, 71, 52–78. [Google Scholar] [CrossRef] [Green Version]
- Kirk, P.; Griffin, J.E.; Savage, R.S.; Ghahramani, Z.; Wild, D.L. Bayesian correlated clustering to integrate multiple datasets. Bioinformatics 2012, 28, 3290–3297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kettenring, J.R. The practice of cluster analysis. J. Classif. 2006, 23, 3–30. [Google Scholar] [CrossRef]
- Kormaksson, M.; Booth, J.G.; Figueroa, M.E.; Melnick, A. Integrative model-based clustering of microarray methylation and expression data. Ann. Appl. Stat. 2012, 1327–1347. [Google Scholar] [CrossRef]
- Wang, W.; Baladandayuthapani, V.; Morris, J.S.; Broom, B.M.; Manyam, G.; Do, K.A. iBAG: Integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics 2013, 29, 149–159. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Zhao, Q.; Zhao, H.; Ma, S. Integrating multidimensional omics data for cancer outcome. Biostatistics 2016, 17, 605–618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chai, H.; Shi, X.; Zhang, Q.; Zhao, Q.; Huang, Y.; Ma, S. Analysis of cancer gene expression data with an assisted robust marker identification approach. Genet. Epidemiol. 2017, 41, 779–789. [Google Scholar] [CrossRef]
- Peng, J.; Zhu, J.; Bergamaschi, A.; Han, W.; Noh, D.-Y.; Pollack, J.R.; Wang, P. Regularized multivariate regression for identifying master predictors with application to integrative genomics study of breast cancer. Ann. Appl. Stat. 2010, 4, 53. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Q.; Jiang, Y.; Ma, S. Robust network-based analysis of the associations between (epi) genetic measurements. J. Mult. Anal. 2018, 168, 119–130. [Google Scholar] [CrossRef]
- Teran Hidalgo, S.J.; Wu, M.; Ma, S. Assisted clustering of gene expression data using ANCut. BMC Genom. 2017, 18, 623. [Google Scholar] [CrossRef] [PubMed]
- Teran Hidalgo, S.J.; Ma, S. Clustering multilayer omics data using MuNCut. BMC Genom. 2018, 19, 198. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Oesterreich, S.; Kim, S.; Park, Y.; Tseng, G.C. Integrative clustering of multi-level omics data for disease subtype discovery using sequential double regularization. Biostatistics 2017, 18, 165–179. [Google Scholar] [CrossRef] [PubMed]
- Huo, Z.; Tseng, G. Integrative sparse K-means with overlapping group lasso in genomic applications for disease subtype discovery. Ann. Appl. Stat. 2017, 11, 1011. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Li, Y.; Bie, R.; Teran Hidalgo, S.J.; Qin, Y.; Wu, M.; Ma, S. Assisted gene expression-based clustering with AWNCut. Stat. Med. 2018, 37, 4386–4403. [Google Scholar] [CrossRef] [PubMed]
- Teran Hidalgo, S.J.; Zhu, T.; Wu, M.; Ma, S. Overlapping clustering of gene expression data using penalized weighted normalized cut. Genet. Epidemiol. 2018, 42, 796–811. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Speicher, N.K.; Pfeifer, N. Integrating different data types by regularized unsupervised multiple kernel learning with application to cancer subtype discovery. Bioinformatics 2015, 31, i268–i275. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, C.-C.; Li, W.; Shen, H.; Laird, P.W.; Zhou, X.J. Discovery of multi-dimensional modules by integrative analysis of cancer genomic data. Nucl. Acids Res. 2012, 40, 9379–9391. [Google Scholar] [CrossRef] [Green Version]
- Weitschek, E.; Felici, G.; Bertolazzi, P. MALA: A Microarray Clustering and Classification Software. In Proceedings of the 23rd International Workshop on Database and Expert Systems Applications, 3–7 September 2012; pp. 201–205. [Google Scholar]
- Wang, B.; Mezlini, A.M.; Demir, F.; Fiume, M.; Tu, Z.; Brudno, M.; Haibe-Kains, B.; Goldenberg, A. Similarity network fusion for aggregating data types on a genomic scale. Nat. Methods 2014, 11, 333. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Wang, D.; Zhang, M.Q.; Gu, J. Fast dimension reduction and integrative clustering of multi-omics data using low-rank approximation: Application to cancer molecular classification. BMC Genom. 2015, 16, 1022. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Tagett, R.; Diaz, D.; Draghici, S. A novel approach for data integration and disease subtyping. Genome Res. 2017, 27, 2025–2039. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Jiang, J.; Wang, W.; Zhou, Z.-H.; Tu, Z. Unsupervised metric fusion by cross diffusion. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2997–3004. [Google Scholar]
- Liu, J.; Wang, C.; Gao, J.; Han, J. Multi-view clustering via joint nonnegative matrix factorization. In Proceedings of the 2013 SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 252–260. [Google Scholar]
- Kalayeh, M.M.; Idrees, H.; Shah, M. NMF-KNN: Image annotation using weighted multi-view non-negative matrix factorization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 184–191. [Google Scholar]
- Huang, J.; Nie, F.; Huang, H.; Ding, C. Robust manifold nonnegative matrix factorization. ACM Trans. Knowl. Discov. Data (TKDD) 2014, 8, 11. [Google Scholar] [CrossRef]
- Zhang, X.; Zong, L.; Liu, X.; Yu, H. Constrained NMF-Based Multi-View Clustering on Unmapped Data. In Proceedings of the AAAI, Austin, TX, USA, 25–30 January 2015; pp. 3174–3180. [Google Scholar]
- Li, S.-Y.; Jiang, Y.; Zhou, Z.-H. Partial multi-view clustering. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; pp. 1968–1974. [Google Scholar]
- De Tayrac, M.; Lê, S.; Aubry, M.; Mosser, J.; Husson, F. Simultaneous analysis of distinct Omics data sets with integration of biological knowledge: Multiple Factor Analysis approach. BMC Genom. 2009, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Hutter, C.M.; Mechanic, L.E.; Chatterjee, N.; Kraft, P.; Gillanders, E.M.; Tank, N.G.E.T. Gene-environment interactions in cancer epidemiology: A National Cancer Institute Think Tank report. Genet. Epidemiol. 2013, 37, 643–657. [Google Scholar] [CrossRef] [PubMed]
- Hunter, D.J. Gene-environment interactions in human diseases. Nat. Rev. Genet. 2005, 6, 287. [Google Scholar] [CrossRef]
- Wu, C.; Cui, Y. A novel method for identifying nonlinear gene—Environment interactions in case–control association studies. Hum. Genet. 2013, 132, 1413–1425. [Google Scholar] [CrossRef]
- Wu, C.; Cui, Y. Boosting signals in gene-based association studies via efficient SNP selection. Brief. Bioinform. 2013, 15, 279–291. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Li, S.; Cui, Y. Genetic association studies: An information content perspective. Curr. Genom. 2012, 13, 566–573. [Google Scholar] [CrossRef]
- Schaid, D.J.; Sinnwell, J.P.; Jenkins, G.D.; McDonnell, S.K.; Ingle, J.N.; Kubo, M.; Goss, P.E.; Costantino, J.P.; Wickerham, D.L.; Weinshilboum, R.M. Using the gene ontology to scan multilevel gene sets for associations in genome wide association studies. Genet. Epidemiol. 2012, 36, 3–16. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Shi, X.; Cui, Y.; Ma, S. A penalized robust semiparametric approach for gene–environment interactions. Statist. Med. 2015, 34, 4016–4030. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Cui, Y.; Ma, S. Integrative analysis of gene–environment interactions under a multi-response partially linear varying coefficient model. Stat. Med. 2014, 33, 4988–4998. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Jiang, Y.; Ren, J.; Cui, Y.; Ma, S. Dissecting gene—Environment interactions: A penalized robust approach accounting for hierarchical structures. Stat. Med. 2018, 37, 437–456. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Zhong, P.-S.; Cui, Y. Additive varying-coefficient model for nonlinear gene-environment interactions. Stat. Appl. Genet. Mol. Biol. 2018, 17. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Zang, Y.; Zhang, S.; Huang, J.; Ma, S. Accommodating missingness in environmental measurements in gene-environment interaction analysis. Genet. Epidemiol. 2017, 41, 523–554. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Ma, S. Robust genetic interaction analysis. Brief. Bioinform. 2018, 1–14. [Google Scholar] [CrossRef]
- Sagonas, C.; Panagakis, Y.; Leidinger, A.; Zafeiriou, S. Robust joint and individual variance explained. In Proceedings of the IEEE International Conference on Computer Vision & Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; p. 6. [Google Scholar]
- Cavill, R.; Jennen, D.; Kleinjans, J.; Briedé, J.J. Transcriptomic and metabolomic data integration. Brief. Bioinform. 2015, 17, 891–901. [Google Scholar] [CrossRef]
- Cambiaghi, A.; Ferrario, M.; Masseroli, M. Analysis of metabolomic data: Tools, current strategies and future challenges for omics data integration. Brief. Bioinform. 2017, 18, 498–510. [Google Scholar] [CrossRef]
- Wanichthanarak, K.; Fahrmann, J.F.; Grapov, D. Genomic, proteomic and metabolomic data integration strategies. Biomark. Insights 2015, 10, S29511. [Google Scholar] [CrossRef]
- Nathoo, F.S.; Kong, L.; Zhu, H. A Review of statistical methods in imaging genetics. arXiv, 2017; arXiv:1707.07332. [Google Scholar]
- Liu, J.; Calhoun, V.D. A review of multivariate analyses in imaging genetics. Front. Neuroinform. 2014, 8, 29. [Google Scholar] [CrossRef] [PubMed]
| Reference | Type | Description |
|---|---|---|
| Richardson et al. [10] | Comprehensive | Review statistical methods for both vertical integration and horizontal integration. Introduce different types of genomic data (DNA, Epigenetic marks, RNA and protein), genomics data resources and annotation databases. |
| Bersanelli et al. [11] | Comprehensive | Review mathematical and methodological aspects of data integration methods, with the following four categories (1) network-free non-Bayesian, (2) network-free Bayesian, (3) network-based non-Bayesian and (4) network-based Bayesian. |
| Hasin et al. [12] | Comprehensive | Different from the studies with emphasis on statistical integration methods, this review focuses on biological perspectives, i.e., the genome first approach, the phenotype first approach and the environment first approach. |
| Huang et al. [13] | Comprehensive | This review summarizes published integration studies, especially the matrix factorization methods, Bayesian methods, network based methods and multiple kernel learning methods. |
| Li et al. [14] | Comprehensive | Review the integration of multi-view biological data from the machine learning perspective. Reviewed methods include Bayesian models and networks, ensemble learning, multi-modal deep learning and multi-modal matrix/tensor factorization. |
| Pucher et al. [15] | Comprehensive (with case study) | Review three methods, sCCA, NMF and MALA and assess the performance on pairwise integration of omics data. Examine the consistence among results identified by different methods. |
| Yu et al. [16] | Comprehensive | This study first summarizes data resources (genomics, transcriptome, epigenomics, metagenomics and interactome) and data structure (vector, matrix, tensor and high-order cube). Methods are reviewed mainly following the bottom-up integration and top-down integration. |
| Zeng et al. [17] | Comprehensive | The statistical learning methods are overviewed from the following aspects: exploratory analysis, clustering methods, network learning, regression based learning and biological knowledge enrichment learning. |
| Rappoport et al. [18] | Clustering (with case study) | Review studies conducting joint clustering of multi-level omics data. Comprehensively assess the performance of nine clustering methods on ten types of cancer from TCGA. |
| Tini et al. [19] | Unsupervised integration (with case study) | Evaluation of five unsupervised integration methods on BXD, Platelet, BRCA data sets, as well as simulated data. Investigate the influences of parameter tuning, complexity of integration (noise level) and feature selection on the performance of integrative analysis. |
| Chalise et al. [20] | Clustering (with case study) | Investigate the performance of seven clustering methods on single-level data and three clustering methods on multi-level data. |
| Wang et al. [21] | Clustering | Discuss the clustering methods in three major groups: direct integrative clustering, clustering of clusters and regulatory integrative clustering. This study is among the first to review integrative clustering with prior biological information such as regulatory structure, pathway and network information. |
| Ickstadt et al. [22] | Bayesian | Review integrative Bayesian methods for gene prioritization, subgroup identification via Bayesian clustering analysis, omics feature selection and network learning. |
| Meng et al. [23] | Dimension Reduction (with case study) | Review dimension reduction methods for integration and examine visualization and interpretation of simultaneous exploratory analyses of multiple data sets based on dimension reduction. |
| Rendleman et al. [24] | Proteogenomics | This study is not another review on the statistical integrative methods. Instead, it discusses integration with an emphasis on the mass spectrometry-based proteomics data. |
| Yan et al. [25] | Graph- and kernel-based (with case study) | Graph- and kernel- based integrative methods have been systematically reviewed and compared using GAW 19 data and TCGA Ovarian and Breast cancer data in this study. Kernel-based methods are generally more computationally expensive. They lead to more complicated but better models than those obtained from the graph-based integrative methods. |
| Wu et al. [present review] | Variable Selection based | This review investigates existing multi-omics integrating studies from the variable selection point of view. This new perspective sheds fresh insight on integrative analysis. |
| Method | Formulation | Data | Package |
|---|---|---|---|
| Sparse CCA [66] | PMD + L1 penalty PMD + fused LASSO | comparative genomic hybridization (CGH) data | PMA |
| Sparse mCCA [26] | CCA criteria + LAASO/fused LASSO | DLBCL copy number variation data | PMA |
| Sparse sCCA [26] | Modified CCA criteria + LASSO/fused LASSO | DLBCL data with gene expression and copy number variation data | PMA |
| Sparse PLS [56] | Approximate loss (F norm) + LASSO | Liver toxicity data, arabidopsis data, wine yeast data | mixOmics |
| CollRe [67] | Multiple least square loss + L1 penalty/ridge/fused LASSO | Neoadjuvant breast cancer data with gene expression and CNV | N/A |
| PCIA [71] | Co-inertia-based loss + LASSO/network penalty | NCI-60 cancer cell lines gene expression and protein abundance data | PCIA |
| iCluster [72] | Complete data loglikelihood + L1 penalty | Lung cancer gene expression and copy number data | iCluster |
| iCluster [73] | Complete data loglikelihood + L1 penalty/fused LASSO/Elastic Net | Breast cancer DNA methylation and gene expression data | iCluster |
| iCluster+ [74] | Complete data loglikelihood + L1 penalty | (1) CCLE data with copy number variation, gene expression and mutation (2) TCGA CRC data with DNA copy number promoter methylation and mRNA expression | iClusterPlus |
| JIVE [27] | Approximation loss + L1 penalty | TCGA GBM data with gene expression and miRNA | r.JIVE |
| LRM [90] | Approximation Loss (F norm) + L1 penalty | TCGA | Github * |
| ARMI [91] | Multiple LAD loss + L1 penalty | (1) TCGA SKCM gene expression and CNV (2) TCGA LUAD gene expression and CNV | Github * |
| remMap [92] | Least square loss + L1 penalty + L2 penalty | Breast cancer with RNA transcript level and DNA copy numbers | remMap |
| Robust network [93] | Semiparametric LAD loss + MCP + group MCP + network penalty | TCGA cutaneous melanoma gene expression and CNV | Github * |
| GST-iCluster [96] | Complete data loglikelihood + L1 penalty + approximated sparse overlapping group LASSO | (1) TCGA breast cancer mRNA, methylation and CNV (2) TCGA breast cancer mRNA and miRNA | GSTiCluster |
| IS K-means [97] | BCSS + L1 penalty | (1) TCGA breast cancer mRNA, CNV and methylation (2) METABRIC breast cancer mRNA and CNV (3) Three leukemia transcriptomic datasets | IS-Kmeans |
| Reference | Methods Compared | Dataset | Major Conclusion |
|---|---|---|---|
| Rappoport et al. [18] | K-means; Spectral clustering; LRAcluster [108] PINS [109] SNF [107,110] rMKL-LPP [104] MCCA [26] MultiNMF [105,111,112,113,114,115] iClusterBayes [75] | TCGA Cancer Data: AML, BIC, COAD, GBM, KIRC, LIHC, LUSC, SKCM, OV and SARC | MCCA has the best prediction performance under prognosis. rMKL-LPP outperforms the rest methods in terms of the largest number of significantly enriched clinical labels in clusters. Multi-omics integration is not always superior over single-level analysis. |
| Tini et al. [19] | MCCA [26] JIVE [27] MCIA [65] MFA [116] SNF [107] | Murine liver (BXD), Platelet reactivity and breast cancer (BRCA). | For integrating more than two omics data, MFA performs best on simulated data. Integrating more omics data leads to noises and SNF is the most robust method. |
| Pucher et al. [25] | sCCA [26] NMF [105] MALA [106] | The LUAD, the KIRC and the COAD data sets | For pairwise integration of omics data, sCCA has the best identification performance and is most computationally efficient. The consistency among results identified from different methods is low. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Zhou, F.; Ren, J.; Li, X.; Jiang, Y.; Ma, S. A Selective Review of Multi-Level Omics Data Integration Using Variable Selection. High-Throughput 2019, 8, 4. https://doi.org/10.3390/ht8010004
Wu C, Zhou F, Ren J, Li X, Jiang Y, Ma S. A Selective Review of Multi-Level Omics Data Integration Using Variable Selection. High-Throughput. 2019; 8(1):4. https://doi.org/10.3390/ht8010004
Chicago/Turabian StyleWu, Cen, Fei Zhou, Jie Ren, Xiaoxi Li, Yu Jiang, and Shuangge Ma. 2019. "A Selective Review of Multi-Level Omics Data Integration Using Variable Selection" High-Throughput 8, no. 1: 4. https://doi.org/10.3390/ht8010004
APA StyleWu, C., Zhou, F., Ren, J., Li, X., Jiang, Y., & Ma, S. (2019). A Selective Review of Multi-Level Omics Data Integration Using Variable Selection. High-Throughput, 8(1), 4. https://doi.org/10.3390/ht8010004






