Linear and Non-Linear Optimal Control Methods to Determine the Best Chemotherapy Schedule for Most Effectively Inhibiting Tumor Growth
Abstract
1. Introduction
2. Materials and Methods
2.1. LQR Optimal Control Background
2.2. SDRE Non-Linear Optimal Control Background
2.3. Anticancer Treatment Evaluation Metrics
3. Results
3.1. The Optimal Control Approach Applied in Tumor Growth Inhibition Optimal Chemotherapy Determination
3.2. Linear Optimal Control for Efficient Tumor Growth Eradication
ARX and LQR-Based Gemcitabine Dosage Optimization for Periodic Tumor Treatment Scenarios
3.3. Non-Linear Optimal Control for Efficient Tumor Growth Eradication
- : represents the proliferating portion of tumor cells, which actively contribute to the tumor’s growth. This state reflects the cells that remain unaffected by the drug’s cytotoxic effects at time .
- : represent the tumor’s cells in progressive stages of damage due to the chemotherapy drug. These compartments capture the delayed effect of the drug, where damaged cells are passing through increasingly severe states of damage, before eventually dying.
3.3.1. Optimized Chemotherapy Dosages in Periodic Tumor Treatment Scenarios Using SDRE Optimal Control and the Introduced Here “Augmented” Simeoni et al.’s TGI Non-Linear State-Space Dynamic Model
3.3.2. Optimized Chemotherapy Dosages in Intermittent Tumor Treatment Cases Using the Introduced Here “Augmented” Simeoni et al.’s TGI Non-Linear State-Space Dynamic Model and SDRE Optimal Control
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ledzewicz, U.; Schaettler, H. Optimizing Chemotherapeutic Anti-cancer Treatment and the Tumor Microenvironment: An Analysis of Mathematical Models: Quantitative Modeling and Simulations. In Systems Biology of Tumor Microenvironment; Advances in Experimental Medicine and Biology; Springer: London, UK, 2016; pp. 209–223. [Google Scholar] [CrossRef]
- Bahrami, K.; Kim, M. Optimal control of multiplicative control systems arising from cancer therapy. IEEE Trans. Autom. Control 1975, 20, 537–542. [Google Scholar] [CrossRef]
- Swan, G.W.; Vincent, T.L. Optimal control analysis in the chemotherapy of IgG multiple myeloma. Bull. Math. Biol. 1977, 39, 317–337. [Google Scholar] [CrossRef]
- De Pillis, L.G.; Radunskaya, A. A Mathematical Tumor Model with Immune Resistance and Drug Therapy: An Optimal Control Approach. Comput. Math. Methods Med. 2001, 3, 79–100. [Google Scholar] [CrossRef]
- De Pillis, L.G.; Radunskaya, A. The dynamics of an optimally controlled tumor model: A case study. Math. Comput. Model. 2003, 37, 1221–1244. [Google Scholar] [CrossRef]
- De Pillis, L.G.; Eladdadi, A.; Radunskaya, A. Optimal control of mixed immunotherapy and chemotherapy of tumors. J. Biol. Syst. 2008, 16, 51. [Google Scholar] [CrossRef]
- De Pillis, L.G.; Eladdadi, A.; Radunskaya, A.E. Modeling cancer-immune responses to therapy. J. Pharmacokinet. Pharmacodyn. 2014, 41, 461–478. [Google Scholar] [CrossRef]
- Rihan, F.A.; Lakshmanan, S.; Maurer, H. Optimal control of tumour-immune model with time-delay and immuno-chemotherapy. Appl. Math. Comput. 2019, 353, 147–165. [Google Scholar] [CrossRef]
- Swan, G.W. Optimal control in some cancer chemotherapy problems. Int. J. Syst. Sci. 1980, 11, 223–237. [Google Scholar] [CrossRef]
- Swan, G.W. General Applications of Optimal Control Theory in Cancer Chemotherapy. Math. Med. Biol. 1988, 5, 303–316. [Google Scholar] [CrossRef]
- Murray, J.M. Optimal control for a cancer chemotherapy problem with general growth and loss functions. Math. Biosci. 1990, 98, 273–287. [Google Scholar] [CrossRef]
- Swierniak, A.; Polanski, A.; Kimmel, M. Optimal control problems arising in cell-cycle-specific cancer chemotherapy. Cell Prolif. 1996, 29, 117–139. [Google Scholar] [CrossRef] [PubMed]
- Panetta, J.C.; Fister, K.R. Optimal Control Applied to Competing Chemotherapeutic Cell-Kill Strategies. SIAM J. Appl. Math. 2003, 63, 1954–1971. [Google Scholar] [CrossRef]
- Castiglione, F.; Piccoli, B. Cancer immunotherapy, mathematical modeling and optimal control. J. Theor. Biol. 2007, 247, 723–732. [Google Scholar] [CrossRef] [PubMed]
- Itik, M.; Salamci, M.U.; Banks, S.P. Optimal control of drug therapy in cancer treatment. Nonlinear Anal. Theory Methods Appl. 2009, 71, e1473–e1486. [Google Scholar] [CrossRef]
- Moradi, H.; Vossoughi, G.; Salarieh, H. Optimal robust control of drug delivery in cancer chemotherapy: A comparison between three control approaches. Comput. Methods Programs Biomed. 2013, 112, 69–83. [Google Scholar] [CrossRef]
- Ghaffari, A.; Nazari, M.; Arab, F. Optimal Finite Cancer Treatment Duration by Using Mixed Vaccine Therapy and Chemotherapy: State Dependent Riccati Equation Control. J. Appl. Math. 2014, 2014, 363109. [Google Scholar] [CrossRef]
- Kim, K.S.; Cho, G.; Jung, I.H. Optimal treatment strategy for a tumor model under immune suppression. Comput. Math. Methods Med. 2014, 2014, 206287. [Google Scholar] [CrossRef]
- Hadjiandreou, M.M.; Mitsis, G.D. Mathematical Modeling of Tumor Growth, Drug-Resistance, Toxicity, and Optimal Therapy Design. IEEE Trans. Biomed. Eng. 2014, 61, 415–425. [Google Scholar] [CrossRef]
- Schättler, H.; Ledzewicz, U. Optimal Control of Mathematical Models for Antiangiogenic Treatments. In Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2015; pp. 171–235. [Google Scholar] [CrossRef]
- Wang, S.; Schattler, H. Optimal control of a mathematical model for cancer chemotherapy under tumor heterogeneity. Math. Biosci. Eng. 2016, 13, 1223–1240. [Google Scholar] [CrossRef]
- Moore, H. How to mathematically optimize drug regimens using optimal control. J. Pharmacokinet. Pharmacodyn. 2018, 45, 127–137. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Assiri, T.; Atangana, A. Optimal control for cancer treatment mathematical model using Atangana–Baleanu–Caputo fractional derivative. Adv. Differ. Equ. 2020, 2020, 334. [Google Scholar] [CrossRef]
- Jarrett, A.M.; Faghihi, D.; Hormuth, D.A.; Lima, E.A.; Virostko, J.; Biros, G.; Patt, D.; Yankeelov, T.E. Optimal Control Theory for Personalized Therapeutic Regimens in Oncology: Background, History, Challenges, and Opportunities. J. Clin. Med. 2020, 9, 1314. [Google Scholar] [CrossRef] [PubMed]
- Angaroni, F.; Graudenzi, A.; Rossignolo, M.; Maspero, D.; Calarco, T.; Piazza, R.; Montangero, S.; Antoniotti, M. An Optimal Control Framework for the Automated Design of Personalized Cancer Treatments. Front. Bioeng. Biotechnol. 2020, 8, 523. [Google Scholar] [CrossRef] [PubMed]
- Lecca, P. Control Theory and Cancer Chemotherapy: How They Interact. Front. Bioeng. Biotechnol. 2021, 8, 621269. [Google Scholar] [CrossRef]
- Bodzioch, M.; Bajger, P.; Foryś, U. Angiogenesis and chemotherapy resistance: Optimizing chemotherapy scheduling using mathematical modeling. J. Cancer Res. Clin. Oncol. 2021, 147, 2281–2299. [Google Scholar] [CrossRef]
- Haddad, G.; Kebir, A.; Raissi, N.; Bouhali, A.; Miled, S.B. Optimal control model of tumor treatment in the context of cancer stem cell. Math. Biosci. Eng. 2022, 19, 4627–4642. [Google Scholar] [CrossRef]
- Mavromatakis, S.; Liliopoulos, S.G.; Stavrakakis, G.S. Determination of the pharmaceutical treatment-dosage for cancer patients using non-linear optimal control techniques. In Proceedings of the 2020 24th International Conference on Circuits, Systems, Communications and Computers (CSCC), Chania, Greece, 19–22 July 2020; pp. 106–111. [Google Scholar] [CrossRef]
- Mavromatakis, S.; Liliopoulos, S.G.; Stavrakakis, G.S. Optimized intermittent pharmaceutical treatment of cancer using non-linear optimal control techniques. WSEAS Trans. Biol. Biomed. 2020, 17, 67–75. [Google Scholar] [CrossRef]
- Liliopoulos, S.G.; Stavrakakis, G.S. Discrete ARMA model applied for tumor growth inhibition modeling and LQR-based chemotherapy optimization. WSEAS Trans. Biol. Biomed. 2021, 18, 141–145. [Google Scholar] [CrossRef]
- Simeoni, M.; Magni, P.; Cammia, C.; De Nicolao, G.; Croci, V.; Pesenti, E.; Germani, M.; Poggesi, I.; Rocchetti, M. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004, 64, 1094–1101. [Google Scholar] [CrossRef]
- Liliopoulos, S.G.; Stavrakakis, G.S.; Dimas, K.S. Advanced non-linear mathematical model for the prediction of the activity of a putative anticancer agent in human-to-mouse cancer xenografts. Anticancer Res. 2020, 40, 5181–5189. [Google Scholar] [CrossRef]
- Bilalis, P.; Skoulas, D.; Karatzas, A.; Marakis, J.; Stamogiannos, A.; Tsimblouli, C.; Sereti, E.; Stratikos, E.; Dimas, K.; Vlassopoulos, D.; et al. Self-healing pH- and enzyme stimuli-responsive hydrogels for targeted delivery of gemcitabine to treat pancreatic cancer. Biomacromolecules 2018, 19, 3840–3852. [Google Scholar] [CrossRef] [PubMed]
- Kalman, R.E.; Koepcke, R.W. Optimal Synthesis of Linear Sampling Control Systems Using Generalized Performance Indexes. J. Fluids Eng. 1958, 80, 1820–1826. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice-Hall: Boston, MA, USA, 2010. [Google Scholar]
- Pearson, D. Approximation Methods in Optimal Control I. Sub-optimal Control. Int. J. Electron. 1962, 13, 453–469. [Google Scholar] [CrossRef]
- Banks, H.T.; Lewis, B.M.; Tran, H.T. Nonlinear feedback controllers and compensators: A state-dependent Riccati equation approach. Comput. Optim. Appl. 2007, 37, 177–218. [Google Scholar] [CrossRef]
- Liliopoulos, S.G.; Stavrakakis, G.S.; Dimas, K.S. A Comparative Analysis of ARX and ANFIS Models for Tumor Growth Prediction Under Single and Multi-agent Chemotherapy. Anticancer Res. 2024, 44, 2425–2436. [Google Scholar] [CrossRef]
- Liliopoulos, S. Prediction of the Cancer Patients’ Response to Their Therapeutical Treatment with Non-Linear Forecasting Techniques. Master’s Thesis, School of Electrical and Computer Engineering, Technical University of Crete, Chania, Greece, 2023. [Google Scholar] [CrossRef]
- Raguz, S.; Yagüe, E. Resistance to chemotherapy: New treatments and novel insights into an old problem. Br. J. Cancer 2008, 99, 387–391. [Google Scholar] [CrossRef]
- Berry, S.R.; Cosby, R.; Asmis, T.; Chan, K.; Hammad, N.; Krzyzanowska, M.K. Continuous versus intermittent chemotherapy strategies in metastatic colorectal cancer: A systematic review and meta-analysis. Ann. Oncol. 2015, 26, 477–485. [Google Scholar] [CrossRef]
- Cazzaniga, M.E.; Biganzoli, L.; Cortesi, L.; De Placido, S.; Donadio, M.; Fabi, A.; Ferro, A.; Generali, D.; Lorusso, V.; Milani, A.; et al. Treating advanced breast cancer with metronomic chemotherapy: What is known, what is new and what is the future? OncoTargets Ther. 2019, 12, 2989–2997. [Google Scholar] [CrossRef]
- Wichmann, V.; Eigeliene, N.; Saarenheimo, J.; Jekunen, A. Recent clinical evidence on metronomic dosing in controlled clinical trials: A systematic literature review. Acta Oncol. 2020, 59, 775–785. [Google Scholar] [CrossRef]
- Cazzaniga, E.; Cordani, N.; Capici, S.; Cogliati, V.; Riva, F.; Cerrito, M.G. Metronomic Chemotherapy. Cancers 2021, 13, 2236. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emani-Naeini, A. Feedback Control of Dynamic Systems, 6th ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- The MathWorks Inc. MATLAB, 9.7.0.1190202 (R2019b); The MathWorks Inc.: Natick, MA, USA, 2022. [Google Scholar]
- Alfarouk, K.O.; Stock, C.; Taylor, S.; Walsh, M.; Muddathir, A.K.; Verduzco, D.; Bashir, A.H.; Mohammed, O.Y.; Elhassan, G.O.; Harguindey, S.; et al. Resistance to cancer chemotherapy: Failure in drug response from ADME to P-gp. Cancer Cell Int. 2015, 15, 71. [Google Scholar] [CrossRef] [PubMed]
- Onishi, T.; Sasaki, T.; Hoshina, A. Intermittent Chemotherapy Is a Treatment Choice for Advanced Urothelial Cancer. Oncology 2012, 83, 50–56. [Google Scholar] [CrossRef]
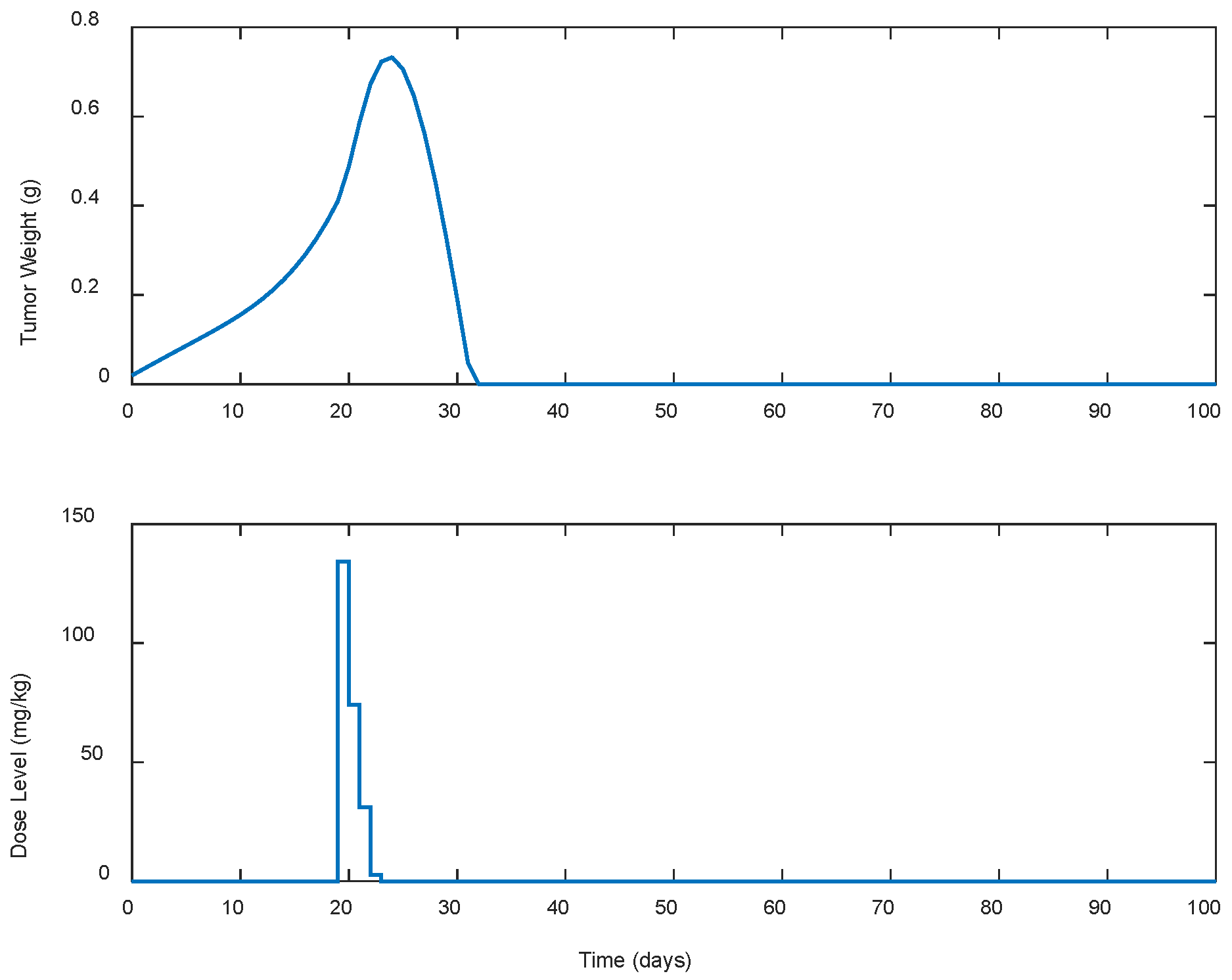
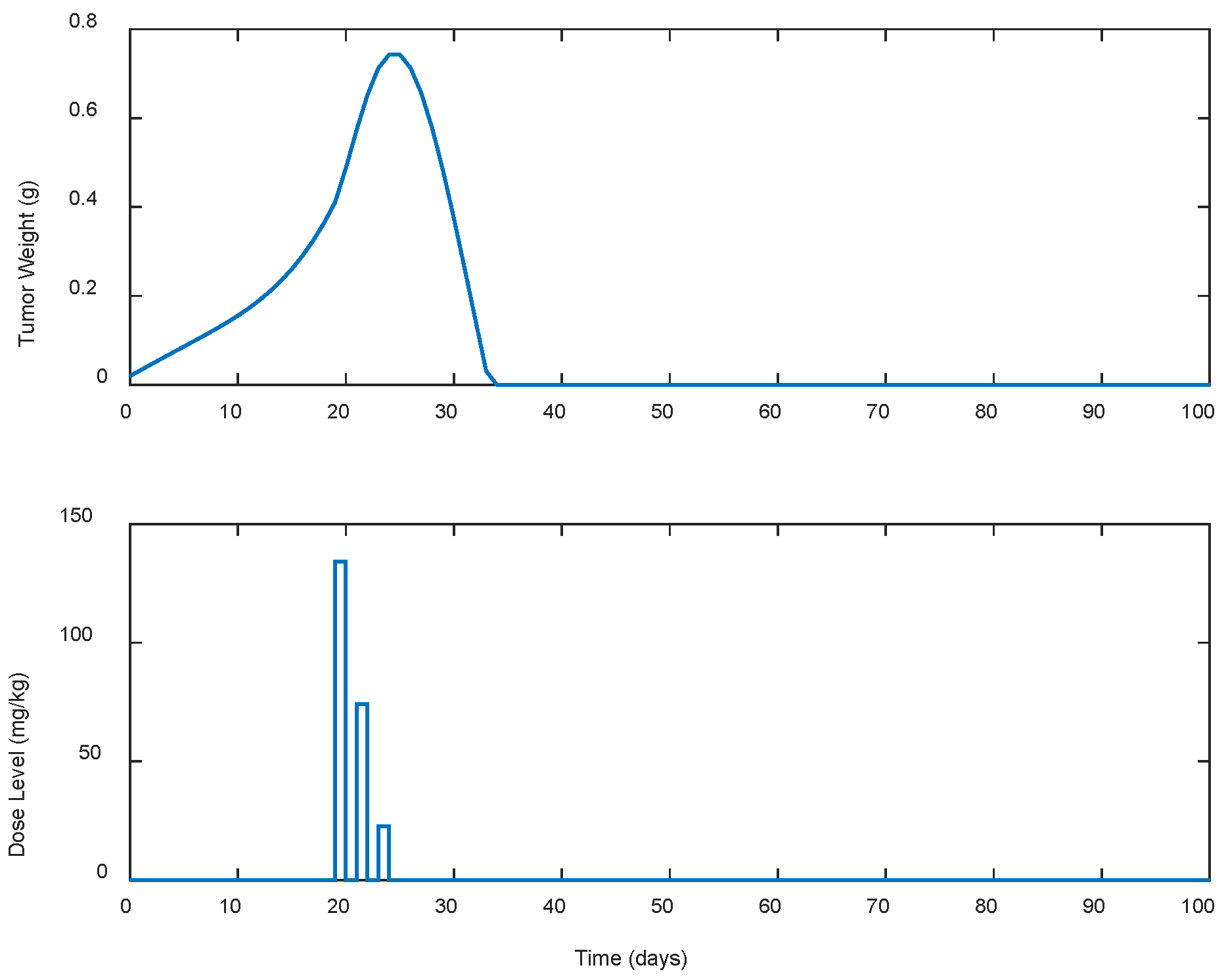
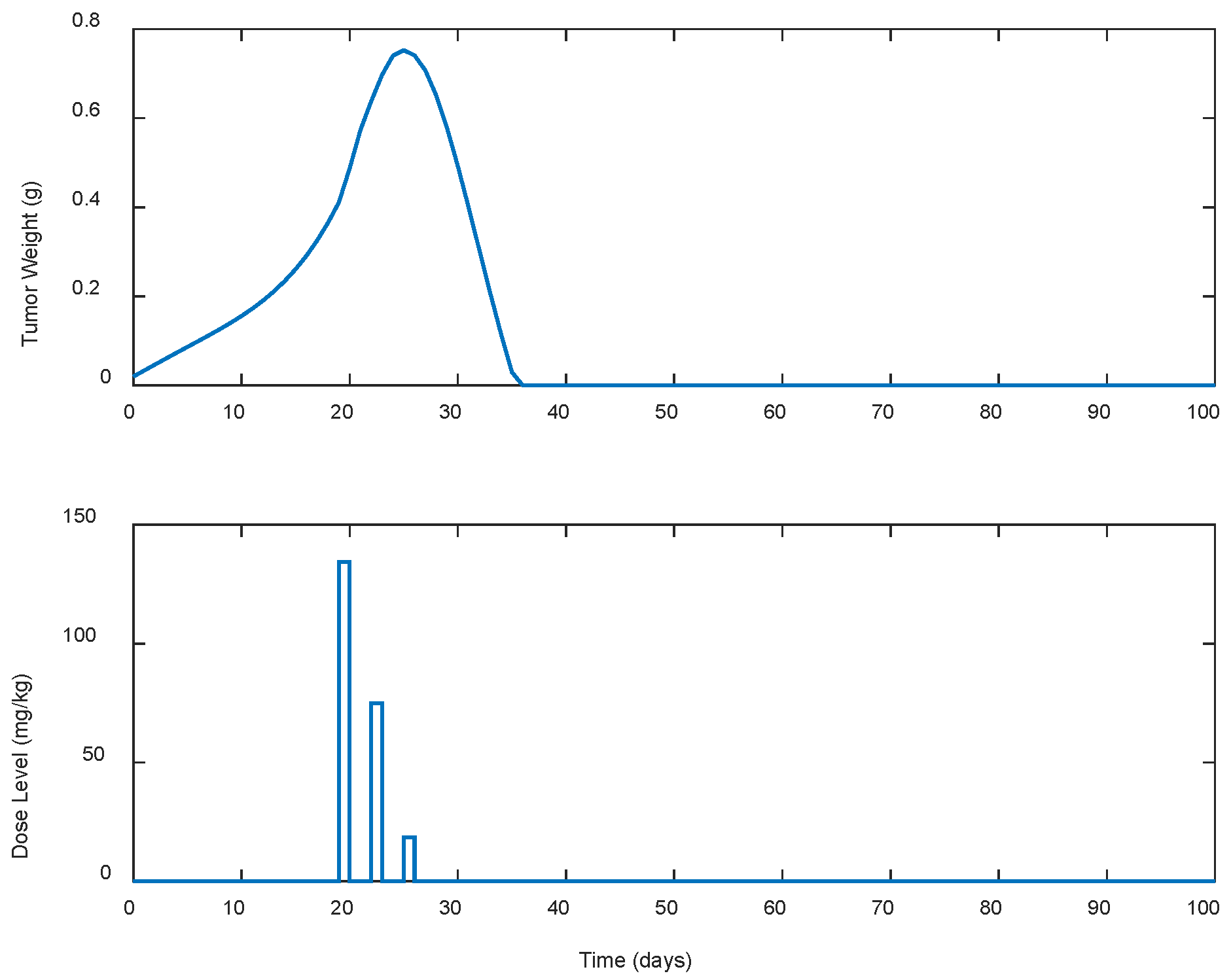
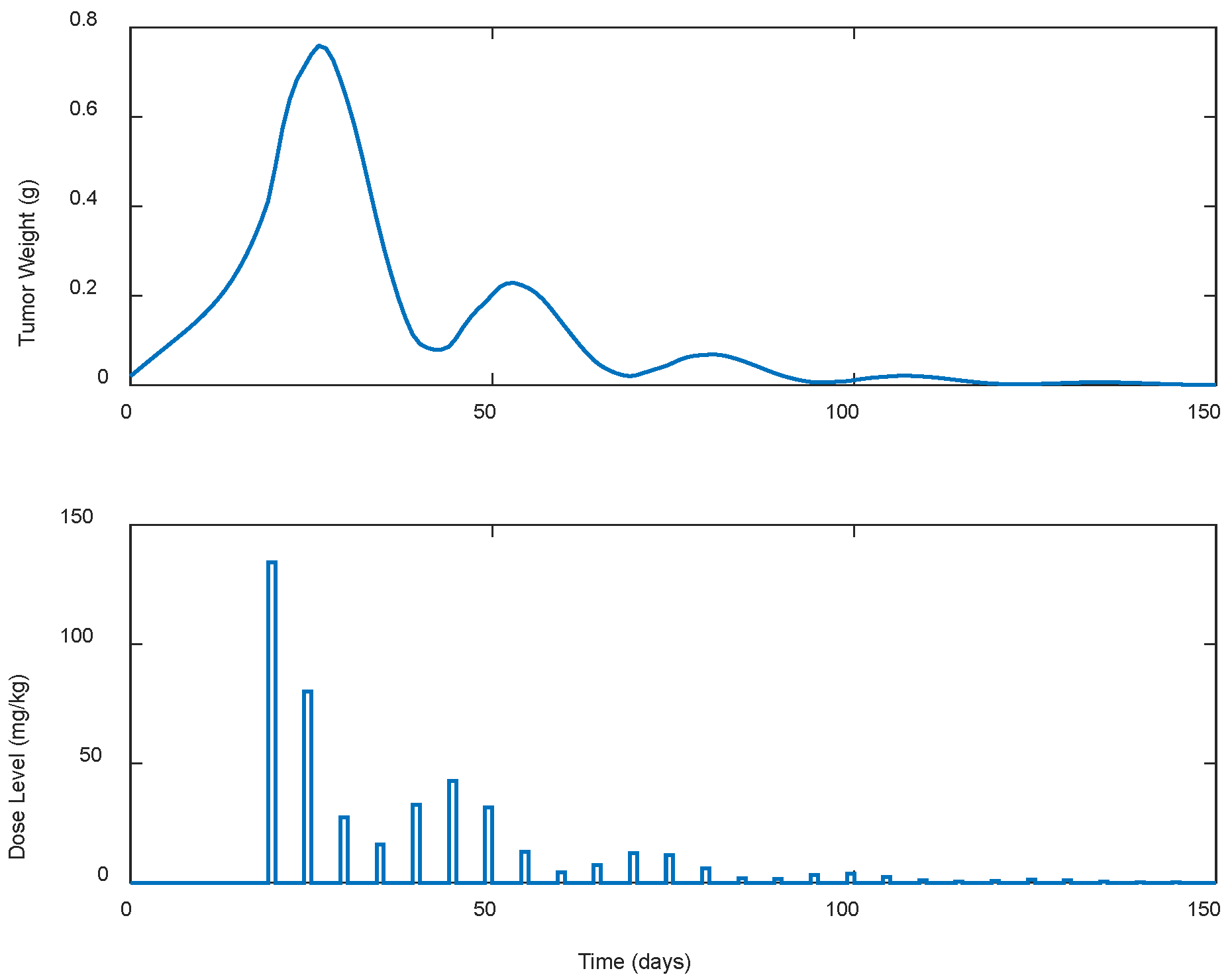
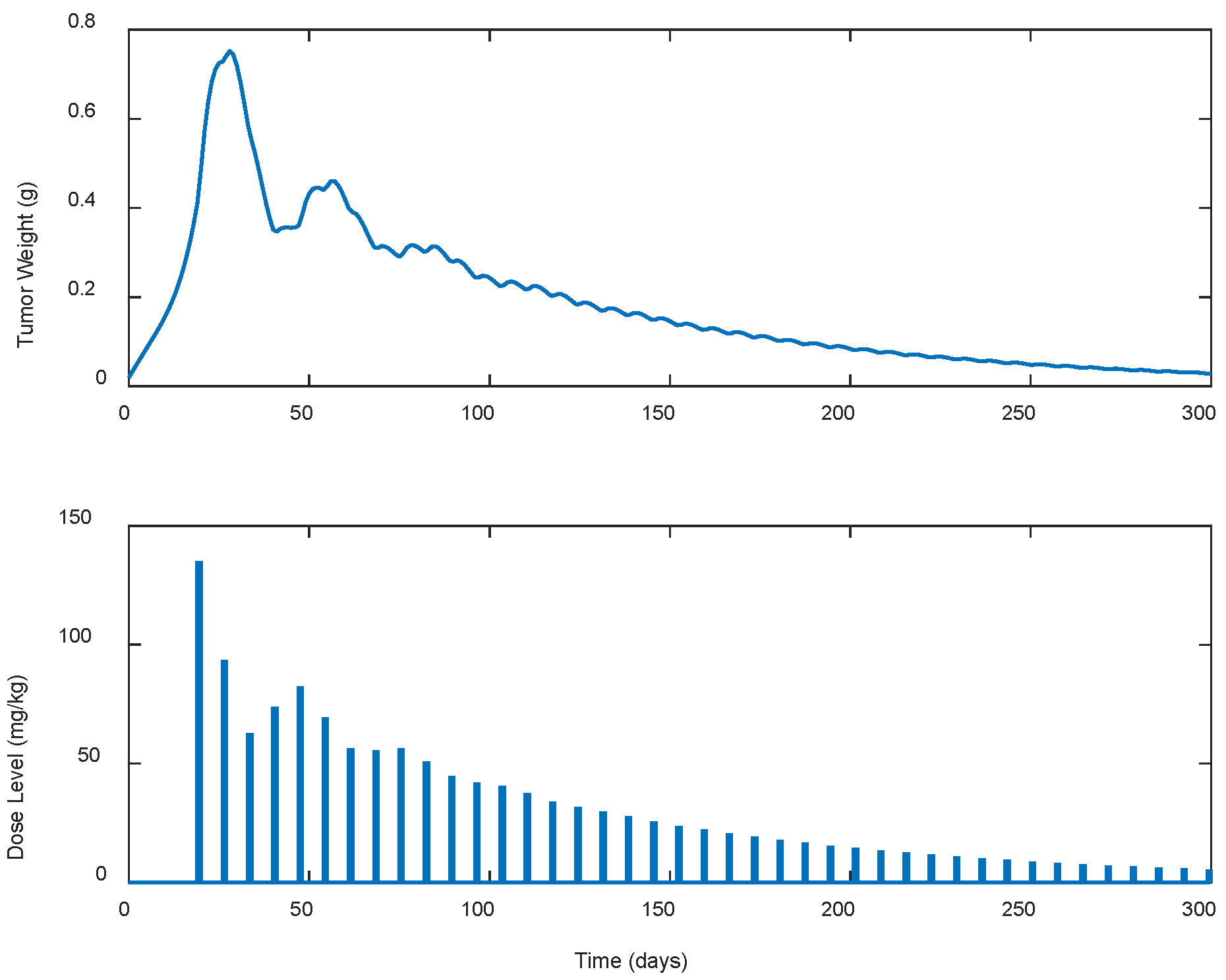
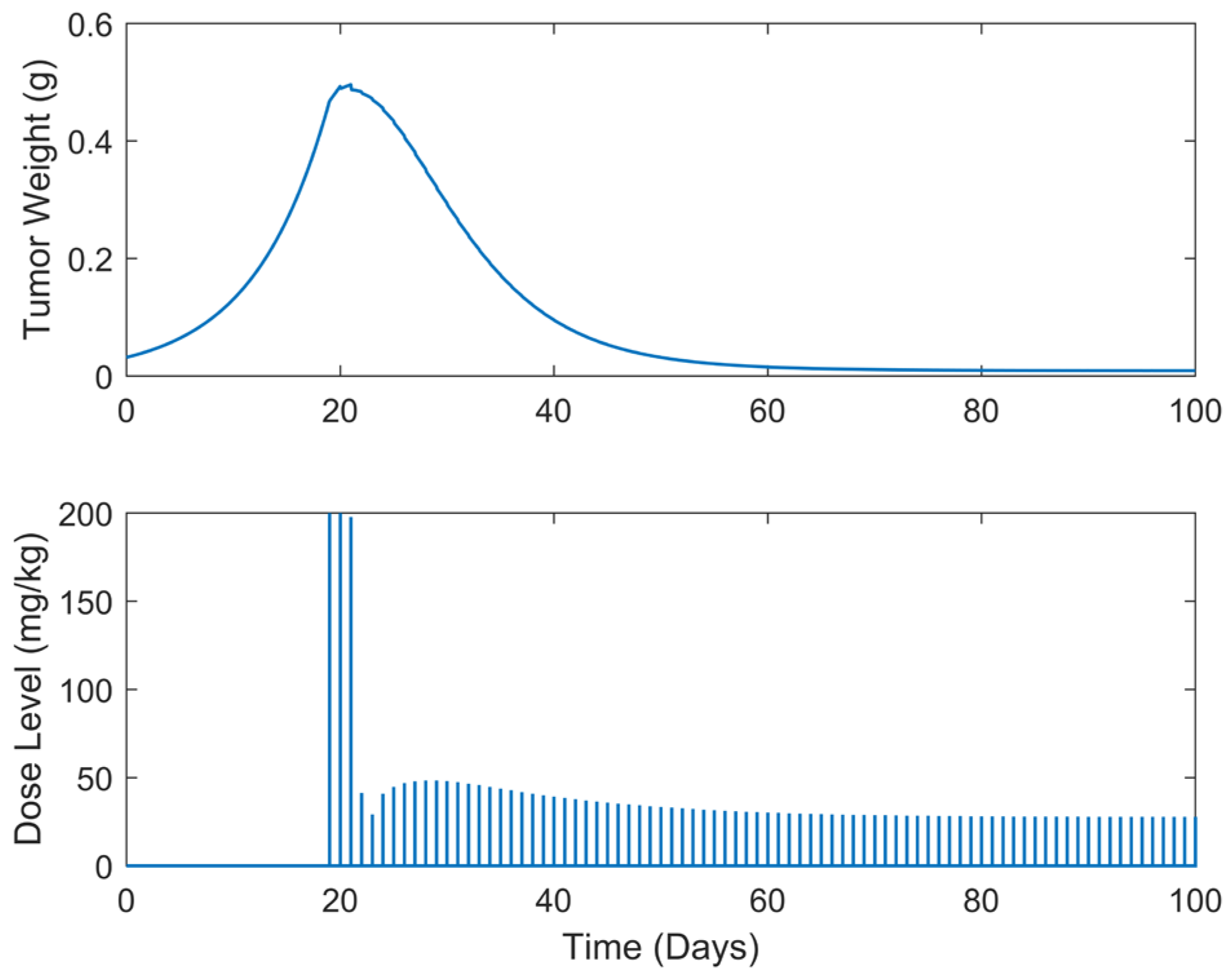
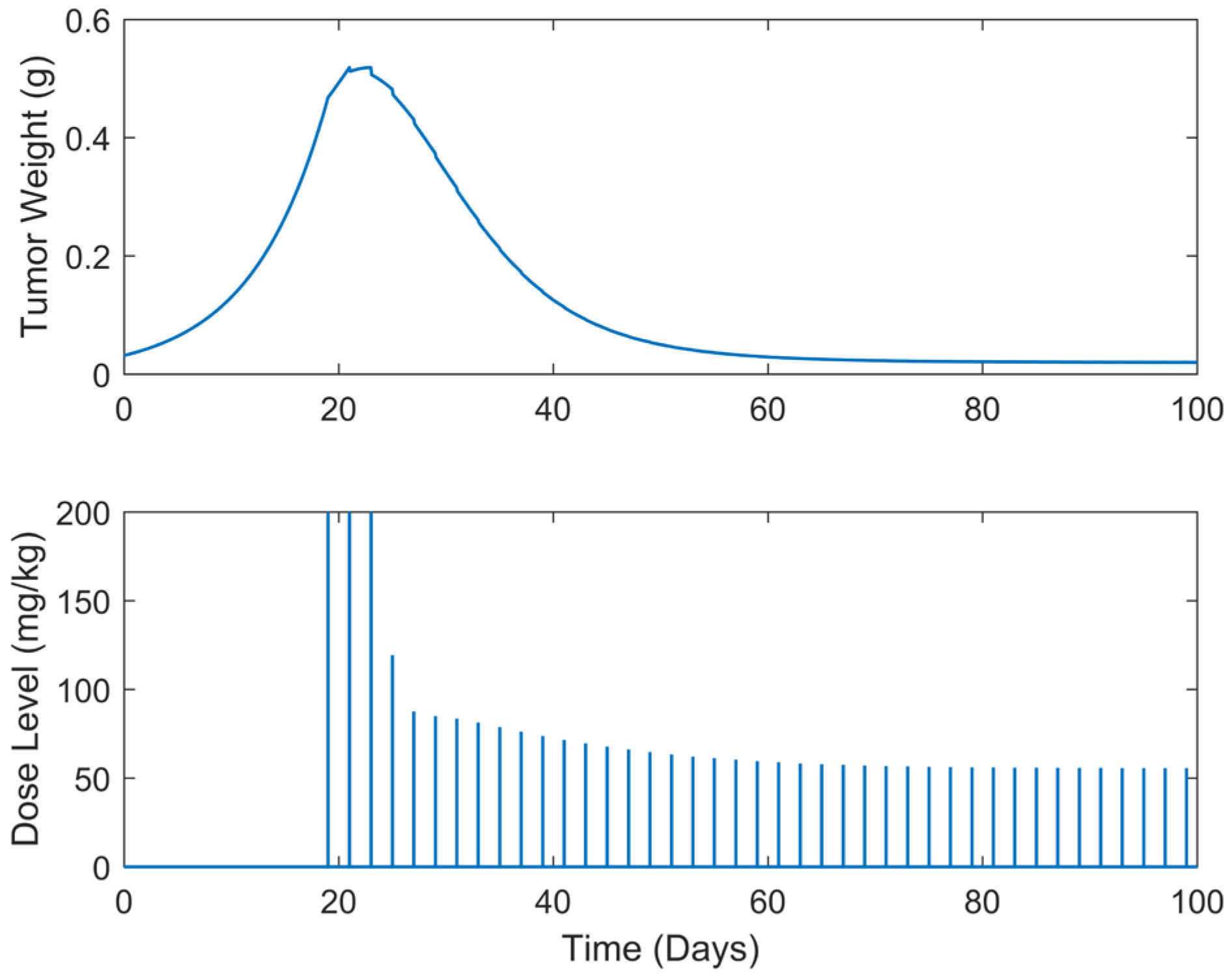
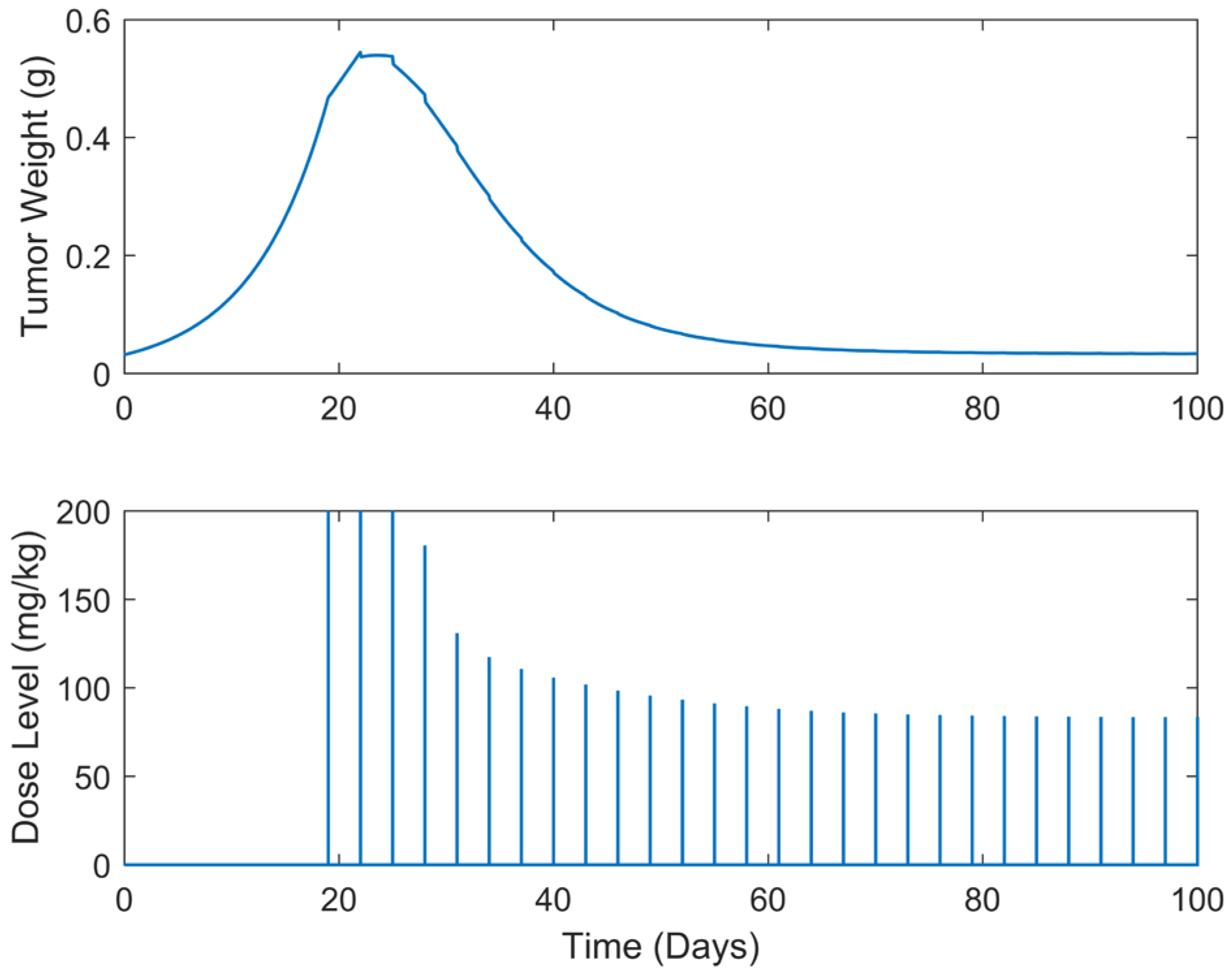

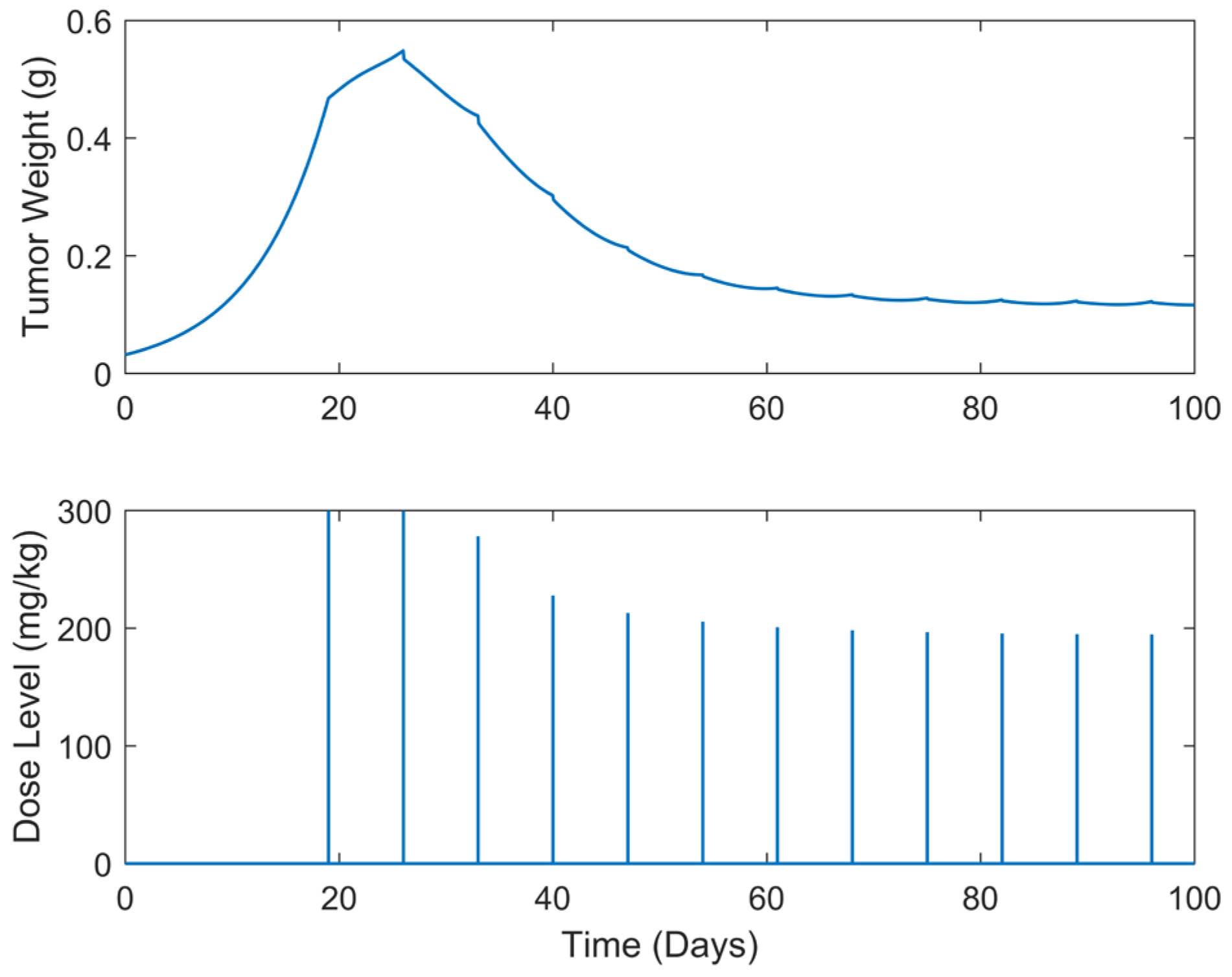

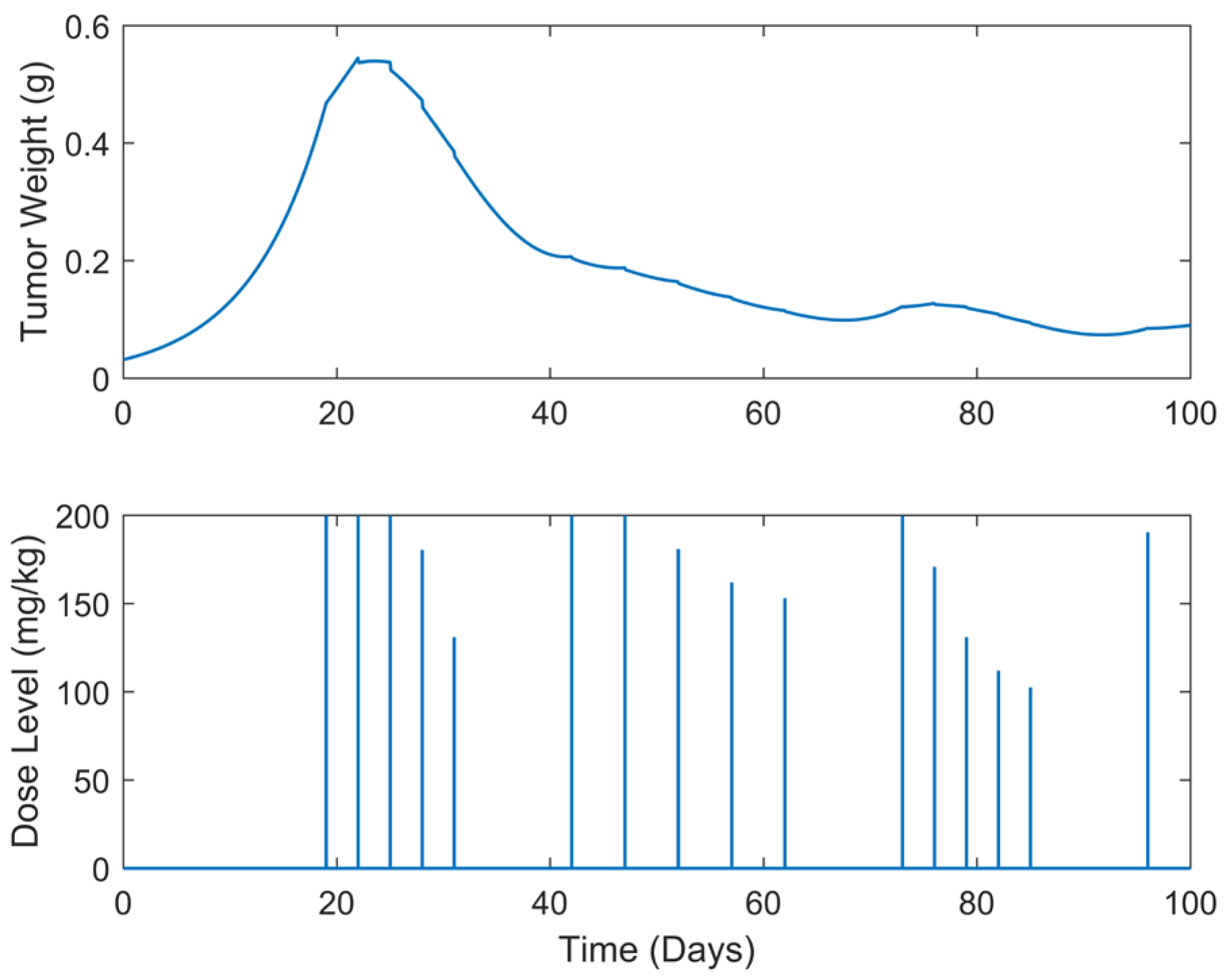
| Case | Dose Schedule | (mg/kg) | (g) | (Days) |
|---|---|---|---|---|
| A.1 | continuous | 241.93 | 0.7325 | 33 |
| A.2 | every 2 days | 230.96 | 0.7428 | 35 |
| A.3 | every 3 days | 227.59 | 0.7522 | 37 |
| A.4 | every 5 days | 437.21 | 0.7591 | 148 |
| A.5 | every 7 days | 1296.45 | 0.7523 | >300 |
| Case | Dose Schedule | (mg/kg) | (g) | (Days) |
|---|---|---|---|---|
| B.1 | continuous | 3234.63 | 0.4957 | >100 |
| B.2 | every 2 days | 3062.82 | 0.5188 | >100 |
| B.3 | every 3 days | 3002.18 | 0.5447 | >100 |
| B.4 | every 5 days | 2844.42 | 0.5970 | >100 |
| B.5 | every 7 days | 2705.71 | 0.5486 | >100 |
| Case | Dose Schedule | (Days) | (mg/kg) | (g) | (Days) |
|---|---|---|---|---|---|
| B.6 | q3dx5, q5dx5 | 7 | 2804.91 | 0.5447 | >100 |
| B.7 | q3dx5, q5dx5 | 10 | 2714.38 | 0.5447 | >100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liliopoulos, S.G.; Stavrakakis, G.S.; Dimas, K.S. Linear and Non-Linear Optimal Control Methods to Determine the Best Chemotherapy Schedule for Most Effectively Inhibiting Tumor Growth. Biomedicines 2025, 13, 315. https://doi.org/10.3390/biomedicines13020315
Liliopoulos SG, Stavrakakis GS, Dimas KS. Linear and Non-Linear Optimal Control Methods to Determine the Best Chemotherapy Schedule for Most Effectively Inhibiting Tumor Growth. Biomedicines. 2025; 13(2):315. https://doi.org/10.3390/biomedicines13020315
Chicago/Turabian StyleLiliopoulos, Sotirios G., George S. Stavrakakis, and Konstantinos S. Dimas. 2025. "Linear and Non-Linear Optimal Control Methods to Determine the Best Chemotherapy Schedule for Most Effectively Inhibiting Tumor Growth" Biomedicines 13, no. 2: 315. https://doi.org/10.3390/biomedicines13020315
APA StyleLiliopoulos, S. G., Stavrakakis, G. S., & Dimas, K. S. (2025). Linear and Non-Linear Optimal Control Methods to Determine the Best Chemotherapy Schedule for Most Effectively Inhibiting Tumor Growth. Biomedicines, 13(2), 315. https://doi.org/10.3390/biomedicines13020315







