Modeling of the In Vitro Release Kinetics of Sonosensitive Targeted Liposomes
Abstract
1. Introduction
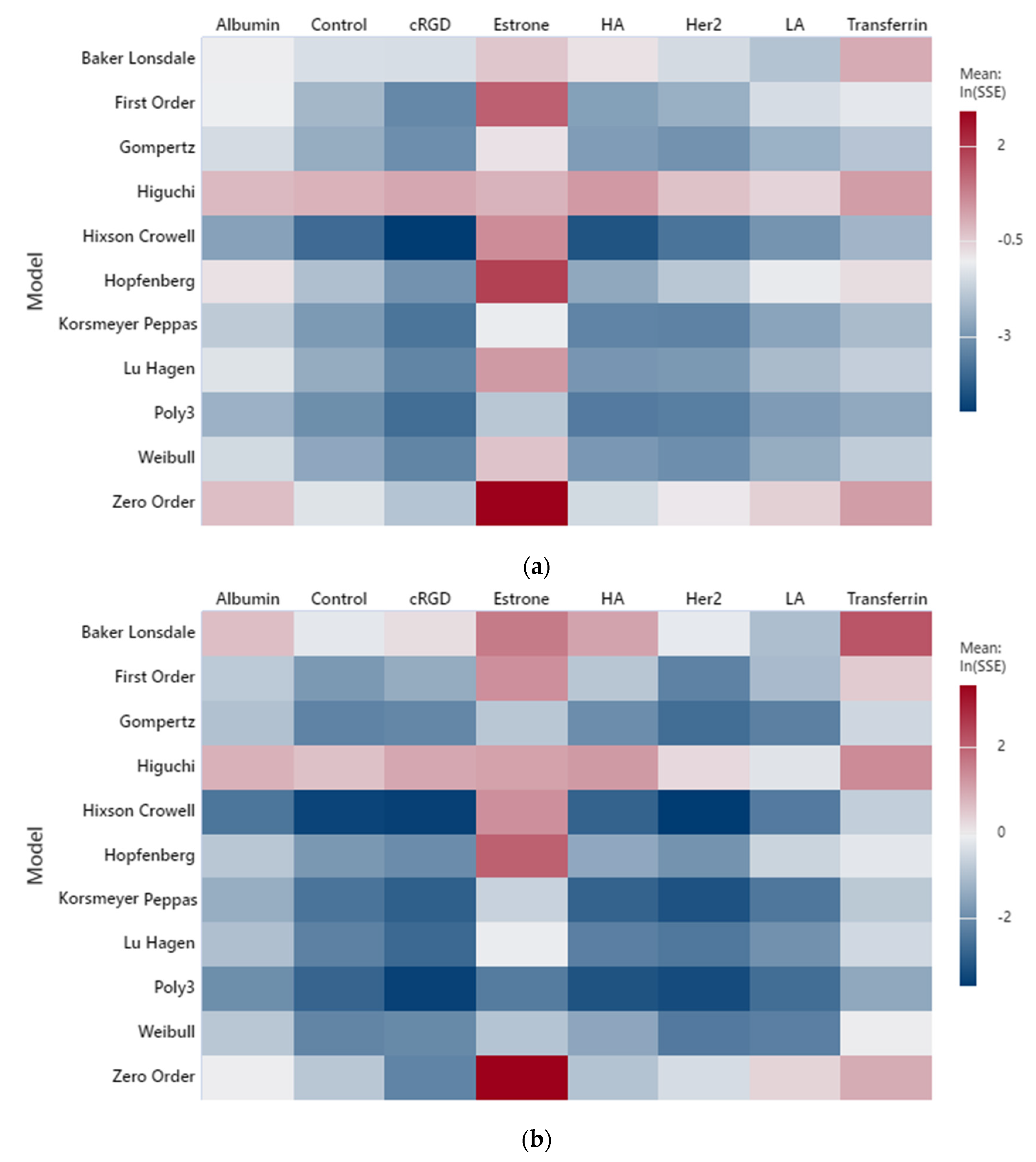
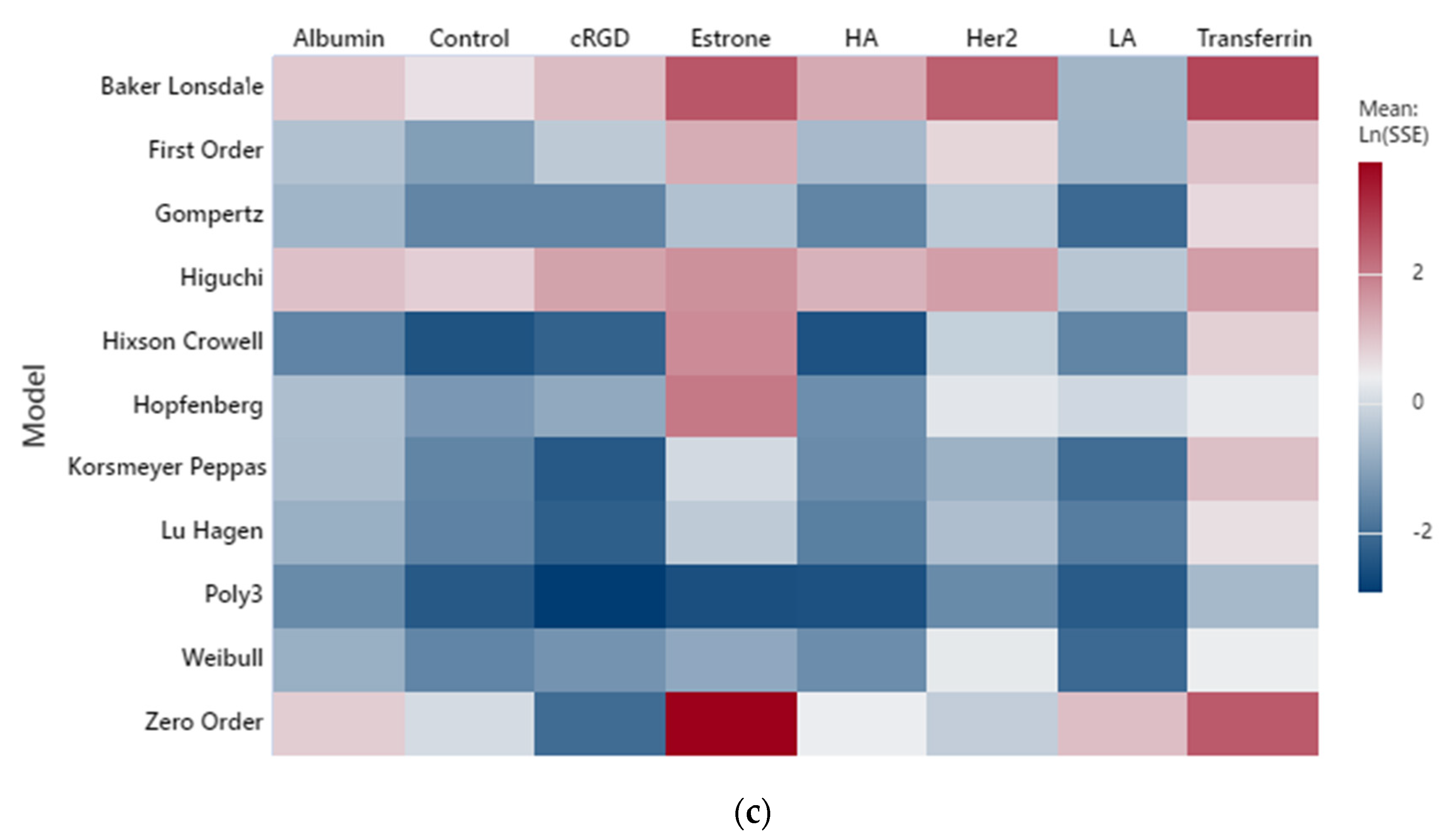
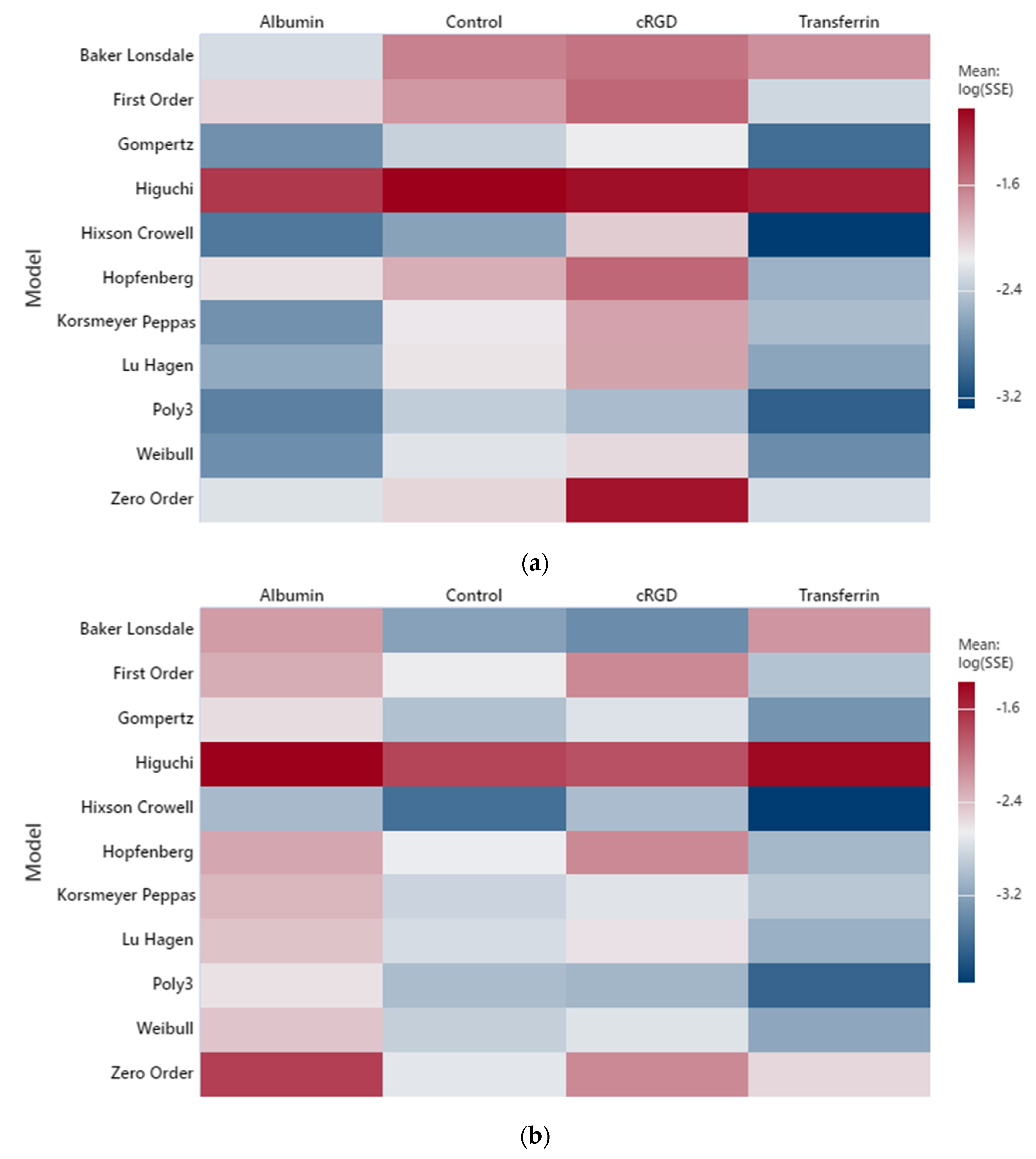
2. Results and Discussion
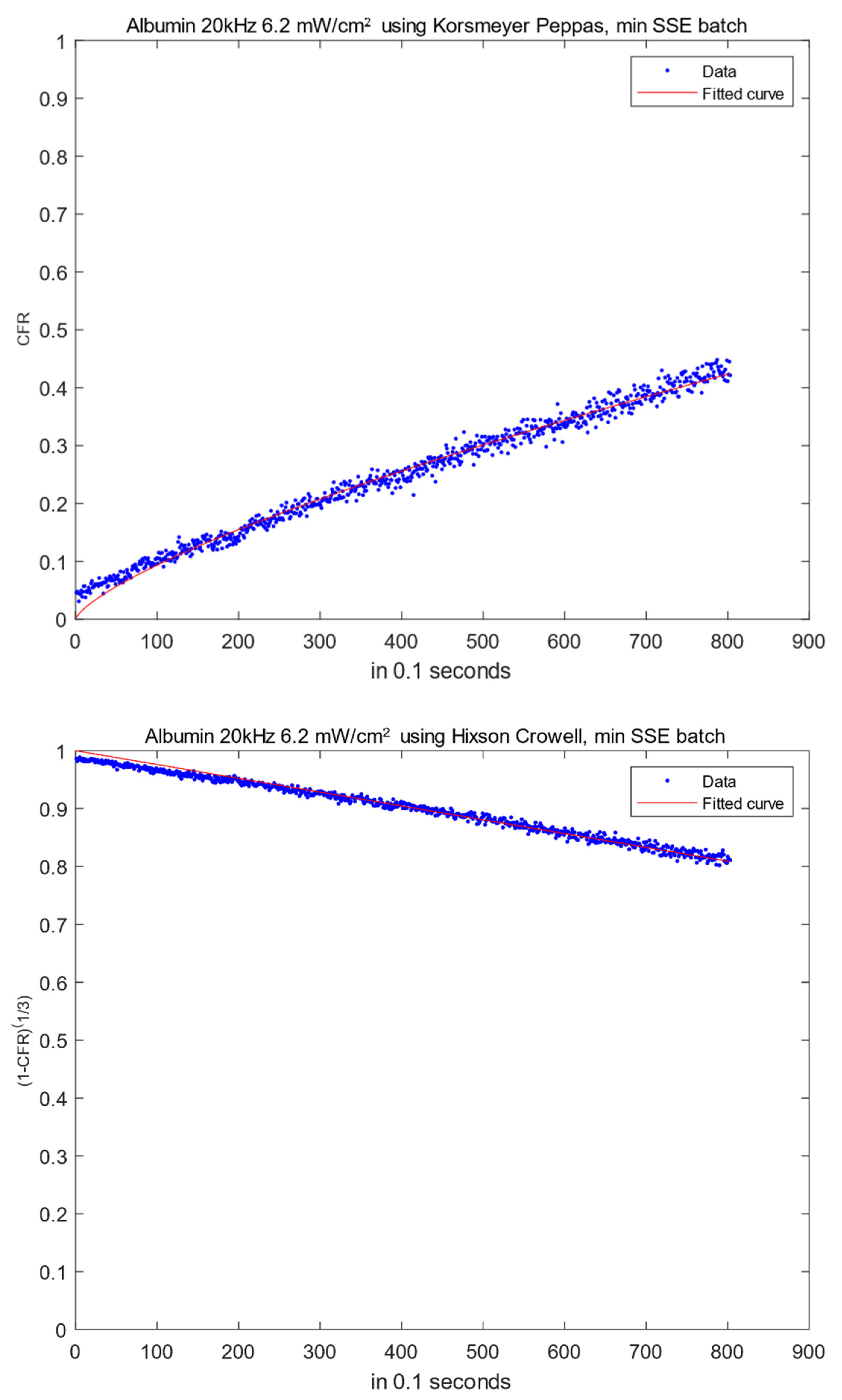
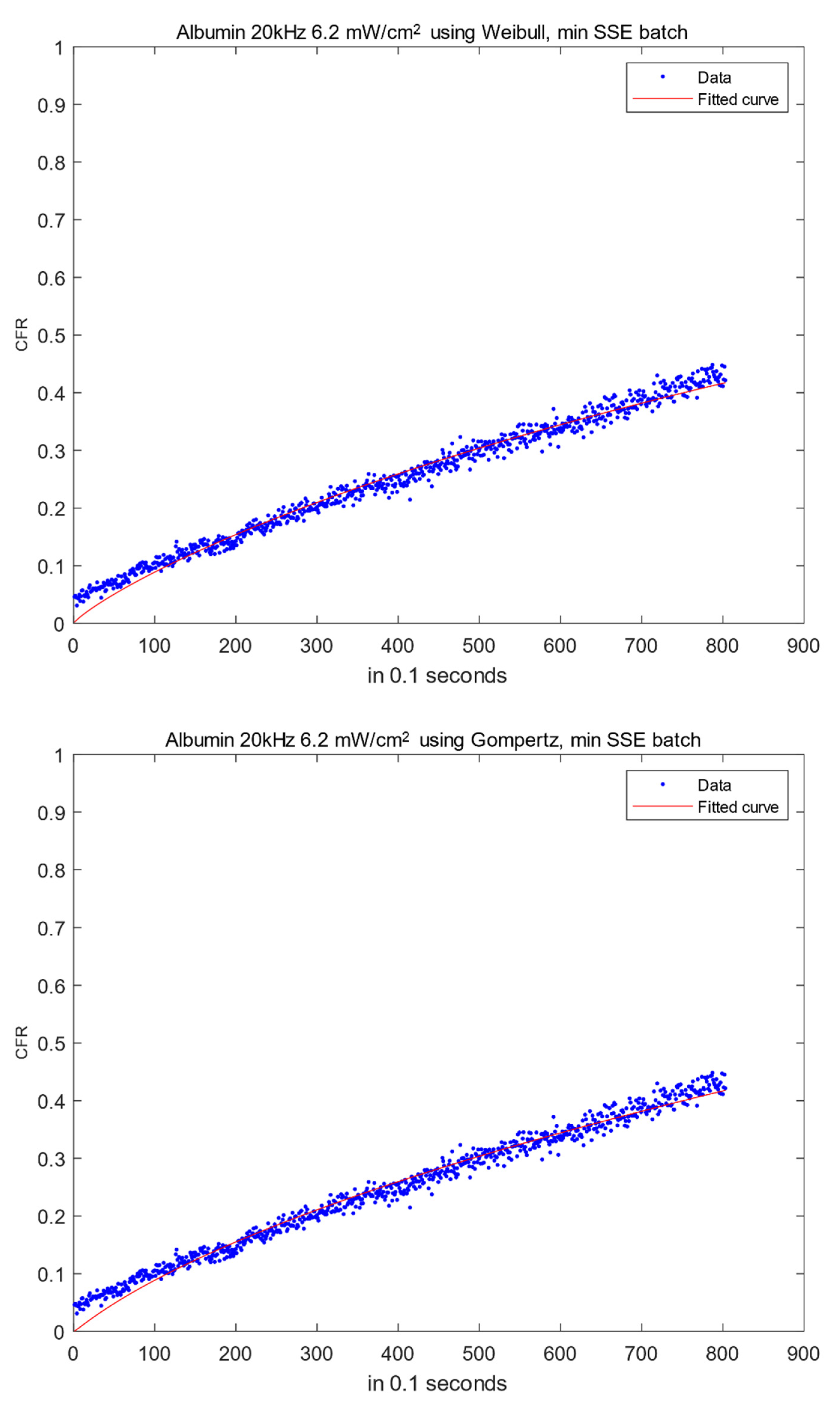
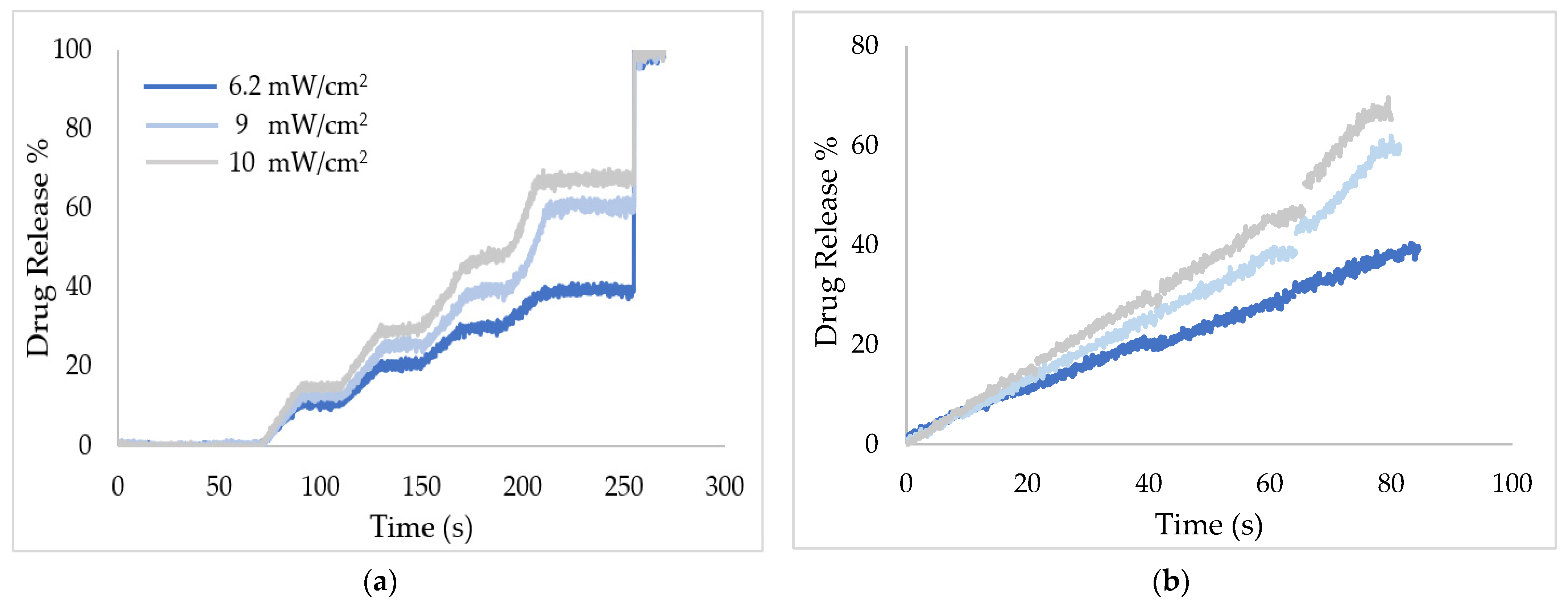
2.1. Low-Frequency Data Fitting
2.2. High-Frequency Data Fitting
3. Materials and Methods
3.1. Materials
3.2. Synthesis of Control Liposomes
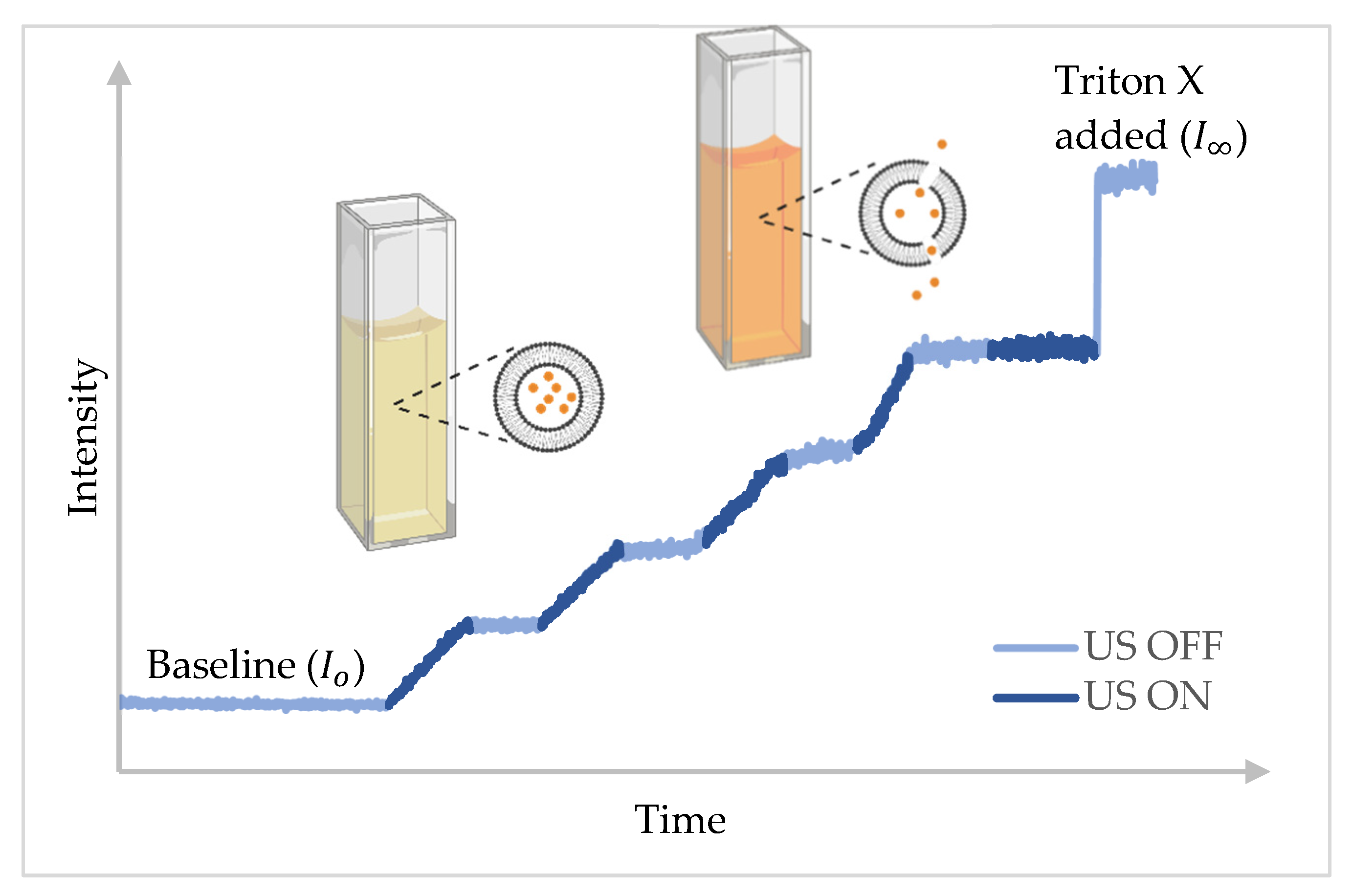
3.3. Data Acquisition
3.4. Data Formatting and Processing
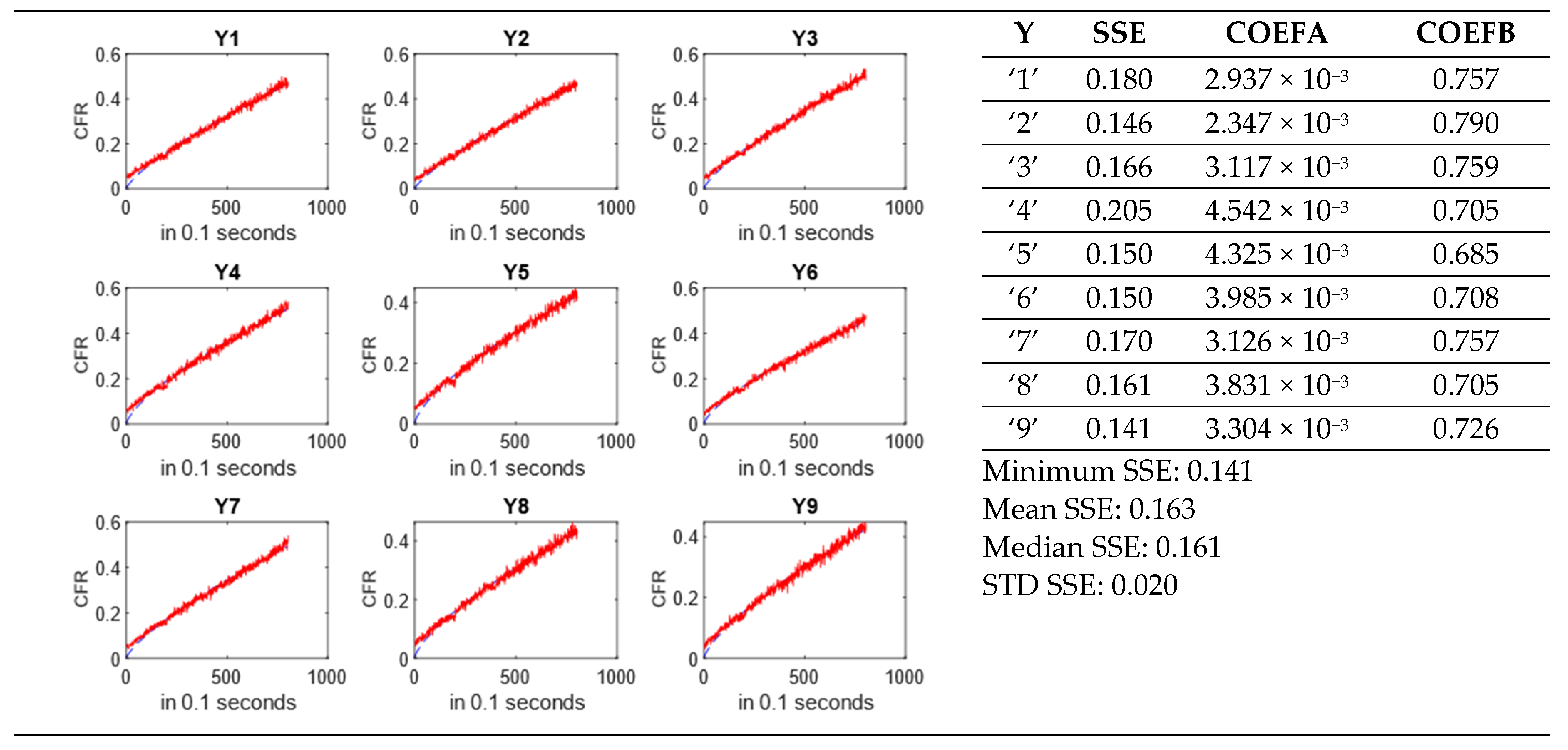
3.5. Kinetic Models for Drug Release and Error Estimation
3.6. MATLAB Codes
- ○
- Estimated model coefficient(s) for each run.
- ○
- SSE values for each run with a statistical summary.
- ○
- Plots of CFR vs. time for each run based on the selected model.
- ○
- A summary page, including a summary plot of all the moieties and power densities in the spreadsheet.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| amount of drug released at time t | |
| initial amount of drug in the solution (usually ) | |
| total amount of drug released (≈total amount in the dosage system) | |
| drug concentration at time t | |
| initial drug concentration | |
| total drug concentration | |
| saturation concentration (solubility) of drug at given temperature | |
| initial amount of drug encapsulated in the DDS | |
| drug solubility in the matrix | |
| initial amount of drug encapsulated in the DDS | |
| amount of drug remaining in the DDS at time t | |
| percentage release at time t | |
| maximum dissolution | |
| surface area of the DDS | |
| D | diffusion coefficient |
| constant related to surface, shape, and density of particles | |
| number of particles | |
| thickness of the diffusion layer | |
| radius of a spherical matrix | |
| half thickness of the system | |
| timescale parameter | |
| shape parameter (release curve in Weibull, dissolution rate in Gompertz, and nanoparticles shape in Hopfenberg) | |
| equivalence of undissolved proportion at time t = 1 | |
| erosion rate constant | |
| model release constants 1 | |
1 |
References
- Cancer. Available online: https://www.who.int/news-room/fact-sheets/detail/cancer (accessed on 17 July 2022).
- Brown, D.L. Cellular Mechanisms of Chemotherapy. In Clinical Guide to Antineoplastic Therapy: A Chemotherapy Handbook; Oncology Nursing Society (ONS): Pittsburgh, PA, USA, 2014; pp. 1–23. [Google Scholar]
- Longley, D.B.; Johnston, P.G. Molecular Mechanisms of Drug Resistance. J. Pathol. 2005, 205, 275–292. [Google Scholar] [CrossRef] [PubMed]
- Devita, V.T.; Serpick, A.A.; Carbone, P.P. Combination Chemotherapy in the Treatment of Advanced Hodgkin’s Disease. Ann. Intern. Med. 1970, 73, 881–895. [Google Scholar] [CrossRef]
- Fisher, R.I.; Gaynor, E.R.; Dahlberg, S.; Oken, M.M.; Grogan, T.M.; Mize, E.M.; Glick, J.H.; Coltman, C.A.; Miller, T.P. Comparison of a Standard Regimen (CHOP) with Three Intensive Chemotherapy Regimens for Advanced Non-Hodgkin’s Lymphoma. N. Engl. J. Med. 1993, 328, 1002–1006. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.E.; Savin, M.A.; Holmes, F.A.; O’Shaughnessy, J.A.; Blum, J.L.; Vukelja, S.; McIntyre, K.J.; Pippen, J.E.; Bordelon, J.H.; Kirby, R.; et al. Phase III Trial Comparing Doxorubicin plus Cyclophosphamide with Docetaxel plus Cyclophosphamide as Adjuvant Therapy for Operable Breast Cancer. J. Clin. Oncol. 2006, 24, 5381–5387. [Google Scholar] [CrossRef] [PubMed]
- Yoshino, T.; Oki, E.; Misumi, T.; Kotaka, M.; Manaka, D.; Eto, T.; Hasegawa, J.; Takagane, A.; Nakamura, M.; Kato, T.; et al. Final Analysis of 3 Versus 6 Months of Adjuvant Oxaliplatin and Fluoropyrimidine-Based Therapy in Patients with Stage III Colon Cancer: The Randomized Phase III ACHIEVE Trial. J. Clin. Oncol. 2022, 350, 3419–3429. [Google Scholar] [CrossRef]
- Xia, W.; Tao, Z.; Zhu, B.; Zhang, W.; Liu, C.; Chen, S.; Song, M. Targeted Delivery of Drugs and Genes Using Polymer Nanocarriers for Cancer Therapy. Int. J. Mol. Sci. 2021, 22, 9118. [Google Scholar] [CrossRef]
- Sawant, R.M.; Hurley, J.P.; Salmaso, S.; Kale, A.; Tolcheva, E.; Levchenko, T.S.; Torchilin, V.P. “SMART” drug Delivery Systems: Double-Targeted pH-Responsive Pharmaceutical Nanocarriers. Bioconjug. Chem. 2006, 17, 943–949. [Google Scholar] [CrossRef]
- Ghavami, M.; Shiraishi, T.; Nielsen, P.E. Enzyme-Triggered Release of the Antisense Octaarginine-PNA Conjugate from Phospholipase A2 Sensitive Liposomes. ACS Appl. Bio Mater. 2020, 3, 1018–1025. [Google Scholar] [CrossRef]
- De Matos, M.B.C.; Deckers, R.; Van Elburg, B.; Lajoinie, G.; De Miranda, B.S.; Versluis, M.; Schiffelers, R.; Kok, R.J. Ultrasound-Sensitive Liposomes for Triggered Macromolecular Drug Delivery: Formulation and in Vitro Characterization. Front. Pharmacol. 2019, 10, 1–15. [Google Scholar] [CrossRef]
- Arias-Alpizar, G.; Kong, L.; Vlieg, R.C.; Rabe, A.; Papadopoulou, P.; Meijer, M.S.; Bonnet, S.; Vogel, S.; van Noort, J.; Kros, A.; et al. Light-Triggered Switching of Liposome Surface Charge Directs Delivery of Membrane Impermeable Payloads in Vivo. Nat. Commun. 2020, 11, 3638. [Google Scholar] [CrossRef]
- Rapp, T.L.; DeForest, C.A. Targeting Drug Delivery with Light: A Highly Focused Approach. Adv. Drug Deliv. Rev. 2021, 171, 94–107. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, R. Trigger-Responsive Nanoparticles: Control Switches for Cancer Therapy. Nanomedicine 2011, 6, 1657–1660. [Google Scholar] [CrossRef]
- Salkho, N.M. Acoustically Activated Release of Estrone-Targeted Liposomes Used for Breast Cancer Treatment. Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2016. Available online: https://dspace.aus.edu:8443/xmlui/handle/11073/8101 (accessed on 17 July 2022).
- Kawak, P. Ultrasound Triggered Release of Estrone-Targeted Liposomes. Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2017. Available online: https://dspace.aus.edu:8443/xmlui/handle/11073/8858 (accessed on 17 July 2022).
- Turki, R.Z. Preparation of Albumin-Targeted Liposomes and Their Release Characteristics Using Ultrasound. Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2016. Available online: https://dspace.aus.edu:8443/xmlui/handle/11073/8107 (accessed on 17 July 2022).
- Awad, N.S.; Paul, V.; Al-Sayah, M.H.; Husseini, G.A. Ultrasonically Controlled Albumin-Conjugated Liposomes for Breast Cancer Therapy. Artif. Cells Nanomed. Biotechnol. 2019, 47, 705–714. [Google Scholar] [CrossRef] [PubMed]
- Kawak, P. Ultrasound Triggered Drug Delivery of Transferrin Coupled Liposomes Carrying the Drug Doxorubicin. Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2020. Available online: https://dspace.aus.edu:8443/xmlui/handle/11073/19715 (accessed on 17 July 2022).
- Elamir, A.; Ajith, S.; Sawaftah, N.A.; Abuwatfa, W.; Mukhopadhyay, D.; Paul, V.; Al-Sayah, M.H.; Awad, N.; Husseini, G.A. Ultrasound-Triggered Herceptin Liposomes for Breast Cancer Therapy. Sci. Rep. 2021, 11, 7545. [Google Scholar] [CrossRef]
- Ben Daya, S.M.; Paul, V.; Awad, N.S.; Al Sawaftah, N.M.; Al Sayah, M.H.; Husseini, G.A. Targeting Breast Cancer Using Hyaluronic Acid-Conjugated Liposomes Triggered with Ultrasound. J. Biomed. Nanotechnol. 2021, 17, 90–99. [Google Scholar] [CrossRef]
- AlSawaftah, N.M.; Paul, V.; Kosaji, D.; Khabbaz, L.; Awad, N.S.; Husseini, G.A. Ultrasound-Sensitive cRGD-Modified Liposomes as a Novel Drug Delivery System. Artif. Cells Nanomed. Biotechnol. 2022, 50, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Abusamra, R. Using Lactose and Ultrasound to Deliver Chemotherapeuitcs. Master’s Thesis, American University of Sharjah, Sharjah, United Arab Emirates, 2019. Available online: https://dspace.aus.edu/xmlui/handle/11073/16440 (accessed on 17 July 2022).
- AlSawaftah, N.M.; Awad, N.S.; Paul, V.; Kawak, P.S.; Al-Sayah, M.H.; Husseini, G.A. Transferrin-Modified Liposomes Triggered with Ultrasound to Treat HeLa Cells. Sci. Rep. 2021, 11, 11589. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ma, H.; Yao, J. ERα, a Key Target for Cancer Therapy: A Review. Onco. Targets. Ther. 2020, 13, 2183–2191. [Google Scholar] [CrossRef]
- Salkho, N.M.; Paul, V.; Kawak, P.; Vitor, R.F.; Martins, A.M.; Al-Sayah, M.H.; Husseini, G.A. Ultrasonically Controlled Estrone-Modified Liposomes for Estrogen-Positive Breast Cancer Therapy. Artif. Cells Nanomed. Biotechnol. 2018, 46, 462–472. [Google Scholar] [CrossRef]
- Neumann, E.; Frei, E.; Funk, D.; Becker, M.D.; Schrenk, H.; Müller-Ladner, U.; Fiehn, C. Native Albumin for Targeted Drug Delivery. Expert Opin. Drug Deliv. 2010, 7, 915–925. [Google Scholar] [CrossRef]
- Danhier, F.; Vroman, B.; Lecouturier, N.; Crokart, N.; Pourcelle, V.; Freichels, H.; Jérôme, C.; Marchand-Brynaert, J.; Feron, O.; Préat, V. Targeting of Tumor Endothelium by RGD-Grafted PLGA-Nanoparticles Loaded with Paclitaxel. J. Control. Release 2009, 140, 166–173. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Lin, Y.; Zhang, X.; Feng, C.; Lu, Y.; Gao, Y.; Dong, C. Cyclic RGD Peptide-Modified Liposomal Drug Delivery System for Targeted Oral Apatinib Administration: Enhanced Cellular Uptake and Improved Therapeutic Effects. Int. J. Nanomed. 2017, 12, 1941–1958. [Google Scholar] [CrossRef] [PubMed]
- Eloy, J.O.; Petrilli, R.; Brueggemeier, R.W.; Marchetti, J.M.; Lee, R.J. Rapamycin-Loaded Immunoliposomes Functionalized with Trastuzumab: A Strategy to Enhance Cytotoxicity to HER2 Positive Breast Cancer Cells. Anticancer Agents Med. Chem. 2017, 17, 48–56. [Google Scholar] [CrossRef]
- Qhattal, H.S.S.; Liu, X. Characterization of CD44-Mediated Cancer Cell Uptake and Intracellular Distribution of Hyaluronan-Grafted Liposomes. Mol. Pharm. 2011, 8, 1233–1246. [Google Scholar] [CrossRef]
- Bansal, D.; Yadav, K.; Pandey, V.; Ganeshpurkar, A.; Agnihotri, A.; Dubey, N. Lactobionic Acid Coupled Liposomes: An Innovative Strategy for Targeting Hepatocellular Carcinoma. Drug Deliv. 2016, 23, 140–146. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.; Sun, Z.; Liu, R.; Liu, X.; Zhang, Y.; Zhou, Y.; Qiu, Y.; Zhang, X. Transferrin-Conjugated Erianin-Loaded Liposomes Suppress the Growth of Liver Cancer by Modulating Oxidative Stress. Front. Oncol. 2021, 11, 727605. [Google Scholar] [CrossRef]
- Soni, V.; Kohli, D.V.; Jain, S.K. Transferrin-Conjugated Liposomal System for Improved Delivery of 5-Fluorouracil to Brain. J. Drug Target. 2008, 16, 73–78. [Google Scholar] [CrossRef]
- Bruschi, M.L. (Ed.) Mathematical Models of Drug Release. In Strategies to Modify the Drug Release from Pharmaceutical Systems; Woodhead Publishing: Cambridge, UK, 2015; pp. 63–86. [Google Scholar] [CrossRef]
- Dash, S.; Murthy, P.N.; Nath, L.; Chowdhury, P. Kinetic Modeling on Drug Release from Controlled Drug Delivery Systems. Acta Pol. Pharm. Drug Res. 2010, 67, 217–223. [Google Scholar]
- Lu, T.; ten Hagen, T.L.M. A Novel Kinetic Model to Describe the Ultra-Fast Triggered Release of Thermosensitive Liposomal Drug Delivery Systems. J. Control. Release 2020, 324, 669–678. [Google Scholar] [CrossRef]
| Type | Advantages | Disadvantages |
|---|---|---|
| visible/near-infrared light |
|
|
| pH |
|
|
| magnetic field |
|
|
| ultrasound |
|
|
| microwave |
|
|
| Targeting Moiety | Tumor-Overexpressed Receptor(s) | Reference |
|---|---|---|
| estrone (ES) | ER+ breast cancer | [25,26] |
| albumin | Gp60, SPARC and hnRNPs overexpressed in MDA-MB-453 breast cancer, lung cancer, metastatic pancreatic adenocarcinoma, and melanoma | [18,27] |
| cyclic arginylglycylaspartic acid (cRGD) | αvβ3 integrin overexpressed in pancreatic, renal, and breast cancer | [28,29] |
| herceptin (HER2) | HER2 overexpressed in breast, ovarian, gastric, and prostate cancer | [20,30] |
| hyaluronic acid (HA) | CD44 overexpressed in breast, lung, colorectal, gastric, renal hepatocellular, pancreatic, cervical cancers, and melanomas | [21,31] |
| lactobionic acid (LA) | ASGRP overexpressed in liver cancer | [23,32] |
| transferrin (Tf) | Tf receptors overexpressed on all the rapidly dividing normal and malignant cells such as liver, cervical and ovarian cancers, leukemia, neuroblastoma, and glioblastoma | [33,34] |
| Model | Model Expression 1 | Modified Expression | Conditions and Uses |
|---|---|---|---|
| zero-order |
| ||
| first-order |
| ||
| Higuchi |
| ||
| Hixson–Crowell |
| ||
| Korsmeyer–Peppas (power law) |
| ||
| Baker–Lonsdale |
| ||
| Weibull |
| ||
| Gompertz |
| ||
| Hopfenberg |
| ||
| Lu–Hagen |
|
| Moiety | Power Density (mW/cm2) | |||||
|---|---|---|---|---|---|---|
| 6.2 | 9 | 10 | ||||
| a | b | a | b | a | b | |
| albumin | 3.50 × 10−3 | 0.73 | 3.25 × 10−3 | 0.79 | 5.70 × 10−3 | 0.74 |
| cRGD | 1.32 × 10−3 | 0.86 | 9.83 × 10−4 | 0.95 | 9.40 × 10−4 | 0.99 |
| estrone | 5.33 × 10−2 | 0.41 | 8.32 × 10−2 | 0.36 | 1.11 × 10−1 | 0.32 |
| HA | 1.67 × 10−3 | 0.85 | 2.52 × 10−3 | 0.85 | 4.78 × 10−3 | 0.78 |
| Her2 | 3.48 × 10−3 | 0.77 | 4.46 × 10−3 | 0.77 | 3.35 × 10−3 | 0.87 |
| LA | 3.33 × 10−3 | 0.72 | 5.57 × 10−3 | 0.69 | 9.45 × 10−3 | 0.64 |
| transferrin | 5.61 × 10−3 | 0.73 | 6.64 × 10−3 | 0.75 | 1.70 × 10−2 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlMajed, Z.; Salkho, N.M.; Sulieman, H.; Husseini, G.A. Modeling of the In Vitro Release Kinetics of Sonosensitive Targeted Liposomes. Biomedicines 2022, 10, 3139. https://doi.org/10.3390/biomedicines10123139
AlMajed Z, Salkho NM, Sulieman H, Husseini GA. Modeling of the In Vitro Release Kinetics of Sonosensitive Targeted Liposomes. Biomedicines. 2022; 10(12):3139. https://doi.org/10.3390/biomedicines10123139
Chicago/Turabian StyleAlMajed, Zeyad, Najla M. Salkho, Hana Sulieman, and Ghaleb A. Husseini. 2022. "Modeling of the In Vitro Release Kinetics of Sonosensitive Targeted Liposomes" Biomedicines 10, no. 12: 3139. https://doi.org/10.3390/biomedicines10123139
APA StyleAlMajed, Z., Salkho, N. M., Sulieman, H., & Husseini, G. A. (2022). Modeling of the In Vitro Release Kinetics of Sonosensitive Targeted Liposomes. Biomedicines, 10(12), 3139. https://doi.org/10.3390/biomedicines10123139








