Unusual Mathematical Approaches Untangle Nervous Dynamics
Abstract
:1. Introduction
2. Mathematics and the Anatomy on the Central Nervous System
2.1. Macroscopic Scale: Braid Groups, Nerve Fibers and Somatotopic Maps
- (a)
- Simple changes in the location and arrangement of nerves could explain the activity of the central nervous system.
- (b)
- The external inputs follow specific nervous paths which are assessable in the mathematical terms of braid groups.
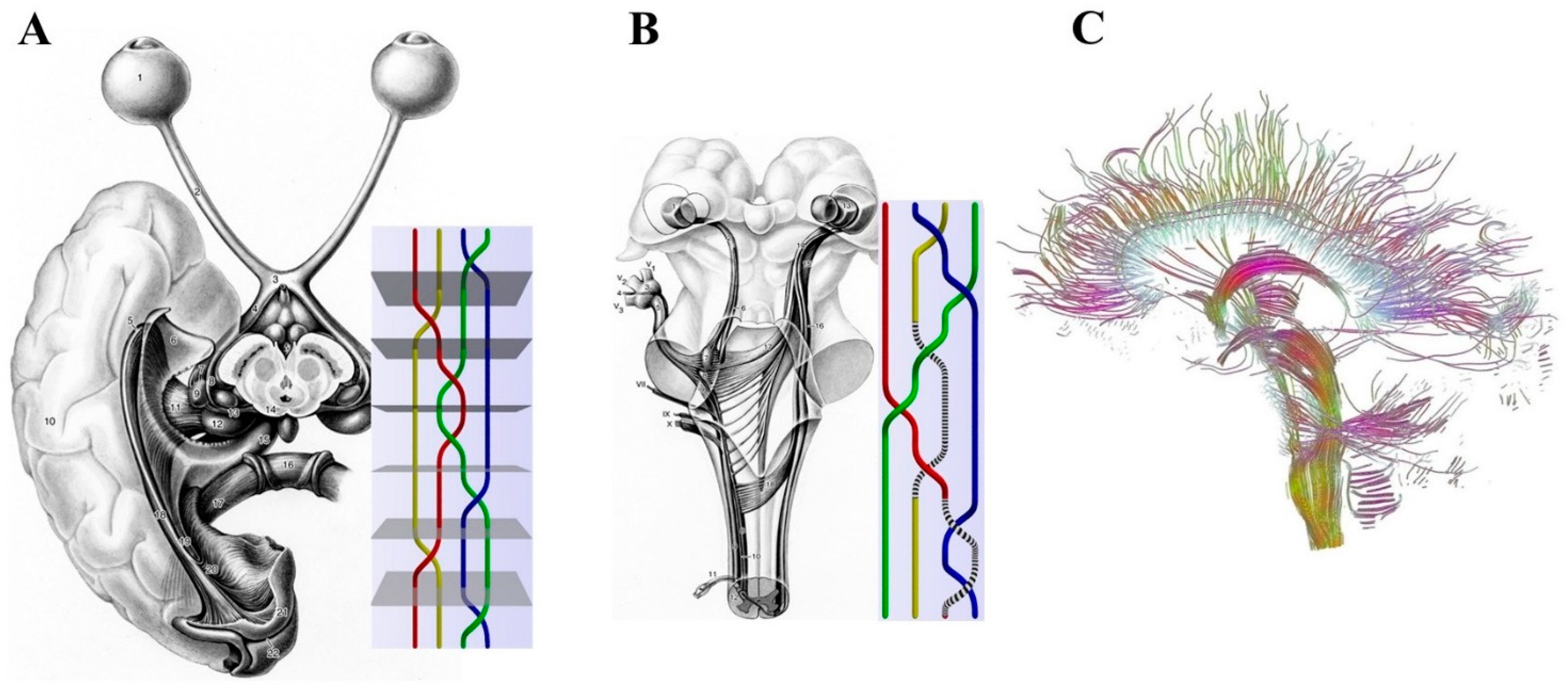
2.2. Mesoscopic Scale: Are There Elliptic Curves in the Brain?
2.3. Microscopic Scale: Towards a Transient Microconnectome Made of Tunneling Nanotubes?
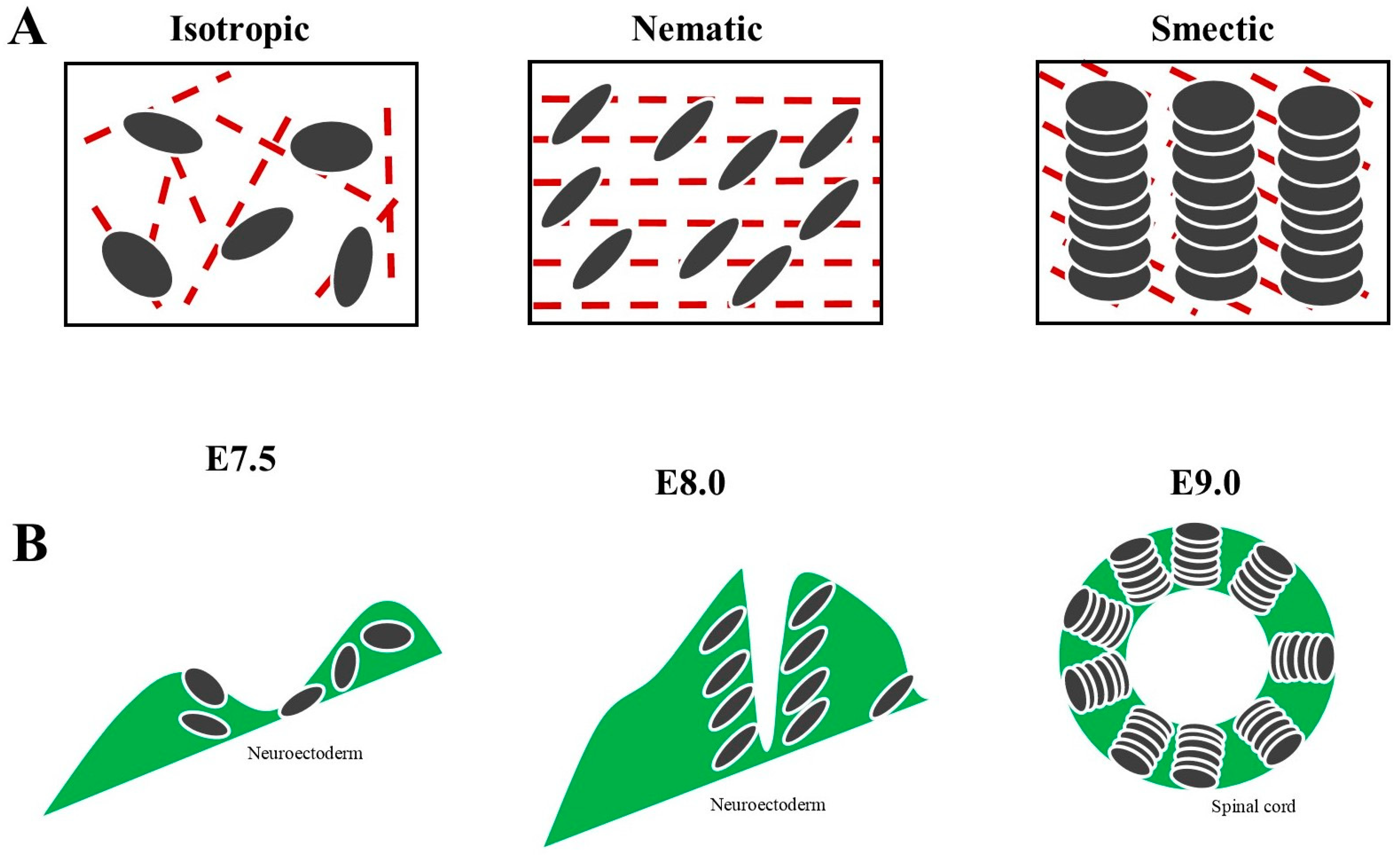
3. Mathematics and the Embryonic Development of the Nervous System
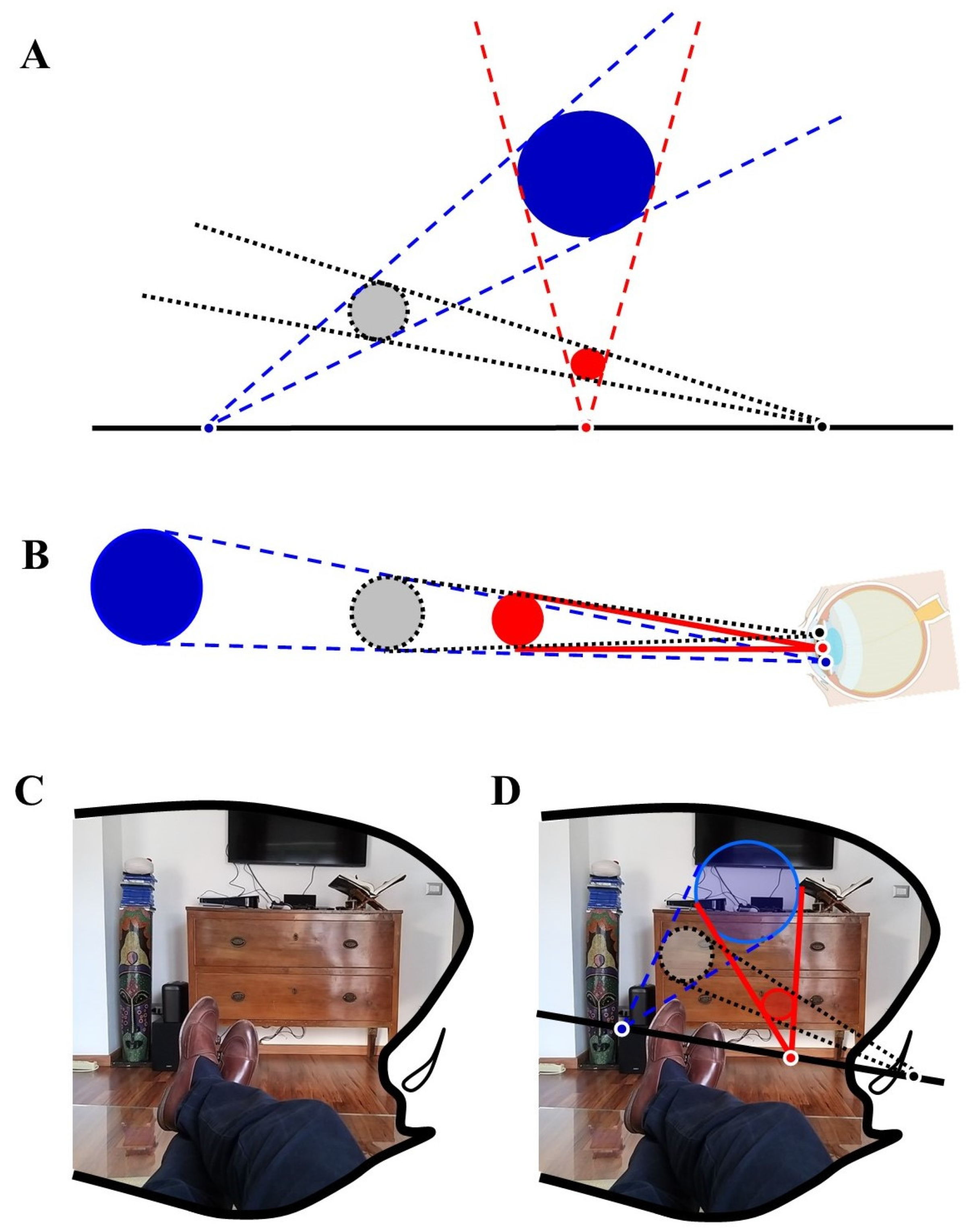
4. Mathematics and Visual Perception
5. Discussion
- (1)
- If X is paracompact, H (X, K) is the set of homotopy classes from X into K.
- (2)
- If X is paracompact space of finite covering dimension, then Lurie’s theory of stacks is equivalent to the Joyal–Jardine homotopy theory.
- (1)
- The customary concept of equality suggests the occurrence of a strict relationship between two entities (say, two neurons or two neural waves on the brain surface).
- (2)
- Lurie’s concept of equivalence of ∞-topos suggests that two entities (say, two neurons or two neural waves on the brain surface) stand in relation to each other in many ways.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benacerraf, P. What Numbers Could not Be. Philos. Rev. 1965, 74, 47–73. [Google Scholar] [CrossRef]
- Maddy, P. Believing the Axioms, II. J. Symb. Log. 1988, 53, 736–764. [Google Scholar] [CrossRef] [Green Version]
- Beckers, S.; Eberhardt, F.; Halpern, J.Y. Approximate Causal Abstraction. arXiv 2019, arXiv:1906.11583v2. [Google Scholar]
- Wigner, E. The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Commun. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- Lakoff, G.; Nunez, R. Where Mathematics Come from: How the Embodied Mind Brings Mathematics into Being, Reprint ed.; Basic Books: New York, NY, USA, 2001; ISBN 978-0465037711. [Google Scholar]
- Sejnowski, T.J. The unreasonable effectiveness of deep learning in artificial intelligence. Proc. Natl. Acad. Sci. USA 2020, 117, 30033–30038. [Google Scholar] [CrossRef] [Green Version]
- Giusti, C.; Ghrist, R.; Bassett, D. Two’s company, three (or more) is a simplex: Algebraic-topological tools for understanding higher-order structure in neural data. J. Comput. Neurosci. 2016, 41, 596. [Google Scholar] [CrossRef] [Green Version]
- Morone, F.; Roth, K.; Min, B.; Stanley, H.E.; Makse, H.A. Model of brain activation predicts the neural collective influence map of the brain. Proc. Natl. Acad. Sci. USA 2017, 114, 3849–3854. [Google Scholar] [CrossRef] [Green Version]
- Kang, J.; Pae, C.; Park, H.J. Energy landscape analysis of the subcortical brain network unravels system properties beneath resting state dynamics. Neuroimage 2017, 149, 153–164. [Google Scholar] [CrossRef]
- Yamazaki, T.; Igarashi, J.; Yamaura, H. Human-scale Brain Simulation via Supercomputer: A Case Study on the Cerebellum. Neuroscience 2021, 462, 235–246. [Google Scholar] [CrossRef]
- Friston, K.J.; Williams, S.; Howard, S.; Frackowiak, R.S.; Turner, R. Movement-related effects in fMRI time-series. Magn. Reson. Med. 1996, 35, 346–355. [Google Scholar] [CrossRef]
- Bhagalia, R.; Kim, B. Spin saturation artifact correction using slice-to-volume registration motion estimates for fMRI time series. Med. Phys. 2008, 35, 424–434. [Google Scholar] [CrossRef] [PubMed]
- Whittingstall, K.; Bartels, A.; Singh, V.; Kwon, S.; Logothetis, N.K. Integration of EEG source imaging and fMRI during continuous viewing of natural movies. Magn. Reson. Imaging 2010, 28, 1135–1142. [Google Scholar] [CrossRef] [PubMed]
- Ostwald, D.; Porcaro, C.; Bagshaw, A.P. Voxel-wise information theoretic EEG-fMRI feature integration. NeuroImage 2011, 55, 1270–1286. [Google Scholar] [CrossRef] [PubMed]
- Mirsattari, S.M.; Ives, J.R.; Leung, L.S.; Menon, R.S. EEG monitoring during functional MRI in animal models. Epilepsia 2007, 48 (Suppl. S4), 37–46. [Google Scholar] [CrossRef] [PubMed]
- Stoll, S.; Infanti, E.; de Haas, B.; Schwarzkopf, D.S. Pitfalls in post hoc analyses of population receptive field data. Neuroimage 2022, 263, 119557. [Google Scholar] [CrossRef]
- Perez, D.L.; Nicholson, T.R.; Asadi-Pooya, A.A.; Bègue, I.; Butler, M.; Carson, A.J.; David, A.S.; Deeley, Q.; Diez, I.; Edwards, M.J.; et al. Neuroimaging in Functional Neurological Disorder: State of the Field and Research Agenda. NeuroImage Clin. 2021, 30, 102623. [Google Scholar] [CrossRef]
- Raimondo, L.; Oliveira, A.; Heij, J.; Priovoulos, N.; Kundu, P.; Leoni, R.F.; van der Zwaag, W. Advances in resting state fMRI acquisitions for functional connectomics. NeuroImage 2021, 243, 118503. [Google Scholar] [CrossRef]
- Lukyanova, O.; Nikitin, O. Modeling of extrasynaptic information transfer in neural networks using braid theory. Procedia Comput. Sci. 2018, 145, 306–311. [Google Scholar] [CrossRef]
- Cromwell, P.R. Knots and Links; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Artin, E. Theory of braids. Ann. Math. 1947, 48, 101–126. [Google Scholar] [CrossRef]
- Alexander, J. A lemma on a system of knotted curves. Proc. Natl. Acad. Sci. USA 1923, 9, 93–95. [Google Scholar] [CrossRef] [Green Version]
- Birman, J.S. Knots, links, and mapping class groups. In Annals of Math Study; Princeton University Press: Princeton, NJ, USA, 1974; Volume 82. [Google Scholar]
- Bailles, A.; Collinet, C.; Philippe, J.-M.; Lenne, P.-F.; Munro, E.; Lecuit, T. Genetic induction and mechanochemical propagation of a morphogenetic wave. Nature 2019, 572, 467–473. [Google Scholar] [CrossRef] [PubMed]
- Frieden, B.R.; Gatenby, R.A. Signal transmission through elements of the cytoskeleton form an optimized information network in eukaryotic cells. Sci. Rep. 2019, 9, 6110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reimann, M.W.; Horlemann, A.-L.; Ramaswamy, S.; Muller, E.B.; Markram, H. Morphological Diversity Strongly Constrains Synaptic Connectivity and Plasticity. Cereb. Cortex 2017, 27, 4570–4585. [Google Scholar] [CrossRef] [Green Version]
- Lukyanova, O.; Nikitin, O. Neuronal topology as set of braids: Information processing, transformation and dynamics. Opt. Mem. Neural Netw. 2017, 26, 172–181. [Google Scholar] [CrossRef]
- Wu, F.Y. Knot theory and statistical mechanics. Rev. Mod. Phys. 1992, 64, 1099–1131. [Google Scholar] [CrossRef]
- Guillamón-Vivancos, T.; Aníbal-Martínez, M.; Puche, L.; Moreno-Bravo, J.A.; Valdeolmillos, M.; Martini, F.J.; López-Bendito, G. Input-dependent segregation of visual and somatosensory circuits in the mouse superior colliculus. Science 2022, 377, 845–850. [Google Scholar] [CrossRef] [PubMed]
- Imam, N.; Finlay, B.L. Self-organization of cortical areas in the development and evolution of neocortex. Proc. Natl. Acad. Sci. USA 2020, 117, 29212–29220. [Google Scholar] [CrossRef]
- A Journey through the Mathematical Theory of Braids. Available online: http://matematita.science.unitn.it/braids/summary.html (accessed on 31 October 2021).
- Nieuwenhuys, R.; Voogd, J.; van Huijzen, C. The Human Central Nervous System, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Diffusion Tensor MRI Datasets. Available online: http://www.sci.utah.edu/~gk/DTI-data/ (accessed on 31 October 2021).
- Gebel, J.; Pethő, A.; Zimmer, H.G. Computing Integral Points on Elliptic Curves. Acta Arith. 1994, 68, 171–192. [Google Scholar] [CrossRef] [Green Version]
- Heath-Brown, D.R. The average analytic rank of elliptic curves. Duke Math. J. 2004, 122, 591–623. [Google Scholar] [CrossRef] [Green Version]
- Alizadeh, M.; Kozlowski, L.; Muller, J.; Ashraf, N.; Shahrampour, S.; Mohamed, F.B.; Wu, C.; Sharan, A. Hemispheric Regional Based Analysis of Diffusion Tensor Imaging and Diffusion Tensor Tractography in Patients with Temporal Lobe Epilepsy and Correlation with Patient outcomes. Sci. Rep. 2019, 9, 215. [Google Scholar] [CrossRef] [Green Version]
- Kühne, L. Equidistribution in Families of Abelian Varieties and Uniformity. arXiv 2021, arXiv:2101.10272. [Google Scholar]
- Smith, A. 2∞-Selmer groups, 2∞-class groups, and Goldfeld’s conjecture. arXiv 2017, arXiv:1702.02325. [Google Scholar]
- Tozzi, A.; Peters, J.F.; Fingelkurts, A.A.; Fingelkurts, A.A.; Marijuán, P.C. Brain projective reality: Novel clothes for the emperor. Reply to comments on “Topodynamics of metastable brains” by Tozzi et al. Phys. Life Rev. 2017, 21, 46–55. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, S.; Iglesias, P.A. Controlling excitable wave behaviors through the tuning of three parameters. Biol. Cybern. 2019, 113, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Lovecchio, E.; Allegrini, P.; Geneston, E.; West, B.J.; Grigolini, P. From self-organized to extended criticality. Front. Physiol. 2012, 3, 98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chvykov, P.; Berrueta, T.A.; Vardhan, A.; Savoie, W.; Samland, A.; Murphey, T.D.; Wiesenfeld, K.; Goldman, D.I.; England, J.L. Low rattling: A predictive principle for self-organization in active collectives. Science 2021, 371, 90–95. [Google Scholar] [CrossRef]
- Linneweber, G.A.; Andriatsilavo, M.; Dutta, S.B.; Bengochea, M.; Hellbruegge, L.; Liu, G.; Ejsmont, R.K.; Straw, A.D.; Wernet, M.; Hiesinger, P.R.; et al. A neurodevelopmental origin of behavioral individuality in the Drosophila visual system. Science 2020, 367, 1112–1119. [Google Scholar] [CrossRef]
- Shyer, A.E.; Rodrigues, A.R.; Schroeder, G.G.; Kassianidou, E.; Kumar, S.; Harland, R.M. Emergent cellular self-organization and mechanosensation initiate follicle pattern in the avian skin. Science 2017, 357, 811–815. [Google Scholar] [CrossRef] [Green Version]
- Montis, R.; Fusaro, L.; Falqui, A.; Hursthouse, M.B.; Tumanov, N.; Coles, S.J.; Threlfall, T.L.; Horton, P.N.; Sougrat, R.; Lafontaine, A.; et al. Complex structures arising from the self-assembly of a simple organic salt. Nature 2021, 590, 275–278. [Google Scholar] [CrossRef]
- Bengson, J.J.; Kelley, T.A.; Zhang, X.; Wang, J.-L.; Mangun, G.R. Spontaneous Neural Fluctuations Predict Decisions to Attend. J. Cogn. Neurosci. 2014, 26, 2578–2584. [Google Scholar] [CrossRef]
- Ribrault, C.; Sekimoto, K.; Triller, A. From the stochasticity of molecular processes to the variability of synaptic transmission. Nat. Rev. Neurosci. 2011, 12, 375–387. [Google Scholar] [CrossRef] [PubMed]
- Zare, M.; Grigolini, P. Criticality and avalanches in neural networks. Chaos Solitons Fractals 2013, 55, 80–94. [Google Scholar] [CrossRef]
- Wang, B.; Ewang, H.; Normoyle, K.P.; Ejackson, K.; Espitler, K.; Sharrock, M.F.; Miller, C.M.; Ebest, C.; Ellano, D.; Du, R. Brain temperature and its fundamental properties: A review for clinical neuroscientists. Front. Neurosci. 2014, 8, 307. [Google Scholar] [CrossRef] [PubMed]
- Papo, D. Functional significance of complex fluctuations in brain activity: From resting state to cognitive neuroscience. Front. Syst. Neurosci. 2014, 8, 112. [Google Scholar] [CrossRef] [Green Version]
- Sporns, O.; Tononi, G.; Kötter, R. The Human Connectome: A Structural Description of the Human Brain. PLoS Comput. Biol. 2005, 1, e42. [Google Scholar] [CrossRef]
- Reese, T.M.; Brzoska, A.; Yott, D.T.; Kelleher, D.J. Analyzing Self-Similar and Fractal Properties of the C. elegans Neural Network. PLoS ONE 2012, 7, e40483. [Google Scholar] [CrossRef] [Green Version]
- Betzel, R.F.; Griffa, A.; Avena-Koenigsberger, A.; Goñi, J.; Thiran, J.-P.; Hagmann, P.; Sporns, O. Multi-scale community organization of the human structural connectome and its relationship with resting-state functional connectivity. Netw. Sci. 2013, 1, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Pang, J.C.; Gollo, L.L.; Roberts, J.A. Stochastic synchronization of dynamics on the human connectome. NeuroImage 2021, 229, 117738. [Google Scholar] [CrossRef]
- Goodman, S.; Naphade, S.; Khan, M.; Sharma, J.; Cherqui, S. Macrophage polarization impacts tunneling nanotube formation and intercellular organelle trafficking. Sci. Rep. 2019, 9, 14529. [Google Scholar] [CrossRef] [Green Version]
- Ariazi, J.; Benowitz, A.; De Biasi, V.; Boer, M.D.; Cherqui, S.; Cui, H.; Douillet, N.; Eugenin, E.A.; Favre, D.; Goodman, S.; et al. Tunneling Nanotubes and Gap Junctions–Their Role in Long-Range Intercellular Communication during Development, Health, and Disease Conditions. Front. Mol. Neurosci. 2017, 10, 333. [Google Scholar] [CrossRef]
- Sartori-Rupp, A.; Cervantes, D.C.; Pepe, A.; Gousset, K.; Delage, E.; Corroyer-Dulmont, S.; Schmitt, C.; Krijnse-Locker, J.; Zurzolo, C. Correlative cryo-electron microscopy reveals the structure of TNTs in neuronal cells. Nat. Commun. 2019, 10, 342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abounit, S.; Zurzolo, C. Wiring through tunneling nanotubes—From electrical signals to organelle transfer. J. Cell Sci. 2012, 125, 1089–1098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Gerdes, H.-H. Long-distance electrical coupling via tunneling nanotubes. Biochim. Et Biophys. Acta (BBA) Biomembr. 2012, 1818, 2082–2086. [Google Scholar] [CrossRef] [PubMed]
- Austefjord, M.W.; Gerdes, H.-H.; Wang, X. Tunneling nanotubes. Commun. Integr. Biol. 2014, 7, e27934. [Google Scholar] [CrossRef] [PubMed]
- Costanzo, M.; Abounit, S.; Marzo, L.; Danckaert, A.; Chamoun, Z.; Roux, P.; Zurzolo, C. Transfer of polyglutamine aggregates in neuronal cells occurs in tunneling nanotubes. J. Cell Sci. 2013, 126, 3678–3685. [Google Scholar] [CrossRef] [Green Version]
- Gurke, S.; Barroso, J.F.V.; Gerdes, H.-H. The art of cellular communication: Tunneling nanotubes bridge the divide. Histochem. Cell Biol. 2008, 129, 539–550. [Google Scholar] [CrossRef] [Green Version]
- Seyed-Razavi, Y.; Hickey, M.J.; Kuffová, L.; McMenamin, P.G.; Chinnery, H.R. Membrane nanotubes in myeloid cells in the adult mouse cornea represent a novel mode of immune cell interaction. Immunol. Cell Biol. 2012, 91, 89–95. [Google Scholar] [CrossRef]
- Van Essen, D.C.; Smith, S.M.; Barch, D.M.; Behrens, T.E.J.; Yacoub, E.; Ugurbil, K. The WU-Minn Human Connectome Project: An overview. NeuroImage 2013, 80, 62–79. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.W. On Growth and Form; Dover Pubns: Mineola, NY, USA, 1992; ISBN 0486671356. [Google Scholar]
- Barriga, E.H.; Franze, K.; Charras, G.; Mayor, R. Tissue stiffening coordinates morphogenesis by triggering collective cell migration in vivo. Nature 2018, 554, 523–527. [Google Scholar] [CrossRef]
- Chan, C.J.; Costanzo, M.; Ruiz-Herrero, T.; Mönke, G.; Petrie, R.J.; Bergert, M.; Diz-Munoz, A.; Mahadevan, L.; Hiiragi, T. Hydraulic control of mammalian embryo size and cell fate. Nature 2019, 571, 112–116. [Google Scholar] [CrossRef]
- Box, K.; Joyce, B.W.; Devenport, D. Epithelial geometry regulates spindle orientation and progenitor fate during formation of the mammalian epidermis. eLife 2019, 8, e47102. [Google Scholar] [CrossRef] [PubMed]
- Dabaghian, Y.; Brandt, V.L.; Frank, L.M. Reconceiving the hippocampal map as a topological template. eLife 2014, 3, e03476. [Google Scholar] [CrossRef]
- Babichev, A.; Dabaghian, Y.A. Topological Schemas of Memory Spaces. Front. Comput. Neurosci. 2018, 12, 27. [Google Scholar] [CrossRef] [PubMed]
- Dabaghian, Y. Through synapses to spatial memory maps via a topological model. Sci. Rep. 2019, 9, 572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, W.; Guo, X.; Cao, Y.; Mondo, J.A.; Campanale, J.P.; Montell, B.J.; Burrous, H.; Streichan, S.; Gov, N.; Rappel, W.-J.; et al. Tissue topography steers migrating Drosophila border cells. Science 2020, 370, 987–990. [Google Scholar] [CrossRef]
- Kebschull, J.M.; Richman, E.B.; Ringach, N.; Friedmann, D.; Albarran, E.; Kolluru, S.S.; Jones, R.C.; Allen, W.E.; Wang, Y.; Cho, S.W.; et al. Cerebellar nuclei evolved by repeatedly duplicating a conserved cell-type set. Science 2020, 370, abd5059. [Google Scholar] [CrossRef]
- Karzbrun, E.; Khankhel, A.H.; Megale, H.C.; Glasauer, S.M.K.; Wyle, Y.; Britton, G.; Warmflash, A.; Kosik, K.S.; Siggia, E.D.; Shraiman, B.I.; et al. Human neural tube morphogenesis in vitro by geometric constraints. Nature 2021, 599, 268–272. [Google Scholar] [CrossRef]
- Herrera-Rincon, C.; Pai, V.P.; Moran, K.M.; Lemire, J.M.; Levin, M. The brain is required for normal muscle and nerve patterning during early Xenopus development. Nat. Commun. 2017, 8, 587. [Google Scholar]
- Soldatov, R.; Kaucka, M.; Kastriti, M.E.; Petersen, J.; Chontorotzea, T.; Englmaier , L.; Akkuratova , N.; Yang , Y.; Häring , M.; Dyachuk , V.; et al. Spatiotemporal structure of cell fate decisions in murine neural crest. Science 2019, 364, eaas9536. [Google Scholar] [CrossRef] [Green Version]
- Xie, M.; Kamenev, D.; Kaucka, M.; Kastriti, M.E.; Zhou, B.; Artemov, A.V.; Storer, M.; Fried, K.; Adameyko, I.; Dyachuk, V.; et al. Schwann cell precursors contribute to skeletal formation during embryonic development in mice and zebrafish. Proc. Natl. Acad. Sci. USA 2019, 116, 15068–15073. [Google Scholar] [CrossRef] [Green Version]
- Qian, Q.; Nakamura, J.; Fallahi, S.; Gardner, G.C.; Manfra, M.J. Possible nematic to smectic phase transition in a two-dimensional electron gas at half-filling. Nat. Commun. 2017, 8, 1536. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartmann, R.; Singh, P.K.; Pearce, P.; Mok, R.; Song, B.; Díaz-Pascual, F.; Dunkel, J.; Drescher, K. Emergence of three-dimensional order and structure in growing biofilms. Nat. Phys. 2018, 15, 251–256. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ladouceur, A.-M.; Parmar, B.S.; Biedzinski, S.; Wall, J.; Tope, S.G.; Cohn, D.; Kim, A.; Soubry, N.; Reyes-Lamothe, R.; Weber, S.C. Clusters of bacterial RNA polymerase are biomolecular condensates that assemble through liquid–liquid phase separation. Proc. Natl. Acad. Sci. USA 2020, 117, 18540–18549. [Google Scholar] [CrossRef] [PubMed]
- Brangwynne, C.P.; Eckmann, C.R.; Courson, D.S.; Rybarska, A.; Hoege, C.; Gharakhani, J.; Julicher, F.; Hyman, A.A. Germline P Granules Are Liquid Droplets That Localize by Controlled Dissolution/Condensation. Science 2009, 324, 1729–1732. [Google Scholar] [CrossRef] [PubMed]
- Strom, A.R.; Emelyanov, A.V.; Mir, M.; Fyodorov, D.V.; Darzacq, X.; Karpen, G.H. Phase separation drives heterochromatin domain formation. Nature 2017, 547, 241–245. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Le, S.; Lee, M.; Fan, J.-S.; Yang, D.; Yan, J.; Jedd, G. Fungal Wound Healing through Instantaneous Protoplasmic Gelation. Curr. Biol. 2020, 31, 271–282.e5. [Google Scholar] [CrossRef]
- Boke, E.; Ruer, M.; Wühr, M.; Coughlin, M.; Lemaitre, R.; Gygi, S.P.; Alberti, S.; Drechsel, D.; Hyman, A.A.; Mitchison, T.J. Amyloid-like Self-Assembly of a Cellular Compartment. Cell 2016, 166, 637–650. [Google Scholar] [CrossRef] [Green Version]
- Quiroz, F.G.; Fiore, V.F.; Levorse, J.; Polak, L.; Wong, E.; Pasolli, H.A.; Fuchs, E. Liquid-liquid phase separation drives skin barrier formation. Science 2020, 367, aax9554. [Google Scholar] [CrossRef]
- Iwabata, K.; Sugai, U.; Seki, Y.; Furue, H.; Sakaguchi, K. Applications of Biomaterials to Liquid Crystals. Molecules 2013, 18, 4703–4717. [Google Scholar] [CrossRef]
- Mitov, M. Cholesteric liquid crystals in living matter. Soft Matter 2017, 13, 4176–4209. [Google Scholar] [CrossRef]
- Sargazi, M.; Linford, M.R.; Kaykhaii, M. Liquid Crystals in Analytical Chemistry: A Review. Crit. Rev. Anal. Chem. 2018, 49, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Termine, R.; Golemme, A. Charge Mobility in Discotic Liquid Crystals. Int. J. Mol. Sci. 2021, 22, 877. [Google Scholar] [CrossRef] [PubMed]
- Bisoyi, H.K.; Li, Q. Liquid Crystals: Versatile Self-Organized Smart Soft Materials. Chem. Rev. 2021, 122, 4887–4926. [Google Scholar] [CrossRef] [PubMed]
- Mundoor, H.; Wu, J.-S.; Wensink, H.H.; Smalyukh, I.I. Thermally reconfigurable monoclinic nematic colloidal fluids. Nature 2021, 590, 268–274. [Google Scholar] [CrossRef] [PubMed]
- Mundoor, H.; Park, S.; Senyuk, B.; Wensink, H.H.; Smalyukh, I.I. Hybrid molecular-colloidal liquid crystals. Science 2018, 360, 768–771. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, D.; Samiullah, M.H. Photo-Responsive Shape-Memory and Shape-Changing Liquid-Crystal Polymer Networks. Materials 2013, 6, 116–142. [Google Scholar] [CrossRef]
- Chen, V.S.; Morrison, J.P.; Southwell, M.F.; Foley, J.F.; Bolon, B.; Elmore, S.A. Histology Atlas of the Developing Prenatal and Postnatal Mouse Central Nervous System, with Emphasis on Prenatal Days E7.5 to E18.5. Toxicol. Pathol. 2017, 45, 705–744. [Google Scholar] [CrossRef] [Green Version]
- McDonald, N.A.; Fetter, R.D.; Shen, K. Assembly of synaptic active zones requires phase separation of scaffold molecules. Nature 2020, 588, 454–458. [Google Scholar] [CrossRef] [PubMed]
- Kießling, T.R.; Stange, R.; Käs, A.J.; Fritsch, A.W. Thermorheology of living cells—Impact of temperature variations on cell mechanics. New J. Phys. 2013, 15, 045026. [Google Scholar] [CrossRef]
- Sotoma, S.; Zhong, C.; Kah, J.C.Y.; Yamashita, H.; Plakhotnik, T.; Harada, Y.; Suzuki, M. In situ measurements of intracellular thermal conductivity using heater-thermometer hybrid diamond nanosensors. Sci. Adv. 2021, 7, eabd7888. [Google Scholar] [CrossRef]
- Tanimoto, R.; Hiraiwa, T.; Nakai, Y.; Shindo, Y.; Oka, K.; Hiroi, N.; Funahashi, A. Detection of Temperature Difference in Neuronal Cells. Sci. Rep. 2016, 6, 22071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Ma, J.; Zhan, X.; Yang, L.; Jia, Y. Temperature effect on memristive ion channels. Cogn. Neurodyn. 2019, 13, 601–611. [Google Scholar] [CrossRef]
- Long, M.A.; Fee, M.S. Using temperature to analyse temporal dynamics in the songbird motor pathway. Nature 2008, 456, 189–194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalmbach, A.S.; Waters, J. Brain surface temperature under a craniotomy. J. Neurophysiol. 2012, 108, 3138–3146. [Google Scholar] [CrossRef] [PubMed]
- Jizba, P.; Arimitsu, T. The world according to Renyi: Thermodynamics of fractal systems. AIP Conf. Proc. 2001, 597, 341–348. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. On q-non-extensive statistics with non-Tsallisian entropy. arXiv 2015, arXiv:1501.07386. [Google Scholar] [CrossRef] [Green Version]
- Lu, G.; Saunoriene, L.; Gelžinis, A.; Petrauskiene, V.; Ragulskis, M. Visual integration of vibrating images in time. Opt. Eng. 2018, 57, 093107. [Google Scholar] [CrossRef]
- Bach, M. Optische Täuschungen und Andere Außergewöhnliche Sehphänomene; Amazon.com, Inc.: Bellevue, WA, USA, 2022; ISBN 978-3-942825-97-9. [Google Scholar]
- Slotnick, S.D. Visual Memory and Visual Perception Recruit Common Neural Substrates. Behav. Cogn. Neurosci. Rev. 2004, 3, 207–221. [Google Scholar] [CrossRef] [Green Version]
- Read, J.C. Visual Perception: Monovision Can Bias the Apparent Depth of Moving Objects. Curr. Biol. 2019, 29, R738–R740. [Google Scholar] [CrossRef]
- Read, J.C.; Cumming, B.G. Visual Perception: Neural Networks for Stereopsis. Curr. Biol. 2017, 27, R594–R596. [Google Scholar] [CrossRef] [Green Version]
- Fleming, R.W. Visual perception: Colour brings shape into stark relief. Curr. Biol. 2022, 32, R272–R273. [Google Scholar] [CrossRef] [PubMed]
- Wexler, M.; van Boxtel, J.J. Depth perception by the active observer. Trends Cogn. Sci. 2005, 9, 431–438. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.K.; Liu, X.; Wu, Y.; Zhang, J.; Yuan, J.; Zhang, Z.; Tsai, D.P. A Meta-device for Intelligent Depth Perception. Adv. Mater. 2022, 2107465. [Google Scholar] [CrossRef]
- Read, J.C. Binocular Vision and Stereopsis Across the Animal Kingdom. Annu. Rev. Vis. Sci. 2021, 7, 389–415. [Google Scholar] [CrossRef]
- Chopin, A.; Chan, S.W.; Guellai, B.; Bavelier, D.; Levi, D.M. Binocular non-stereoscopic cues can deceive clinical tests of stereopsis. Sci. Rep. 2019, 9, 5789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitsudo, H. Neural Mechanism Underlying Stereoscopic Depth Perception: Why are the Two Eyes Aligned? Brain Nerve 2021, 3, 1225–1229. [Google Scholar] [CrossRef]
- Ding, J.; Levi, D.M. A unified model for binocular fusion and depth perception. Vis. Res. 2020, 180, 11–36. [Google Scholar] [CrossRef]
- Thompson, L.; Ji, M.; Rokers, B.; Rosenberg, A. Contributions of binocular and monocular cues to motion-in-depth perception. J. Vis. 2019, 19, 2. [Google Scholar] [CrossRef] [Green Version]
- Harris, J.M.; Wilcox, L.M. The role of monocularly visible regions in depth and surface perception. Vis. Res. 2009, 49, 2666–2685. [Google Scholar] [CrossRef] [Green Version]
- Forrester, J.V.; Dick, A.D.; McMenamin, P.G.; Roberts, F.; Pearlman, E. Physiology of vision and the visual system. In The Eye, 4th ed.; Saunders Ltd.: Philadelphia, PA, USA, 2016; pp. 269–337.e2. [Google Scholar] [CrossRef]
- Schaeffel, F. Vergleichende Betrachtung von Lichtempfindlichkeit, Tiefenwahrnehmung und Bewegungswahrnehmung bei Tier und Mensch Comparative analysis of light sensitivity, depth and motion perception in animals and humans. Der Ophthalmol. 2017, 114, 997–1007. [Google Scholar] [CrossRef]
- Anzai, A.; DeAngelis, G.C. Neural computations underlying depth perception. Curr. Opin. Neurobiol. 2010, 20, 367–375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boone, H.C.; Samonds, J.M.; Crouse, E.C.; Barr, C.; Priebe, N.J.; McGee, A.W. Natural binocular depth discrimination behavior in mice explained by visual cortical activity. Curr. Biol. 2021, 31, 2191–2198.e3. [Google Scholar] [CrossRef] [PubMed]
- Walker, W. Monge’s Theorem in Many Dimensions. Math. Gaz. 1976, 60, 185–188. [Google Scholar] [CrossRef]
- Balajti, Z.; Dudás, I. The Monge theorem and its application in engineering practice. Int. J. Adv. Manuf. Technol. 2017, 91, 739–749. [Google Scholar] [CrossRef]
- Ermis, T.; Gelisgen, O. Does the monge theorem apply to some non-euclidean geometries? Glob. J. Adv. Res. Class. Mod. Geom. 2021, 10, 122–127. [Google Scholar]
- Mach, E. Contributions to the Analysis of Sensations; The Open Court Publishing Co.: Chicago, IL, USA, 1897. [Google Scholar]
- Gjorevski, N.; Nikolaev, M.; Brown, T.E.; Mitrofanova, O.; Brandenberg, N.; DelRio, F.W.; Yavitt, F.M.; Liberali, P.; Anseth, K.S.; Lutolf, M.P. Tissue geometry drives deterministic organoid patterning. Science 2022, 375, eaaw9021. [Google Scholar] [CrossRef]
- Kra, I. Cohomology of kleinian groups. Proc. Natl. Acad. Sci. USA 1969, 63, 655–660. [Google Scholar] [CrossRef] [Green Version]
- Dummit, D.S.; Foote, R.M. Abstract Algebra, 3rd ed.; WolframAlpha: Hoboken, NJ, USA, 2003; ISBN 0-471-43334-9. [Google Scholar]
- Stasheff, J.D. Continuous cohomology of groups and classifying spaces. Bull. Am. Math. Soc. 1978, 84, 513–531. [Google Scholar] [CrossRef] [Green Version]
- Minchenko, A.; Ovchinnikov, A. Triviality of differential Galois cohomology of linear differential algebraic groups. Commun. Algebra 2019, 47, 5094–5100. [Google Scholar] [CrossRef]
- Lurie, J. On Infinity Topoi. arXiv 2003, arXiv:math/0306109. [Google Scholar]
- Lurie, J. Higher Topos Theory. arXiv 2008, arXiv:math/0608040. [Google Scholar]
- Grothendieck, A. Sur quelques points d’algèbre homologique, I. Tohoku Math. J. 1957, 9, 119–221. [Google Scholar] [CrossRef]
- Serre, J.-P. Faisceaux Algebriques Coherents. Ann. Math. 1955, 61, 197. [Google Scholar] [CrossRef]
- Domokos, G.; Jerolmack, D.J.; Kun, F.; Török, J. Plato’s cube and the natural geometry of fragmentation. Proc. Natl. Acad. Sci. USA 2020, 117, 18178–18185. [Google Scholar] [CrossRef] [PubMed]
- Twarock, R.; Luque, A. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat. Commun. 2019, 10, 4414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palotás, J.; Martens, J.; Berden, G.; Oomens, J. The infrared spectrum of protonated buckminsterfullerene C60H+. Nat. Astron. 2019, 4, 240–245. [Google Scholar] [CrossRef]
- McGrath, R.; Sharma, H.R.; Smerdon, J.A.; Ledieu, J. The memory of surfaces: Epitaxial growth on quasi-crystals. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2012, 370, 2930–2948. [Google Scholar] [CrossRef]
- Koju, V.; Robertson, W.M. Excitation of Bloch-like surface waves in quasi-crystals and aperiodic dielectric multilayers. Opt. Lett. 2016, 41, 2915–2918. [Google Scholar] [CrossRef]
- Mustafa, M.-E.; Amin, M.; Siddiqui, O.; Tahir, F.A. Quasi-Crystal Metasurface for Simultaneous Half- and Quarter-Wave Plate Operation. Sci. Rep. 2018, 8, 15743. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.-Y.; Mason, T.G. A Brownian quasi-crystal of pre-assembled colloidal Penrose tiles. Nature 2018, 561, 94–99. [Google Scholar] [CrossRef]
- Bosi, S.; Da Ros, T.; Spalluto, G.; Prato, M. Fullerene derivatives: An attractive tool for biological applications. Eur. J. Med. Chem. 2003, 38, 913–923. [Google Scholar] [CrossRef]
- Nierengarten, I.; Nierengarten, J.-F. Fullerene Sugar Balls: A New Class of Biologically Active Fullerene Derivatives. Chem. Asian J. 2014, 9, 1436–1444. [Google Scholar] [CrossRef]
- Kazemzadeh, H.; Mozafari, M. Fullerene-based delivery systems. Drug Discov. Today 2019, 24, 898–905. [Google Scholar] [CrossRef]
- Gülseren, G.; Saylam, A.; Marion, A.; Özçubukçu, S. Fullerene-Based Mimics of Biocatalysts Show Remarkable Activity and Modularity. ACS Appl. Mater. Interfaces 2021, 13, 45854–45863. [Google Scholar] [CrossRef] [PubMed]
- Tozzi, A.; Peters, J.F.; Ori, O. Fullerenic-topological tools for honeycomb nanomechanics. Toward a fullerenic approach to brain functions. Full- Nanotub. Carbon Nanostruct. 2017, 25, 282–288. [Google Scholar] [CrossRef]
- Tozzi, A.; Peters, J.F.; Ori, O. Cracking the barcode of fullerene-like cortical microcolumns. Neurosci. Lett. 2017, 644, 100–106. [Google Scholar] [CrossRef] [PubMed]
- Telley, L.; Agirman, G.; Prados, J.; Amberg, N.; Fièvre, S.; Oberst, P.; Bartolini, G.; Vitali, I.; Cadilhac, C.; Hippenmeyer, S.; et al. Temporal patterning of apical progenitors and their daughter neurons in the developing neocortex. Science 2019, 364, eaav2522. [Google Scholar] [CrossRef] [Green Version]
- Daoud, A.M.P.; Popovic, M.; Dondorp, W.J.; Bustos, M.T.; Bredenoord, A.L.; Lopes, S.M.C.D.S.; Brink, S.C.V.D.; Roelen, B.; De Wert, G.M.W.R.; Heindryckx, B. Modelling human embryogenesis: Embryo-like structures spark ethical and policy debate. Hum. Reprod. Updat. 2020, 26, 779–798. [Google Scholar] [CrossRef]
- Yang, J.; Fu, H.; Tam, C.; Liu, P. Expanded potential: The key to synthetic embryo? Curr. Opin. Genet. Dev. 2020, 64, 72–77. [Google Scholar] [CrossRef]
- Tomoda, K.; Kime, C. Synthetic embryology: Early mammalian embryo modeling systems from cell cultures. Dev. Growth Differ. 2021, 63, 116–126. [Google Scholar] [CrossRef]
- Tarazi, S.; Aguilera-Castrejon, A.; Joubran, C.; Ghanem, N.; Ashouokhi, S.; Roncato, F.; Wildschutz, E.; Haddad, M.; Oldak, B.; Gomez-Cesar, E.; et al. Post-gastrulation synthetic embryos generated ex utero from mouse naive ESCs. Cell 2022, 185, 3290–3306. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tozzi, A.; Mariniello, L. Unusual Mathematical Approaches Untangle Nervous Dynamics. Biomedicines 2022, 10, 2581. https://doi.org/10.3390/biomedicines10102581
Tozzi A, Mariniello L. Unusual Mathematical Approaches Untangle Nervous Dynamics. Biomedicines. 2022; 10(10):2581. https://doi.org/10.3390/biomedicines10102581
Chicago/Turabian StyleTozzi, Arturo, and Lucio Mariniello. 2022. "Unusual Mathematical Approaches Untangle Nervous Dynamics" Biomedicines 10, no. 10: 2581. https://doi.org/10.3390/biomedicines10102581
APA StyleTozzi, A., & Mariniello, L. (2022). Unusual Mathematical Approaches Untangle Nervous Dynamics. Biomedicines, 10(10), 2581. https://doi.org/10.3390/biomedicines10102581







