Pigeons: A Novel GUI Software for Analysing and Parsing High Density Heterologous Oligonucleotide Microarray Probe Level Data
Abstract
:1. Introduction
2. Methods and Algorithms
 1”) and a genotype derived from a domesticated landrace (DipC; Parent 2; P2; “
1”) and a genotype derived from a domesticated landrace (DipC; Parent 2; P2; “  2”) was made and a single hybrid seed (F1) allowed to grow and produce an F2 population of seed. This population was planted and recorded at the Tropical Crops Research Unit at the University of Nottingham in 2003. Individual plants were recorded for numerous traits, including “number of stems per plant”. The extremes of the “number of stems per plant” distribution were identified and 10 plants from each extreme had DNA extracted by standard techniques and mixed in equal amounts to produce a bulked sample of “low stem number” (“
2”) was made and a single hybrid seed (F1) allowed to grow and produce an F2 population of seed. This population was planted and recorded at the Tropical Crops Research Unit at the University of Nottingham in 2003. Individual plants were recorded for numerous traits, including “number of stems per plant”. The extremes of the “number of stems per plant” distribution were identified and 10 plants from each extreme had DNA extracted by standard techniques and mixed in equal amounts to produce a bulked sample of “low stem number” (“  3”) and a bulked sample of “high stem number” (“
3”) and a bulked sample of “high stem number” (“  4”), respectively.
4”), respectively.2.1. ATM
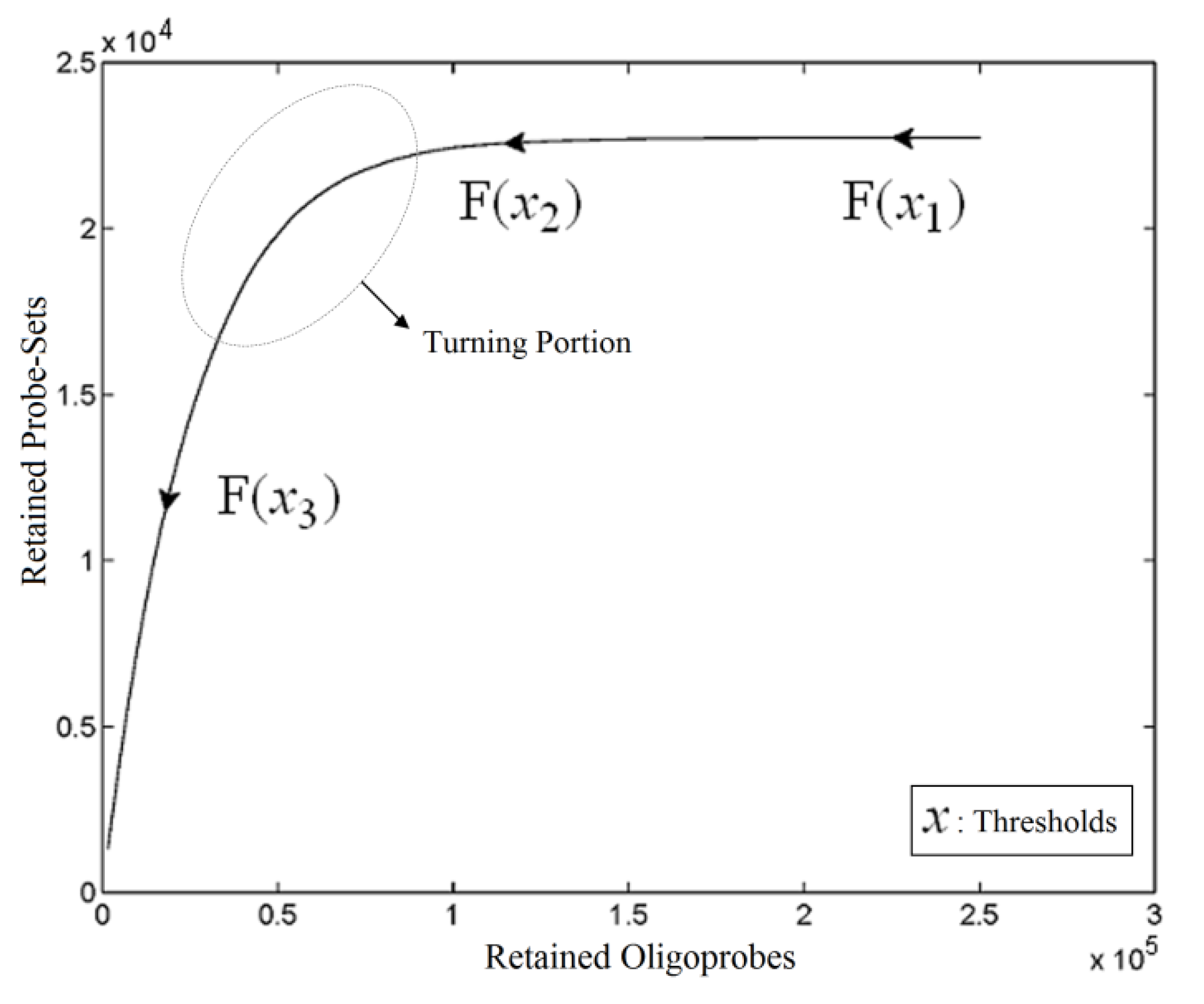
 →
→  2 is defined as follows:
2 is defined as follows:

 =
=  3, let
3, let  be an r-dimensional subspace of
be an r-dimensional subspace of  and
and  ┴ be the orthogonal complement of
┴ be the orthogonal complement of  . Given a matrix B3×r such that the column space of B is
. Given a matrix B3×r such that the column space of B is  , and then for
, and then for  there exists a projector P to project v onto
there exists a projector P to project v onto  along
along  ┴, i.e., Pv = u, u ϵ
┴, i.e., Pv = u, u ϵ  . The unique linear operator P can be acquired by P = B(BTB)-1BT, in particular, if B constitutes orthonormal bases, then P = BBT. During simplification of the system, the goal at this stage is to minimize the loss of information relevant to the problem of concern. As a consequence, given B (e.g., [0,0,1]T) and n numbers of vectors of thresholds with their retention units, and after linear transformation of each vector vi ϵ
. The unique linear operator P can be acquired by P = B(BTB)-1BT, in particular, if B constitutes orthonormal bases, then P = BBT. During simplification of the system, the goal at this stage is to minimize the loss of information relevant to the problem of concern. As a consequence, given B (e.g., [0,0,1]T) and n numbers of vectors of thresholds with their retention units, and after linear transformation of each vector vi ϵ  , i = 1,…, n we will then gain a learning data set D = {ui: Pvi = ui ϵ
, i = 1,…, n we will then gain a learning data set D = {ui: Pvi = ui ϵ  that ideally has the most informative features for turning portion discovery. Suppose that all the data vectors in TP have been projected onto a particular area, we define the area as a hotspot D′ such that
that ideally has the most informative features for turning portion discovery. Suppose that all the data vectors in TP have been projected onto a particular area, we define the area as a hotspot D′ such that

 , the weighted within-class sum of squares, to quantify how good the quality of clustering models is, the FCM attempts to find the best allocation of data to clusters with a gradual membership matrix M. Given a number of clusters c (1 < c < n), then the learning data set
, the weighted within-class sum of squares, to quantify how good the quality of clustering models is, the FCM attempts to find the best allocation of data to clusters with a gradual membership matrix M. Given a number of clusters c (1 < c < n), then the learning data set  is dominated by fuzzy sets
is dominated by fuzzy sets  and the fuzzy partition matrix M =[mij]c×n, where
and the fuzzy partition matrix M =[mij]c×n, where  and
and  . For the individual entries in M, mij are the membership degree of element uj ϵ D to cluster i, i.e.,
. For the individual entries in M, mij are the membership degree of element uj ϵ D to cluster i, i.e.,  . Let
. Let  be a set of cluster prototypes so that each cluster
be a set of cluster prototypes so that each cluster  is represented with a cluster centre vector ωi, and the objective function with two constraints can then be defined as below:
is represented with a cluster centre vector ωi, and the objective function with two constraints can then be defined as below:



 >1 is termed the “fuzzifier” or weighting exponent, and dij is the distance between object uj and cluster centre ωi, within ATM, the Euclidean inner product norm denoted by ‖∙‖ is taken, i.e., dij = ‖uj - ωi‖. The purpose of the clustering algorithm is to obtain the solution M and Ω minimizing the cost function
>1 is termed the “fuzzifier” or weighting exponent, and dij is the distance between object uj and cluster centre ωi, within ATM, the Euclidean inner product norm denoted by ‖∙‖ is taken, i.e., dij = ‖uj - ωi‖. The purpose of the clustering algorithm is to obtain the solution M and Ω minimizing the cost function  , and this can be carried out by:
, and this can be carried out by:


 is minimized by an alternating optimization (AO) scheme, i.e., the membership degrees are first optimized given recently fixed cluster parameters, followed by optimizing the cluster prototypes given currently fixed membership degrees. This reiterative procedure will be repeated until the cluster centres have reached equilibrium which is equivalent in mathematics to the optimal objective function
is minimized by an alternating optimization (AO) scheme, i.e., the membership degrees are first optimized given recently fixed cluster parameters, followed by optimizing the cluster prototypes given currently fixed membership degrees. This reiterative procedure will be repeated until the cluster centres have reached equilibrium which is equivalent in mathematics to the optimal objective function  .
. ,
,  ) are concentrated for the purpose of deciphering since most of elements of
) are concentrated for the purpose of deciphering since most of elements of  are very likely to be projected from vectors in stagnant phase while data points near the beginning of the sharp drop have mostly fallen into
are very likely to be projected from vectors in stagnant phase while data points near the beginning of the sharp drop have mostly fallen into  . Thus, we let D′ be the subset of the union of the two clusters and set the infimum and the supremum of J according to the objects whose membership values are the maximum of
. Thus, we let D′ be the subset of the union of the two clusters and set the infimum and the supremum of J according to the objects whose membership values are the maximum of  and
and  , i.e.,
, i.e.,

 and
and  have them in common with various membership values. Owing to the grayness characteristic and the continuity of the learning-like curve, we believe that a good threshold value for parsing the Affymetrix chip description files would come from a projected object that simultaneously belongs to the two clusters with remarkable membership degrees. As a result, the fuzzy boundary can enable us to offer a more reasonable selection of threshold boundary cut-offs. Two indices, l and k, are utilised to determine the highly likely threshold boundary cut-offs and the automated threshold value, determined by
have them in common with various membership values. Owing to the grayness characteristic and the continuity of the learning-like curve, we believe that a good threshold value for parsing the Affymetrix chip description files would come from a projected object that simultaneously belongs to the two clusters with remarkable membership degrees. As a result, the fuzzy boundary can enable us to offer a more reasonable selection of threshold boundary cut-offs. Two indices, l and k, are utilised to determine the highly likely threshold boundary cut-offs and the automated threshold value, determined by

 and another closed interval [xl,xk] is constructed as the target interval I'. Let be u the arithmetic mean of the elements of
and another closed interval [xl,xk] is constructed as the target interval I'. Let be u the arithmetic mean of the elements of  , and xATM can also be calculated by linear interpolation or by the Lagrange polynomial, as shown in the following formulae:
, and xATM can also be calculated by linear interpolation or by the Lagrange polynomial, as shown in the following formulae:

2.2. DFC
 1 &
1 &  2 for the two parent samples and with
2 for the two parent samples and with  3 &
3 &  4 for the two F2 bulks. In practice, these F2 bulks are constructed from the pooled DNA of F2 individuals. These are derived from the controlled cross between the parental genotypes with allocation to the contrasting bulk based upon a specific trait of interest. The phenotype classification is a necessary prerequisite for the numerical analysis of potential SFP markers.
4 for the two F2 bulks. In practice, these F2 bulks are constructed from the pooled DNA of F2 individuals. These are derived from the controlled cross between the parental genotypes with allocation to the contrasting bulk based upon a specific trait of interest. The phenotype classification is a necessary prerequisite for the numerical analysis of potential SFP markers.  1 and
1 and  3 are classified into one type under a single trait experiment whereas
3 are classified into one type under a single trait experiment whereas  2 and
2 and  4 belong to the other trait version—the prerequisite can be denoted as
4 belong to the other trait version—the prerequisite can be denoted as  . Let N be the number of genes and #(
. Let N be the number of genes and #(  ) be the cardinal number of a probe-set
) be the cardinal number of a probe-set  then each chip can be represented as follows:
then each chip can be represented as follows:



 and that between the offspring
and that between the offspring  , a number of logical criteria are applied to globally screen and search Affymetrix’s single oligoprobes for SFP markers. For
, a number of logical criteria are applied to globally screen and search Affymetrix’s single oligoprobes for SFP markers. For  , let the first condition be bijm > xATM since any signals whose intensities are below the threshold should not be used for good probes in the analysis of heterologous data—this satisfies the demand of the XSpecies technology. When the first criterion holds, the DFC enables the procedure to run the second condition with the two fold-change indicators FCij1 and FCij2, FCij1 ≥ ϵ1 and FCij2 ≥ ϵ2, to measure whether
, let the first condition be bijm > xATM since any signals whose intensities are below the threshold should not be used for good probes in the analysis of heterologous data—this satisfies the demand of the XSpecies technology. When the first criterion holds, the DFC enables the procedure to run the second condition with the two fold-change indicators FCij1 and FCij2, FCij1 ≥ ϵ1 and FCij2 ≥ ϵ2, to measure whether  still holds at the genomic level. The FC approach is commonly used in microarray data analysis to identify differentially expressed genes (DEGs) between a treatment and a control. Calculated as the ratio of two conditions/samples, the FC gives the absolute ratio of normalized intensities in a non-log scale. We extend the same concept in our approach by introducing an additional FC—one ratio assesses the differential hybridisation within G1 and the other assesses the differential hybridisation within G2. The extra FC tests whether the difference in phenotype could result from a difference in genotype at a single locus. Therefore, when there are any differentially hybridised oligonucleotides for the feature of interest between the two parental genotypes, the inherited attribute of
still holds at the genomic level. The FC approach is commonly used in microarray data analysis to identify differentially expressed genes (DEGs) between a treatment and a control. Calculated as the ratio of two conditions/samples, the FC gives the absolute ratio of normalized intensities in a non-log scale. We extend the same concept in our approach by introducing an additional FC—one ratio assesses the differential hybridisation within G1 and the other assesses the differential hybridisation within G2. The extra FC tests whether the difference in phenotype could result from a difference in genotype at a single locus. Therefore, when there are any differentially hybridised oligonucleotides for the feature of interest between the two parental genotypes, the inherited attribute of  would imply that we could expect those differentially hybridised oligonucleotides to have also been transmitted into the F2 individuals. In a word, the corresponding fold-change of the F2 is introduced as a cross-check mechanism for identifying SFPs which are consistent between parental genotype/trait and bulk genotype/trait. The mixture of F2 genotypes (which are bulked according to the trait difference which segregates within the cross) should mean that the attribute difference is only detected when the location of the parental SFP is close to the gene controlling the trait difference. The accuracy of this approach is dependent upon bulk size used. Smaller bulk sizes will lead to the identification of SFPs which are located distantly from (and probably on different chromosomes to) the target trait associated SFPs. Oligo-probes that satisfy the second criterion above are potential SFP markers distinguishing the two phenotypes and could be further tested and used for genetic mapping of the gene controlling the phenotypic difference.
would imply that we could expect those differentially hybridised oligonucleotides to have also been transmitted into the F2 individuals. In a word, the corresponding fold-change of the F2 is introduced as a cross-check mechanism for identifying SFPs which are consistent between parental genotype/trait and bulk genotype/trait. The mixture of F2 genotypes (which are bulked according to the trait difference which segregates within the cross) should mean that the attribute difference is only detected when the location of the parental SFP is close to the gene controlling the trait difference. The accuracy of this approach is dependent upon bulk size used. Smaller bulk sizes will lead to the identification of SFPs which are located distantly from (and probably on different chromosomes to) the target trait associated SFPs. Oligo-probes that satisfy the second criterion above are potential SFP markers distinguishing the two phenotypes and could be further tested and used for genetic mapping of the gene controlling the phenotypic difference.2.3. POST
 the value is calculated by the following formula:
the value is calculated by the following formula:

 . The MA-value is named after the MA plot, a very useful tool in cDNA and GeneChip® microarray data analysis [17,18,19], and is the average intensity ratio between parental samples and F2 bulks in a base 2 logarithmic scale with a mnemonic for subtraction and a mnemonic for addition. The POST then uses the MA-value and a single sample t-test to statistically assess differentially hybridised oligonucleotides between the parent group and the offspring group and to test in a probe-set i whether or not there is significant difference between an interrogated probe k and the other probes in that probe-set, in terms of their log ratios. As a test statistic, the average of the MA-values of each of the probe-pairs except the probe k is denoted by ρik and determined by:
. The MA-value is named after the MA plot, a very useful tool in cDNA and GeneChip® microarray data analysis [17,18,19], and is the average intensity ratio between parental samples and F2 bulks in a base 2 logarithmic scale with a mnemonic for subtraction and a mnemonic for addition. The POST then uses the MA-value and a single sample t-test to statistically assess differentially hybridised oligonucleotides between the parent group and the offspring group and to test in a probe-set i whether or not there is significant difference between an interrogated probe k and the other probes in that probe-set, in terms of their log ratios. As a test statistic, the average of the MA-values of each of the probe-pairs except the probe k is denoted by ρik and determined by:



 , …, k - 1, k + 1, …, #(Bi} and let δi(1) ≤ δi(2) ≤… δi(ni) be the observations of Δik written in ascending order. We define the sample γ-trimmed mean δik to account for probe-specific fluctuations in a probe-set i and its value is calculated by
, …, k - 1, k + 1, …, #(Bi} and let δi(1) ≤ δi(2) ≤… δi(ni) be the observations of Δik written in ascending order. We define the sample γ-trimmed mean δik to account for probe-specific fluctuations in a probe-set i and its value is calculated by



3. Results and Discussion
3.1. Software Implementation
3.2. Case Studies of ATM
| Species | Selected Cut-off | Automated Threshold Mapping (ATM) | Reference | |||
|---|---|---|---|---|---|---|
| % | Suggested Cut-off | Target Interval | Tolerance Interval | |||
| Brassica oleracea L. | 400 | 2.17 | 391.34 a | [351,426] a | [272,454] a | Hammond et al. 2005 [3] |
| Thlaspi caerulescens | 300 | 10.54 | 331.63 a | [297,363] a | [234,387] a | Hammond et al. 2006 [4] |
| Musa (Banana) | 550 | 10.47 | 492.40 b | [399,586] b | [305,698] b | Davey et al. 2009 [7] |
| Equine (Horse) | 100 | 5.93 | 94.07 a | [82,106] a | [65,119] a | Graham et al. 2010 [22] |
| Ovine (Sheep) | 450 | 6.93 | 481.20 b | [381,582] b | [284,694] b | Graham et al. 2011 [23] |
3.3. Examples of an SFP Screen
 , as defined in the methodology section. The probe-level raw data were then background-adjusted and quantile-normalized using the RMA method [18,19] so that these preprocessed intensity signals could be carried over into high level analyses.
, as defined in the methodology section. The probe-level raw data were then background-adjusted and quantile-normalized using the RMA method [18,19] so that these preprocessed intensity signals could be carried over into high level analyses.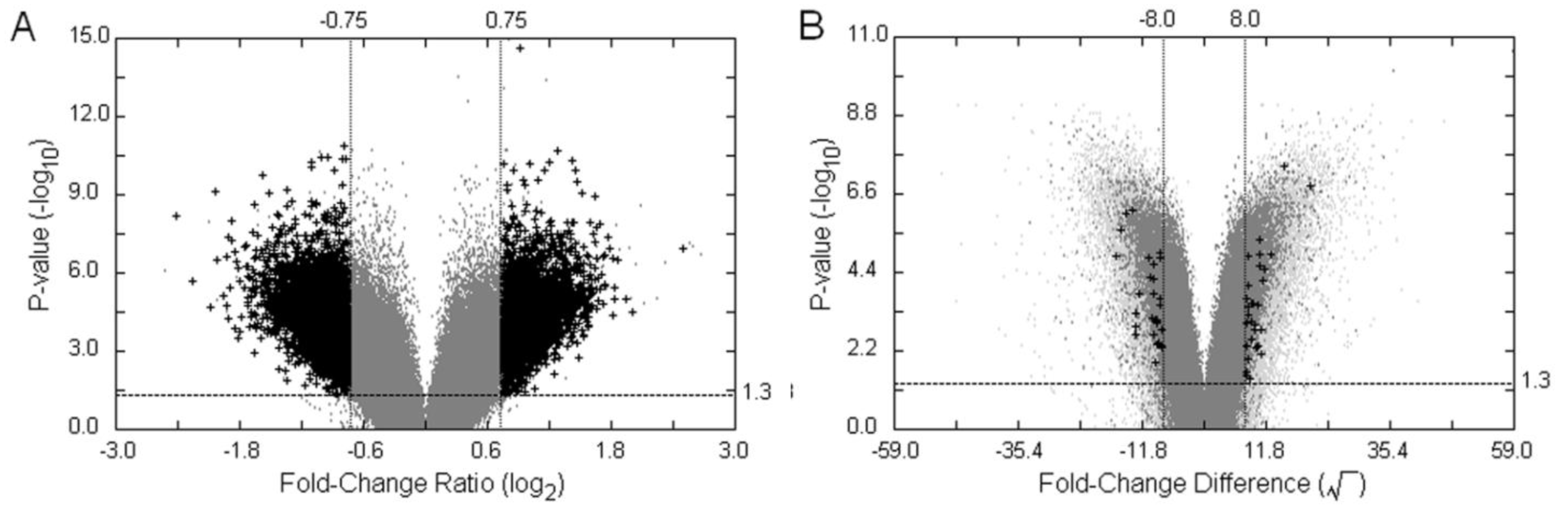
| Method | Filtering Criteria | Number of potentiallydifferential hybridization d | ||||
|---|---|---|---|---|---|---|
| VP | p-value a | MA-value | FCF2 | TH b,c | Probe-pairs | Probe-Sets |
| VP1 | <0.05 | ≥|0.75| | - | - | 13,694 | 10,492 |
| VP2 | <0.05 | ≥|0.75| | ≥1.5 | - | 7903 | 6722 |
| VP3 | <0.05 | ≥|0.75| | - | >93.04 | 125 | 124 |
| VP4 | <0.05 | ≥|0.75| | ≥1.5 | >93.04 | 10 | 10 |
| TVP e | p-value a | FCD-value | FCF2 | FCP | Probe-pairs | Probe-Sets |
| TVP1 | <0.05 | ≥|8.0| | - | - | 1,637 | 1,563 |
| TVP2 | <0.05 | ≥|8.0| | ≥1.5 | - | 59 | 59 |
| TVP3 | <0.05 | ≥|8.0| | - | >2 | 50 | 50 |
| TVP4 | <0.05 | ≥|8.0| | ≥1.5 | >2 | 8 | 8 |
| DFC | FCP | FCF2 | TH b,c | Probe-pairs | Probe-Sets | |
| DFC1 | ≥2 | ≥1.5 | - | 3,360 | 3,132 | |
| DFC2 | ≥2 | ≥1.5 | >93.04 | 5 | 5 | |

4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Wang, J. Computational biology of genome expression and regulation—A review of microarray bioinformatics. J. Environ. Pathol. Toxicol. Oncol. 2008, 27, 157–179. [Google Scholar] [CrossRef]
- Kumar, R.M. The widely used diagnostics “DNA microarrays”—A review. Am. J. Infect. Dis. 2009, 5, 214–225. [Google Scholar] [CrossRef]
- Hammond, J.P.; Broadley, M.R.; Craigon, D.J.; Higgins, J.; Emmerson, Z.F.; Townsend, H.J.; White, P.J.; May, S.T. Using genomic DNA-based probe-selection to improve the sensitivity of high-density oligonucleotide arrays when applied to heterologous species. Plant Methods 2005, 1, 10. [Google Scholar] [CrossRef]
- Hammond, J.P.; Bowen, H.C.; White, P.J.; Mills, V.; Pyke, K.A.; Baker, A.J.; Whiting, S.N.; May, S.T.; Broadley, M.R. A comparison of the Thlaspi caerulescens and Thlaspi arvense shoot transcriptomes. New Phytol. 2006, 170, 239–260. [Google Scholar] [CrossRef]
- Graham, N.S.; Broadley, M.R.; Hammond, J.P.; White, P.J.; May, S.T. Optimising the analysis of transcript data using high density oligonucleotide arrays and genomic DNA-based probe selection. BMC Genomics 2007, 8, 344. [Google Scholar] [CrossRef]
- Broadley, M.R.; White, P.J.; Hammond, J.P.; Graham, N.S.; Bowen, H.C.; Emmerson, Z.F.; Fray, R.G.; Iannetta, P.P.M.; McNicol, J.W.; May, S.T. Evidence of neutral transcriptome evolution in plants. New Phytol. 2008, 180, 587–593. [Google Scholar] [CrossRef]
- Davey, M.W.; Graham, N.S.; Vanholme, B.; Swennen, R.; May, S.T.; Keulemans, J. Heterologous oligonucleotide microarrays for transcriptomics in a non-model species; A proof-of-concept study of drought stress in Musa. BMC Genomics 2009, 10, 436. [Google Scholar] [CrossRef] [Green Version]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 790–842. [Google Scholar]
- Xu, R.; Wunsch, D., II. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef]
- Schena, M.; Shalon, D.; Heller, R.; Chai, A.; Brown, P.O.; Davis, R.W. Parallel human genome analysis: Microarray-based expression monitoring of 1,000 genes. Proc. Natl Acad. Sci. USA 1996, 93, 10614–10619. [Google Scholar] [CrossRef]
- Cui, X.; Churchill, G.A. Statistical tests for differential expression in cDNA microarray experiments. Genome Biol. 2003, 4, 210. [Google Scholar] [CrossRef] [Green Version]
- Kooperberg, C.; Aragaki, A.; Strand, A.D.; Olson, J.M. Significance testing for small microarray experiments. Stat. Med. 2005, 24, 2281–2298. [Google Scholar] [CrossRef]
- Mayes, S.; Stadler, S.; Basu, S.; Murchie, E.; Massawe, F.; Kilian, A.; Roberts, J.A.; Mohler, V.; Wenzel, G.; Beena, R.; et al. BAMLINK—A cross disciplinary programme to enhance the role of bambara groundnut (Vigna subterranea L. Verdc.) for food security in Africa and India. Acta Hortic. 2009, 806, 137–150. [Google Scholar]
- Basu, S.; Mayes, S.; Davey, M.; Roberts, J.A.; Azam-Ali, S.N.; Mithren, R.; Pasquet, R.S. Inheritance of “domestication” traits in bambara groundnut (Vigna subterranea L. Verdc.). Euphytica 2007, 157, 59–68. [Google Scholar] [CrossRef]
- Bezdek, J. Pattern Recognition with Fuzzy Objective Function Algorithms, 1st ed.; Plenum Press: New York, NY, USA, 1981; pp. 95–154. [Google Scholar]
- Jeffery, I.B.; Higgins, D.G.; Culhane, A.C. Comparison and evaluation of methods for generating differentially expressed gene lists from microarray data. BMC Bioinform. 2006, 7, 359. [Google Scholar] [CrossRef]
- Dudoit, S.; Yang, Y.H.; Callow, M.J.; Speed, T.P. Statistical methods for identifying genes with differential expression in replicated cDNA microarray experiments. Stat. Sin. 2002, 12, 111–139. [Google Scholar]
- Irizarry, R.A.; Hobbs, B.; Collin, F.; Beazer-Barclay, Y.D.; Antonellis, K.J.; Scherf, U.; Speed, T.P. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics 2003, 4, 249–264. [Google Scholar] [CrossRef]
- Bolstad, B.M.; Irizarry, R.A.; Astrand, M.; Speed, T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef]
- Tukey, J.W.; McLaughlin, D.H. Less vulnerable confidence and significance procedures for location based on a single sample: Trimming/Winsorization 1. Sankhya A 1963, 25, 331–352. [Google Scholar]
- Patel, K.R.; Mudholkar, G.S.; Fernando, J.L.I. Student’s t approximations for three simple robust estimators. J. Am. Stat. Assoc. 1988, 83, 1203–1210. [Google Scholar]
- Graham, N.S.; Clutterbuck, A.L.; James, N.; Lea, R.G.; Mobasheri, A.; Broadley, M.R.; May, S.T. Equine transcriptome quantification using human GeneChip arrays can be improved using genomic DNA hybridisation and probe selection. Vet. J. 2010, 186, 323–327. [Google Scholar] [CrossRef]
- Graham, N.S.; May, S.T.; Daniel, Z.C.T.R.; Emmerson, Z.F.; Brameld, J.M.; Parr, T. Use of the Affymetrix Human GeneChip array and genomic DNA hybridisation probe selection to study ovine transcriptomes. Animal 2011, 5, 861–866. [Google Scholar] [CrossRef]
- Fukuyama, Y.; Sugeno, M. A New Method of Choosing the Number of Clusters for the Fuzzy C-Mean Method. Available online: http://citeseer.uark.edu:8080/citeseerx/showciting;jsessionid=1AF0955F44EC87078947AADEDE29D50C?cid=664813 (accessed on 10 December 2013).
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. B 1995, 57, 289–300. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lai, H.-M.; May, S.T.; Mayes, S. Pigeons: A Novel GUI Software for Analysing and Parsing High Density Heterologous Oligonucleotide Microarray Probe Level Data. Microarrays 2014, 3, 1-23. https://doi.org/10.3390/microarrays3010001
Lai H-M, May ST, Mayes S. Pigeons: A Novel GUI Software for Analysing and Parsing High Density Heterologous Oligonucleotide Microarray Probe Level Data. Microarrays. 2014; 3(1):1-23. https://doi.org/10.3390/microarrays3010001
Chicago/Turabian StyleLai, Hung-Ming, Sean T. May, and Sean Mayes. 2014. "Pigeons: A Novel GUI Software for Analysing and Parsing High Density Heterologous Oligonucleotide Microarray Probe Level Data" Microarrays 3, no. 1: 1-23. https://doi.org/10.3390/microarrays3010001




