Model-Based Optimization of Scaffold Geometry and Operating Conditions of Radial Flow Packed-Bed Bioreactors for Therapeutic Applications
Abstract
:1. Introduction
2. Materials and Methods
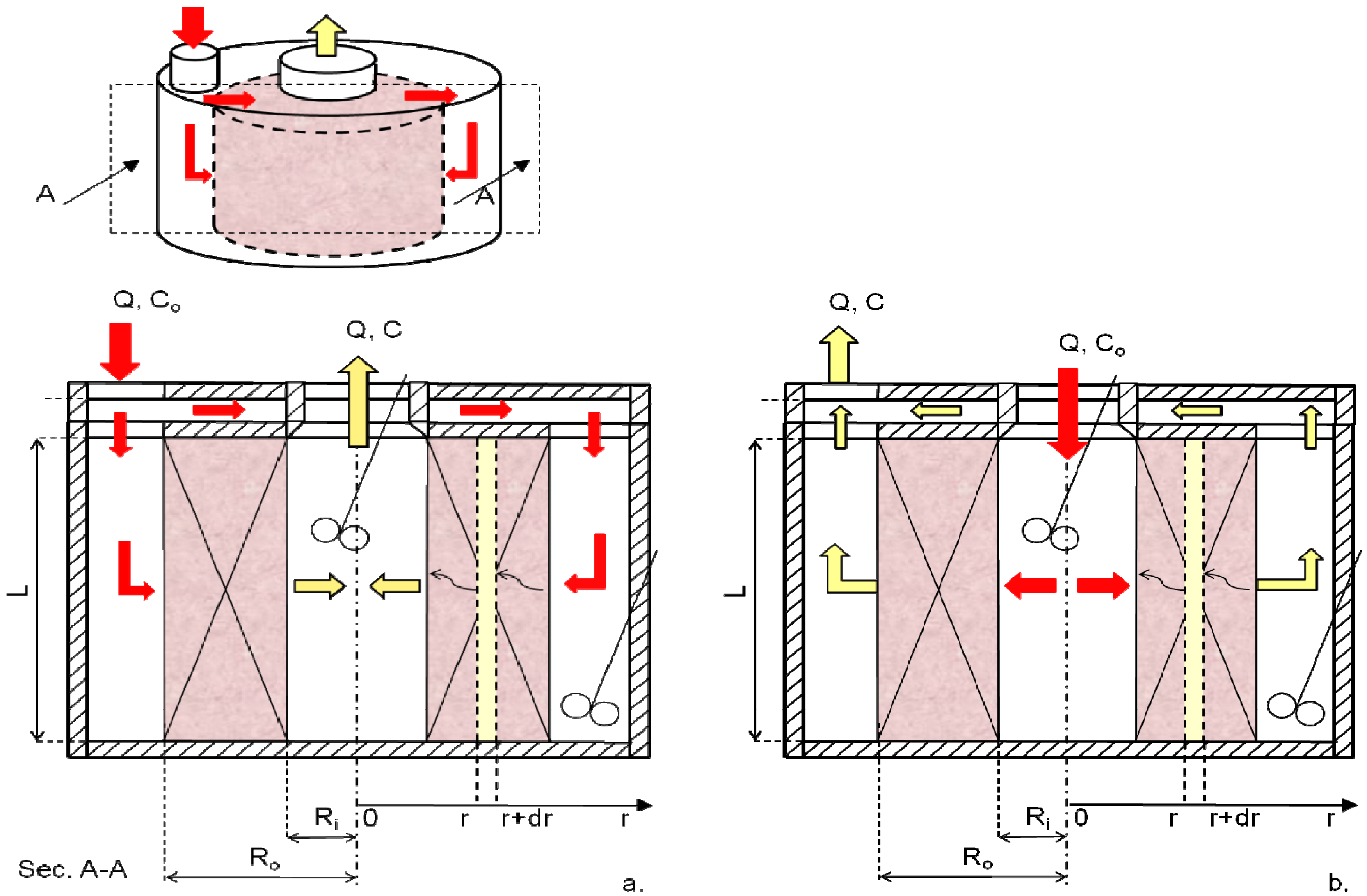
2.1. Model Development
2.1.1. Convection-Enhanced Transport Model of rPBB
- axial symmetry;
- steady-state conditions;
- incompressible fluid;
- isothermal conditions;
- transport in the construct is described according to a pseudo-homogeneous approach;
- construct is described as an isotropic porous medium with Darcy permeability k;
- uniform cell distribution CC;
- no cell lysis or apoptosis;
- solute concentration in the construct does not vary along the axial and angular coordinates;
- momentum transport in the construct is described according to the Darcy equation;
- dissolved oxygen is transported across the construct by convection and dispersion;
- cells consume oxygen according to Michaelis-Menten kinetics, with a maximal cell-specific consumption rate G and a Michaelis constant KM.
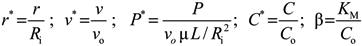
- continuity equation
- momentum conservation (Darcy equation)
- mass conservation
- B.C.1inward flow (γ = −1) r* = 1 p* = 0
- B.C.2
- B.C.3
2.1.2. Diffusion-Limited Transport Model of rPBB
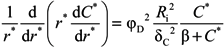
- B.C.1r* = 1 C* = 1
- B.C.2
2.1.3. Convection-Enhanced Transport Model of aPBB
- momentum conservation (Darcy equation)
- mass conservation
- B.C.1z* = 1 P* = 0
- B.C.2
- B.C.3
2.2. Dimensionless Groups
2.2.1. Convection-Enhanced Transport Model of rPBB
| Group Definition | Description |
|---|---|
| 1. γ | perfusion flow direction parameter |
| 2. k L/Ri3 | dimensionless Darcy permeability of construct |
| 3. Ri/δC | inner radius-to-thickness ratio of the construct |
| 4. vo δC/DC | maximal radial Peclet number, Perad,max |
| 5. √(VmaxδC2/(DC Co)) | Thiele modulus, φC |
| 6. KM/Co | saturation parameter, β |
2.2.2. Diffusion-Limited Transport Model of rPBB
2.2.3. Convection-Enhanced Transport Model of rPBB
2.3. Computational Methods
| Dimensionless Group | Values |
|---|---|
| 1. perfusion flow direction parameter, γ | −1 (inwards), 1 (outwards) |
| 2. dimensionless Darcy permeability of construct, k L/Ri3 | 2.24 × 10−10−2.24 × 10−4 |
| 3. construct curvature, Ri/δC | 0.1–10 |
| 4. maximal radial Peclet number, Perad,max | 49 |
| 5. Thiele modulus, φC or φD | 1–20 |
| 6. saturation parameter, β | 0.019 |
| Symbol | Model Parameter | Value | Units | Reference |
|---|---|---|---|---|
| Co | oxygen inlet concentration | 0.216 | mol/m3 | [53] |
| D | oxygen diffusivity in water | 2.64 × 10−9 | m2/s | [52] |
| Deff | effective oxygen diffusivity in the construct | 1.85 × 10−9 | m2/s | [50] |
| DC | oxygen dispersivity in the construct | 2 × 10−8 | m2/s | [49] |
| KM | oxygen Michaelis constant | 4.05 × 10−3 | mol/m3 | [54] |
| k | Darcy permeability of construct | 1.4 × 10−13 | m2 | [55] |
| L | scaffold length | 0.2 | m | |
| vo | maximal inlet superficial velocity | 1.98 × 10−4 | m/s | [36] |
| δC | scaffold thickness | 0.005 | m | [36] |
| μ | medium viscosity | 6.92 × 10−4 | Pa s | [53] |
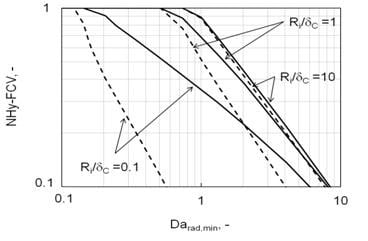
3. Results and Discussion
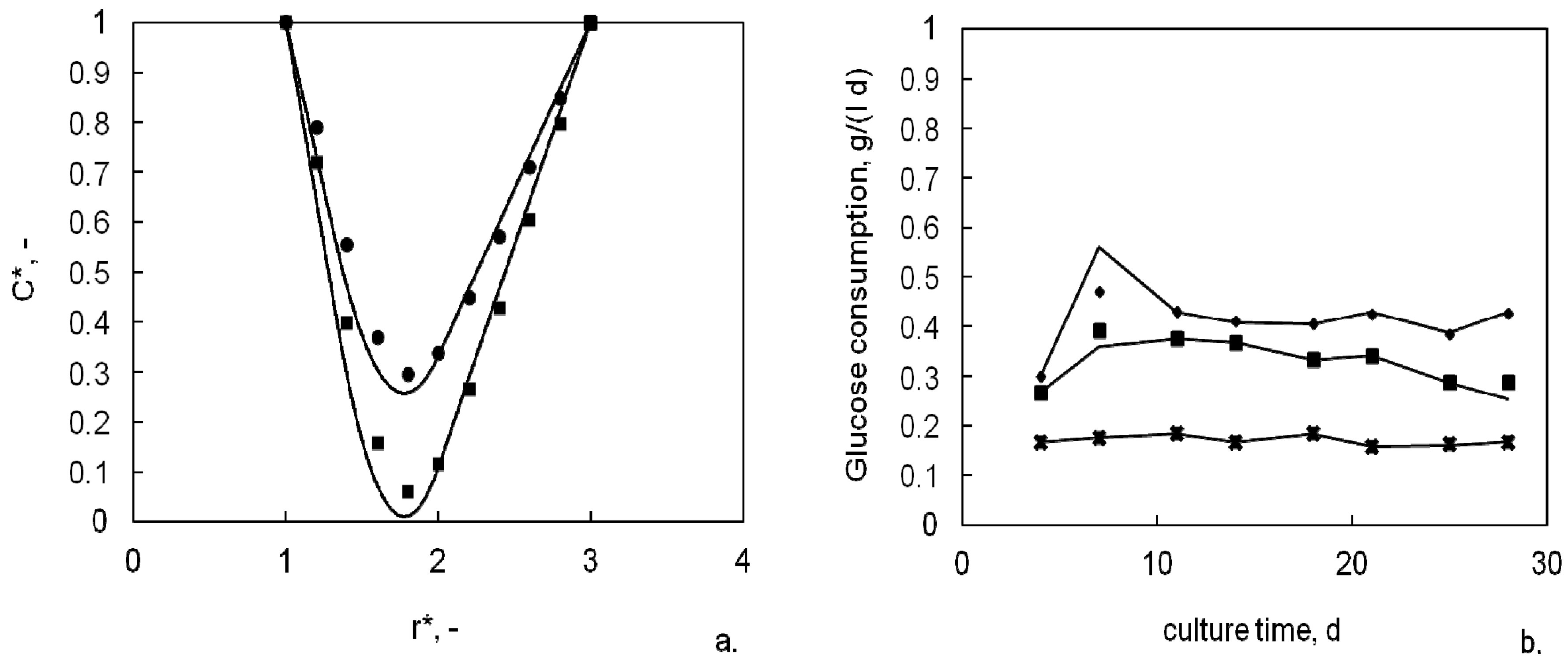
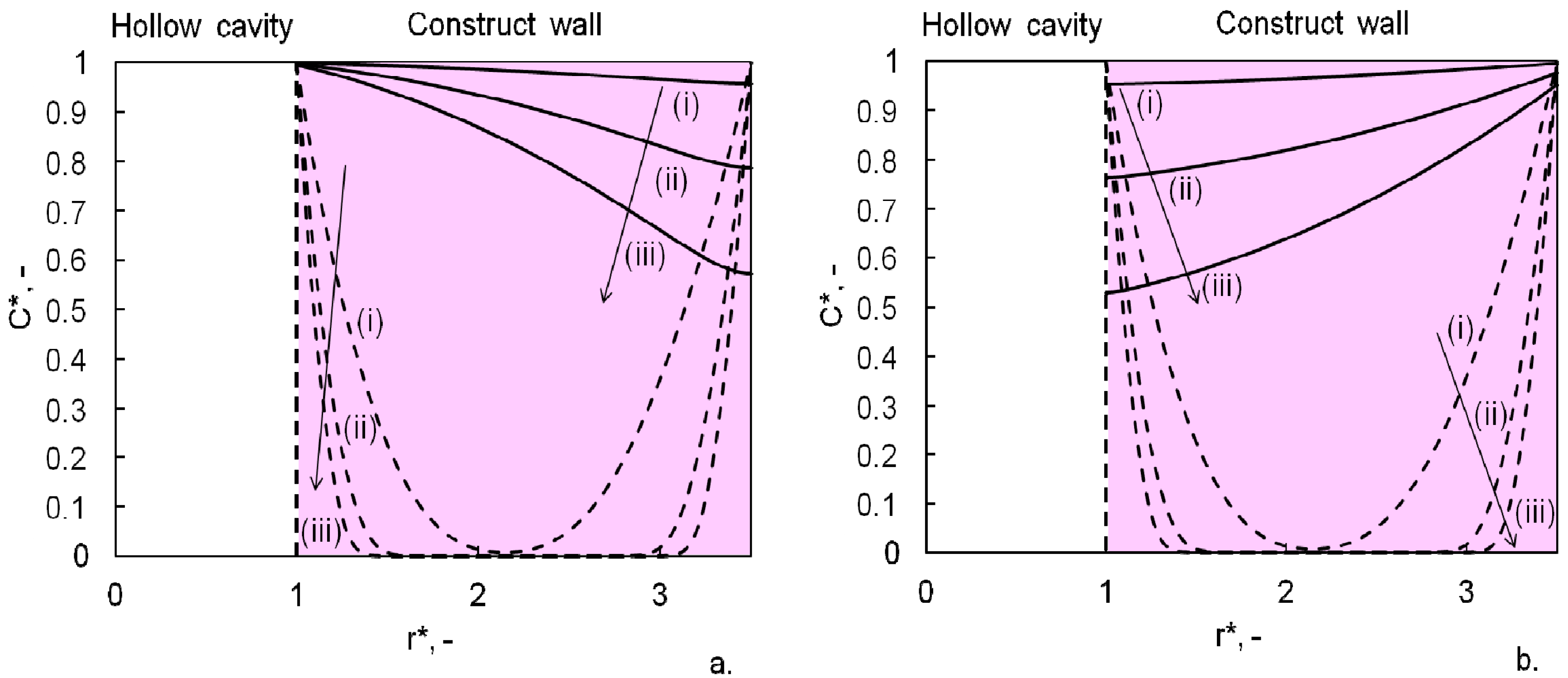
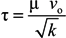

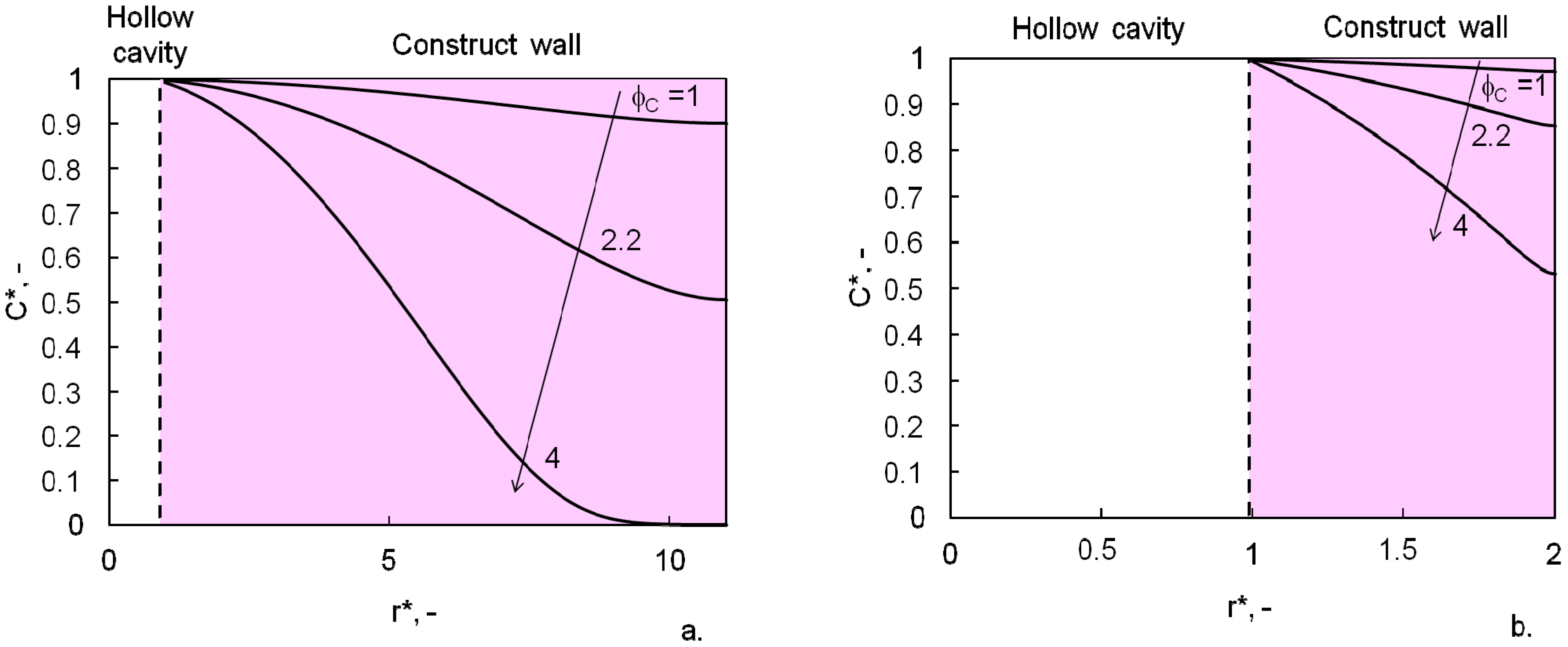
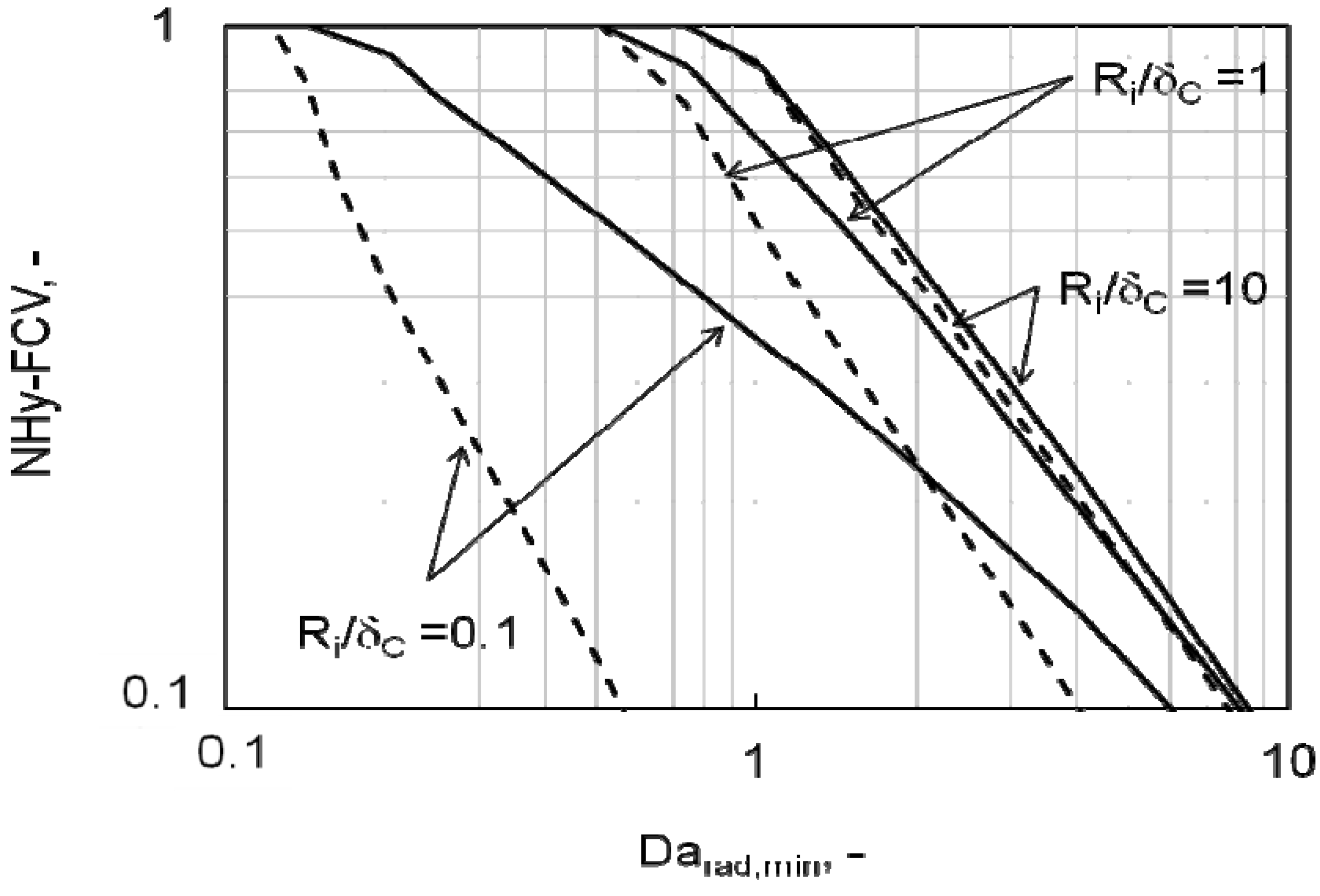
4. Conclusions
Nomenclature
| C | dissolved oxygen concentration in the construct [mol/m3] |
| CC | cell concentration in the construct [cells/m3] |
| Co | dissolved oxygen concentration in the feed [mol/m3] |
| D | oxygen diffusion coefficient in water [m2/s] |
| Darad,min = VmaxδC/(voCo) | minimal radial Damköhler number in the construct [-] |
| DC | oxygen dispersion coefficient in the construct [m2/s] |
| Deff = D·ε | effective oxygen diffusion coefficient in the construct [m2/s] |
| G | maximal cell-specific oxygen metabolic consumption rate [mol/(s cell)] |
| KM | Michaelis constant for oxygen consumption [mol/m3] |
| k | Darcy permeability of construct [m2] |
| L | construct length [m] |
| NHy-FCV | non-hypoxic fractional construct volume [-] |
| P | pressure [Pa] |
| Peax = uo·L/DC | axial Peclet number [-] |
| Perad,max = vo·δC/DC | maximal radial Peclet number [-] |
| Q | medium feed flow rate [m3/s] |
| Ri | construct inner radius [m] |
| Ro | construct outer radius [m] |
| r | radial coordinate [m] |
| u | axial superficial velocity [m/s] |
| uo | axial superficial velocity entering the construct [m/s] |
| Vmax = CCG | maximal metabolic consumption rate of oxygen [mol/(m3s)] |
| v | radial velocity in construct [m/s] |
| vo | maximal radial velocity in construct at r = Ri [m/s] |
| z | axial coordinate [m] |
Greek Symbols
| β = KM/Co | saturation parameter [-] |
| γ | perfusion flow direction parameter [-] |
| δC = Ro − Ri | thickness of construct annular wall [m] |
| ε | construct porosity [-] |
| μ | medium viscosity [Pa∙s] |
| φC = √(Vmax·δC/(DC·Co)) | Thiele modulus in construct perfused with medium [-] |
| φD = √(Vmax·δC/(Deff·Co)) | Thiele modulus in construct under static operation [-] |
| τ | average shear stress in construct [Pa] |
Superscripts and Subscripts
| ax | axial |
| C | construct |
| max | maximal |
| rad | radial |
| * | dimensionless |
Acknowledgments
Conflicts of Interest
References
- Langer, R.; Vacanti, J.P.; Vacanti, C.A.; Atala, A.; Freed, L.E.; Vunjak-Novakovic, G. Tissue engineering: Biomedical applications. Tissue Eng. 1995, 1, 151–161. [Google Scholar] [CrossRef]
- VandeVord, P.J.; Nasser, S.; Wooley, P.H. Immunological responses to bone soluble proteins in recipients of bone allografts. J. Orthop. Res. 2005, 23, 1059–1064. [Google Scholar] [CrossRef]
- Zeilinger, K.; Holland, G.; Sauer, I.M.; Efimova, E.; Kardassis, D.; Obermayer, N.; Liu, M.; Neuhaus, P.; Gerlach, J.C. Time course of primary liver cell reorganization in three-dimensional high-density bioreactors for extracorporeal liver support: An immunohistochemical and ultrastructural study. Tissue Eng. 2004, 10, 1113–1124. [Google Scholar]
- Rotem, A.; Toner, M.; Bhatia, S.N.; Foy, B.D.; Tomkins, R.G.; Yarmush, M.L. Oxygen is a factor determining in vitro tissue assembly: Effects on attachment and spreading of hepatocytes. Biotechnol. Bioeng. 1994, 43, 654–660. [Google Scholar] [CrossRef]
- Catapano, G.; de Bartolo, L.; Lombardi, C.P.; Drioli, E. The effect of oxygen transport resistances on the viability and functions of isolated rat hepatocytes. Int. J. Artif. Organs 1996, 19, 31–41. [Google Scholar]
- Allen, J.W.; Khetani, S.R.; Bhatia, S.N. In vitro zonation and toxicity in a hepatocyte bioreactor. Toxicol. Sci. 2005, 84, 110–119. [Google Scholar] [CrossRef]
- Volkmer, E.; Drosse, I.; Otto, S.; Stangellmayer, A.; Stengele, M.; Kallukalam, B.C.; Mutschler, W.; Schieker, M. Hypoxia in static and dynamic 3D culture systems for tissue engineering of bone. Tissue Eng. Part A 2008, 14, 1331–1340. [Google Scholar] [CrossRef]
- Griffith, C.K.; George, S.C. The effect of hypoxia on in vitro prevascularization of a thick soft tissue. Tissue Eng. Part A 2009, 15, 2423–2434. [Google Scholar] [CrossRef]
- Catapano, G. Mass transfer limitations to the performance of membrane bioartificial liver support devices. Int. J. Artif. Organs 1996, 19, 51–68. [Google Scholar]
- Wendt, D.; Marsano, A.; Jakob, M.; Heberer, M.; Martin, I. Oscillating perfusion of cell suspensions through three-dimensional scaffolds enhances cell seeding efficiency and uniformity. Biotechnol. Bioeng. 2003, 84, 205–214. [Google Scholar] [CrossRef]
- Glicklis, R.; Shapiro, L.; Agbaria, R.; Merchuk, J.C.; Cohen, S. Hepatocyte behavior within three-dimensional porous alginate scaffolds. Biotechnol. Bioeng. 2000, 67, 344–353. [Google Scholar] [CrossRef]
- Gaspar, D.A.; Gomide, V.; Monteiro, F.J. The role of perfusion bioreactors in bone tissue engineering. Biomatter 2012, 2, 1–9. [Google Scholar] [CrossRef]
- Muschler, G.F.; Nakamoto, C.; Griffith, L. Engineering principles of clinical cell-based tissue engineering. J. Bone Joint Surg. 2004, 86, 1541–1558. [Google Scholar]
- Griffith, C.K.; George, S.C. Diffusion limits of an in vitro thick prevascularized tissue. Tissue Eng. 2005, 11, 257–266. [Google Scholar] [CrossRef]
- Jaesung, P.; Yawen, L.; Berthiaume, F.; Toner, M.; Yarmush, M.L.; Tilles, A.W. Radial flow hepatocyte bioreactor using stacked microfabricated grooved substrates. Biotechnol. Bioeng. 2008, 99, 455–467. [Google Scholar] [CrossRef]
- Niu, M.; Hammond, P.; Coger, R.N. The effectiveness of a novel cartridge-based bioreactor design in supporting liver cells. Tissue Eng. Part A 2009, 15, 2903–2916. [Google Scholar] [CrossRef]
- Granet, C.; Laroche, N.; Vico, L.; Alexandre, C.; Lafage-Proust, M.H. Rotating wall vessel, promising bioreactors for osteoblastic cell culture: Comparison with other 3D conditions. Med. Biol. Eng. Comput. 1998, 36, 513–519. [Google Scholar] [CrossRef]
- Sikavitsas, V.I.; Bancroft, G.N.; Mikos, A.G. Formation of three-dimensional cell/polymer constructs for bone tissue engineering in a spinner flask and a rotating wall vessel bioreactor. J. Biomed. Mater. Res. 2002, 62, 36–48. [Google Scholar]
- Catapano, G.; Gerlach, J.C. Bioreactors for liver tissue engineering. On-line encyclopedia of tissue engineering. Topics in Tissue Engineering; Ashammakhi, N., Reis, R., Chiellini, E., Eds.; Biomaterials and Tissue Engineering Group: Oulu, Finland, 2007; Volume 3, Chaper 8. pp. 1–42. Available online: http://www.oulu.fi/spareparts/ebook_topics_in_t_e_vol3/ (accessed on 27 December 2013).
- Radisic, M.; Deen, W.; Langer, R.; Vunjak-Novakovic, G. Mathematical model of oxygen distribution in engineered cardic tissue with parallel channel array perfused with culture medium containing oxygen carriers. Am. J. Physiol. Heart Circ. Physiol. 2005, 288, H1278–H1289. [Google Scholar]
- Sullivan, J.P.; Palmer, A.F. Targeted oxygen delivery within hepatic hollow fiber bioreactors via supplementation of hemoglobin-based oxygen carriers. Biotechnol. Prog. 2006, 22, 1374–1387. [Google Scholar]
- McClelland, R.E.; Coger, R.N. Use of micropathways to improve oxygen transport in a hepatic system. Trans. ASME 2000, 122, 268–273. [Google Scholar]
- McClelland, R.E.; Coger, R.N. Effects of enhanced O2 transport on hepatocytes packed within a bioartificial liver device. Tissue Eng. 2004, 10, 253–266. [Google Scholar] [CrossRef]
- Kim, S.S.; Sundback, C.A.; Kaihara, S.; Benvenuto, M.S.; Kim, B.-S.; Mooney, D.J.; Vacanti, J.P. Dynamic seeding and in vitro culture of hepatocytes in a flow perfusion system. Tissue Eng. 2000, 6, 39–44. [Google Scholar] [CrossRef]
- Bancroft, G.N.; Sikavitsas, V.I.; van der Dolder, J.; Sheffield, T.L.; Ambrose, C.G.; Jansen, J.A.; Mikos, A.G. Fluid flow increases mineralized matrix deposition in 3D perfusion culture of marrow stromal osteoblasts in a dose-dependent manner. Proc. Natl. Acad. Sci. USA 2002, 99, 12600–12605. [Google Scholar] [CrossRef]
- Warnock, J.N.; Bratch, K.; Al-Rubeai, M. Packed-bed bioreactors. In Bioreactors for Tissue Engineering, 1st ed.; Chauduri, J., Al-Rubeai, M., Eds.; Springer Verlag: Dordrecht, The Netherlands, 2005; pp. 87–114. [Google Scholar]
- Fröhlich, M.; Grayson, W.L.; Marolt, D.; Gimble, J.M.; Kregar-Velikonja, N.; Vunjak-Novakovic, G. Bone grafts engineered from human adipose-derived stem cells in perfusion bioreactor culture. Tissue Eng. 2010, 16, 179–189. [Google Scholar]
- Piret, J.M.; Devens, D.A.; Cooney, C.L. Nutrient and metabolite gradients in mammalian-cell hollow fiber bioreactors. Can. J. Chem. Eng. 1991, 69, 421–428. [Google Scholar] [CrossRef]
- Fassnacht, D.; Pörtner, R. Experimental and theoretical considerations on oxygen supply for animal cell growth in fixed-bed reactors. J. Biotechnol. 1999, 72, 169–184. [Google Scholar] [CrossRef]
- Singh, H.; Ang, E.S.; Lim, T.T.; Hutmacher, D.W. Flow modeling in a novel non-perfusion conical bioreactor. Biotechnol. Bioeng. 2007, 97, 1291–1299. [Google Scholar] [CrossRef]
- Kurosawa, H.; Markl, H.; Niebhur-Redder, C.; Matsamura, M. Dialysis bioreactor with radial flow fixed bed for animal cell culture. J. Ferment. Bioeng. 1991, 72, 41–45. [Google Scholar]
- Kino-Oka, M.; Taya, M. Design and operation of a radial flow bioreactor for reconstruction of cultured tissues. In Bioreactors for Tissue Engineering, 1st ed.; Chauduri, J., Al-Rubeai, M., Eds.; Springer Verlag: Dordrecht, The Netherlands, 2005; pp. 115–133. [Google Scholar]
- Guillouzo, A.; Guguen-Guillouzo, C. Evolving concepts in liver tissue modeling and implications for in vitro toxicology. Expert Opin. Drug Metab. Toxicol. 2008, 4, 1279–1294. [Google Scholar] [CrossRef]
- Kitagawa, T.; Yamaoka, T.; Iwase, R.; Murakami, A. Three-dimensional cell seeding and growth in radial-flow perfusion bioreactor for in vitro tissue reconstruction. Biotechnol. Bioeng. 2006, 93, 947–954. [Google Scholar] [CrossRef]
- Xie, Y.; Hardouin, P.; Zhu, Z.; Tang, T.; Dai, K.; Lu, J. Three-dimensional flow perfusion culture system for stem cell proliferation inside the critical-size β-tricalcium phosphate scaffold. Tissue Eng. 2006, 12, 3535–3543. [Google Scholar] [CrossRef]
- Olivier, V.; Hivart, P.; Descamps, M.; Hardouin, P. In vitro culture of large bone substitutes in a new bioreactor: Importance of the flow direction. Biomed. Mater. 2007, 2, 174–180. [Google Scholar] [CrossRef]
- Kawada, M.; Nagamori, S.; Aizaki, H.; Fukaya, K.; Niiya, M.; Matsuura, T.; Sujino, H.; Hasumura, S.; Yashida, H.; Mizutani, S.; et al. Massive culture of human liver cancer cells in a newly developed radial flow bioreactor system: Ultrafine structure of functionally enhanced hepatocarcinoma cell lines. In Vitro Cell Dev. Biol. Anim. 1998, 34, 109–115. [Google Scholar] [CrossRef]
- Hongo, T.; Kajikawa, M.; Ishida, S.; Ozawa, S.; Ohno, Y.; Sawada, J.; Umezawa, A.; Ishikawa, Y.; Kobayashi, T.; Honda, H. Three-dimensional high-density culture of HepG2 cells in a 5-mL radial flow bioreactor for construction of artificial liver. J. Biosci. Bioeng. 2005, 99, 237–244. [Google Scholar] [CrossRef]
- Miskon, A.; Sasaki, N.; Yamaoka, T.; Uyama, H.; Kodama, M. Radial flow type bioreactor for bioartificial liver assist using PTFE non-woven fabric coated with poly-amino acid urethane copolymer. Macromol. Symp. 2007, 249-250, 151–158. [Google Scholar] [CrossRef]
- Morsiani, E.; Galavotti, D.; Puviani, A.C.; Valieri, L.; Brogli, M.; Tosatti, S.; Pazzi, P.; Azzena, G. Radial flow bioreactor outperforms hollow-fiber modulus as a perfusing culture system for primary porcine hepatocytes. Transplant. Proc. 2000, 32, 2715–2718. [Google Scholar] [CrossRef]
- Morsiani, E.; Brogli, M.; Galavotti, D.; Bellini, T.; Ricci, D.; Pazzi, P.; Puviani, A.C. Long-term expression of highly differentiated functions by isolated porcine hepatocytes perfused in a radial-flow bioreactor. Artif. Organs 2001, 25, 740–748. [Google Scholar] [CrossRef]
- Saito, M.; Matsuura, T.; Masaki, T.; Maehashi, H.; Shimizu, K.; Hataba, Y.; Iwahori, T.; Suzuki, T.; Braet, F. Reconstruction of liver organoid using bioreactor. World J. Gastroenterol. 2006, 12, 1881–1888. [Google Scholar]
- Ishii, Y.; Saito, R.; Marushima, H.; Ito, R.; Sakamoto, T.; Yanaga, K. Hepatic reconstruction from fetal porcine liver cells using a radial flow bioreactor. World J. Gastroenterol. 2008, 14, 2740–2747. [Google Scholar] [CrossRef]
- Tharakan, J.P.; Chau, P.C. Modeling and analysis of radial flow mammalian cell culture. Biotechnol. Bioeng. 1987, 29, 657–671. [Google Scholar] [CrossRef]
- Cima, L.G.; Blanch, H.W.; Wilke, C.R. A theoretical and experimental evaluation of a novel radial-flow hollow fiber reactor for mammalian cell culture. Bioprocess Eng. 1990, 5, 19–30. [Google Scholar] [CrossRef]
- Böhmann, A.; Pörtner, R.; Schmieding, J.; Kasche, V.; Markl, H. The membrane dialysis bioreactor with integrated radial-flow fixed bed—A new approach for continuous cultivation of animal cells. Cytotechnology 1992, 9, 51–57. [Google Scholar] [CrossRef]
- Pörtner, R.; Platas, O.B.; Fassnacht, D.; Nehring, D.; Czermak, P.; Markl, H. Fixed bed reactors for the cultivation of mammalian cells: Design, performance and scale-up. Open Biotechnol. J. 2007, 1, 41–46. [Google Scholar]
- Chang, H.C.; Saucier, M.; Calo, J.M. Design criterion for radial flow fixed-bed reactors. AIChE J. 1983, 29, 1039–1041. [Google Scholar] [CrossRef]
- Delgado, J. A critical review of dispersion in packed beds. Heat Mass Transfer 2006, 42, 279–310. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 4th ed.; Prentice Hall: Westford, MA, USA, 2006; pp. 946–943. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2007; pp. 545–568. [Google Scholar]
- Han, P.; Bartels, D.M. Temperature dependence of oxygen diffusion in H2O and D2O. J. Phys. Chem. 1996, 100, 5597–5602. [Google Scholar] [CrossRef]
- Abdullah, N.S.; Das, D.B.; Ye, H.; Cui, Z.F. 3-D bone tissue growth in hollow fibre membrane bioreactor: Implications of various process parameters on tissue nutrition. Int. J. Artif. Organs 2006, 29, 841–851. [Google Scholar]
- Zahm, A.M.; Bucaro, M.A.; Ayyaswamy, P.S.; Srinivas, V.; Shapiro, I.M.; Adams, C.S.; Mukundakrishnan, K. Numerical modeling of oxygen distribution in cortical and cancellous bone: Oxygen availability governs osteonal and trabecular dimensions. Am. J. Physiol. Cell Physiol. 2010, 229, C922–C929. [Google Scholar]
- Chen, G.; Palmer, A.F. Hemoglobin-based oxygen carrier and convection enhanced oxygen transport in a hollow fiber bioreactor. Biotechnol. Bioeng. 2009, 102, 1603–1612. [Google Scholar] [CrossRef]
- Loiacono, L.A.; Shapiro, D.S. Detection of hypoxia at the cellular level. Crit. Care Clin. 2010, 26, 409–421. [Google Scholar] [CrossRef]
- Clarke, B. Normal bone anatomy. Clin. J. Am. Soc. Nephrol. 2008, 3, S131–S139. [Google Scholar] [CrossRef]
- Tortora, G.J.; Derrickson, B. Principles of Anatomy and Physiology, 11th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Ponzi, P.R.; Kaye, L.A. Effect of flow maldistribution on conversion and selectivity in radial flow fixed-bed reactors. AIChE J. 1979, 25, 100–108. [Google Scholar] [CrossRef]
- Komarova, S.V.; Ataullakhanov, F.I.; Globus, R.K. Bioenergetics and mitochondrial transmembrane potential during differentiation of cultured osteoblasts. Am. J. Physiol. Cell Physiol. 2000, 279, C1220–C1229. [Google Scholar]
- Balis, U.J.; Behnia, K.; Dwarakanath, B.; Bhatia, S.N.; Sullivan, S.J.; Yarmush, M.L.; Toner, M. Oxygen consumption characteristics of porcine hepatocytes. Metab. Eng. 1999, 1, 49–62. [Google Scholar] [CrossRef]
- Mehta, K.; Mehta, G.; Takayama, S.; Linderman, J. Quantitative inference of cellular parameters from microfluidic cell culture systems. Biotechnol. Bioeng. 2009, 103, 966–974. [Google Scholar] [CrossRef]
- Wang, S.; Tarbell, J.M. Effect of fluid flow on smooth muscle in a 3-dimensional collagen gel model. Arterioscler. Thromb. Vasc. Biol. 2000, 20, 2220–2225. [Google Scholar] [CrossRef]
- Christi, Y. Hydrodynamic damage to animal cells. Crit. Rev. Biotechnol. 2001, 21, 67–110. [Google Scholar] [CrossRef]
- Navdeep, S.; Chandel, G.R.; Budinger, S. The cellular basis for diverse responses to oxygen. Free Radic. Biol. Med. 2007, 42, 165–174. [Google Scholar] [CrossRef]
- Moustafa, T.; Badr, S.; Hassan, M.; Abba, I.A. Effect of flow direction on the behavior of radial flow catalytic reactors. Asia-Pac. J. Chem. Eng. 2012, 7, 307–316. [Google Scholar] [CrossRef]
- Rowley, J.A.; Timmins, M.; Galbraith, W.; Garvin, J.; Kosovsky, M.; Heidaran, M. Oxygen consumption as a predictor of growth and differentiation of MC3T3-E1 osteoblasts on 3D biodegradable scaffolds. Mol. Biol. Cell 2002, 13, 345a. [Google Scholar]
- Kretzmer, G.; Schügerl, K. Response of mammalian cells to shear stress. Appl. Microbiol. Biotechnol. 1991, 34, 613–616. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Donato, D.; Napoli, I.E.D.; Catapano, G. Model-Based Optimization of Scaffold Geometry and Operating Conditions of Radial Flow Packed-Bed Bioreactors for Therapeutic Applications. Processes 2014, 2, 34-57. https://doi.org/10.3390/pr2010034
Donato D, Napoli IED, Catapano G. Model-Based Optimization of Scaffold Geometry and Operating Conditions of Radial Flow Packed-Bed Bioreactors for Therapeutic Applications. Processes. 2014; 2(1):34-57. https://doi.org/10.3390/pr2010034
Chicago/Turabian StyleDonato, Danilo, Ilaria E. De Napoli, and Gerardo Catapano. 2014. "Model-Based Optimization of Scaffold Geometry and Operating Conditions of Radial Flow Packed-Bed Bioreactors for Therapeutic Applications" Processes 2, no. 1: 34-57. https://doi.org/10.3390/pr2010034