Characterization of a Laterally Oscillating Microresonator Operating in the Nonlinear Region
Abstract
:1. Introduction
2. Design and Modelling
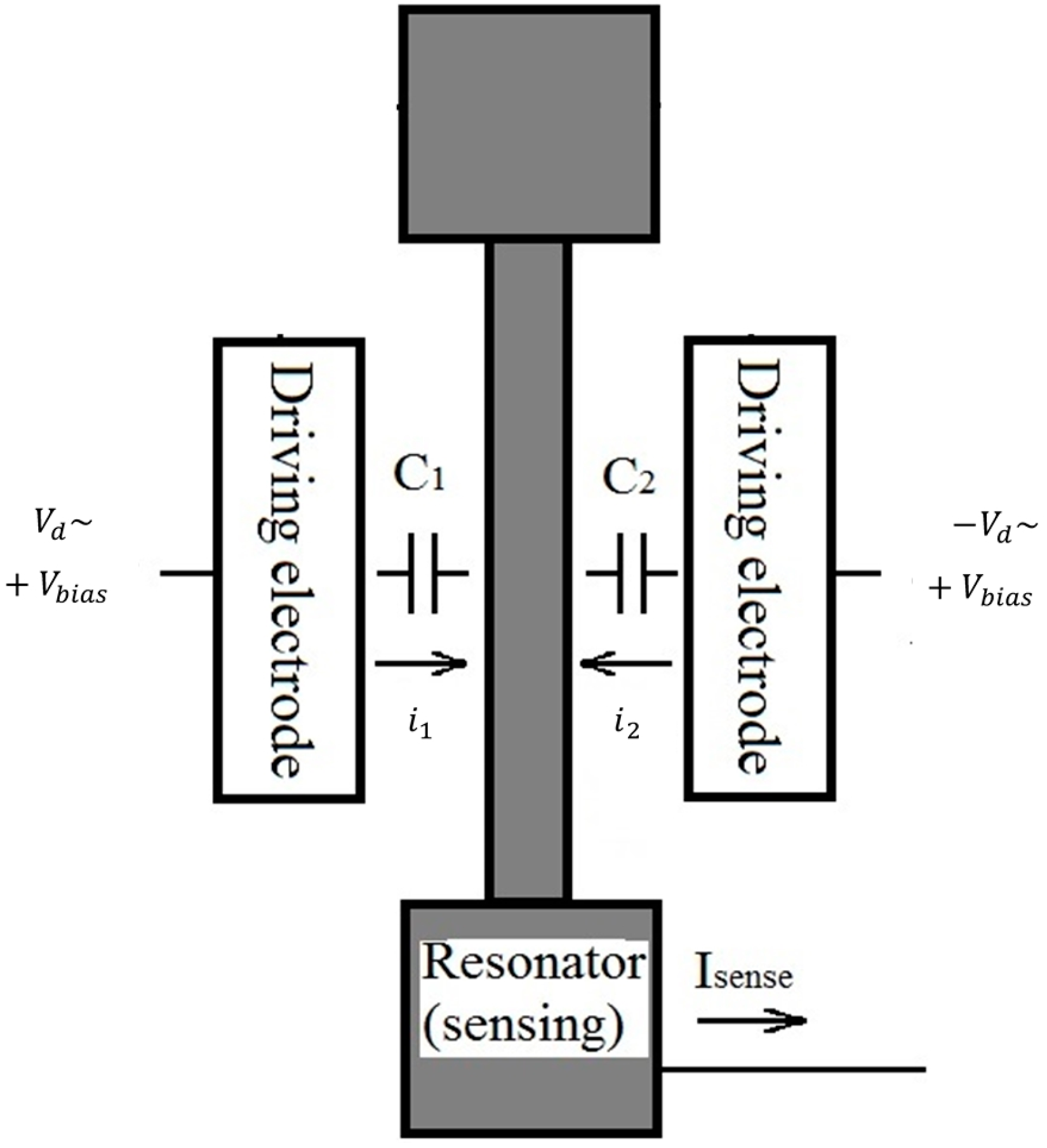
2.1. Lumped Model of Microresonator
2.2. Analytical Solution to the Duffing Equation
2.3. Effective Mass of System
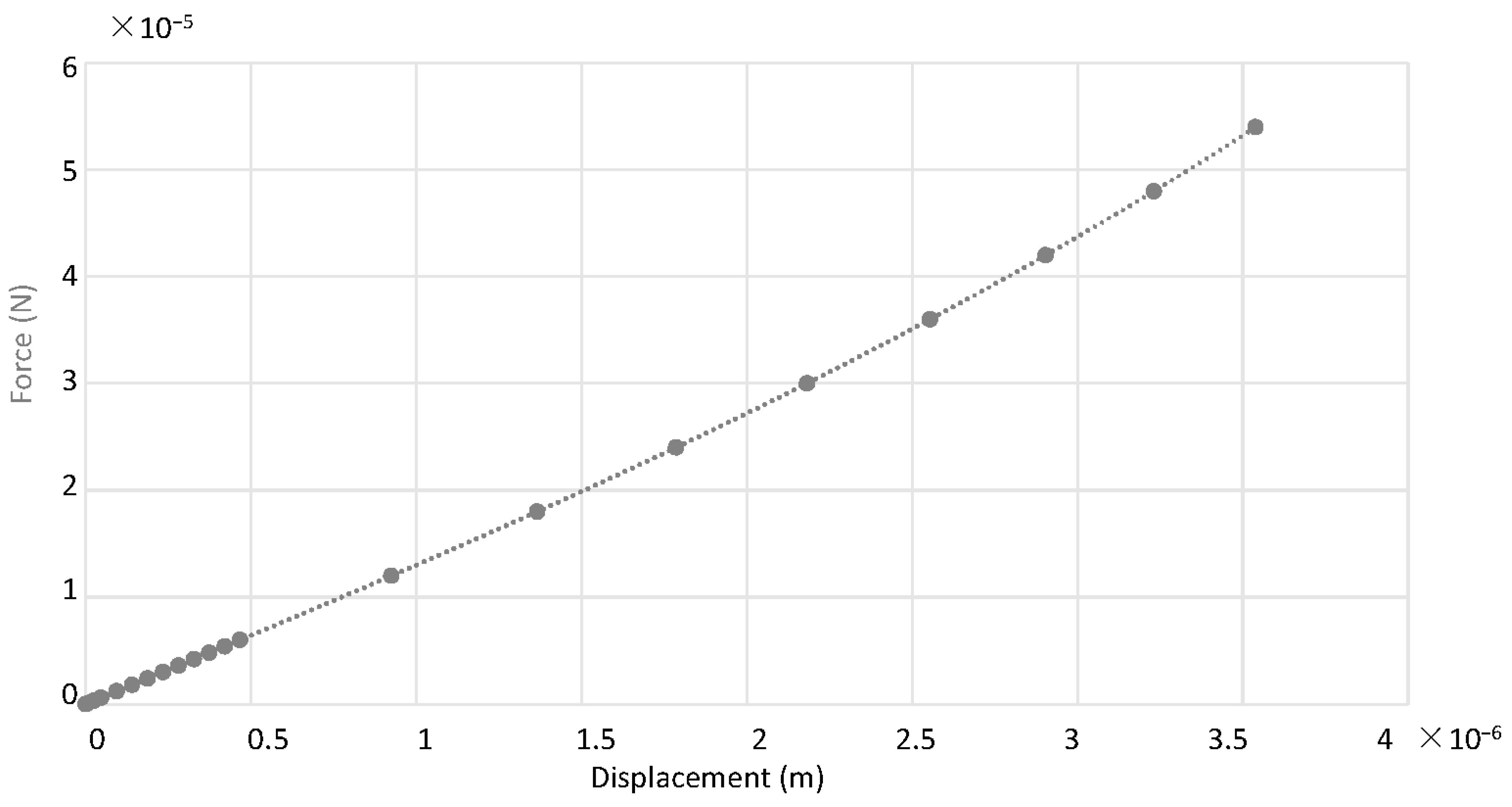
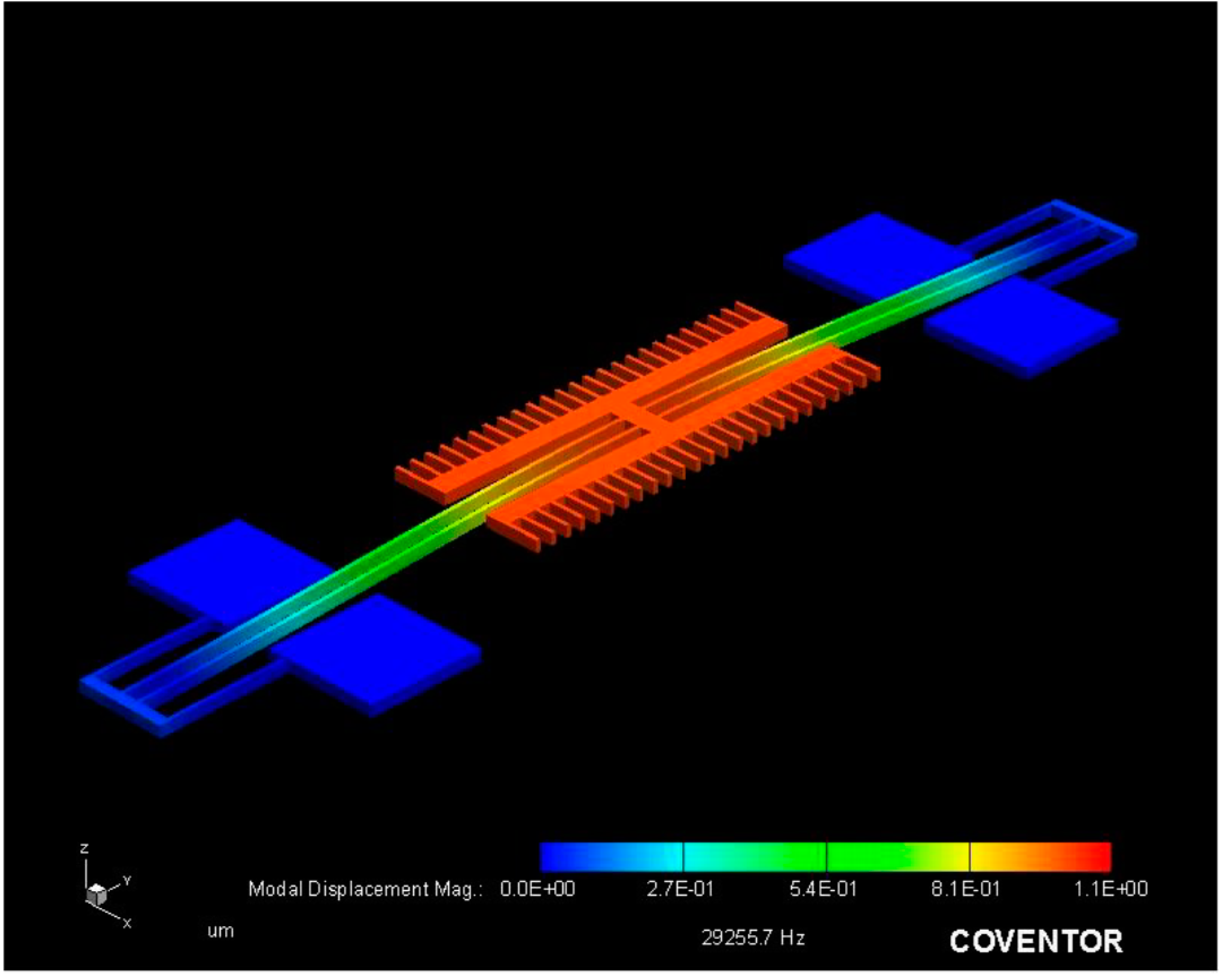
2.4. Static and Modal Analysis of the Microresonator
2.5. Electrostatic Force Acting on Resonator
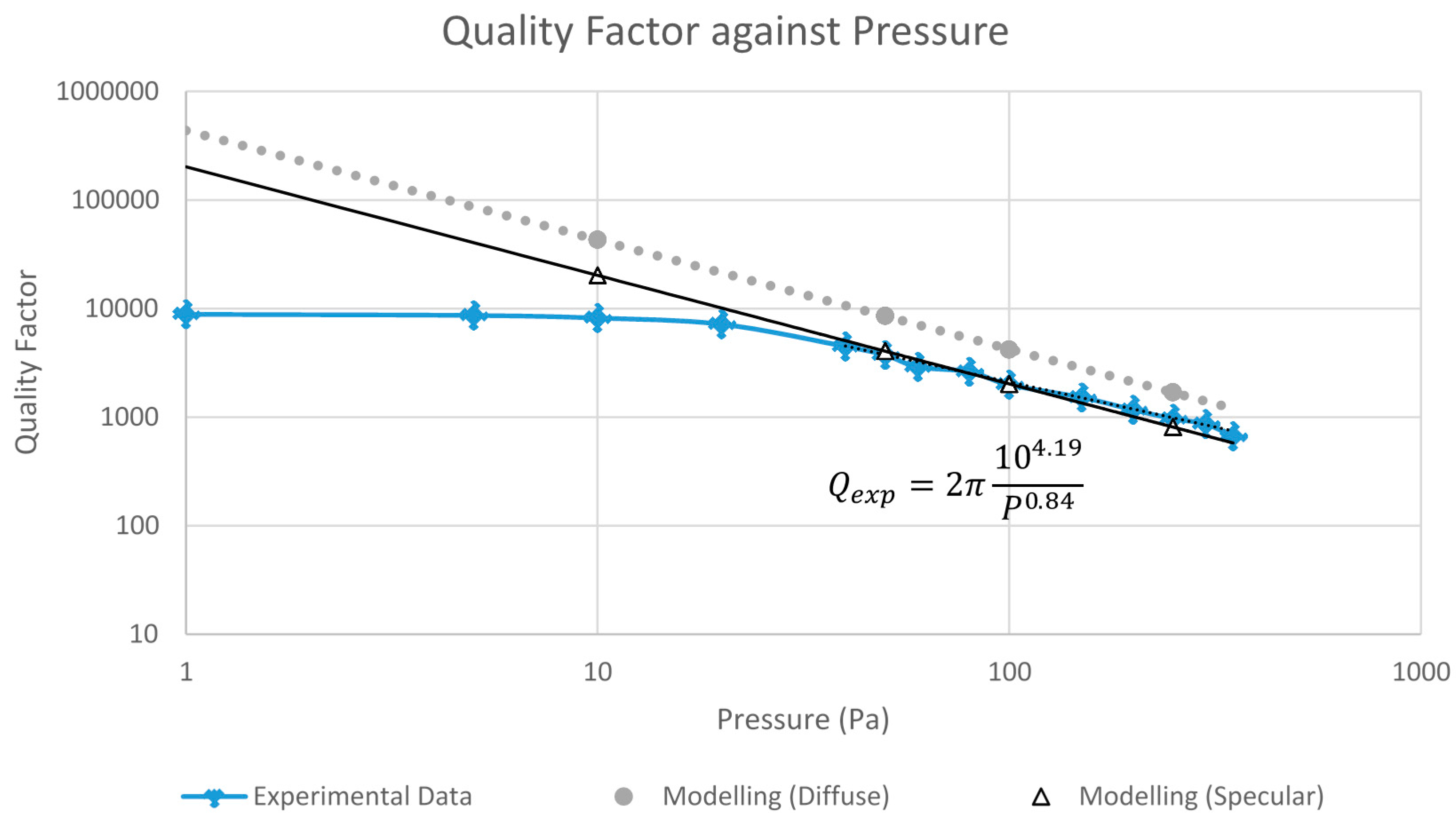
2.6. Damping Analysis
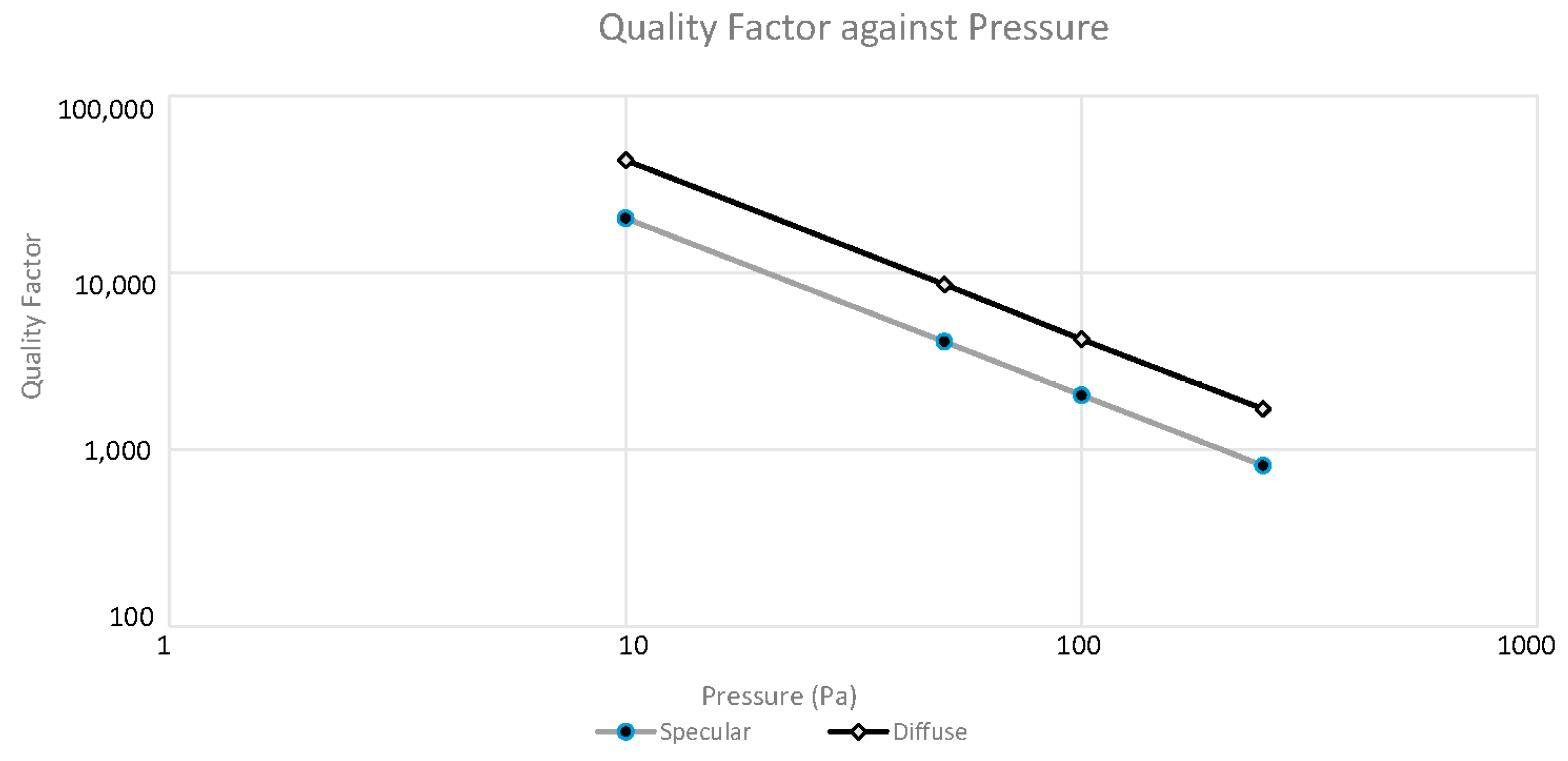
2.6.1. Air Damping of Structures Vibrating in an Unbounded Space
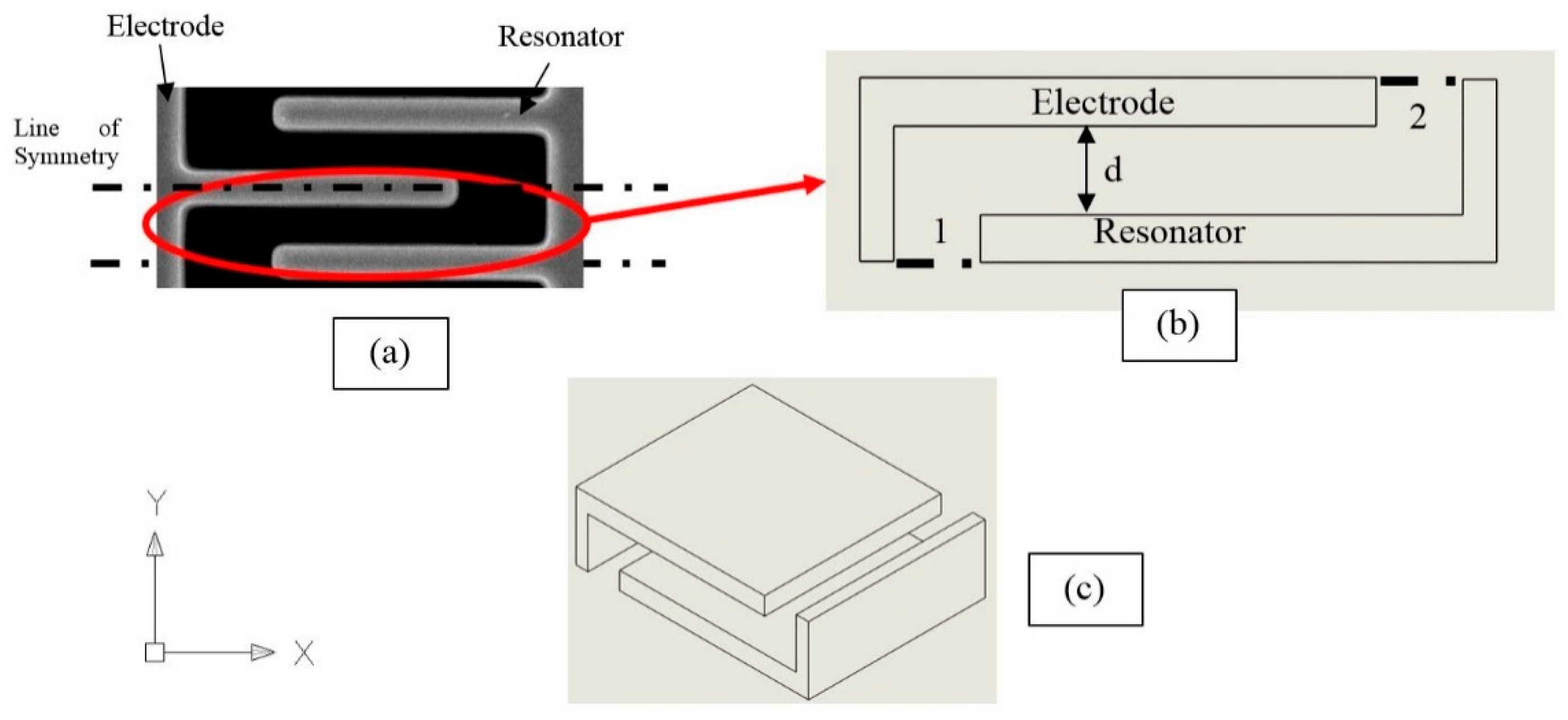
2.6.2. Slide Film Damping between the Comb Fingers
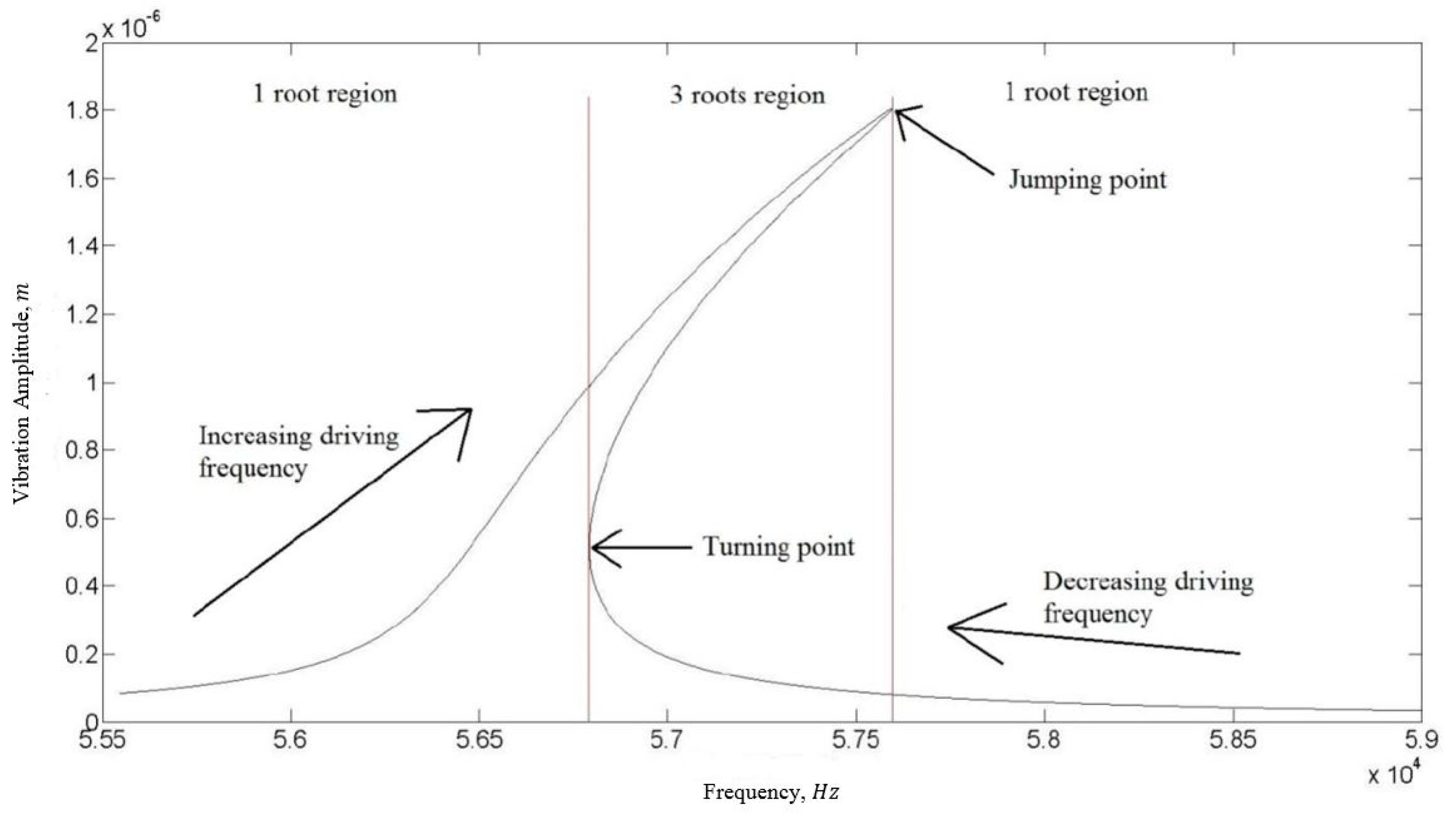
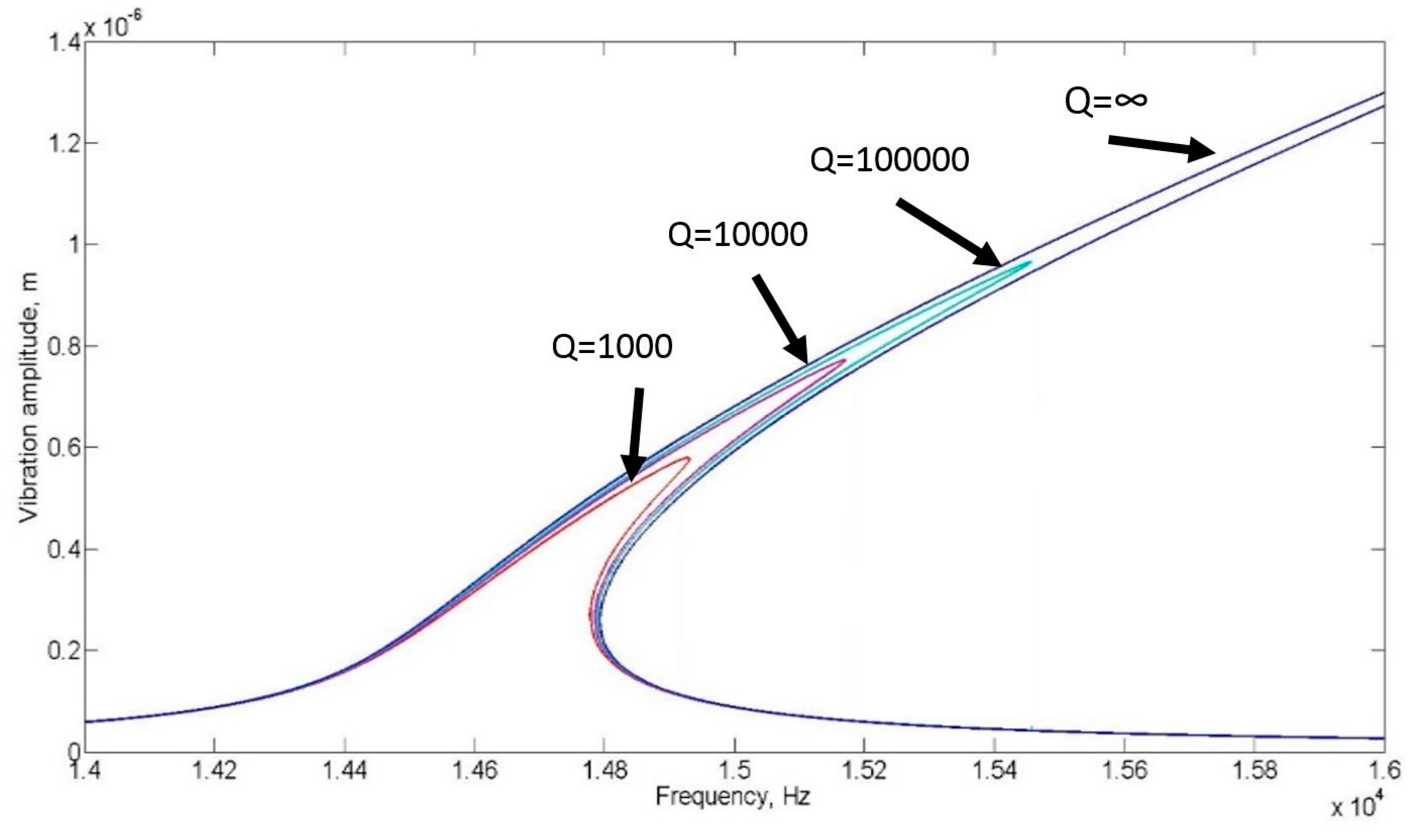
2.7. The Quality Factor of a Nonlinear Resonator
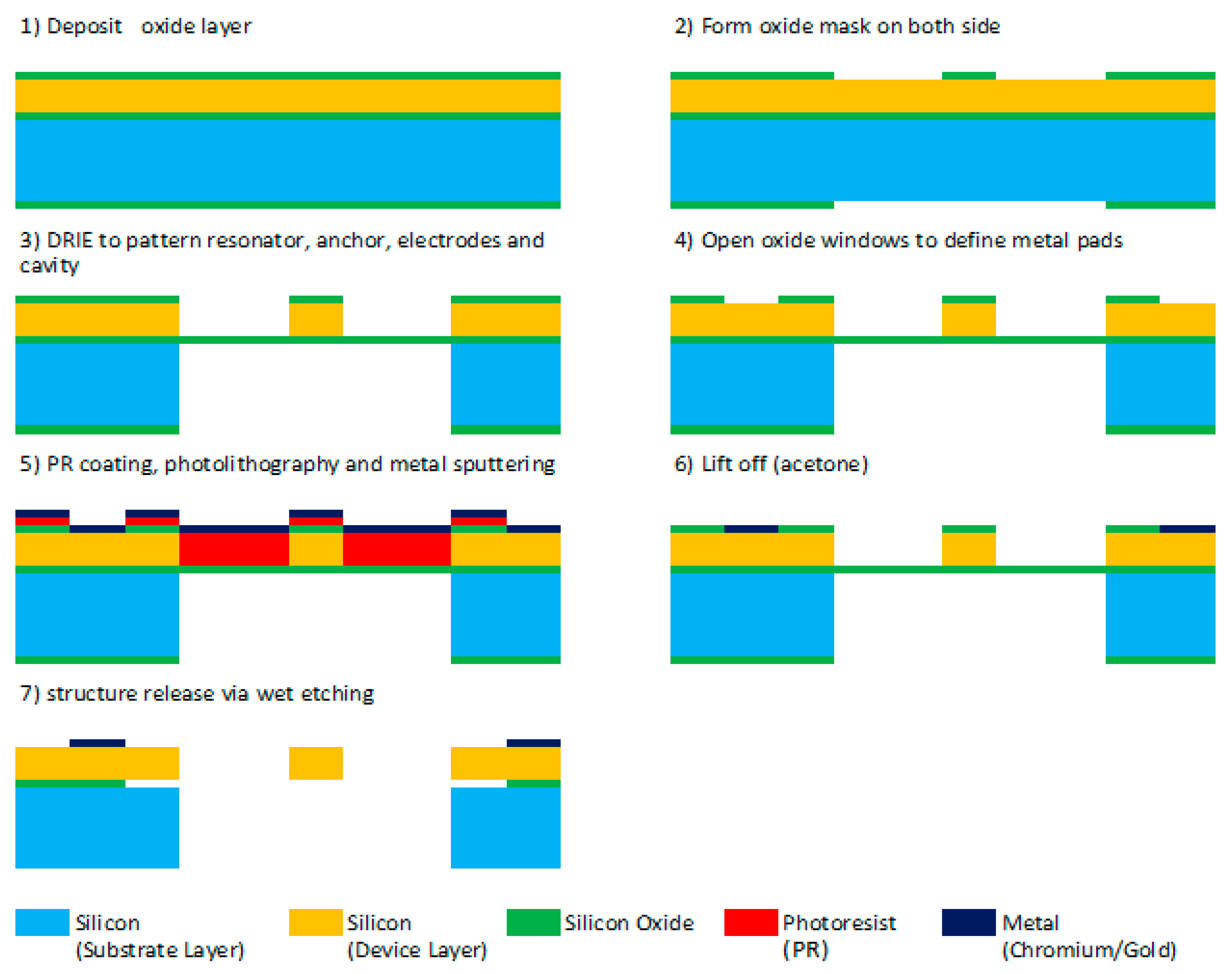
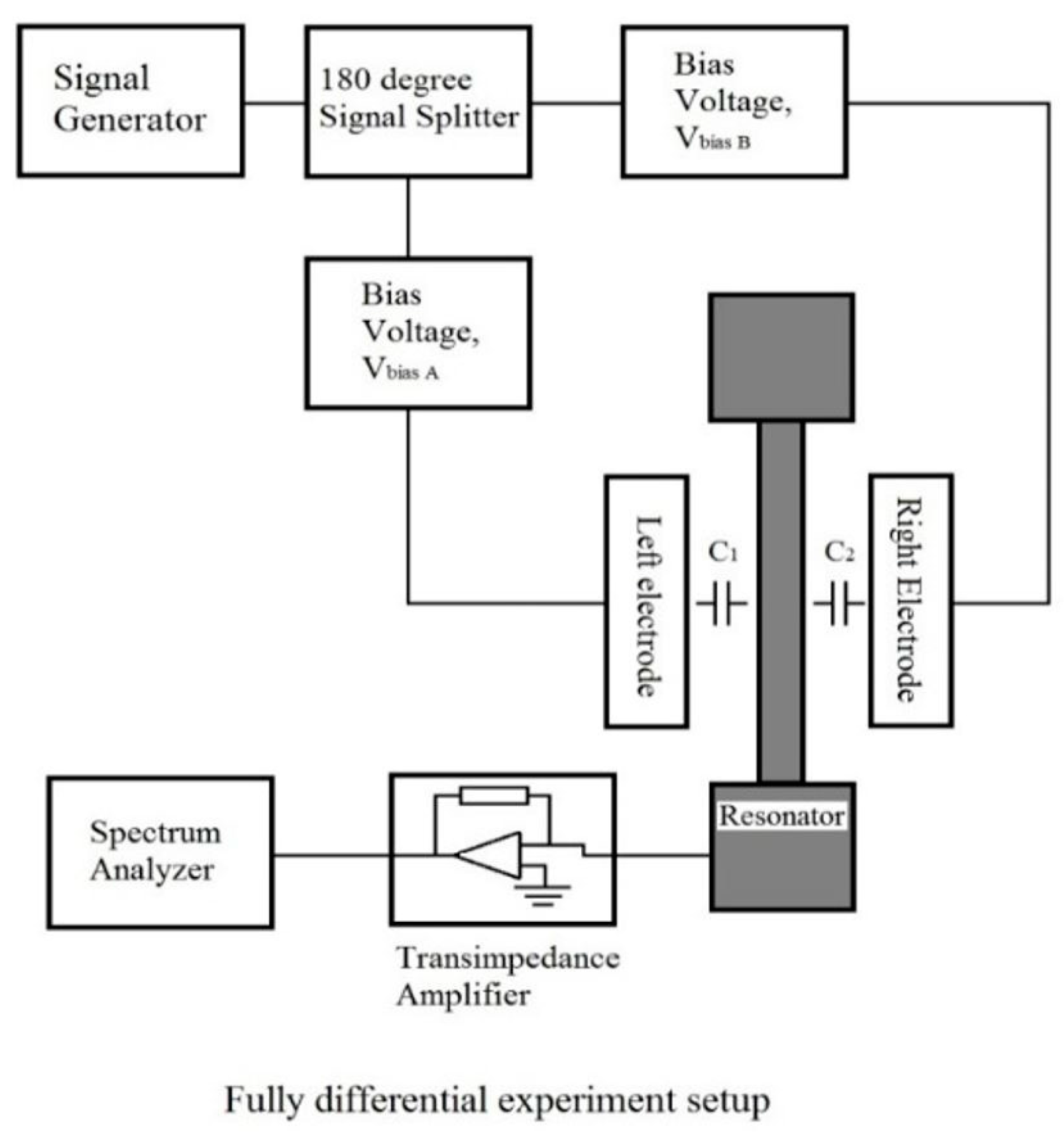
3. Fabrication and Experimental Setup
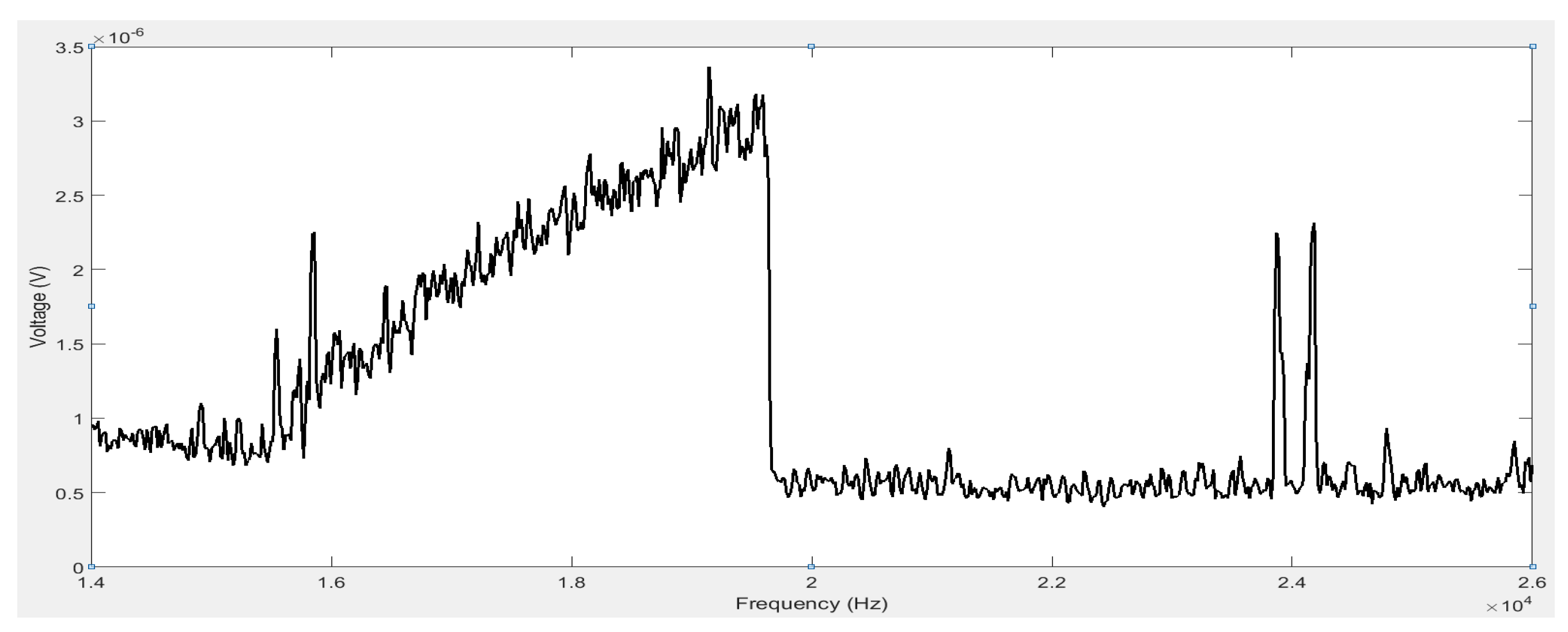
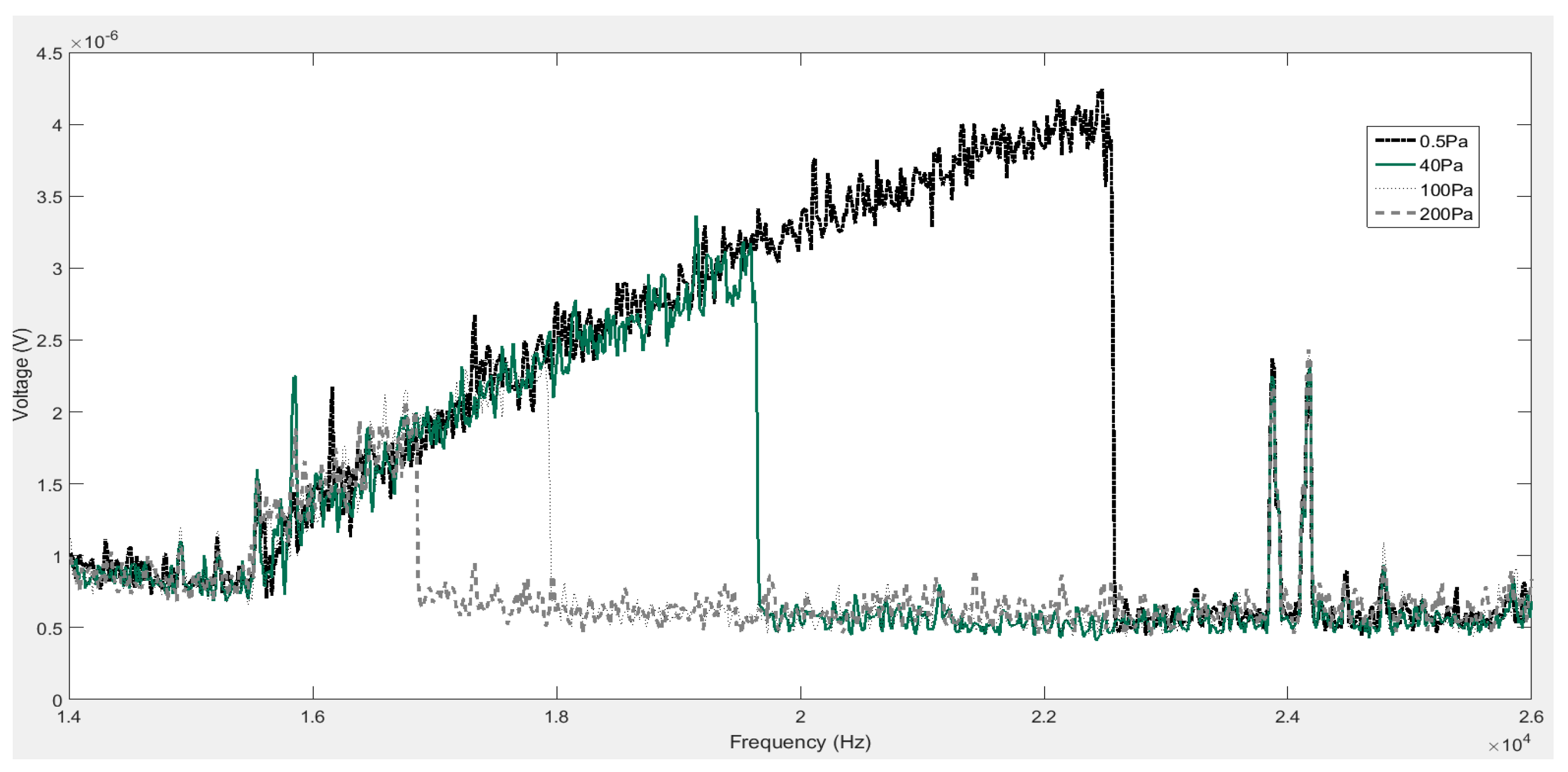
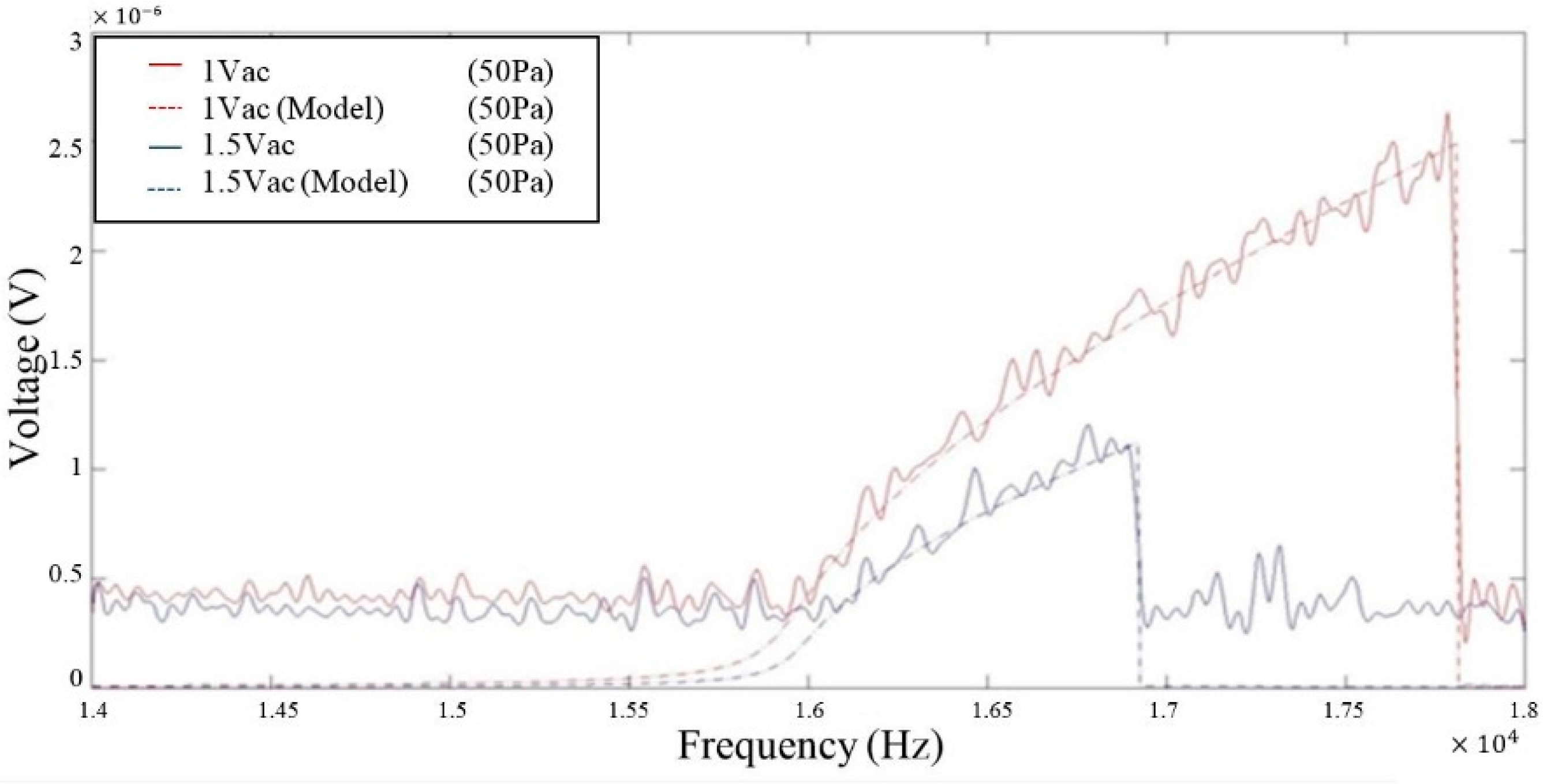
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marek, J.; Gómez, U.-M. MEMS (micro-electro-mechanical systems) for automotive and consumer electronics. In Chips 2020—A Guide to the Future of Nanoelectronics; Springer: Heidelberg, Germany; pp. 293–314.
- Chiu, S.-R.; Chen, J.-Y.; Teng, L.-T.; Sue, C.-Y.; Lin, S.-T.; Hsu, Y.-W.; Su, Y. A vibrating micro-resonator design for gyroscope applications using TIA. In Proceedings of the 2010 5th International on Microsystems Packaging Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 20–22 October 2010; pp. 1–4.
- Ramlan, R.; Brennan, M.J.; Mace, B.R.; Kovacic, I. Potential benefits of a non-linear stiffness in an energy harvesting device. Nonlinear Dyn. 2010, 59, 545–558. [Google Scholar] [CrossRef]
- Miki, D.; Honzumi, M.; Suzuki, Y.; Kasagi, N. Large-amplitude MEMS electret generator with nonlinear spring. In Proceedings of the 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS), Wanchai, Hong Kong, China, 24–28 January 2010; pp. 176–179.
- Zhang, W.; Turner, K.L. Application of parametric resonance amplification in a single-crystal silicon micro-oscillator based mass sensor. Sens. Actuators A Phys. 2005, 122, 23–30. [Google Scholar] [CrossRef]
- Rayleigh, L. Theory of Sound, 2nd ed.; Dover Publications: New York, NY, USA, 1945. [Google Scholar]
- Kaajakari, V. Theory and Analysis of MEMS Resonators. Available online: http://www.ieee-uffc.org/frequency-control/learning/pdf/Kaajakari-MEMS_Resonators_v2b.pdf (accessed on 28 July 2016).
- Landau, L.D.; Lifshitz, E.M. Mechanics, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 1999. [Google Scholar]
- Kaajakari, V.; Mattila, T.; Oja, A.; Seppa, H. Nonlinear limits for single-crystal silicon microresonators. J. Microelectromech. Syst. 2004, 13, 715–724. [Google Scholar] [CrossRef]
- Kamiński, M.; Corigliano, A. Numerical solution of the Duffing equation with random coefficients. Meccanica 2015, 50, 1841–1853. [Google Scholar] [CrossRef]
- Solution Techniques for Cubic Expressions and Root Finding. Available online: https://www.e-education.psu.edu/png520/m11_p6.html (accessed on 28 July 2016).
- Tang, W.C.K. Electrostatic Comb Drive for Resonant Sensor and Actuator Applications. Ph.D. Thesis, University of California, Oakland, CA, USA, 1990. [Google Scholar]
- Martin, M.J.; Houston, B.H.; Baldwin, W.J.; Zalalutdinov, M.K. Damping models for microcantilevers, bridges, and torsional resonators in the free-molecular-flow regime. J. Microelectromech. Syst. 2008, 17, 503–511. [Google Scholar] [CrossRef]
- Hong, G.; Ye, W. A macromodel for squeeze-film air damping in the free-molecule regime. Phys. Fluid. 2010. [Google Scholar] [CrossRef]
- Leung, R.; Cheung, H.; Gang, H.; Ye, W. A Monte Carlo simulation approach for the modeling of free-molecule squeeze-film damping of flexible microresonators. Microfluid. Nanofluid. 2010, 9, 809–818. [Google Scholar] [CrossRef]
- Alexander, F.J.; Garcia, A.L. The direct simulation Monte Carlo method. Comput. Phys. 1997, 11, 588–593. [Google Scholar] [CrossRef]
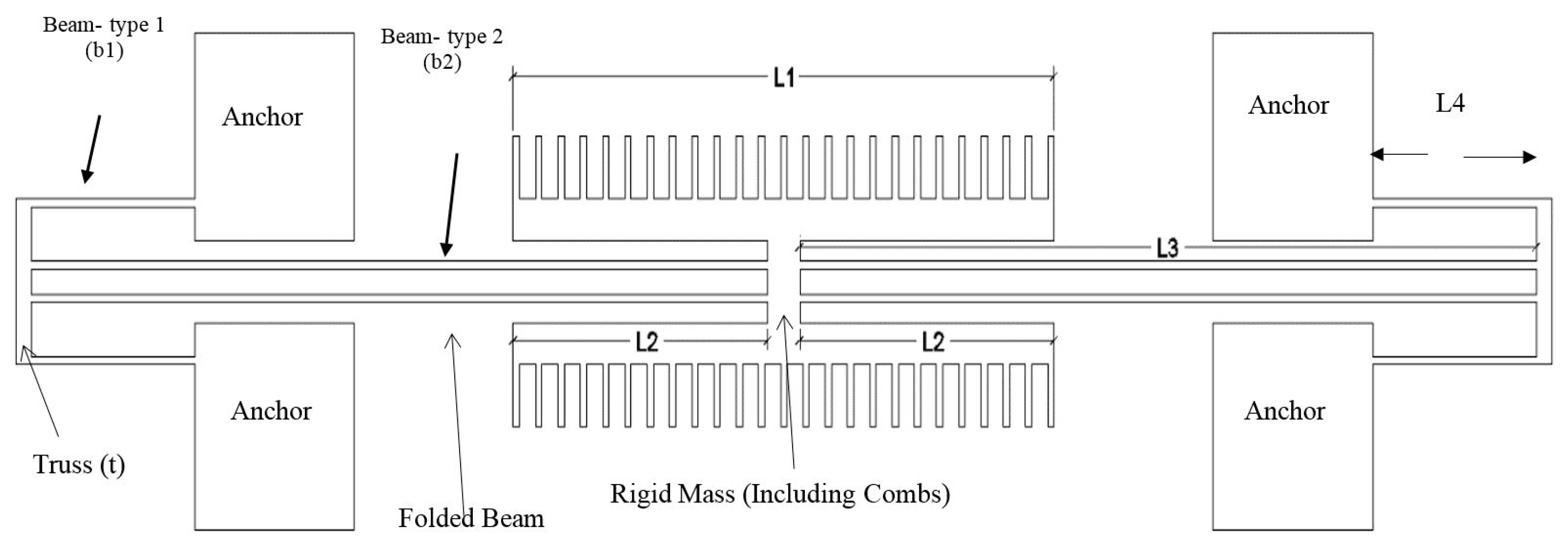



| L1 | L2 | L3 | L4 | Beam Width |
|---|---|---|---|---|
| 340 µm | 160 µm | 463 µm | 103 µm | 4 µm |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramanan, A.; Teoh, Y.X.; Ma, W.; Ye, W. Characterization of a Laterally Oscillating Microresonator Operating in the Nonlinear Region. Micromachines 2016, 7, 132. https://doi.org/10.3390/mi7080132
Ramanan A, Teoh YX, Ma W, Ye W. Characterization of a Laterally Oscillating Microresonator Operating in the Nonlinear Region. Micromachines. 2016; 7(8):132. https://doi.org/10.3390/mi7080132
Chicago/Turabian StyleRamanan, Aditya, Yu Xuan Teoh, Wei Ma, and Wenjing Ye. 2016. "Characterization of a Laterally Oscillating Microresonator Operating in the Nonlinear Region" Micromachines 7, no. 8: 132. https://doi.org/10.3390/mi7080132






