Artificial Roughness Encoding with a Bio-inspired MEMS-based Tactile Sensor Array
Abstract
:1. Introduction
2. Materials
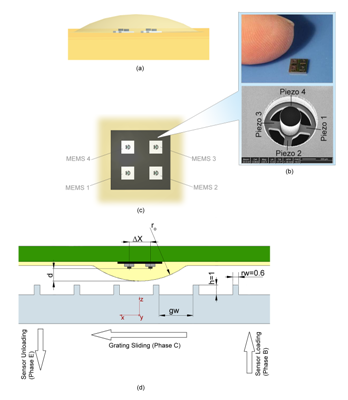
2.1. MEMS Sensor Array
2.2. Packaging
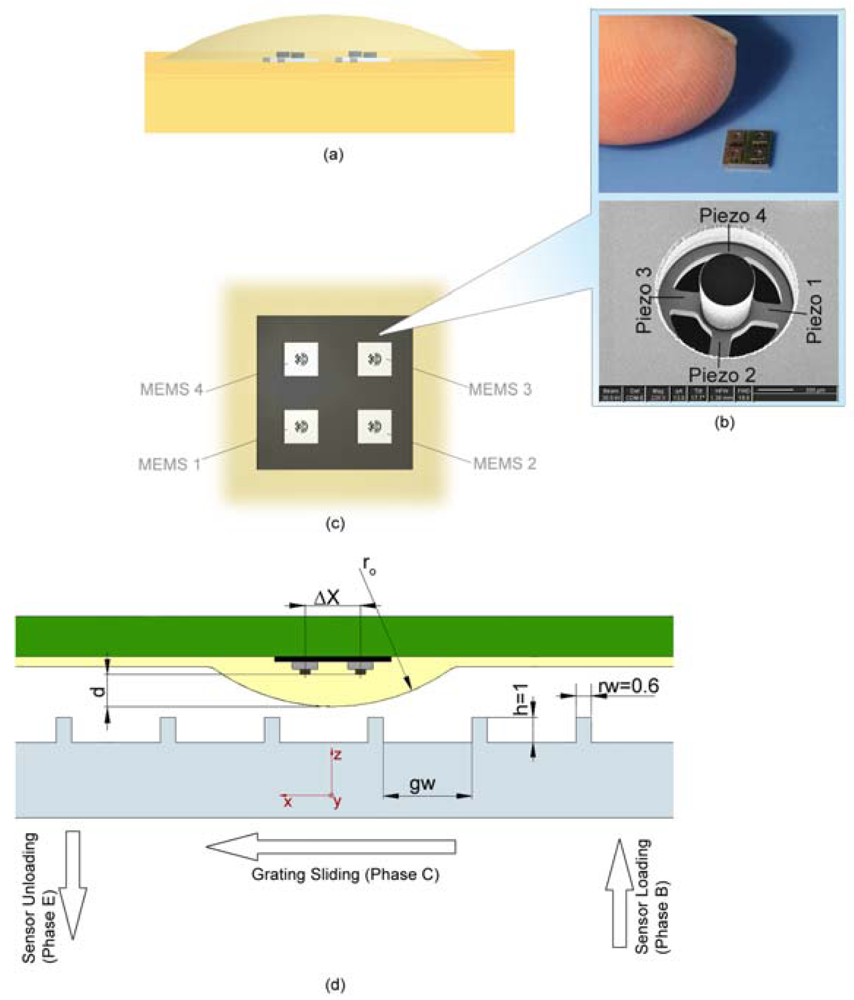
2.3. Readout Electronics
3. Methods
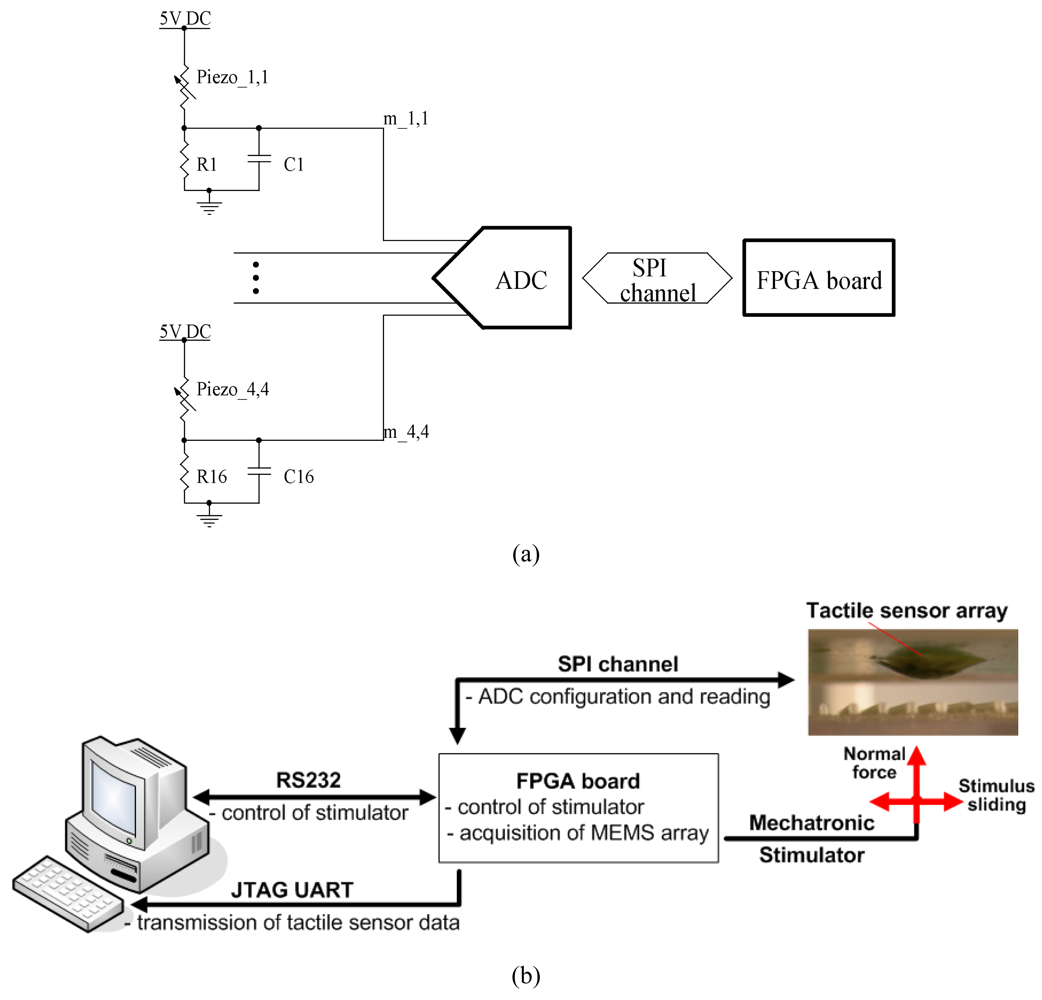
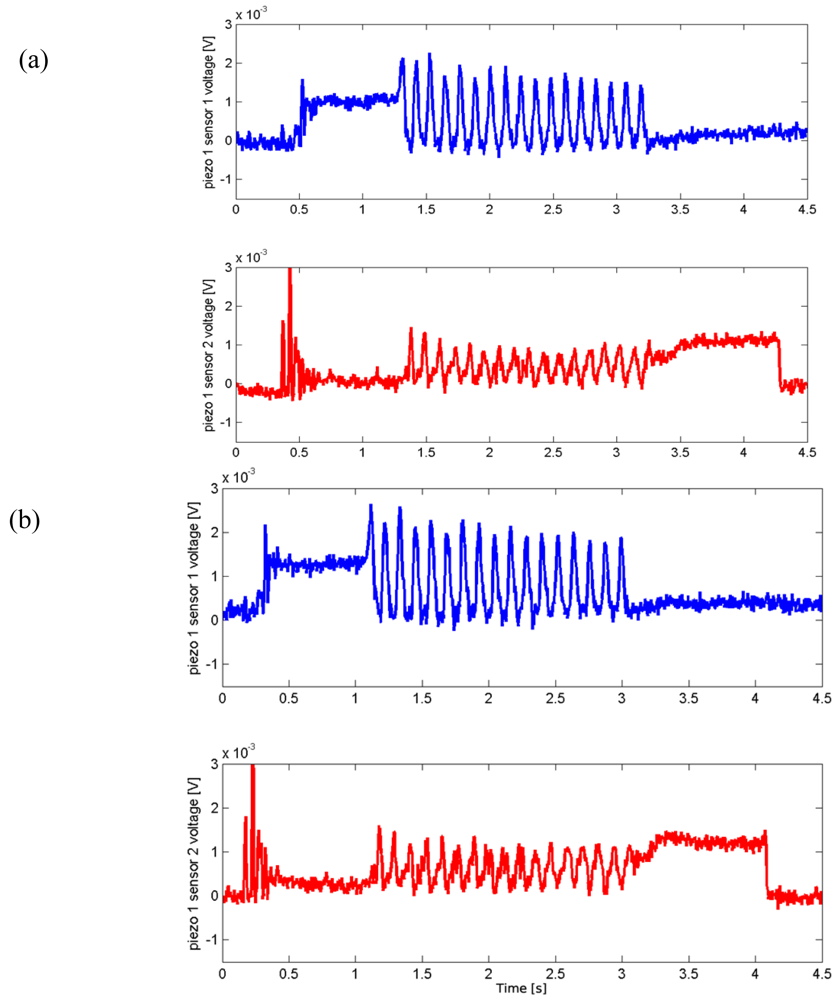
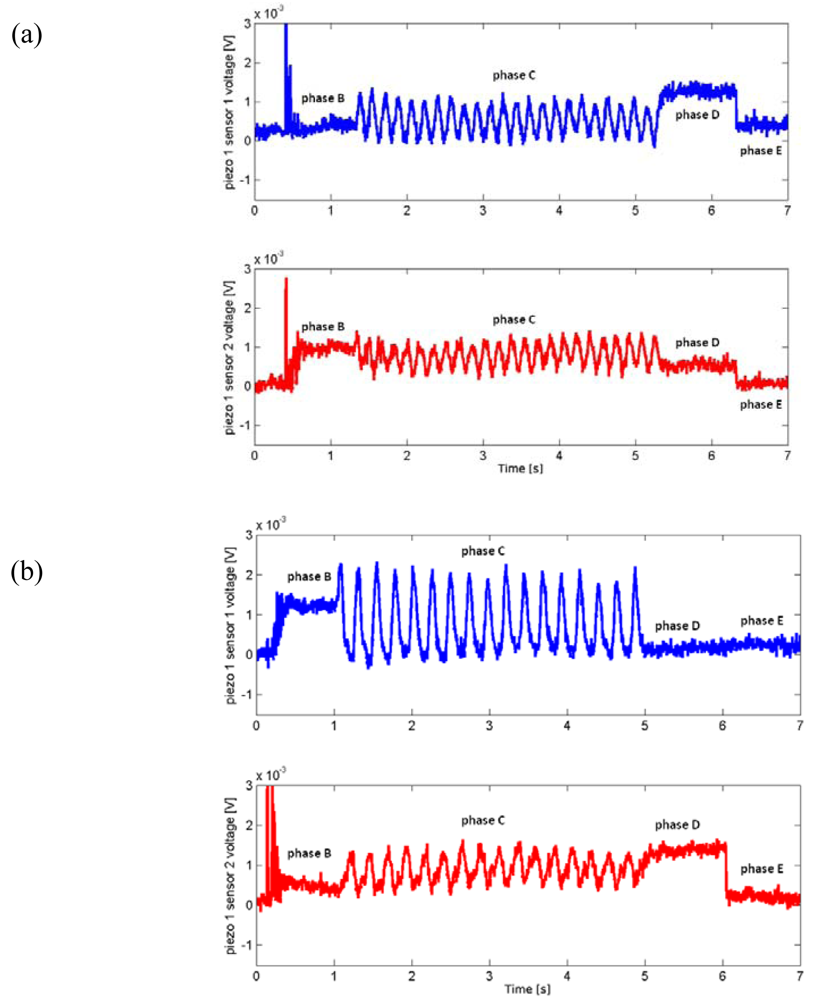
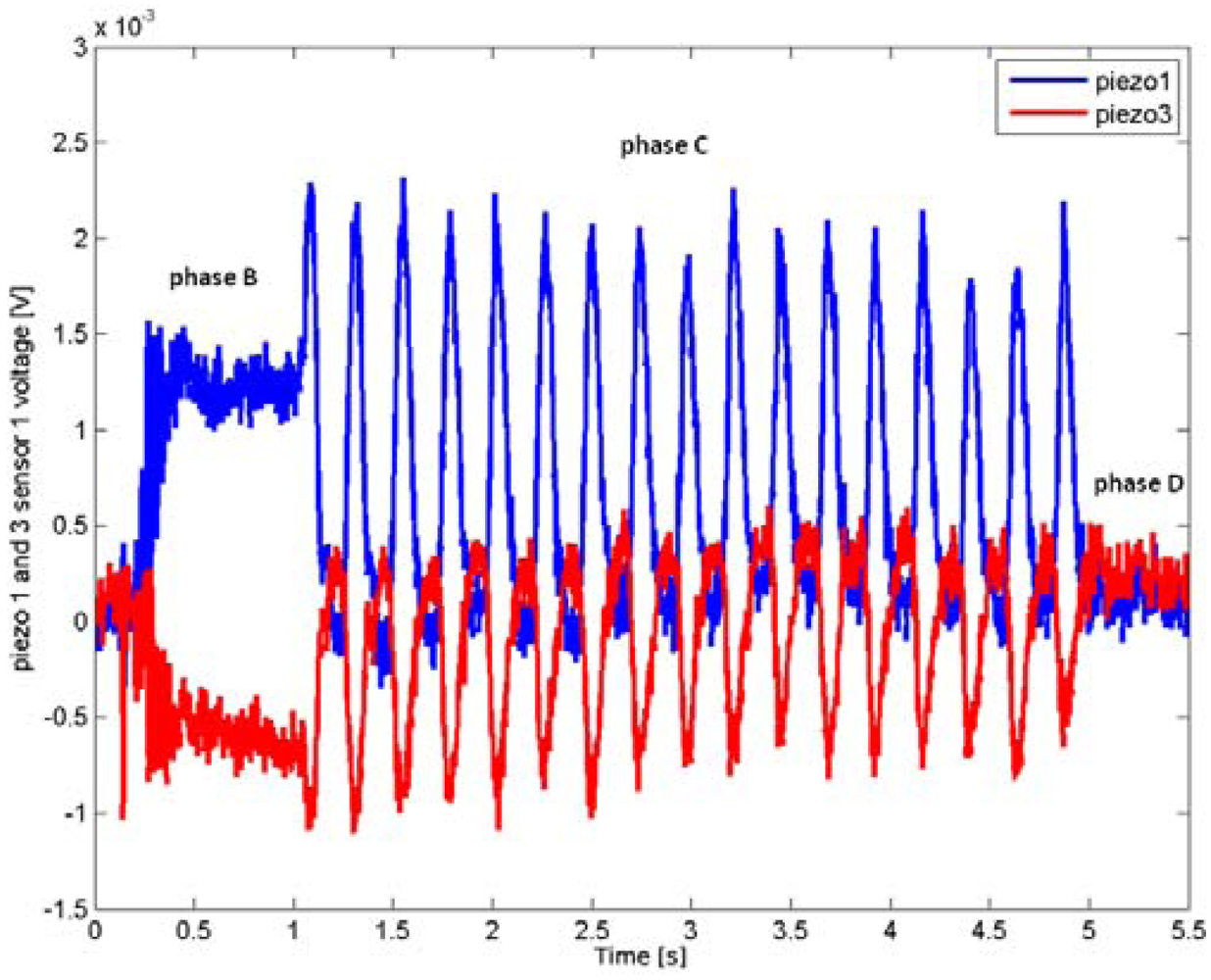
3.1. Experimental Protocol
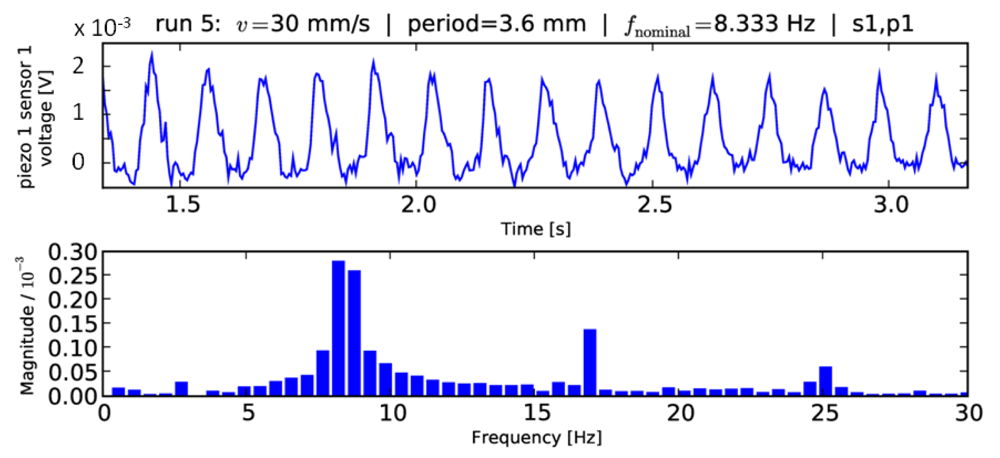
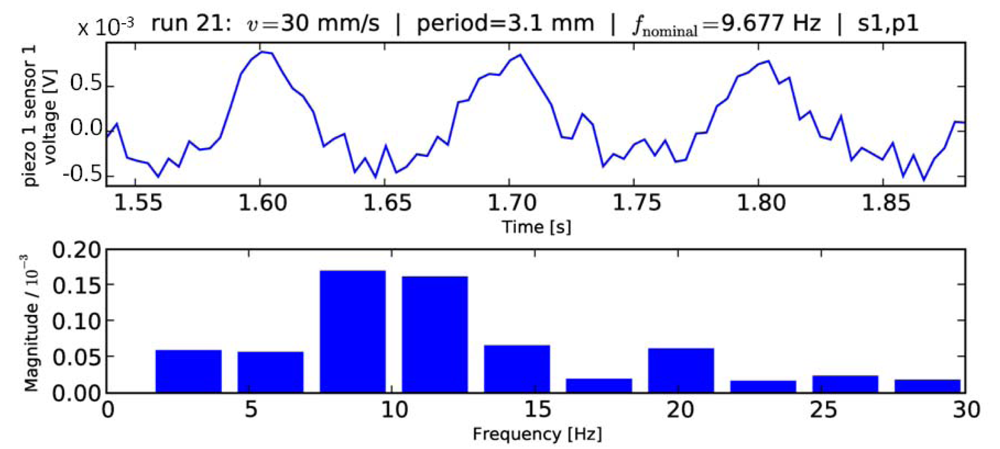
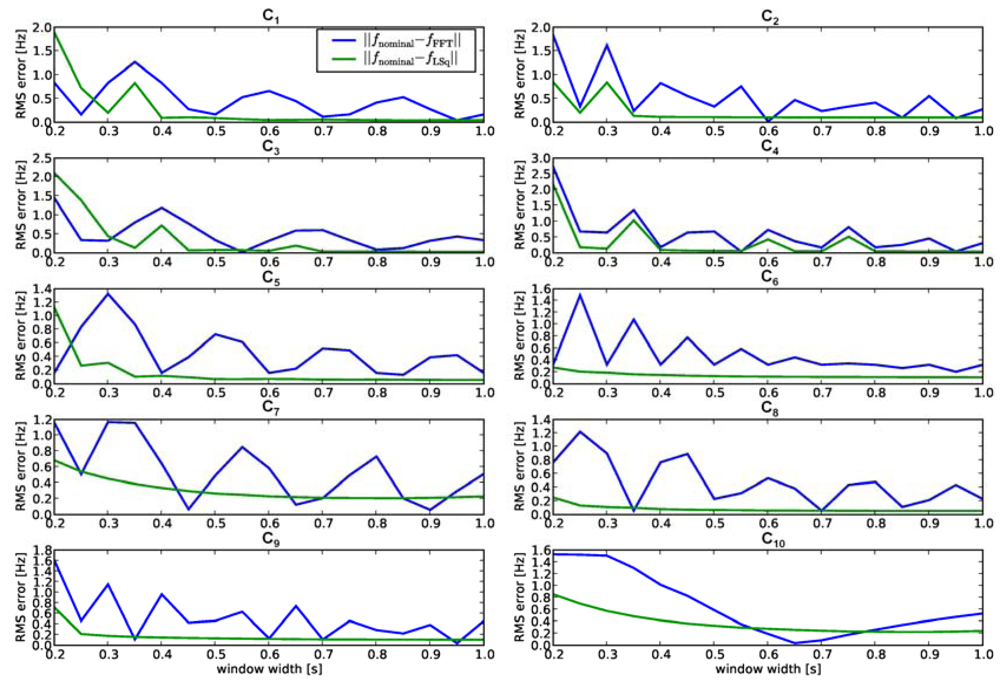
3.2. Common Frequency Detection
Preprocessing
Fast Fourier Transform
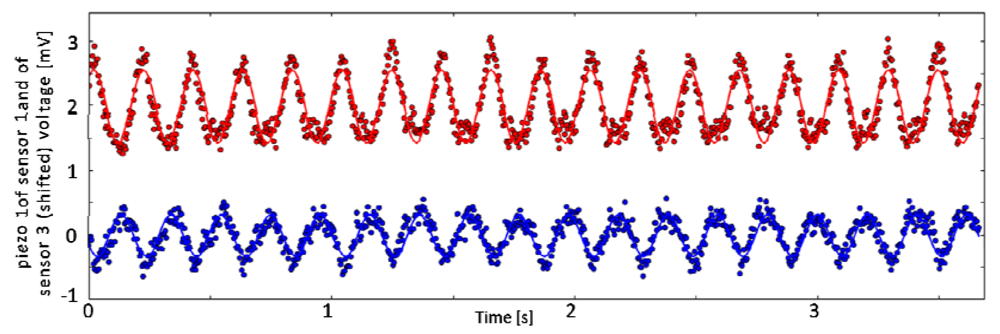
Least squares fitting
- –
- mi,j is the signal obtained from the i-th piezoresistor of the j-th MEMS unit of the 2×2 array;
- –
- Bi,j and Ai,j are the offset and the amplitude of the sine waves used for fitting each mi,j;
- –
- – ti,j is an offset time which well fits the sine waves with data acquired during the exploration phase;
- –
- f is the common principal frequency coming out from the output signals using the analysis described below; observe that f is expected to be the same for all the outputs of the sensor array.
3.3. Error Parameters and Repeatability
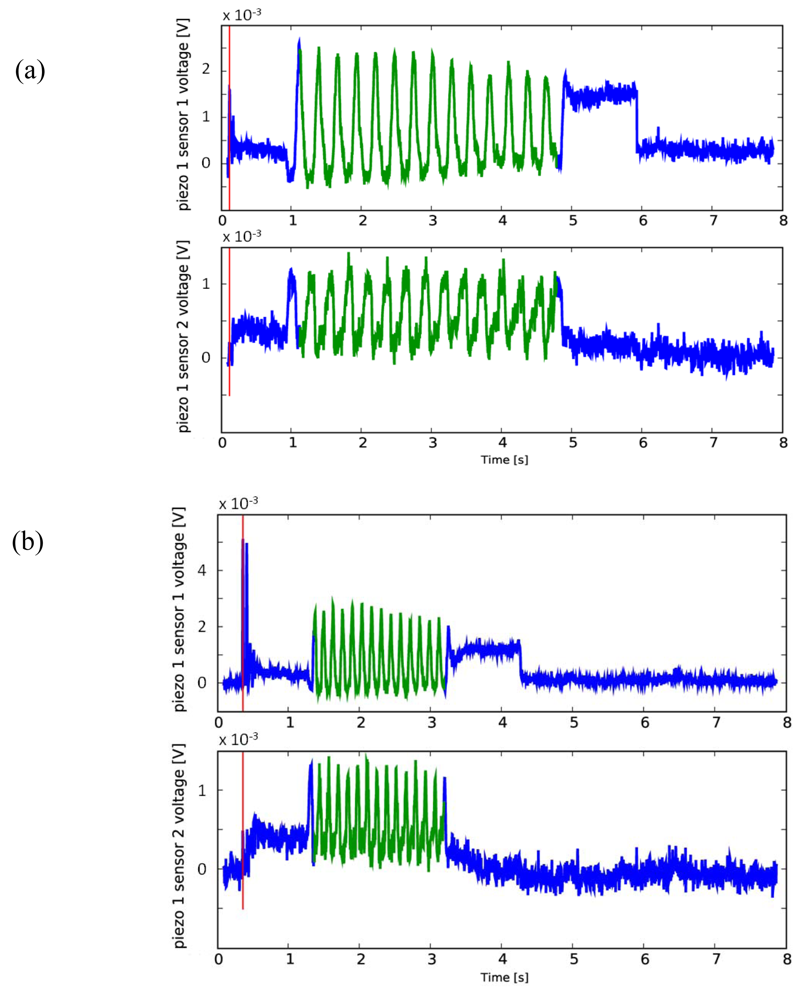
4. Experimental Results
Fast Fourier Transform
Least Squares Fitting
Repeatability
Static Imaging
5. Discussion
6. Conclusions and Future Work
Acknowledgments
References and Notes
- Johnson, K.O.; Yoshioka, T. Neural mechanisms of tactile form and texture perception. In The Somatosensory System: Deciphering the Brain's Own Body Image; Nelson, RJ, Ed.; CRC Press LLC: Boca Raton, FL, USA, 2001; pp. 73–101. [Google Scholar]
- Jones, L.A.; Lederman, S.J. Tactile Sensing. In Human Hand Function; Jones, LA, Lederman, SJ, Eds.; Oxford University Press: New York, NY, USA, 2006; pp. 44–74. [Google Scholar]
- Hollins, M.; Faldowski, R.; Rao, S.; Young, F. Perceptual dimensions of tactile surface texture: a multidimensional scaling analysis. Percept. Psychophys. 1993, 54, 697–705. [Google Scholar]
- Yoshioka, T.; Bensmaïa, S.J.; Craig, J.C.; Hsiao, S.S. Texture perception through direct and indirect touch: An analysis of perceptual space for tactile textures in two modes of exploration. Somatos. Mot. Res. 2007, 24, 53–70. [Google Scholar]
- Meftah, E.M.; Belingard, L.; Chapman, C.E. Relative effects of the spatial and temporal characteristics of scanned surfaces on human perception of tactile roughness using passive touch. Exp. Brain. Res. 2000, 132, 351–361. [Google Scholar]
- Smith, M.; Chapman, C.E.; Deslandes, M.; Langlais, J.S.; Thibodeau, M.P. Role of Friction and Tangential Force Variation in Subjective Scaling of Tactile Roughness. Exp. Brain. Res. 2002, 144, 211–223. [Google Scholar]
- Lawrence, M.A.; Kitada, R.; Klatzky, R.L.; Lederman, S.J. Haptic roughness perception of linear gratings via bare finger or rigid probe. Perception 2007, 36, 547–557. [Google Scholar]
- Klatzky, R.L.; Lederman, S.J.; Hamilton, C.; Grindley, M.; Swendsen, R.H. Feeling textures through a probe: Effects of probe and surface geometry and exploratory factors. Percept. Psychophys. 2003, 65, 613–631. [Google Scholar]
- LaMotte, R.H.; Srinivasan, MA. Surface microgeometry: Neural encoding and perception. Information Processing in the Somatosensory System. In Wenner-Gren Intl. Symposium Series; Franzen, O, Westman, J, Eds.; Macmillan Press: New York, NY, USA, 1991; pp. 49–58. [Google Scholar]
- Scheibert, J.; Leurent, S.; Prevost, A.; Debrégas, G. The role of fingerprints in the coding of tactile information probed with a biomimetic sensor. Science 2009, 323, 1503–1506. [Google Scholar]
- Srinivasan, M.A.; Whitehouse, JM; LaMotte, RH. Tactile detection of slip: Surface microgeometry and peripheral neural codes. J. Neurophysiol. 1990, 63, 1323–1332. [Google Scholar]
- Hollins, M.; Risner, S.R. Evidence for the duplex theory of tactile texture perception. Percept. Psychophys. 2000, 62, 695–705. [Google Scholar]
- Yoshioka, T.; Gibb, B.; Dorsch, A.K.; Hsiao, S.S.; Johnson, K.O. Neural coding mechanisms underlying perceived roughness of finely textured surfaces. J. Neurosci. 2001, 21, 6905–6916. [Google Scholar]
- Konyo, M.; Maeno, T.; Yoshida, A.; Tadokoro, S. Roughness sense display representing temporal frequency changes of tactile information in response to hand movements. Proceedings of the First Joint Eurohaptics Conference and Symposium on Haptic Interface for Virtual Environment and Teleoperator Systems 2005, 609–610. [Google Scholar]
- Konyo, M.; Yoshida, A.; Tadokoro, S.; Saiwaki, N. A tactile synthesis method using multiple frequency vibrations for representing virtual touch. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems 2005, Edmonton, Canada, 2-6 August, 2005; pp. 3965–3971.
- Lee, M.H.; Nicholls, H.R. Tactile sensing for mechatronics: A state of the art survey. Mechatronics 1999, 9, 1–31. [Google Scholar]
- Maheshwari, V.; Saraf, R.F. Tactile devices to sense touch on a par with a human finger. Angew Chem. Int. Edit. 2008, 47, 7808–7826. [Google Scholar]
- Kim, S.H.; Engel, J.; Liu, C.; Jones, D.L. Texture classification using a polymer-based MEMS tactile sensor. J. Micromech. Microeng. 2005, 15, 912–920. [Google Scholar]
- Mukaibo, Y.; Shirado, H.; Konyo, M; Maeno, T. Development of a texture sensor emulating the tissue structure and perceptual mechanism of human fingers. Proceedings of the IEEE International Conference on Robotics and Automation 2005, Barcelona, Spain, 18-22 April 2005; pp. 2565–2570.
- Okamoto, S.; Konyo, M.; Mukaibo, Y.; Maeno, T.; Tadokoro, S. Real-time estimation of touch feeling factors using human finger mimetic tactile sensors. Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems 2006, Beijing, China, October 2006; pp. 3581–3586.
- Scheibert, J.; Prevost, A.; Debrégas, G.; Rousier, R.; Rey, P. A Novel Biomimetic Haptic Sensor to study the Physics of Touch. Proceedings of Méchanotransduction, 2004.
- Shimojo, M.; Ishikawa, M. An active touch sensing method using a spatial filtering tactile sensor. Proceedings of the IEEE International Conference on Robotics and Automation 1993, Seoul, Korea, May 1993; pp. 948–954.
- Hosoda, K.; Tada, Y.; Asada, M. Anthropomorphic robotic soft fingertip with randomly distributed receptors. Robot. Auton. Systems 2006, 54, 104–109. [Google Scholar]
- Fishel, J.A.; Santos, V.J.; Loeb, G.E. A Robust Micro-Vibration Sensor for Biomimetic Fingertips. Proceedings of the IEEE 2nd Biennial IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics 2008, Scottsdale, AZ, USA, 19-22 October, 2008; pp. 659–663.
- Wettels, N.; Santos, V.J.; Johansson, R.S.; Loeb, G.E. Biomimetic Tactile Sensor Array. Adv. Robot. 2008, 22, 829–849. [Google Scholar]
- Maheshwari, V.; Saraf, R.F. High-resolution thin-film device to sense texture by touch. Science 2006, 312, 1501–1504. [Google Scholar]
- Johansson, R.S.; Vallbo, Å.B. Tactile sensibility in the human hand: relative and absolute densities of four types of mechanoreceptive units in glabrous skin. J. Physiol. (Lond.) 1979, 286, 283–300. [Google Scholar]
- Beccai, L.; Roccella, S.; Arena, A.; Valvo, F.; Valdastri, P.; Menciassi, A.; Carrozza, M.C. Design and fabrication of a hybrid silicon three-axial force sensor for biomechanical applications. Sens. Actuator A-Phys. 2005, 120, 370–382. [Google Scholar]
- Beccai, L.; Roccella, S.; Ascari, L.; Valdastri, P.; Sieber, A.; Carrozza, M.C.; Dario, P. Development and Experimental Analysis of a Soft Compliant Tactile Microsensor for Anthropomorphic Artificial Hand. IEEE-ASME Trans. Mechatron. 2008, 13, 158–168. [Google Scholar]
- Oddo, C.M.; Valdastri, P.; Beccai, L.; Roccella, S.; Carrozza, M.C.; Dario, P. Investigation on calibration methods for multi-axis, linear and redundant force sensors. Meas. Sci. Technol. 2007, 18, 623–631. [Google Scholar]
- Vásárhelyi, G.; Fodor, B.; Roska, T. Tactile sensing-processing: interface-cover geometry and the inverse-elastic problem. Sens. Actuat. A-Phys. 2007, 140, 8–18. [Google Scholar]
- Carrozza, M.C.; Cappiello, G.; Micera, S.; Edin, B.B.; Beccai, L.; Cipriani, C. Design of a cybernetic hand for perception and action. Biol. Cybern. 2006, 95, 629–644. [Google Scholar]
- Beccai, L.; Roccella, S.; Oddo, C.; Carrozza, M.C. Sensing fingertip for bio-inspired tactile encoding. In Proceedings of the First Italian Conference on Bioengineering; Burattini, R, Contro, R, Dario, P, Landini, L, Eds.; Pàtron editore: Bologna, Italy, 2008; p. 787. [Google Scholar]
- Vásárhelyi, G.; Ádám, M.; Vázsonyi, É; Bársony, I; Dücső, C. Effects of the elastic cover on tactile sensor arrays. Sens. Actuat. A-Phys. 2006, 132, 245–251. [Google Scholar]
- Shimojo, M. Mechanical filtering effect of elastic cover for tactile sensor. IEEE Trans. Rob. Autom. 1997, 13, 128–132. [Google Scholar]
- Lederman, S.J. Tactile roughness of grooved surfaces: the touching process and effects of macro- and microsurface structure. Percept. Psychophys. 1974, 16, 385–395. [Google Scholar]
- Darian-Smith, I.; Oke, L.E. Peripheral neural representation of the spatial frequency of a grating moving across the monkey's finger pad. J. Physiol.-London 1980, 309, 117–133. [Google Scholar]
| Grating number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| gw (mm) | 2.0 | 2.5 | 3.0 | 3.5 |
| Δp (mm) | 2.6 | 3.1 | 3.6 | 4.1 |
| Expected frequency vs. Δp and v | Δp = 4.1 mm | Δp = 3.6 mm | Δp = 3.1 mm | Δp = 2.6 mm |
|---|---|---|---|---|
| v = 15 mm/s | 3.66 Hz | 4.17 Hz | 4.84 Hz | 5.77 Hz |
| v = 30 mm/s | 7.32 Hz | 8.33 Hz | 9.68 Hz | 11.54 Hz |
| v = 48 mm/s | 11.71 Hz (not tested) | 13.33 Hz (not tested) | 15.48 Hz | 18.46 Hz |
| Measurement run | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1-4 | 5-8 | 9-12 | 13-16 | 17-20 | 21-24 | 25-28 | 29-32 | 33-36 | 37-40 | |
| fnominal [Hz] | 4.17 | 8.33 | 3.66 | 7.32 | 4.84 | 9.68 | 15.48 | 5.77 | 11.54 | 18.46 |
| C | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
| Δp [mm] | 3.6 | 3.6 | 4.1 | 4.1 | 3.1 | 3.1 | 3.1 | 2.6 | 2.6 | 2.6 |
| v [mm/s] | 15 | 30 | 15 | 30 | 15 | 30 | 48 | 15 | 30 | 48 |
| piezo1,1 vs. piezo2,1 | ||||||||||
| εFFT | 0.072 | 0.135 | 0.113 | 0.182 | 0.078 | 0.168 | 0.286 | 0.033 | 0.053 | 0.063 |
| [%] | 1.72 | 1.62 | 3.1 | 2.49 | 1.62 | 1.73 | 1.85 | 0.57 | 0.46 | 0.34 |
| εLSq | 0.038 | 0.105 | 0.027 | 0.058 | 0.052 | 0.123 | 0.257 | 0.053 | 0.124 | 0.272 |
| [%] | 0.91 | 1.26 | 0.73 | 0.79 | 1.08 | 1.27 | 1.66 | 0.93 | 1.07 | 1.47 |
| piezo4,1 vs. piezo2,1 | ||||||||||
| εFFT | 0.072 | 0.135 | 0.1 | 0.152 | 0.075 | 0.165 | 0.257 | 0.036 | 0.059 | 0.189 |
| [%] | 1.72 | 1.61 | 2.74 | 2.08 | 1.56 | 1.7 | 1.66 | 0.62 | 0.52 | 1.03 |
| εLSq | 0.04 | 0.127 | 0.029 | 0.063 | 0.06 | 0.126 | 0.262 | 0.055 | 0.123 | 0.266 |
| [%] | 0.97 | 1.52 | 0.,78 | 0.87 | 1.24 | 1.31 | 1.69 | 0.95 | 1.07 | 1.44 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Oddo, C.M.; Beccai, L.; Felder, M.; Giovacchini, F.; Carrozza, M.C. Artificial Roughness Encoding with a Bio-inspired MEMS-based Tactile Sensor Array. Sensors 2009, 9, 3161-3183. https://doi.org/10.3390/s90503161
Oddo CM, Beccai L, Felder M, Giovacchini F, Carrozza MC. Artificial Roughness Encoding with a Bio-inspired MEMS-based Tactile Sensor Array. Sensors. 2009; 9(5):3161-3183. https://doi.org/10.3390/s90503161
Chicago/Turabian StyleOddo, Calogero Maria, Lucia Beccai, Martin Felder, Francesco Giovacchini, and Maria Chiara Carrozza. 2009. "Artificial Roughness Encoding with a Bio-inspired MEMS-based Tactile Sensor Array" Sensors 9, no. 5: 3161-3183. https://doi.org/10.3390/s90503161