Digital Mirror Device Application in Reduction of Wave-front Phase Errors
Abstract
:1. Introduction
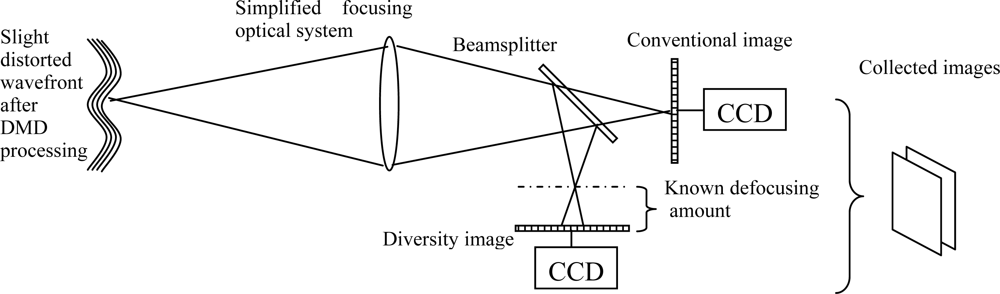
2. Correction Principle and Method
2.1 First step: adaptive optical correction using DMD
2.2 Second step: PDS correction
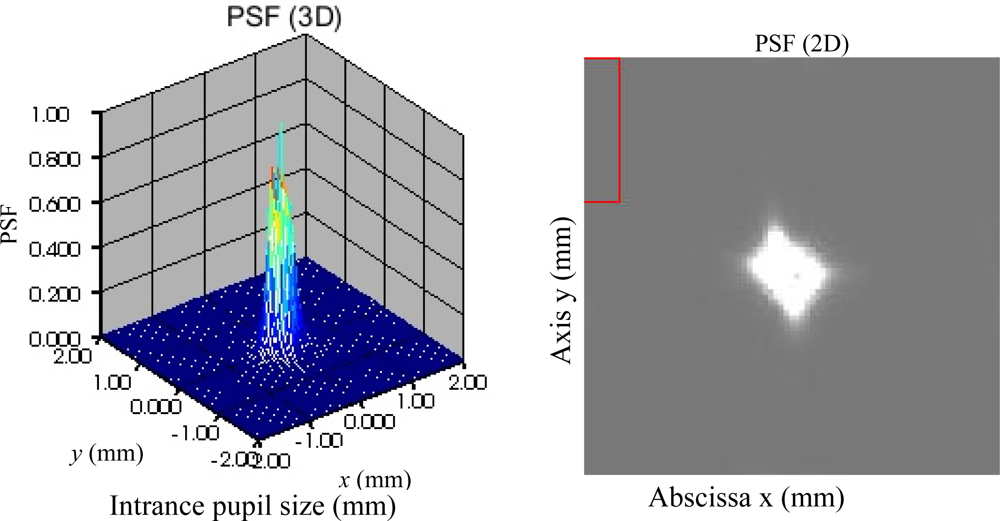
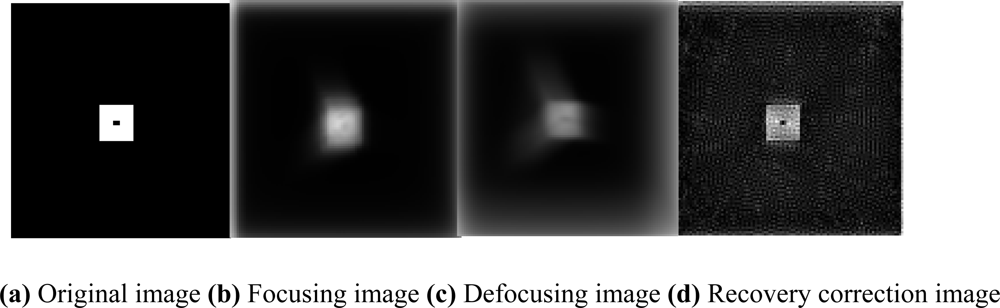
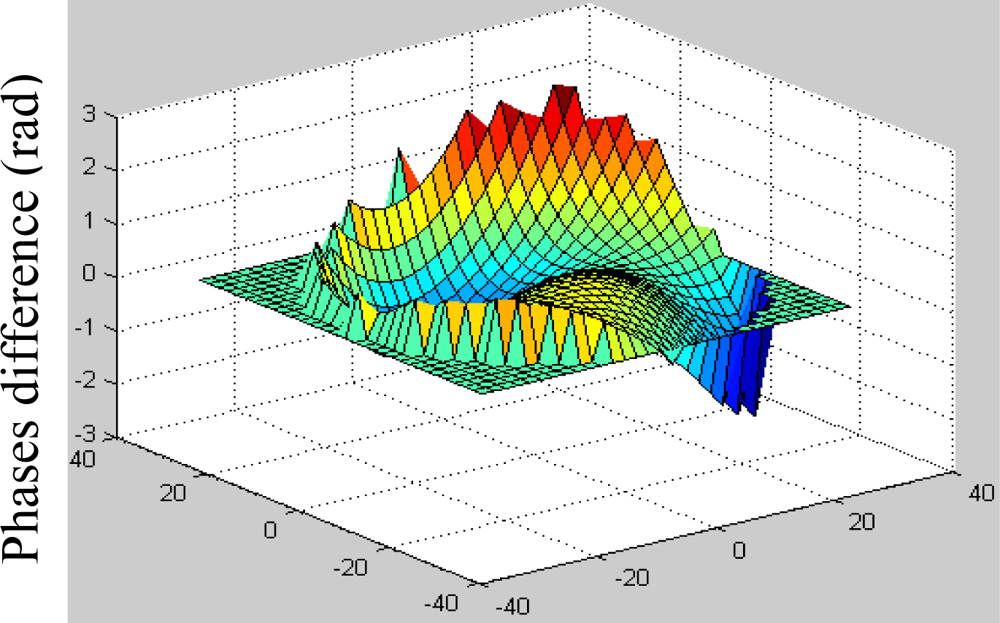
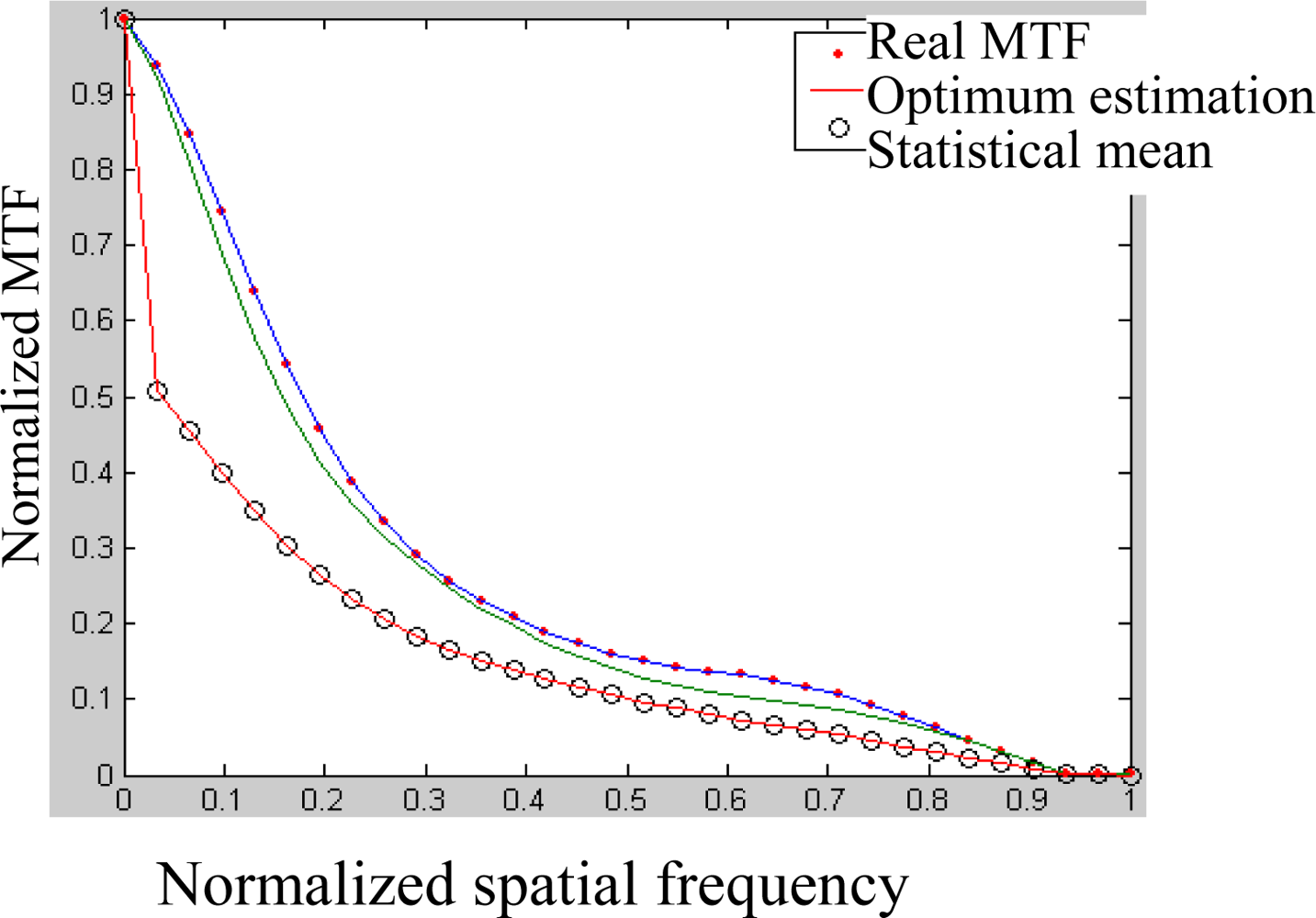
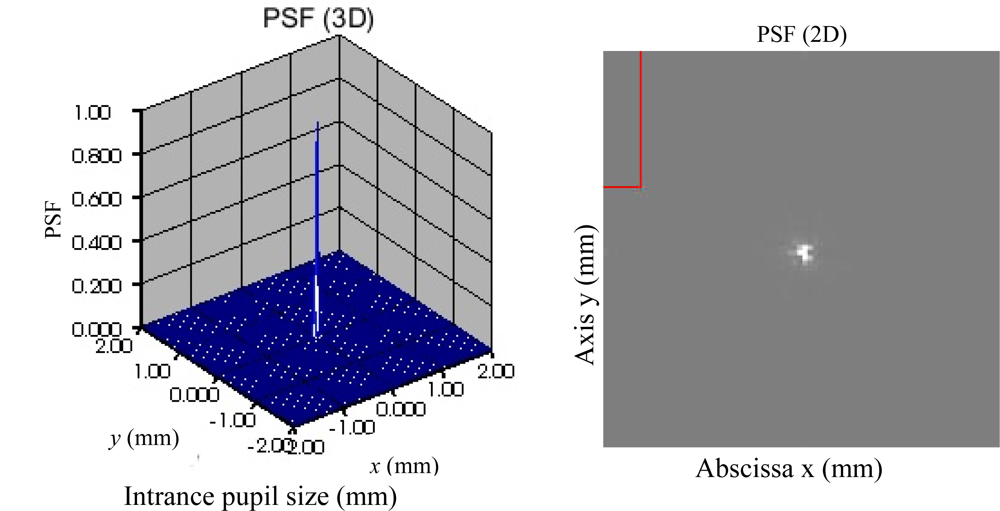
3. Experimental Results
4. Conclusions
Acknowledgments
References and Notes
- Pond, J.E.; Welch, C.T.; Sutton, G.W. Side Mounted IR Window Aero-optic and Aero-thermal Analysis. SPIE 1999, 3705, 266–275. [Google Scholar]
- Dixon, W.P. Image Degradation Caused by Thermal Gradients in Windows. AIAA, 30th Aerospace Sciences Meeting & Exhibit, Reno, NV 1992, 0705, 1–6. [Google Scholar]
- Sun, X.H.; Hong, H.Y.; Zhang, T.X. Image Reconstruction Method under Aero-optic Effect Based on ARTUR Algorithm. Infrared and Laser Engineering 2003, 4, 377–381. [Google Scholar]
- Lu, X.F.; Zhang, T.X.; Hong, H.Y. Image Correction Method with Pixel Deviation Caused by Aero-optics Effects. Infrared and Laser Engineering 2007, 5, 758–761. [Google Scholar]
- Zhang, J.R. 2002; pp. 1–44.
- Choudhury, P.R. MEMS and MOEMS Technology and Applications. SPIE Press. Washington (USA) 2000, 12. [Google Scholar]
- Zeng, Y.P.; Sun, X.Y.; Chen, W.J. Effect on the Phase Measuring Profilometer to the Spatio-temporal Characteristic of DMD. Optical Technique 2004, 2, 29–32. [Google Scholar]
- Li, Y.; Su, X.Y.; Wu, Q.Y. Study of Effect on the Phase Measuring Profilometer to the Spatiotemporal Characteristic of DMD. Laser Journal 2005, 26, 57–58. [Google Scholar]
- Hornbeck, L.J. Deformable Mirror Spatial Light Modulators. SPIE Proceedings on Critical Review Series 1989, 1150, 86–102. [Google Scholar]
- Borecki, M. Intelligent Fiber Optic Sensor for Estimating the Concentration of a Mixture-Design and Working Principle. Sensors 2007, 7, 384–399. [Google Scholar]
- El-Sherif, M.; Bansal, L.; Yuan, J. Fiber Optic Sensors For Detection of Toxic and Biological Threats. Sensors 2007, 7, 3100–3118. [Google Scholar]
- Elosua, C.; Bariain, C.; Matias, I.; Rodriguez, A.; Colacio, E.; Salinas-Castillo, A.; Segura-Carretero, A.; Fernandez-Gutiérrez, A. Pyridine Vapors Detection by an Optical Fibre Sensor. Sensors 2008, 8, 847–859. [Google Scholar]
- Parisi, A.; Cino, A.; Busacca, A.; Cherchi, M.; Riva-Sanseverino, S. Integrated Optic Surface Plasmon Resonance Measurements in a Borosilicate Glass Substrate. Sensors 2008, 8, 7113–7124. [Google Scholar]
- Richter, R. Classification Metrics for Improved Atmospheric Correction of Multispectral VNIR Imagery. Sensors 2008, 8, 6999–7011. [Google Scholar]
- Seldin, J.H; Paxman, RG. Phase-Diverse Speckle Reconstruction of Solar Data. In Image Reconstruction and Restoration. SPIE 1994, 2302, 268–280. [Google Scholar]
- Paxman, R.G.; Seldin, J.H. Fine-Resolution Astronomical Imaging with Phase-Diversity Speckle. Digital Image Recovery and Synthesis II, SPIE 1993, 2029, 287–298. [Google Scholar]
- Perreault, J.A.; Bifano, T.G.; Levine, B.M. Adaptive Optic Correction Using Silicon Based Deformable Mirrors. SPIE 1999, 3760, 12–22. [Google Scholar]
- Fried, D.L. Adaptive Optics Development, A 30-year Personal Perspective. Proceedings of SPIE 2001, 4376, 11–13. [Google Scholar]
- Thelen, B.J.; Carrara, D.A.; Paxman, R.G. Fine-resolution Imagery of Extended Objects Observed Through Volume Turbulence Using Phase-diverse Speckle. SPIE 1999, 3763, 102–111. [Google Scholar]
- Baba, N.S.; Tomita, H.Y.; Miura, N.K. Iterative Reconstruction Method in Phase Diversity Imaging. Applied Optics 1994, 33, 4428–4433. [Google Scholar]
- Carreas, R.A.; Tarr, G.; Restaino, S.; Loos, G. Concurrent Computation of Zernike Coefficients Used in a Phase Diversity Algorithm for Optical Aberration Correction. SPIE, Image and Signal Processing for Remote Sensing 1994, 2315, 363–370. [Google Scholar]


© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, Y.; Liu, Y.; Wang, S. Digital Mirror Device Application in Reduction of Wave-front Phase Errors. Sensors 2009, 9, 2345-2351. https://doi.org/10.3390/s90402345
Zhang Y, Liu Y, Wang S. Digital Mirror Device Application in Reduction of Wave-front Phase Errors. Sensors. 2009; 9(4):2345-2351. https://doi.org/10.3390/s90402345
Chicago/Turabian StyleZhang, Yaping, Yan Liu, and Shuxue Wang. 2009. "Digital Mirror Device Application in Reduction of Wave-front Phase Errors" Sensors 9, no. 4: 2345-2351. https://doi.org/10.3390/s90402345
APA StyleZhang, Y., Liu, Y., & Wang, S. (2009). Digital Mirror Device Application in Reduction of Wave-front Phase Errors. Sensors, 9(4), 2345-2351. https://doi.org/10.3390/s90402345




