1. Introduction
Increased functionality of MEMS has lead to the development of micro-structures that are more and more complex. Besides, modeling tools have not kept the pace with this growth. Indeed, the simulation of a device allows to optimize its design, to improve its performance, and to minimize development time and cost by avoiding unnecessary design cycles and foundry runs. To achieve these objectives, the development of new and more efficient modeling techniques adapted to the requirements of MEMS, has to be carried out [
1].
Several numerical methods have been proposed for the simulation of MEMS. Lumped or reduced order models and semi-analytical methods [
2][
3] allow to predict the behaviour of simple micro-structures. However they are no longer applicable for devices, such as comb drives, electrostatic motors or deflectable 3D micromirrors, where fringing electrostatic fields are dominant [
4][
5][
6]. The FE method can accurately compute these fringing effects at the expense of a dense discretization near the corners of the device [
7]. Further the FE modeling of MEMS accounting for their movement needs a completely new mesh and computation for each new position what is specially expensive when dealing with 3D models.
The scope of this work is to introduce a perturbation method for the FE modeling of electrostatically actuated MEMS. An unperturbed problem is first solved in a large mesh taking advantage of any symmetry and excluding additional regions and thus avoiding their mesh. Its solution is applied as a source to the further computations of the perturbed problems when conductive regions are added [
8][
9][
10]. It benefits from the use of different subproblem-adapted meshes, this way the computational efficiency increases as the size of each sub-problem diminishes [
9]. For some positions where the coupling between regions is significant, an iterative procedure is required to ensure an accurate solution. Successive perturbations in each region are thus calculated not only from the original source region to the added conductor but also from the latter to the former. A global-to-local method for static electric field calculations is presented in [
11]. Herein, the mesh of the local domain is included in the one of the global domain, whereas in the proposed perturbation method, the meshes of the perturbing regions are independent of the meshes of the unperturbed domain, which is a clear advantage with respect to the classical FE approach.
As test case, we consider a micro-beam subjected to an electrostatic field created by a micro-capacitor. The micro-beam is meshed independently of the complete domain between the two electrodes of the device. The electrostatic field is computed in the vicinity of the corners of the micro-beam by means of the perturbation method. For the sake of validation, results are compared to those calculated by the conventional FE approach. Furthermore, the accuracy of the perturbation method is discussed as a function of the extension of the reduced domain.
3. Perturbation Method
Hereafter, the subscripts
u and
p refer to the unperturbed and perturbed quantities and associated domains, respectively. An unperturbed problem is first defined in Ω without considering the properties of a so-called perturbing region Ω
c,p which will further lead to field distortions [
8][
9][
10]. At the discrete level, this region is not described in the mesh of Ω. The perturbation problem focuses thus on Ω
c,p and its neighborhood, their union Ω
p being adequately defined and meshed will serve as the studied domain. Electric field distortions appear when a perturbing conductive region Ω
c,p is added to the initial configuration. The perturbation problem is defined as an electrostatic problem in Ω
p.
Particularizing
(1a-b-c) for both the unperturbed and perturbed problems, we obtain [
8]
Equations (4b) and
(5b) assume that no charge density exists in the considered regions. Subtracting the unperturbed equations from the perturbed ones, one gets [
8]
with the field perturbations [
8]:
e =
ep −
eu and
d =
dp −
du. Note that if
εp ≠
εu, an additional source term given by the unperturbed solution (
εp—
εu)
eu is considered in
(6c). For the sake of simplicity,
εp and
εu are kept equal.
For added perfect conductors, carrying floating potentials, one must have
n ⨯
ep∣
∂Ωc,p= 0 and consequently
n ⨯
e ∣
∂Ωc,p= −
n ⨯
e ∣
∂Ωc,p. This leads to the following condition on the perturbation electric scalar potential
This way, υu acts as a source for the perturbation problem.
Two independent meshes are used. A mesh of the whole domain without any additional conductive regions and a mesh of the perturbing regions. A projection of the results between one mesh and the other is then required.
4. Iterative Sequence of Perturbation Electric Scalar Potential Problems
When the perturbing region Ωc,p is close to the original source field, an iterative sequence has to be carried out. Each region gives a suitable correction as a perturbation with an accuracy dependent of the fineness of its mesh.
For each iteration
i (
i = 0,1,…), we determine the electric scalar potential
υ2i in Ω, with
υ0=
υu. The projection of this solution from its original mesh to that of the added conductor Ω
c,p gives a source
υs,2i+1 for a perturbation problem. This way, we obtain a potential
υ2i+1 in ∂Ω
c,p that will counterbalance the potential in ∂Ω
c. A new source
υs,2i+2 for the initial configuration has then to be calculated. This is done by projecting
υ2i+1 from its support mesh to that of Ω as follows
A new perturbation electric scalar potential problem is defined in Ω as
with Dirichlet BC
υ2i+2 = −
υs,2i+2∣
∂Ωc.
This iterative process is repeated until convergence for a given tolerance.
5. Application
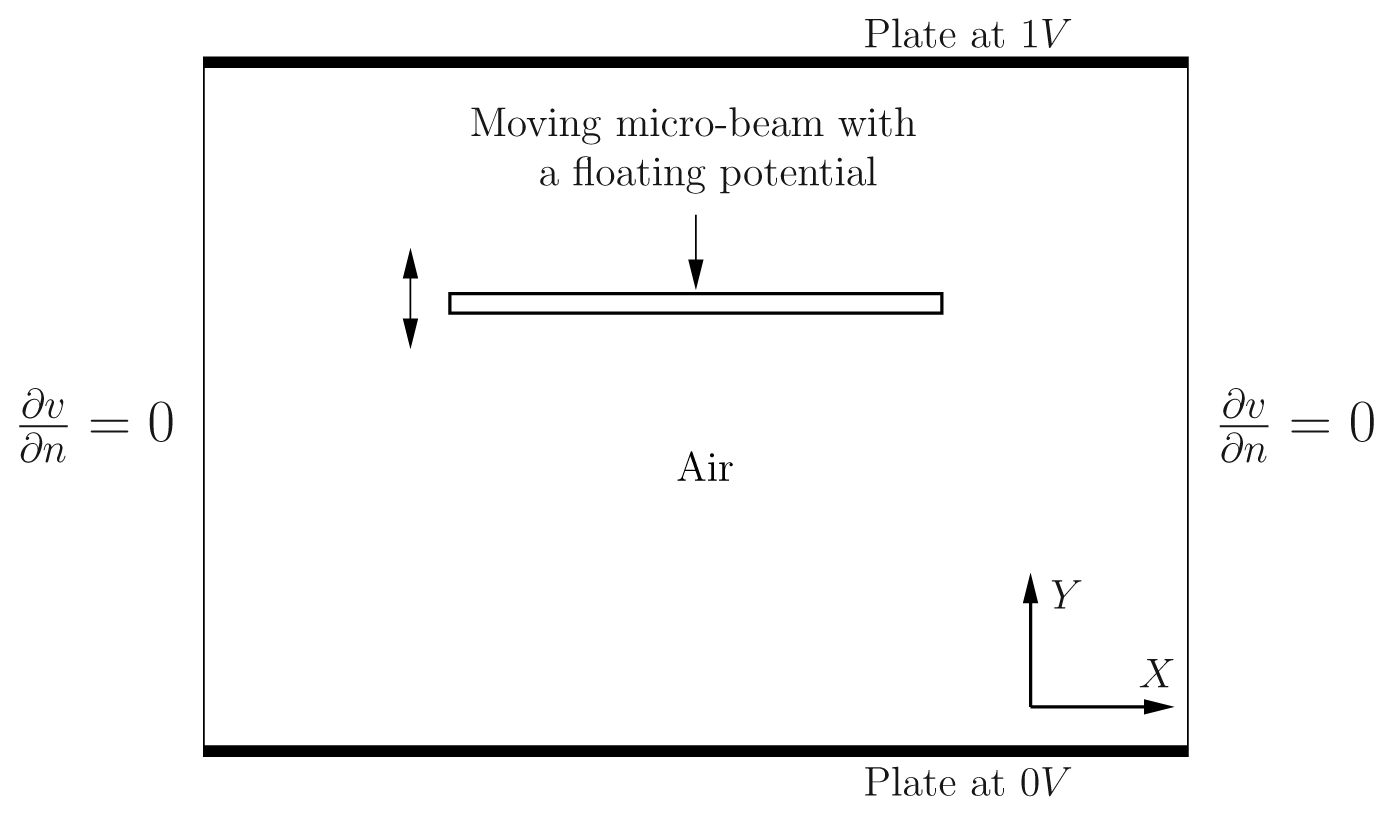
A parallel-plate capacitor (
Fig. 1) is considered as a 2-D FE test case to illustrate and validate the perturbation method for electrostatic field distortions (length of plates= 200
μm, distance between plates: d = 200
μm). The conducting parts Ω
c of the capacitor are two electrodes between which the difference of electric potential is ΔV= 1V (upper electrode fixed to 1V). The perturbing conductive region Ω
c,p is a micro-beam (length= 100
μm, width= 10
μm). This perturbing region is placed at a distance
d1 of the electrode at 1V.
First, we study the accuracy of the perturbation method as a function of the size of the perturbing domain. In this case,
d1 = 75
μm.
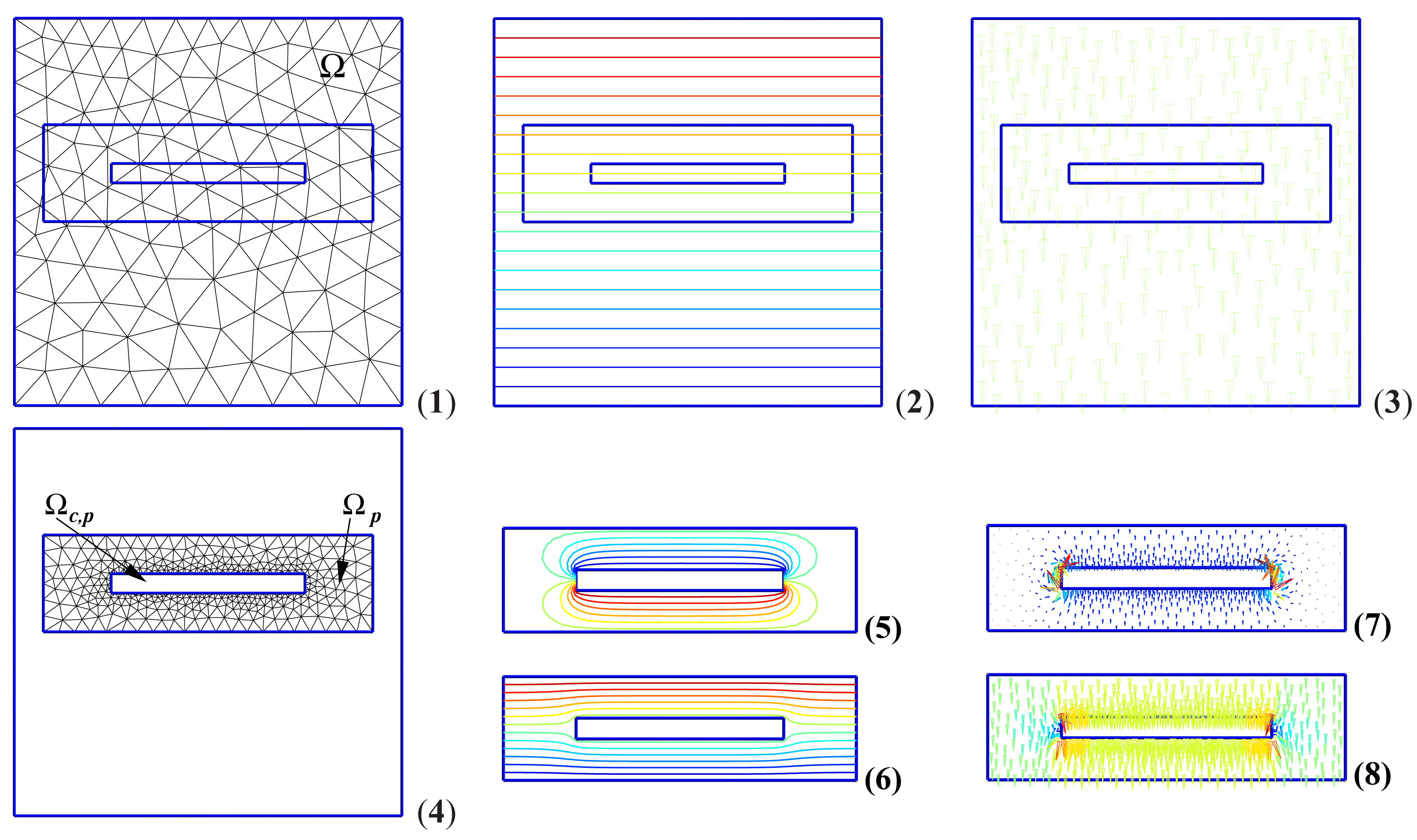
Fig. 3 shows examples of meshes for the perturbing problems. An adapted mesh, specially fine in the vicinity of the corners of the micro-beam is used. Note that any intersection of perturbation problem boundaries with the unperturbed problem material regions is allowed.
The electrostatic field between the plates of the capacitor is first calculated in the absence of the micro-beam. The solution of this problem is then evaluated on the added micro-beam and used as a source for the so-called perturbation problem.
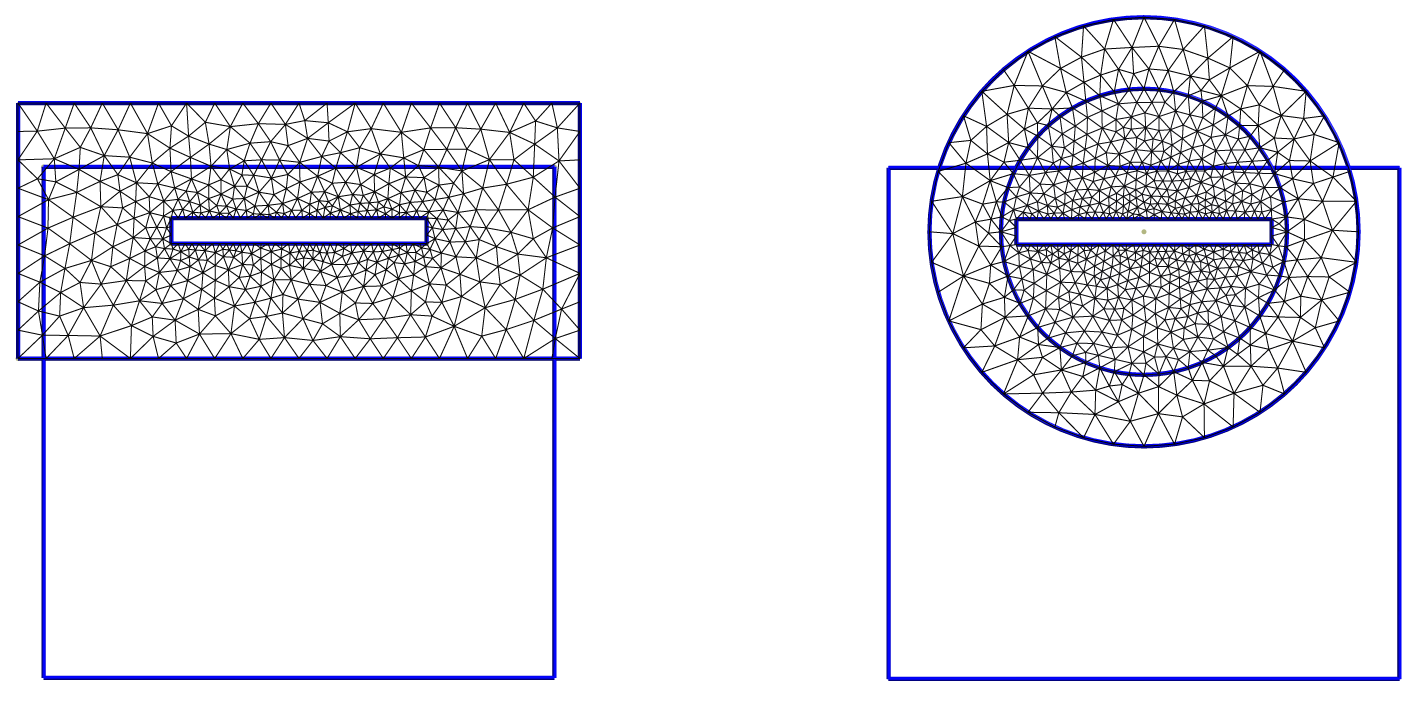
In
Fig. 4(
left), the local electric field is depicted for different sizes of the perturbation domain. The first one is a rectangular bounded perturbation region (length= 170
μm, width= 50
μm). The second one is a rectangular perturbation domain as well (length= 180
μm, width= 150
μm). The third one is an extended perturbation region to infinity through a shell transformation [
15].
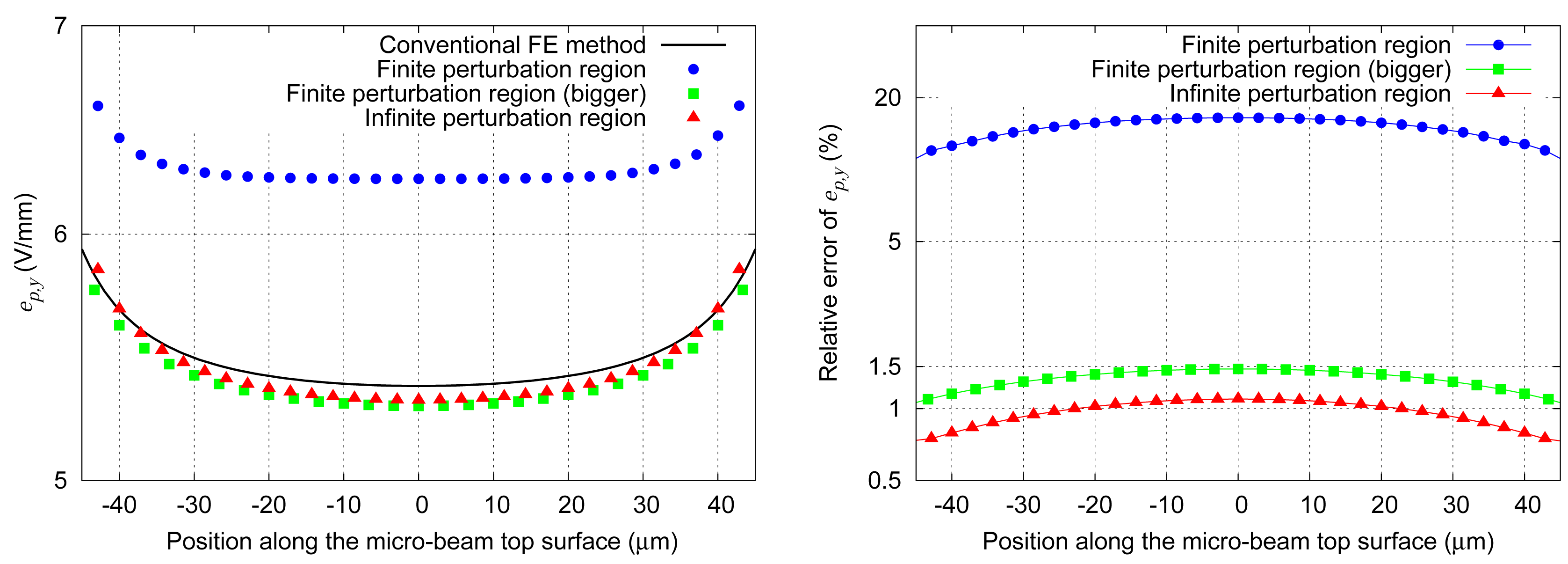
Comparing with the conventional FE solution, we observe that the relative error of the local electric field is under 1.2% when the perturbation domain is extended to infinity through a shell transformation (
Fig. 4(
right)). This justifies our choice for this kind of perturbation region for the whole of our study.
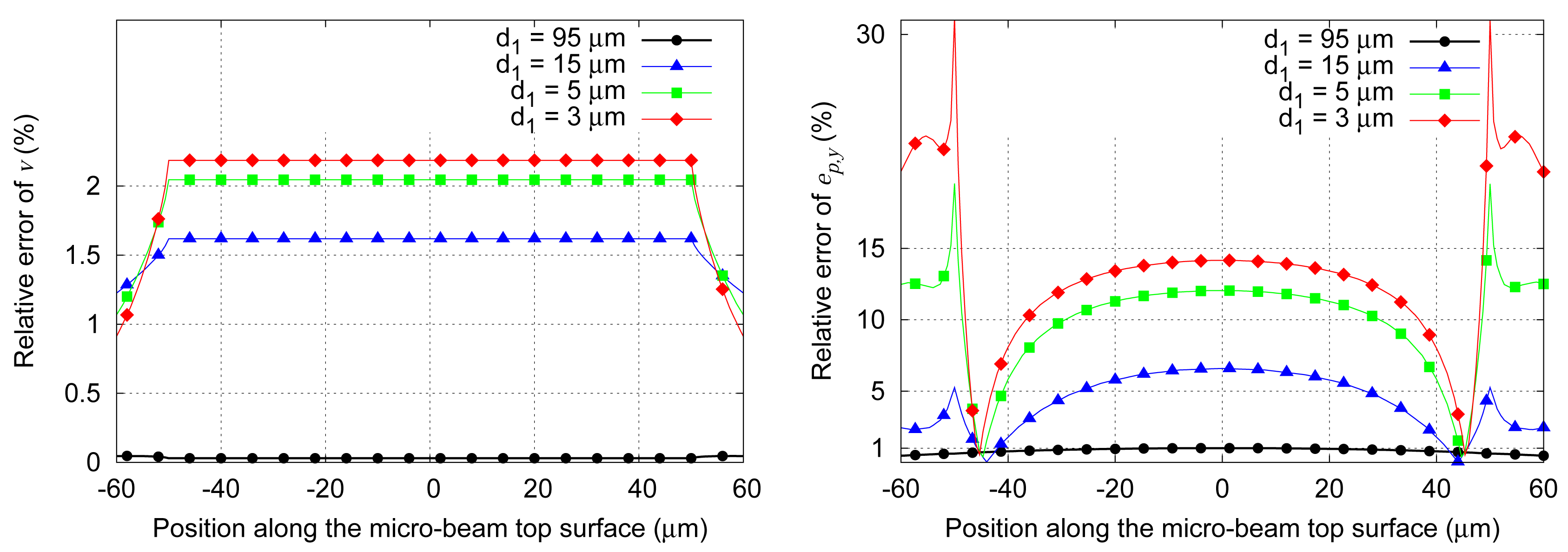
The relative error of the electric potential and the electric field near the micro-beam increases when the latter is close to electrode at 1V (
Fig. 5) what highlights a significant coupling of these regions. A more accurate solution for close positions needs an iterative process to calculate successive perturbations in each region.
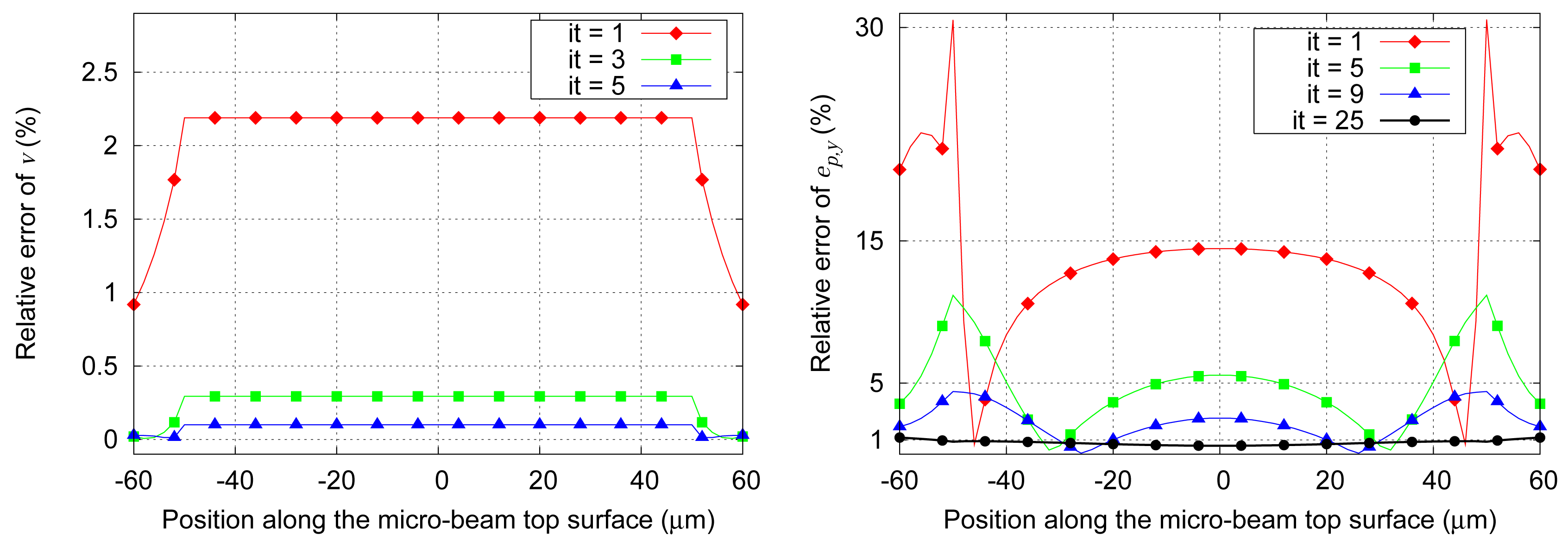
To illustrate the iterative perturbation process, the distance
d1 = 3
μm is chosen as an example (
Fig. 6). Successive perturbation problems defined in each region are solved.
At iteration 0, the unperturbed electric potential scalar is computed in the whole domain Ω. Projecting this quantity in the domain Ω
p at iteration 1 leads to a perturbed electric potential scalar
υp ensuing the electric field perturbation
ep. The relative error of the electric scalar potential computed near the micro- beam with respect to the conventional FE technique is bigger than 2% (
Fig. 6(
left)). Besides, the difference between the
y-components of
ep and the reference solution (FE) is considerable (relative error up to 32%) which is due to a strong coupling between these regions (
Fig. 6 (
right)). At iteration 2,
υ is projected from its mesh to that of Ω where a new perturbation problem is solved and its solution is projected again in Ω
p (at iteration 3). The relative error of the local electric field at iteration 25 is reduced to 1%.
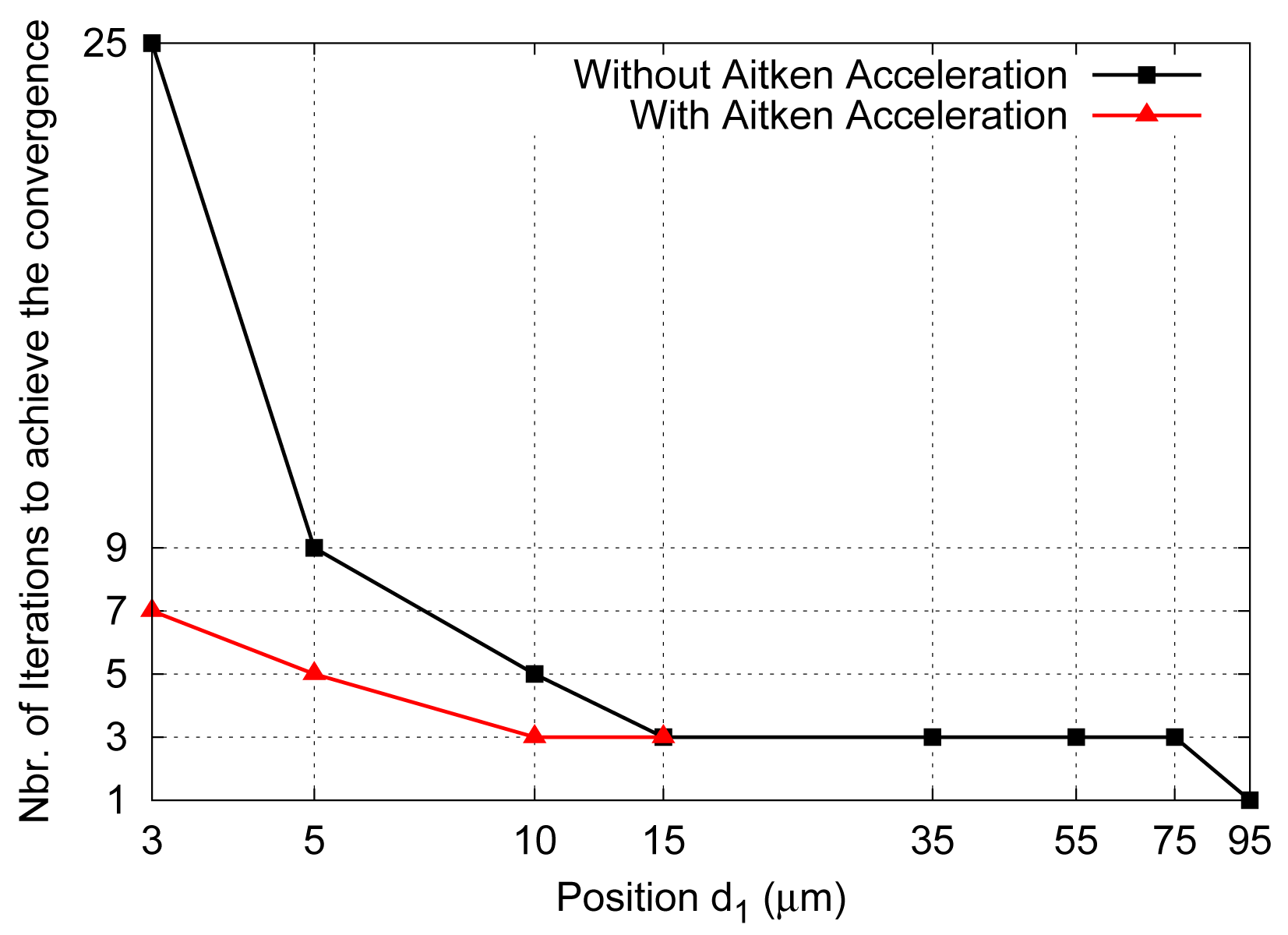
In order to highlight the relationship between the distance separating the micro-beam and electrode at 1V and the number of iterations required to achieve the convergence without and with Aitken ac-celeration [
16], several positions
d1 of the micro-device are considered (
Fig. 7). For each of them, the perturbation problem is solved and an iterative process is carried out till the relative error of the local electric field is smaller than 1%.
As expected, several iterations are needed to obtain an accurate solution when the micro-beam is close to the considered electrode. When the Aitken accelaration is used, the number of iterations is reduced.
6. Conclusion
A perturbation method for computing electrostatic field distortions due to the presence of conductive micro-structure has been presented. First, an unperturbed problem (in the absence of certain conductors) is solved with the conventional FE method in the complete domain. Second, a perturbation problem is solved in a reduced region with an additional conductor using the solution of the unperturbed problem as a source.
In order to illustrate and validate this method, we considered a 2-D FE model of a capacitor and a moving micro-beam. Results are compared to those obtained by the conventional FE method. When the moving region is close to the electrostatic field source, several iterations are required to obtain an accurate solution. Successive perturbations in each region are thus calculated not only from the original source region to the added conductive perturbing domain, but also from the latter to the former. The Aitken acceleration has been applied to improve the convergence of the iterative process.