Ultra Low-Power Algorithm Design for Implantable Devices: Application to Epilepsy Prostheses
Abstract
:1. Introduction
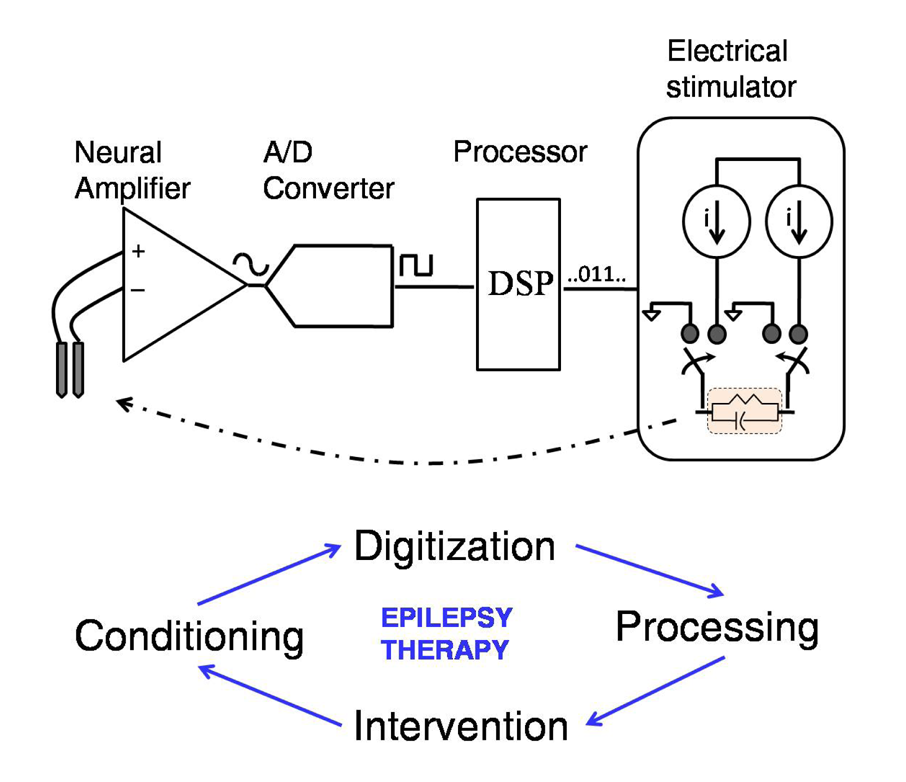
2. Components of a Closed-Loop Epilepsy Prosthesis
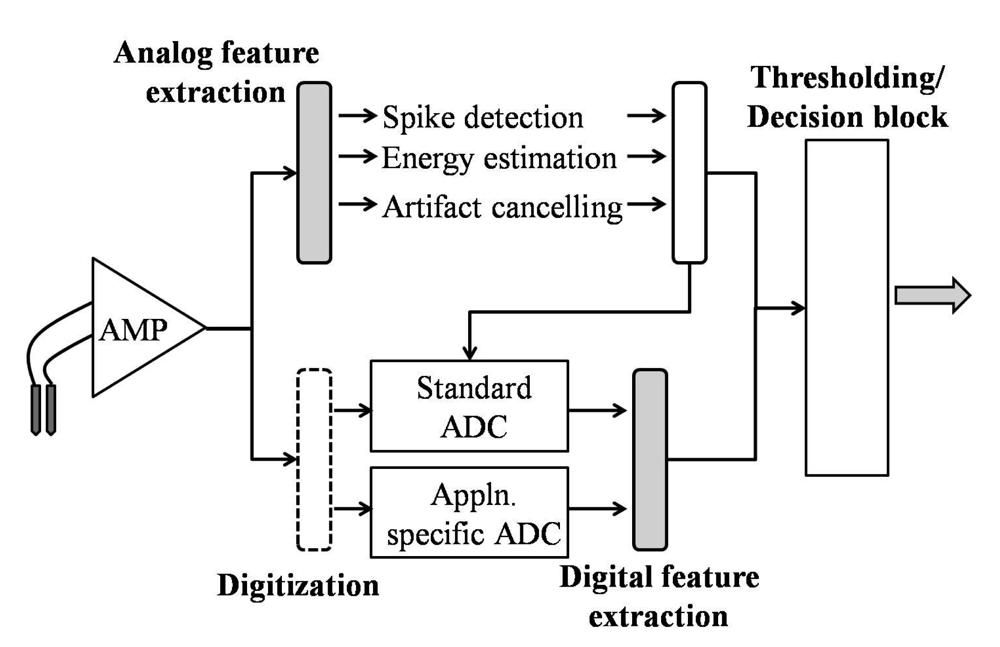
2.1. Feature Extraction/Signal Processing
3. Digital Feature Extraction-Applied to Seizure Detection Algorithms
3.1. Terminology
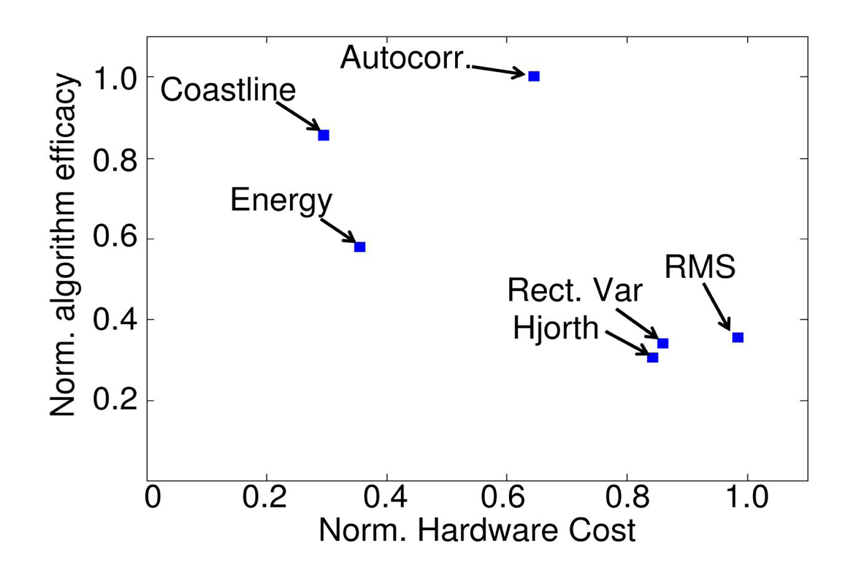
3.2. Seizure Detection Features
4. Low-Power Algorithm Design Techniques
4.1. Mathematical Approximation
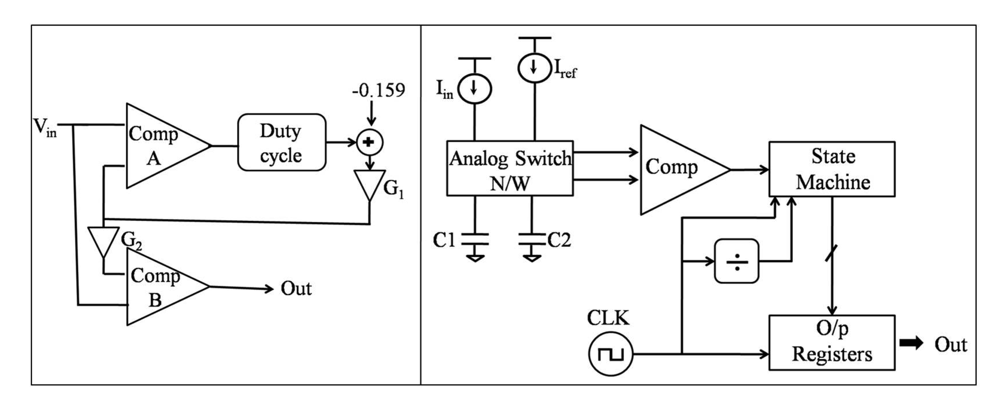
4.1.1. Division
4.1.2. Windowing and Averaging
4.1.3. Frequency Analysis
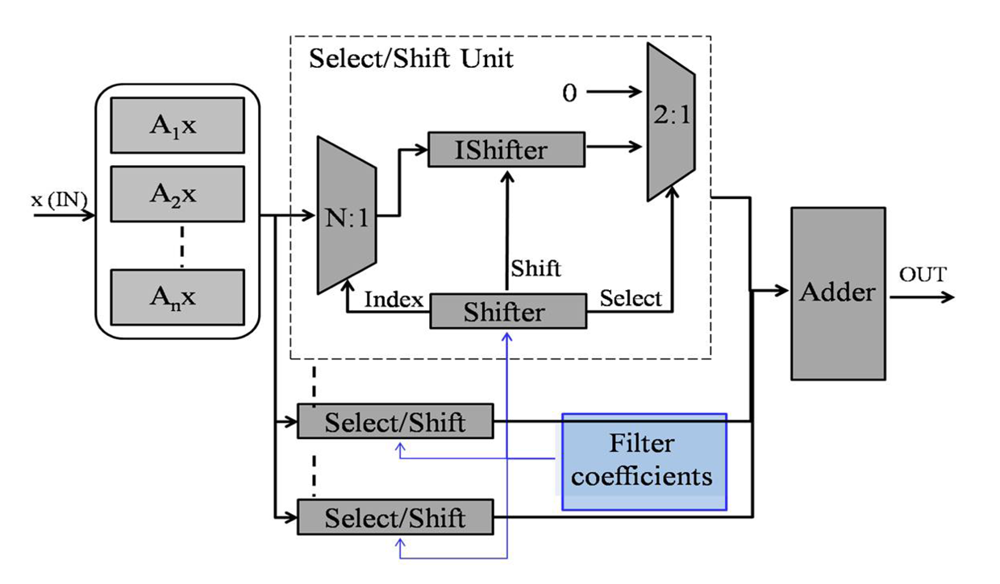
4.2. Algorithm-Specific Approximation
4.3. System-Level Design Techniques
4.3.1. Choice of Optimal VDD for Minimal Energy or Power
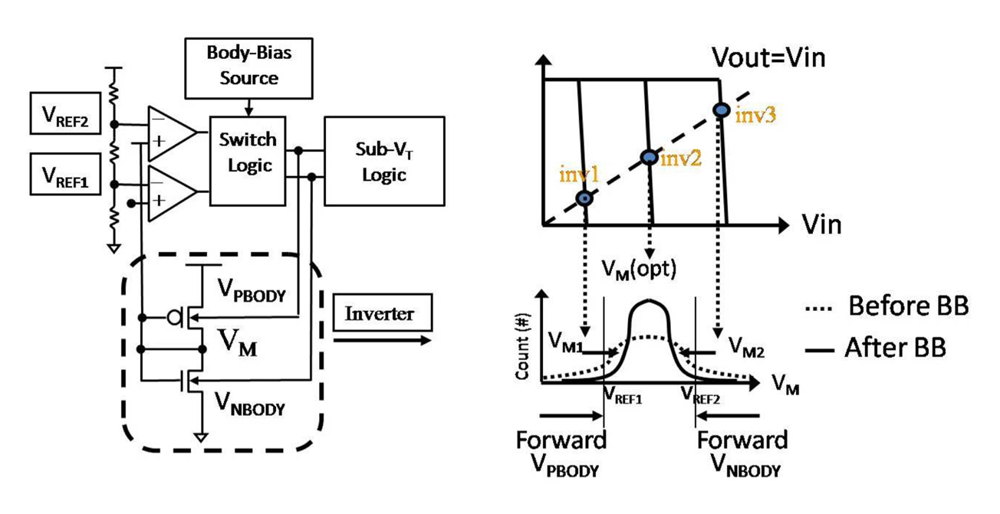
4.3.2. Adaptive Beta Ration Modulation (ABRM) for Enhanced System Robustness
4.4. Block-Level Design Techniques
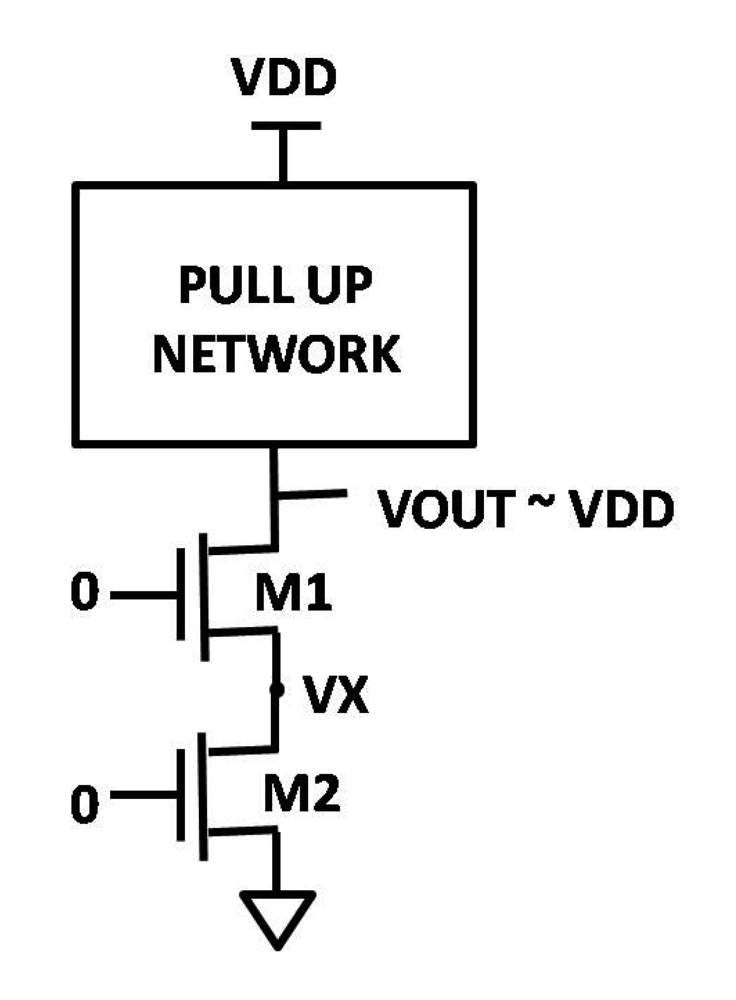
4.4.1. Leakage Reduction Using Stacking Effect
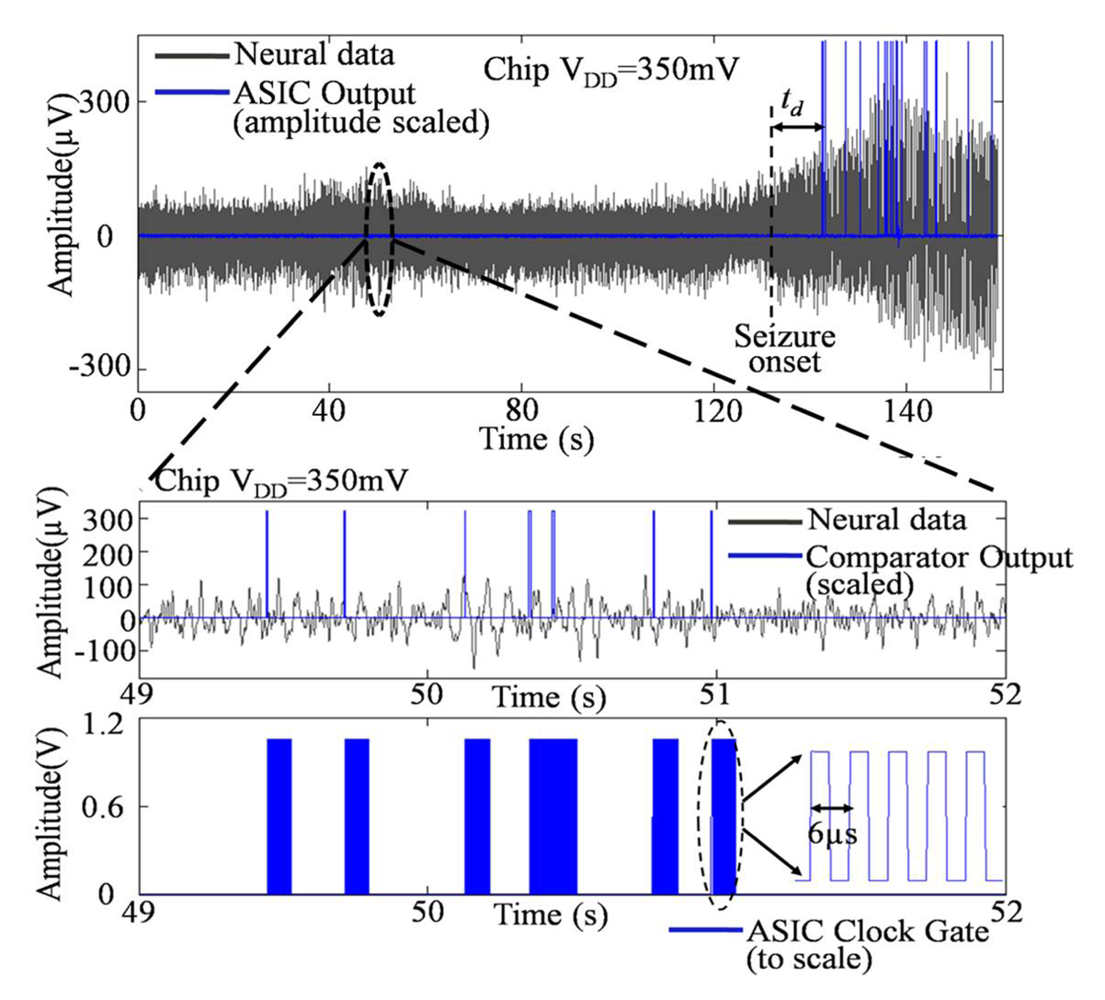
4.4.2. Clock and Power Gating
5. Conclusions











| Seizure detection features | |
|---|---|
| Time domain | Frequency domain |
| Energy | Edge frequency |
| Coastline/Line length | Spectral power |
| Hjorth variance | Dominant frequency |
| RMS amplitude | Dominant bandwidth |
| Non-linear energy | Wavelet energy |
| Autocorrelation | |
| Rectified variance energy | |
| Feature | Mean Baseline (X) | Mean Seizure (Y) | Average Difference (d = Ȳ − X̄) | t Value | Pr(|T| > t) Ha: d! = 0 | Area of Overlap (A) | Power a = 0.05 (P) |
|---|---|---|---|---|---|---|---|
| Energy | 380.64 | 4990.47 | 4727.04 | 2.44 | 0.071 | 0.43 | 0.698 |
| Coastline | 2741.29 | 7192.26 | 4450.98 | 8.32 | 0.0011 | 0.16 | 0.999 |
| Hjorth | 378.48 | 3702.97 | 3324.48 | 4.87 | 0.0082 | 0.09 | 0.996 |
| RMS | 16.43 | 60.12 | 43.69 | 4.61 | 0.01 | 0.08 | 0.994 |
| Autocorrelation | 1726.9 | 3934.8 | 2207.9 | 4.32 | 0.0125 | 0.31 | 0.9657 |
| Abs. Variance | 1.44 × 105 | 2.40 × 106 | 2.25 × 106 | 2.56 | 0.0626 | 0.65 | 0.7355 |
| SEFa | 36.92 | 36.94 | 0.01 | 0.05 | 0.9566 | 0.79 | 0.0502 |
| SEFb | 72.23 | 75.09 | 2.86 | 0.8 | 0.4705 | 0.58 | 0.0579 |
| Sp Powera | 589.81 | 4486.4 | 3896.59 | 3.18 | 0.0335 | 0.16 | 0.8133 |
| Sp Powerb | 1744.4 | 8509.6 | 6765.2 | 2.36 | 0.0782 | 0.15 | 0.4575 |
| Dom Peak | 30.27 | 29.72 | −0.56 | 0.46 | 0.6709 | 0.87 | 0.0664 |
| Peak BW | 9.79 | 9.56 | −0.24 | 0.36 | 0.738 | 0.87 | 0.0571 |
| Mathematical Operation | Implementation | Norm. Hardware Cost |
|---|---|---|
| Barrel shift Addition | 10-bit | 1× |
| (a) RPL | 1.43 × | |
| (b) CLA | 1.05× | |
| Subtraction | (a) RPL | 1.53× |
| (b) CLA | 1.15× | |
| Multiplication | (a) CSA | 17.53× |
| (b) Wallace-tree | 21.35× | |
| Division | (a) RPL | 9.98 × |
| (b) CLA | 9.33 × | |
| Square root | (a) RPL | 15.06× |
| (b) CLA | 16.54× |
| Coefficients | Decomposition |
|---|---|
| X0 = 103 = 01100111 | 25 (0011)x + (0111)x |
| X1 = 139 = 10001011 | 27 (0001)x + (1011)x |
| Supply Voltage | With Power-Gating | Without Power-Gating | ||||
|---|---|---|---|---|---|---|
| Leakage Energy | Dynamic Energy | Total Energy | Leakage Energy | Dynamic Energy | Total Energy | |
| 1.1-V | 0.53-pJ | 4.75-pJ | 5.28-pJ | 14000-pJ | 4.75-pJ | 14005-pJ |
| 0.6-V | 0.27-pJ | 0.88-pJ | 1.15-pJ | 2610-pJ | 0.88-pJ | 2611-pJ |
| 0.1-V | 10.9-pJ | 0.81-pJ | 11.31-pJ | 160-pJ | 0.81-pJ | 161-pJ |
References
- Begley, C.E.; Famulari, M.; Annegers, J.F.; Lairson, D.R.; Reynolds, T.F.; Coan, S.; Dubinsky, S.; Newmark, M.E.; Leibson, C.; So, E.L.; Rocca, W.A. The cost of Epilepsy in the United States: An estimate from population-based clinical and survey data. Epilepsia 2000, 41, 342–351. [Google Scholar]
- Morrell, M.J. Antiepileptic medications for the treatment of epilepsy. Semin. Neuorol. 2002, 22, 247–258. [Google Scholar]
- Labar, D.; Murphy, J.; Tecoma, E. Vagus nerve stimulation for medication-resistant generalized epilepsy. Neurology 1999, 52, 1510–1512. [Google Scholar]
- Graves, N.M.; Fisher, R.S. Neurostimulation for epilepsy, including a pilot study of anterior nucleus stimulation. Clin. Neurosurg. 2005, 52, 127–34. [Google Scholar]
- Ghai, R.S.; Bikson, M.; Durand, D.M. Effects of applied electric fields on low-calcium epileptiform activity in the CA1 region of rat hippocampal slices. J. Neurophysiol. 2000, 84, 274–280. [Google Scholar]
- Velasco, M.; Velasco, F.; Velasco, A.L.; Boleaga, B.; Jimenez, F.; Brito, F.; Marquez, I. Subacute electrical stimulation of the hippocampus blocks intractable temporal lobe seizures and paroxysmal EEG activities. Epilepsia 2000, 41, 158–169. [Google Scholar]
- Psatta, D.M. Control of chronic experimental temporal lobe epilepsy by feedback caudatum stimulations. Epilepsia 1983, 24, 444–454. [Google Scholar]
- Nakagawa, M.; Durand, D.M. Effects of applied currents on spontaneous epileptiform activity induced by low calcium in the rat hippocampus. Brain Res. 1998, 806, 186–195. [Google Scholar]
- Osorio, I.; Frei, M.; Sunderam, S. Automated seizure abatement in humans using electrical stimulation. Ann. Neurol. 2005, 57, 258–268. [Google Scholar]
- Sun, F.T.; Morrell, M.J.; Wharen, R.E. Responsive Cortical Stimulation for the Treatment of Epilepsy. Neurotherapeutics 2008, 5, 68–74. [Google Scholar]
- Osorio, I.; Frei, M.G.; Manly, B.F.J.; Sunderam, S.; Bhavaraju, N.C.; Wilkinson, S.B. An Introduction to contingent (Closed-Loop) brain electrical stimulation for seizure blockage, to ultra-short-term clinical trials, and to multidimensional statistical analysis of therapeutic efficacy. J Clin. Neurophysiol. 2001, 18, 533–544. [Google Scholar]
- McCreery, D.B.; Yuen, T.G.H.; Agnew, W.; Bullara, L.A. A characterization of the effects on neuronal excitability due to prolonged microstimulation with chronically implanted microelectrodes. IEEE Trans. Biomed. Eng. 1997, 44, 931–939. [Google Scholar]
- McIntyre, E.J. Electrical stimulation of neural tissue to evoke behavioral responses. J. Neurosci. Methods 1996, 65, 1–17. [Google Scholar]
- McCreery, D.; Agnew, W.; Yuen, T.; Bullara, L. Charge density and charge per phase as cofactors in neural injury induced by electrical stimulation. IEEE Trans. Biomed. Eng. 1990, 37, 996–1001. [Google Scholar]
- Peters, T.; Bhavaraju, N.; Frei, M.; Osorio, I. Network system for automated seizure detection and contingent delivery of therapy. J. Clin. Neurophysiol. 2001, 18, 545–549. [Google Scholar]
- Kossoff, E.H.; Ritzl, E.K.; Politsky, J.M.; Murro, A.M.; Smith, J.R.; Duckrow, R.B.; Spencer, D.D.; Bergey, G.K. Effect of an external responsive neurostimulator on seizures and electrographic discharges during subdural electrode monitoring. Epilepsia 2004, 45, 1560–1567. [Google Scholar]
- Raghunathan, S.; Gupta, S.K.; Ward, M.P.; Worth, R.M.; Roy, K.; Irazoqui, P.P. The design and hardware implementation of a low-power real-time seizure detection algorithm. J. Neural. Eng. 2009, 6, 56005. [Google Scholar]
- Verma, N.; Shoeb, A.; Bohorquez, J.; Dawson, J.; Guttag, J.; Chandrakasan, A. A Micro-power EEG acquisition SoC with integrated feature extraction processor for a chronic seizure detection system. IEEE J. Solid-State Circuits 2010, 45, 804–816. [Google Scholar]
- Bhavaraju, N.C.; Frei, M.G.; Osorio, I. Analog Seizure Detection and Performance Evaluation. IEEE Trans. Biomed. Eng. 2006, 53, 238–245. [Google Scholar]
- Harrison, R.R.; Kier, R.J.; Chestek, C.A.; Gilja, V.; Nuyujikian, P.; Ryu, S.; Greger, B.; Solzbacher, F.; Shenoy, K.V. Wireless neural recording with single low-power integrated circuit. IEEE Trans. Neural. Syst. Rehabil. Eng. 2009, 17, 322–29. [Google Scholar]
- Kim, S.; Tathireddy, P.; Normann, R.; Solzbacher, F. Thermal impact of an active 3-d microelectrode array implanted in the brain. IEEE Trans. Neural. Syst. Rehabil. Eng. 2007, 15, 493–501. [Google Scholar]
- LaManna, J.C.; McCracken, K.A.; Patil, M.; Prohaska, O.J. Stimulus-activated changes in brain tissue temperature in the anesthetized rat. Metab. Brain Dis. 1989, 4, 225–237. [Google Scholar]
- Jochum, T.; Denison, T.; Wolf, P. Integrated circuit amplifiers for multi-electrode intracortical recording. J. Neural Eng. 2009, 6, 012001. [Google Scholar]
- Harrison, R.R. The design of integrated circuits to observe brain activity. Proc. IEEE 2008, 96, 1203–1216. [Google Scholar]
- White, A.M.; Williams, P.A.; Ferraro, D.J.; Clark, S.; Kadam, S.D.; Dudek, F.E.; Staley, K.J. Efficient unsupervised algorithms for the detection of seizures in continuous EEG recordings from rats after brain injury. J. Neurosci. Methods 2006, 152, 255–66. [Google Scholar]
- Greene, B.R.; Faul, S.; Marnane, W.P.; Lightbody, G.; Korotchikova, I.; Boylan, G.B. A comparison of quantitative EEG features for neonatal seizure detection. Clin. Neurophysiol. 2008, 119, 1248–1261. [Google Scholar]
- Harrison, R.R. A low-power integrated circuit for adaptive detection of action potentials in noisy signals. Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Cancun, Mexico; 2003; pp. 3325–3328. [Google Scholar]
- Harrison, R.R.; Santhanam, G.; Shenoy, K.V. Local field potential measurement with low-power analog integrated circuit. Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, Canada; 2004; pp. 4067–4070. [Google Scholar]
- Harrison, R.R.; Kier, R.J.; Chestek, C.A.; Gilja, V.; Nuyujikian, P.; Ryu, S.; Greger, B.; Solzbacher, F.; Shenoy, K.V. Wireless neural recording with single low-powered integrated circuit. IEEE Trans. Neural. Syst. Rehabil. Eng. 2009, 17, 322–329. [Google Scholar]
- Aksenov, E.V.; Ljashenko, A.V.; Plotnikov, A.V.; Prilutskiy, D.A.; Selishchev, S.V.; Vetvetskiy, E.V. Biomedical data acquisition systems based on sigma-delta analogue-to-digital converters. Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Istanbul, Turkey; 2001; pp. 3336–3337. [Google Scholar]
- Yang, H.; Sarpeshkar, R. A time-based energy-efficient analog-to-digital converter. IEEE J. Solid-State Circuits 2005, 40, 1590–1601. [Google Scholar]
- Yang, H.; Sarpeshkar, R. A Bio-inspired ultra-energy-efficient analog-to-digital converter for biomedical applications. IEEE Trans. Circuit. Syst. 2006, 53, 2349–2356. [Google Scholar]
- Hyung-Il, K.; Roy, K. Ultra-Low Power DLMS Adaptive Filterfor Hearing Aid Applications. Proceedings of the International Symposium on Low Power Electronics and Design, Huntington Beach, CA, USA, 6–7 Auguest 2001; pp. 352–357.
- Spencer, S.S.; Williamson, P.D.; Spencer, D.D.; Mattson, R.H. Human hippocampal seizure spread studied by depth and subdural recording: The hippocampal commissure. Epilepsia 1987, 28, 479–489. [Google Scholar]
- Talathi, S.S.; Hwang, D.U.; Spano, M.L.; Simonotto, J.; Furman, M.D.; Myers, S.M.; Winters, J.T.; Ditto, W.L.; Carney, P.R. Non-parametric early seizure detection in an animal model of temporal lobe epilepsy. J. Neural Eng. 2008, 5, 85–98. [Google Scholar]
- Raghunathan, S.; Gupta, S.K.; Markandeya, H.S.; Roy, K.; Irazoqui, P.P. A hardware-algorithm co-design approach to optimize seizure detection algorithms for implantable applications. J. Neurosci. Methods 2010, 193, 106–117. [Google Scholar]
- Mormann, F.; Andrzejak, R.G.; Elger, C.E.; Lehnertz, K. Seizure prediction: The long and winding road. Brain 2007, 130, 314–33. [Google Scholar]
- Hellier, J.L.; Dudek, F.E. Chemoconvulsant model of chronic spontaneous seizures. Curr. Protoc. Neurosci. 2005, 9, 1911–1919. [Google Scholar]
- Hjorth, B. EEG analysis based on time domain properties. Electroencephalogr. Clin. Neurophysiol. 1970, 29, 306–310. [Google Scholar]
- Hjorth, B. The physical significance of time domain descriptors in EEG analysis. Electroencephalogr. Clini. Neurophysiol. 1973, 34, 321–325. [Google Scholar]
- Gotman, J.; Flanagan, D.; Zhang, J. Automatic seizure detection in the newborn: Methods and initial evaluation. Electroencephalogr. Clin. Neurophysiol. 1997, 103, 356–362. [Google Scholar]
- Hudson, R.J.; Stanski, D.R.; Saidman, L.J.; Meathe, E. A model for studying depth of anesthesia and acute tolerance to thiopental. Anesthesiology 1983, 59, 301–308. [Google Scholar]
- Fell, J.; Roschke, J.; Mann, K.; Schaffner, C. Discrimination of sleep stages: A comparison between spectral and nonlinear EEG measures. Electroencephalogr. Clin. Neurophysiol. 1996, 98, 401–410. [Google Scholar]
- He, S.; Torkelson, M. A new approach to pipeline FFT processor. Proceedings of IPPS ′96, The 10th International Parallel Processing Symposium, Honolulu, HI, USA, 15–19 April 1996; pp. 766–770.
- Markandeya, H.S.; Karakonstantis, G.; Raghunathan, S.; Irazoqui, P.P.; Roy, K. Low-Power DWT-Based Quasi-Averaging Algorithm and Architecture for Epileptic Seizure Detection. Proceedings of the 2010 ACM/IEEE International Symposium on Low Power Electronics and Design, Austin, TX, USA; 2010; pp. 301–306. [Google Scholar]
- Karakonstantis, G.; Roy, K. An Optimal Algorithm for Low Power Multiplierless FIR Filter Design using Chebychev Criterion. Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA; 2007. [Google Scholar]
- Aziz, J.N.Y.; Karakiewicz, R.; Genov, R.; Bardakjian, B.L.; Derchansky, M.; Carlen, P.L. Towards Real-Time In-Implant Epileptic Seizure Prediction. Proceedings of the 28th IEEE EMBS Annual International Conference, New York, NY, USA, 30 Auguest–3 September 2006; pp. 5476–5479.
- Haas, S.M.; Frei, M.G.; Osorio, I. Strategies for adapting automated seizure detection algorithms. Med. Eng. Phys. 2007, 29, 895–909. [Google Scholar]
- Khan, Y.U.; Gotman, J. Wavelet based automatic seizure detection in intracerebral electroencephalogram. Clin. Neurophysiol. 2003, 114, 898–908. [Google Scholar]
- Litt, B.; D'Allesandro, M.; Esteller, R.; Echauz, J.; Vachtsevanos, G. Translating Seizure Detection, Prediction and Brain Stimulation Into Implantable Devices for Epilepsy. Proceedings of the 1st International IEEE EMBS Conference on Neural Engineering, Capri Island, Italy; 2003; pp. 485–488. [Google Scholar]
- Raghunathan, S.; Ward, M.P.; Roy, K.; Irazoqui, P.P. A low-power implantable event-based seizure detection algorithm. Proceeedings of the 4th International IEEE EMBS Conference on Neural Engineering, Antalya, Turkey; 2009; pp. 151–154. [Google Scholar]
- Drew, T. Division approximation for implantable medical devices. U.S. Patent US7526340, 28 April 2009. [Google Scholar]
- Kamboh, A.; Raetz, M.; Oweiss, K.; Mason, A. Area-power efficient VLSI implementation of multichannel DWT for data compression in implantable neuroprosthetics. IEEE Trans. Circuit. Syst. 2007, 1, 128–135. [Google Scholar]
- Raychowdhury, A.; Paul, B.C.; Bhunia, S.; Roy, K. Computing with subthreshold leakage: Device/circuit/architecture co-design for ultralow-power subthreshold operation. IEEE Trans. Very Large S. I. Syst. 2005, 13, 1213–1224. [Google Scholar]
- Calhoun, B.H.; Chandrakasan, A. Characterizing and Modeling Minimum Energy Operation for Subthreshold Circuits. Proceedings of the 2004 International Symposium on Low Power Electronics and Design, Newport Beach, CA, USA; 2004; pp. 90–95. [Google Scholar]
- Gupta, S.K.; Raychowdhury, A.; Roy, K. Digital computation in subthreshold region for ultralow-power operation: A device–circuit–architecture codesign perspective. Proc. IEEE 2010, 98, 160–190. [Google Scholar]
- Tschanz, J.; Narendra, S.; Ye, Y.; Bloechel, B.; Borkar, S.; De, V. Dynamic sleep transistor and body bias for active leakage power control of microprocessors. IEEE J. Solid-State Circuits 2003, 38, 1838–1845. [Google Scholar]
- Roy, K.; Kulkarni, J.P.; Hwang, M.E. Process Tolerant Ultralow Voltage Digital Sub-threshold Design. Proceedings of the IEEE Topical Meeting Silicon Monolithic Integrated Circuits in RF Systems, Orlando, FL, USA; 2008; pp. 2574–2577. [Google Scholar]
- Johnson, M.C.; Somasekhar, D.; Chiou, L.y.; Roy, K. Leakage Control With Efficient Use of Transistor Stacks in Single Threshold CMOS. IEEE Trans. Very Large Syst. Intergr. Syst. 2002, 10, 1–5. [Google Scholar]
- Rabaey, J. Digital Integrated Circuits: A Design Perspective; Prentice Hall: Duluth, GA, USA, 1996. [Google Scholar]
- Johnson, M.C.; Somasekhar, D.; Roy, K. Models and Algorithms for Bounds on Leakage in CMOS Circuits. IEEE Trans. Comput.-Aid. Des. Integr. Circuits Syst. 1999, 18, 714–725. [Google Scholar]
- Li, H.; Bhunia, S.; Chen, Y.; Vijaykumar, T.N.; Roy, K. Deterministic clock gating for microprocessor power reduction. Proceedings of The Ninth International Symposium on High-Performance Computer Architecture, Washington, DC, USA; 2003; pp. 113–122. [Google Scholar]
- Jiang, H.; Marek-Sadowska, M.; Nassif, S.R. Benefits and costs of power-gating technique. Proceedings of The IEEE International Conference on Computer Design: VLSI in Computers and Processors, Washington, DC, USA; 2005; pp. 559–566. [Google Scholar]
- Seok, M.; Hanson, S.; Lin, Y.S.; Foo, Z.; Kim, D.; Lee, Y.; Liu, N.; D, S.; Blaauw, D. Phoenix: An Ultra-low Power Processor for Cubic Millimeter Sensor Systems. Proceedings of the 46th Design Automation Conference, DAC 2009, San Francisco, CA, USA, 26–31 July 2009.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Raghunathan, S.; Gupta, S.K.; Markandeya, H.S.; Irazoqui, P.P.; Roy, K. Ultra Low-Power Algorithm Design for Implantable Devices: Application to Epilepsy Prostheses. J. Low Power Electron. Appl. 2011, 1, 175-203. https://doi.org/10.3390/jlpea1010175
Raghunathan S, Gupta SK, Markandeya HS, Irazoqui PP, Roy K. Ultra Low-Power Algorithm Design for Implantable Devices: Application to Epilepsy Prostheses. Journal of Low Power Electronics and Applications. 2011; 1(1):175-203. https://doi.org/10.3390/jlpea1010175
Chicago/Turabian StyleRaghunathan, Shriram, Sumeet K. Gupta, Himanshu S. Markandeya, Pedro P. Irazoqui, and Kaushik Roy. 2011. "Ultra Low-Power Algorithm Design for Implantable Devices: Application to Epilepsy Prostheses" Journal of Low Power Electronics and Applications 1, no. 1: 175-203. https://doi.org/10.3390/jlpea1010175





