Real-Time Forecast of Hydrologically Sensitive Areas in the Salmon Creek Watershed, New York State, Using an Online Prediction Tool
Abstract
:1. Introduction
2. The HSA Prediction Tool
2.1. The Framework of the HSA Prediction Tool
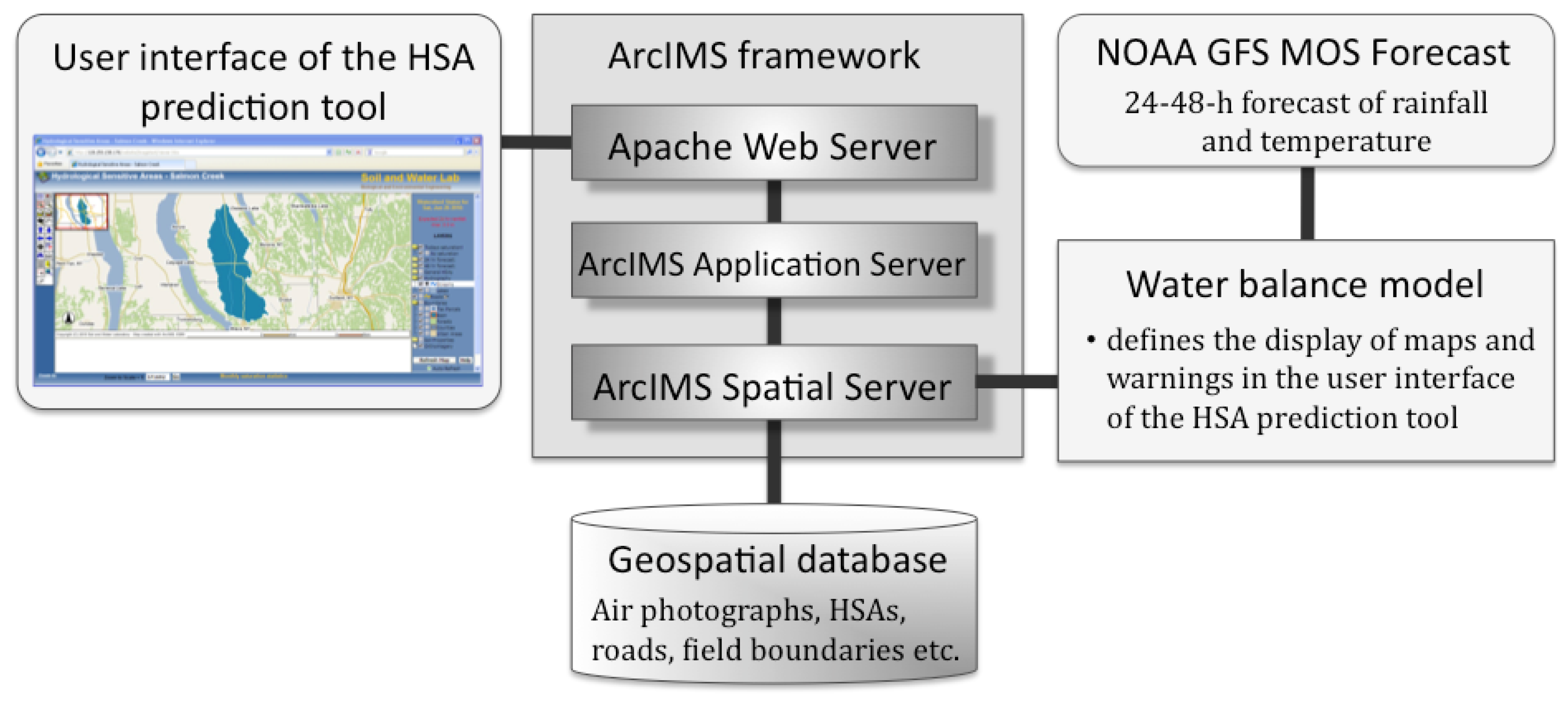
2.2. The Semi-Distributed VSA Water Balance Model
2.2.1. The VSA Hydrology Concept Based on the Soil Conservation Service (SCS)-Curve Number (CN)
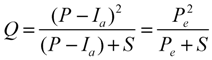
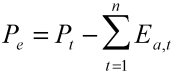
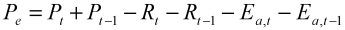
2.2.2. Model Discretization and Variable Source Area Prediction
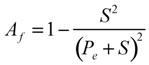
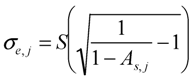
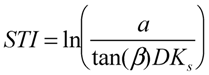
2.2.3. Model Input, Output and Calibration Parameters
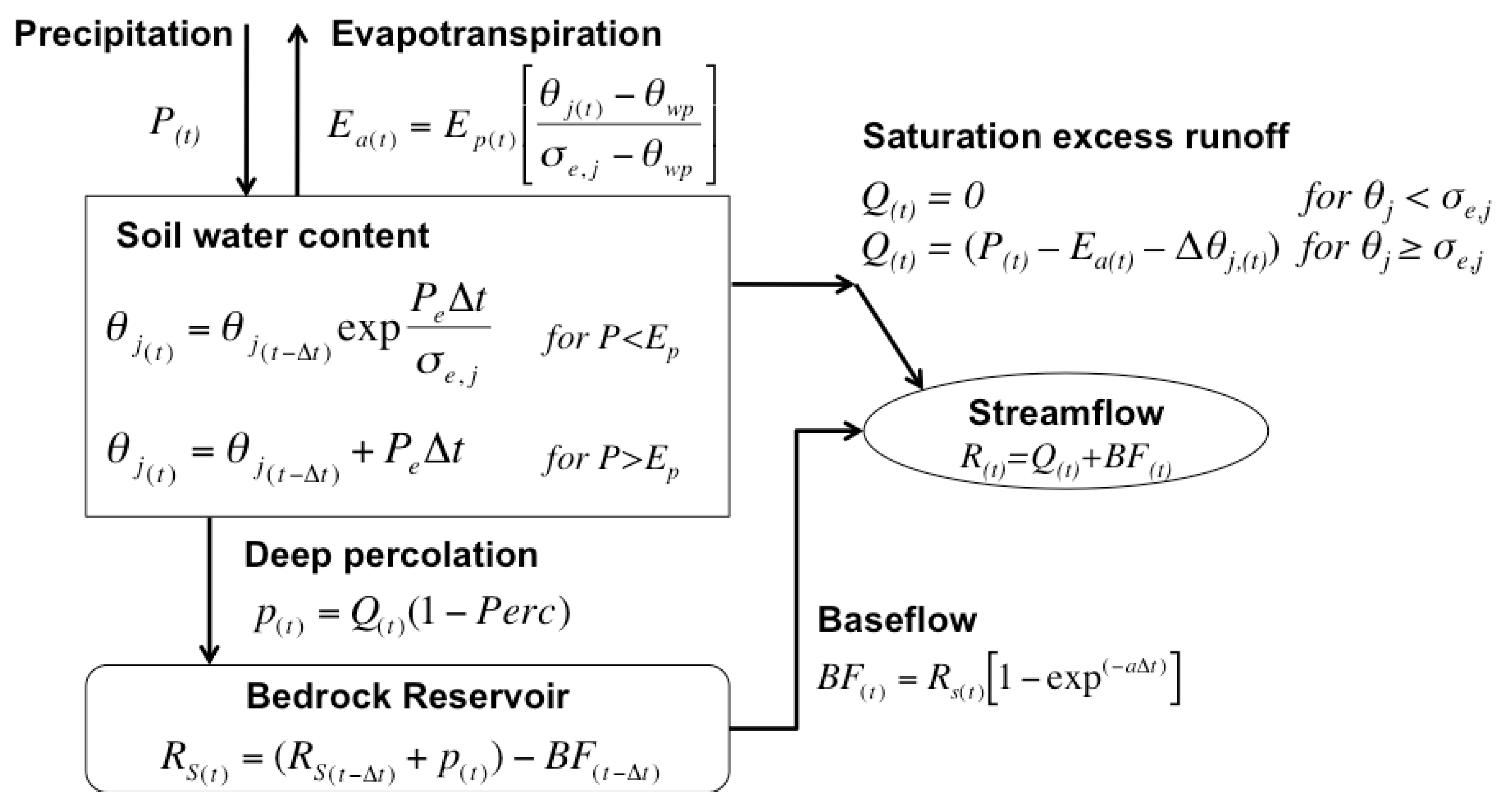
2.3. Hydrologic Forecasting
| Categories | GFS precipitation scale (in.) | Precipitation (mm) used in the VSA water balance model |
|---|---|---|
| 0 | 0 | 0.0 |
| 1 | 0.01–0.09 | 2.3 |
| 2 | 0.10–0.24 | 6.1 |
| 3 | 0.25–0.49 | 12.5 |
| 4 | 0.50–0.99 | 25.2 |
| 5 | 1.00–1.99 | 50.6 |
| 6 | ≥2 | 76.2 |
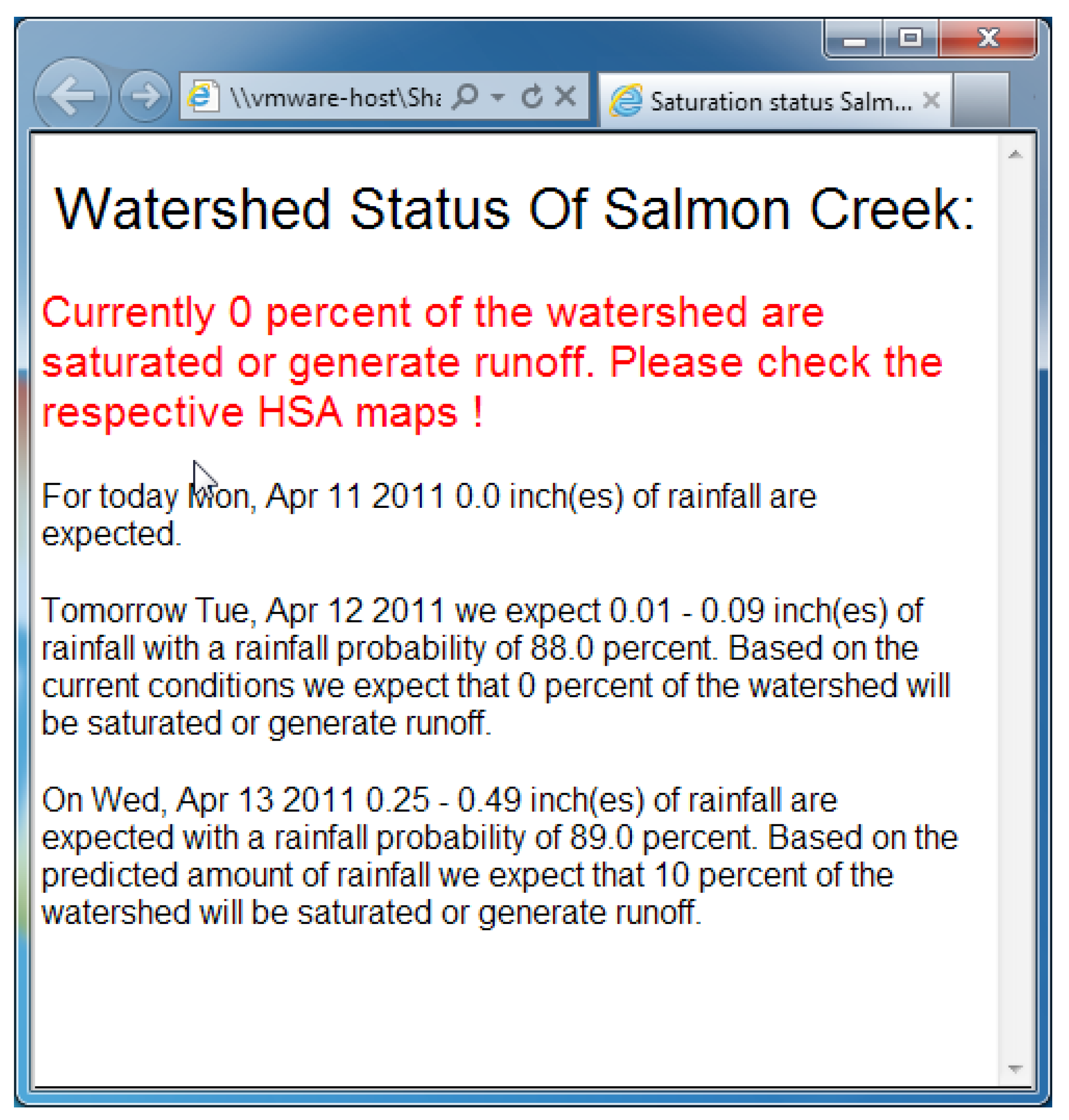
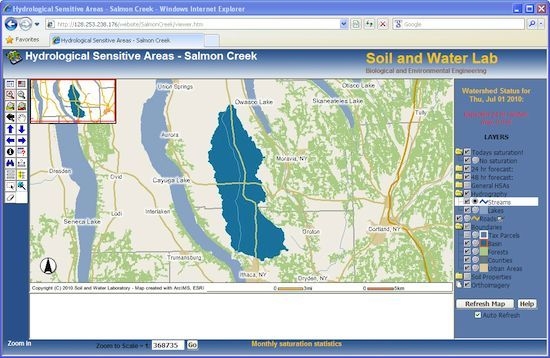
2.4. User Interface of the HSA Prediction Tool


2.4.1. Graphical Output of Predicted HSA Risk Maps
2.4.2. Geospatial Data
3. Application of the HSA Prediction Tool: Proof of Concept
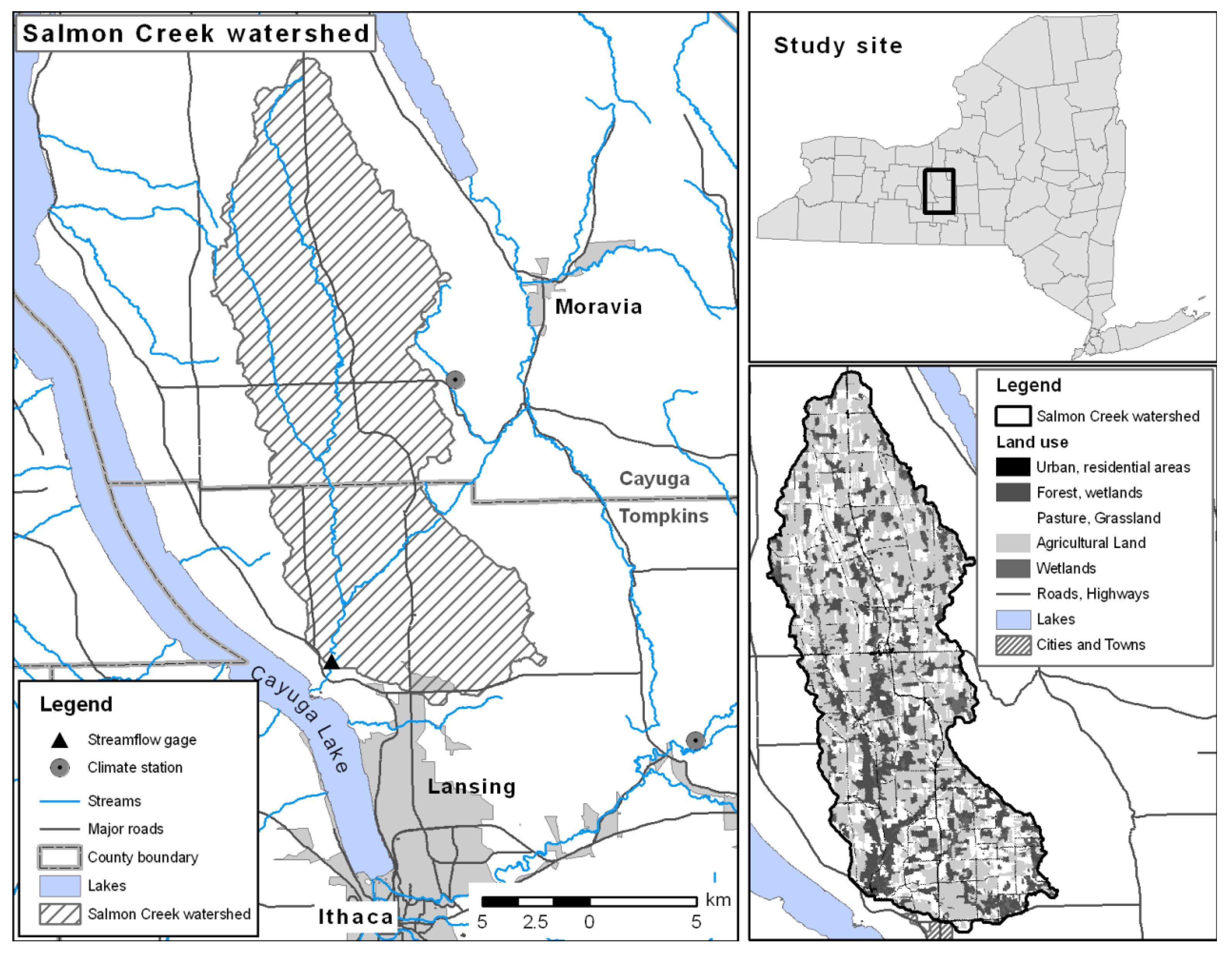
3.1. Input Data
3.1.1. Geospatial Database
| Data | Resolution/Scale | Source | Description |
|---|---|---|---|
| Air photographs | 2 m | NY State GIS Clearinghouse [65] | Natural color image. Cayuga County 2007, Tompkins County 2006. |
| DEM | 10 m | NYS DEC, USGS [66] | Elevation, slope, flow direction, flow accumulation, HSAs |
| Forest | 30 m | Multi-Resolution Land Characteristics (MRLC) Consortium [67] | Land Use, Land Cover data set, 2001 |
| Lakes | 1:2,000,000 | National Atlas, New York State [66] | Lakes and surface water bodies |
| Roads | 1:100,000 | U.S. Census Bureau [66] | |
| Soils | 1:15,840 (Cayuga County) 1:20,000 (Tompkins County) | SSURGO (USDA-NRCS Soil Data Mart) [64] | Soil depth, saturated hydraulic conductivity, drainage class, flood frequency |
| Streams | 1:100,000 | U.S. Census Bureau [66] | Hydrography |
| Tax Parcels | 1:10,000 | Tompkins County and Cayuga County Clerkʼs Office [66] | Municipal Tax Parcels (year 2000) |
| Urban areas | 1:100,000 | U.S. Census Bureau [66] | Urbanized areas and municipalities |
| Meteorological data | Northeastern Regional Climate Center [68] | Daily minimum and maximum temperature and total daily precipitation | |
| Streamflow data | U.S. Geological Survey [69] | Daily streamflow data | |
| GFS MOS forecast data | NOAA National Weather Service [70] | Extended range GFS-Based Model Output Statistics (MOS) |
3.1.2. Weather Data
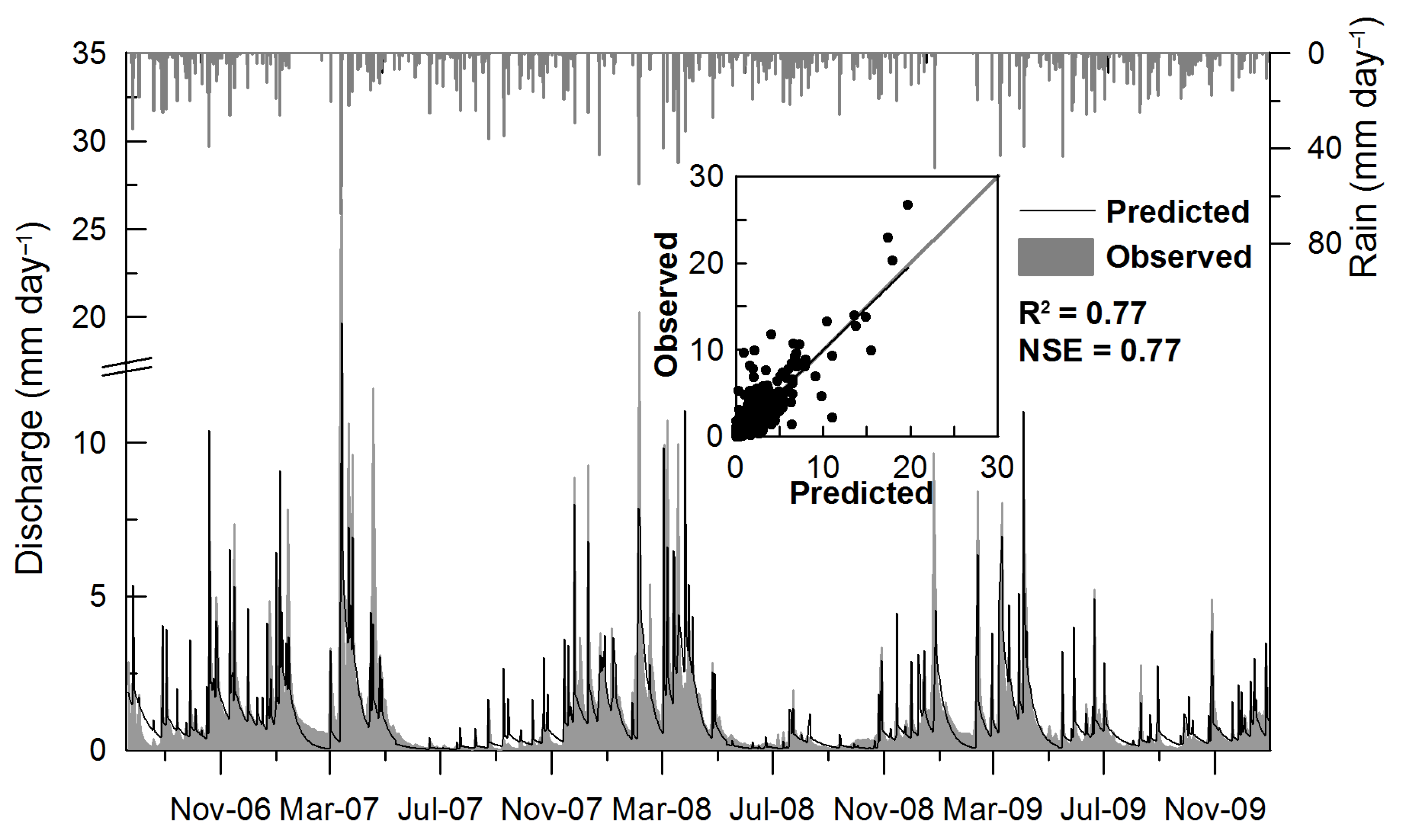
3.2. VSA Water Balance Model Calibration and Validation
| Period | Modeled | Measured | Goodness of fit | |||||
|---|---|---|---|---|---|---|---|---|
| Minimum (mm·day−1) | Mean (mm·day−1) | Maximum (mm·day−1) | Minimum (mm·day−1) | Mean (mm·day−1) | Maximum (mm·day−1) | E a | R² b | |
| 2006 | 0.37 | 1.45 | 10.41 | 0.11 | 1.41 | 13.25 | 0.74 | 0.74 |
| 2007 | 0.02 | 1.09 | 21.39 | 0.02 | 1.30 | 26.71 | 0.80 | 0.82 |
| 2008 | 0.04 | 1.12 | 17.90 | 0.04 | 1.20 | 20.30 | 0.68 | 0.71 |
| 2009 | 0.06 | 0.99 | 13.74 | 0.05 | 0.96 | 12.72 | 0.82 | 0.83 |
| Calibration period | 0.37 | 1.45 | 10.41 | 0.11 | 1.41 | 13.25 | 0.76 | 0.76 |
| Validation period | 0.04 | 0.87 | 14.85 | 0.04 | 0.88 | 13.78 | 0.78 | 0.79 |
| Entire Period c | 0.02 | 1.11 | 21.39 | 0.02 | 1.19 | 26.71 | 0.77 | 0.77 |
3.3. Accuracy of HSA Predictions for Salmon Creek Watershed
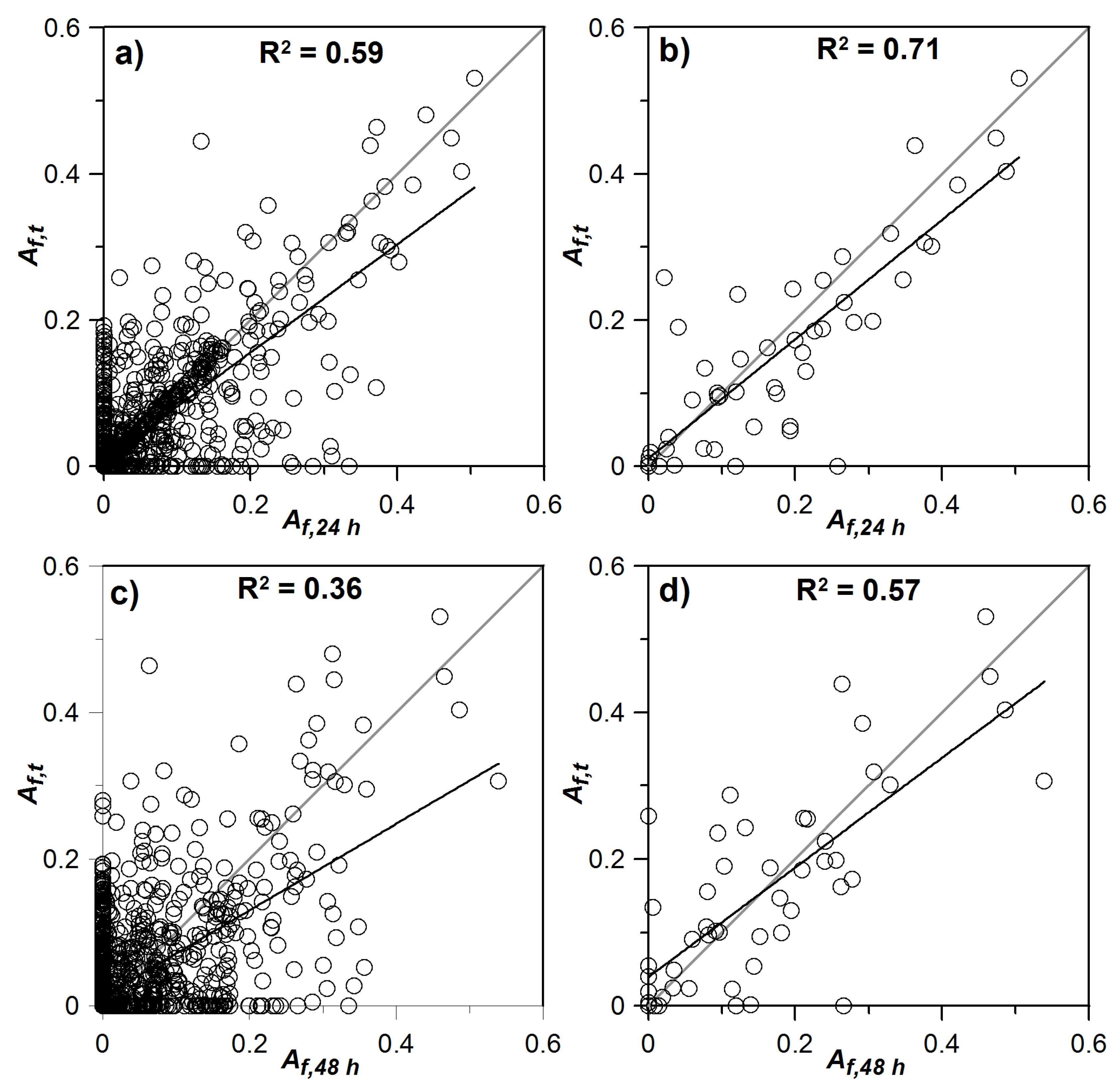
| Comparison sets | Wetness classes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All | n.s. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Af,t vs. Af,24 h | 0.81 | 0.92 | 0.66 | 0.54 | 0.50 | 0.67 | 0.67 | 1 | n.a. | n.a. | n.a. | n.a. |
| Af,t vs. Af,48 h | 0.70 | 0.87 | 0.41 | 0.24 | 0.25 | 0.17 | 0.67 | 1 | n.a. | n.a. | n.a. | n.a. |
| Af,24 h vs. Af,48 h | 0.79 | 0.92 | 0.54 | 0.46 | 0.48 | 0.54 | 0.50 | 1 | n.a. | n.a. | n.a. | n.a. |
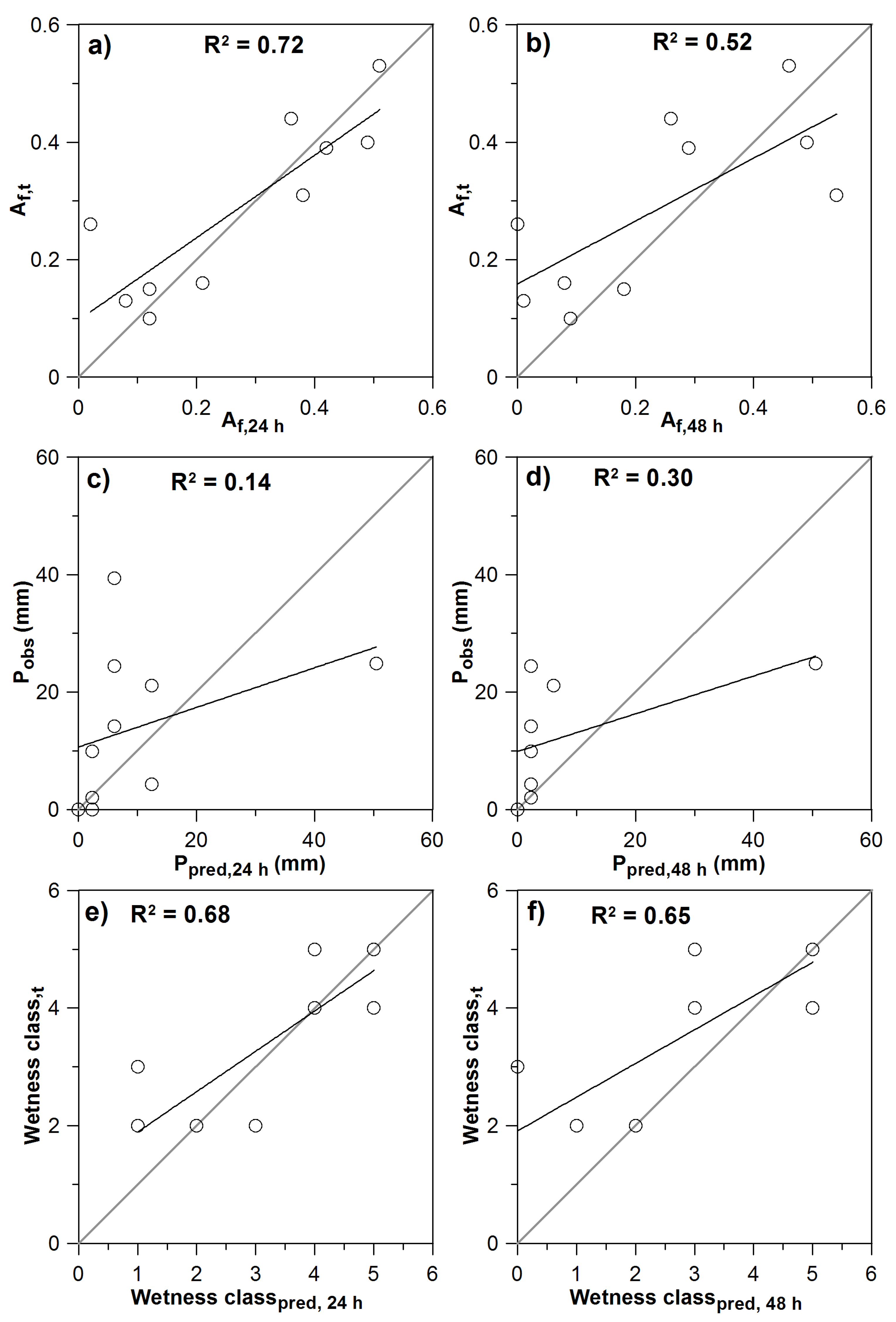
3.4. Predicted Saturation Dynamics
| Time period | Wetness class | Average number of rainfall days | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| January | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 7.87 |
| Febuary | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 0.71 | 3.50 |
| March | 0.82 | 0.82 | 0.82 | 0.82 | 0.82 | 0.82 | 0.76 | 0.76 | 0.76 | 0.76 | 8.50 |
| April | 0.62 | 0.55 | 0.41 | 0.41 | 0.38 | 0.38 | 0.38 | 0.38 | 0.38 | 0.38 | 14.50 |
| May | 0.05 | 10.00 | |||||||||
| June | 0.29 | 0.16 | 0.03 | 15.50 | |||||||
| July | 0.36 | 0.31 | 0.26 | 0.24 | 0.24 | 0.19 | 0.19 | 0.17 | 0.12 | 0.10 | 18.08 |
| August | 0.26 | 0.21 | 0.14 | 0.09 | 0.07 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 | 14.33 |
| September | 0.42 | 0.28 | 0.22 | 0.22 | 0.22 | 0.22 | 0.11 | 0.11 | 0.11 | 0.11 | 12.00 |
| October | 0.61 | 0.57 | 0.46 | 0.41 | 0.37 | 0.37 | 0.35 | 0.28 | 0.22 | 0.22 | 15.33 |
| Novemember | 0.55 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.50 | 0.48 | 0.23 | 13.33 |
| Decemember | 0.77 | 0.73 | 0.73 | 0.68 | 0.68 | 0.68 | 0.68 | 0.68 | 0.68 | 0.68 | 7.33 |
| Annual average | 0.51 | 0.44 | 0.38 | 0.36 | 0.35 | 0.34 | 0.32 | 0.31 | 0.29 | 0.26 | 140.27 |
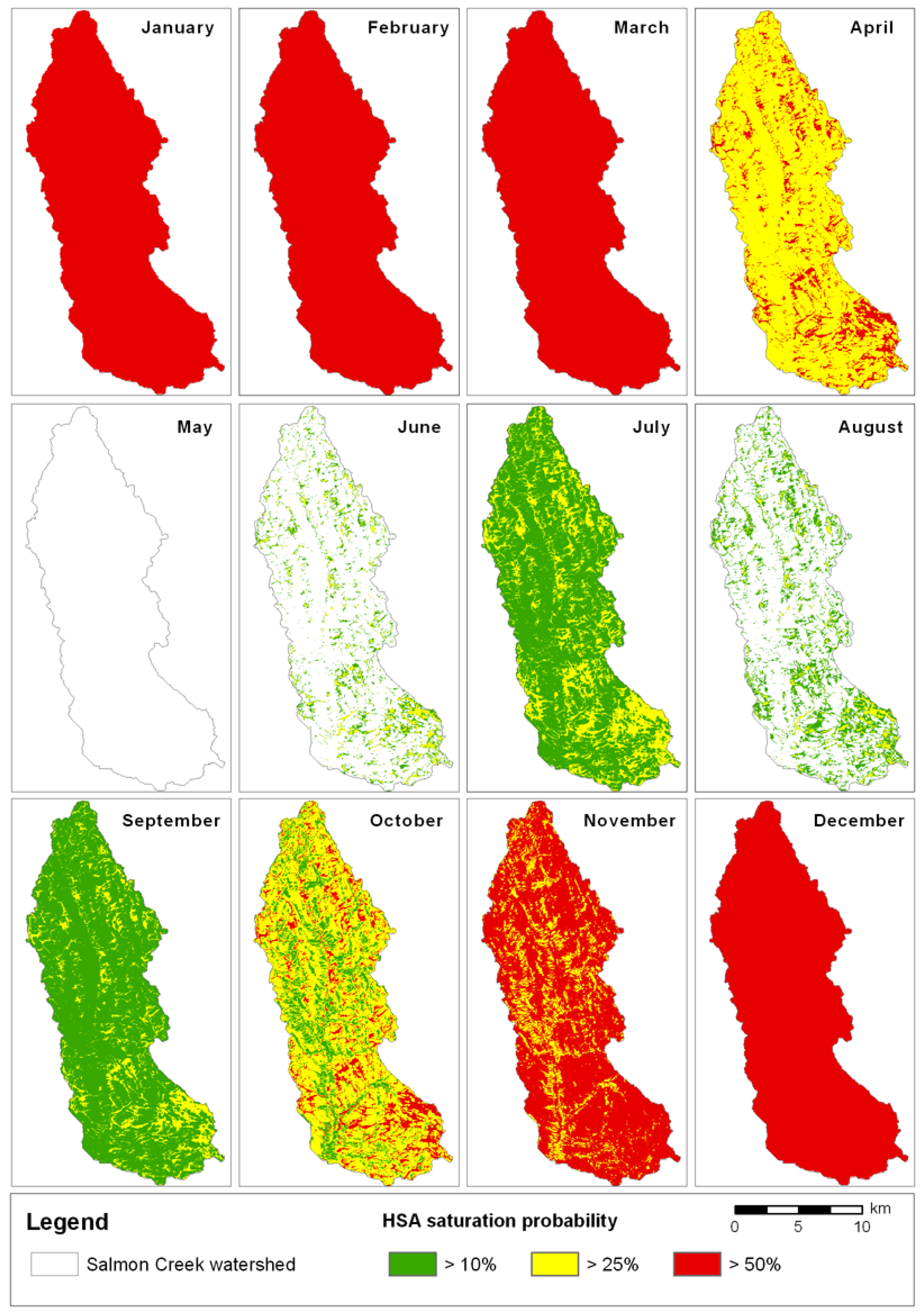
4. Management Implications and Conclusions
Acknowledgments
Conflict of Interest
References
- Andraski, T.W.; Bundy, L.G. Relationships between phosphorus levels in soil and in runoff from corn production systems. J. Environ. Qual. 2003, 32, 310–316. [Google Scholar]
- Ekholm, P.; Kallio, K.; Salo, S.; Pietilainen, O.P.; Rekolainen, S.; Laine, Y.; Joukola, M. Relationship between catchment characteristics and nutrient concentrations in an agricultural river system. Water Res. 2000, 34, 3709–3716. [Google Scholar] [CrossRef]
- Puckett, L.J. Identifying the major sources of nutrient water-pollution. Environ. Sci. Tech. 1995, 29, A408–A414. [Google Scholar]
- Sharpley, A.N.; McDowell, R.W.; Weld, J.L.; Kleinman, P.J.A. Assessing site vulnerability to phosphorus loss in an agricultural watershed. J. Eviron. Qual. 2001, 30, 2026–2036. [Google Scholar]
- Brannan, K.M.; Mostaghimi, S.; McClellan, P.W.; Inamdar, S. Animal waste BMP impacts on sediment and nutrient losses in runoff from the Owl Run watershed. Trans. Am. Soc. Agric. Eng. 2000, 43, 1155–1166. [Google Scholar]
- Gitau, M.W.; Veith, T.L.; Gburek, W.J.; Jarrett, A.R. Watershed-level BMP selection and placement in the Town Brook watershed, NY. J. Am. Water Resour. Assoc. 2006, 42, 1565–1581. [Google Scholar] [CrossRef]
- Lee, K.; Isenhart, T.M.; Schultz, R.C.; Mickelson, S.K. Multispecies riparian buffers trap sediment and nutrients during rainfall simulations. J. Environ. Qual. 2000, 29, 1200–1205. [Google Scholar]
- Sorrano, P.A.; Hubler, S.L.; Carpenter, S.R.; Lathrop, R.C. Phosphorus loads to surface waters: A simple model to account for spatial pattern of land use. Ecol. Appl. 1996, 6, 865–878. [Google Scholar] [CrossRef]
- Walter, M.T.; Brooks, E.S.; Walter, M.F.; Steenhuis, T.S.; Scott, C.A.; Boll, J. Evaluation of soluble phosphorus transport from manure-applied fields under various spreading strategies. J. Soil Water Conserv. 2001, 56, 329–336. [Google Scholar]
- Walter, M.T.; Shaw, S.B. Discussion of curve number hydrology in water quality modeling: Uses, abuses, and future directions by Garen and Moore. J. Am. Water Resour. Assoc. 2005, 41, 1491–1492. [Google Scholar] [CrossRef]
- Buchanan, B.P.; Falbo, K.; Schneider, R.L.; Easton, Z.M.; Walter, M.T. Hydrologic impact of roadside ditch networks in an agricultural watershed: Implications for non-point source pollution. Hydro. Process. 2012. [Google Scholar] [CrossRef]
- McDowell, R.W.; Wilcock, R.J. Particulate phosphorus transport within stream flow of an agricultural catchment. J. Environ. Qual. 2004, 33, 2111–2121. [Google Scholar] [CrossRef]
- Scanlon, T.M.; Kiely, G.; Xie, Q. A nested catchment approach for defining the hydrological controls on non-point phosphorus transport. J. Hydrol. 2004, 291, 218–231. [Google Scholar] [CrossRef]
- Dahlke, H.E.; Easton, Z.M.; Walter, T.M.; Steenhuis, T.S. Field test of the variable source area interpretation of the curve number rainfall-runoff equation. J. Irrig. Drain. Eng. 2012, 138, 235–244. [Google Scholar]
- Dunne, T.; Leopold, L. Water in Environmental Planning; W.H. Freeman and Company: New York, NY, USA, 1978. [Google Scholar]
- Dunne, T.; Black, R.D. Partial area contributions to storm runoff in a small New England watershed. Water Resour. Res. 1970, 6, 1296–1311. [Google Scholar]
- Hewlett, J.D.; Hibbert, A.R. Factors Affecting the Response of Small Watersheds to Precipitation in Humid Regions. In Forest Hydrology; Sopper, W.E., Lull, H.W., Eds.; Pergamon Press: Oxford, UK, 1967; pp. 275–290. [Google Scholar]
- Easton, Z.M.; Fuka, D.R.; Walter, M.T.; Cowan, D.M.; Schneiderman, E.M.; Steenhuis, T.S. Re-conceptualizing the soil and water assessment tool (SWAT) model to predict runoff from variable source areas. J. Hydrol. 2008, 348, 279–291. [Google Scholar] [CrossRef]
- Easton, Z.M.; Gerard-Marchant, P.; Walter, M.T.; Petrovic, A.M.; Steenhuis, T.S. Hydrologic assessment of a urban variable source watershed in the Northeast U.S. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Needelman, B.A.; Gburek, W.J.; Petersen, G.W.; Sharpley, A.N.; Kleinman, P.J. Surface runoff along two agricultural hillslopes with contrasting soils. Soil Sci. Soc. Am. J. 2004, 68, 914–923. [Google Scholar]
- Srinivasan, M.S.; Gburek, W.J.; Hamlett, J.M. Dynamics of stormflow generation: A field study in east-central Pennsylvania, USA. Hydrol. Process. 2002, 16, 649–665. [Google Scholar] [CrossRef]
- Walter, M.T.; Walter, M.F.; Brooks, E.S.; Steenhuis, T.S.; Boll, J.; Weiler, K.R. Hydrologically sensitive areas: Variable source area hydrology implications for water quality risk assessment. J. Soil Water Conserv. 2000, 55, 277–284. [Google Scholar]
- Walter, M.T.; Mehta, V.K.; Marrone, A.M.; Boll, J.; Steenhuis, T.S.; Walter, M.F. Simple estimation of prevalence of Hortonian flow in New York City watersheds. J. Irrig. Drain. Eng. 2003, 8, 214–218. [Google Scholar]
- Collick, A.S.; Easton, Z.M.; Montalto, F.A.; Gao, B.; Kim, Y.; Day, L.; Steenhuis, T.S. Hydrological evaluation of septic disposal field design in sloping terrains. J. Environ. Eng. 2006, 132, 1289–1297. [Google Scholar]
- Dahlke, H.E.; Easton, Z.M.; Fuka, D.R.; Lyon, S.W.; Steenhuis, T.S. Modeling variable source area dynamics in a CEAP watershed. Ecohydrology 2009, 2, 337–349. [Google Scholar] [CrossRef]
- Schneiderman, E.M.; Steenhuis, T.S.; Thongs, D.J.; Easton, Z.M.; Zion, M.S.; Mendoza, G.F.; Walter, M.T.; Neal, A.L. Incorporating variable source area hydrology into the curve number based Generalized Watershed Loading Function model. Hydrol. Process. 2007, 21, 3420–3430. [Google Scholar] [CrossRef]
- Walter, M.T.; Walter, M.F. The New York City Watershed Agricultural Program! WAP: A model for comprehensive planning for water quality and agricultural economic viability. Water Resour. Impact 1999, 15, 5–8. [Google Scholar]
- Gburek, W.J.; Drungil, C.C.; Srinivasan, M.S.; Needelman, B.A.; Woodward, D.E. Variable-source area controls on phosphorus transport: Bridging the gap between research and design. J. Soil Water Conserv. 2002, 57, 534–543. [Google Scholar]
- Marjerison, R.D.; Easton, Z.M.; Dahlke, H.E.; Walter, M.T. A P-Index transport factor based on variable source area hydrology for New York State. J. Soil Water Conserv. 2011, 66, 149–157. [Google Scholar]
- Gburek, W.J.; Sharpley, A.N.; Heathwaite, L.; Folmar, G.J. Phosphorus management at the watershed scale: A modification of the phosphorus index. J. Environ. Qual. 2000, 29, 130–144. [Google Scholar]
- Pionke, H.B.; Gburek, W.J.; Sharpley, A.N.; Schnabel, R.R. Flow and nutrient export patterns for an agricultural hill-land watershed. Water Resour. Res. 1996, 32, 1795–1804. [Google Scholar] [CrossRef]
- Page, T.; Haygarth, P.M.; Beven, K.J.; Joynes, A.; Butler, T.; Keeler, C.; Freer, J.; Owens, P.N.; Wood, G.A. Spatial variability of soil phosphorus in relation to the topographic index and critical source areas: Sampling for assessing risk to water quality. J. Environ. Qual. 2005, 34, 2263–2277. [Google Scholar] [CrossRef]
- Czymmek, K.J.; Ketterings, Q.M.; Geohring, L.D.; Albrecht, G.L. The New York Phosphorus Runoff Index: User’s Manual and Documentation; 2003; CSS Extension Publication E03-13. [Google Scholar]
- Dahlke, H.E.; Easton, Z.M.; Lyon, S.W.; Destouni, G.; Walter, T.; Steenhuis, T.S. Dissecting the variable source area concept—Subsurface flow pathways and water mixing processes in a hillslope. J. Hydrol. 2012, 420–421, 125–141. [Google Scholar]
- Agnew, L.J.; Lyon, S.; Gérard-Marchant, P.; Collins, V.B.; Lembo, A.J.; Steenhuis, T.S.; Walter, M.T. Identifying hydrologically sensitive areas: Bridging science and application. J. Environ. Manag. 2006, 78, 64–76. [Google Scholar]
- Cheng, X.; Dahlke, H.E.; Shaw, S.B.; Marjerison, R.D.; Yearick, C.; DeGloria, S.D.; Walter, M.T. Improving risk estimates of runoff producing areas: Formulating variable source areas as a bivariate process. Water Resour. Res. 2013. submitted. [Google Scholar]
- Shaw, S.B.; Walter, M.T. Improving runoff risk estimates: Formulating runoff as a bivariate process using the SCS curve number method. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Adeli, A.; Bala, F.M.; Rowe, D.E.; Owens, P.R. Effects of drying intervals and repeated rain events on runoff nutrient dynamics from soil treated with broiler litter. J. Sustain. Agric. 2006, 28, 67–83. [Google Scholar] [CrossRef]
- Allen, B.L.; Mallarino, A.R. Effect of liquid swine manure rate, incorporation, and timing of rainfall on phosphorus loss with surface runoff. J. Environ. Qual. 2008, 37, 125–137. [Google Scholar] [CrossRef]
- Hanrahan, L.R.; Jokela, W.E.; Knapp, J.R. Dairy diet phosphorus and rainfall timing effects on runoff phosphorus from land-applied manure. J. Environ. Q. 2009, 38, 212–217. [Google Scholar] [CrossRef]
- Schroeder, P.D.; Radcliffe, D.E.; Cabrera, M.L. Rainfall timing and poultry litter application rate effects on phosphorus loss in surface runoff. J. Environ. Q. 2004, 33, 2201–2209. [Google Scholar] [CrossRef]
- Sistani, K.R.; Torbert, H.A.; Way, T.R.; Bolster, C.H.; Pote, D.H.; Warren, J.G. Broiler litter application method and runoff timing effects on nutrient and Escherichia coli losses from tall fescue pasture. J. Environ. Q. 2009, 38, 1216–1223. [Google Scholar]
- Smith, D.R.; Owens, P.R.; Leytem, A.B.; Warnemuende, E.A. Nutrient losses from manure and fertilizer applications as impacted by time to first runoff event. Environ. Pollut. 2007, 147, 131–137. [Google Scholar] [CrossRef]
- Edwards, D.R.; Daniel, T.C. Drying interval effects on runoff—From fescue plots receiving swine manure. Trans. Am. Soc. Agric. Eng. 1993, 36, 1673–1678. [Google Scholar]
- Edwards, D.R.; Daniel, T.C.; Moore, P.A.; Vendrell, P.F. Drying interval effects on quality of runoff from fescue plots treated with poultry litter. Trans. Am. Soc. Agric. Eng. 1994, 37, 837–843. [Google Scholar]
- Endale, D.M.; Franklin, D.H.; Calvert, V.H., II. Rainfall Timing Effect on Concentrations of Testosterone and Estradiol in Surface Runoff From Broiler Litter Applied to Grassed Plots. In Proceedings of the American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America (ASA-CSSA-SSSA) Annual Meeting, Pittsburg, PA, USA, 1–5 November 2009.
- Westerman, P.W.; Donnelly, T.L.; Overcash, M.R. Erosion of soil and poultry manure—A laboratory study. Trans. Am. Soc. Agric. Eng. 1983, 26, 1070. [Google Scholar]
- Vadas, P.A.; Jokela, W.E.; Franklin, D.H.; Endagle, D.M. The effect of rain and runoff when assessing timing of manure application and dissolved phosphorus loss in runoff. J. Am. Water Resour. Assoc. 2011, 47, 877–886. [Google Scholar]
- Steenhuis, T.S.; Winchell, M.; Rossing, J.; Zollweg, J.A.; Walter, M.F. SCS Runoff equation revisited for variable-source runoff areas. J. Irrig. Drain. Eng. 1995, 121, 234–238. [Google Scholar] [CrossRef]
- Lyon, S.W.; Gérard-Marchant, P.; Walter, M.T.; Steenhuis, T.S. Using a topographic index to distribute variable source area runoff predicted with the SCS-Curve Number equation. Hydrol. Process. 2004, 18, 2757–2771. [Google Scholar] [CrossRef]
- Thornthwaite, C.W.; Mather, J.R. The Water Balance; Publication No. 8; Laboratory of Climatology: Centerton, NJ, USA, 1955. [Google Scholar]
- Ambroise, B.; Beven, K.; Freer, J. Toward a generalization of the TOPMODEL concepts: Topographic indices of hydrological similarity. Water Resour. Res. 1996, 32, 2135–2145. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically-based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar]
- Lyon, S.W.; Lembo, A.J.; Walter, M.T.; Steenhuis, T.S. Defining probability of saturation with indicator kriging on hard and soft data. Adv. Water Resour. 2006, 29, 181–193. [Google Scholar]
- Lyon, S.W.; Seibert, J.; Lembo, A.J.; Walter, M.T.; Steenhuis, T.S. Geostatistical investigation into the temporal evolution of spatial structure in a shallow water table. Hydrol. Earth Syst. Sci. 2006, 10, 113–125. [Google Scholar] [CrossRef] [Green Version]
- Rallison, R.E. Origin and Evolution of the SCS Runoff Equation. In Proceedings of Symposium on Watershed Management, Boise, ID, USA, 21–23 July 1980; pp. 912–924.
- United States Department of Agriculture, Soil Conservation Service (USDA-SCS), National Engineering Handbook, Part 630 Hydrology; USDA-SCS: Mountain View, WY, USA, 1972; Section 4, Chapter 10.
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large scale parameters. Mon. Weath. Rev. 1972, 100, 81–92. [Google Scholar]
- Walter, M.T.; Brooks, E.S.; McCool, D.K.; King, L.G.; Molnau, M.; Boll, J. Process-based snowmelt modeling: Does it require more input data than temperature-index modeling? J. Hydrol. 2005, 300, 65–75. [Google Scholar] [CrossRef]
- Glahn, H.R.; Lowry, D.A. The use of Model Output Statistics (MOS) in objective weather forecasting. J. Appl. Meteor. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Kanamitsu, M. Description of the NMC global data assimilation and forecast system. Weather Forecast 1989, 4, 335–342. [Google Scholar] [CrossRef]
- Maloney, J.C.; Gilbert, K.K.; Baker, M.N.; Shafer, P.E. GFS-based MOS Guidance—The Extended-Range Alphanumeric Messages from the 0000/1200 UTC Forecast Cycles; MDL Technical Procedures Bulletin No. 2010-01; NOAA’s National Weather Service Meteorological Development Lab: Silver Spring, MD, USA, 2010. [Google Scholar]
- Hydrologically Sensitive Areas Model. Available online: http://hsadss.bee.cornell.edu/SalmonCreek/ (accessed on 23 June 2013).
- Soil Survey Staff, Natural Resources Conservation Service, United States Department of Agriculture, Soil Survey Geographic (SSURGO) Database for [Tompkins County, Cayuga County, New York State]. Available online: http://soildatamart.nrcs.usda.gov (accessed on 20 June 2008).
- NYSGIS Clearinghouse. Available online: http://gis.ny.gov/gisdata/ (accessed on 23 June 2013).
- CUGIR—Cornell University Geospatial Information Repository Home Page. Available online: http://cugir.mannlib.cornell.edu (accessed on 23 June 2013).
- Multi-Resolution Land Characteristics Consortium (MRLC) Home Page. Available online: http://www.mrlc.gov (accessed on 23 June 2013).
- Northeast Regional Climate Center Home Page. Available online: http://www.nrcc.cornell.edu/ (accessed on 23 June 2013).
- U.S. Geological Survey Web Page, National Water Information System: Web Interface. Available online: http://waterdata.usgs.gov (accessed on 23 June 2013).
- NOAA’s National Weather Services Meteorological Development Lab Web Page, GFS-Based Model Output Statistics (MOS) Equation Refresh of GFS MOS (MAV and MEX) Effective 3 March 2010 1200 UTC. Available online: http://www.nws.noaa.gov/tdl/synop/gfs.php (accessed on 23 June 2013).
- Steenhuis, T.S.; van der Molen, W.H. The Thornthwaite-mather procedure as a simple engineering method to predict recharge. J. Hydrol. 1986, 84, 221–229. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part 1—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Edwards, W.M.; Owens, L.B. Large storm effects on total soil erosion. J. Soil Water Conserv. 1991, 46, 75–77. [Google Scholar]
- Pionke, H.B.; Gburek, W.J.; Schnabel, R.R.; Sharpley, A.N.; Elwinger, G.F. Seasonal flow, nutrient concentrations and loading patterns in stream flow draining an agricultural hill-land watershed. J. Hydrol. 1999, 220, 62–73. [Google Scholar]
- Smith, S.J.; Sharpley, A.N.; Williams, J.R.; Berg, W.A.; Coleman, G.A. Sediment-Nutrient Transport during Severe Storms. In Proceedings of the 5th Interagency Sedimentation Conference, Las Vegas, NV, USA, 18–21 March 1991; Fan, S.S., Kuo, Y.H., Eds.; Federal Energy Regulatory Commission: Washington, DC, USA, 1991; pp. 48–55. [Google Scholar]
- Vanni, M.J.; Renwick, W.H.; Headworth, J.L.; Auch, J.D.; Schaus, M.H. Dissolved and particulate nutrient flux from three adjacent agricultural watersheds: A 5-year study. Biogeochemistry 2001, 54, 85–114. [Google Scholar] [CrossRef]
- Easton, Z.M.; Walter, M.T.; Steenhuis, T.S. Combined monitoring and modeling indicate the most effective agricultural best management practices. J. Environ. Qual. 2008, 37, 1798–1809. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dahlke, H.E.; Easton, Z.M.; Fuka, D.R.; Walter, M.T.; Steenhuis, T.S. Real-Time Forecast of Hydrologically Sensitive Areas in the Salmon Creek Watershed, New York State, Using an Online Prediction Tool. Water 2013, 5, 917-944. https://doi.org/10.3390/w5030917
Dahlke HE, Easton ZM, Fuka DR, Walter MT, Steenhuis TS. Real-Time Forecast of Hydrologically Sensitive Areas in the Salmon Creek Watershed, New York State, Using an Online Prediction Tool. Water. 2013; 5(3):917-944. https://doi.org/10.3390/w5030917
Chicago/Turabian StyleDahlke, Helen E., Zachary M. Easton, Daniel R. Fuka, M. Todd Walter, and Tammo S. Steenhuis. 2013. "Real-Time Forecast of Hydrologically Sensitive Areas in the Salmon Creek Watershed, New York State, Using an Online Prediction Tool" Water 5, no. 3: 917-944. https://doi.org/10.3390/w5030917