Quantifying the Relative Contributions of Forest Change and Climatic Variability to Hydrology in Large Watersheds: A Critical Review of Research Methods
Abstract
:1. Introduction
2. Research Methods
2.1. Hydrological Modeling
2.2. Trend Analysis
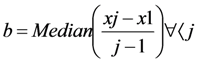

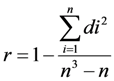
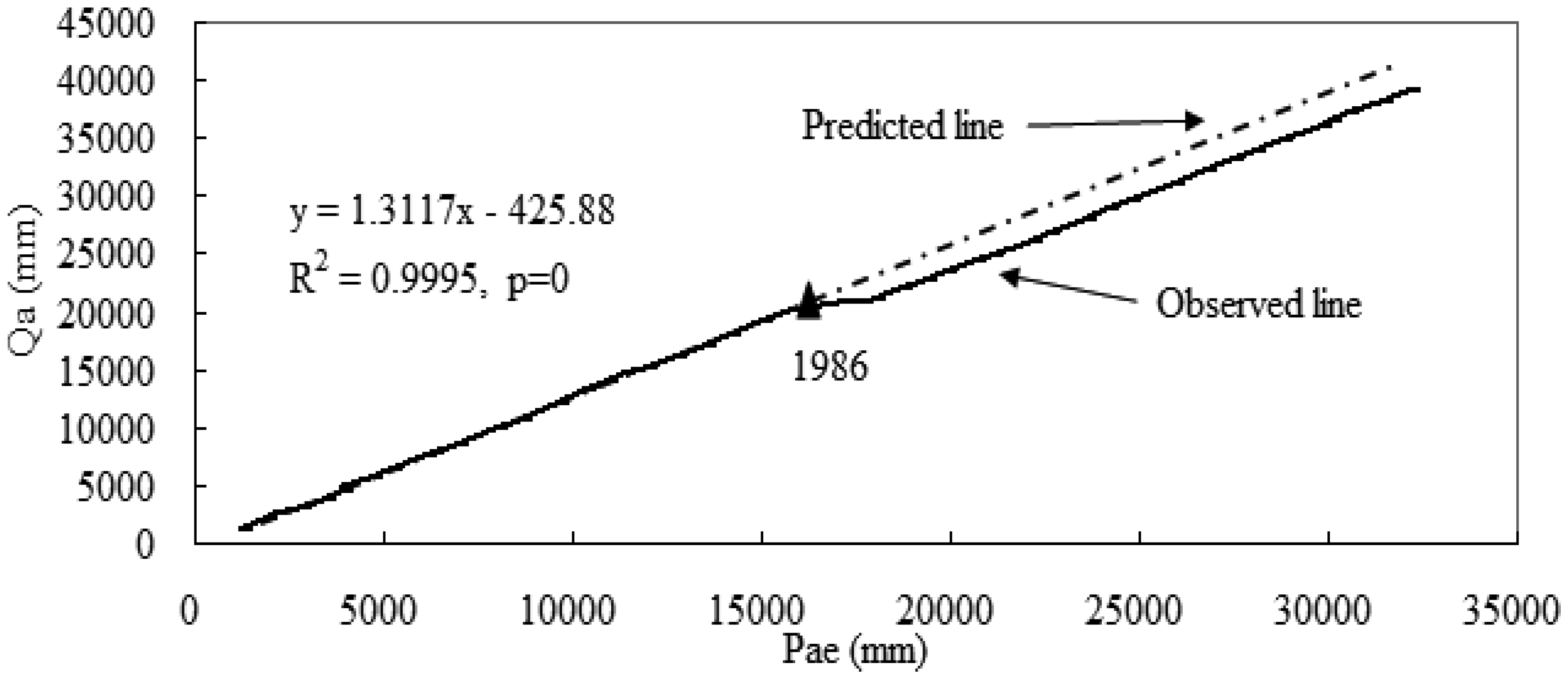
2.3. Double Mass Curves
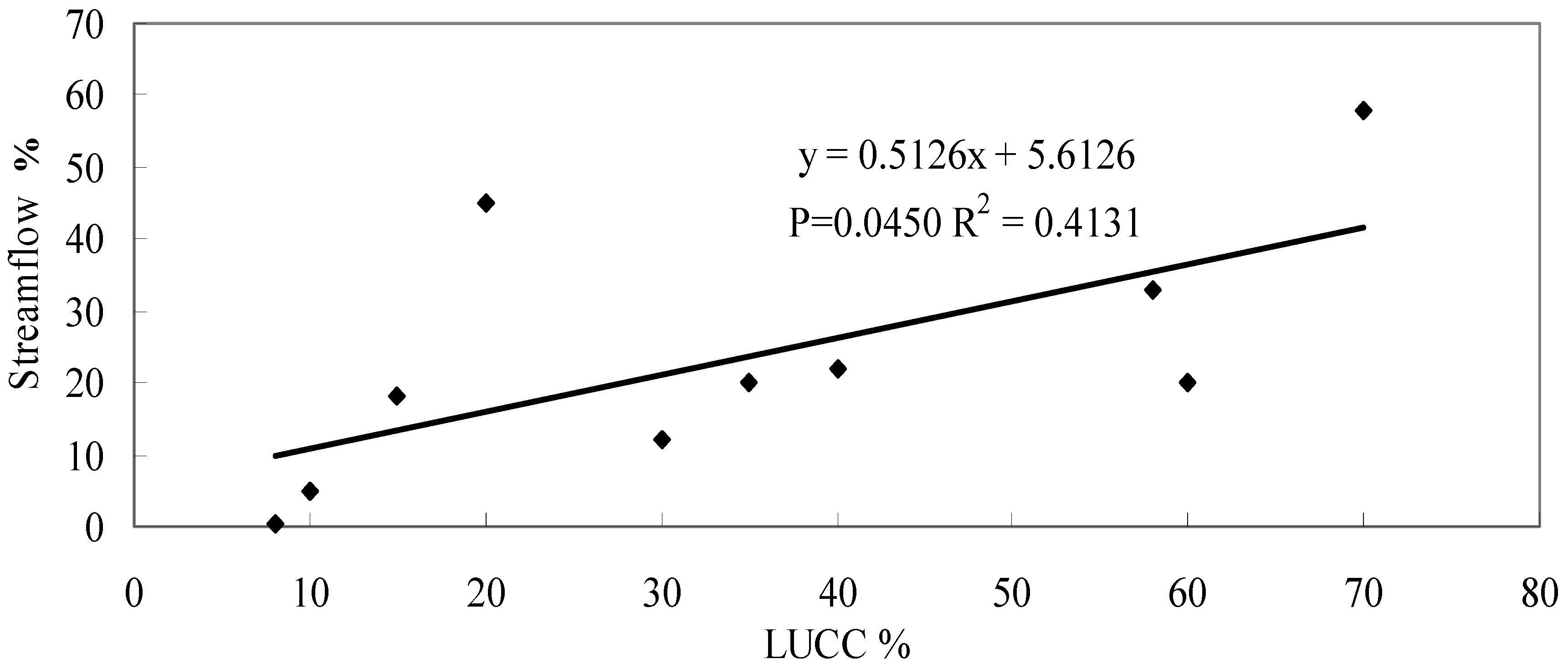
2.4. Quasi-Paired Watershed Method
2.5. Sensitivity-Based Approach

2.6. Simple Water Balance
2.7. Time Trend Method
2.8. Tomer-Schilling Framework
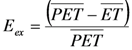
3. Research Progress
| Method | Watershed (km2) | Forest change or land use change (%) at a watershed | Relative contribution (%) | References | |
|---|---|---|---|---|---|
| Climate variability | Forest change/land use change | ||||
| Hydrological Modeling | The source regions of Yellow River (1.22 × 105 km2) | 0.13%~34.03% area change in woodland and shrub/grassland | 65%–95% | 6%–16% | [56] |
| Heihe River watershed (1506 km2) | 4.5% of the catchment area was changed mainly from shrubland and sparse | 95.8% | 9.6% | [57] | |
| Suomo Watershed (2536 km2) | Forest area decreased by 17%, open woodland increased by 8%, grassland area increased by 10% | 60%–80% | 20% | [62] | |
| Hydrological Modeling | The upper Yangtze River watershed (13,721~1,005,501 km2) | Human activities | 55%–73.3% | 28.5%–46.7% | [63] |
| Chaobai River watershed (57,001 km2) | Human activities | 34% | 64% | [64] | |
| Araguaia River watershed, Brazil (385,000 km2) | 55% Deforestation | 33% | 67% | [65] | |
| Trend Analysis | Shiyang river watershed (389~1614 km2) | Area change in Forest, crop and grassland | 64.5%–87.9% | 12.1%–35.5% | [66] |
| Hun–Tai River watershed (1112~11,203 km2) | Human activities | 43% | 57% | [67] | |
| Pyrenees Watershed, Spain (3.25 × 104 km2) | The increase of agricultural land | 70% | 30% | [68] | |
| Wuding River watershed (30,261 km2) | 43% (The soil conservation measures) | 13% | 87% | [45] | |
| Qingshui River watershed (436 km2) | Cropland decreased by 72.1%, woodland increased by 963.60% and residential area increased by 576.07% | 46.79% | 53.21% | [69] | |
| Taoer River watershed (41,600 km2) | Paddy field increased by 2%, upland increased by 15.10%, forest decreased by 10.60% | 45% | 55% | [61] | |
| ColumbiaRiver watershed, Canada (385,000 km2) | Human activities | 48%–55% | 45%–52% | [70] | |
| Double Mass Curves | The Willow River watershed, Canada (2,860 km2) | 19.7% Deforestation | 55% | 45% | [26] |
| The Upper Zagunao River watershed (2528km2) | 15.5% Deforestation | 42.5% | 57.5% | [71] | |
| Quasi-paired Watershed Method | Yulin, 8.28 km2 Xinlin, 28 km2 | Forest cover increased from 20% to 80% | / | 8.61% | [30] |
| Sensitivity-Based Approach | Upper catchment of the Yellow River Watershed (222,551 km2) | Human activities | 50% | 40% | [55] |
| Baiyangdian Lake (3,465 km2) | Construction of water conservation facilities | 38%–40% | 60%–62% | [52] | |
| The headwaters of the Yellow River Watershed (1.32 × 105 km2) | Water and soil conservation engineering | 30% | 70% | [72] | |
| Sensitivity-Based Approach | The Loess Plateau (1,279–9,289 km2) | Water and soil conservation engineering | 21%–57% | 43%–79% | [21] |
| Crawford River watershed, Darlot Creek watershed, Tinana Creek watershed (698–1,174 km2) | Afforestation 13.4%–23.5% | 21%–49% | 61%–64% | [73] | |
| Simple Water Balance | Yiluo River watershed (1.89 × 105 km2) | Water and soil conservation engineering | 21.75% | 78.26% | [40] |
| Time Trend Method | Seven paired catchments from Australia, New Zealand, and South Africa (0.18–3.44 km2) | Clearing vegetation 32%–100% Afforestation 67%–83% Forest conversion 100% | 10%–72% | 28%–98% | [55] |
| The upper reach of the Weihe River (1.35 × 105 km2) | Human activities | 40% | 60% | [64] | |
| Plata watershed, Paragury(3.2 × 104 km2) | Forest land converted to cropland | 41%–53% | 51%–59% | [74] | |
| Tomer-Schilling Framework | Four candidate Midwest watersheds | Changes in agricultural land cover | Increase/decreased Pex and Eex | Increased Pex and decreased Eex | [50] |
4. Future Research Challenges and Research Priorities

Acknowledgments
Conflicts of Interest
References
- Andreassian, V. Waters and forests: From historical controversy to scientific debate. J. Hydrol. 2004, 291, 1–27. [Google Scholar] [CrossRef]
- Bosch, J.M.; Hewlett, J.L. A review of catchment experiments to determine the effects of vegetation changes on water yield and evapotranspiration. J. Hydrol. 1982, 55, 3–23. [Google Scholar] [CrossRef]
- Hibbert, A.R. Forest Treatment Effects on Water Yield. In Proceedings of International Symposium on Forest Hydrology, Fort Collins, CO, USA, 6–8 September 1967; Sopper, W.E., Lull, H.W., Eds.; p. 813.
- Jackson, R.B.; Jobbágy, E.G.; Avissar, R.; Roy, S.B.; Barrett, D.J.; Cook, C.W.; Farley, K.A.; le Maitre, D.C.; McCarl, B.A.; Murray, B.C. Trading water for carbon with biological carbon sequestration. Science 2005, 310, 944–1947. [Google Scholar]
- MacDonald, L.H.; Stednick, J.D. Forests and Water: A State-of-the-Art Review for Colorado; CWRRI Completion Report No. 196; Colorado Water Resources Research Institute, Colorado State University: Fort Collins, CO, USA, 2003. [Google Scholar]
- Price, K. Effects of watershed topography, soils, land use, and climate on baseflow hydrology in humid regions: A review. Progr. Phys. Geogr. 2011, 35, 465–492. [Google Scholar] [CrossRef]
- Price, K.; Jackson, C.R.; Parker, A.J.; Reitan, T.; Dowd, J.; Cyterski, M. Effects of watershed land use and geomorphology on stream low flows during severe drought conditions in the southern Blue Ridge Mountains, Georgia and North Carolina, USA. Water Resour. Res. 2011, 47, W02516. [Google Scholar]
- Gao, X.; Sorooshian, S.; Gupta, H.V. Sensitivity analysis of the biosphere-atmosphere transfer scheme. J. Geophys. Res. 1996, 101, 7279–7289. [Google Scholar] [CrossRef]
- Pitman, A.J. Assessing the sensitivity of a land-surface scheme to the parameter values using a single column method. J. Clim. 1994, 7, 1856–1869. [Google Scholar] [CrossRef]
- Wilson, M.F.; Henderson-Sellers, A.; Dickinson, R.E.; Kennedy, P.J. Sensitivity of the Biosphere-Atmosphere Transfere Scheme (BATS) to the inclusion of variable soil characteristics. J. Appl. Meteorol. Climatol. 1987, 26, 341–362. [Google Scholar] [CrossRef]
- Wilson, M.F.; Henderson-Sellers, A.; Dickinson, R.E.; Kennedy, P.J. Investigation of the sensitivity of the land-surface parameterization of the NCAR Community Climate Model in regions of tundra vegetation. Climatology 1987, 7, 319–343. [Google Scholar] [CrossRef]
- Karvonen, T.; Koivusalo, H.; Jauhiainen, M.; Palko, J.; Weppling, K. A hydrological model for predicting runoff from different land use areas. J. Hydrol. 1999, 217, 253–256. [Google Scholar] [CrossRef]
- Zhang, A.J.; Zhang, C.; Fu, G.B.; Wang, B.D.; Bao, Z.X.; Zheng, H.X. Assessments of impacts of climate change and human activities on runoff with swat for the Huifa River Basin, northeast China. Water Resour Manage 2012, 26, 2199–2217. [Google Scholar] [CrossRef]
- Chen, J.F.; Li, X.B.; Zhang, M. Simulating the impacts of climate variation and land-cover changes on basin hydrology: A case study of the Suomo Basin. Sci. China Ser. D 2005, 48, 1501–1509. [Google Scholar] [CrossRef]
- Cuo, L.; Giambelluca, T.W.; Ziegler, A.D. Lumped parameter sensitivity analysis of a distributed hydrological model within tropical and temperate catchments. Hydrol. Process. 2011, 25, 2405–2421. [Google Scholar] [CrossRef]
- Sun, W.Y.; Bosilovich, M.G. Planetary boundary layer and surface layer sensitivity to land surface parameters. Boundary Lay. Meteorol. 1996, 77, 353–378. [Google Scholar] [CrossRef]
- Stonesifer, C.S. Modeling the cumulative effects of forest fire on watershed hydrology: A post-fire application of the Distributed Hydrology-Soil-Vegetation Model (DHSVM). J. Hydrol. 2007, 10, 282–290. [Google Scholar]
- Christiaens, K.; Feyen, J. Analysis of uncertainties associated with different methods to determine soil hydraulic properties and their propagation in the distributed hydrological MIKE SHE model. J. Hydrol. 2001, 246, 63–81. [Google Scholar] [CrossRef]
- Beven, K. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42, W03S04. [Google Scholar] [CrossRef]
- Zhang, X.P.; Zhang, L.; Zhao, J. Responses of stream flow to changes in climate and land use/cover in the Loess Plateau, China. Water Resour. Res. 2008, 44, W00A07. [Google Scholar]
- Sheng, Y.; Michio, H. Statistical interpretation of the impact of forest growth on stream flow of the Sameura Basin, Japan. Environ. Monit. Assess. 2005, 104, 369–384. [Google Scholar] [CrossRef]
- Wilcox, B.P.; Huang, Y. Woody plant encroachment paradox: Rivers rebound as degraded grasslands convert to woodlands. Geophys. Res. Lett. 2010, 37, L07402. [Google Scholar]
- Zhou, G.Y.; Wei, X.H.; Luo, Y.; Zhang, M.F.; Li, Y.; Qiao, Y.; Liu, H.; Wang, C. Forest recovery and river discharge at the regional scale of Guangdong Province, China. Water Resour. Res. 2010, 46, W09503. [Google Scholar]
- Peña-Arancibia, J.L.; van Dijk, A.I.J.M.; Guerschman, J.P.; Mulligan, M.; Bruijnzeel, L.A.; McVicar, T.R. Detecting changes in stream flow after partial woodland clearing in two large catchments in the seasonal tropics. J. Hydrol. 2012, 416–417, 60–71. [Google Scholar]
- Wei, X.H.; Zhang, M.F. Quantifying stream flow change caused by forest disturbance at a large spatial scale: A single watershed study. Water Resour. Res. 2010, 46, W12525. [Google Scholar]
- Buttle, J.M.; Metcalfe, R.A. Boreal forest disturbance and stream flow response, northeastern Ontario. Can. J. Fish. Aquat. Sci. 2000, 57, 5–18. [Google Scholar] [CrossRef]
- Siriwardena, L.; Finlayson, B.L.; McMahon, T.A. The impact of land use change on catchment hydrology in large catchments: The Comet River, Central Queensland, Australia. J. Hydrol. 2006, 326, 199–214. [Google Scholar] [CrossRef]
- Wigbout, M. Limitations in the use of double mass curves. J. Hydrol. 1973, 12, 132–138. [Google Scholar]
- Yao, Y.F.; Cai, T.J.; Wei, X.H.; Zhang, M.F.; Ju, C.Y. Effect of forest recovery on summer streamflow in small forested watersheds, Northeastern China. Hydrol. Process. 2011, 26, 1208–1214. [Google Scholar]
- Koster, R.D.; Suarez, M.J. A simple framework for examining the interannual variability of land surface moisture fluxes. J. Clim. 1999, 12, 1911–1917. [Google Scholar] [CrossRef]
- Box, G.; Cox, D. An analysis of transformations, J.R. Stat. Soc. B 1964, 26, 211–252. [Google Scholar]
- Box, G.; Pierce, D. Distribution of residual autocorrelations in autoregressive integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Buttle, J.M. Identifying Hydrological Responses to Basin Restoration: An Example from Southern Ontario. In Watershed Restoration Management: Physical, Chemical, and Biological Considerations; McDonnell, J.J., Stribling, J.B., Neville, L.R., Leopold, D.J., Eds.; American Water Resources Association: Herndon, VA, USA, 1996; pp. 5–13. [Google Scholar]
- Zhang, M.F.; Wei, X.H. The effects of forest disturbance on hydrology in two contrasted watersheds. Hydrol. Processes. 2013. submitted for publication. [Google Scholar]
- Zhang, M.F.; Wei, X. Alteration of flow regimes caused by large-scale forest disturbance: A case study from a large watershed in the interior of British Columbia, Canada. Ecohydrology 2013, in press. [Google Scholar]
- Dooge, J.C.I.; Bruen, M.; Parmentier, B. A simple model for estimating the sensitivity of runoff to long–term changes in precipitation without a change in vegetation. Adv. Water Resour. 1999, 23, 153–163. [Google Scholar]
- Jones, R.N.; Chiew, F.H.S.; Boughton, W.C.; Zang, L. Estimating the sensitivity of mean annual runoff to climate change using selected hydrological models. Adv. Water Resour. 2006, 29, 1419–1429. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. The response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z.F.; Cui, B.S.; Sun, T. Temporal trends of hydro-climatic variables and runoff response to climatic variability and vegetation changes in the Yiluo River Basin, China. Hydrol. Process. 2009, 23, 3030–3039. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Predicting the Effect of Vegetation Changes on Catchment Average Water Balance; Technical Report 99/12; Cooperative Research Centre for Catchment Hydrology. CSIRO Land and Water: Clayton South, Australia, 1999. [Google Scholar]
- Ponce, V.M.; Shetty, A.V. A conceptual-model of catchment water-balance: 1. Formulation and calibration. J. Hydrol. 1995, 173, 27–40. [Google Scholar] [CrossRef]
- Budyko, M.I. The Heat Balance of the Earth’s Surface; U.S. Department of Commerce: Dordrecht, The Netherland, 1958; p. 259. [Google Scholar]
- Budyko, M.I. Climate and Life; Academic Press: San Diego, CA, USA, 1974; p. 508. [Google Scholar]
- Li, L.J.; Zhang, L.; Wang, H.; Wang, J.; Yang, J.W.; Jiang, D.J.; Li, J.Y.; Qin, D.Y. Assessing the impact of climate variability and human activities on streamflow from the Wuding River Basin in China. Hydrol. Proces. 2007, 21, 3485–3491. [Google Scholar] [CrossRef]
- Zhang, L.; Hickel, K.; Dawes, W.R.; Chiew, F.H.S.; Western, A.W.; Briggs, P.R. A rational function approach for estimating mean annual evapotranspiration. Water Resour. Res. 2004, 40, W02502. [Google Scholar]
- Xu, C.Y.; Gong, L.B.; Jiang, T.; Chen, D.L.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Zhao, F.F.; Zhang, L.; Xu, Z.X.; Scott, D.F. Evaluation of methods for estimating the effects of vegetation change and climate variability on streamflow. Water Resour. Res. 2010, 46, W03505. [Google Scholar]
- Guardiola-Claramonte, M.; Troch, P.A.; Breshears, D.D.; Huxman, T.E.; Switanek, M.B.; Durcik, M.; Cobb, N.S. Decreased streamflow in semi-arid basins following drought-induced tree die-off: A counter-intuitive and indirect climate impact on hydrology. J. Hydrol. 2011, 406, 225–233. [Google Scholar] [CrossRef]
- Tomer, M.D.; Schilling, K.E. A simple approach to distinguish land-use and climate-change effects on watershed hydrology. J. Hydrol. 2009, 376, 24–33. [Google Scholar] [CrossRef]
- Tootle, G.A.; Singh, A.K.; Piechota, T.C.; Farnham, I. Long lead-time forecasting of US streamflow using partial least squares regression. J. Hydrol. Eng. 2007, 12, 442–451. [Google Scholar] [CrossRef]
- Hu, S.S.; Zheng, H.X.; Liu, C.M.; Yu, J.J.; Wang, Z.G. Assessing the impacts of climate variability and human activities on streamflow in the water source area of Baiyangdian Lake. Acta Geograph. Sinica 2012, 67, 62–70. [Google Scholar]
- Zhang, L.; Zhao, F.F.; Chen, Y.; Dixon, R.N.M. Estimating effects of plantation expansion and climate variability on streamflow for catchments in Australia. Water Resour. Res. 2011, 47, W12539. [Google Scholar]
- Zhang, S.R.; Lu, X.X. Hydrological responses to precipitation variation and diverse human activities in a mountainous tributary of the lower Xijiang, China. Catena 2009, 77, 130–142. [Google Scholar]
- Zhao, F.F.; Xu, Z.X.; Zhang, L.; Zuo, D.P. Streamflow response to climate variability and human activities in the upper catchment of the Yellow River Basin. Sci. China Ser. E 2009, 52, 1–8. [Google Scholar]
- Chen, L.Q.; Liu, C.M. Influence of climate and land-cover change on runoff of the source regions of Yellow River. China Environ. Sci. 2007, 27, 559–565. [Google Scholar]
- Li, Z.; Liu, W.Z.; Zhang, X.C.; Zheng, F.L. Impacts of landuse change and climate variability on hydrology in an agriculture catchment on the Loess Plateau of China. J. Hydrol. 2009, 377, 35–42. [Google Scholar] [CrossRef]
- Guo, H.; Hu, Q.; Jiang, T. Annual and seasonal streamflow responses to climate and land-cover changes in the Poyang Lake Basin, China. J. Hydrol. 2008, 355, 106–122. [Google Scholar] [CrossRef]
- Hao, X.M.; Chen, Y.N.; Xu, C.C.; Li, W.H. Impacts of climate change and human activities on the surfaces runoff in the Tarim River Basin over the last fifty years. Water Resour. Manag. 2008, 22, 1159–1171. [Google Scholar] [CrossRef]
- Chen, J.F.; Li, X.B.; Zhang, M. Impacts of climate variability and land cover change on hydrology using model simulation in Suomuo Basin. Sci. China Ser. D 2004, 34, 668–674. [Google Scholar]
- Li, L.J.; Li, B.; Liang, L.Q.; Li, J.Y.; Liu, Y.M. Effect of climate change and land use on stream flow in the upper and middle reaches of the Taoer River, northeastern China. For. Stud. China 2010, 12, 107–115. [Google Scholar]
- Montenegro, S.; Ragab, R. Impact of possible climate and land use changes in the semi arid regions: A case study from North Eastern Brazil. J. Hydrol. 2012, 434–435, 55–68. [Google Scholar] [CrossRef]
- Xia, J.; Wang, M.L. Runoff changes and distributed hydrologic simulation in the upper reaches of Yangtze River. Resour. Sci. 2008, 30, 962–967. [Google Scholar]
- Wang, G.S.; Xia, J.; Wan, D.H.; Ye, A.Z. A Distributed monthly water balance model for identifying hydrological response to climate changes and human activities. J. Nat. Resour. 2006, 21, 86–91. [Google Scholar]
- Coe, M.; Latrubesse, E.; Ferreira, M.; Amsler, M. The effects of deforestation and climate variability on the streamflow of the Araguaia River, Brazil. Biogeochemistry 2011, 105, 119–131. [Google Scholar] [CrossRef]
- Ma, Z.M.; Kang, S.Z.; Zhang, L.; Tong, L. Analysis of impacts of climate variability and human activity on stream flow for a river basin in arid region of northwest China. J. Hydrol. 2008, 352, 239–249. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Guan, D.X.; Jin, C.J.; Wang, A.Z.; Wu, J.B.; Yuan, F.H. Analysis of impacts of climate variability and human activity on streamflow for a river basin in northeast China. J. Hydrol. 2011, 410, 239–247. [Google Scholar] [CrossRef]
- Beguería, S.; López-Moreno, J.I.; Lorente, A.; Seeger, M.; García-Ruiz, J.M. Assessing the effect of climate oscillations and land-use changes on streamflow in the central Spanish Pyrenees. Ambio 2003, 32, 283–286. [Google Scholar]
- Tang, L.X.; Zhang, Z.Q.; Wang, X.J.; Wang, S.P.; Zha, T.G. Streamflow response to climate and landuse changes in Qingshui River watershed in the loess hilly-gully region of Western Shanxi Province, China. Chin. J. Plant Ecol. 2010, 34, 800–810. [Google Scholar]
- Naik, P.K.; Jay, D.A. Human and climate impacts on Columbia River hydrology and salmonids. River Res. Appl. 2011, 27, 1270–1276. [Google Scholar] [CrossRef]
- Zhang, M.F.; Wei, X.H.; Sun, P.S.; Liu, S.R. The effect of forest harvesting and climatic variability on runoff in a large watershed: The case study in the Upper Minjiang River of Yangtze River Basin. J. Hydrol. 2012, 464–465, 1–11. [Google Scholar] [CrossRef]
- Zheng, H.X.; Zhang, L.; Zhu, C.; Liu, C.M.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the Yellow River Basin. Water Resour. Res. 2009, 45, W00A19. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhang, Y.Q.; Vaze, J.; Wang, B.D. Separating effects of vegetation change and climate variability using hydrological modelling and sensitivity-based approaches. J. Hydrol. 2012, 420–421, 403–418. [Google Scholar]
- Doylea, M.E.; Vicente, B.R. Attribution of the river flow growth in the Plata Basin. Int. J. Climatol. 2011, 31, 2234–2248. [Google Scholar] [CrossRef]
- Tague, C.; Grant, G.E.; Farrell, M.; Choate, J.; Jefferson, A. Deep groundwater mediates streamflow response to climate warming in the Oregon Cascades. Clim. Change 2008, 86, 189–210. [Google Scholar] [CrossRef]
- Van Wateren-de Hoog, B. A regional model to assess the hydrological sensitivity of medium size catchments to climate variability. Hydrol. Process. 1998, 12, 43–56. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Entekhabi, D.; Bras, R.L.; Ivanov, V.Y. Controls on runoff generation and scale-dependence in a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2007, 11, 1683–1701. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Soulsby, C.; Waldron, S.; Malcolm, I.A.; Bacon, P.J.; Dunn, S.M. Conceptualization of runoff processes using a geographical information system and tracers in a nested mesoscale catchment. Hydrol. Process. 2007, 21, 1289–1307. [Google Scholar] [CrossRef]
- Christophersen, N.; Neal, C.; Hooper, R.P.; Vogt, R.D.; Andersen, S. Modeling streamwater chemistry as a mixture of soilwater end-members—A step towards 2nd-generation acidification models. J. Hydrol. 1990, 116, 307–320. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. A review and evaluation of catchment transit time modeling. J. Hydrol. 2006, 330, 543–563. [Google Scholar] [CrossRef]
- Soulsby, C.; Tetzlaff, D.; Hrachowitz, M. Tracers and transit times: Windows for viewing catchment scale storage? Hydrol. Process. 2009, 23, 3503–3507. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wei, X.; Liu, W.; Zhou, P. Quantifying the Relative Contributions of Forest Change and Climatic Variability to Hydrology in Large Watersheds: A Critical Review of Research Methods. Water 2013, 5, 728-746. https://doi.org/10.3390/w5020728
Wei X, Liu W, Zhou P. Quantifying the Relative Contributions of Forest Change and Climatic Variability to Hydrology in Large Watersheds: A Critical Review of Research Methods. Water. 2013; 5(2):728-746. https://doi.org/10.3390/w5020728
Chicago/Turabian StyleWei, Xiaohua, Wenfei Liu, and Peicong Zhou. 2013. "Quantifying the Relative Contributions of Forest Change and Climatic Variability to Hydrology in Large Watersheds: A Critical Review of Research Methods" Water 5, no. 2: 728-746. https://doi.org/10.3390/w5020728
APA StyleWei, X., Liu, W., & Zhou, P. (2013). Quantifying the Relative Contributions of Forest Change and Climatic Variability to Hydrology in Large Watersheds: A Critical Review of Research Methods. Water, 5(2), 728-746. https://doi.org/10.3390/w5020728




