PSO-Based Algorithm Applied to Quadcopter Micro Air Vehicle Controller Design
Abstract
:1. Introduction
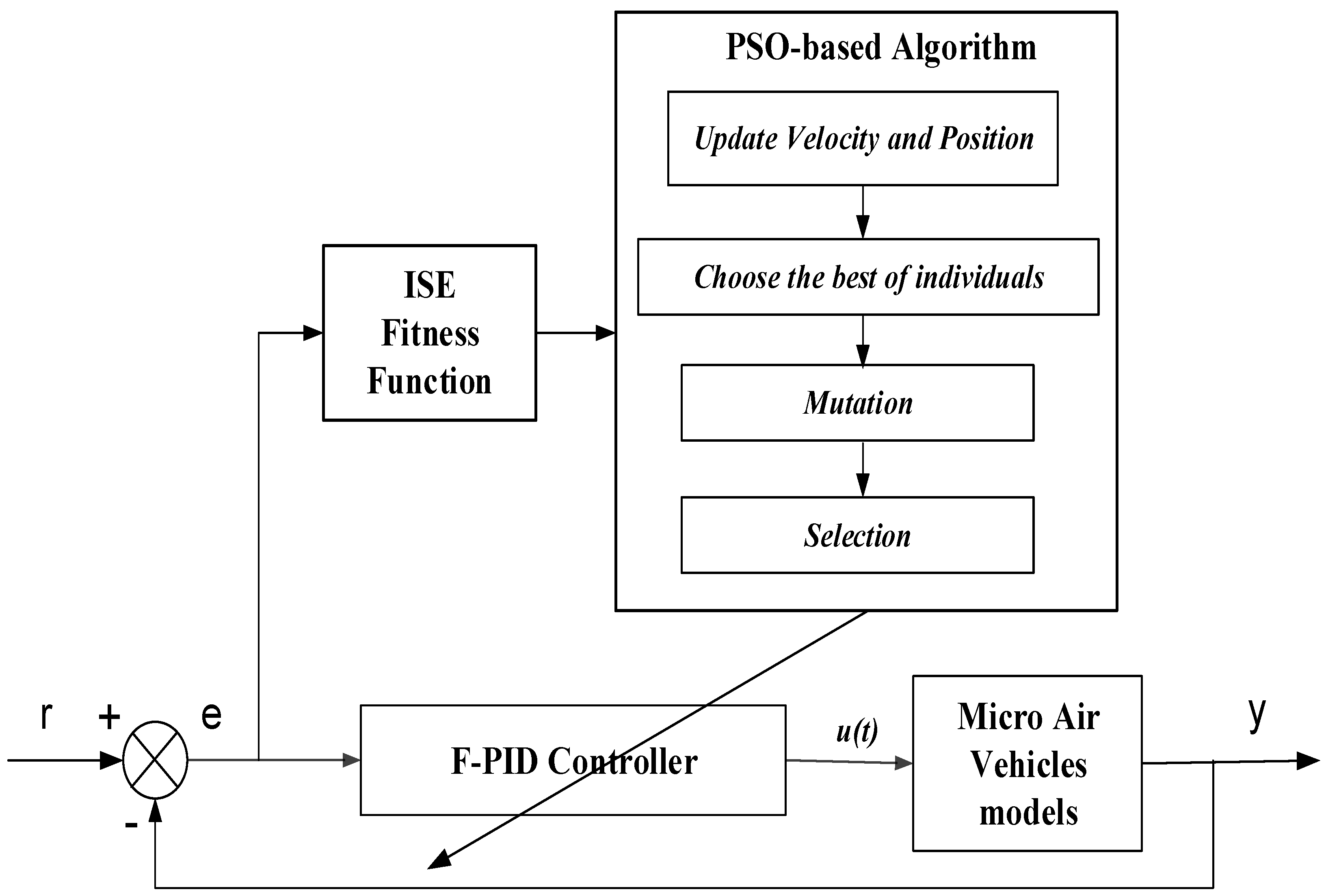
2. PSO-Based Algorithm Applied Controller Design
3. Quadcopter as a Micro Air Vehicle
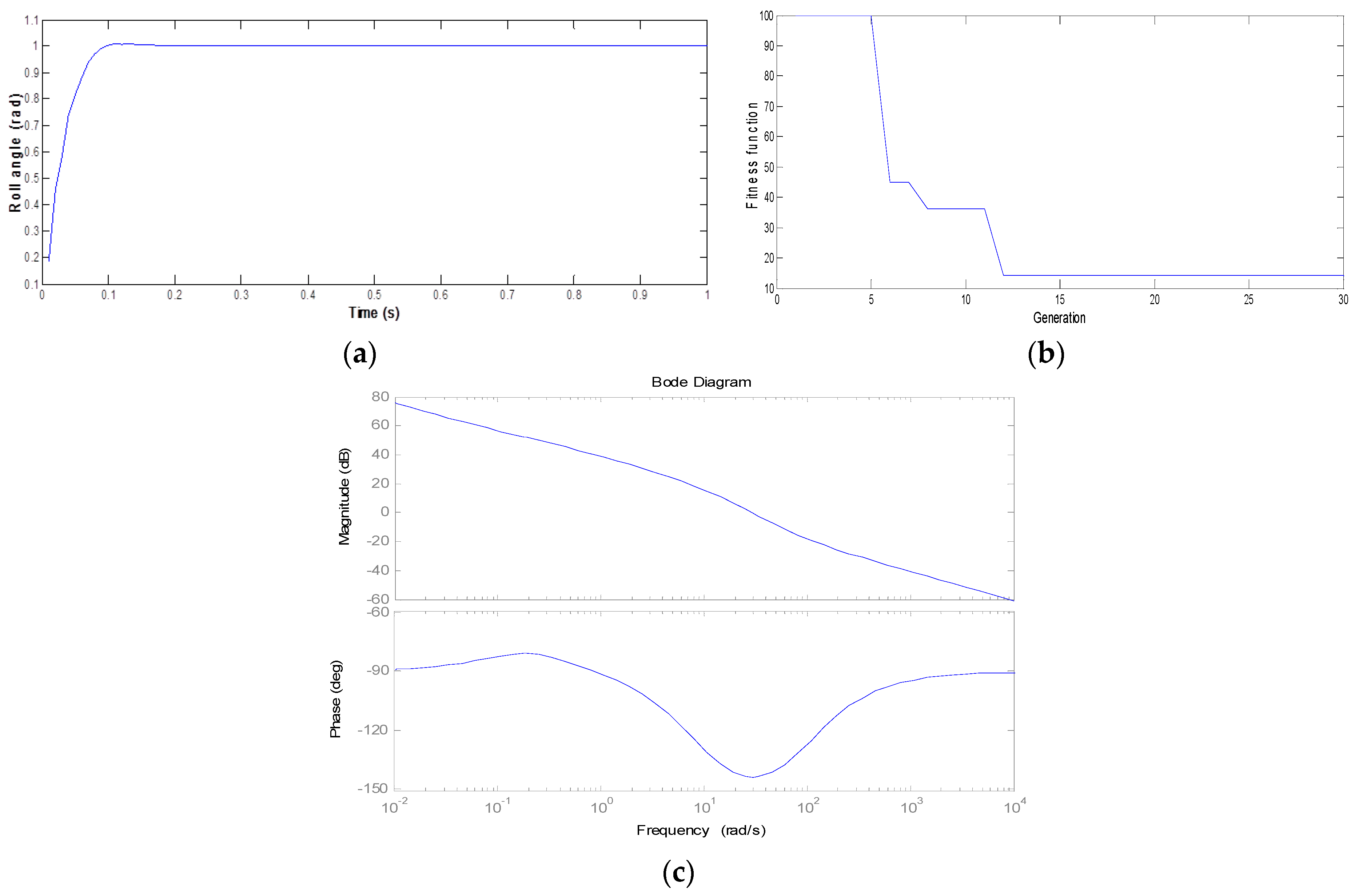
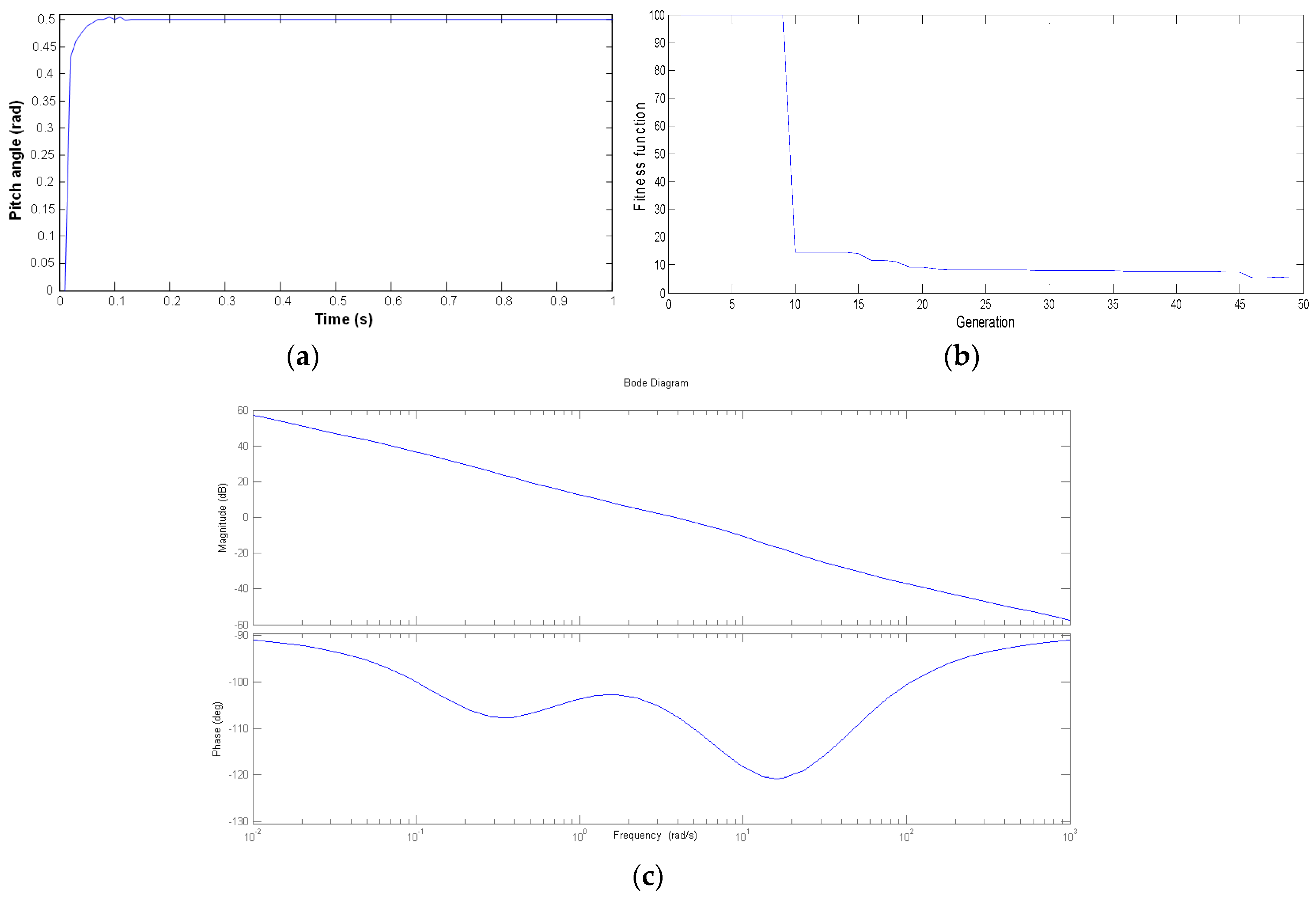
4. Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Fourth IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948.
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, San Diego, CA, USA, 16–19 July 2000; pp. 84–88.
- Liu, B.; Wang, L.; Lin, Y.H. An effective PSO-based memetic algorithm for flow shop scheduling. IEEE Trans. Syst. Man. Cybern. 2007, 37, 18–27. [Google Scholar] [CrossRef]
- Solihin, M.I.; Akmeliawati, R. PSO-based optimization of state feedback tracking controller for a flexible link manipulator. In Proceedings of the International Conference of Soft Computing and Pattern Recognition (SoCPaR 2009), Malacca, Malaysia, 4–7 December 2009; pp. 72–76.
- Mirjalili, S.; Hashim, S.Z.M. A new hybrid PSOGSA algorithm for function optimization. In Proceedings of the International Conference on Computer and Information Application (ICCIA), Tianjin, China, 3–5 December 2010; pp. 374–377.
- Menhas, M.I.; Fei, M.R.; Wang, L.; Fu, X. A novel hybrid binary PSO algorithm. In Advances in Swarm Intelligence; Springer: Berlin, Germany, 2011; Volume 6728, pp. 93–100. [Google Scholar]
- Ghodrati, A.; Lotfi, S. A hybrid CS/PSO algorithm for global optimization. In Intelligent Information and Database Systems; Springer: Berlin, Germany, 2012; Volume 7198, pp. 89–98. [Google Scholar]
- Esmin, A.A.A.; Matwin, S. HPSOM: A hybrid particle swarm optimization algorithm with genetic mutation. Int. J. Innov. Comput. Inf. Control 2013, 9, 1919–1934. [Google Scholar]
- Koyuncua, E.; Erolb, R. PSO based approach for scheduling NPD projects including overlapping process. Comput. Ind. Eng. 2015, 85, 316–327. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin, Germany, 2003. [Google Scholar]
- Zhao, Z.Y.; Tomizuka, M.; Isaka, S. Fuzzy gain scheduling of PID controllers. In Proceedings of the First IEEE Conference on Control Applications, Dayton, OH, USA, 13 September 1992; pp. 698–703.
- Sanchez, E.N.; Becerra, H.M.; Velez, C.M. Combining fuzzy, PID and regulation control for an autonomous mini-helicopter. Inf. Sci. 2007, 177, 1999–2022. [Google Scholar] [CrossRef]
- Juang, Y.T.; Chang, Y.T.; Huang, C.P. Design of fuzzy PID controllers using modified triangular membership functions. Inf. Sci. 2008, 178, 1325–1333. [Google Scholar] [CrossRef]
- Tan, W.; Liu, J.; Chen, T.; Marquez, H.J. Comparison of some well-known PID tuning formulas. Comput. Chem. Eng. 2006, 30, 1416–1423. [Google Scholar] [CrossRef]
- Passino, K.M.; Yurkovich, S. Fuzzy Control; Addison-Wesley: Reading, MA, USA, 1998. [Google Scholar]
- Precup, R.E.; David, R.C.; Petriu, E.M.; Preitl, S.; Radac, M.B. Fuzzy logic-based adaptive gravitational search algorithm for optimal tuning of fuzzy controlled servo systems. IET Control Theory Appl. 2013, 7, 99–107. [Google Scholar] [CrossRef]
- Bouabdallah, S.; Noth, A.; Siegwart, R. PID vs LQ control techniques applied to an indoor micro quadrotor. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendal, Japan, 28 September–2 October 2004; pp. 2451–2456.
- Bouabdallah, S. Design and Control of Quadrotors with Application to Autonomous Flying. Ph.D. Thesis, Ecole Polytechnique Federale de Lausanne, Lausanne, Switzerland, December 2006. [Google Scholar]
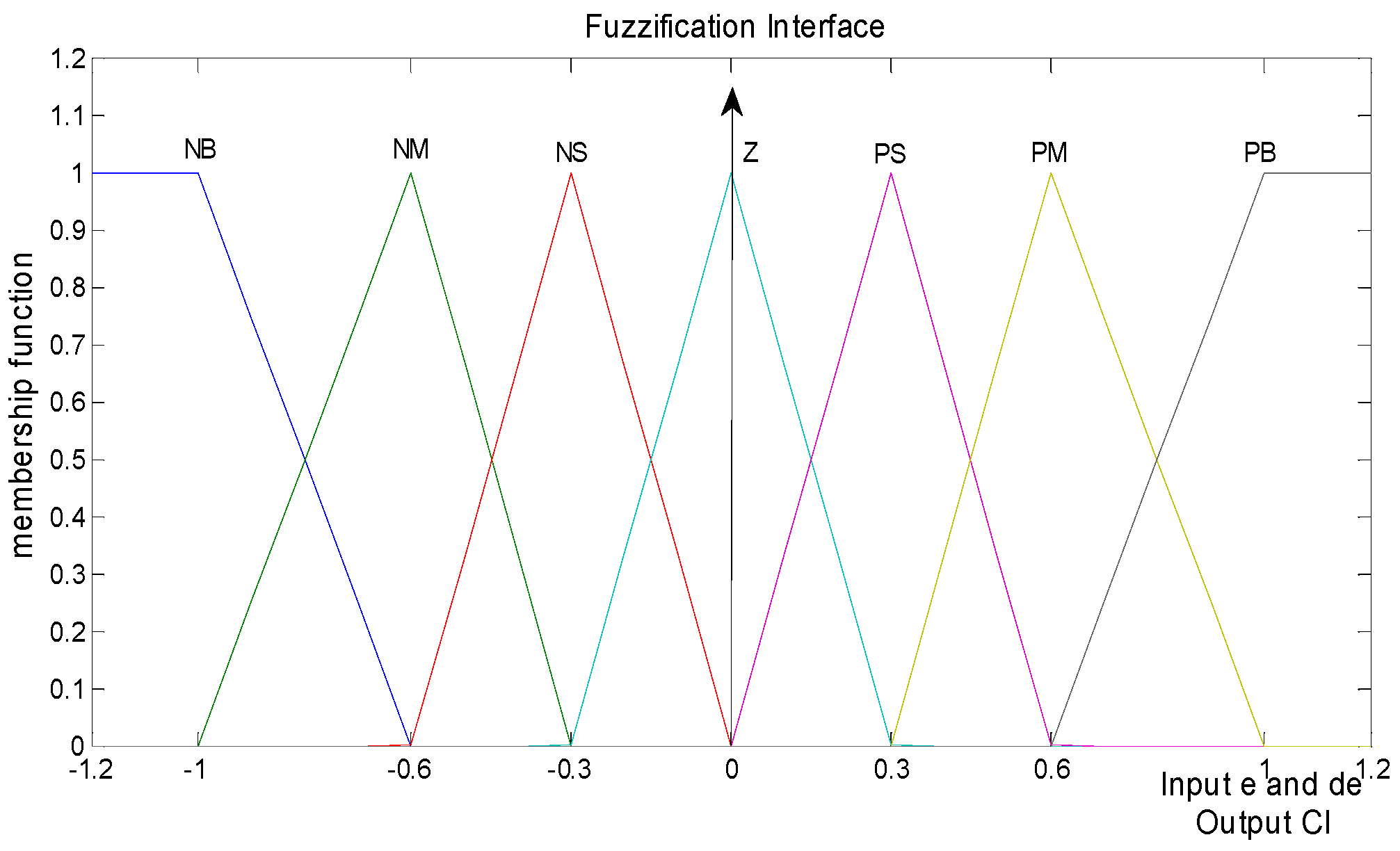


| CI(t) | e(t) | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZE | PS | PM | PB | ||
| de(t) | NB | ZE | NS | NS | NM | NM | NB | NB |
| NM | PS | ZE | NS | NS | NM | NM | NB | |
| NS | PS | PS | ZE | NS | NS | NM | NM | |
| ZE | PS | NM | PS | ZE | NS | NS | NM | |
| PS | PM | PM | PS | PS | ZE | NS | NS | |
| PM | PB | PM | PM | PS | PS | ZE | NS | |
| PB | PB | PB | PM | PM | PS | PS | ZE | |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, H.-K.; Chiou, J.-S. PSO-Based Algorithm Applied to Quadcopter Micro Air Vehicle Controller Design. Micromachines 2016, 7, 168. https://doi.org/10.3390/mi7090168
Tran H-K, Chiou J-S. PSO-Based Algorithm Applied to Quadcopter Micro Air Vehicle Controller Design. Micromachines. 2016; 7(9):168. https://doi.org/10.3390/mi7090168
Chicago/Turabian StyleTran, Huu-Khoa, and Juing-Shian Chiou. 2016. "PSO-Based Algorithm Applied to Quadcopter Micro Air Vehicle Controller Design" Micromachines 7, no. 9: 168. https://doi.org/10.3390/mi7090168






